Interpreting joint SNP analysis results: when are two distinct signals really two distinct signals?

Abstract

In genetic association studies, much effort has focused on moving beyond the initial single nucleotide polymorphism (SNP)-by-SNP analysis. One approach is to re-analyze a chromosomal region where an association has been detected, jointly analyzing the SNP thought to best represent that association with each additional SNP in the region. Such joint analyses may help identify additional, statistically independent association signals. However, it is possible for a single genetic effect to produce joint SNP results that would typically be interpreted as two distinct effects (e.g. both SNPs are significant in the joint model). We present a general approach that can (1) identify conditions under which a single variant could produce a given joint SNP result, and (2) use these conditions to identify variants from a list of known SNPs (e.g. 1000 Genomes) as candidates that could produce the observed signal. We apply this method to our previously reported joint result for smoking involving rs16969968 and rs588765 in CHRNA5. We demonstrate that it is theoretically possible for a joint SNP result suggestive of two independent signals to be produced by a single causal variant. Furthermore, this variant need not be highly correlated with the two tested SNPs nor must it have a large odds ratio. Our method aids in interpretation of joint SNP results by identifying new candidate variants for biological causation that would be missed by traditional approaches. Also, it can connect association findings that may seem disparate due to lack of high correlations among the associated SNPs.

Introduction

In genetic association studies of a complex disease, a chromosomal region that contains one variant associated with a phenotype often harbors additional SNPs that also display statistically significant association with the phenotype. In such situations, it is common to report the most significantly associated SNP in the region or a highly correlated proxy that has biological support from other sources. An important next step is to interpret the remaining associations. The remaining associations in the region may be due to linkage disequilibrium (LD) with the reported SNP or may represent additional distinct genetic effects. One commonly used approach to discern distinct associations in a chromosomal region is joint SNP analysis [Cordell and Clayton 2002; Ma, et al. 2010]. In application to a dichotomous phenotype, a single logistic regression model can be used to jointly estimate the odds ratios of multiple SNPs at the same time. Often, the reported SNP is paired with each additional SNP in the region in the model. If the odds ratios are significant for both SNPs, they are typically interpreted as representing two distinct effects on the phenotype. This approach has been useful in identifying multiple distinct association signals in complex diseases such as smoking [Saccone, et al. 2009; Saccone, et al. 2010], psoriasis [Cargill, et al. 2007], diabetes [Zeggini, et al. 2008], rheumatoid arthritis [Plenge, et al. 2007], and systemic lupus erythematosus [Graham, et al. 2008].

However, although joint SNP analysis results (univariate and joint odds ratios for two SNPs) may suggest that there are two distinct genetic effects in the region, it cannot guarantee that this is the case. The associations may, in fact, be produced by one underlying causal variant. In this paper, we introduce a method that identifies conditions under which observed univariate and joint results for two SNPs can be produced by a single causal SNP, D. This method identifies properties of D (minor allele frequency, pair-wise correlations to the two SNPs, and odds ratio) that would give rise to an observed joint SNP analysis result of two SNPs. Real SNPs that match an identified minor allele frequency and pair-wise correlations can be considered candidates for D. We demonstrate the utility of this method by applying it to our previously reported joint SNP results for nicotine dependence [Saccone, et al. 2009].

Methods

Notation

A, B = Two SNPs in a theoretical three-SNP model whose associations to the phenotype are solely produced by correlations to the causal variant.

D = The causative SNP in the above three-SNP model giving rise to the joint results for A and B

A, B = two SNPs that are each significant in joint SNP association result in a specific real dataset¹

r_xy = pair-wise correlation between SNPs where X and Y ∈ {A,B,D}

A₁, B₁, D₁ = major alleles of A, B, and D respectively

A₂, B₂, D₂ = minor alleles of A, B, and D respectively

P(X) = allele frequency of X where X ∈ {A₁,A₂,B₁,B₂,D₁,D₂}

A_i-B_j-D_K = haplotype of SNPs A, B, and D where i, j, k ∈ {1,2}

P_ijk = population level haplotype frequency for A_i-B_j-D_K

P_ijk^case = haplotype frequencies for A_i-B_j-D_k among cases

P_ijk^control = haplotype frequencies for A_i-B_j-D_k among controls

K = Population disease prevalence

f_ij = Probability of disease given genotype D_iD_j where I, j ∈ {1,2} (i.e. penetrance)

R_ij = relative risk of D_iD_j compared to D₁D₁ where I, j ∈ {1,2}

OR_X = odds ratio of X in a logistic regression (LR) with X as the only genetic predictor, X ∈ {A,B,D}

OR_X|Y = odds ratio of X in a LR with X and Y as the only genetic predictors, X, Y ∈ {A,B,D}.

N = Number of copies of haplotypes used in three-SNP model generation step

¹Other notation for quantities related to A and B follows the notations given for A and B (e.g. OR_A = odds ratio of A).

OVERVIEW

We will describe a general method that, given two real SNPs A and B, each significant in a joint analysis, will determine properties (minor allele frequency, pair-wise correlations to A and B, and odds ratio) that if possessed by an additional SNP, D, would produce the observed association results of A and B in the absence of any true causal effect of A and B. Such a D could be the biological cause of the observed joint signal and thus would be of interest for further investigation. Any D satisfying the conditions generated by this method will produce the observed results for A and B (i.e. the conditions are sufficient but need not be necessary). We will then use these theoretical properties of D to identify candidates from a database of known SNPs (e.g. 1000 Genomes) [Genomes Project 2010]. Our presentation focuses on additive, dominant, and recessive models but generalizes to other models.

I: GENERATING THREE-SNP MODELS WITH FIXED ALLELE FREQUENCIES AND CORRELATION FOR A AND B AND WHERE D IS CAUSAL

We consider diplotype models consisting of three SNPs (A, B, and D), where D has a direct impact on the phenotype (disease) and any association between A and B and the phenotype is due solely to their correlation to D. Each such model is entirely specified by a set of 3-SNP haplotype frequencies, P_ijk where i,j,k ∈ {1,2], and a trio of penetrance values for the genotypes of D, (f₁₁, f₁₂, f₂₂). We will show how to construct such models and compute the corresponding univariate and joint odds ratios for A and B in the following 4 steps.

Step 1: Generate a set of frequencies for (A-B-D) haplotypes such that P(A₂), P(B₂) and r_AB will match the a priori values for P(A₂), P(B₂) and rAB

From the values of P(A₂), P(B₂), and rAB, we can estimate the population-level frequencies of the four haplotypes of A and B (A₁-B₁, A₁-B₂, A₂-B₁, A₂-B₂). After setting haplotype frequencies for (A-B) to match the population-level values for (A-B), each two-SNP haplotype frequency is split into two 3-SNP haplotype frequencies, i.e. P_ij1 + P_ij2 ≡ freq(A_i-B_j-D₁) + freq(A_i-B_j-D₂) = freq(A_i-B_j). This extends the set of four haplotype frequencies of A and B into multiple (or in theory an infinite number of) sets of 8 haplotype frequencies for (A-B-D).

We operationalize this process in the following finite manner:

1. Instantiate the A-B haplotype frequencies in a total of N (A-B) haplotypes, rounding to the nearest unit (e.g. if N=100, and the 4 haplotypes are equally frequent, we would use 25 copies of each haplotype).

2. Since D₂ is the minor allele for D, there should be ≤ N/2 copies of D₂ among the N instantiated haplotypes. For each integer X in [1,N/2], consider all the distinct ways that X copies of the D₂ allele can be distributed across the 4 two-locus haplotype classes for A-B (instantiated in a total of N haplotypes. (e.g. if X = 1 and each of the 4 two-locus haplotypes was instantiated in at least 1 copy, there would be 4 distinct ways the copy of D₂ could be placed.) All remaining instantiated haplotypes would carry a copy of D₁.

3. By stepping through all the ways X copies of D₂ could be distributed among the N two-SNP haplotypes and dividing the number of each resulting 3-SNP haplotype by the N, we generate a finite list of sets of haplotype frequencies {P_ijk,| i,j,k ∈ {1,2}}, each of which has values for P(A₂), P(B₂), and r_AB essentially matching the values of P(A₂), P(B₂), and r_AB. Across the sets of P_ijk, the values of P(D₂) will only range up to 50%, and pair-wise correlations of D to A and B (r_AD, r_BD) will range between complete repulsion and complete coupling.

Step 2: For each set of haplotype frequencies from Step 1, generate multiple three-SNP models of disease

We consider the most commonly used disease models for D (additive, dominant, recessive), and fix the disease prevalence (K) to the relevant value for the given phenotype. Then, given a relative risk value (R₁₂ for additive disease model and R₂₂ for dominant and recessive disease models) and one set of haplotype frequencies {P_ijk|I,j,k ∈{1,2,3}} from Step 1, the values of f₁₁, f₁₂, and f₂₂ can be calculated using equations S1a (additive), S1b (dominant), and S1c (recessive) (see Supporting Information). By ranging through the three disease models (additive, dominant, recessive) and stepping through values for R₁₂ or R₂₂ that range between protective (R₁₂, R₂₂ < 1) and risk (R₁₂, R₂₂ > 1) effects (for example, 1 to 10 by an increment of 0.1 for risk effect and reciprocal of each risk value for protective effect), we end up with many three-SNP models, each composed of a set of haplotype frequencies {P_ijk} and a triple of penetrance values for D, (f₁₁, f₁₂, f₂₂).

Step 3: Calculate case/control haplotype frequencies for each three-SNP model

From a three-SNP disease model (i.e. a set of haplotype frequencies for A_i-B_j-D_k and a triple penetrance values for D), we first calculate haplotype frequencies in cases and controls (followed by corresponding genotype frequencies) using the formulas derived below.

We derive equations for the 8 haplotype frequencies in cases and the 8 haplotype frequencies in controls assuming Hardy-Weinberg equilibrium (HWE) in the population. For example, for haplotype frequency of A₁-B₁-D₁ among the cases (P₁₁₁^case), the equation is as follows (See Supporting Information for proof):

$${P_{111}}^{\mathit{case}}=\frac{P_{111}\left(f_{11}P\right(D_1)+f_{12}P(D_2\left)\right)}{K}$$ Eq. 1

The additional 15 equations (one for P₁₁₁^control and 2 for each of the 7 other haplotypes) for haplotype frequencies in cases and controls are computed in a similar fashion (see Supporting Information).

Step 4: Estimate odds ratios for each generated three-SNP models (i.e. OR_A, OR_B, OR_A|B, OR_B|A, and OR_D)

For a given three-SNP model, we use Eq.1 to Eq. 16 to calculate P₁₁₁^case, P₁₁₂^case, …, P₂₂₂^case, and P₁₁₁^control, P₁₁₂^control, …, P₂₂₂^control. Under HWE in the population, the resulting 8 haplotype frequencies in controls and 8 haplotype frequencies in cases specify genotype frequencies of A, B and D in cases and in controls. We obtain OR_A, OR_B, OR_D, OR_A|B, and OR_B|A for each three-SNP model by running logistic regression models predicting case status from (1) SNP A, (2) SNP B, (3) SNPs A and B, and (4) SNP D using genotype frequencies among cases and controls as weights.

II: IDENTIFYING REAL SNPS THAT ARE CANDIDATES FOR D

Step 1: Identify three-SNP models that are consistent with the results observed for A and B

We begin with the set of generated three-SNP models with OR_A, OR_B, OR_A|B, and OR_B|A matching the observed odds ratios for A and B (OR_A, OR_B, OR_A|B, and OR_B|A) to obtain a set of “grid-based theoretical candidate models.” We call this set S_point because it is based on point estimates of OR_A, OR_B, OR_A|B, and OR_B|A from a real dataset. Any real SNP with MAF, correlation to A and B, and odds ratio corresponding to a three-SNP model in this set (i.e. matching the values of P(D₂), r_AD, r_BD, and OR_D), would be statistically indistinguishable from being entirely responsible for the observed results for A and B. Because we have considered only additive, recessive, and dominant models, and we have stepped through a grid of possible allele frequencies and penetrances, S_point does not include all theoretical candidates.

Although our primary interest is in determining when a single variant could account for an observed joint result, we acknowledge that observed point estimate results are subject to error and do not typically match true population parameters perfectly. For this reason, we also consider an expanded set, S₉₅, of three-SNP models based on the 95% confidence intervals and confidence regions of the odds ratio estimates. That is, this set, S₉₅, is filtered not on the single point estimate of univariate and joint odds ratios for A and B, but includes any model such that

$$({\mathrm{OR}}_{\mathrm{A}},{\mathrm{OR}}_{\mathrm{B}},{\mathrm{OR}}_{A\mid B},{\mathrm{OR}}_{B\mid A})\in (95\%\text{C.I. for}{\mathrm{OR}}_{\underset{¯}{A}})\times (95\%\text{C.I. for}{\mathrm{OR}}_{\underset{¯}{B}})\times (95\%\text{joint C.R. for}{\mathrm{OR}}_{\underset{¯}{A}\mid \underset{¯}{B}}\text{and}{\mathrm{OR}}_{\underset{¯}{B}\mid \underset{¯}{A}})$$

where the 95% Confidence Region (C.R.) of OR_A|B and OR_B|A is generated using the R package ellipse which generates a C.R. based on point estimates, variance, and covariance of two odds ratios [Murdoch, et. al. 2007].

Step 2: Match real data to consistent three-SNP models

A set of three-SNP models matching the observed results, S_point (or S₉₅), is then compared to a list of known variants (e.g. catalogued in 1000 Genomes). The list is filtered to retain only those real SNPs with allele frequencies and correlations to A and B that match a model in S_point (or S₉₅). We call these real SNPs candidates for D.

At this point there are several possible outcomes:

1. If there are no candidates (and particularly if there are no “broad-sense” candidates that match S₉₅), then under the models examined (e.g. additive, dominant, recessive with certain ranges for relative risks), no SNPs from 1000 Genomes can theoretically be the sole cause of associations seen at A and B. We have no evidence against the usual interpretation that A and B represent two distinct association signals.

2. If there are candidates that match S_point (or S₉₅), we would wish to examine the OR, in our real association study dataset, for each candidate. The goal is to identify whether or not these candidate SNPs also have the corresponding odds ratios to be in S_point or S₉₅, and in particular to rule out the ones that do not. This step requires either measured or estimated genotypes of the SNP in the applied dataset. Therefore we have the following options

   • 2.1If a candidate is already genotyped in the current dataset, we perform association analysis to determine its odds ratio.
   • 2.2If a candidate is not genotyped, but can be imputed (accurately) from the current data, the imputed genotypes for SNPs could be evaluated as in 2.1. Confirmatory genotyping should be considered as well.
   • 2.3If a candidate is not genotyped and cannot be accurately imputed in the current dataset, it can be flagged as a target for future genotyping.

Any candidate that does not have matching odds ratios is ruled out as potential SNP D. For the candidates that do possess matching odds ratios, association analyses of the candidate alone and candidate together with A and B (a 3 SNP joint analysis) could be compared to determine if the candidate accounts for the joint analysis result of A and B. More specifically, we examine whether or not adding A and B to a model with D (a 3 SNP joint analysis) adds substantially to the phenotypic variance explained by D alone. We divide this difference by the variance explained by just A and B; this ratio is the proportion of variance explained by A and B that is not accounted for by D. Additionally, −2log likelihoods from the model that includes A, B, and D can be subtracted from a model that includes D alone. Under the null (A and B do not add to the signal from D), the difference is chi-square distributed with 2 degrees of freedom. If resulting p-value is significant, it indicates that adding A and B to the model with D substantially increases model fitness, suggesting that D does not account for the effects observed at A and B.

AN APPLICATION: A JOINT RESULT RELATED TO NICOTINE DEPENDENCE

An interesting joint SNP result involving rs16969968 and rs588765 (two SNPs located in the CHRNA5 gene in chromosome 15q25.1) and nicotine dependence has been previously reported in multiple datasets [Saccone, et al. 2009; Saccone, et al. 2010]. In the initial report using data from the Collaborative Genetic Study of Nicotine Dependence (COGEND), univariate analysis found that rs16969968 (SNP A) was strongly associated with nicotine dependence while rs588765 (SNP B) was not significantly associated with nicotine dependence [Saccone, et al. 2009]. However, joint analyses of A and B strengthened the evidence for association for B without weakening the strength of A's association, suggesting two distinct findings [Saccone, et al. 2009]. This pattern of univariate and joint analysis association evidence was subsequently confirmed, with genome-wide significance, for the two SNPs in a large collaborative meta-analysis of heavy/light smoking [Saccone, et al. 2010].

We applied the general method described above to the COGEND European-American sample (sample size=2053) to investigate the possibility that this joint analysis result could have arisen from a single third SNP. Cases are nicotine dependent based on the Fagerström Test for Nicotine Dependence (FTND) [Heatherton, et al. 1989; Heatherton, et al. 1991], with FTND score ≥ 4. Controls have no lifetime dependence to nicotine and have FTND score ≤ 1.

We used 1000 Genomes estimates for the population-level frequencies and correlation between these variants to represent rs16969968 and rs588765 in the three-SNP models. Here, P(A₂) = 0.42, P(B₂) = 0.39, and r_AB = −0.68 (1000 Genomes, August 2010 release) (Table I). Using the steps described in the previous section, and using a total haplotype count of N=100, we generated a mesh of sets of P_ijk consistent with the estimated frequencies for haplotypes of A and B. N thus determines the step size in sampling between the minimum and maximum values of the pair-wise correlation values between D and A and D and B (r_AD and r_BD). For each generated set of haplotype frequencies of A-B-D, we generated values of f₁₁, f₁₂, and f₂₂ using the equations S1a, S1b, and S1c by stepping through values of R₁₂ (additive model) and R₂₂ (dominant and recessive models) from 1 and 10 in increments of 0.1 to generate models where D₂ increases risk and the reciprocal of each value for R₁₂ and R₂₂ to generate models where D₂'s effect is protective.

Table I.

Table of observed properties values of rs16969968 (SNP A) and rs588765 (SNP B). Minor allele frequencies of A and B and pair-wise correlation between the two SNPs are obtained from the 1000 Genomes European reference panel to match the ancestry background of the COGEND European-American (EA) dataset. Odds ratio estimates and 95% C.I. of OR_A, OR_B, OR_A|B, and OR_B|A and covariance between OR_A|B and OR_B|A are calculated from the COGEND EA sample (1062 cases, 991 controls).

	RS16969968 (A)	Rs588765 (B)
MAF in 1000 Genomes	0.42	0.39
Pair-wise correlation in 1000 Genomes	r = −0.68
Univariate OR (L95%,U95%)	1.39 (1.22,1.58)	0.91 (0.80,1.03)
Joint SNP OR (L95%,U95%)	1.55 (1.31,1.83)	1.19 (1.01,1.39)
Covariance between joint SNP OR estimates	4.52 × 10−3

Table I lists the point estimates and the 95% C.I.s of OR_A, OR_B, OR_A|B, and OR_B|A, as well as the covariance value used to calculate the 95% C.R. of OR_A|B and OR_B|A. We examined the 2793 SNPs in 1000 Genomes (August 2010 release) that lie in the ~500Kb region centered at rs16969968 (Chr15:78,711,803-79,263,811) as possible candidates for a single explanatory SNP. This region is flanked by recombination hotspots and spans well beyond the gene cluster (70kb in length) that includes rs16969968 and rs588765. Of these 2793 SNPs, 212 SNPs were genotyped in COGEND. The remaining 2561 SNPs were imputed in COGEND samples using the BEAGLE software (version 3.3.1) with a reference panel of 283 individuals of European origin from the 1000 Genomes (August 2010 release) prepared by the BEAGLE developers (http://bochet.gcc.biostat.washington.edu/beagle/) [Browning and Browning 2009]. The minor allele frequencies and (signed) pair-wise correlations to rs16969968 and rs599765 were calculated from the same reference panel using the verbose option of LDmax [Abecasis and Cookson 2000].

We used these values to filter the generated set of models to determine a set of candidates to be evaluated.

A BROADER EXPLORATION OF JOINT EFFECTS CAUSED BY A SINGLE VARIANT

Finally, we performed a more general exploration of models that share essential features with our example from real data, that is, a scenario wherein a single causative variant creates a substantial univariate association for locus A and a second association for locus B which is seen only in joint analysis with A.

As in the real COGEND data example, we fixed P(A₂) = 0.42, P(B₂) = 0.39, and r_AB = −0.68. However, this portion of the study examined a range of odds ratios of potential interest, rather than just the specific empirical values from that example. As before, we generated all combinations of P_ijk possible from a total haplotype count of 100, and for each of the 3 disease models generated the values of f₁₁, f₁₂, and f₂₂ using the equations S1a, S1b, and S1c and ranging the value of R₁₂ for additive model and R₂₂ for dominant and recessive models between 1 and 10 by an increment of 0.1 for risk effect of D₂ and the reciprocal of each values of R₁₂ and R₂₂ for protective effect of D₂.

We examined the subset of models with the following properties: (1) A is associated with disease with effect sizes comparable to those typically seen in GWAS (1.30 ≤ OR_A ≤ 2.00), (2) B does not show strong association when analyzed alone (0.91 ≤ OR_B ≤ 1.10), and (3) A and B both show association to disease when analyzed together in a joint model (1.30 ≤ OR_A|B ≤ 2.00, 1.30 ≤ OR_B|A ≤ 2.00). The results of these examinations provide important and surprising insights.

Results

BROADER EXPLORATION OF JOINT EFFECTS CAUSED BY A SINGLE VARIANT

For models where a single causative SNP, D, can give rise to odds ratios for non-causative SNPs A and B where 1.3 ≤ OR_A ≤ 2.0, 0.91 ≤ OR_B ≤ 1.1, 1.3 ≤ OR_A|B ≤ 2.0 and 1.3 ≤ OR_B|A ≤ 2.0, we observed the following:

1. Such disease causing SNPs are not required to be highly correlated to A nor B

Figure 1a illustrates the range of pair-wise correlations (r_AD and r_BD) between the disease causing SNP, D, and the two null SNPs, A and B, under additive disease models. Three-SNP models with low to moderate effect size of D (0.33 ≤ OR_D ≤ 3.0) are highlighted with filled red circles; remaining three-SNP models are open black circles. We see that the correlation between the disease causing SNP, D, and both SNPs, A and B, is modest for these three-SNP models, with r² between D and A ≤ 0.45 and between D and B ≤ 0.03 (More specifically, r_AD ∈ [−0.67, −0.15] ∪ [0.11, 0.53], corresponding to signed r² ∈ [−0.45, −0.02] ∪ [0.01, 0.28] and r_BD ∈ [−0.15, 0.18], corresponding to signed r² ∈ [−0.02, 0.03]). This figure illustrates the surprising fact that even when the correlation between B and D is 0, B can become significant in a joint analysis with A while simultaneously strengthening the association between A and the phenotype. The fact that r_AD and r_BD can be moderate indicates that the typical approach of considering only SNPs highly correlated with A or B as candidates to explain the associations observed at A and B is insufficient – such an approach could not identify these Ds. This is true even for disease causing SNPs of moderate effect size (e.g. 0.33 ≤ OR_D ≤ 3.00, identified by red dots in figure 1a).

Figure 1.

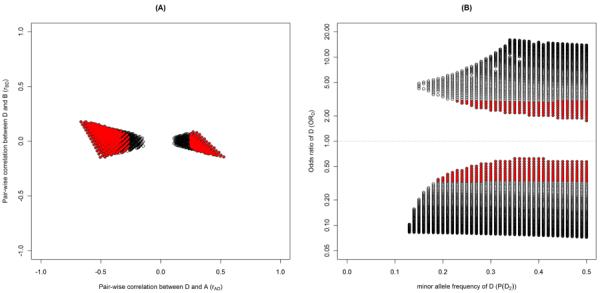
a. Plot of D's pair-wise correlation to A (r_AD) and to B (r_BD) among the three-SNP models that produced the following odds ratios for A and B under additive disease model for D; 1.30 ≤ OR_A ≤ 2.00, 0.91 ≤ OR_B ≤ 1.10, 1.30 ≤ ORA|B ≤ 2.00, and 1.30 ≤ OR_B|A ≤ 2.00. Each open circle indicates a combination of D's theoretical properties (P(D₂), r_AD, r_BD, OR_D). Red filled-in circles indicate Ds that have odds ratios between 0.33 and 3.00.

b. Plot of D's minor allele frequencies (P(D₂)) and odds ratios (OR_D) among the three-SNP models that produced the following odds ratios for A and B under additive disease model for D; 1.30 ≤ OR_A ≤ 2.00, 0.91 ≤ OR_B ≤ 1.10, 1.30 ≤ ORA|B ≤ 2.00, and 1.30 ≤ OR_B|A ≤ 2.00. Each open circle indicates a combination of D's theoretical properties (P(D₂), r_AD, r_BD, OR_D). Red filled-in circles indicate Ds that have odds ratios between 0.33 and 3.00.

Under dominant and recessive models, D showed similar modest values of r_AD and r_BD. For dominant models, r_AD ∈ [−0.67, −0.16] ∪ [0.12, 0.53] and r_BD ∈ [−0.15, 0.18] corresponding to signed r² ∈ [−0.45, −0.03] ∪ [0.01, 0.28] and [−0.02, 0.03] respectively (Figure S1a) and for recessive, r_AD ∈ [−0.67, −0.41] ∪ [0.16, 0.53] and r_BD ∈ [−0.14, 0.18], i.e. signed r² ∈ [−0.45, −0.17] ∪ [0.03, 0.28] and [−0.02, 0.03] respectively (Figure S2a).

2. Such disease causing SNPs are not required to have low MAF or large odds ratios

The range of MAF for possible disease causing D versus the corresponding odds ratio of D under additive disease model with the given properties is illustrated in Figure 1b. This two dimensional figure shows that the disease causing SNPs from such models, cannot be small and have a wide range of values (0.13 ≤ P(D₂) ≤ 0.50). D also can have modest odds ratios as low as 1.75. Again, we have highlighted the three-SNP models with modest odds ratios of D (0.33 ≤ OR_D ≤ 3.0) in red.

D under dominant disease model can have lower MAF than for the additive model (0.06 ≤ P(D₂) ≤ 0.50) but still can have modest odds ratios as low as 2.13 (Figure S1b). D under recessive models must have MAFs that are common (0.21≤ P(D₂) ≤ 0.50) and can have odds ratios as low as 2.07 (Figure S2b).

To confirm that D does account for A and B's effects on the phenotype in these models, we compared the amount of variance explained (R², the coefficient of determination) in two logistic regression models; D alone and A, B, and D together. In these two models, the amount of variance explained was the same, indicating that A and B did not add to the explained phenotypic variance accounted by D alone. Thus D accounts for the effects of A and B.

APPLICATION TO NICOTINE DEPENDENCE

We did not find any three-SNP models that could individually account for the point estimates of OR_A, OR_B, OR_A|B and OR_B|A in the COGEND data under additive, dominant, or recessive disease models. In other words, S_point is empty. One way to see this concretely is to note that under all three disease models, all of the three-SNP models examined whose OR_A and OR_B matched the point estimates of OR_A and OR_B resulted in values for OR_A|B in the range [1.68, 1.72] and values for OR_B|A in the range [1.32, 1.36]. The point estimates from COGEND for these values (OR_A|B = 1.55, OR_B|A = 1.19) both fall outside these ranges. This suggests that it is unlikely that any single SNP acting under a common disease model produced the joint analysis results observed in the COGEND data. Because the set of candidate models, S_point, is empty, no comparison to the 1000 Genomes SNPs was needed.

S₉₅, the less restrictive set of three-SNP models in which allele frequencies and correlations precisely match observed values but odds ratios need only lie within a confidence region (i.e. (OR_A, OR_B, OR_A|B, OR_B|A) ∈ (95%C.I. for OR_A) × (95%C.I. for OR_B) × (95% joint C.R. for OR_A|B and OR_B|A), was not empty. Figure 2a shows, for additive disease models, the combinations of minor allele frequencies and odds ratios for D (i.e. P(D₂) and OR_D respectively) for which a single additively acting causative SNP, D, could give rise to joint SNP results in the S₉₅ for rs16969968 and rs588765 in COGEND. The large area depicted indicates that in theory, many SNPs could be candidates for such a D, producing joint SNP results within the somewhat broad space formed by the C.I. and C.R.: (1.22,1.58) × (0.80,1.03) × (95% joint C.R. for OR_A|B and OR_B|A). We note that under an additive disease model, D must be common (MAF ≥ 6%) and can have modest odds ratios (as small as 1.37). These results were based on 3-SNP models generated with N = 100 (number of haplotypes), which thus determines the density of the plotted gray circles. A larger N would result in a higher density of gray circles, but is not expected to change the overall shape.

Figure 2a–c.

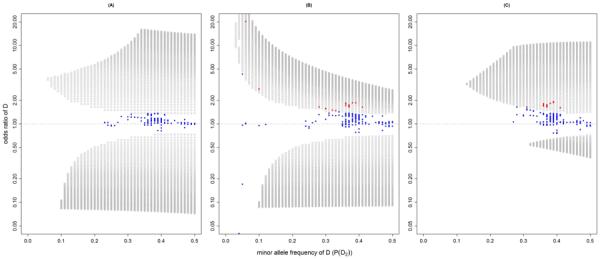
Plot of D's minor allele frequencies (P(D₂)) and odds ratios (OR_D) from S₉₅ under additive (a), dominant (b) and recessive (c) disease models for D. Each open circle indicates a combination of D's theoretical properties (P(D₂), r_AD, r_BD, OR_D). Blue dots indicate candidates for D from 1000 Genomes that do not have matching odds ratios and are therefore ruled out as potential causal Ds. Red dots indicate candidates that possess matching odds ratio.

Because S₉₅ was not empty, we filtered S₉₅ against the 2793 SNPs listed in the 1000 Genomes that lie in the ~500Kb region centered at rs16969968. Under additive model, we found 362 SNPs that match MAF, r_AD and r_BD. Out of these 362 candidates, 25 were previously genotyped, and 320 could be imputed well (using a lenient threshold of estimated allelic R² ≥ 0.4). The remaining 17 potential candidate SNPs were not imputable in COGEND and cannot be tested at this time (Table SII). We tested the 345 genotyped and well-imputed SNPs in COGEND to obtain odds ratios and plot them against P(D₂) and OR_D (Figure 2a, blue dots). None of these SNPs possessed an appropriate odds ratio to remain as a candidate.

For models in S₉₅ under dominant disease models, we similarly plot P(D₂) and OR_D (Figure 2b). As we found for additive models, dominant S₉₅ models cover a large area in this space. These models include less common (MAF can be as low as 2%) causative SNPs, which must have very large odds ratios, as well as common SNPs, which may have modest effects (e.g. MAF = 0.41, OR_D = 1.40).

The same list of 2793 real SNPs was filtered against S₉₅ under dominant disease model for D. There was a total of 370 SNPs that possess MAF, r_AD, and r_BD values that fall within S₉₅. Of the 370 candidates, 25 were previously genotyped and 323 were imputed well COGEND. The remaining 22 candidates were not imputable in COGEND (Table SII). Figure 2b shows that out of the 348 candidates, 329 did not have matching odds ratios (blue dots) leaving 19 SNPs (red dots) that have odds ratios to remain as candidates for D under dominant disease models in S₉₅ (Table SII).

Lastly, Figure 2c plots P(D₂) and OR_D that for models in S₉₅ under recessive disease models. Compared to additive and dominant models, we find models in S₉₅ covering a smaller area in these dimensions. In these models the causative SNPs must be common (MAF ≥ 13%). Still, D can have modest odds ratios (OR_D ≥ 1.38). The 2793 real SNPs were filtered against the recessive disease models in S₉₅. A total of 307 SNPs had MAF, r_AD, and r_BD values that match S₉₅. Of these candidates, 23 were previously genotyped and 275 were imputed in COGEND. The 9 that were not imputable in COGEND remain as potential candidates and are listed in Table SII. Figure 2c shows that out of the 298 candidates, 280 did not have matching odds ratios to remain as candidates (blue dots) and 18 SNPs (red dots) remain as candidates for D under the recessive disease models in S₉₅ (Table SII).

Finally, we wish to determine if any of the 37 candidates (dominant and recessive models) can account for rs16969968 and rs588765, in the sense that adding both these SNPs to the model with D alone does not increase the variance explained. Each candidate was tested in the COGEND dataset alone and together with both additional SNPs rs16969968 and rs588765 in logistic regression models with the appropriate genotyping coding for D (dominant or recessive). In COGEND, we found that none of the candidates could account for all of the variance explained by rs16969968 and rs588765; 29% to 98% of the variance explained by rs16969968 and rs588765 was not contributed by the candidates. Also using tests based on −2log likelihood differences, for each candidate D, the model including D, rs16969968, and rs588765 provided a significantly better fit to the data than the model that includes D alone (last column of Table SII). Therefore, we conclude that none of the candidates fully account for the originally observed associations of rs16969968 and rs588765.

Discussion and Conclusions

We have presented a novel approach that provides a list of candidate SNPs that could produce observed associations of two SNPs, A and B, to a phenotype in a joint analysis. Typically, only variants that have high r² with either A or B are considered as potential candidates, as they are clearly “tagged” by either SNP. Our method demonstrates that lower correlation SNPs could cause such phenomena and provides a systematic approach to identify candidates that may represent a single effect underlying the associations of A and B. In addition, these candidates may have only modest correlation to the observed association signals. Therefore our approach is important because it (1) identifies potential causal candidates that would be missed by the traditional approach of searching for causal variants among the “tags” that are highly correlated with the statistically identified SNPs, and (2) it has the potential to connect association signals that might have seemed disparate due to lack of high pair-wise correlations among the SNPs. This method can be applied to any joint SNP analysis finding for two SNPs and a dichotomous trait. Our SAS (Cary, NC) code is available upon request.

Based on a scenario in which SNP A is associated in univariate analysis and SNP B is associated only after joint analysis with A, we observed that even with modest effect sizes, the causative SNP D can have moderate to low pair-wise correlations to A and B. This is striking since examining only highly correlated SNP (r² ≥ 0.8) is typically thought to be sufficient to identify SNPs whose statistical associations are due to the same causal source. However in our simulations we found A and B, whose significant associations to the phenotype were due solely to causative SNP D, were not required to be highly correlated to D. In fact, D's pair-wise correlations to A and B were limited to modest to low values. This makes sense, since if either A or B were highly correlated to D, then any joint SNP analysis with the highly correlated variant would yield only one significant association (representing D). Our demonstration that high correlation does not necessarily identify key candidates that represent the same underlying joint signal has some parallels to a previous simulation study of single SNP association results which showed that two highly correlated SNPs do not necessarily have highly correlated test results [Nielsen, et al. 2008]. Our findings and theirs both caution against relying solely on high pair-wise correlation among SNPs to make inferences from association findings to identify variants underlying observed association signals.

Our work shows that it is possible for two apparently distinct signals to be explained by a single underlying causal variant. This is the flip-side of a previous simulation-based demonstration that it is possible for an association signal at a single common SNP to be explained by multiple rare causal variants that co-occur on the haplotype background (synthetic association) [Dickson, et al. 2010]. In both studies, results show that relying on high correlations with observed association signals to identify causal variants is not adequate and will miss many potential causal variants.

It is important to note that even though our three-SNP models are set up so that D is the single causal variant, this does not guarantee that any candidate identified by our approach is indeed the underlying causal SNP for a given joint analysis finding. The candidate list alerts researchers as to (some of the SNPs) which have this potential. Biological assays or functional evidence are ultimately required to establish causal relationships, either of a pair of SNPs A and B or of a single SNP D, to the disease.

In our application to nicotine dependence association results in COGEND, we found no convincing evidence that a third SNP D is responsible for the joint results observed at rs16969968 (A) and rs588765 (B). First, S_point is empty, meaning that no single SNP, under the models examined (additive, dominant, recessive), would in theory produce the precise odds ratio point estimates observed in COGEND. Second, none of the 37 candidates identified using S₉₅ could account for the effects of rs16969968 and rs588765 in a 3 SNP logistic regression, which indicates that these candidates are not the underlying variants. Lastly, it is important to note that a great deal of biological support is emerging for the functional effects of rs16969968 [Bierut, et al. 2008] and of rs588765 or its high r² proxies [Smith, et al. 2011; Wang, et al. 2009]. This biological evidence supports the idea of distinct roles for these two loci in nicotine dependence, thereby supporting the thesis that the two SNPs represent two different effects.

The candidates from the 1000 Genomes for D in S₉₅ could connect our nicotine findings in CHRNA5 to variants in IREB2, CHRNA3, CHRNB4, and ADAMTS7 where the candidates are located. The genes IREB2, CHRNA3, and CHRNB4 contain other variants with strong correlation to rs16969968 or rs588765 and previously have been reported in relation to smoking. Our analysis also revealed a potential connection between smoking loci and ADAMTS7 (Table SIII). Interestingly, ADAMTS7 (rs1994016) was recently reported as associated with coronary artery disease (CAD), a phenotype closely related to smoking [Reilly, et al. 2011]. Increased attention to potential overlap or relationships between associations for smoking behavior and heart disease may therefore be warranted.

It is important to note that the process of identifying broad-sense candidates for a joint result (i.e. SNPs in S₉₅) is influenced by the accuracy of the estimates of OR_A, OR_B, OR_A|B, and OR_B|A. More accurate estimates of the odds ratios (i.e. tighter confidence interval) will force the SNPs in S₉₅ to more closely represent the observed joint SNP analysis result. Also, in generation of three-SNP models, it is important to select population-level values for P(A₂), P(B₂), and r_AB from an appropriate reference that represents the ancestral make up of the real data well. If inaccurate population values were used, the generated three-SNP models would deviate from the values of P(A₂), P(B₂), and r_AB observed in the real dataset. Use of an appropriate reference is also important when performing imputation in the applied study dataset, and differing imputation strategies may yield differing results. However, imputation is only involved in the final filtering step to identify “real” candidates that match the theoretical properties in S_point or S₉₅. We first retain only those real SNPs with matching allele frequencies and correlation. As in all cases involving imputed variants of interest, confirmatory genotyping remains important.

Our work highlights the usefulness of reporting odds ratios and confidence intervals for both SNPs that are included in a joint analysis. Oftentimes, when joint analyses are carried out using a selected SNP (SNP A) already known to be disease-associated, only the second SNP's result (SNP B) is reported from the joint model. Odds ratios of both SNPs are important for interpretation of joint SNP association results, and can be used by our method to identify potential candidates for a single causal SNP.

In conclusion, our method identifies theoretical properties sufficient for a single underlying variant to be the sole cause of a specific joint SNP analysis result and can be applied systematically to identify real candidate causal SNPs (e.g. from the 1000 Genomes data). We have shown that these candidates would not necessarily be obvious from current approaches. In addition, our method can connect association signals that might otherwise be thought to be distinct. This work provides information that can aid in designing follow-up studies to further elucidate the genetic underpinnings of diseases.