The quantal nature of Ca²⁺ sparks and in situ operation of the ryanodine receptor array in cardiac cells

Abstract

Intracellular Ca²⁺ release in many types of cells is mediated by ryanodine receptor Ca²⁺ release channels (RyRCs) that are assembled into two-dimensional paracrystalline arrays in the endoplasmic/sarcoplasmic reticulum. However, the in situ operating mechanism of the RyRC array is unknown. Here, we found that the elementary Ca²⁺ release events, Ca²⁺ sparks from individual RyRC arrays in rat ventricular myocytes, exhibit quantized Ca²⁺ release flux. Analysis of the quantal property of Ca²⁺ sparks provided a view of unitary Ca²⁺ current and gating kinetics of the RyRC in intact cells and revealed that spark activation involves dynamic recruitment of small, variable cohorts of RyRCs. Intriguingly, interplay of RyRCs in multichannel sparks renders an unusual, thermodynamically irreversible mode of channel gating that is unshared by an RyRC acting solo, nor by RyRCs in vitro. Furthermore, an array-based inhibitory feedback, overriding the regenerative Ca²⁺-induced Ca²⁺ release of RyRCs, provides a supramolecular mechanism for the microscopic stability of intracellular Ca²⁺ signaling.

The ryanodine receptor Ca²⁺ release channel (RyRC) is a prototypical member of the Ca²⁺ release channel superfamily located in the endoplasmic reticulum/sarcoplasmic reticulum (SR) of eukaryotic cells and plays a pivotal role in intracellular Ca²⁺ signaling (1-5). Instances of local Ca²⁺ release, in the form of “Ca²⁺ sparks” or their equivalents, constitute the elementary Ca²⁺ signaling events in heart, brain, and muscle cells (6-12). Intriguingly, RyRCs in intact cells are almost exclusively found at discrete spark-generating sites, where ≈100 channels are assembled into two-dimensional paracrystalline arrays (13-15). This pattern of RyRC organization seems to be highly conserved from crustaceans to vertebrates (13, 15, 16), suggesting that array formation is critical to RyRC-mediated Ca²⁺ signaling in vivo. Thus, understanding array-based RyRC behavior is of fundamental importance for elucidation of intracellular Ca²⁺ signaling mechanism.

Despite a wealth of information on behavior of RyRCs in planar lipid bilayers and other cell-free systems (5, 17-20), little is known on how RyRCs operate in situ; many fundamental issues regarding the genesis and termination of Ca²⁺ sparks remain unanswered (5, 21, 22). Based on in vitro properties of RyRCs, the classic Ca²⁺-induced Ca²⁺ release (CICR) mechanism (23) would predict an all-or-none activation of the RyRC array and an everlasting local Ca²⁺ release, which cannot explain the prompt termination of Ca²⁺ sparks and the microstability of intracellular signaling (24, 25). The relatively constant Ca²⁺ spark rise time (≈10 ms in the heart) indicates a stereotypical open time of RyRCs (25) whereas RyRCs in vitro always follow exponential open-time distributions (5, 17, 20). The brief spark duration also contrasts sharply with the coupled gating (19) kinetics of RyRCs, in which the open time of physically linked channels acting in unison is prolonged by orders of magnitude (up to 2,500 ms) (20). These paradoxical observations underscore that in vivo operation of RyRCs may involve gating mechanisms that are apparently absent in cell-free systems. Alternatively, the formation of RyRC array may endow the channels with new regulatory mechanisms that are unshared by a corresponding set of solitary RyRCs.

In the present study, we sought to investigate RyRC operation in their native arrays. Because intracellular location of RyRC arrays makes them inaccessible to electrophysiological means, we devised an optical approach to analyze the Ca²⁺ release flux underlying the spark (I_spark) in intact cardiac myocytes. By splitting I_spark from individual RyRC arrays into single-channel components, we provided a view of the in situ gating of a single RyRC and demonstrated that array-based interaction between RyRCs renders an unusual, irreversible channel behavior and contributes to the microscopic stability of intracellular Ca²⁺ signaling.

Methods

Confocal Ca²⁺ Imaging. Enzymatically isolated adult rat cardiac myocytes were loaded with the Ca²⁺ indicator, fluo-4-AM, as described (26). Confocal line-scan imaging was performed by using a Zeiss LSM 410 or LSM510 confocal microscope equipped with an argon laser (488 nm) and ×40, 1.3 N.A. oil immersion objective. Line-scan images were acquired at sampling rates of 0.38-1.4 ms/line and 0.07 μm/pixel, with radial and axial resolutions of 0.4 and 1.0 μm, respectively. Assuming that the indicator responds to [Ca²⁺] with little kinetic delay, local Ca²⁺ concentrations were determined by using the formula [Ca²⁺] = k_dR/(k_d/[Ca²⁺]_rest ± 1 - R) (6), where R = F/F₀, the resting Ca²⁺ concentration [Ca²⁺]_rest = 100 nM, and the dissociation constant k_d = 1.1 μM. To resolve the quantal property of I_spark, cautions were given to ensure that the focal plane was placed precisely at the tip of the patch pipette throughout the experiments. Environmental vibration was carefully isolated from the recording system so as not to introduce low frequency noise into spark time courses.

Cell-Attached Patch Clamp. Cell-attached patch clamp was established in either GΩ-seal or loose-seal configuration, with glass patch pipettes of 4-5 MΩ. In the loose-seal patches, the membrane potential was determined by proportionally dividing the test voltages between the pipette resistance and the seal resistance (15-30 MΩ) (26). The standard patch pipette filling solution consisted of (in mM) 120 tetraethylammonium chloride, 1 CaCl₂, 0.01 tetrodotoxin, and 10 Hepes (pH 7.4). The standard superfusion solution contained (in mM) 135 NaCl, 1 CaCl₂, 4 KCl, 1 MgCl₂, 10 glucose, and 10 Hepes (pH 7.4). All experiments were performed at room temperature (23-25°C).

Results

Ca²⁺ Spark Release Flux Exhibited Quantal Substructure. To gain insight into the behavior of RyRCs in situ, we combined confocal microscopy and cell-attached patch clamp technique to activate Ca²⁺ sparks by single L-type Ca²⁺ channel (LCC) current (i_LCC) (26). In freshly isolated rat ventricular myocytes loaded with the Ca²⁺-indicator fluo-4, Ca²⁺ sparks could be triggered by i_LCC under the GΩ-seal patch clamp conditions when the pipette contained 20 mM Ca²⁺ and 10 μM FPL64176, an LCC agonist (Fig. 1A). Likewise, Ca²⁺ sparks could also be evoked in loose-seal patches during a sequence of depolarization (0.1 Hz) to 0 mV in the presence of 1 mM Ca²⁺ in the pipette (Fig. 2A). The loose-seal method allows repetitive activation of Ca²⁺ sparks from in-focus release sites, minimizing the optical blurring associated with out-of-focus events (26).

Fig. 1.

Measurement of Ca²⁺ release flux of Ca²⁺ sparks (I_spark). (A) Simultaneous recordings of single LCC currents and triggered sparks in a GΩ-sealed patch. The pipette contained 20 mM Ca²⁺ and 10 μM FPL64176, an LCC agonist. (B) Representative recordings showing that repolarizations from +60 mV to resting membrane potential (-70 mV) evoked LCC tail current of 0.67 pA. (C) Under the loose-seal patch clamp conditions, the unitary tail current in B produced a tail Ca²⁺ sparklet when the SR Ca²⁺ release was disabled by 10 mM caffeine and 10 μM thapsigargin. Nine tail sparklets with >50 ms duration were averaged to improve the signal-to-noise ratio. (D) The time course (open circles) of the averaged sparklet in C was fitted to the equation ΔC = C_∞i (1 - exp(-t/τ) with i fixed at 0.67 pA, yielding C_∞ = 62 nM/pA and τ = 9.7 ms.

Fig. 2.

I_spark exhibits quantal substructure. (A)Ca²⁺ sparks triggered in loose-seal patch clamp condition when the SR function was intact. The pipette contained 1 mM Ca²⁺ without FPL64176. (B) Calibration of I_spark by fitting the spark rising phase to the equation in Fig. 1D using the determined C_∞ and τ. The traces shown are for the sparks in A (I_spark = 4.43, 3.47, and 2.26 pA, respectively). (C) I_spark distribution (bars) and its multi-Gaussian components (red curve) for all 384 sparks in 31 patches, and the fitting with Eq. 1 rendered a_j = 13.9, 25.5, 19.5, 12.4, 4.5, 3.1, and 1.0 (j = 1 to 7), b = 0.058, and q = 1.24 pA. (D) Evoked Ca²⁺ sparks in the presence of 100 μM tetracaine. (E) Estimation of I_spark for events in D (I_spark = 1.17 and 1.12 pA, respectively). (F) Histogram of I_spark in the presence of tetracaine (n = 11 cells). Multi-Gaussian fitting (red curve) as in C yielded a₁ = 24.5, a₂ = 7.0, and a_j < 1 for j = 3 to 7, b = 0.077, and q = 1.22 pA.

To measure I_spark, which relates directly to the unitary Ca²⁺ flux of RyRCs and the number of channels involved, we created a calibration standard with the aid of “Ca²⁺ sparklet” (26) produced by i_LCC. Specifically, LCC sparklets due to the “tail” i_LCC on repolarization from ≈+60 mV (i_LCC ≈ 0) to ≈-70 mV (i_LCC = -0.67 pA measured separately in GΩ-seal patches, Fig. 1B) were obtained in myocytes whose SR Ca²⁺ release was abolished by thapsigargin and caffeine. A subset of fully developed “tail” sparklets (longer than 50 ms) was then averaged to improve the signal-to-noise ratio (Fig. 1C). From the resultant high-resolution LCC sparklet, we derived the time course of local Ca²⁺ concentration as a function of the injected Ca²⁺ influx (Fig. 1D). The I_spark of any given Ca²⁺ spark was then deduced by fitting its rising phase to the known relationship (Fig. 2B). Because sparklets and sparks were obtained with identical imaging settings, sharing the same microenvironments with respect to Ca²⁺ diffusion, buffering, and indicator binding, the use of LCC sparklet as the “yardstick” to gauge I_spark should be essentially model- and parameter-independent.

Our measurement of 384 sparks from 31 patches (Fig. 2C) showed that I_spark varied widely from ≈1 to 10 pA. Notably, the I_spark did not vary continuously but exhibited prominent peaks that were separated at roughly equal intervals (Fig. 2C), suggesting a quantal substructure in the I_spark. By analogy to the classic analysis of quantal release of neurotransmitters (27), the entire histogram of I_spark was fitted to a multicomponent Gaussian function:

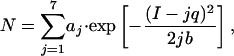1

where N is the frequency of observations, a_j and b are constants. The fitting yielded a quantal unit of current q = 1.24 pA. By contrast, a similar quantal pattern was not found in the I_spark of spontaneous sparks acquired at random locations (data not shown), indicating that in-focus detection is a prerequisite to revealing the fine I_spark substructure.

Splitting the Elementary Ca²⁺ Sparks. It is noteworthy that the subpopulation of the smallest I_spark in Fig. 2C consists of only a single q (number of q, n_q = 1), suggesting that the q is the smallest building block of Ca²⁺ release flux underlying the spark. Because ultrastructural studies so far (13-16) do not support any subgrouping of RyRCs within an array in cardiac myocytes, it is most probable that the subpopulation of n_q = 1 represent Ca²⁺ sparks of a single RyRC, and the sparks of higher n_q are from multiple RyRCs. To test this hypothesis directly, we devised experiments (Fig. 2D) in which tetracaine was included in the patch pipette at a concentration (100 μM) suitable to block a significant fraction of RyRCs (18). Because inclusion of tetracaine in the patch pipette should reduce the availability of RyRCs only locally, we do not expect a significant change in the “leaky-pump” balance and therefore the SR Ca²⁺ load. In the presence of tetracaine, Ca²⁺ sparks evoked beneath the tip of the patch pipette may either be unaffected if they were from a single channel, or be split into smaller sparks if they were multichannel events. We found that 100 μM tetracaine markedly reduced the amplitudes of Ca²⁺ sparks by decreasing the I_spark (Fig. 2E). Nevertheless, the histogram of decreased I_spark still exhibited quantized variation with the q (1.22 pA) unit unchanged (Fig. 2F). The vast majority of I_spark corresponded to only one (70%) or two (22%) quantal units, with sparks of higher n_q essentially eliminated. This result suggests that Ca²⁺ sparks with large I_spark can be split into subtler events. That tetracaine could neither destroy the quantal structure nor alter the q value indicates that a q arises from the all-or-none Ca²⁺ release of a single RyRC.

Dynamic Recruitment of RyRCs in an Array. The identification of q as the single RyRC Ca²⁺ release flux enabled us to analyze the recruitment of RyRCs in individual arrays. As shown in Fig. 3A, I_spark varied widely, even for those from the same patch. Notably, I_spark data points tended to aggregate into regular clusters in the scatter plot. Autocorrelation analysis of I_spark distribution (Fig. 3B) in patches displaying a sufficient number (no less than 15) of events revealed that the I_spark indeed exhibited a periodicity of around 1.2 pA (Fig. 3C, n = 24 patches). These observations indicate that the quantal substructure of I_spark is an inherent property of Ca²⁺ sparks from individual arrays.

Fig. 3.

Dynamic recruitment of RyRCs from individual release sites. (A) Scatter plots of I_spark from three representative loose-seal patches. The arrowheads indicate the quantal levels determined by the procedure in B. Small vertical displacements were added to separate overlapping symbols. (B) Autocorrelation function of I_spark data for patches [a] and [b] in A. I_spark histogram was constructed with a bin width of 0.1 pA and, after a minimal (3-kernel) smoothing, its autocorrelation function was then determined with a routine coded in interactive data language (IDL). The cyclic peaks at regular intervals in the autocorrelation function reflect the quantal variation of I_spark. A q is determined for each patch by the first non-zero peak. (C) Distribution of q determined by using autocorrelation analysis (n = 24 patches). Gaussian fitting using the equation N = a·exp[-(I - q)²/2b] yielded a = 11.2, b = 0.030, and q = 1.18 pA. (D) Distribution of n_q (I_spark/q, rounded to the nearest integer) in sparks from two representative patches, showing that variable cohorts of RyRCs were recruited from individual RyRC arrays. (E) All-events distribution of n_q in Ca²⁺ sparks from all tested patches.

By counting the n_q involved in each Ca²⁺ spark, we found that the vast majority (88%) of sparks involve multiple (up to 8) RyRCs whereas still 12% of them are single-channel events (n_q = 1) (Fig. 3E). The wide variation of n_q for the same-patch events (Fig. 3D) contrasts sharply with the notion that Ca²⁺ sparks are an all-or-none phenomenon (6, 28) and excludes the possibility that Ca²⁺ sparks involve the entire array (≈100 RyRCs) (29) or any fixed number of RyRCs. Instead, our data indicate that small, variable cohorts of RyRCs are recruited dynamically from a large population of RyRCs in an array.

In Situ Gating Kinesics of a Single RyRC. The ability to visualize single-channel Ca²⁺ sparks afforded an unprecedented opportunity to probe the gating behavior of a single RyRC in their native physiological environment. Previous studies indicated that RyRC gating in lipid bilayers exhibits an exponential distribution of open duration (17, 20, 25), which cannot explain the stereotyped Ca²⁺ release duration of typical Ca²⁺ sparks (25). To probe whether and how gating of a single RyRC differs in vitro vs. in situ, RyRC open duration in situ was measured by the rise time of single-channel Ca²⁺ sparks. Fig. 4A shows two examples of single-channel sparks, with brief (4.5 ms) and long (41 ms) rise time, respectively. The ensemble data show that the channel open duration followed approximately an exponential distribution with a time constant of 11.6 ms (Fig. 4B). Hence, the in situ gating kinetics of a single RyRC seem to resemble that in lipid bilayers (with a slow open time constant of 13.6 ms) (20), indicating that the mechanism for the stereotyped spark duration must exist at the supramolecular level.

Fig. 4.

In situ kinetics of a single RyRC. (A) Line-scan images (Upper) and their surface plots (Lower) of two single-RyRC Ca²⁺ sparks with short (4.5 ms, Left) and long (41 ms, Right) rise times, respectively. The different rise times resulted in different spark amplitudes. (B) Distribution of rise time for single-RyRC Ca²⁺ sparks. Mono-exponential fitting (red curve) yielded a time constant of 11.6 ms.

Transition to an Irreversible Mode of Gating for Interacting RyRs. To probe whether RyRC behavior is reshaped by array-based interplay of Ca²⁺ release channels, we next measured the rise time of multichannel sparks and categorized the data according to their corresponding n_q. Surprisingly, with the increase of n_q, the rise-time histogram was progressively transformed from an exponential distribution for n_q = 1 (Fig. 4B) to a leftward skewed distribution for n_q = 2 or 3 (Fig. 5A), and finally to a nearly Gaussian distribution for n_q ≥ 4 (Fig. 5B).

Fig. 5.

Interaction of RyRCs reshapes local Ca²⁺ release kinetics. (A) Distribution of rise time for Ca²⁺ sparks of n_q = 2 or 3. Note that the histograms become modal as compared with Fig. 4C. (B) Distribution of spark rise time for n_q ≥ 4. The red curve represents the fitting to a Gaussian function. (C) Relationship between the average rise time and the n_q of Ca²⁺ sparks. Data are expressed as mean ± SE.

For Markovian channels or channel groups uncoupled from external free energy, microscopic reversibility requires that the distribution of the unit active open time always be the sum of positively weighted decaying exponentials (30-32). Although single-RyRC gating in situ basically satisfies thermodynamic reversibility, the n_q-dependent, nonexponential open time distributions for n_q ≥ 2 indicate that, when more than one RyRC is activated in a spark, thermodynamic irreversibility ensues. Our observations illustrate that the gating of an ion channel can transit from a thermodynamically reversible to an irreversible mode due to functional channel-channel interaction.

To further delineate the nature of intra-array interaction of RyRCs, we examined the influence of n_q on averaged spark rise time. Fig. 5C shows that, with the n_q increased from 1 to 7, averaged spark rise time was decreased monotonically from 15.0 ± 1.9 to 8.4 ± 0.8 ms (mean ± SE.). In other words, the more RyRCs recruited in a spark, the faster the spark terminates. It follows that the interaction between RyRCs in their native array is predominantly inhibitory.

Discussion

Ca²⁺ sparks and equivalent localized Ca²⁺ release events have been found in all types of muscle cells, neurons, and some nonexcitable cells and are generally accepted as the elementary events of endoplasmic reticulum/SR-mediated Ca²⁺ signaling (6-12). A major finding reported here is that the elementary Ca²⁺ sparks actually comprise a finer substructure by virtue of quantized I_spark. The quantal nature of Ca²⁺ sparks has been established on the basis of the distinct, regular peaks in the I_spark histogram for a large number of in-focus sparks, the periodicity in I_spark data from individual patches, and the splitting of sparks by decreasing RyRC availability using tetracaine. The lack of such quantal substructure for spontaneous events, with their apparent I_spark distorted by out-of-focus blurring, adds to the credence that the quantal substructure of in-focus events is real.

The ability to identify the quantal property of I_spark depends on the variation of data. To minimize detection error, we carefully optimized the recording condition (see Methods) and adopted a new generation of confocal microscope. Nevertheless, the q still exhibited a significant cell-to-cell variation (Fig. 3C, variation factor S = 0.146, defined as for the equation in Fig. 3C legend). This variation should, in part, reflect the photon shot noise associated with fluorescence measurement and the heterogeneity of release units among cells. The cell-to-cell variation in [Ca²⁺]_rest [S = 0.152 measured with indo-1 ratiometric confocal microscopy (33)], by affecting F/F₀, could result in additional variation in q measurement, but its contribution should be partially alleviated because of the positive correlation between [Ca²⁺]_rest and the SR Ca²⁺ load (and therefore the RyR Ca²⁺ release flux). Mathematically, neighboring Gaussian peaks can be resolved when S < 0.5. For experimental data with a sufficient number of observations, the quantal peaks would be resolvable with an S considerably smaller than 0.5, as demonstrated in Fig. 2C for n_q = 1, 2, and 3. It is noteworthy that the distribution of I_spark becomes smeared at n_q higher than 4 (Fig. 2C) because the S value increases at increasing n_q.

On the basis that ultrastructural studies reveal no subgrouping of cardiac RyRCs within array (13-16), a straightforward interpretation is that the q is from a single RyRC. This finding is further supported by several lines of evidence. First, the tiniest I_spark consists of only a single q (Fig. 2C), indicating that the q constitutes the smallest building block of I_spark. Second, local application of tetracaine can diminish I_spark of n_q > 1, but not the q per se (Fig. 2F), indicating that the q is pharmacologically indivisible under the present conditions. Third, the rise time constant (11.6 ms) of the Ca²⁺ sparks with n_q = 1 is in good agreement with the major slow component of single cardiac RyRC open duration (13.6 ms) (20) (the fast component of RyR open duration, if it exists, would be difficult to resolve with current optical measurement). In contrast, it is far briefer than that for coupled gating of multiple RyRCs in lipid bilayers (286 ms) (20). In addition, lipid bilayer studies have estimated that a single RyRC in vitro under quasi-physiological conditions carries a Ca²⁺ flux of 0.5 to 1.4 pA, depending on the exact ionic conditions used (34-36). The q of 1.2 pA falls right within this range and reflects the RyRC Ca²⁺ release flux in intact functioning cells.

Splitting Ca²⁺ sparks into quantal units has permitted us to dissect RyRC array operation in the genesis of Ca²⁺ sparks. It has been controversial whether spark activation involves a single RyRC, a few RyRCs, or the entire RyRC array (6, 10, 28-30, 37, 38). Our results demonstrated that spark origin cannot be any fixed number of channels, nor the entire array. Rather, RyRC recruitment in sparks involves variable cohorts of channels from individual arrays. Although most sparks involve multiple channels, still 12% of sparks are single-channel events. Given the large number (≈100) of RyRCs in a cardiac RyRC array, this result implies that only a small fraction of RyRCs in an array are activated, with the overall activation probability on the order of 0.01 ≈ 0.1 per spark. Such a low activation probability should reserve a wide margin of array activation for various physiological regulations (e.g., during cardiac adrenergic stimulation).

As compared with single-channel sparks, the scarcity of brief or long events at higher n_q (comparing Fig. 5 A and B with Fig. 4C) suggests that coupling of RyRCs has the effect of synchronizing Ca²⁺ release duration, both prolonging shorter openings and curtailing longer ones. The prolongation effect is expected if RyRCs are solely coupled by the regenerative CICR mechanism (23). However, the n_q-dependent curtailment of long-duration events suggests that RyRC Ca²⁺ release must also exert a negative feedback to the release machinery. The inverse relationship between n_q and the averaged spark rise time (Fig. 5C) supports this notion and further suggests that the inhibitory component predominates over the coupling among RyRCs.

The inhibitory feedback overriding the regenerative CICR may represent the long-sought mechanism for the termination and stability of intracellular Ca²⁺ release. We have previously shown that a model RyRC array based on in vitro RyRC properties and local CICR fails to reproduce proper termination of Ca²⁺ sparks and cannot account for the microscopic stability of intracellular Ca²⁺ release (24, 25). In light of the present finding, we incorporated an inhibitory coupling by introducing a strong Ca²⁺-dependent inactivation of RyRCs (Fig. 6A). Monte Carlo simulations of the new model recapitulated salient features of Ca²⁺ sparks, including the prompt termination of sparks, the inverse relationship between n_q and release time (Fig. 6B), and the exponential-to-modal transition of Ca²⁺ release duration (Fig. 6C). As a proof of principle, the model showed that the dual role of permeating Ca²⁺ as both agonist and antagonist (3-5, 23, 39, 40) of RyRCs could afford the link by which the free energy in the trans-SR Ca²⁺ gradients drives the irreversible gating of RyRCs. It is also noteworthy that the inhibitory mechanism inactivates some naive RyRCs before they could ever be fired in a spark (Fig. 6A), resulting in a limited availability of RyRCs in the array.

Fig. 6.

Monte Carlo simulations of a model RyRC array. (A) A snapshot (Right, 1 ms after ignition of a simulated “spark”) of the simulation of RyRC model array with excitatory and inhibitory interactions (Left). The stochastic “cardiac couplon” model of Stern et al. (24) was used, modified by increasing the rate constant for Ca²⁺-dependent inactivation of the resting-state RyRC 200-fold. (B) Average release duration of simulated sparks as a function of n_q. The n_q was defined as the peak number of simultaneously open RyRCs, and the release duration was determined as the time at which the number of open RyRCs first fell below half of its peak value. (C) Release-duration statistics of model-generated “sparks.” Note that the model recapitulated salient features of cardiac RyRC arrays in the genesis and termination of Ca²⁺ sparks.

It should be noted that a strong local Ca²⁺-dependent inactivation is only one of the candidate mechanisms for spark termination and does not exclude other possibilities, such as regulations from luminal side of SR. In the latter case, there is substantial evidence for luminal Ca²⁺ activation of RyR (40), but local depletion of SR Ca²⁺ during a spark remains an open question. It has been recently shown that no detectable Ca²⁺ gradients exist between the junctional SR (presumably the release sites) and the longitudinal SR (presumably the uptake site) during an action potential-elicited release (41). This finding indicates that the SR network is well-connected, allowing for rapid internal diffusion. Thus, experimental measurements leave it uncertain whether a sufficient diffusion resistance exists within the SR to sustain such local depletion during a spark.

Clustering of signaling proteins is an intriguing phenomenon of cell biology (42, 43). Our present study revealed that clustering of RyRCs into arrays endows interacting channels with unique properties. The n_q-dependent transition from a thermodynamically reversible to an irreversible mode of gating, which results in the stereotyped duration of Ca²⁺ sparks, has been heretofore unseen in any ion channels acting solo. The curtailment of active duration in multi-RyRC sparks is also in contrast to the much prolonged open duration in coupled gating of RyRCs in vitro (20), suggesting that not all array-based RyRC properties can be reproduced in a cell-free system.

In summary, we have investigated unitary properties and functional interaction of RyRCs in their native array in intact cardiac myocytes. We found that the number of RyRCs involved in a spark varies dynamically from one to many, which endows Ca²⁺ sparks with quantal substructure. The interplay of RyRCs in multiquantum sparks results in a thermodynamically irreversible operation of the Ca²⁺ release channel and stereotyped Ca²⁺ spark durations. The predominant inhibitory nature of RyRC interaction confines and abbreviates the excitation in the channel array, thus contributing to the microscopic stability of intracellular Ca²⁺ signaling.