Early phase trial design for assessing several dose levels for toxicity and efficacy for targeted agents

Abstract

Background

Traditional phase I trials are designed to be conservative. Many times a traditional phase I trial design stops at a dose level below the maximal tolerated dose (MTD), thus potentially treating patients at a suboptimal level in all subsequent trials. This has been confirmed by our recent simulation studies.

Purpose

We propose a phase I/II trial design to determine the most promising dose level in terms of toxicity and efficacy for cytostatic or targeted agents. This design evaluates three dose levels for efficacy and toxicity using a modified phase II selection design. The dose levels include the phase I recommended dose (RD) in addition to the dose levels immediately below and above that level.

Methods

This phase I/II trial design uses a two-step approach. In the first step, a traditional phase I trial design is used to get close to a good dose level. The second step consists of a modified selection design, randomizing patients to three dose levels: the phase I RD level and the dose levels immediately below and above the phase I RD level. Both efficacy and toxicity are used to determine a good or best dose level. Appropriate toxicity stopping rules in the phase II portion of the trial are implemented as part of such a trial. We perform simulation studies for a variety of toxicity and efficacy scenarios to determine the operating characteristics of this design and compare those to our originally proposed trial where we only explore dose levels at and below the phase I RD in the second phase of the trial, as well as to the traditional setting where a phase I trial is followed by a single-arm phase II trial at the phase I RD.

Results

The 3-arm modified selection design exploring the dose levels immediately above and below as well as the RD performs as well or better than the 2-arm modified selection design or the single-arm design for almost all toxicity and efficacy scenario combinations tested.

Conclusion

We demonstrate that this design has a higher success rate at identifying a good or best dose level when exploring dose levels immediately above and below the RD in the early phase II setting, in most cases without needing larger sample sizes.

Background

We recently developed a phase I/II trial design to determine the most promising dose level in terms of toxicity and efficacy for targeted agents [1,2]. This phase I/II trial design uses a two-step approach. In the first step, a traditional phase I trial design is used to get close to a good dose level. The second step consists of a modified selection design, randomizing patients to two dose levels at or below the phase I recommended dose (RD) level, and using both efficacy and toxicity to determine a good or best dose level. We evaluated the operating characteristics of that design using simulation studies for various toxicity and efficacy scenarios [1,2]. Phase I trial designs traditionally use a small number of patients in order to minimize the number of patients being treated at suboptimal levels or at dose levels that are too toxic [3]. As a consequence, the variability of toxicity estimates at a certain dose level is high, and we sometimes go forward in subsequent trials with suboptimal dose levels [4]. This design offers the opportunity to examine a few dose levels close to the RD in greater detail for both toxicity and efficacy before going forward with a specific dose level in a larger efficacy trial. We found that exploring a few dose levels in the phase II setting increases the success rate of determining a good or best dose level for future larger efficacy studies. We also showed that this increase in success rate in most scenarios investigated does not require larger sample sizes compared to the traditional setting, where the phase II trial evaluates efficacy of a new agent at the dose level determined by the preceding phase I trial.

Here we expand upon this concept by also exploring the dose level immediately above the phase I RD level. Traditional phase I trials are designed to be conservative. Many times, a traditional phase I trial design stops at a dose level below the maximal tolerated dose (MTD) [4], thus potentially treating patients at a suboptimal level in all subsequent trials. Considering the dose level above the RD may be a valid option, especially for some of the cytostatic or targeted agents, when we anticipate that toxicity is less of a concern than it is for more traditional cytotoxic agents. Continuous toxicity monitoring and appropriate toxicity stopping rules will need to be implemented. We perform simulation studies to determine the operating characteristics of this trial and compare those to our originally proposed trial where we only explore dose levels at and below the phase I RD in the second phase of the trial, as well as to the traditional setting where a phase I trial is followed by a single-arm phase II trial at the phase I RD.

A recent example where we would have benefited from such a trial design was observed with carfilzomib, which is a next-generation proteasome inhibitor that is currently developed for use in patients with multiple myeloma. It was developed to increase efficacy while reducing toxicity in this patient population. This agent is currently being tested in a number of clinical trials and has shown preliminary efficacy at a dose level of 27 mg/m² in combination with other agents. However, there is evidence from early therapeutic studies that a higher dose level of 56 mg/m² may be more efficacious, while still maintaining an acceptable toxicity profile. A protocol is currently being developed by the SWOG Myeloma Committee to formally test that hypothesis. More specifically, this will be a randomized phase II study comparing two dose levels of carfilzomib in combination with dexamethasone for multiple myeloma patients with relapsed or refractory disease. It would have been beneficial to more carefully determine the efficacy and toxicity for several dose levels at an earlier stage of drug development.

In the summer of 2008, a workshop sponsored by the Clinical Trial Design Task Force of the Investigational Drug Steering Committee discussed the changing role of phase I clinical trials. Ivy et al. [5] summarized the findings of this workshop. The main phase I trial designs discussed at that workshop were the traditional 3 + 3 designs, the continual reassessment method (CRM), as well as accelerated titration designs. O’Quigley [6] introduced the CRM, a Bayesian adaptive design for dose finding. Numerous modifications have been made over the years to add flexibility. Unlike the standard 3 + 3 design, the CRM requires the investigator to specify a number of design components in order to develop the trial design. Simon et al. [7] developed a family of accelerated titration designs and proposed the use of an accompanying dose toxicity model. The main features of these designs are a rapid initial dose escalation and intra-patient dose escalation. Penel et al. [4] compared the performance of 270 phase I trials published between 1997 and 2008 that either used a 3 + 3 trial design or a variation of the accelerated titration design. Accelerated titration was used in approximately 10% of those trials. They showed that the average sample size needed in these trials to determine the MTD was comparable, but the number of patients treated at dose levels below the RD was found to be significantly smaller in the accelerated titration design. Rogatko et al. [8] compared the literature of phase I trials and found that only 1.6% of dose-finding trials used novel designs, such as the accelerated titration or CRM. Despite enthusiasm for novel dose-finding designs in the statistical community, they are not yet finding widespread acceptance in the clinic.

The main goal in phase I trials for traditional cytotoxic agents is to determine the MTD. The underlying premise is that both efficacy and toxicity increase monotonically with increasing dose levels. Only toxicity, not efficacy, is monitored during a traditional phase I trial. The premise for phase I trials for cytostatic or targeted agents is generally different. Since the agent is designed to specifically interfere with a molecular pathway directly related to specific characteristics of the tumor, it is hypothesized to be less toxic than a traditional cytotoxic agent. Toxicity does not necessarily increase with increasing dose levels but is anticipated to level off after it reaches a maximum toxicity level. Likewise, efficacy does not necessarily increase monotonically with increasing dose levels either but may plateau after it reaches maximal efficacy; higher dose levels past this point may no longer yield higher efficacy. Thus, the goal of a dose-finding trial for targeted agents should be to determine the dose level that provides highest efficacy, or a prespecified minimal efficacy, while assuring the safety of that dose level. A variety of CRMs have been proposed for this purpose (see, e.g. Refs. [9,10]). Hunsberger et al. [11] recently proposed a dose escalation trial for targeted therapies similar to the traditional 3 + 3 phase I trial, but with dose escalation solely based on response, assuming that no significant toxicity will occur. These proposed trial designs address the issue of finding such a dose and have good statistical properties. None of these trial designs appear to have found widespread acceptance in the clinical trials community yet.

The phase I/II trial design that we recently evaluated [1,2] uses a two-step approach. The first step consists of a traditional phase I trial design, such as the 3 + 3 design, accelerated titration, or CRM design, with the goal to get close to a good dose level. We will refer to the dose level this traditional phase I trial determines to be the best dose to go forward with in a phase II setting as the phase I RD level, or RD level. As the second step, we used a modified selection design, randomizing patients to two dose levels (at the RD level and the level below) and using both efficacy and toxicity to determine a good or best dose level. Throughout this article, we refer to the highest dose level with a probability of dose limiting toxicity (DLT) <33% as the MTD.

The conservatism of phase I trial designs was confirmed by our simulation studies (see Table 1 in Ref. [1]), which showed the chosen RD level was below the MTD at least 30% of the time in each scenario that did not have negligible toxicity for all dose levels (toxicity probability of 5% for all dose levels). For these toxicity scenarios with nonnegligible toxicity for at least some of the dose levels, we found the probability of correctly identifying the MTD, that is, the RD level coinciding with the MTD, ranges from 22% to 31%. Similarly, the probability of identifying the dose level immediately below the MTD as the RD ranges between 21% and 30% for those same scenarios. Thus, in many cases, we may miss a potentially good or best dose level when going forward with phase II trials restricting ourselves to dose levels at the RD and below.

Here, we explore the possible benefits of randomizing patients in the phase II portion of this proposed trial to three different dose levels (arms): the phase I RD level (RD), the dose level immediately below (RD−), and the dose level immediately above that level (RD + ). We anticipate that such a trial design is particularly useful for newer targeted agents with a toxicity profile anticipated to be far better than for traditional cytotoxic agents, and for which the potential for missing a good or best dose level with respect to efficacy would far outweigh the risks of exploring the dose level above the RD. Appropriate toxicity stopping rules in the phase II portion of the trial will be implemented as part of such a trial. Any dose level of the phase II trial will be considered unsafe if the toxicity in that arm crosses a predefined toxicity boundary. In addition, we implement continuous toxicity monitoring for the RD+ arm, and accrual to that arm will be terminated immediately if at any time this dose level appears too toxic.

Underlying model assumptions

In general, toxicity and efficacy are closely linked. Each dose level has a specific average toxicity and efficacy associated with it. We thus simulate the toxicity and efficacy data using a correlated bivariate logistic regression model. We use the same model assumptions that were used in our previous article [1] and measure the correlation using an odds ratio relating the two end points [12].

Let the marginal probabilities (for toxicity and efficacy) be logistic and depend on the parameter β. For an observation with covariate vector x, the marginal probabilities are then given by

$$Pr(Y=1)=\frac{exp(x\beta )}{1+exp(x\beta )}$$ (1)

Let p_ij be the joint probability for toxicity i = (0,1) and efficacy j = (0,1). The odds ratio ψ is defined by ψ = p₁₁ p₀₀/p₁₀ p_01. For a description of bivariate odds ratio models, see the book by McCullagh [13]. The joint probability p₁₁ can be expressed in terms of the marginal probabilities p₁ and p₂ as follows [14]

$$p_{11}=\{\begin{array}{c}{(2(\psi -1))}^{-1}\left(a-\sqrt{a^2+b}\right)\\ p_1{p}_2\end{array}\text{for}\begin{array}{c}\psi \ne 0\\ \psi =0\end{array}$$ (2)

where a = 1 + (p₁ + p₂)(ψ − 1) and b = −4ψ(ψ − 1) p₁p₂, and p₁ and p₂ denote the marginal probabilities for toxicity and efficacy, respectively.

We also introduced the concept of a good and best dose level. In this context, the best dose is defined as the dose level that maximizes efficacy while assuring safety, and a good dose is defined as a dose level where efficacy is above a predefined boundary while maintaining safety. Targeted agents are often difficult and expensive to manufacture in larger quantities, and a smaller dose provides economic benefit. Thus, under some circumstances, a good dose may even be preferable to the best dose.

Simulation studies

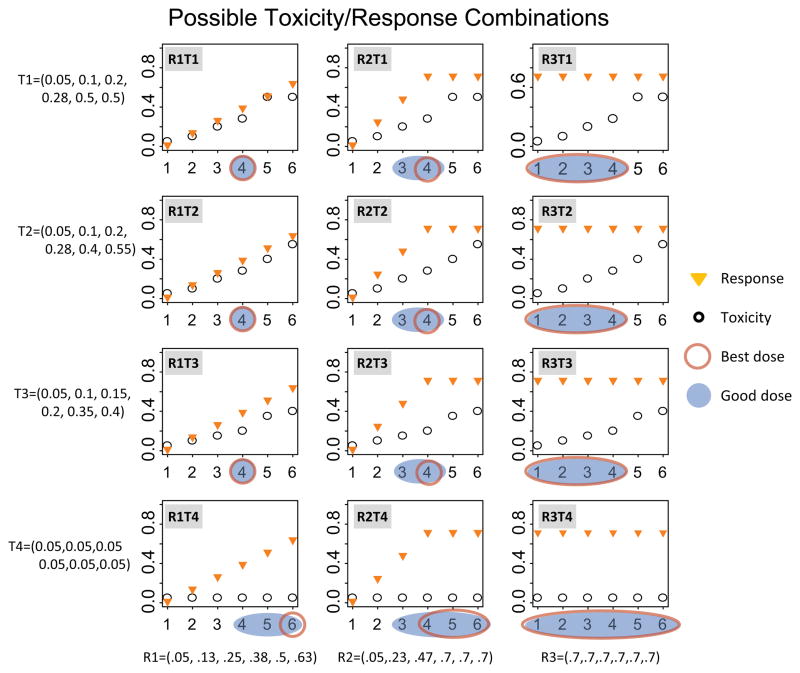
We evaluate the same four toxicity and three efficacy scenarios as before (Figure 1). More specifically, the toxicity scenarios are as follows. Scenario T1 assumes that toxicity increases until a maximum toxicity is achieved after which it levels off. Toxicity scenarios T2 and T3 assume that toxicity increases monotonically with dose level, where the increase is steeper for T2 than T3. Finally, toxicity scenario T4 assumes negligible toxicity.

Figure 1.

Possible response and toxicity scenario combinations as a function of dose level. Plotted are the marginal probabilities of response and toxicity as a function of dose level.

Orange triangles indicate the probability of response and black circles indicate the probability of toxicity. Best and good dose levels are shown for all scenarios. A blue shaded area indicates a good dose level and a red oval indicates a best dose level.

Similarly, we evaluate three efficacy scenarios (Figure 1). We refer to those scenarios loosely as response scenarios. Response could be any binary efficacy outcome that is sensible in a specific disease type. Examples include but are not limited to response by response evaluation criteria in solid tumors (RECIST), overall survival or progression free survival at a specific time point, or disease control rate. Response scenario R1: This scenario assumes a continuous increase in response with increasing dose level within the dose levels considered. In this case, the leveling-off could occur outside the dose ranges considered. Response scenario R2: In scenario 2, we assume an increase in response for the first four dose levels after which it levels off. This also most closely resembles the scenario expected for a cytotoxic agent. Response scenario R3: Scenario 3 describes the scenario where the response is independent of the dose level within the range considered. The marginal distributions together with the actual numerical values of the 12 efficacy and toxicity scenario combinations are illustrated in Figure 1.

We assume six dose levels, and use the same simulation studies for the phase I part as we did in Ref. [1] to determine the probability of recommending a specific dose level for each scenario in the phase I trial using a traditional ‘3 + 3’ trial design. A CRM or an accelerated titration design could also be used for this step. We chose the 3 + 3 design as it is still the most commonly used phase I design in oncology clinical trials. Table 1 in Ref. [1] summarizes the results of our simulation studies for the phase I portion of the trial. We used 1000 simulations. We chose a high correlation or odds ratio between efficacy and toxicity for simulating our efficacy and toxicity data. The log odds ratio we chose for all our simulation studies is 4.6. Our simulations confirmed that the 3 + 3 design is very conservative. The probability of reaching the level above the MTD is in general small. In the scenarios with dose level 4 being the MTD, the probability of correctly identifying the MTD or the dose level below is similar and in general somewhere between 20% and 30%.

In our simulation studies for the phase II portion, we determine the power of the efficacy test, the probability of the dose levels being tested to be too toxic, and the probability of correctly determining the best dose. We use a modified selection design for this step. A traditional selection design [15] selects the best arm based on efficacy alone. We modified the selection design to select the best arm based on efficacy and toxicity.

We randomize 48 patients to three dose levels (arms), the RD determined in phase I (arm 2), the dose level immediately above the RD (RD+, arm 1), and the dose level immediately below the RD (RD−, arm 3). The hypothesis test for response used in this example tests H0: p = 0.05 versus HA: p = 0.30. The toxicity limit in our simulations is defined to be 33%, which means that if 33% or more patients experience a DLT in a certain dose level, this dose level is considered to be unsafe for any of the arms and will not be chosen in our selection design. In addition, we implemented a strict toxicity stopping rule for the RD + (arm 1) level. For that level, we apply continuous toxicity monitoring. We use the traditional 3 + 3 phase I criteria for the first six patients, and stop accrual to this dose level if at any time two patients experience a DLT; after the first six patients, we immediately terminate accrual to this dose level at any time that 33% or more patients experience a DLT.

In our simulation studies, arm 1 is chosen if accrual is not halted based on our toxicity stopping rule, if the efficacy is above the efficacy boundary, and if the observed efficacy is larger than the efficacy in arms 2 and 3. Arm 2 is chosen if the toxicity is below the toxicity boundary, if the efficacy is above the efficacy boundary, if arm 1 was not chosen, and if the observed efficacy is larger than the efficacy in arm 3. Finally, arm 3 is chosen if the toxicity is below the toxicity boundary, if the efficacy is above the efficacy boundary, and if neither arm 1 nor arm 2 is chosen. These three probabilities do not add up to 1 as no arm is chosen if the toxicity is too high or the efficacy is not large enough.

Results

Figure 1 summarizes the 12 toxicity and efficacy scenario combinations, their respective MTD, good dose, and best dose levels. For some scenarios, there is only one best dose and one good dose, whereas for others, several or even all dose levels are considered good or even best by our definition.

We first simulate the phase I part of the trial using a 3 + 3 design and determine for each toxicity and efficacy scenario combination and for each dose level, the probability of a specific dose level being the RD for the phase II part of the trial. This is explained in greater detail in Ref [1].

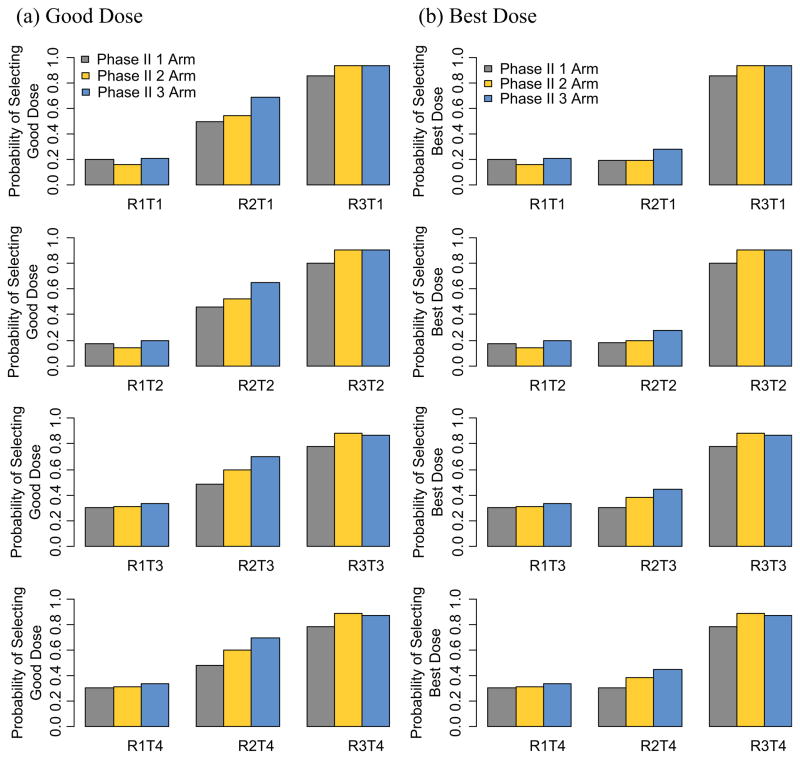
We then simulate a randomized selection design where patients are randomized to three different dose levels, RD, RD+, and RD−, and determine the power in terms of the efficacy hypothesis of each arm (dose level) and the probability of ≥33% of patients having a DLT in each arm. We next combine the two steps of the trial and determine the overall probability of reaching a specific dose level. Finally, we evaluate the overall probability of picking good and best dose levels using this phase I/II design as a sum of the probabilities of the different possible ways to select a good or best dose level (Figure 3).

Figure 3.

Overall probability (phase I and phase II combined) of selecting the best or a good dose level using one, two or three arms in the phase II selection design.

We also compare our results to two other design options, each of them using the same phase I trial but a different phase II trial design: One using a traditional single-arm phase II trial at the RD level and the other one using a modified randomized selection design with two dose levels – RD (arm 1) and RD− (arm 2). In our simulation studies for the 2-arm design, arm 1 is chosen if the toxicity is below the toxicity boundary, the efficacy is above the efficacy boundary, and if the observed efficacy is larger than the efficacy in arm 2. Arm 2 is chosen if the toxicity is below the toxicity boundary, if the efficacy is above the efficacy, and if arm 1 was not chosen. In our simulation studies for the single-arm design, the arm is chosen if the toxicity is below the toxicity boundary and the efficacy is above the efficacy boundary.

We use the same total sample size, 48 patients, for all three trial designs and determine the probability of correctly picking the best dose level and a good dose level using the definitions above. The same toxicity and efficacy selection criteria are used in all three trials. Due to the discreteness of the binomial distribution, the alpha levels that are determined by the efficacy boundary in the three examples are slightly different. The one-sided alpha levels and corresponding critical values are 0.03 and 6 for the single-arm, 0.03 and 4 for each of the arms in the 2-arm selection design, and 0.04 and 3 for each of the three arms in the 3-arm selection design, respectively.

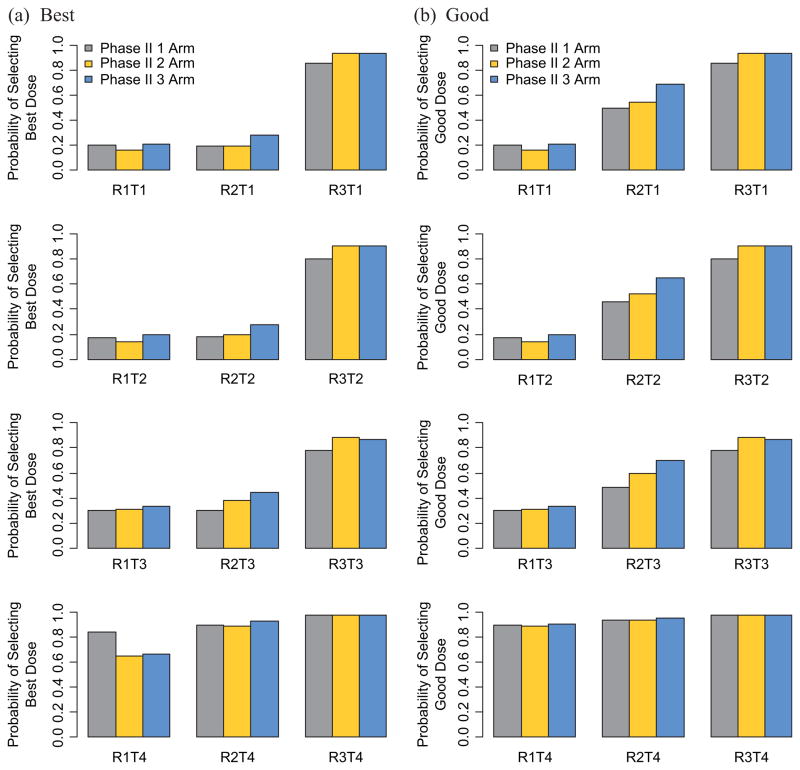
When studying a new agent, toxicity needs to be monitored continuously, even in the phase II setting. Figure 2 shows the probability of halting accrual in the phase II portion of the trial to a specific arm (dose level) due to toxicity for the various scenarios and the three different phase II modified selection designs. In the traditional single-arm phase II trial, patients are only accrued to the RD level (middle column of the graphs). In the 2-arm selection design, patients are randomized between RD− (left column of the graphs) and RD. Finally, in our proposed design, patients are randomized between RD−, RD and RD+ (right column of the graphs). In general, the probability of stopping at the RD− level is low (below 5%), at the RD level, it is between 10% and 20%, and at the RD+ level, it is high (above 50%). This also means that the probability of halting accrual to the RD + level in the 3-arm selection design is large and thus a good safeguard in the phase II portion of the trial against selecting a dose level that may potentially be harmful. Recall that we use continuous toxicity monitoring in the RD+ level. The median number of patients enrolled in the RD+ level, if that level is too toxic, ranges between 3 and 6.

Figure 2.

Probability of stopping due to toxicity for the various scenarios and the three different phase II designs. For the single-arm phase II design, all patients are treated at the RD level; in the 2-arm phase II design, patients are randomized to RD and RD−; in the 3-arm phase II design, patients are randomized to RD, RD+, and RD−: (a) good dose level and (b) best dose level.

RD: phase II RD level; RD+ : dose level immediately above phase II RD level; RD−: dose level immediately below phase II RD level.

Figure 3 shows the overall probability of selecting a good or best dose level using the single-, 2-, or 3-arm selection designs described above. These probabilities include the probability of reaching the various dose levels in the phase I portion of the trial. This means that all the possible pathways of yielding a good or best dose level are included.

Discussion

The 3-arm selection design exploring the dose levels immediately above and below as well as the RD performs as well or better than the 2-arm selection design or the single-arm design for almost all toxicity and efficacy scenario combinations tested. In the case of toxicity scenario T4 (nominal 0.05 toxicity for all dose levels), all trial designs perform approximately the same in terms of selecting a good and best dose level. There is one exception which is when determining the best dose level in the R1T4 scenario, where there is only one best dose level (level 6) and the single-arm does slightly better than the other two designs, as we are not exploring the dose levels above level 6.

This phase I/II design exploring dose levels above and below the RD performs particularly well when determining a good or best dose level for the response scenario R2 combined with any of the toxicity scenarios with toxicity larger than nominal toxicity (T1 through T3). R2 is the most likely scenario for a targeted agent for which the response level increases for the first four dose levels, and then levels off after that (for dose levels 5 and 6). These simulation studies confirm that, especially in the setting of targeted agents, it is advantageous to explore RD+ in addition to RD and RD− before launching into a larger efficacy trial. We implemented a rigorous toxicity stopping rule in our simulation studies that terminates accrual to a specific dose level if a pre-specified toxicity boundary is crossed, which in turn yields a high probability of rejecting RD+ due to toxicity (Figure 2). Even with such a rigorous toxicity stopping rule, the probability of reaching a good or best dose level is still significantly larger compared to trials that only explore RD or even RD and RD−.

In general, one needs to be cautious and thorough when determining a good or best dose level for a new agent, taking into account both toxicity and efficacy. The overall goal is to determine such a dose level while minimizing the number of patients being exposed to dose levels that may potentially be too toxic or to dose levels that may not be efficacious. Traditional phase I trial designs use small sample sizes that inherently yield large variability and error rates when determining the MTD. This also implies that there is a large probability (30% or greater in our simulation studies for toxicity scenarios with nonnegligible toxicity) of recommending a suboptimal dose level, thus potentially exposing all future patients to such a dose level. Here, we demonstrate that we have a higher success rate at identifying a good or best dose level when exploring dose levels immediately above and below the RD in the early phase II setting, in most cases without needing larger sample sizes.