Cure Models as a Useful Statistical Tool for Analyzing Survival

Abstract

Cure models are a popular topic within statistical literature but are not as widely known in the clinical literature. Many patients with cancer can be long-term survivors of their disease, and cure models can be a useful tool to analyze and describe cancer survival data. The goal of this article is to review what a cure model is, explain when cure models can be used, and use cure models to describe multiple myeloma survival trends. Multiple myeloma is generally considered an incurable disease, and this article shows that by using cure models, rather than the standard Cox proportional hazards model, we can evaluate whether there is evidence that therapies at the University of Arkansas for Medical Sciences induce a proportion of patients to be long-term survivors.

Introduction

Progress in the treatment of cancer has led to a spate of statistical research to develop cure models. Many analyses of cancer survival data are based on overall survival or progression-free survival (PFS). No patient can be "cured" of death, so in these situations cure models can be used to model long-term survivors rather than cured patients. Cure models can be used to investigate the heterogeneity between patients with cancer who are long-term survivors and those who are not. A straightforward way to identify whether a particular data set might have a subset of long-term survivors is to look at the survival curve. If the survival curve has a plateau at the end of the study, a cure model may be an appropriate and useful way to analyze the data.

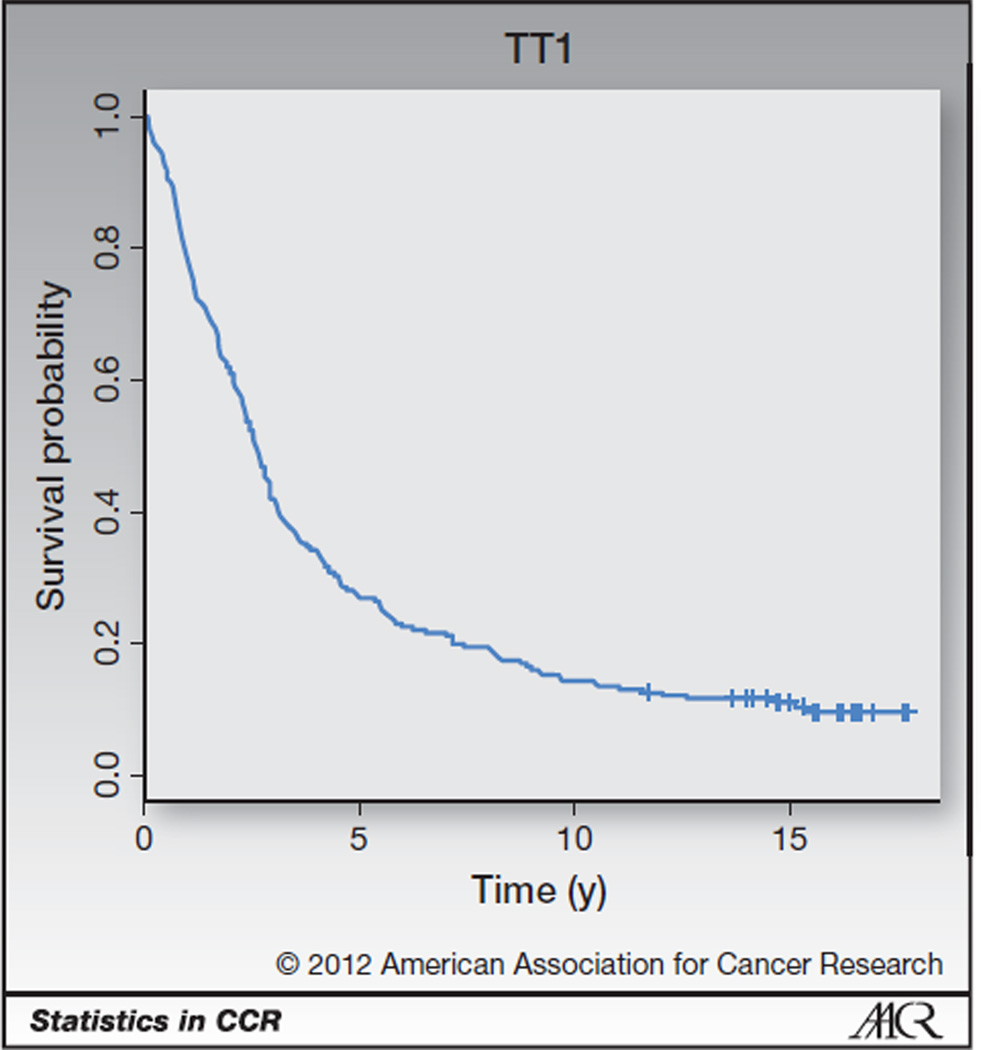
An example of data for which cure models could be useful is provided in Fig. 1, the PFS curve for patients treated on the University of Arkansas for Medical Sciences (UAMS; Little Rock, AR) first Total Therapy study (TT1), which tested a tandem autotransplant approach for patients with multiple myeloma (1, 2). Here, PFS is defined from the time of response to the first of death or progression, with patients last known to be alive without progression censored at the date of last contact. With the current amount of follow-up, there is a flat plateau after 15 years. One way to interpret this curve is that there are 2 groups of patients in this trial. One group of patients are long-term survivors and will not fail during the follow-up of the study, whereas the rest of the patients will fail during the first 15 years of the study.

Figure 1.

PFS curve for TT1 potentially indicates a proportion of long-term survivors. Censoring is marked with a cross.

Cure models can be a useful alternative to the standard Cox proportional hazards models (3) for data with survival trends like those shown in Fig. 1 for several reasons. First, the assumption of proportional hazards can fail when survival curves have plateaus at their tails. Second, survival plots with long plateaus may indicate heterogeneity within a patient population that can be useful to describe explicitly. Cure models allow us to investigate what covariates are associated with either short-term or long-term effects. For example, cure models can allow us to evaluate whether a new therapy is associated with an increase or decrease in the probability of being a long-term survivor or an improvement or detriment in survival for those who are not long-term survivors.

While cure models have been a popular component of statistical literature for the past 20 years or more, they have not been implemented in some areas of the clinical literature. The purpose of this article is to review cure models with the hope that some researchers will find the models a useful alternative to standard survival models when analyzing some types of cancer survival data. To this end, we first describe in a fairly nontechnical manner what cure models are and how they differ from more widely used survival models. Then, we present a cure model analysis of multiple myeloma data from the UAMS. Multiple myeloma is generally considered an incurable disease (4), but researchers at UAMS have developed an approach called Total Therapy that may allow some patients with multiple myeloma to be long-term survivors. The analysis will highlight what additional information can be gained from using a cure model analysis beyond a standard Cox analysis.

Cure Models

There are 2 major classes of cure models, mixture and nonmixture models. Mixture cure models, as the name suggests, explicitly model survival as a mixture of 2 types of patients: those who are cured and those who are not cured. Typically, the probability a patient is cured is modeled with logistic regression. The second component of the model is a survival model for patients who are not cured. There are many options for this, but 2 common models are the Weibull and the Cox models. In words, a mixture cure model can be written as follows:

$$\text{Probability alive at time}t=\text{probability cured}+\text{probability not cured}\times \text{probability alive at time}t\text{if not cured}$$ (A)

Standard survival models, such as the Cox model, do not assume 2 different populations as the mixture cure model does. Many variations of mixture cure models have been proposed in the statistical literature (5–14, to name a few). In our multiple myeloma analyses, we use the logistic Weibull model (15). A nice feature of the logistic Weibull model (and some other mixture models) is that a wide range of researchers understand how to interpret ORs and HRs. The results of the model provide ORs for the probability of being cured and HRs for the survival for patients who are not cured. A benefit of the mixture cure model is that it allows covariates to have different influence on cured patients and on patients who are not cured. For example, a therapy may increase the proportion of patients who are cured (evidenced by a significant OR) but not affect survival for patients who are not cured (evidenced by a nonsignificant HR). A mixture cure model allows us to tease out that relationship.

Nonmixture cure models take a different approach to modeling survival. Many nonmixture cure models can be thought of as Cox proportional hazards models that allow for a cure fraction.

Nonmixture survival models can be written as follows:

$$\text{Probability alive time}t={\text{probability cured}}^{1-S\times (t)},$$ (B)

where 1−S×(t) is an exponent of the probability of being cured and S×(t) is a survival function. Equation B has a very different form than the mixture cure model in equation A. Nonmixture cure models may fit some data better than mixture cure models and vice versa.

For the nonmixture model, covariates can be incorporated both in the model for the probability of being cured and in S×(t). The interpretation of covariates is different with the nonmixture cure model than with the mixture model. Covariates included in S×(t) characterize a "short-term" effect, but the covariates do not describe the survival for those who are not cured because the nonmixture model does not directly model a mixture population. We review the difference in interpretation between mixture and nonmixture models in the data application in the next section. A number of nonmixture cure models have been proposed in the statistical literature (refs. 16–22, among others). We use a Weibull nonmixture model in the data application.

Using Cure Models to Investigate Survival in Multiple Myeloma

We apply several survival models to multiple myeloma survival data from the UAMS to elucidate information on long-term survivors among patients with multiple myeloma. The UAMS conducted 3 Total Therapy trials with the intent of inducing some patients with multiple myeloma to be long-term survivors. The first study, TT1, tested a tandem autotransplant approach (1, 2). The second study showed that the addition of thalidomide, TT2⁺, improved results compared with the same regimen without thalidomide, TT2⁻ (23). TT3, the third study, incorporated both thalidomide and bortezomib in induction (24, 25).

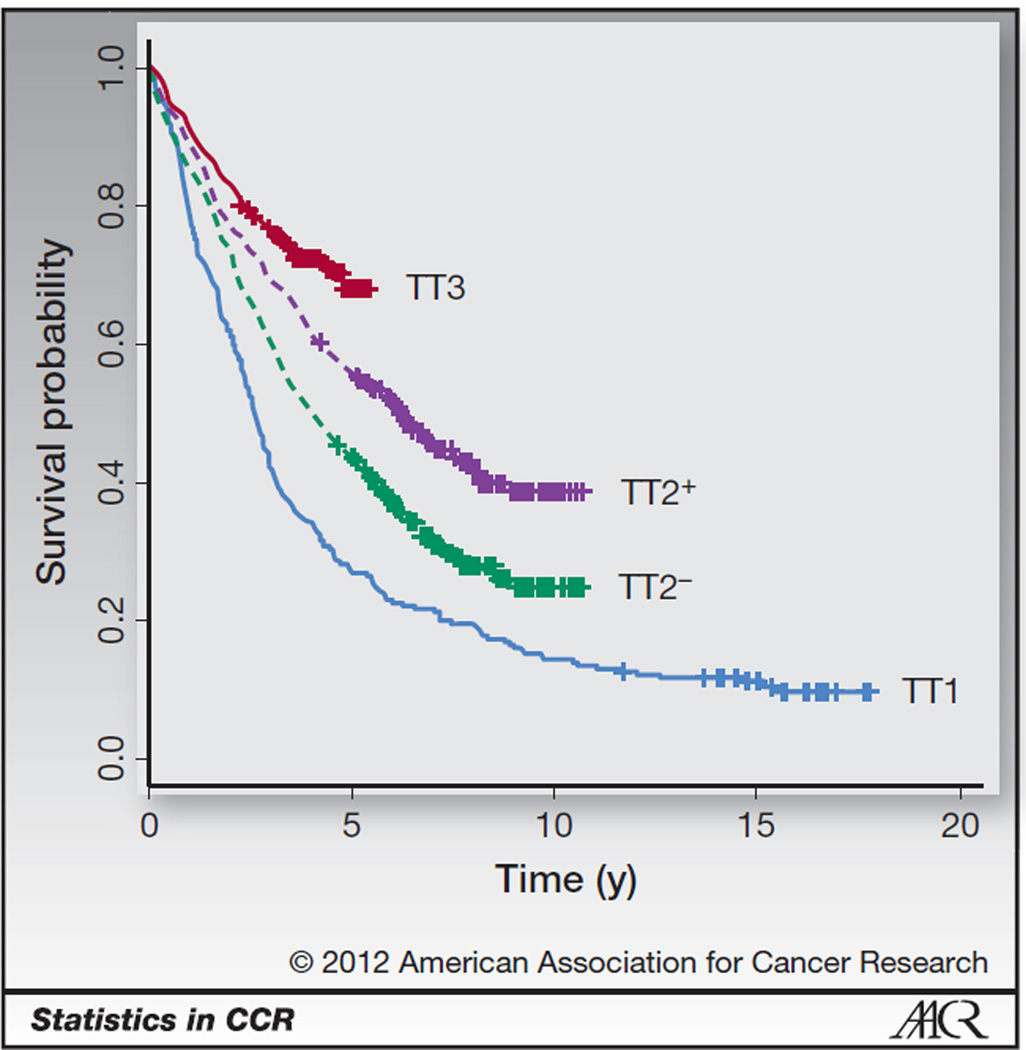
Kaplan–Meier plots of PFS for the Total Therapy regimens (Fig. 2) indicate that there may be some long-term survivors on these regimens. Here PFS is defined from the time of response to the first of death or progression, with patients last known to be alive without progression censored at the date of last contact. In each of the 4 curves in Fig. 2, there appears to be evidence of an emerging plateau, indicating that a proportion of patients from each of the Total Therapy regimens may be long-term survivors. The more recent regimens plateau at a higher level, indicating that the proportion of long-term survivors may have increased over the development of the regimens.

Figure 2.

PFS plots for the Total Therapy regimens. Censoring is marked with a cross.

A standard survival analysis would use the Cox model to test whether PFS has improved over the regimens. Results for a Cox model [HRs, 95% confidence intervals (CI), and P values] adjusting for the potential prognostic factors age and presence of any cytogenetic abnormalities are provided in Table 1. In this model, HRs less than 1 indicate improved PFS. The results from this model suggest that PFS is significantly improved in TT2⁻, TT2⁺, and TT3 compared with TT1, which matches the interpretation of the PFS curves in Fig. 2. In addition, we can see that increasing age and presence of cytogenetic abnormalities are associated with decreased PFS.

Table 1.

Cox model regression results

	HR (95% CI)	P
TT1 (ref.)
TT2−	0.65 (0.53–0.79)	<0.001
TT2+	0.45 (0.36–0.55)	<0.001
TT3	0.29 (0.22–0.37)	<0.001
Age	1.02 (1.01–1.02)	<0.001
Cytogenetic abnormalities	1.72 (1.48–2.01)	<0.001

The Cox model allows us to test whether PFS is the same among the Total Therapy regimens while controlling for other covariates and provides an overall summary of PFS. When survival curves plateau, as shown in Fig. 2, there is an indication that a proportion of patients could be long-term survivors of multiple myeloma. A cure model could estimate the proportion of long-term survivors with each therapy and could test whether the proportions have changed over the regimens. In addition, cure models can characterize the survival of patients who are not long-term survivors.

First, we summarize results from a Weibull mixture cure model, with technical details of the parameterization provided in the Supplementary Material. In this model, ORs greater than 1 indicate an increase in the proportion of long-term survivors and HRs less than 1 indicate an improvement in survival among patients who are not long-term survivors. Results adjusted for age and cytogenetic abnormalities are provided in Table 1. The results from this model suggest that the proportions of long-term survivors have increased over the regimens and that PFS among those who are not long-term survivors is improved in TT2⁺ compared with TT1. PFS among those who are not long-term survivors is not significantly improved in TT3 relative to TT1. This nonsignificant result could be due to the more limited follow-up in TT3 compared with the other regimens or it could be that the large improvement in PFS observed in Fig. 2 is due to TT3 having a larger proportion of patients who are long-term survivors. Among all regimens, older age is associated with a decreased probability of being a long-term survivor but is not significantly associated with short-term PFS. Presence of cytogenetic abnormalities is associated with a decreased probability of being a long-term survivor and worse PFS for those who are not long-term survivors.

We can also use nonmixture cure models to study the trends in the multiple myeloma data. We summarize a Weibull nonmixture cure model, with technical details of the parameterization provided in the Supplementary Material. For the long-term part of the model, HRs less than 1 indicate an increase in the proportion of long-term survivors, whereas for the short-term model HRs more than 1 indicate an improvement in short-term survival. We note that, in contrast to the mixture model, the HRs for short-term survival in this model cannot be interpreted as HRs for patients who are not cured. Results are summarized in Table 3. These results suggest that significantly more patients on TT2⁺ and TT3 are long-term survivors than on TT1 and that there is no significant difference in the long-term survivor proportions between TT2⁻ and TT1. Higher age and presence of cytogenetic abnormalities were both associated with decreased probability of being a long-term survivor. None of the covariates had a significant short-term effect. Overall, the nonmixture model indicates that the TT2⁺ and TT3 patients had improved PFS compared with TT1 patients and that the improvement is due to an increase in the proportion of patients who are long-term survivors.

Table 3.

Weibull nonmixture cure model regression results

	Estimate (95% CI)	P
Long-term survivor model (HR)
TT1 (ref.)
TT2−	0.85 (0.48–1.49)	0.57
TT2+	0.50 (0.18–0.79)	0.003
TT3	0.18 (0.10–0.31)	<0.001
Age	1.13 (0.995–1.03)	0.16
Cytogenetic abnormalities	1.17 (1.07–2.14)	0.019
Short-term survival model (HR)
TT1 (ref.)
TT2−	0.51 (0.88–1.53)	0.66
TT2+	0.72 (0.39–1.32)	0.29
TT3	1.72 (0.90–3.29)	0.10
Age	1.00 (0.98–1.02)	0.80
Cytogenetic abnormalities	1.18 (0.80–1.75)	0.40

An alternative summary of the results from Tables 1 and 3, on the coefficient scale rather than the HR and OR scale, is provided in the Supplementary Material.

We use TT3 to emphasize the difference in interpretation between the Cox model (Table 1) and the cure models (Tables 1 and 3). From the Cox model results (Table 1), we conclude that PFS is significantly improved in TT3 compared with TT1 (HR = 0.29, P < 0.0001). From the mixture cure model results in Table 2, we conclude that a larger proportion of patients are cured in TT3 than TT1 (OR = 20.23, P < 0.001), but there is no evidence that survival among patients who are not cured is different in TT3 compared with TT1 (HR = 0.92, P = 0.78). From the nonmixture cure model (Table 3), we conclude that a larger proportion of patients are cured in TT3 compared with TT1 (HR = 0.18, P < 0.001), but there is no evidence that short-term survival is different in TT3 compared with TT1 (HR = 1.72, P = 0.10). We note that the mixture cure model compares cure proportions on the OR scale whereas the nonmixture cure model uses the HR scale.

Table 2.

Weibull mixture cure model regression results

	Estimate (95% CI)	P
Long-term survivor model (OR)
TT1 (ref.)
TT2−	4.75 (2.22–10.18)	0.036
TT2+	2.36 (1.06–5.26)	<0.001
TT3	20.23 (9.11–44.90)	<0.001
Age	0.97 (0.95–0.97)	0.018
Cytogenetic abnormalities	0.42 (0.25–0.70)	0.001
Short-term survival model (HR)
TT1 (ref.)
TT2−	0.77 (0.59–1.00)	0.052
TT2+	0.66 (0.48–0.93)	0.017
TT3	0.92 (0.52–1.64)	0.78
Age	1.00 (0.999–1.02)	0.25
Cytogenetic abnormalities	1.41 (1.15–1.73)	0.001

Results from mixture and nonmixture cure models can provide estimates of the probability of being a long-term survivor. An unadjusted logistic Weibull mixture cure model (only including covariates for the Total Therapy regimens in long- and short-term models) estimated the proportion of cured patients in TT1, TT2⁻, TT2⁺, and TT3 to be 10%, 16%, 29%, and 60%, respectively. An unadjusted Weibull nonmixture cure model estimated the proportion of cured patients in TT1, TT2⁻, TT2⁺, and TT3 to be 9%, 11%, 27%, and 60%, respectively. The long-term survivor estimates are similar in the 2 models, and both models estimate an increasing trend in long-term survivor proportions.

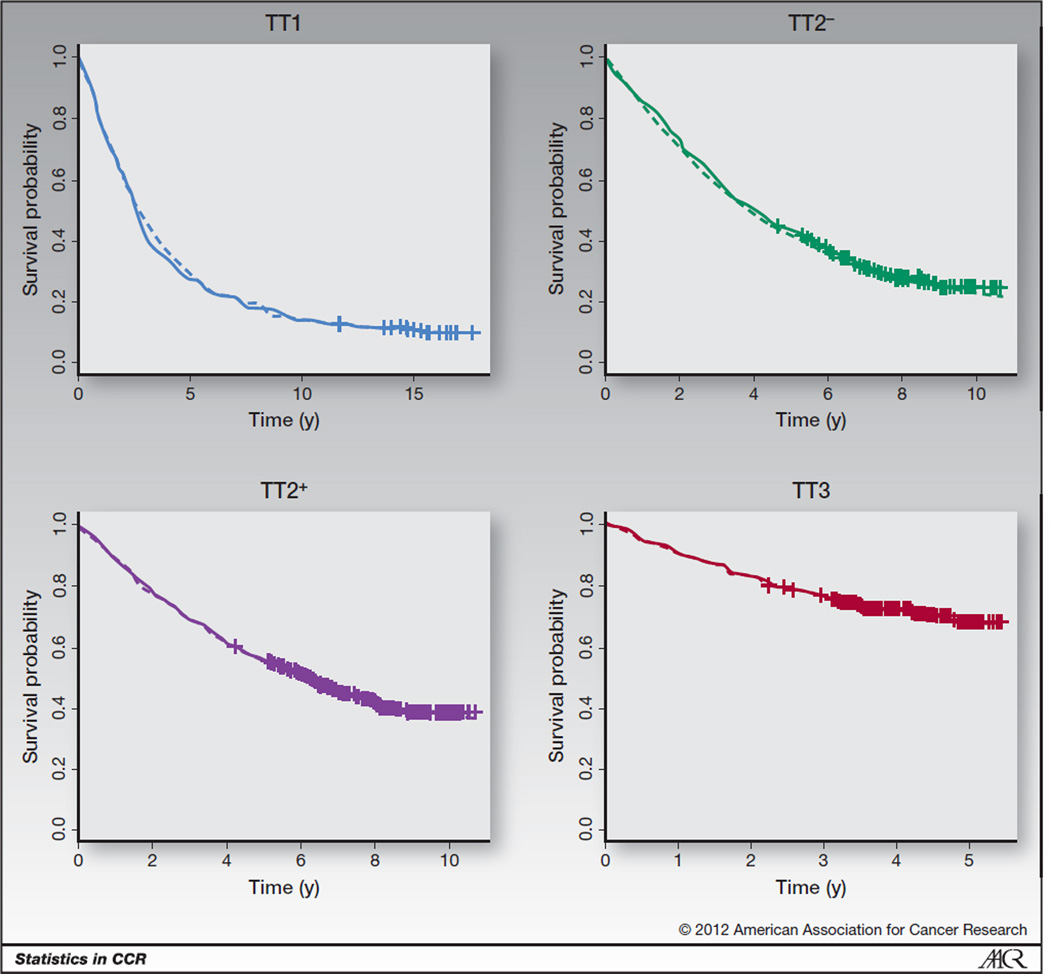
For each regimen, Fig. 3 has Kaplan–Meier survival plots along plots based on the unadjusted Weibull mixture cure model and Weibull nonmixture cure model. The model-based survival curves fit the Kaplan–Meier curves so closely that it is difficult to distinguish among the 3 curves on the plot. Figure 3 indicates that both the mixture and nonmixture cure models fit the multiple myeloma data well and can be a useful tool to describe the trends across regimens.

Figure 3.

PFS plots for the Total Therapy regimens. Kaplan–Meier estimates are solid lines, mixture model curves are dashed lines, and nonmixture models are dash–dot lines. Censoring is marked with a cross.

Regimens TT1–TT3 were tested in sequential studies, and thus the length of follow-up available and amount of censoring differ between the studies, with TT1 having the most follow-up and least censoring and TT3 having the least follow-up and most censoring. As with other survival models, additional follow-up and less censoring will lead to smaller standard errors relative to the sample size. The increased variance associated with the shorter follow-up of TT3 is reflected in the CIs in Tables 1–3. Cure models may not be appropriate for data with too short of follow-up to identify a plateau in the tail. In this application, TT3 has the shortest follow-up, with under 6 years and has a suggestion of a plateau only in the last year of follow-up. We replicated the unadjusted analyses with just the TT3 subset to evaluate the stability of the TT3 results. The estimates of long-term survivors were nearly identical, and the model-based survival curves were almost indistinguishable (data not shown).

Discussion

Cure models are an underused statistical tool. Cure models have been well developed in the statistical literature, but the models are not as common in the clinical literature. For cancers in which some patients may be long-term survivors, cure models can be an interesting way to characterize and study patients’ survival. There are 2 general classes of cure models, mixture and nonmixture models. Both classes can describe short-term and long-term effects. Choosing between the 2 models is a matter of preference and fit. In this application, both classes fit the data well, so either class is useful for testing and inference.

The cure model analyses for the multiple myeloma data provide additional information beyond the standard Cox model analysis. PFS has improved from TT1 to TT3, and cure models indicate that the gains in survival were primarily due to more patients being long-term survivors. The short-term survival trends have not shown drastic improvements.

While the application of this article focused on multiple myeloma, the statistical tools reviewed above could be useful for a wide range of cancers. Therapies for a number of cancer types are believed to induce a cure among a subset of patients. Disease sites where this may be the case include Burkitt lymphoma and Hodgkin disease (26), head and neck cancer (27), colon cancer (28), melanoma (29), and acute promyelocytic and myeloid leukemia (30–32).

Some statistical research has been done on testing whether there is evidence of a cured proportion based on mixture cure models (33, for example), but none of the proposed statistical approaches has software available. More research in this area is warranted.