Attention-dependent reductions in burstiness and action potential height in macaque area V4

Abstract

Attention improves the encoding of visual stimuli. One mechanism that is implicated in facilitating sensory encoding is the firing of action potentials in bursts. We tested the hypothesis that when spatial attention is directed to a stimulus, this causes an increase in burst firing to the attended stimulus. To the contrary, we found an attention-dependent reduction in burstiness among putative pyramidal neurons in macaque area V4. We accounted for this using a conductance-based Hodgkin-Huxley style model in which attentional modulation stems from scaling excitation and inhibition. The model exhibited attention-dependent increases in firing rate and made the surprising and correct prediction that when attention is directed into a neuron’s receptive field, this reduces action potential height. The model thus provided a unified explanation for three distinct forms of attentional modulation, two of them novel, and implicates scaling of the responses of excitatory and inhibitory input populations in mediating attention.

The role of burst firing in sensory processing is unknown. Previous studies have argued that bursts may play a privileged role in sensory encoding, as they have been shown to carry sensory information and propagate more reliably than individual action potentials¹. In thalamus, neurons in burst mode show greater sensitivity to incoming stimuli, while non-bursting responses are more graded and exhibit better linear summation². In primary visual and auditory cortex, bursts of action potentials have been found to exhibit sharper tuning to stimulus features than isolated spikes^3-5 and make a larger contribution to receptive field (RF) properties⁶. Burst firing in cortex may also play a central role in selective communication⁷ and in regulating synaptic integration and plasticity^8-9. Further, studies in the zebra finch song system and the pyramidal neurons of the weakly electric fish have found evidence that burst firing plays a role in detecting highly specific, behaviorally relevant events¹.

If burst firing is important for encoding and transmission of sensory information, then burst rate might be expected to increase when attention is directed to a stimulus. To test this hypothesis, we recorded responses in macaque area V4, an intermediate stage of processing in the ventral visual processing stream, which previous lesion studies and single unit recording studies have implicated in selective attention ^10-11. We compared the burstiness of neural responses when attention was directed into or away from individual neurons’ receptive fields. Contrary to the hypothesis that burst firing should increase with attention, we found that it is significantly reduced.

We describe a conductance-based Hodgkin-Huxley style neuron model that accounts for both the attention-dependent increases in rate previously reported as well as the reductions in burst firing observed in the current study. The model further predicted that the height of action potentials should decrease with attention. We found a significant attention-dependent reduction in action potential height that is comparable to the reductions predicted by the model. Taken together, the present findings show that attention reduces burst firing and spike height, and suggests that attentional modulation depends on a relatively simple mechanism: an attention-dependent increase in excitatory and inhibitory synaptic conductances.

RESULTS

Attention-dependent reduction in burstiness

To investigate the role of burst firing in macaque area V4, we compared the burstiness of neural responses when attention was directed into or away from individual neurons’ receptive fields (RFs), using an attention-demanding tracking task. V4 neurons can be separated into narrow and broad spiking categories, corresponding to putative fast spiking interneurons and pyramidal neurons¹². We use the term “putative” here because the relationship between broad/narrow spiking width and pyramid/interneuron is not one-to-one. A small fraction of neurons (10-15%) are broad spiking interneurons, and several studies have found examples of narrow spiking pyramidal neurons^13-15.

Consistent with in vitro physiology, putative pyramidal neurons exhibit a much larger degree of burst spiking, often firing doublets and triplets of spikes at short interspike intervals¹⁶. Figure 1 shows two example broad spiking (putative pyramidal) neurons that exhibited an attention-dependent reduction in burstiness. Both neurons showed a robust increase in firing rate with attention. The mean firing rate of the first neuron increased from 36.2 to 48.4 Hz (33.6% increase with attention directed into the RF), while the mean firing rate of the second neuron of the increased from 7.1 Hz to 12.1 Hz (69.8% increase).

Figure 1. Attention-dependent reduction in the burstiness.

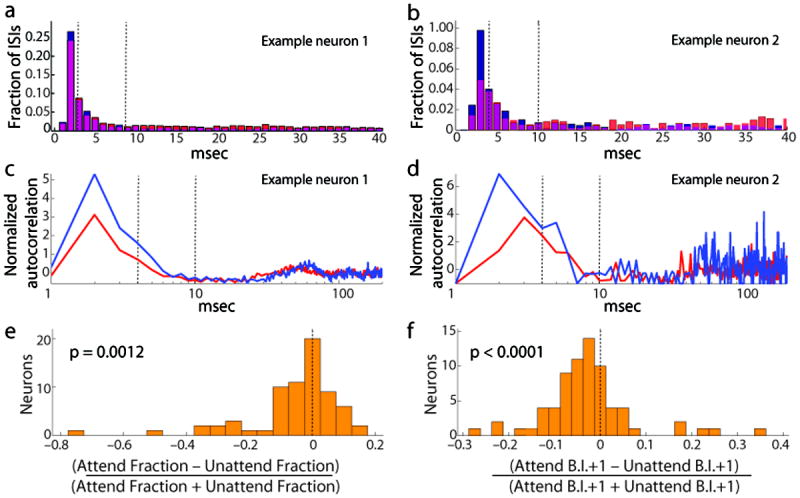
a: Interspike interval (ISI) histogram for an example neuron, with the two attention conditions superimposed (red: attend into receptive field (RF), blue: attend away). Note the higher fraction of short ISIs among the unattended trials (blue). c: Attention-dependent reduction of the normalized autocorrelation function at short time lags (log scale) for the same neuron. Note the reduction in the peak of the autocorrelation function in the attended condition (red) relative to the unattended condition (blue), indicative of a reduction in burst firing. b, d: Same as panels a and c, for a different example neuron. e: Distribution of changes in burst fraction (ISI < 4 msec), normalized by sum, among 69 broad spiking neurons, indicating significant attention-dependent reduction in the fraction of action potentials within bursts with attention. (Two units (not shown) did not have ISIs < 4 msec in either attention condition.) f: Distribution of changes in burst index (B.I.), normalized by sum, also indicating significant attention-dependent reduction in burst fraction with attention (N=71).

To quantify the degree of burst firing across the two attention conditions, we examined the interspike interval (ISI) distributions of each neuron. Examples for these two neurons are shown in panels 1a and 1b. We hypothesized that if burst firing were critical for sensory encoding, we would see an attention-dependent increase in burstiness, which we could measure as an increase in the percentage of short interspike intervals. Contrary to this prediction, we found an attention-dependent reduction in the proportion of short interspike intervals (< 4 msec) for both of our example neurons, reflecting a reduction in the proportion of burst events. Note that despite the increase in firing rate, which would be expected to result in an increase in the fraction of short ISIs, both neurons showed reductions with attention.

We quantified this across the neuronal population, and found a systematic reduction in burst firing among broad spiking neurons when attention was directed into the neuron’s receptive field. These neurons had a significantly higher percentage of short interspike intervals in the unattended condition, indicating a reduction in burstiness with attention (Wilcoxon signed rank test, p = 0.00097, N=71). We did not observe a significant reduction in burstiness among narrow spiking neurons (p = 0.20, N = 47). For each neuron, we also computed a burst attention modulation index (B.A.I.), which was the difference in the percentage of ISIs < 4msec across the two attention conditions, normalized by their sum. Broad spiking neurons showed a significant reduction in this burst index (p= 0.0012, Figure 1e, see also Supplemental Figure 1a). This reduction tended to occur among neurons with lower firing rates (Supplemental Figure 2). In contrast, we did not see a significant reduction among narrow spiking neurons (p= 0.61). The difference between the B.A.I. distributions of the two populations was significant (Mann-Whitney U test, p= 0.025).

Slow fluctuations in firing rate are an important source of the variability in the V4 sustained response¹⁷ that may reflect a more general feature of cortical activity^18-19. These slow fluctuations are reduced by attention¹⁷. To rule out the possibility that the observed reduction in burst firing might be an artifact of this attention-dependent reduction in low frequency fluctuations, we developed a second, autocorrelation-based burst metric. This metric subtracted out the effects of low frequency fluctuations, thereby isolating the contribution of burst firing events at short delays from longer timescale fluctuations (see Methods). As with the ISI-based burst metric, the majority of broad spiking neurons showed reductions in this index (Wilcoxon signed rank test, p<0.0001, Figure 1f. See also Supplemental Figure 1b.) We again found no evidence for changes in burst firing with attention among narrow spiking neurons (shown in green) (p = 0.67). Reductions in burstiness were significant among broad spiking neurons collected in each individual animal, using either metric (p<0.05). Neither animal’s narrow spiking neurons showed significant modulation of burstiness using either metric.

This reduction in burstiness among broad, but not narrow, spiking population may reflect a cell-type difference in attentional modulation of burst firing. However, it is important to note that narrow spiking neurons do not tend to fire bursts of action potentials, limiting our ability to observe a reduction in burstiness. Furthermore, the mean firing rate among narrow spiking neurons was higher than among broad spiking neurons, making it difficult to rule out that differences between classes stem from differences in their mean rate. Across the combined population of narrow and broad spiking neurons, we observed a significant reduction in burstiness with either burstiness metric (p < 0.05).

The Scaled Conductance Model of Attention

Cortical pyramidal neurons become less bursty in response to depolarization²⁰ and during the transition from sleep to quiet wakefulness²¹. This suggests that the attention-dependent reductions in burstiness we observed could potentially result from an attention-dependent increase in neuronal depolarization. To formalize this, we developed a conductance-based Hodgkin-Huxley style model that exhibited burst spiking and evaluated how attention-dependent increases in synaptic activity, resulting in increased mean depolarization, might modulate its burst firing.

The Scaled Conductance Model of Attention (Figure 2a) is based on a single-compartment model of burst firing in CA1 pyramidal neurons²². The model includes several active conductance channels, including Hodgkin-Huxley type voltage-dependent conductances that drive action potentials, as well as several calcium dependent channels that regulate after hyperpolarization and spike adaptation. The model includes muscarinic potassium channels and persistent sodium channels that contribute to burst spiking. Previous work examined in detail the role of these two channels in modulating bursting activity in pyramidal neurons²².

Figure 2. Scaled Conductance Model of Attention.

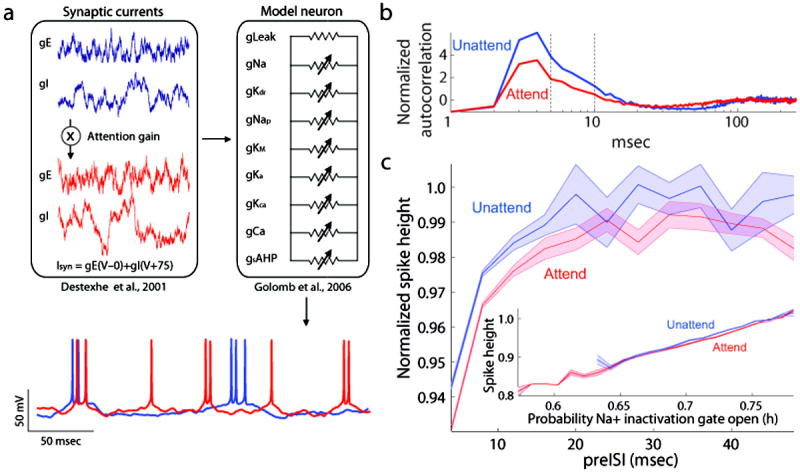
a: Schematic of model neuron (right) and fluctuating synaptic inputs (left). Below, example intracellular traces produced by the model in the attended (red) and unattended (blue) conditions. b: Model reproduced the attention-dependent reduction in burstiness seen in our V4 neurons, as shown by the reduction in the peak of the normalized autocorrelation function in the attended condition (red) relative to the unattended condition (blue). This reduction was comparable to the peak reduction we observed in V4 neurons (compare to Figures 1c and 1d). c: Model prediction of an attention-dependent reduction in extracellular action potential height. Note the predicted spike-independent-reduction in height, reflected in the downward shift of spike height curve when attention was directed into the receptive field. Inset: Attention-dependent reduction in action potential height for matched levels of sodium inactivation. Extracellular action potential height is plotted as a function of the sodium inactivation variable, h, 0.6 msec before the peak of the action potential. h corresponds to the probability that the sodium inactivation particle is not blocking the channel. When h was large, more sodium channels were available to participate in the action potential, leading to spikes of higher amplitude. In addition to this dependence of spike height on sodium channel inactivation (p < 0.0001, R_s = 0.96 attended, R_s = 0.95 unattended), the modeled predicted an attention-dependent reduction in spike height. This can be seen by the vertical shift between the height in the unattended condition (blue) and the attended condition (red).

We incorporated attention-dependent changes in synaptic input to examine how this modulates burst firing. Synaptic inputs were modeled as fluctuating excitatory and inhibitory conductances, representing synaptic inputs summed across populations of Poisson spiking inhibitory and excitatory neurons²³. We assumed that attention proportionally increased both excitatory and inhibitory conductances, consistent with evidence that spatial attention increases activity among both pyramidal and inhibitory neurons¹², and with the normalization model of attention, which posits that attention increases the activity of both excitatory and inhibitory neurons^11,24.

Within the model, attention-dependent increases in excitatory and inhibitory synaptic conductances caused a net depolarization, which resulted in an attention-dependent increase in firing rate. Depolarization also activated the muscarine-sensitive potassium channel, which has been shown to reduce burst firing in pyramidal neurons^20-21,25. The attention-dependent increase in model input conductances gave rise to a reduction in burstiness that was comparable to what we observed experimentally (Figure 2b; compare with Figures 1c-d). At the same time, model neuron’s firing rate increased from 27.4Hz to 39.9Hz, a gain change within the physiological range we observed. The model thus offers a simple, unified explanation for attention-dependent increases in firing rate and reductions in burst rate.

The voltage-dependent muscarine-sensitive potassium channel in our model is directly activated by depolarization. This led to the prediction that even after periods of time in which no spiking occurred, attentional modulation of sub-threshold depolarization should reduce the neuron’s propensity to burst. To test this, we examined whether attention modulated the burstiness of neurons after periods of neuronal silence. Since the firing rates during these periods were identically zero, mechanisms that modulate burst firing by varying spike rate would not be expected to yield a change in the neuron’s propensity to burst. For each neuron, we identified spikes that were preceded by 200 msec of silence, and then calculated the difference in the percentage of post ISIs < 4msec across the two attention conditions, normalized by their sum. Among the broad spiking neurons, we found a significant reduction with attention (Wilcoxon signed rank test, p = 0.0061).

We also compared, on a cell-by-cell basis, the strength of the attention-dependent reduction of this measure across all time periods vs. periods following at least 200 msec of quiescence, by computing the difference of these measures divided by their sum. If spike-dependent mechanisms played an essential role in this reduction, we would expect a decrease in the strength of this modulation following periods without spiking activity. Instead, we found a significant enhancement in this attention-dependent modulation of burstiness during quiescent periods (median −0.029 across all times vs. −0.094 following silence; Wilcoxon signed rank test, p < 0.0001), arguing against a spike-dependent mechanism. This result is consistent with our proposal, in which sub-threshold depolarization is sufficient to yield reduction of burst firing.

In addition to providing a simple explanation for these two forms of attentional modulation, the model made the novel prediction of an attention-dependent reduction in action potential height (Figure 2c). This is illustrated in Figure 2c, which shows the model neuron’s extracellular action potential amplitude as a function of preceding interspike interval (preISI). In both attention conditions the model predicted a reduction in action potential height for spikes immediately following a prior action potential. This activity-dependent reduction in action potential height arose from the inactivation of Na⁺ channels caused by the depolarization during the preceding action potential, consistent with the findings of intracellular studies^26-29. In addition to this spike-history-dependent effect, the model made the novel prediction of an additional decrease in action potential height with attention. In Figure 2c, this additional reduction is reflected in the downward shift of spike height curve when attention was directed into the receptive field. This reduction in spike amplitude resulted, in part, from additional inactivation of sodium channels stemming from increased depolarization with attention. However, we also observed a reduction in height that was independent of sodium channel inactivation (Figure 2c, inset). This reduction reflected increased excitatory and inhibitory conductances, which drove the neuron towards the excitatory and inhibitory reversal potentials, which are both below the maximum depolarization state reached during action potential generation.

Action potential shape depends on spike history

To test these predictions, we measured action potentials of each neuron as a function of preceding interspike interval (preISI) and attention condition. We first considered whether we would observe the activity-dependent reduction in spike height predicted by the model, which to our knowledge, had not been examined in the awake primate. As can be seen for an example V4 neuron in the inset of Figure 3a, action potentials were reduced in amplitude as the interspike interval decreases. Here, we normalized spike height (voltage difference from peak to trough) by the mean height of the action potentials that were preceded by long ISIs (> 100 msec) and were therefore largely unadapted. For each neuron, we then computed a height adaptation index (H.A.I.), defined as the mean normalized height of all action potentials with short preISIs (< 4 msec). For the example neuron in the inset to Figure 3a, the HAI was 0.87, which corresponded to a 13% decrease in the height of action potentials that were preceded within 4 msec by another spike, which was highly significant (Wilcoxon signed rank test, p ≪ 0.0001). The effect of spike history dependent adaptation was also highly significant across the population. The distribution of HAIs was significantly less than one (Wilcoxon signed rank test, p ≪ 0.0001), and 74/112 neurons (66.3%) showed individually significant height adaptation (Wilcoxon signed rank test, p < 0.001; 52/67 (77.6%) broad spiking (2 excluded), 22/43 (51.2%) narrow spiking).

Figure 3. Narrow spiking neurons show less spike-history dependent height adaptation than do broad spiking neurons.

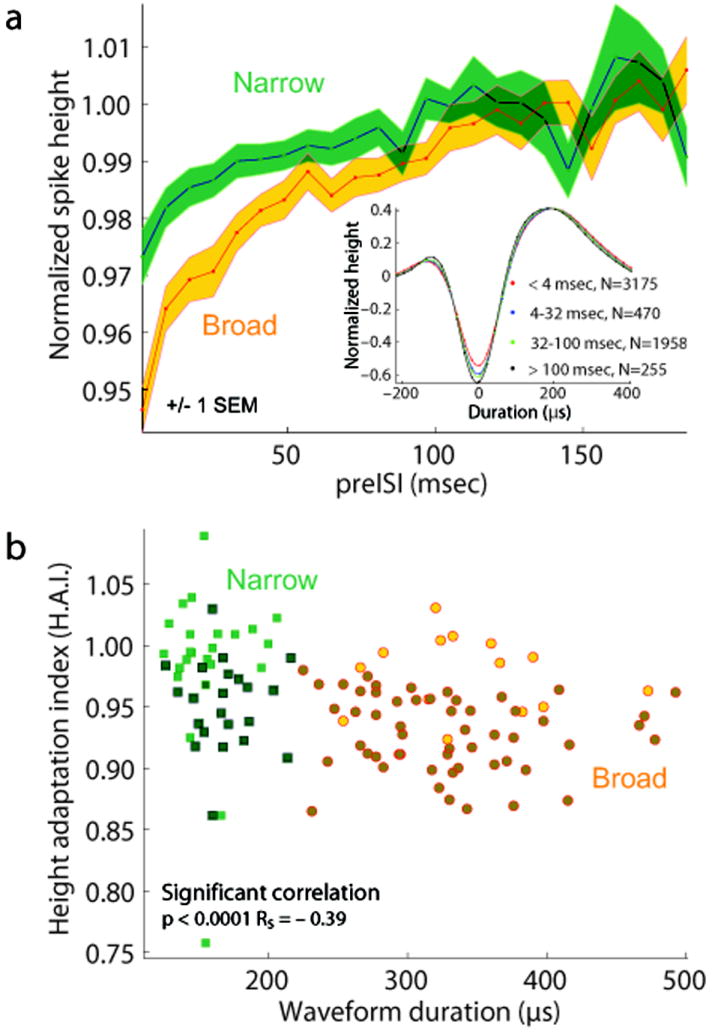
a: Time course of height adaptation among narrow and broad spiking neurons. Green and yellow lines show population average spike heights for narrow and broad-spiking populations, normalized to the unadapted spike height. Shaded regions correspond to +/- 1 SEM around the population means, bin size 8 msec. Inset shows the spike history dependence of action potential shape for an individual neuron. Each trace corresponds to the mean waveform of all action potentials evoked by the example neuron during the sustained period of the stimulus-evoked response, following the interspike interval (preISI) indicated in the figure legend. Spike amplitudes were all normalized to the amplitude of largely unadapted spikes preceded by ISIs > 100 msec. Spike amplitudes grew increasingly reduced at shorter preISIs. Thin shaded regions correspond to +/- 1 SEM of the interpolated waveform traces. b: Significant correlation between mean waveform duration and spike height adaptation index (HAI) (Spearman’s rank correlation, p < 0.0001, Rs = –0.39). For each neuron, the height adaptation index was computed by taking the mean normalized height of all action potentials with short preISIs (< 4 msec). Narrow spiking neurons’ action potentials (green squares, N = 43) were less adapted than broad spiking neurons (orange circles, N = 69). Darker symbols correspond to neurons with significant height adaptation (p < 0.001). The difference between height adaptation among narrow and broad spiking neurons was significant (Mann U Whitney test, p < 0.0001).

Two classes of neurons can be distinguished in area V4, based on the duration of their action potentials: narrow spiking neurons (putative fast-spiking inhibitory interneurons (FS)) and broad spiking neurons (putative pyramidal neurons)¹². Intracellular studies have found minimal height adaptation among FS cells^28,30,31. If narrow spiking neurons largely correspond to FS neurons, they should therefore exhibit less spike height adaptation than do broad spiking neurons. Consistent with this hypothesis, V4 broad spiking neurons had significantly stronger spike-history-dependent height reduction than did narrow spiking neurons (Mann-Whitney U test, p < 0.0001, median broad HAI 0.9336, median narrow HAI 0.9726). The broad spiking neurons also showed stronger reductions in action potential height than did narrow spiking neurons, as a function of inter-spike interval (Figure 3a). In intracellular studies, this reduced adaptation among FS neurons has been shown to arise largely from the short duration of their action potentials, which results in fewer inactivated sodium channels³². Consistent with this finding, we also observed a significant correlation between HAI and mean action potential duration, with broader neurons showing stronger reductions in spike height (Figure 3b; Spearman’s rank correlation, p < 0.0001 R_s = −0.39).

Attention-dependent reductions in action potential height

As predicted by our model, we found a small but significant reduction in action potential height with attention. This can be seen for an example broad spiking neuron in Figure 4a. Consistent with the model prediction, action potentials elicited in the unattended condition (blue line) are consistently larger in amplitude than those elicited in the attended condition (red line), across matched preISI bins. To examine the distribution of this attention effect across the population, we computed an Attention Height Index (A.H.I.), which quantified the change in spike height when attention was directed into the receptive field. The A.H.I. index was computed as: (normalized attended height −normalized unattended height) / (normalized attended height + normalized unattended height). Across the population, the distribution was significantly less than zero, corresponding to a reduction in action potential height with attention (Wilcoxon signed rank test; entire population, median A.H.I. = −0.0034, p = 0.00063; broad −0.0033, p = 0.019; narrow −0.0035, p = 0.0041).

Figure 4. Attention-dependent reduction in action potential height.

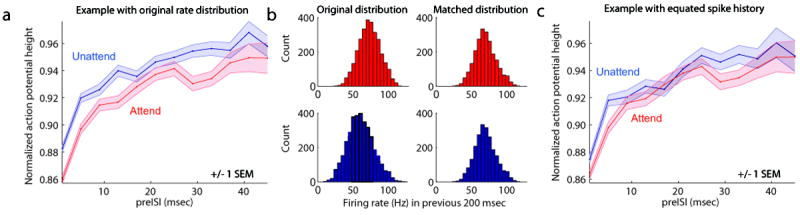
a: Consistent with the SCA model prediction, action potentials elicited in the unattended condition (blue line) were consistently larger in amplitude than those elicited in the attended condition (red line), across matched preISI bins. Shaded regions correspond to +/- 1 SEM, bin size 4 msec. b: Method for equating recent spike history across attention conditions, for example neuron shown in a. Left panels show distribution of firing rates (spikes per second) during the 200 msec period preceding each spike in the attend receptive field (red) and attend away (blue) conditions. The distribution was shifted to the right with attention (red), because firing rates were higher with attention. To equate spike history across attention conditions, we conducted the following procedure. Within each bin, we randomly discarded spikes from whichever attention condition had more spikes. This allowed us to compare action potentials that were matched in preceding spike history. Right panels show distributions of spike counts, equated across attention conditions, after applying this spike-history matching procedure, to control for differences in spike-history-dependent adaptation. c: Action potentials continued to show attention-dependent reductions in amplitude, after the application of the spike-history matching procedure illustrated in b.

The proposed model predicted that spike height would be reduced by two distinct attention-dependent mechanisms, and we observed evidence for both. First, attention was assumed to increase synaptic conductances. These conductances, as well as voltage-gated conductances they activate such as the M-current, were predicted to reduce action potential height. This is because their reversal potentials are hyperpolarized, relative to the peak depolarization reached during the action potential. As a result, an increase in synaptic conductances would cause an increase in hyperpolarizing currents, which in turn would reduce action potential amplitude³³. In addition, the model predicted that an increase in firing rate would add to this reduction in spike amplitude. This is because each action potential would inactivate sodium channels, which de-inactivate over time. During this recovery period, fewer channels would be available to contribute to the next action potential, reducing its amplitude. This phenomenon is known as spike height adaptation. Increasing firing rate would reduce the average interspike interval, causing more spikes to fall within this adaptation window. Since attention increases firing rate, the model predicted that in addition to any reduction in action potential amplitude caused by increases in synaptic conductance, attention would also reduce action potential height indirectly, via an increase in spike height adaptation.

To test the model, it was therefore essential to isolate these two hypothesized sources of attention-dependent spike amplitude reduction. To control for spike-history-dependent adaptation, we used several methods designed to equate action potential history across attention conditions. Spike-history-dependent adaptation occurs over relatively short time periods (see Figures 2c, 3a). Therefore, we conducted control analyses designed to equate the number of spikes within this adaptation window, across attention conditions. 200 msec was chosen as a conservative estimate of the spike adaptation window, chosen to exceed the period over which action potentials were observed to recover from the adaptation caused by the prior spike (see Figure 3a). First, we counted the number of spikes that preceded each action potential within a 200 msec adaptation window. The distribution of firing rates falling within the adaptation window during each attention condition is shown for an example neuron in the left panels of Figure 4b. The distribution is shifted to the right with attention (red), because firing rates were higher with attention. We then equated spike history across attention conditions, as follows. Within each bin, we randomly discarded spikes from whichever attention condition had more spikes. The resulting matched history distribution can be seen for the example neuron in the right panels of Figure 4b. After equating recent spike history in this manner, we continued to find a significant attention-dependent reduction in A.H.I., both for the example neuron (Figure 4c), and across the population (Wilcoxon signed rank test, p = 0.0044). Reductions in A.H.I. were significant in each animal (p < 0.05). Within the 200 msec adaptation window, additional spikes occurring within shorter intervals would be expected to contribute more to spike height reduction than spikes occurring at longer intervals. We thus repeated the analysis to equate spike count over shorter periods of adaptation 10, 25, 50, 100 msec. We found that the reduction in spike height was statistically significant (p<0.05) across all windows.

The above analysis equated spike count across the pre-spike period over which we observed measurable spike-history-dependent adaptation. However, it is possible that differences in mean firing rate could have contributed to spike height adaptation over longer time periods. We controlled for this by recomputing the A.H.I. over trials that were matched in firing rate across attention conditions. First, we counted the number of action potentials that occurred when the attended or unattended stimulus paused with the receptive field. We then selected trials with matched numbers of spike counts in both attention conditions. Since we frequently had more trials with a given spike count in one attention condition than the other, we randomly discarded trials from the more numerous condition until the number of trials at each spike count was identical across attention conditions. We repeated this for all observed spike counts, thereby identically matching spike count distributions across attention conditions. We then computed the A.H.I. from the resulting rate-matched trials. For each neuron, we repeated this random selection process 100 times, and averaged the resulting trial-matched A.H.I. After matching rates in this manner, we found that action potential heights were still significantly reduced in magnitude (one tailed Wilcoxon signed rank test, p=0.023, median A.H.I. −0.0016). As a final test, we combined the two controls. First, we performed the rate-matching procedure to exactly match firing rates across the two attention conditions. After selecting this rate-matched subset of trials, we then equated recent spike history by selecting from these trials subsets of action potentials that were exactly matched in the number of preceding spikes in a 200 msec spike adaptation window. After performing this combined firing rate and spike history control, action potential height was significantly reduced by attention (one-tailed Wilcoxon signed rank test, p = 0.023, median A.H.I. −0.0021). We repeated this analysis across the full range of spike adaptation windows. For all windows, spike height was significantly reduced by attention (p <0.05, one-tailed Wilcoxon signed rank test, for 10, 25, 50, 100, and 200 msec bins). We thus conclude that, after accounting for differences in spike-history-dependent adaptation, attention reduces action potential height, as predicted by the model.

DISCUSSION

The present study advances our understanding of the neural mechanisms underlying attention in several ways. It provides the first evidence for an attention-dependent modulation of burstiness. The observed reduction in burstiness with attention contradicts the widely held view that bursts are a privileged communication channel. If bursts did convey information with greater fidelity than isolated spikes, we would expect bursts to increase when stimuli are task relevant, and attention is directed toward them. The reduction in burst firing is instead consistent with the view that bursts are a source of response variability that is reduced so as to improve neuronal signaling of attended stimuli. Burst firing has also been implicated in other aspects of cortical computation, including plasticity^8-9, synaptic integration^1,9, and communication to select subpopulations⁷. Thus the attention-dependent changes in burst firing observed in the current study are likely to have important consequences for these aspects of cortical computation.

One previous study examined attentional modulation of burst firing and did not find evidence for a change³⁴. This study measured the raw rate of spikes with short ISIs. This would be expected to increase with attention-dependent increases in firing rate potentially masking a reduction in burst firing. Indeed, when we applied this metric, we failed to detect a reduction. They also examined the relationship between raw burst rate and firing rate across neurons. This comparison is less sensitive than the within-cell comparison used here. We failed to detect the observed reduction in burst firing when we apply this second metric. Thus, while the conclusions of the two studies differ, the difference likely stems from differences in the sensitivity of the analyses adopted.

To account for this attention-dependent reduction in burstiness, we developed the Scaled Conductance Model of Attention (SCA). This model was inspired by a previous model where burst firing depends, in part, on the interaction between voltage-gated muscarinic potassium conductances and fast persistent sodium channels²². Our model posited that attention-dependent increases in depolarization activate these muscarinic channels, reducing burst firing. This proposal is consistent with the finding that cortical pyramidal neurons become less bursty when they are depolarized^20,21. Burstiness has also been found to be reduced with elevated levels of arousal²¹. The present findings thus support the hypothesis that mechanisms of selective attention are shared, in part, with those mediating changes in arousal³⁵. We hypothesize that attention and arousal share in common an increase in depolarization that, in the case of selective attention, is mediated by spatially selective feedback signals, such as those generated by the oculomotor system³⁶.

Alternative models of burst firing, such as ‘ping-pong’ models that incorporate back propagation of action potentials between somatic and dendritic compartments^37-39, could also potentially account for our findings. However, we observed significant attention-dependent reductions in burstiness that were undiminished following periods of silence. Thus, differences in spiking activity are not necessary to generate the observed reduction in burstiness. This argues against the necessity of the spike-dependent burst mechanism featured in these models to account for attention-dependent reductions in burstiness. Rather, we propose that attention-dependent reductions in burst firing result from periods of heightened subthreshold depolarization. Though technically difficult, this prediction could be tested directly using intracellular recording methods in monkeys during the performance of attention-demanding tasks⁴⁰.

Within the SCA model, attention increases excitation and inhibition in tandem. This is not strictly necessary: attention-dependent reduction in spike height and the reduction in burst firing can be observed in a model in which only excitatory conductances are increased. However, conjoint increases in inhibitory conductances (whose reversal potentials are more hyperpolarized than are excitatory conductances) did contribute strongly in the model to spike height reduction and helped keep the attention-dependent increase in spike rate within the experimentally observed range. The assumption that increases in excitation are accompanied by increases in inhibition is also consistent with experiments showing that changes in excitation are often found to be accompanied by corresponding changes in inhibition, as might be expected from the fact that excitatory neurons drive inhibitory neurons⁴¹. It is further supported by the finding that attention causes increases in the firing rates of both broad spiking (putative excitatory) and narrow spiking (putative inhibitory) neurons¹².

The second significant innovation in the present study was the use of the extracellular action potential shape, coupled with conductance-based models to provide a ‘window’ into the state variables that modulate spike amplitude^26-31,42. While a few studies have examined changes in extracellular action potential height in the rodent^42-45 this is, to our knowledge, the first study in the non-human primate to use changes in spike-shape to make inferences about neural mechanisms underlying changes in cognitive state. Specifically, our model made the novel prediction of an attention-dependent reduction in action potential height. Consistent with this, we found a small yet measurable attention-dependent reduction in action potential height among both broad and narrow spiking V4 neurons. Not only does this finding link a very low level phenomenon– action potential shape—to a high level phenomenon–attention–it is a specific and surprising prediction of the proposed model, which is the first channel-level model of attention to be tested empirically. This study therefore takes a significant step toward the longstanding goal of achieving a mechanistic, reductionist understanding of attention.

METHODS

Statistical Analysis

Non-parametric tests were used to avoid assumptions inherent in parametric tests. P-values are reported for each test, except where multiple tests were performed and the results in each were significant at the p<0.05 level. P-values greater than 0.0001 have been rounded to two significant digits.

Electrophysiology and receptive field characterization

All procedures were approved by the Salk Institute Institutional Animal Care and Use Committee (IACUC) and conformed to NIH guidelines for the humane care and use of animals in research. Monkeys were prepared for neuronal recording following procedures as described previously¹². Recordings were made from tungsten electrodes (FHC, Bowdoin, ME 04287) that were advanced until action potentials of single neurons could be isolated based on action potential waveform shape. Neuronal signals were recorded extracellularly, filtered (Butterworth filter, 6-pole, 3db cutoffs at 154 Hz and 8.8 kHz), and stored using the Multichannel Acquisition Processor system (Plexon, Inc., Houston, TX). Spike waveforms crossing a negative threshold, which was set to exclude noise, were stored for later off-line analysis. Units were identified as isolated in offline analysis (Offline Sorter, Plexon, Inc., Houston, TX) if the first three principle components of their waveform shape formed a clearly separable cluster from noise and other units. After isolating one or more neurons, receptive fields were mapped using a subspace reverse correlation procedure^46,12. In this procedure, Gabor stimuli (eight orientations, six colors, 80% luminance contrast, 1.2 cycles per degree, Gabor Gaussian half-width 2°) were flashed to determine a single stimulus location that would elicit a robust visual response. When multiple neurons were recorded simultaneously, the features and location of the stimulus were selected to excite the best-isolated units.

Stimulus presentation and eye movement monitoring

Stimuli were presented on a computer monitor (Sony Trinitron Multiscan, TC, 640 × 480 pixel resolution, 120 Hz) placed 57 cm from the eye. Experimental control was handled by NIMH Cortex software (http://www.cortex.salk.edu).

Eye position was continuously monitored with an infrared eye tracking system (240 Hz, ETL-400; ISCAN, Inc.).

Task and stimuli

Two monkeys performed a multiple-object tracking task that has been used to study attention in humans^47-48 and non-human primates^12,16-17. The animals began each trial by fixating a central point and maintained fixation until the end of the trial. After 200 msec, four identical Gabor stimuli appeared (40% luminance contrast). The color and orientation of these stimuli were chosen based on the subspace reverse correlation map to produce a strong response. The positions of the stimuli were selected to fall at regular intervals along an invisible ring of equal eccentricity, selected such that all of the stimuli fell outside of the neurons’ receptive fields. One or two stimuli were then cued as targets by a brief elevation in luminance. All four stimuli then moved along independent, randomly generated trajectories that positioned the stimuli at four new, equally eccentric positions. This placed one of the stimuli at the center of the neuron’s receptive field and the others outside the receptive field. The trajectories were designed to match stimulation history across the two attention conditions, by using the identical trajectories in the attended and unattended trials, and by preventing all but one stimulus from entering the receptive field. The stimuli then paused for 1000 msec before moving to a final set of equally eccentric positions and stopping. At this point, the fixation point disappeared, signaling the animal to make a saccade to each cued target. To minimize the development of spatial biases, the starting and ending positions for the target and non-target stimuli were symmetrically balanced. Correct identification of the targets resulted in a liquid reward.

Measurement of action potential shape

Action potential waveforms were obtained from the Plexon Multichannel Acquisition Processor system, which digitized the waveforms to 25 microseconds (μs). To calculate the height of an action potential, we subtracted the trough from the peak of the waveform. To calculate waveform duration, we spline-interpolated the waveforms from 25 μs to a resolution of 0.05 μs and then calculated the time from the trough to the peak¹². We then normalized these measures by the mean height or duration of action potentials in the stimulus-free fixation period to reduce the effects of long timescale drift in action potential shape (see Supplemental Figure 3). Two broad spiking neurons did not have any action potentials with a preISI < 4 msec, and were excluded from height adaptation index (HAI) analyses.

Broad and narrow spiking classification

As described previously¹², we divided neurons into narrow and broad spiking subpopulations based on waveform duration. We defined waveform duration to be the time from the trough to the peak of the average waveform¹². We selected this metric on the basis of studies showing that this measure best distinguishes putative pyramidal neurons from putative fast-spiking interneurons in the neocortex⁴⁹. The distribution of spike waveform duration was significantly bimodal across all isolated cells with biphasic spike waveforms (N = 202, Hartigan’s dip test, p < 0.0001), and also across the subset of these cells with significant visual responses (N = 118, Hartigan’s dip test, p < 0.01). Narrow and broad spiking neurons were separated based on the trough between the two modes of the waveform duration distribution, with narrow spiking neurons defined as those ranging in duration from 120 to 224 μs and broad-spiking neurons defined as those ranging in duration from 225 to 500 μs.

Inclusion criteria

We recorded from 206 well-isolated neurons from two male adult macaques (N = 53 Monkey B, N = 153 Monkey M). We restricted our discharge pattern analyses to units whose response on trials when attention was directed away from the RF exceeded 5 Hz, averaged over the final 500 msec of the stimulus pause period, and was significantly greater than the mean spontaneous firing rate averaged over the 250 msec preceding the onset of the Gabor stimuli (Mann-Whitney U test, p < 0.05). This resulted in 84 neurons being excluded. In addition, four units were excluded because their waveforms did not have the typical biphasic shape, with a trough followed by a clearly defined peak, and they could not therefore be classified as narrow or broad spiking. This resulted in 118 neurons that met these selection criteria. For the waveform adaptation analyses we excluded six additional neurons, resulting in 112 neurons. Two of these were excluded because only mean waveform data was available, and the other four were excluded as the peak of many of their waveforms could not be determined. Unless otherwise specified, analysis of spiking statistics was restricted to the final 800 msec of the pause period (the “sustained period”), which excluded periods of transient response as stimuli entered or exited the receptive field, and thus the mean firing rate was relatively stationary.

Burst analysis

We computed two burst measures: an ISI-based metric that calculated the percentage of interspike intervals less than 4 msec, and an autocorrelation function based metric. For the second measure, we calculated the autocorrelation function of the neuron separately for each attention condition for the correct 2 of 4 tracking trials. We then subtracted the shuffle predictor for that condition. The shuffle predictor is defined as the mean cross-correlation across all pairs of trials of an individual neuron. By subtracting the predictor, we remove any trial-locked fluctuations in spiking that result from repeated presentation of the stimulus. After this subtraction, we normalized the result by the shuffle predictor at each time lag. This defines the normalized autocorrelation function, depicted for example neurons in Figures 1c and 1d. To further isolate changes in burst firing from changes in low-frequency fluctuations in firing rate, we defined a filter that served to eliminate contributions to the autocorrelation from rate fluctuations below 10 Hz, the range where we have previously reported shared fluctuations in firing rate over the neuronal population¹⁷. It was created by taking the inverse fast Fourier transform of the following equation:

$$\mathit{if\; freq}<\mathit{22.5},\mathit{then}{\left(1+e^{\frac{-(\mathit{freq}-11.5)}{0.75}}\right)}^{-1},\mathit{otherwise}{\left(1+e^{\frac{(\mathit{freq}-33.5)}{0.75}}\right)}^{-1}.$$

The burstiness index (B.I.) was computed as the sum of the product of the described filter with normalized autocorrelation defined above. As an additional control analysis to further isolate attention-dependent reductions in burst firing from slow fluctuations, we also applied a spike jitter analysis (Supplemental Figure 4)¹⁹.

Single compartment model

We implemented the Golomb single-compartment model described in previous work²². A schematic of the model can be seen in Figure 4a. The model was implemented using MATLAB (Mathworks, Natick, MA) software with a temporal resolution of 0.02 ms, and is constructed of coupled differential equations according to a Hodgkin-Huxley-type scheme. The model includes many of the currents known to exist in the soma and proximal dendrites of pyramidal neurons, including the transient Na⁺ current (I_Na) the delayed rectifier K⁺ current (I_Kdr) that generate spikes. In the original paper, the authors use a fast-slow analysis to demonstrate that bursting in the model arises from the interplay of the slow timescale of the muscarinic-sensitive K⁺ current (I_M) and the fast timescale of the transient and persistent Na⁺ currents (I_Na and I_Nap)²². Just as varying the conductances of these currents varies the intrinsic burstiness of the model neuron, differences in expression of the persistent Na⁺ channel may underlie some of the variability in burstiness seen across pyramidal neurons in different cortical layers⁵⁰.

While these four currents are sufficient to give rise to most of the model behavior, we included the other currents found in the full non-zero [CA²⁺] Golomb model²². This includes an A-type K⁺ current (I_A), the high-threshold Ca²⁺ current (I_Ca), and two Ca²⁺ activated K⁺ currents: the fast Ca²⁺-activated K⁺ current (I_Kca) which contribute to rapid spike repolarization and the slow Ca²⁺-activated K⁺ current (I_sAHP), which mediates a slow after-hyperpolarization and spike frequency adaptation. In total, the current balance equation is:

$$C\frac{\mathit{dV}}{\mathit{dt}}=-g_L(V-V_L)-I_{\mathit{Na}}-I_{\mathit{Nap}}-I_{\mathit{Kdr}}-I_M-I_A-I_{\mathit{Ca}}-I_{\mathit{Kca}}-I_{\mathit{sAHP}}+I_{\mathit{syn}}$$

where C = 1μF/cm², g_L = 0.05 mS/cm², V_L = −70 mV, and I_syn is the synaptic current (see following section). The ionic currents are: I_Na(V, h) = g_Nam_∞³(V)h(V – V_Na), I_Nap(V) = g_Napp_∞(V)(V – V_Na), I_Kdr(V, n) = g_Kdrn⁴(V – V_K), I_A(V, b) = g_Aa_∞³(V)b(V – V_K), I_M(V, z) = g_Mz(V – V_K), g_Car²(V – V_Ca), I_Kca(V, c) = g_Cd_∞([Ca²⁺]_i)c(V – V_K), I_sAHP(V, q) = g_sAHPq(V – V_K). The reversal potentials are V_Na = 55 mV, V_K = −90 mV, V_Ca = 120 mV. All conductances are equal to or within the range of parameters used in the original paper²²: g_Na = 35 mS/cm², g_NaP= 0.3 mS/cm², g_Kdr = 6 mS/cm², g_A = 1.4 mS/cm², g_M = 1 mS/cm², g_Ca=0.02 mS/cm², g_Kca = 10 mS/cm², g_sAHP = 5 mS/cm². The dynamics of calcium concentration inside the compartment are:

$$\frac{d[{\mathit{Ca}}^{2+}]}{\mathit{dt}}=-\upsilon I_{\mathit{Ca}}-\frac{\left[{\mathit{Ca}}^{2+}\right]}{{\tau }_{\mathit{Ca}}}$$

where υ = 0.13 cm²/(ms×μA), τ_Ca = 13 msec. The kinetics equations are identical to those used in the original paper¹⁵. Extracellular action potentials were modeled as the first derivative of the intracellular voltage.

Synaptic input to model

To simulate conditions in vivo, we modified the Golomb model by replacing the applied current with a synaptic current, I_syn (Figure 2a). This synaptic current was generated by a point-conductance model to approximate fluctuating synaptic activity seen in vivo²³. This current is the sum of independent excitatory and inhibitory conductances, g_e(t) and g_i(t):

$$I_{\mathit{syn}}=g_e(t)(v-0)+g_i(t)(v-75).$$

Each of these conductances is described by one-variable stochastic processes similar to an Ornstein-Uhlenbeck process²³, and is equivalent to the sum of many Poisson processes smoothed by a synaptic time constant. The time constants for the excitatory and inhibitory conductances were 2.71 and 10.49 msec respectively. The mean of the inhibitory conductance was twice as strong as the excitatory conductance, but we obtained qualitatively similar results when we varied the relative balance of these conductances.

To simulate attentional modulation, we scaled the synaptic inputs to the model. We accomplished this by proportionally increasing the means of the excitatory and inhibitory conductances by an attentional factor, A, and scaling the standard deviations of these processes by the square root of A. By the central limit theorem, summing a large population of Poisson inputs results in a Gaussian random variable with a mean equal to the number of inputs and a variance that is proportional to the mean (standard deviation proportional to the square root of the mean). Thus, the scaling applied here is equivalent to scaling of the rate parameters of a large population of Poisson synaptic inputs.

Supplementary Material

1

Figure S1. Attention-dependent reduction in burst firing among broad, but not narrow, spiking neurons. a: Reduction in fraction of ISIs < 4 msec with attention. Each point corresponds to one neuron. Note that most of the broad spiking neurons (45 of 71) fall below the line of unity, indicating greater burstiness in the unattended condition. Blue crosses indicate example units in Figure 1. b: Attention-dependent reduction in the burstiness index (B.I.) among broad, but not narrow, spiking neurons. Note that most of the broad spiking neurons (51 of 71), fall below the line of unity, again indicating greater burstiness in the unattended condition. Blue crosses correspond to example units in Figure 1. Significance values, Wilcoxon signed rank test.

Figure S2. Attention-dependent reductions in burstiness occur among low-firing rate broad spiking neurons. upper panel: Among broad spiking neurons (N=71), there was a non-significant trend towards greater attention-dependent reductions in burstiness (B.A.I.) among lower firing rate neurons. lower panel: B.A.I. as a function of firing rate in the unattended condition for the narrow spiking neurons (N=47). B.A.I values of -1 and +1 for two narrow spiking neurons occurred because these neurons had no spikes with ISIs < 4 msec in one of the two attention conditions. When these two narrow spiking outliers were removed, the correlation between unattended firing rate and B.A.I. remained non-significant (Spearman’s rank correlation, p = 0.65).

Figure S3. Removing gradual drifts in action potential height. During extracellular recording, gradual changes in the position of the electrode, relative to the recorded neuron, occasionally result in slow changes in action potential height and duration, but for most neurons this drift was modest compared to the variance in action potential height over the course of a recording session. The example neuron shown here is one of the most extreme examples of this slow drift in waveform height (top panel). To correct for this, we normalized the height of each action potential by the average height of the 50 most recent action potentials recorded in the pre-stimulus fixation period. The top panel shows the height of action potentials in the preceding prestimulus period, the middle panels the unnormalized height during the stimulus-evoked response period, and the bottom panel the resulting normalized height in the sustained period. Red dots correspond to action potentials in correctly performed attend receptive field trials, blue dots correspond to action potentials in correct attend away trials.

Figure S4. Jitter procedure for isolating the effects of attention-dependent reductions in slow fluctuations from changes in burst firing. a: Raw normalized autocorrelation function averaged across narrow (green) and broad spiking neurons (yellow). Dark lines show values computed over trials in which attention was directed away from RF, light lines from trials when attention was directed into RF. b: Identical format to a, but after applying the jitter procedure described by Smith & Kohn (2008) to exclude fast response fluctuations while preserving slow fluctuations¹⁹. See Methods. c: Autocorrelation function after subtracting slow fluctuations (b) from raw autocorrelation (a), to isolate fast fluctuations (bursts). d: Scatterplot showing reduction in burst index computed from autocorrelation functions after removal of slow fluctuations. Each point corresponds to one neuron. Broad spiking neurons (yellow, N=71) are significantly shifted below the line of unity (Wilcoxon signed rank test, p<0.001), indicating a significant reduction in burst rate, after controlling for the effect of slow fluctuations. Narrow spiking neurons (N=47) showed no significant change in bursting.