A latent class model for defining severe hemorrhage: Experience from the PRospective, Observational, Multicenter, Major Trauma Transfusion (PROMMTT) Study

Abstract

Background

Several predictive models have been developed to identify trauma patients who have had severe hemorrhage (SH) and may need a massive transfusion protocol (MTP). However, almost all these models define SH as the transfusion of ≥10 units of red blood cells (RBCs) within 24 hours of ED admission (aka massive transfusion, MT). This definition excludes some patients with SH, especially those who die before a 10^th unit of RBCs could be transfused, which calls the validity of these prediction models into question. We show how a latent class model could improve the accuracy of identifying the SH patients.

Methods

Modeling SH classification as a latent variable, we estimate the posterior probability of a patient in SH based on ED admission variables (SBP, HR, pH, Hemoglobin), the 24-hour blood product utilization (plasma:RBCs and platelets: RBCs ratios), and 24-hour survival status. We define the SH subgroup as those having a posterior probability of ≥0.5. We compare our new classification of SH with that of the traditional MT using data from PROMMTT study.

Results

Of 1245 patients, 913 had complete data which were used in the latent class model. About 25.3% of patients were classified as SH. The overall agreement between the MT and SH classifications was 83.8%. However, among 49 patients who died before receiving the 10^th unit of RBCs 41 (84%) were classified as SH. Seven of the remaining 8 (87.5%) who were not classified as SH had head injury.

Conclusion

Our definition of SH based on the aforementioned latent class model has an advantage of improving on the traditional MT definition by identifying SH patients who die before receiving the 10^th unit of RBCs. We recommend further improvements to more accurately classify SH patients that could replace the traditional definition of MT for use in developing prediction algorithms.

Level of Evidence

II, Prospective

INTRODUCTION

When trauma patients first come to medical attention, there is no immediate or reliable indicator of their amount of blood loss or rate of continuing hemorrhage. Yet clinicians need this information urgently to initiate appropriate resuscitation strategies. Several predictive models have been developed to identify trauma patients who have had severe hemorrhage (SH) and potentially are in need of receiving a massive transfusion protocol (MTP). Examples include the work of McLaughlin et al.,¹ the TASH-score² and the ABC score.³ However, almost all these models define SH as the transfusion of ≥10 units of red blood cells (RBCs) within 24 hours of ED admission, also known as massive transfusion (MT). This definition ignores important information such as variability in patients’ conditions and providers’ transfusion strategies. It also excludes patients with SH who die before a tenth unit of RBCs is transfused, which calls the validity of these prediction models into question.

Donated blood products are a scarce resource, and transfusion can pose significant risks. While it has been reported that MTPs reduce morbidity and mortality^4–6 as well as associated costs,⁷ use of aggressive transfusion should be restricted to patients who truly need an MTP. Aspects of the blood transfusion protocol used to treat severely injured trauma patients, such as early prediction of patients in need of MT and optimal blood product transfusion ratios, have attracted intense clinical/translational research interest due to their significant potential impact on patient survival rates.^8–16

In the past, MT protocols usually started with crystalloids, followed by RBCs. Plasma and platelets were not transfused unless one of the following events occurred: ≥6 RBC units had been transfused, persistent hypotension that was unresponsive to crystalloid infusion had been observed, abnormal coagulation laboratory parameters had been documented, or obvious microvascular bleeding had occurred.¹⁵ Brohi et al.¹⁶ and MacLeod et al.¹⁷ documented the early presence of coagulopathy in 25% of trauma patients upon ED admission and its association with increased mortality risk.^{16, 17} Since then, a number of observational studies have reported beneficial effects among MT patients who were administered a higher ratio of plasma and platelets. ^18–23 Because of survival bias, debate persists about the validity of these findings and results from randomized clinical trials have not been reported although several are ongoing.

In addition to its role in identifying trauma patients at greatest potential benefit of transfusion strategies that mitigate or prevent coagulopathy (e.g., high plasma:RBC and platelet:RBC ratios), the traditional definition of MT is recognized as the “gold standard” for evaluating algorithm performance for early prediction of patients in need of an MTP activation. Hemorrhagic deaths occur rapidly, within a median time of 2.7 hours of injury.²³ Also Cotton et al.⁴ showed that early implementation of MTP is critical. Therefore, it is important that for medical personnel have available physiologic and/or laboratory data within minutes of a trauma patient’s arrival to the ED to accurately predict patients who suffered SH and rapidly activate an evidenced based MT protocol.

Previous research has considered the association between survival and 24-hour cumulative plasma:RBC and platelet:RBC ratios that are assumed constant from the initial to final transfusion, ignoring the time-varying nature of blood transfusions. Research in this area has been hindered by both the difficulty of collecting data on the timing of each blood product transfusion and the lack of appropriate statistical analysis methods. Holcomb et al.²² studied the relationship between survival and plasma: RBC and platelet:RBC ratios at 6 and 24 hours. Snyder et al.⁸ further divided the first 24 hours into 12 time intervals, calculated each patient’s plasma:RBC ratio within each interval, then included the plasma:RBC ratio as a time-dependent covariate in a Cox proportional hazards model for survival.⁸ However, such time-dependent ratio estimation is not only highly sensitive to the specification of the time intervals, but also ignores the correlation between censoring mechanisms (e.g., due to surgical interventions) and the transfusion procedure.²³

Despite the high level of research activity, several critical questions remain unanswered. The most important include disagreements regarding the current definition of MT, because it is measured as the total sum of RBC units received by hour 24 after ED admission. Kashuk et al.²⁴ redefined MT patients as those who receive at least 6 units of RBCs within 6 hours after ED admission. However, many injured, severely hemorrhaging trauma patients either die within the first few hours of ED admission or achieve hemostasis due to surgical or other interventions before the sixth or the tenth unit of RBCs is transfused. Additionally, the reported survival advantage among MT patients who received a higher ratio of plasma and platelets may simply reflect the fact that they lived long enough to achieve higher ratios.⁸ Studies that have addressed the question of high vs. low plasma and platelet ratios assumed that the ratio of plasma and platelets did not change appreciably in the early hours after ED admission during which a trauma patient receives transfusions. However, recent evidence suggests otherwise.²³

For many years, behavioral scientists and epidemiologists have used latent class (LC) modeling to define behavioral and other outcomes that are not directly observable (e.g., happiness).²⁵ Since SH may not be directly observable upon ED admission, it seems appropriate to model it as a latent variable. Another distinct application of LC analysis is to evaluate the performance of diagnostic screening tools in the absence of a “gold standard”.²⁶ The overall objective of this study is to demonstrate how a latent class model could be used to more accurately and completely classify SH patients than the traditional MT definition. We show that our SH definition improves upon the traditional MT definition by identifying SH patients who died or achieved hemostasis before receiving the tenth unit of RBCs.

METHODS

The preliminary model described here was developed initially using a retrospective data set with only 6 and 24 hour cumulative transfusion data.^{22, 27} However, our ongoing research is motivated by PROMMTT, which is a 10-center prospective observational study of trauma patients admitted directly from the scene of injury to a Level 1 Trauma Center. PROMMTT has collected detailed data on the timing as well as the type of each single blood product transfusion over the first 24 hours after ED admission. PROMMTT enrolled 1,245 trauma patients receiving transfusions and 297 patients received ≥10 units of RBCs.²⁸ The collection of large-scale, time-dependent, complex data through PROMMTT has produced an awareness of the urgent need for advanced statistical analysis methods. To illustrate the utility of latent class modeling in trauma transfusion research, we applied the preliminary statistical model developed in the retrospective study ^{22, 27} to PROMMTT data. We are currently extending this preliminary model to incorporate PROMMTT’s time-varying transfusion data and provide new insights into SH patients.

Latent class analysis

Latent class analysis is a statistical method that traditionally has been used for finding subtypes of related characteristics (latent classes) from multiple categorical variables.^{29, 30} These methods are ideally suited to find distinct diagnostic categories among multiple symptoms in patients. More recent improvements to the traditional LC analysis allow covariates in a logistic regression model to predict latent class membership.⁹ In this paper we assume that the entire trauma study population consists of 2 subgroups: M = 1 if a patient is SH and M = 0 otherwise. Let Z denote the baseline covariates available at ED arrival, A denote the treatment (plasma:RBC and platelet:RBC ratios), Ỹ denote the logarithm of the total amount of RBCs transfused within 24 hours, and U denote survival status of the patient at 24 hours. We can observe Ỹ only if the patient survives 24 hours (i.e., U = 1). Let Y denote the logarithm of the observed total amount of RBC transfused within 24 hours or up to death, whichever comes first. That is, Ỹ =Y if U=1 and Ỹ≥Y if U=0. We developed an LC model with three components as described in detail here.

(M1). A logistic regression model for predicting the latent class M (whether or not a patient is classified as SH), based on four patient ED arrival conditions (coded ‘low’ or ‘high’) with cut-points suggested by the literature.^{1, 3, 31–36} These characteristics included SBP (≤90mmHg or >90mmHg), Heart Rate (<120 bmp or ≥120 bmp), pH (≤7.25 or >7.25), and Hemoglobin (≤9 or >9) measured at ED admission and collectively called baseline predictors (Z). The conditional probability of a patient being classified as SH given the values of the observed baseline covariates, Z, can be estimated through estimated coefficients of the above logistic regression.

(M2). A linear regression model for the log-transformed 24 hours RBCs utilization:

For this component of the LC model we used a linear regression model for predicting the log-transformed Ỹ based on the information at ED arrival, Z, the latent classification for SH from model from step M1, the cumulative 24-hour ratios A (Platelets: RBC and Plasma:RBC ratios), and the interaction terms between latent variable SH and the cumulative 24-hour ratios A (Platelets: RBC and Plasma:RBC ratios).

(M3). A logistic regression model for 24 hour survival (U):

In this component of the LC model, we consider 24-hour survival as the outcome variable in a logistic regression model with the patient ED arrival information, Z, the latent classification M (SH or non-SH), the log-transformed RBC utilization during the first 24-hours (Y), pH, the cumulative 24-hour ratios A (Platelets: RBC and Plasma:RBC ratios), and the interaction terms between latent variable SH and the cumulative 24-hour ratios (Platelets: RBC and Plasma:RBC ratios).

Under the assumption that physicians’ decisions for choosing treatment A for a patients is independent of the unobserved latent variable M, the complete data likelihood is represented by, L(Z,M,A,Ỹ,U) = f(Z)P(M|Z)f(A|Z,M)f(Ỹ|A,M,Z)P(U|Ỹ,A,M,Z), where P(M|Z) is described by the logistic model in M1, f(Ỹ|A,M,Z) is the density function for log-transformed Ỹ with a mean that is a function of treatment A, latent SH (M), and baseline covariates (Z), standard deviation σ which is modeled as a linear regression described in M2, and P(U|Ỹ,A,M,Z) which is described by logistic model introduced in M3. Additional details regarding the model assumptions are described elsewhere. ²⁷

Since M and part of the Ỹ are not directly observed (e.g., patient died during the first 24 hours), the expectation-maximization (EM) algorithm ³⁷ was used to estimate model parameters. The EM algorithm is an iterative method for finding maximum likelihood estimates of parameters in statistical models, where the model depends on unobserved latent variables. The EM iteration alternates between performing an expectation (E) step, which creates a function for the expectation of the likelihood function evaluated using the current estimate for the parameters, and a maximization (M) step, which computes parameters maximizing the expected likelihood function found on the E step. These parameter estimates are then used to determine the distribution of the latent variables in the next E step. In our situation, we first computed the unobserved values based on the first logistic regression equation (M1) with setting initial values for the latent class membership M to be the observed traditional MT status, and updated the parameters using the computed values at various iterations. This procedure is repeated until a specified criterion for convergence is achieved. The regression coefficients on the final round of iteration are reported. Using bootstrap method we estimated the standard errors of the estimators of the parameters along with their 95% confidence intervals (CIs). With these estimated parameters, the posterior probability of M=1, given all the observed variables (Z, A, Y, U), is calculated using P(M=1|Z, A, Y, U) = L(Z,M = 1,A,Y,U)/[L(Z,M = 1, A, Y, U) + L(Z,M = 0, A, Y, U)]. A patient is classified as SH if P(M = 1|Z,A, Y, U) ≥ 0.5. Among patients who died before receiving 10 units of RBC, we compared characteristics of patients by their SH classification with t-test and Chi-Square test, depending on the type of variables.

RESULTS

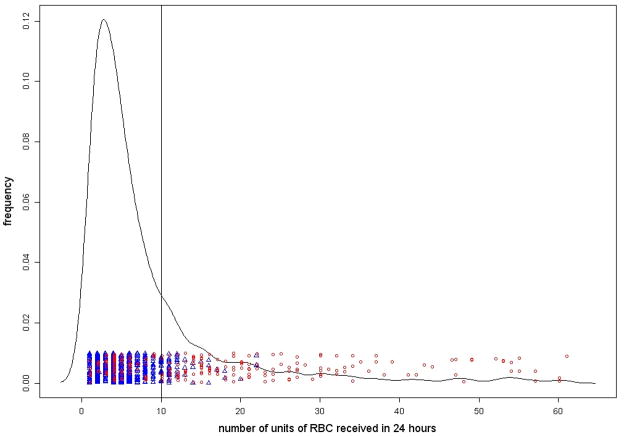
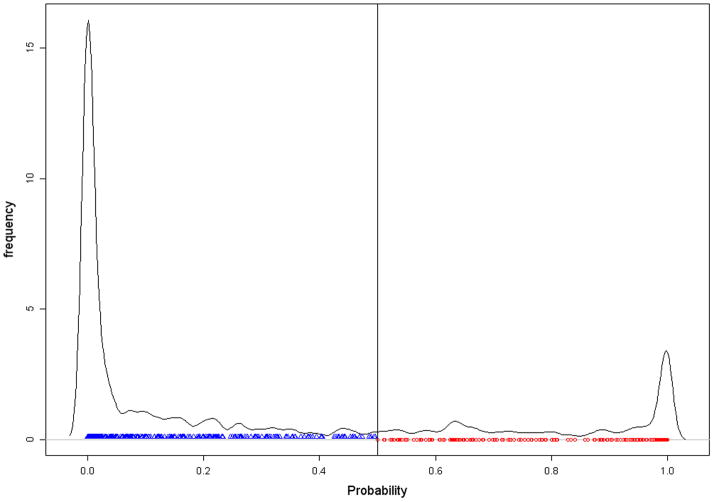
Of 1245 patients, 913 had complete data needed for the latent class model. Most of the characteristics of the subset of 913 patients with compete data were similar to those for the full dataset. Based on our definition of SH, 25.3% of patients (231/913) were classified as SH but only 215 of the 913 (i.e., 23.5%) were MT. The overall agreement between the two classifications was 83.8%. As shown in Figure 1(a), the number of RBC units received by SH patients ranged from 1–61, but the same for MT patients ranged from 10–61.

Figure 1.

Figure 1(a): Graphical presentation of the traditional MT classification (≥10 RBC units) based on PROMMTT data

Figure 1(b): Graphical presentation of the SH classification based on latent class model using posterior probability ≥ 0.5 based on the PROMMTT data

Eighty-four percent (41/49 =0.84) of patients who died before receiving a 10^th unit of RBCs within 24 hours were classified as SH. As shown in Table 2, except for 6- and 24-hour RBC utilization, there were significant differences between the 41 patients who were classified as SH, and the 8 patients who were not classified as SH, but died before receiving the 10^th unit of RBCs. In addition, there were significant differences between these two subgroups with respect to mean SBP (P =0.01). The distribution of causes of injury for the 8 patients included, 25% gunshots, 25% motor vehicle accidents, 25% pedestrian accidents, 12.5% falls, and 12.5% All-Terrain Vehicle (ATV).

Table 2.

The characteristics table for the 8 (49 - 41) patients that were not classified as SH by latent class model among the 49 died before receiving 10 units of RBC, 41 classified as SH by latent class model died non-MT and 49 died non-MT

	N=49	N=41	N=8	P-value
Patient characteristics
Age	44.71±25.57	45.53±25.52	40.63±27.16	0.626
Men (%)	67.35	70.73	50.00	0.253
Penetrating injury (%)	16.33	14.63	25.00	0.468
Systolic blood pressure (mmHg)	114.53±37.85	108.51±33.51	145.38±45.92	0.010
Diastolic blood pressure (mmHg)	74.73±25.22	71.53±25.33	92.83±16.29	0.055
Heart rate (bpm)	106.1±35.86	107.66±35.86	98.13±37.24	0.497
Respiratory rate	24±9.45	24.3±10.35	22.5±3.54	0.819
Temperature (°C)	35.52±1.22	35.57±1.11	35.3±1.78	0.660
pH	7.21±0.16	7.2±0.17	7.27±0.12	0.275
International Normalized Ratio	1.64±0.69	1.65±0.74	1.58±0.41	0.782
Base deficit	−8.88±5.8	−9.22±5.85	−7.15±5.59	0.362
Glasgow Coma Scale	4.73±3.73	4.79±3.92	4.43±2.7	0.817
Injury severity score	38.31±18.72	37.15±18.88	44.25±17.88	0.331
Blood products usage
RBC 0–6 hrs (units)	4.21±2.07	4.15±2.13	4.50±1.85	0.669
RBC 0–24 hrs (units)	4.49±2.06	4.44±2.16	4.75±1.58	0.701
FFP 0–6 hrs (units)	2.73±2.92	2.15±2.14	5.75±4.46	<0.001
FFP 0–24 hrs (units)	2.92±3.01	2.32±2.2	6.00±4.66	<0.001
Platelets 0–6 hrs (units)	1.22±2.44	0.44±1.58	5.25±2.12	<0.001
Platelets 0–24 hrs (units)	1.29±2.43	0.49±1.6	5.38±1.77	<0.001
FFP:RBC ratio 0–24 hrs	0.63±0.61	0.52±0.54	1.20±0.67	<0.001
Platelet:RBC ratio 0–24 hrs	0.26±0.52	0.07±0.23	1.21±0.54	<0.001

Estimated parameters along with standard errors and 95% CIs are provided in Table 3. Though, statistically Hemoglobin, SBP, HR were not significant contributor to the first part of the model (M1), all these three variables significantly contributed to the second component (M2) of the model. In addition, in the second component of the model (M2) significant interactions were observed between latent variable SH (M) and 24-hours plasma:RBC ratio. Although the interaction between latent variable SH (M) and 24-hours platelets:RBC ratio was not statistically significant, in order to provide greater flexibility in modeling we kept both interactions in the second and third (M2, M3) components of the LC model.

Table 3.

Estimated Regression Coefficients along with Standard Errors and 95% Confidence Intervals (CIs)

Variables	Coefficients	SE	95% CI for Coefficients
			Lower	Upper
Model M1
(Intercept)	−2.46	0.36	−3.10	−1.68
Systolic blood pressure	0.04	0.30	−0.57	0.61
Heart rate	−0.03	0.28	−0.59	0.48
pH	1.64	0.35	0.84	2.20
Hemoglobin	0.64	0.45	−0.32	1.46
Model M2
(Intercept)	0.93	0.05	0.83	1.04
Latent SH	3.40	0.73	2.05	4.56
FFP:RBC ratio	0.15	0.06	0.05	0.27
Platelet:RBC ratio	0.99	0.18	0.60	1.27
Systolic blood pressure	0.18	0.07	0.05	0.29
Heart rate	0.14	0.07	0.02	0.28
pH	0.26	0.07	0.12	0.39
Hemoglobin	0.26	0.11	0.01	0.45
Latent SH*FFP:RBC ratio	−1.49	0.42	−2.42	−0.76
Latent SH*PLT:RBC ratio	−1.46	1.08	−2.64	1.45
σ̂	0.66	0.02	0.62	0.70
Model M3
(Intercept)	20.48	32.67	14.74	95.00
Latent SH	−7.65	15.45	−30.22	1.49
Log(RBC 24-Hour)	−4.42	6.33	−20.35	−3.72
FFP:RBC ratio	−2.94	5.22	−13.72	4.32
Platelet:RBC ratio	−2.61	12.96	−17.73	8.23
pH	0.57	2.13	−0.95	5.46
Latent SH*FFP:RBC ratio	2.24	6.23	−7.75	12.32
Latent SH*PLT:RBC ratio	9.96	19.11	−2.36	41.73

SH= severe hemorrhage; FFP=fresh frozen plasma; RBC=red blood cells; PLT=platelets;

DISCUSSION

To our knowledge we are the first to introduce LC models to trauma transfusion research. Instead of using observed outcomes (e.g., ≥10 units of RBCs transfused) to define MT patients, we define SH based on posterior probability of ≥0.5 calculated from initial ED arrival variables (SBP, HR, pH, Hemoglobin), the 24-hour blood products utilization, and plasma:RBC and platelets: RBCs ratios. Based on our definition, about 25% of patients were classified as SH and the overall agreement between the MT and SH classifications was 83.8%. Moreover, among 49 patients who died before receiving the tenth unit of RBCs, 41 (84%) were classified as SH. Seven of the remaining 8 (87.5%) patients who were not classified as SH had head injury. These findings suggest that our LC model identifies a very large portion of patients who died before receiving the tenth unit of RBCs but were excluded from the traditional MT. Patient outcome, such as survival, is affected not only by the transfusion protocol received but also by the residual effect of the injury (e.g. any additional surgical and lifesaving interventions such as laparotomy) and the patient’s ongoing exposure to the hospital environment. Key information including highly influential variables and their timing or sequence may not be captured in the datasets currently available to data analysts. Utilizing all available information will create a more accurate identification of SH patients that is not limited to the subset of patients who survive long enough to receive 10 RBC units within 24 hours of ED admission.

The PROMMTT dataset included 1245 patients but because of missing values in at least one of the variables used in our LC model, we only used 913 patients who had complete data needed for the LC model. Though we did not find any significant differences in characteristics of the patients in the full dataset and the subgroup who had complete information, we consider this as a limitation of our approach. However, others have shown that multiple imputation³⁸ can be applied to LC analysis assuming the missingness is completely at random.³⁹ Since we expect that the missing patterns in trauma data are not at random, our future research will focus on addressing missing data problems by using the multiple imputation technique³⁸ with sensitivity analyses for potential non-ignorable missing. Another limitation of latent class models is that they all have to be fully parametric and therefore may not be robust to model misspecification. Potential nonidentifiability of parameters in the LC regression model is a well-recognized statistical problem but in the LC analysis literature, identifiability examinations have focused on local identifiability (i.e., within a small enough neighborhood that no two values for the parameters result in the same distribution). Huang and Bandeen-Roche ⁴⁰ discussed sufficient conditions for the local identifiability of LC models with polytomous variables. Additionally, the ability to achieve a high ratio in Plasma:RBC or Platelets:RBC is highly dependent on the duration of the massive transfusion protocol. A physician may choose to give 1:1 ratio but it may not be logistically feasible due to availability of these blood products. This has implications on meeting the underlying assumption for the LC model. Our future research plan will introduce the latest in recurrent event data analysis to incorporate time-dependent blood product transfusion rates (whether RBC, plasma, or platelet) in order to avoid the unstable behavior of conventionally-computed plasma and platelet ratios. This methodology provides an opportunity to overcome time-dependent confounding in the assessment of the effects of transfusion rates on survival.

In conclusion, we demonstrated an application of LC models for identifying a subgroup of patients in PROMMTT who may have suffered from blood loss during the first 24 hours from ED admission. Further, we have shown that our SH definition improves upon the traditional MT definition by identifying 84% of SH patients who died or achieved hemostasis before receiving the 10^th unit of RBCs. Our effort in demonstrating our current latent class model helps to initiate a conversation between statisticians, epidemiologists, clinicians, and other scientists to work together in order to come up with a meaningful approach to identify the subgroup of trauma patients who have truly suffered SH and are in need of massive transfusion protocol. After a new “gold standard” of SH is accepted, we will proceed to build new and enhanced predictive algorithms using the new definition of SH.

Table 1.

Comparison of latent class classification of SH based on Cutoff=0.5 with that of traditional MT (≥10 RBC units)

	Conventional non-MT	Conventional MT	Total
Latent non-SH	616	66	682
Latent SH	82	149	231
Total	698	215	913

MT=Massive transfusion; SH= severe hemorrhage