Ordinal response prediction using bootstrap aggregation, with application to a high-throughput methylation dataset

Summary

Many investigators conducting translational research are performing high-throughput genomic experiments and then developing multigenic classifiers using the resulting high-dimensional dataset. In a large number of applications, the class to be predicted may be inherently ordinal. Examples of ordinal outcomes include Tumor-Node-Metastasis (TNM) stage (I, II, III, IV); drug toxicity evaluated as none, mild, moderate, or severe; and response to treatment classified as complete response, partial response, stable disease, or progressive disease. While one can apply nominal response classification methods to ordinal response data, in so doing some information is lost that may improve the predictive performance of the classifier. This study examined the effectiveness of alternative ordinal splitting functions combined with bootstrap aggregation for classifying an ordinal response. We demonstrate that the ordinal impurity and ordered twoing methods have desirable properties for classifying ordinal response data and both perform well in comparison to other previously described methods. Developing a multigenic classifier is a common goal for microarray studies, and therefore application of the ordinal ensemble methods is demonstrated on a high-throughput methylation dataset.

1. Introduction

In a large number of biomedical and health survey applications, the response to be compared or predicted is ordinal. Examples of ordinal outcomes include Tumor-Node-Metastasis (TNM) stage (I, II, III, IV); drug toxicity evaluated as ‘none,’ ‘mild,’ ‘moderate,’ or ‘severe;’ and response to treatment classified as complete response, partial response, stable disease, or progressive disease. These outcomes are ordinal; that is, while there is an inherent ordering present among the responses, there is no known underlying numerical relationship between the responses. While one can apply nominal response classification methods to ordinal response data, in so doing important information is lost that may improve the predictive performance of the classifier. Specifically, for many applications such as gene expression microarray studies, it is likely of interest to identify covariates (i.e., genes) that are monotonically associated with the ordinal response. Application of nominal response methods for classification may not fare well in identifying monotonic associations. Furthermore, for ordinal response data, parameters other than classifier accuracy may be the more important measures of classifier performance.

Common to all high-throughput genomic datasets, the data consist of a large number of candidate predictors, p, and a small number of observations, n. There are statistical modeling approaches, such as cumulative logit models, proportional odds models, cumulative link models, or cumulative probit models, that can be used to predict an ordinal response. However, these ordinal modeling approaches are not estimable when p > n. Furthermore, the assumption of independence among the p candidate predictors is violated in data arising from high-throughput genomic experiments. Therefore, when interest lies in class prediction, machine learning approaches are commonly applied when p ≫ n.

Most machine learning methods, such as k-nearest neighbors, support vector machines, and neural networks, are useful for classifying observations into nominal response categories. Alternative methods for deriving a classification tree (CT) for predicting ordinal responses have been described, yet these ordinal CTs are not routinely used since CTs are characteristically unstable learners [1]. Recently, ensemble learning methods, which do not require reduction of the predictor space prior to classification, have been described and have reported unparalleled accuracy [2, 3, 4, 5, 6]. This study examined the effectiveness of ensemble learning, specifically bootstrap aggregation, on classifying an ordinal response. An overview of classification tree methodology is presented in Section 2, followed by a description of bootstrap aggregation in Section 3. Modifications to the tree induction problem when the response is ordinal are described in Section 4. We examined the performance of four previously described ordinal splitting methods in comparison to the traditional nominal response Gini impurity method by bootstrap aggregation of CTs. A simulation study is presented in Section 5, and in Section 6 we demonstrate the application of the ordinal classification methods when classifying subjects into one of three ordinal classes using methylation data for 1,505 candidate CpG sites.

2. Classification trees

Formally, the learning data set consists of n observations such that ℒ = {(x₁, ω₁),…, (x_n, ω_n)}, where each observation belongs to one of G classes, denoted ω_i ∈ (1,…, G), and the covariates are stored in the p-dimensional vector of predictors x_i = (x_i1,…, x_ip). To simplify the notation, often ω_i is represented by the class label g. For the ordinal classification problem, the class values of ω are ordered, such that 1 < 2 < … < G. The objective is to derive a classifier ψ which takes x_i as input and accurately outputs ω_i.

Classification trees were developed because problems arose that could not be handled in an easy or natural way by any of the methods that had previously been described (e.g., linear discriminant analysis, k-nearest neighbors) [7]. When deriving a classification tree, all observations in ℒ start together in the root node, t. Then, for each of the p predictor variables, the best binary split is determined, where splits resulting in increasingly more homogeneous nodes with respect to class are desired. Thereafter, among all best splits for the p predictor variables, the very best split is selected for partitioning the observations to the left and right descendant nodes, t_L and t_R, respectively. This process is repeated for all descendant nodes until the terminal nodes are either homogeneous with respect to the class or there are too few observations for further partitioning.

Regardless of the classification tree variant one may use (e.g., CART [7] or C4.5 [8]), the four essential elements needed in the initial tree growing procedure are as follows:

1. a set of binary questions, which comprise the candidate set of splits s;

2. a goodness-of-split criterion ϕ(s,t) that can be evaluated for any split s of any node t;

3. a stop-splitting rule; and

4. a rule for assigning every terminal node one of the C classes.

The goodness-of-split criteria are most often formulated as the decrease in node impurity. As noted by [7], the fundamental aspect in recursive partitioning is the splitting rule, in other words, a well-formulated impurity measure. In this paper, we focus attention to various methods for quantifying goodness-of-split (item 2), and describe splitting criteria for both nominal and ordinal response problems. For node t, the proportion of cases in each of the G classes are the node proportions, defined to be p(g|t) for g = 1,…,G such that p(1|t) +; p(2|t) + … + p(G|t) = 1. For nominal response prediction, an impurity function is a non-negative function i(t) defined on the set (p(1|t),p(2|t),…,p(G|t)) such that the node impurity is largest when all classes are equally mixed together and smallest (i.e., 0) when the node contains only one class. For any node t, the best candidate split s_p of the node divides it into left (t_L) and right (t_R) descendant nodes such that a proportion p_L of the cases in t go into t_L and a proportion of cases p_r go into t_R. Therefore, p_L = p(t_L)/p(t), p_r = p(t_R)/p(t) (where p_L +;p_r = 1) (Figure 1).

Figure 1.

Candidate split s divides node t it into left (t_L) and right (t_R) descendant nodes such that a proportion p_L of the cases in t go into t_L and a proportion of cases p_R go into t_R.

Within-node impurity measures commonly used for nominal response classification are the Gini criterion, defined as

$$i(t)=\sum _g\sum _{h\ne g}p(h|t)p(g|t)=\sum _{g}p(g|t)(1-p(g|t)),$$ (1)

or the Information/Entropy criterion defined as

$$i(t)=-\sum _{g}p(g|t)log[p(g|t)].$$ (2)

Regardless of the impurity measure selected, the candidate split s resulting in the largest decrease in node impurity among the p candidate predictors, assuming Δi ≥ 0, is chosen as the best split, or

$$arg\underset{p}{max}\Delta i(s_p,t),$$ (3)

where for each of the p predictors the decrease in node impurity due to the split s_p is defined as

$$\Delta i(s_p,t)=i(t)-p_{L}i(t_L)-p_{R}i(t_R).$$ (4)

In order for Δi(s_p,t) ≥ 0, i(t) must be a concave function. A non-concave impurity function can be problematic, potentially resulting in Δi(s_p,t) that is negative for some or all candidate splits, so that no splitting is performed. Assuming application of an appropriate splitting function, the predicted class ĝ(t) for a terminal node t is taken to be the class for which p(g|t) is largest, or

$$\widehat{g}(t)=arg\underset{g}{max}p(g|t).$$ (5)

Therefore, the predicted class for observation i that is a member of terminal node t is the predicted class of the terminal node t, formally ĝ_i = arg max_g,i∈tp(g|t).

3. Boostrap aggregating

If the classifier is high dimensional, then the model will tend to overfit the data and hence, is unstable [3]. That is, the model may have low prediction error for the learning dataset but it will have higher prediction error on new test sets. Alternatively, if the classifier is too low dimensional, it may not contain a good fit of the data. While classification trees are readily interpretable, giving insight into important predictor variables, they have been found to be unstable; that is, small changes in the training data yield changes in the final tree constructed. If perturbing the learning set can cause significant changes in the predictor constructed, as is the case with classification trees, then bootstrap aggregating (or ‘bagging’) has been demonstrated to improve accuracy [3].

When bagging, bootstrapped resamples of the original data are used to generate multiple versions of a predictor; these predictors are then combined to form an aggregate classifier. When bagging CTs, a bootstrap learning sample ℒ_b is obtained by sampling the original learning sample ℒ with replacement. An overly large tree T_max,b is then grown using the observations in the bootstrap learning sample ℒ_b and is not pruned. For each terminal node in T_max,b the predicted class is obtained. This process of drawing bootstrap resamples and deriving a CT using ℒ_b is repeated B times.

The aggregate classifier is obtained by combining the predictions over the B classification trees. First, the class-specific prediction indicator is derived for the i^th observation and b^th bootstrap learning sample, and for class g is taken to be

$${\widehat{d}}_{\mathit{\text{igb}}}({\text{x}}_i,{ℒ}_b)=\{\begin{array}{c}1\text{if}{\widehat{g}}_{\mathit{\text{ib}}}=g\\ 0\text{if}{\widehat{g}}_{\mathit{\text{ib}}}\ne g.\end{array}$$ (6)

For each observation i, the bagged estimate consists of G elements equal to the number of the B trees predicting class g at x_i, where the G elements are taken to be

$${\widehat{d}}_{\mathit{\text{ig}},\mathit{\text{bag}}}({\text{x}}_i,ℒ)=\sum _{b=1}^B{\widehat{d}}_{\mathit{\text{igb}}}({\text{x}}_i,{ℒ}_b).$$ (7)

The bagged predicted class for the i^th observation is that class having the majority vote among the B trees,

$${\widehat{D}}_{i,\mathit{\text{bag}}}({\text{x}}_i,ℒ)=arg\underset{g}{max}{\widehat{d}}_{\mathit{\text{ig}},\mathit{\text{bag}}}({\text{x}}_i,ℒ).$$ (8)

4. Ordinal classification

Previously suggested machine learning methods for classifying an ordinal response have been to assign scores to the ordinal categories and then treat these numeric values in a quantitative manner. For example, [9] proposed the use of regression trees to predict an ordinal class by treating the ordinal response as numeric-valued vector and applying some post-processing method to the predicted response (such as rounding) to obtain the predicted ordinal class. They also investigated various post-processing methods (median, mode, mean rounding) within the nodes during the tree construction process to enforce the predictions to always take on a valid class label. This method may be sensible if the ordinal response is based on some underlying continuous measurement distribution. However, often there is no obvious choice for assigning numeric scores to the ordinal response, and different scoring systems can yield different results [10, 11]. Alternative methods for tree induction when predicting an ordinal response have been previously proposed. In this section, these methods are described and shortcomings are highlighted. In addition, a new splitting criteria for an ordinal response which attempts to overcome the shortcomings of the previously described methods is described.

4.1. Generalized Gini index

The Generalized Gini index factors in the cost or loss associated with classifying an observation belonging to class g as h, or C(h|g), into the node impurity measure [7, 12]. The within node impurity is thus defined as

$$i_{\mathit{\text{GG}}}(t)=\sum _g\sum _{h\ne g}C(h|g)p(h|t)p(g|t)$$ (9)

In classifying an ordinal response, it may be assumed that for each combination of true class and predicted class, there is a known loss or cost C(h|g) giving the negative utility of the consequences of predicting h when the true class is g. The cost of misclassifying an observation with ordinal response g as h should satisfy the following conditions:

1. C(h|g)≥ 0, if h ≠ g (costs are non-negative)

2. C(h|g) = 0, if h ≠ g (correct classification costs are 0)

3. C(h|g) > C(h|g) if classes f and g are more dissimilar than classes h and g (costs are positive increasing)

4. C(h|g) = C(h|g) if the dissimilarity between classes f and g is the same as the dissimilarity between classes h and g (costs are symmetric).

The node selection rule is to select the split that maximizes equation (4) where i(t) is defined by equation (9). We note that like the assignment of scores to ordinal categories then treating the assigned scores as numeric responses, assigment of misclassification costs is arbitrary. Moreover, other researchers have shown that incorporation of misclassification costs (equation 9) can result in an impurity function that is not necessarily concave, so that the decrease in node impurity could conceivably be negative for some or all splits [7]. This is problematic because when the decrease in node impurity is negative for all candidate splits, no splitting is performed.

4.2. Ordered twoing

At each node, the ordered twoing method redefines the G-class ordinal problem to G − 1 dichotomous response problems [7, 13]. For each observation i the g^th dichotomous response is defined as

$$C_{\mathit{\text{ig}}}=\{\begin{array}{cc}1& \text{if}{\omega }_{\text{i}}=1,\dots g\\ 0& \text{if}{\omega }_{\text{i}}=g+1,\dots G.\end{array}$$ (10)

For node t and dichotomous superclass C_g, the split that maximizes

$$\varphi (s,t,C_g)=2p_L{p}_R{(p(C_g|t_L)-p(C_g|t_R))}^2$$ (11)

over the p covariates is taken to be the best split for that dichotomous superclass C_g. Then the dichotomous superclass $C_g^{\ast }$ which maximizes ϕ(s, t, C_g) among all dichotomous superclasses is selected for splitting node t. Ordered twoing is more computationally intensive, since for each node containing observations in G classes, the decrease in node impurity for each candidate predictor must be evaluated for each of G − 1 superclasses.

4.3. Criteria for impurity functions when predicting an ordinal response

The properties for nominal response splitting criteria require modifications when interest is in predicting an ordinal response. Specifically, the splitting criteria should reward splits for variables monotonically related to the ordinal response in the tree growing procedure. According to [14], the fundamental question for formulating splitting criteria is in answering the question, “What distribution of the instances between the two children nodes maximizes the goodness-of-split criterion?” As an example, in considering the goal of identifying covariates monotonically associated with a three-level ordinal response, we postulate that it is less desirable for observations in node t to be represented in proportions $(\frac{1}{2},0,\frac{1}{2})$ rather than $(\frac{1}{3},\frac{1}{3},\frac{1}{3})$. Previously, a novel splitting criteria for classification tree growing when the response is ordinal was proposed [15]. Specifically, the ordinal impurity function was proposed to be

$$i(t)=\sum _{g=1}^G|{\stackrel{\sim }{\omega }}_{g+1}-{\stackrel{\sim }{\omega }}_g|F_t(g)[1-F_t(g)],$$ (12)

where ω̃_g represents a score attached to the g^th level of the response ω, and F_t(g) denotes the proportion of observations in node t characterized by a level ω_i ≤ g. A modified version of the ordinal impurity function given in equation 12 which omits the difference between ordinal class scores [15], or

$$i_{\mathit{\text{OS}}}(t)=\sum _{g=1}^G{F}_t(g)[1-F_t(g)],$$ (13)

was also proposed [15]. Equation 13 has been previously demonstrated to be related to an index measuring the strength of association between an ordinal response and nominal covariate [16, 13]. The global, anti-end cut factor, and exclusivity preference properties of this ordinal impurity function have been previously described [13]. Following the tradition of nominal response impurity function properties [7], we provide proof in the Appendix that the splitting function in equation 13 also meets the following ordinal impurity function criteria:

• (ORD.1) the impurity function is required to be a non-negative function i(t) defined on the set (p(1|t),p(2|t),…,p(G|t)) such that the node impurity is largest when classes in the extreme (i.e., g = 1, G) are equally mixed together;

• (ORD.2) i(t) takes on a minimum when node t is homogeneous with respect to class (i.e., (1, 0,…, 0) = 0, (0, 1, 0,…, 0) = 0, …, (0,0,…, 0, 1) = 0; and

• (ORD.3) We require Δi(s_p,t) ≥ 0, so i(t) must be a concave function.

We note that only the first property differs from the properties of impurity functions for nominal response prediction, and emphasize that the Gini criterion does not fulfill the ordinal properties since ORD.1 is violated. Also, inclusion of misclassification costs into the Generalized Gini criterion can violate property ORD.3. Finally, the ordered twoing method is not an impurity-based method since Δi(t) is not used in forming the split. Therefore, only equation 13 fulfills all three ordinal splitting properties.

5. Simulation study

A small simulation study was conducted by generating 100 observations, where 20 observations were generated from each of 5 ordinal classes. Specifically, within each of ω = 1,…, 5 ordinal classes, 20 multivariate normal observations were generated having a mean vector (2ω, 2ω) and covariance matrix

$$\sum =\left[\begin{array}{cc}1& 0.8\\ 0.8& 1\end{array}\right]$$

Noise covariates were added such that: X₃ ∼ Unif(0,1), X₄ ∼ Unif(0,1), X₅ ∼ Unif(0,1), X₆ &sim; N(0,1), X₇ ∼ N(0,1), X₈ ∼ ${\chi }_{\text{2}}^{\text{2}}$. We note that in some ordinal response modeling problems, there may be circumstances where U- and J-shaped predictors may be usefully included in the model. However, we are assuming the researcher is starting from the vantage point of having prior knowledge that a monotonic relationship between the ordinal response and interesting predictor variables exists, so that the restrictive nature of modeling the ordinal response using montonically associated variables is of primary interest. Such is the case with data arising from high-throughput genomic experiments, where an increase in the phenotypic level (stage of disease) may be mechanistically linked through a monotonic association with genotype/gene expression. Bootstrap aggregation was performed using Gini, Generalized Gini with linear cost of misclassification, Generalized Gini with quadratic cost of misclassification, ordered twoing, and the ordinal impurity method with B = 100 unpruned trees in each ensemble. For each tree in the ensemble, the minimum number of observations that must exist in a node, in order for a split to be attempted, was set to five, which means the minimum size that any terminal node in the ensemble could attain is two. Classification performance was assessed in two ways; first, for each bootstrap resample ℒ_b, prediction error was estimated for the corresponding CT using only those observations in the learning dataset that were not in the bootstrap resample, or the “out-of-bag” (OOB) observations, ℒ_b,oob = ℒ − ℒ_b. Second, since the goal of this study is to optimize ordinal classification, the gamma statistic of ordinal association was estimated between the observed responses and ordinal class predictions using ℒ_b,oob. Simulations were conducted using the R programming environment [17], the rpart package [12], and additional R functions for ordinal and ordered twoing splitting developed by the authors were used.

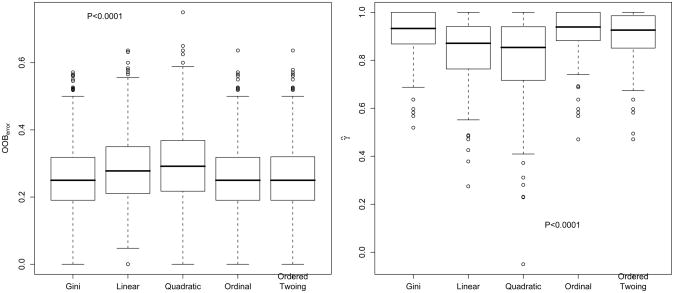
Boxplots of the out-of-bag error estimates for each algorithm are displayed for examining the distribution of the error estimates associated with each algorithm (Figure 2). The ordinal impurity and ordered twoing methods had lower OOB errors in comparison to the other three methods. In addition, boxplots of the gamma statistic for each algorithm revealed the ordinal impurity and ordered twoing methods had the highest gamma statistic (Figure 2). The dependent K-sample design permitted comparison of the K = 5 algorithms by testing for significant differences among the misclassification errors and gamma statistics. The null hypothesis H₀: τ₁ = τ₂ = τ₃ = τ₄ = τ₅ was tested against the alternative that at least one inequality exists using Friedman's test. Both tests were significant at the P < 0.0001 level. Since each impurity method was applied to the same bootstrap resamples, to identify which impurity methods contributed to the observed significant difference between the five methods, pairwise comparisons were performed by applying the Wilcoxon signed rank test. From Tables I and II we conclude that the ordinal and ordered twoing methods had significantly improved performance over the other three methods, but were not different from one another. The Generalized Gini with linear and quadratric costs of misclassifications were also significantly better that Gini, but were not different from one another.

Figure 2.

Right-hand figure: Boxplots of misclassification rates for each of the five impurity methods calculated using out-of-bag observations from the simulation study. Left-hand figure: Boxplots of the gamma statistic for each of the five impurity methods calculated using out-of-bag observations from the simulation study.

Table I.

P-values from the pairwise comparisons of OOB error from the simulation study.

	Linear cost	Quadratic cost	Ordinal	Ordered Twoing
Gini	0.004	0.001	<0.0001	<0.0001
Linear cost		0.64	0.003	0.0002
Quadratic cost			0.01	0.001
Ordinal				0.42

Table II.

P-values from the pairwise comparisons of the gamma ordinal measure of association estimated between the observed responses and ordinal class predictions using the out-of-bag observations from the simulation study.

	Linear cost	Quadratic cost	Ordinal	Ordered Twoing
Gini	0.006	0.002	<0.0001	<0.0001
Linear cost		0.19	0.0002	0.0008
Quadratic cost			0.01	0.03
Ordinal				0.37

6. Case Application

Due to the poor clinical outcome of patients with cirrhosis due to the hepatitis C virus (HCV) who are diagnosed with advanced stage hepatocellular carcinoma (HCC), markers capable of classifying patients are needed. Aberrant methylation likely plays a direct role in altered protein expression levels, since methylation of CpG sites in gene promoter regions affects gene transcription [18]. In fact, epigenetic events such as hypermethylation of tumor suppressor genes have been implicated in carcinogenesis [19]. A cross-sectional study of patients infected with HCV and subjects with a normal functioning liver yielded patients that belong to one of the three ordinal categories: normal functioning liver (N = 20), pre-malignant liver (HCV-cirrhosis, N = 16), or malignant liver (HCV-cirrhosis with hepatocellular carcinoma, N = 20). For each subject, DNA was isolated from their liver sample, bisulfite treated, amplified, and hybridized to an Illumina Goldengate Methylation BeadArray Cancer Panel I. This resulted in expression measures representing “proportion methylated” for 1,505 CpG sites for each subject. Here it was of interest to classify the patients as belonging to one of these three ordinal categories (normal < pre-malignant < malignant) using the 1,505 proportion methylated measurements as predictor variables.

From the full dataset, 100 bootstrap datasets were generated. For each bootstrap resample, a classification tree predicting ordinal class (normal, pre-malignant, malignant) was derived using the Gini, Generalized Gini with linear cost of misclassification, Generalized Gini with quadratic cost of misclassification, ordered twoing, and the ordinal impurity function. Similar to the simulation study, the out-of-bag error was estimated for each bootstrap resample and derived CT as was the gamma statistic measuring the ordinal association between the observed responses and ordinal class predictions. There was a significant difference among the five methods with respect to OOB error, with the ordinal impurity and ordered twoing being significantly lower than the Generalized Gini with either linear or quadratic costs of misclassification, but neither significantly different from the Gini method or one another(Figure 3, Table III). There was a significant difference among the five methods with respect to the gamma statistic, with the ordinal impurity having a significantly higher gamma statistic compared to the other four methods. The ordered twoing was significantly higher than the Generalized Gini with either linear or quadratic cost of misclassification, though not significantly different from the Gini method (Figure 3, Table IV).

Figure 3.

Right-hand figure: Boxplots of misclassification rates for each of the four impurity methods calculated using out-of-bag observations from the case application. Left-hand figure: Boxplots of the gamma statistic for each of the four impurity methods calculated using out-of-bag observations from the case application.

Table III.

P-values from pairwise comparisons of OOB error from the case application.

	Linear cost	Quadratic cost	Ordinal	Ordered Twoing
Gini	0.0003	<0.0001	0.62	0.21
Linear cost		0.49	0.0001	0.001
Quadratic cost			<0.0001	<0.0001
Ordinal				0.11

Table IV.

P-values from the pairwise comparisons of the gamma ordinal measure of association estimated between the observed responses and ordinal class predictions using the out-of-bag observations from the case application.

	Linear cost	Quadratic cost	Ordinal	Ordered Twoing
Gini	<0.0001	<0.0001	0.24	0.20
Linear cost		0.44	<0.0001	<0.0001
Quadratic cost			<0.0001	<0.0001
Ordinal				0.04

7. Discussion

Traditional methods for modeling an ordinal response include multinomial logistic regression, baseline logits, proportional odds, and continuation ratio models. Unfortunately, these models rely upon maximum likelihood and can only be fit when the number of observations (n) is less than the number of covariates (p). However, the purpose of this paper is to demonstrate methods for predicting an ordinal response when the number of covariates exceeds the sample size, which is now common among high-throughput genomic experiments such as with gene expression microarray data. When predicting an ordinal response for datasets where p ≫ n, alternatives to traditional statistical modeling approaches may be applied, such as CTs. We have presented alternatives to the traditional nominal response impurity function, namely an ordinal response impurity function and ordered twoing, and assessed their performance in a simulation study and case application.

Our simulation study was designed to be relevant to ordinal response prediction problems with small sample sizes, since most microarray gene expression studies often include relatively small sample sizes within each class. From our simulation study, we observed that the ordinal impurity and ordered twoing functions had the lowest OOB errors and highest gamma statistics. Since among the eight predictor variables, only two were truly important predictors and both were monotonically associated with the ordinal response, we believe this indicates that the ordinal impurity and ordered twoing functions are the most well-suited for partitioning the ordinal response categories when monotonic associations are present.

For the case application, the ordinal impurity and twoing functions had a significantly lower misclassification errors when compared to the Generalized Gini with either linear or quadratic costs of misclassification. In addition, it has similar error when compared to the Gini impurity function which is commonly used for nominal response classification. It is likely that the methylation dataset, which consisted of 1,505 methylation expression values, included some predictors that separated the classes but were not monotonically associated with the ordinal response. That is, the Gini impurity function may have performed well because it would have been capable of detecting associations between covariates that are not monotonic with the ordinal class. For example, U-shaped predictors will not be preferentially used for partitioning a node when using i_OS(t) but may be used by the Gini impurity. We note that in some modeling problems, there may be circumstances where U- and J-shaped predictors may be usefully included in the model. However, we are assuming the researcher is starting from the vantage point of having prior knowledge that a monotonic relationship between the ordinal response and interesting predictor variables exists, so that the restrictive nature of modeling the ordinal response using montonically associated variables is of primary interest. Such is the case with data arising from high-throughput genomic experiments, where an increase in the phenotypic level (stage of disease) may be mechanistically linked through a monotonic association with genotype/gene expression. We assert that in our case application, U-shaped predictors are not of particular interest when predicting the ordinal response, particularly when we seek to use in our model only covariates likely to be mechanistically associated with the ordinal class, such as genes having a monotonic association with the ordinal response. Therefore, we conclude that either the ordinal impurity function i_OS(t) or ordered twoing should be used for ordinal response prediction in similar situations.

For both the case application and the simulated dataset, the impurity functions were applied when combining CTs with bootstrap aggregation. Bootstrap aggregation is one of now several ensemble learning methods and is the method from which the random forest methodology was derived, the primary difference between the two being that with bagging, all covariates are examined at each node for splitting it into left and right descendent nodes, while with the random forest (RF) method, only a pre-selected number of covariates (m, commonly m = √p) are randomly selected at each node for splitting. Like RF, we used out-of-bag error as a means to assess performance of the bootstrap aggregated trees. The purpose of this manuscript was not to compare different types of ensemble learning methods, but rather, to compare different splitting criterion under the same ensemble learning method framework. We are, however, currently working to implement the ordinal impurity function in the randomForest package [20]. Since variables selected for splitting a single tree are by no means the only important covariates in the predictive structure of the problem, this extension will permit examination of an important byproduct of the random forest algorithm, variable importance measures [6, 20, 21]. R code for the ordinal impurity and ordered twoing method can be obtained by contacting the corresponding author.

Appendix.

Proof of ORD.1

Consider fitting a binary classification tree for predicting an ordinal response. Suppose p(ω₁|t),p(ω₂|t),…,p(ω_G|t) denote the proportion of observations in each of the G classes at node t, such that Σ_gp(ω_g|t) = 1. We first demonstrate that the impurity function is defined on the set (p(1|t),p(2|t),…,p(G|t)) such that the node impurity is largest when classes in the extreme (i.e., g = 1,G) are equally mixed together; in other words i_OS(t) takes on a maximum when (p(ω₁|t), p(ω₂|t),…, p(ω_G|t)) = $(\frac{1}{2},0,\dots ,0,\frac{1}{2})$; Again, recall that F(ω_g|t)= ${\sum }_{k=1}^{g}p({\omega }_k|t)$ and i_OS(t) = ${\sum }_{g=1}^{G}F({\omega }_g|t)(1-F({\omega }_g|t))$. If for any number of G classes, suppose p(ω₁|t) = p(ω_G|t)= $\frac{1}{2}$. Then for all g < G

$$F({\omega }_g|t)=\sum _{k=1}^{g}p({\omega }_k|t)=\frac{1}{2}$$ (14)

and for class G

$$F({\omega }_G|t)=\sum _{k=1}^{G}p({\omega }_k|t)=1$$ (15)

and so the impurity is

$$i_{\mathit{\text{OS}}}(t)=\sum _{k=1}^{G-1}[F({\omega }_k|t)(1-F({\omega }_k|t))]+F({\omega }_G|t)(1-F({\omega }_G|t))=(G-1)\times \frac{1^2}{2}.$$ (16)

This can be easily demonstrated to be a maximum over any other set of node proportions by considering that if either p(1|t) ≠ $\frac{1}{2}$ or p(G|t) ≠ $\frac{1}{2}$, the product terms in the summation will be less than terms comprising equation (15).

Proof of ORD.2

To demonstrate i_OS(t) satisfies ORD.2 by assuming p(ω_g|t) = 1 for some g, for any class g we can rewrite the impurity as

$$i_{\mathit{\text{OS}}}(t)=\sum _{k=1}^{g-1}F({\omega }_k|t)(1-F({\omega }_k|t)+\sum _{k=g}^{G}F({\omega }_k|t)(1-F({\omega }_k|t)).$$ (17)

Then for any j < g,

$$F({\omega }_j|t)=\sum _{k=1}^{j}p({\omega }_k|t)=0$$ (18)

so the first part of equation (16) becomes

$$\sum _{k=1}^{g-1}F({\omega }_k|t)(1-F({\omega }_k|t))=0$$ (19)

and for any j ≥ g

$$F({\omega }_j|t)=\sum _{k=1}^{g}p({\omega }_k|t)=1$$ (20)

which means 1 − F(ω_j|t) = 0 such that the second part of equation (16) becomes 0, and 0+0=0, so that i_OS(t) achieves a minimum if p(ω_g|t) = 1 for some class g.

Proof of ORD.3

To demonstrate that for any split, Δi(s, t) ≥ 0, from above we see that i_OS(t) is a concave function. A simplification of Jensen's Inequality when μ₁ +μ₂ + … + μ_n = 1 and 0 ≤ μ_k ≤ 1 is that for a concave function f, $f({\sum }_{k=1}^n{\mu }_k{x}_k)\le {\sum }_{k=1}^n{\mu }_{k}f(x_k)$. The decrease in node impurity is defined as Δi_OS(t) = i_OS(t)− p_Li_OS(t_L)− p_Ri_OS(t_R). Considering the node proportions satisfy p_L + p_R = 1 and 0 ≤ p_L≤ 1 and 0 ≤ _pR ≤ 1, then

$$p_L{i}_{\mathit{\text{OS}}}(t_L)+p_R{i}_{\mathit{\text{OS}}}(t_R)\le i_{\mathit{\text{OS}}}(p_{L}tL+p_R{t}_R)=i_{\mathit{\text{OS}}}(t)$$ (21)

so that Δi_OS(t) = i_OS(t)− p_Li_OS(t_L)− p_Ri_OS(t_R) will always be ≥ 0.