Constrained Data Decomposition and Regression for Analyzing Healthy Aging from Fiber Tract Diffusion Properties

Abstract

It has been shown that brain structures in normal aging undergo significant changes attributed to neurodevelopmental and neurodegeneration processes as a lifelong, dynamic process. Modeling changes in healthy aging will be necessary to explain differences to neurodegenerative patterns observed in mental illness and neurological disease. Driving application is the analysis of brain white matter properties as a function of age, given a database of diffusion tensor images (DTI) of 86 subjects well-balanced across adulthood. We present a methodology based on constrained PCA (CPCA) for fitting age-related changes of white matter diffusion of fiber tracts. It is shown that CPCA applied to tract functions of diffusion isolates population noise and retains age as a smooth change over time, well represented by the first principal mode. CPCA is therefore applied to a functional data analysis (FDA) problem. Age regression on tract functions reveals a nonlinear trajectory but also age-related changes varying locally along tracts. Four tracts with four different tensor-derived scalar diffusion measures were analyzed, and leave-one-out validation of data compression is shown.

1 Introduction

Unlike earlier hypothesis that brain anatomy and major functions are pretty much established after adolescence and would not change significantly until late adulthood, there is increasing evidence of dynamic, lifelong changes of brain structures and thus plasticity. To examine correlation of age-related brain changes, volumetric measurements such as brain tissue [1] or cortical thickness [2] were proposed. Regression on brain MRI has been used by Davis et al.. [3] to depict age-related shape and volume changes. White matter changes in diffusion tensor imaging (DTI) due to aging were reported by analyzing changes of scalar diffusion measures such as fractional anisotropy (FA) and mean diffusivity (MD) in manually selected brain [4,5] or tract regions [6]. Analysis was most often performed by regional measurements of FA or MD across different age groups, or by linear regression of such measurements versus age. Whereas most of this previous analysis uses manually selected regions of interest strategically placed in subregions of known fiber tract locations, clinical research is often interested in the analysis of whole fiber tracts associated with specific tasks or cognitive function. Age-related changes of tract diffusion properties should therefore be represented at various positions of tracts, informing researchers about anatomical location and type of diffusion changes. This paper presents a methodology for age regression of fiber tract diffusion properties. We follow the work of Goodlett et al.[7] where fiber bundles are parametrized with arc-length and attributed with local diffusion properties summarized across perpendicular cross-sections. These parametrized representations with diffusion attributes can thus represented by functions whose shape represents variation of diffusion as a function of locality, f(s), with s = [0 … l]. Diffusion is a scalar derived from tensors, so that f(s) can be a function of FA or MD, for example. Measuring such tract functions from subjects with different age t results in a set of functions parametrized as f(t, s). Using a constrained PCA technique (CPCA), we demonstrate how the complex shape and time change information encoded in f(t, s) can be simplified to a model where regression on one coefficient efficiently represents locality, type and magnitude of age-related diffusion changes.

This paper is organized as follows: Section 2 describes the concept of constrained PCA. The processing pipelines for population-based segmentation of fiber tracts and for analysis of age-related diffusion changes of tracts are described in section 3. Section 4 summarizes results on several tracts from the healthy aging study, followed by validation experiments (section 5).

2 Constrained Principal Component Analysis (CPCA)

Our problem is defined as follows: Given a set of parametrized functions of diffusivity attributed with age, f(t, s), we would like to isolate the major systematic change of functional shapes with respect to age from population noise. Such a dimensionality reduction cannot be optimally achieved by principal component analysis (PCA) since any decomposition to modes of major variability would not consider the time attribute. We therefore fit the set of functions into a space that is constrained to a smooth change with time. The first or first few of the resulting coefficients can then be used for age regression via polynomial fit.

We propose the use of constrained Principal Component Analysis (CPCA) [8,9] to perform data reduction that incorporates the age or time effect in the observed data. For a set of discretized functions f(t, s) that represents the observed population data at different points of time, we first construct a data matrix Z_t,s indexed by time t along the row and indexed by the tract spatial parametrization s along the column (as in standard PCA). CPCA linearly separates the data matrix given multiple constraint variables or external information about the structure of the data along the row or columns of the observations. For constraint variables α₁,···, α_j, a data matrix M is rewritten as:

$$M=\stackrel{\sim }{M}({\alpha }_1)+\cdots +\stackrel{\sim }{M}({\alpha }_j)+R$$ (1)

where R is the residual data matrix. Unlike standard PCA, CPCA decomposes the individual data matrices for each constraint variable rather than the original unconstrained data matrix. This ensures that the subspaces generated by CPCA encode the effects of the constraint variables. In our tract analysis, we have one constraint variable along the row (time) and Z can be formulated as:

$$Z=\stackrel{\sim }{Z}(t)+R$$ (2)

where Z̃(t) is a projection of each individual function onto the space of polynomials a₀ + a₁t +···+ a_kt^k that smoothly varies with time and R is the residual data matrix. We have chosen the projection to the space of polynomials to constrain the analysis to changes that vary smoothly with time and exclude noise and population variability. Given a matrix of polynomial basis functions B and the matrix of polynomial coefficients that best fit the observed data C, Z̃(t) = BC and Z = BC + R.

Within the constrained CPCA framework, all analysis of the diffusion properties is performed within the subspaces of the constrained data matrix BC and we exclude the residual matrix to ensure that noise is not attributed as age effect. A polynomial up to a degree 4 was used in our experiments.

3 Application to Age-Related White Matter Tract Changes

Driving Application: White Matter Change in Healthy Aging

We have access to a database of high-resolution, 3-Tesla MR images of 100 healthy subjects aged 20 to 76, with 20 subjects per decade divided equally by gender. All subjects are carefully screened for the presence of brain-related disease. Images acquired include T1, T2, MRA, and diffusion tensor images. After screening for image quality of successful DTI scans, 86 DTI could be selected for this study. DTI was done on a Siemens Allegra 3T head-only scanner: One image without diffusion gradients together with diffusion weighted images along six gradient directions with a b-value of 850, repeated 2 times for averaging. TR/TE were 7500/73ms, the matrix size was 64x64, and voxel resolution was isotropic with 2x2x2mm³.

Atlas Building of Tensor Images

The images are initially aligned by affine registration of the non-diffusion weighted images to a template T2 (MNI) image using mutual information, which ensures mapping into a normative brain space. A scalar feature, the greatest eigenvalue of the Hessian of the FA image, is computed for each subject [7]. A diffeomorphic, fluid registration is computed for the set of feature images [10] using the affine alignment as an initalization. The result of the registration is a set of transformations that smoothly map each subject image into a common atlas coordinate system and can also be used to map structures from the atlas back to each subject’s native space. All tensor images deformed into the atlas space are averaged to produce a template tensor image for the atlas, which is used to extract fiber tracts for the white matter structures of interest. We extracted the four bundles genu, splenium, mid corpus callosum (mid-cc) and motor-sensory via fiber tractography in atlas space to ensure correspondence across subjects (Fig. 1 right), using a standard streamline integration method. These tracts were then mapped back into each subjects native space to obtain diffusion measures for that subject. This results in a set of tracts in the atlas space with equivalent geometry but diffusion values extracted from each subject. Validation and comparison to individual tractography has been done, but space constraints prohibit inclusion in this paper. Since subjects have different ages equally distributed between 19 and 68, we therefore get sets of functions represented as f(t, s) with s representing parametrization by arc-length and t subject age. The scalar diffusion measures f can be chosen as FA, MD (trace), axial diffusivity (AD, λ₁) and radial diffusivity (RD, (λ₂ + λ₃)/2).

Fig. 1.

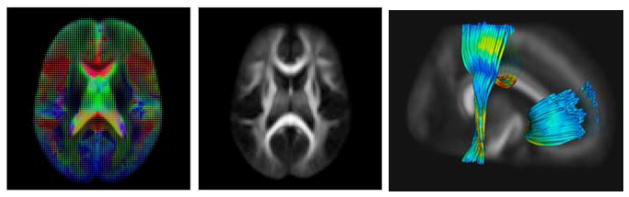
DTI population atlas: Left Tensor field of atlas computed over 86 subjects: Middle: FA map calculated from tensor atlas. Right: Typical fiber bundles used in this study. Mid corpus callosum, sensory-motor and genu tracts are color-coded with FA, with [0 ··· 1] ranging from dark blue over yellow to red.

CPCA on a Set of Functions

Figure 2 illustrates the example of FA of the mid-cc tract represented by a set of functions coded with age. We can observe that FA at the middle part close to the corpus callosum does not change strongly with age but that the sidelobes, i.e. bundle locations close to the cortex, show significant decrease of FA with age. The complexity of age change and the type and amount of change at different tract locations are not visible due to large population variability. We then applied constrained CPCA to the set F A(t, s) in order to decrease dimensionality and determine major shape variation of the FA functions with age. Standard PCA is applied for comparison.

Fig. 2.

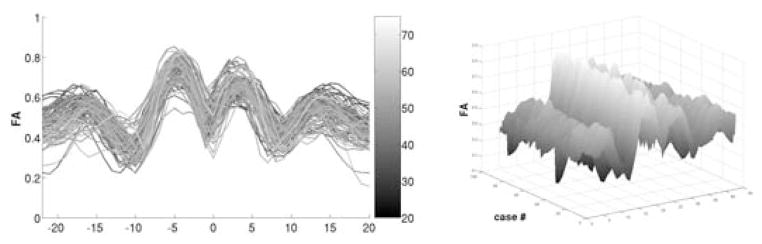
Plot of all mid-cc tract functions of FA shaded by age (left) and 3D representation of the age set sorted by age (young to old from right to left)

Figure 3 illustrates results for PCA (top) and CPCA (bottom) for the mid-cc tract. Plots in the left column show samples projected into the space of the first two principal components and age. Samples are color-coded with age. As expected, PCA does not present obvious structure versus age but CPCA results in a low-dimensional continuous path for the 86 samples. The middle column illustrates projection to only the first component versus age, with overlay of 4th-order regression on age. Again, PCA does not depict a clear relationship to age, but age regression of CPCA (middle, bottom) illustrates a nonlinear continuous change with age, with large changes between age 20 and 30, than flattening till age 50, and accelerated change thereafter. The right column displays the FA tract functions reconstructed from the first component for all 86 subjects. Unlike PCA, CPCA encodes age change of the FA functions, clearly visible as the systematic age-sorted coloring of CPCA and random coloring of PCA.

Fig. 3.

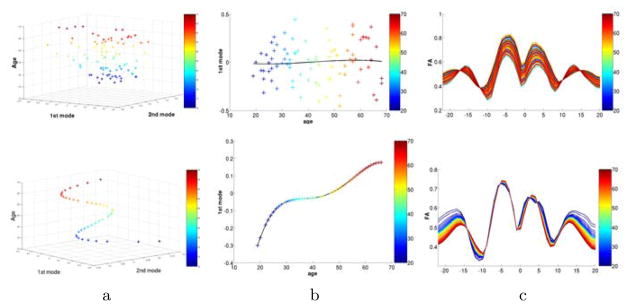
Results of the analysis of FA of the mid-cc tract with standard PCA (top) and constrained CPCA (bottom). Age is encoded in color. a) The first two modes plotted against age. b) Only first mode versus age with overlay of 4th order age regression. c) FA functions of 86 subjects projected onto the first component. Columns b and c demonstrate that data reduction by CPCA does encode a strong age-related relationship not seen in PCA (see random coloring in PCA versus age-sorted coloring in CPCA in column c).

Our main aim is a simplified model of changes of diffusion functions with respect to age. As seen in Fig. 4(b) left for the mid-cc tract, most energy is concentrated on the first component of CPCA. Moreover, age correlation is very strong for the first component but nonsignificant for the others. PCA is shown for comparison. We therefore chose to model the diffusion changes by age regression within the subspace of only the first component. Here, we fit a polynomial up to a degree 4 to the projections of the functions to the first component (see Fig. 3 column b). Using this polynomial fit, we can then reconstruct the expected diffusion properties for each age in the range of interest. Fig. 4(a) illustrates the reconstructions for ages 20,30,40,50 and 60 and for various diffusion properties (FA, MD, AD, RD) along the mid-cc tract. Age is encoded using a gray-scale color map. The figures show nonlinear differences across age and also variations of change patterns as a function of tract location.

Fig. 4.

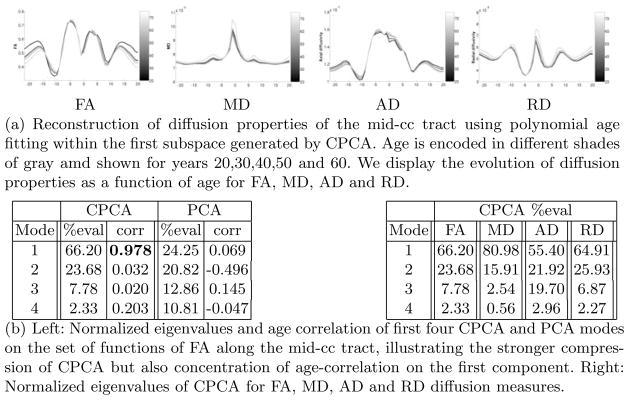
Results of mid-cc tract for four different diffusion measures

4 Results

The CPCA analysis has been applied to the major four fiber tracts genu, splenium, mid-cc and motor-sensory. Fig. 5 displays age-related changes as calculated for these four tracts. We illustrate the reconstructed diffusion functions of FA and MD for age 20, 30, 40, 50 and 60, using projection onto the first CPCA component and 4th-order regression. The plots clearly illustrate that the age-related trajectory of white matter diffusion is nonlinear, i.e. different decades present different changes, and second that diffusion changes vary significantly as a function of tract location. FA in genu, splenium and mid corpus callosum, for example, shows only minor age change in the center region but significant FA decrease in the peripheral parts close to the cortex. The motor-sensory tract (arc-length left to right presents superior to inferior tract location, see also Fig. 1) also demonstrates age-changes of FA close to the cortex but large MD changes along the middle part between cortex and internal capsule. The splenium tract showed much more population variability than the genu, which is reflected in the MD analysis. Major conclusions related to the specific age study might be too preliminary, but this discussion demonstrates how the results could be interpreted by clinical researchers. The caption in Fig. 5 also lists the age correlation for the first component of CPCA which is highly significant for all 4 tracts.

Fig. 5.

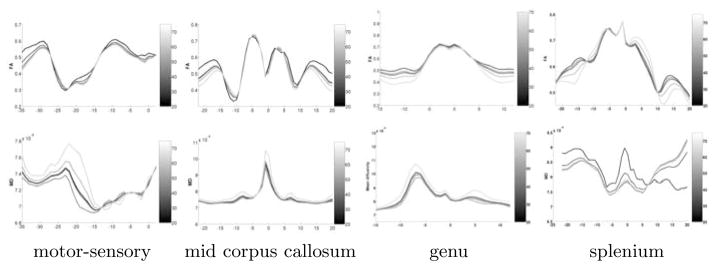
Reconstructed functions of FA (top row) and MD (bottom row) for four fiber tracts. Age is encoded as gray-scale for years 20, 30, 40, 50, and 60. Age-correlation of CPCA was significant for all 4 tracts (0.93, 0.98, 0.85 and 0.95).

5 Validation

We validate the choice of an age-constrained subspace by leave-one-out cross validation. Given a set of N functions, we perform leave-one-out analysis by excluding one function from the set followed by performing data reduction and regression using the reduced set. We then project the one excluded function to the computed first principal component, and compare the projected score against the expected score from the polynomial fitting. We decided to use this approach to validate the data reduction by projection to a lower dimensional subspace and also the age-based fitting within this subspace. This analysis was performed on the subspaces computed by CPCA and regular PCA. The values for the average of the sum_x|proj(x) - fit(x)|² measure for motor-sensory, mid-cc, genu and splenium are (0.01975, 0.02298, 0.01698, 0.03778) for CPCA and (0.02499, 0.03051, 0.02367, 0.12504) for PCA. As seen, the CPCA consistently provides lower prediction error compared to the unconstrained PCA. The prediction error for PCA is higher for the noisy diffusion data in the splenium tract.

6 Discussion

We present a methodology for analyzing age-related changes of white matter measured along fiber tracts. The framework includes population-based mapping of DTI to a common coordinate space, tractography, and representation of tensor-derived scalar diffusion measures along tracts. CPCA constrained to age is then applied to the sets of diffusion functions to reduce dimensionality to the first principal mode. The PCA projections are performed on the curves reconstructed from the polynomials. We thus enforce the dominant eigenvectors to be strongly driven by time and not necessarily be the original eigenvectors. We preferred this global approach versus regression at each spatial position to account for along-tract correlation. Results on major tracts demonstrate feasibility and represent type of changes of FA and MD as reported elsewhere. However, our preliminary analysis predicts that age changes might not be simplified to linear regression but show more complex time and space variations. The strong dimensionality reduction while still encoding age-related changes as a function of tract location might be a benefit for biostatisical analysis. We plan to apply the method to clinical studies of aging and early brain development, with testing for group differences of change trajectories of white matter diffusion. A limitation might be the independent analysis of tensor-derived diffusion parameters. In the future, we will explore joint analysis of multiple features, e.g. FA and tensor norm or AD and RD, or even full tensors.