Estimation of Smooth Growth Trajectories with Controlled Acceleration from Time Series Shape Data

Abstract

Longitudinal shape analysis often relies on the estimation of a realistic continuous growth scenario from data sparsely distributed in time. In this paper, we propose a new type of growth model parameterized by acceleration, whereas standard methods typically control the velocity. This mimics the behavior of biological tissue as a mechanical system driven by external forces. The growth trajectories are estimated as smooth flows of deformations, which are twice differentiable. This differs from piecewise geodesic regression, for which the velocity may be discontinuous. We evaluate our approach on a set of anatomical structures of the same subject, scanned 16 times between 4 and 8 years of age. We show our acceleration based method estimates smooth growth, demonstrating improved regularity compared to piecewise geodesic regression. Leave-several-out experiments show that our method is robust to missing observations, as well as being less sensitive to noise, and is therefore more likely to capture the underlying biological growth.

1 Introduction

The study of time dependent shapes is an emerging field in Computational Anatomy, with potential application to early brain development, aging studies, or the analysis of evolving pathologic structures. As longitudinal data becomes more widely available, the need for computer models of anatomical evolution becomes increasingly important. Two approaches have been followed so far: the first consists in computing a realistic growth scenario from cross-sectional time-series data, like in [4,10,6,3]. The second approach involves estimating several individual growth trajectories and combining them with a framework for 4D registration between growth trajectories or 4D atlas construction, to statistically analyze the growth variability within a population, like in [13,8,14,7,9].

In any case, the methods rely greatly on the estimation of growth models from time series data, which are sparsely distributed in time. Growth models provide a tool to generate shapes at any instant in time (within the interval defined by the data), offering us the opportunity to continuously measure shape properties. This is in contrast to using sparse measurements such as volume or circumference for 1D regression absent the shape information. The problem can be stated as “temporal shape regression” and can be solved by purely descriptive statistical methods like the extension of kernel regression to Riemannian manifolds [4], or by generative statistical models which define a parameterized family of realistic growth models and the one which best fits the actual data is estimated based on a regularized least-square criterion [8,7,2]. We favor this last approach, since it makes explicit the assumptions which drive the estimation of growth trajectories and therefore enables the inclusion of realistic biological priors to constrain the estimation.

The growth model in [7] is based on a continuous flow of diffeomorphisms, with piecewise geodesics interpolating between shapes. This method estimates continuous non-linear growth between shapes, but does not guarantee differentiable growth as the speed of evolution is discontinuous at observation time-points. Our work is motivated by the assumption that the evolution of biological tissue is inherently smooth in time. If we consider the growth of biological tissue as a mechanical system driven by external forces, then the evolution of any particle on an anatomical surface is continuous with continuous derivative and therefore does not change direction instantaneously, as observed in the growth model estimated from [7].

Temporal smoothness can be enforced via smooth interpolation between 3D deformations estimated at discrete time-points, using B-splines or polynomial interpolation as in [11,1]. However, these approaches are not based on the inference of a generic growth model, which captures the dynamics of the shape changes over time.

Based on these considerations, we propose a new growth model parameterized by acceleration, rather than velocity as in the large deformation setting of [12]. The estimated acceleration could be considered an indication of the forces which drive the growth of the anatomical structures. From this parameterization, we gain one order of differentiability and guarantee that shape evolution is smooth in both space and time. We further deviate from the large deformations framework by introducing a new regularization term which accounts for the total amount of acceleration. As a consequence, our model does not constrain the flow of deformation between shapes to be geodesic, or close to a geodesic path. By contrast, the approach in [16] estimates twice differentiable trajectories as random perturbations of geodesic paths.

The evaluation of our new methodology on real anatomical surfaces reveals the differences between our approach and piecewise geodesic regression. Our regression yields a twice differentiable evolution with improved regularity, thus discarding more noise from the data to fit a more realistic growth trajectory. Also, we demonstrate that volume measurements taken out of our 3D shape regression are compatible with a 1D regression of these measurements, whereas piecewise geodesic regression appears to overfit. Lastly, we show via leave-several-out experiments that our method better interpolates between data and is therefore more robust to missing observations. This suggests a greater ability to capture the underlying growth of the anatomical structures.

2 Shape Regression Parameterized by Acceleration

The problem of longitudinal shape regression involves inferring a continuous shape evolution from a discrete set of shapes S_ti observed at time t_i. Shape evolution is modeled as the continuous deformation of a baseline shape S₀, formally defined as R_t = φ_t(S₀) where R_t corresponds to S₀ having undergone the transformation φ_t with t varying continuously within the time interval. The time-varying deformation φ_t is a general transformation from 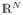to 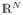with φ₀(S₀) = S₀. The baseline shape is deformed over time to closely match the observed shapes (R_ti ~ S_ti) while the rigidity of the deformation is controlled via a regularity term. This leads to a variational problem in the form of a trade off between fidelity to data and regularity. For measuring shape similarity, we follow the work of [15], modeling shapes as currents.

We define the acceleration field a(x, t) at point x and time t as a vector field of the form

$$a(x,t)=\sum _{i=1}^N{K}^V(x,x_i(t)){\alpha }_i(t)$$ (1)

where x_i are the shape points carrying a point force vector α_i, and $K^V(x,y)=\mathit{exp}(-{\left|\right|x-y\left|\right|}^2/{\lambda }_V^2)$ is a Gaussian kernel of dimension mass⁻¹ with standard deviation λ_V controlling the spatial extent at which the acceleration field varies.

The time-varying point force vectors α_i(t) parameterize a flow of deformation φ_t(x_i(t)) by the integration of the 2nd-order ODE φ̈_t(x_i(t)) = a(x_i(t), t) with initial position x_i(0) and initial velocity ẋ_i(0). The initial positions of the particles are assumed to be fixed at the vertices of the baseline shape, while the initial velocity of the particles have to be determined by the algorithm.

Let x(t), a(t), and α(t) be the concatenation of the x_i(t)’s, a_i(t)’s, and the α_i(t)’s. This parameterization leads to the specific regression criterion

$$E(\stackrel{.}{\mathbf{x}}(0),\mathit{\alpha }(t))=\sum _{t_i}{\left|\right|{\phi }_{t_i}(\mathbf{x}(0))-\mathbf{x}(t_i)\left|\right|}_{W\ast }^2+\gamma {\int }_0^T{\left|\right|\mathbf{a}(t)\left|\right|}_V^{2}dt$$ (2)

where || · ||_W* is the norm on currents and regularity is defined as ${\left|\right|\mathbf{a}(t)\left|\right|}_V^2=\mathit{\alpha }(t)K^V(\mathbf{x}(t),\mathbf{x}(t))\mathit{\alpha }(t)$, interpreted as the ‘total amount of acceleration’, measured using the norm in the reproducing kernel Hilbert space defined by the interpolating kernel [5].

3 Description of the Algorithm

We implement an adaptive step size gradient descent algorithm. The gradient of the criterion (2) with respect to force vectors and initial velocity is written as

$${\nabla }_{{\alpha }_i(t)}E(t)=2\gamma {\alpha }_i(t)+{\eta }_i^{\stackrel{.}{x}}(t)\text{and}{\nabla }_{{\stackrel{.}{x}}_i(0)}E={\eta }_i^{\stackrel{.}{x}}(0)$$ (3)

where variables ${\eta }_i^x(t)$ and ${\eta }_i^{\stackrel{.}{x}}(t)$ satisfy coupled ODEs shown in Appendix A.

During each iteration of gradient descent, the trajectories of shape points are computed by solving the 2nd-order ODE φ̈_t(x_i(t)) = a(x_i(t), t) using a Verlet integration scheme. The auxiliary variables ${\eta }_i^x(t)$ and ${\eta }_i^{\stackrel{.}{x}}(t)$ are computed using an Euler method with prediction/correction. Eventually we compute the gradients given in equation (3). The algorithm may be started with zero initial velocity and force, though we notice faster convergence when initial velocity is determined by registration between the baseline and first target shape as in [15].

4 Experiments

To evaluate our method, we use longitudinal image data from a child that has been scanned 16 times between four and eight years of age. The MRI data is first rigidly aligned to establish a common reference frame. The intracranial volume and lateral ventricles are segmented from each image using an EM based tissue classification algorithm and a level-set based active contour segmentation tool.

We estimate the evolution of the intracranial surface using a regression model based on the piecewise geodesic flow of diffeomorphisms as in [7]. The standard deviation of the Gaussian kernel controlling deformation is set to 50 mm, roughly 30% of the diameter of the baseline intracranial surface. For the scale of currents we use 20 mm, with a regularity weight of 0.1. Finally, time is discretized in increments of 0.0425 years. We also produce a growth trajectory using our proposed method with the same parameter settings as above except we weight regularity by 0.01 (the two weighted terms cannot be compared since they have different ‘physical’ dimension). The parameters were tuned empirically to produce regressions of comparable quality with both methods.

Shape evolution is considerably smoother using our proposed regression model as compared to the piecewise geodesic model. This is particularly evident in the trajectories of the shape points across time, a subset of which are shown in Fig. 1. It is an important distinction that the trajectories estimated by our method are not a smoothing of the piecewise geodesic method. Rather, the trajectories are the result of fundamentally different assumptions on the underlying model which results in a more realistic estimation of growth.

Fig. 1.

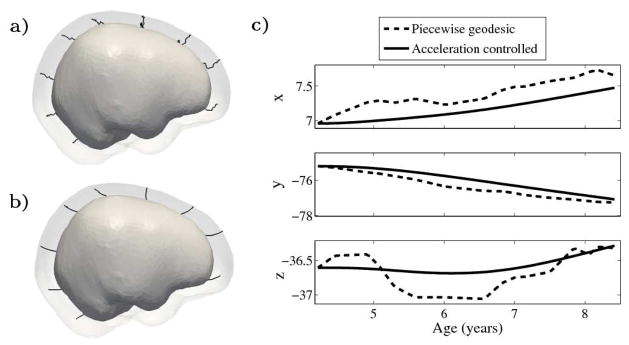
a) and b) Shape evolution from baseline (solid) to final configuration (transparent) using a model based on piecewise geodesics (a) and our method (b) with point trajectories for selected particles displayed as black lines. c) The path of a point on the forebrain is decomposed into coordinates. Growth is estimated using 15 target shapes, highlighting the speed discontinuities present in the piecewise geodesic evolution.

The smoothness constraints imposed by our model limit the shape variation we can capture over short time periods. Consequently, we investigate the accuracy of our model by examining how closely we match the target data: our estimated growth scenario decreases the initial sum of squared residual by 148%, compared to a 153% decrease from the piecewise geodesic method. While our method does not come as close to matching the target data, this suggests that our method is less sensitive to noise and less likely to overfit.

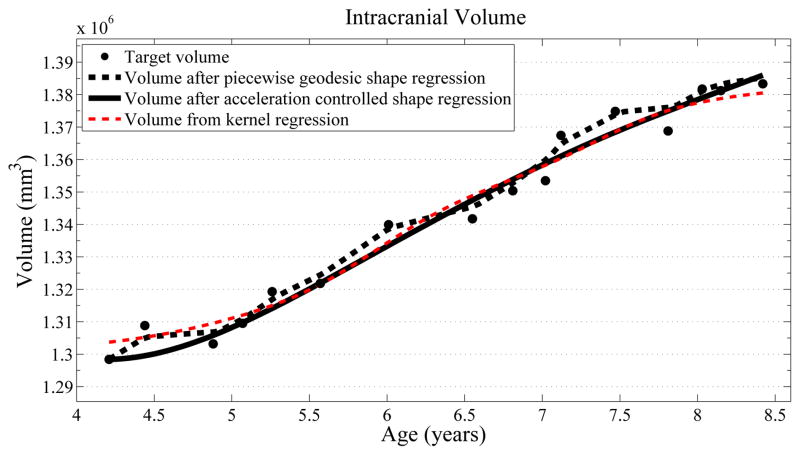
Next, we investigate the application of our model to the study of measurements derived from shape. Here we obtain a continuous non-linear model of volume, shown in Fig. 2. The results are consistent with a 1D regression model, such as kernel regression, applied to the sparse volume measurements. However, we have focused our modeling efforts on capturing the evolution of shape, with continuous volume measurements resulting naturally from the estimated growth. In addition, the piecewise geodesic method appears to be overfitting, producing unrealistic volume measurements, further suggesting that our method is more robust in the presence of noisy data.

Fig. 2.

Volume measurements derived from our growth model are consistent with a kernel regression (σ = 0.5) performed on the sparse volume measurements. Our model describes the continuous evolution of shape and volume is measured after regression.

Finally, we consider the evolution of the lateral ventricles, which exhibit considerably more complexity than the intracranial surface. The horns of the segmented lateral ventricles are as thin as a few millimeters, making regression particularly challenging. As with the intracranial volume, ventricle growth is estimated using a piecewise geodesic model and our acceleration based model. The scale of deformation is set at 6 mm, the scale of currents to 2 mm, and regularity is weighted by 0.1 and 0.01, respectively.

The impact of missing data is examined by performing leave-several-out experiments, the results of which are summarized in Fig. 3. In all experiments, selected target shapes were chosen as uniformly across time as possible. Our method demonstrates robustness with respect to the number of target shapes, with only minimal increase in the coefficient of determination R² when using more than 3 targets. This suggests that our method captures the underlying growth with limited data, as additional target data does not greatly alter the estimation. In contrast, piecewise geodesic regression is more influenced by additional target data and is therefore likely to overfit.

Fig. 3.

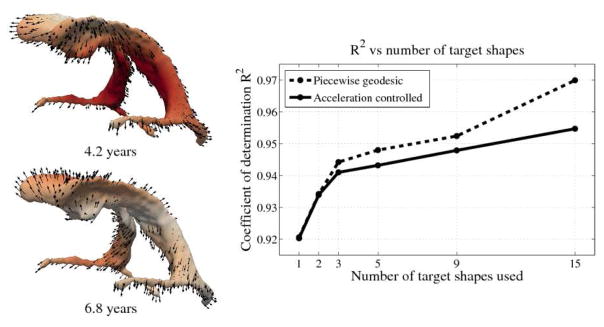
Left: Snapshots from a continuous shape evolution of lateral ventricles estimated by our regression model. Acceleration vectors are displayed on the surface, with color denoting magnitude. Right: The impact of the number of target shapes on R².

5 Conclusion

We have introduced a new 2nd-order regression model for estimating smooth evolution from time dependent shapes. This is based on a new way of parameterizing growth by acceleration rather than velocity. We show on real anatomical data that, compared to the standard piecewise geodesic model, our method is less sensitive to noise introduced during segmentation and is robust to missing data, and is therefore more likely to characterize the underlying biological growth. The evolution of volume extracted after shape regression was shown to be compatible with a 1D regression on the observed volume measurements. Our method may be improved by additionally solving for initial positions of the shape points as in [7], to address the apparent underestimation of initial volume in Fig. 2.

Note that the new concept introduced in this paper has been implemented for 3D-surface data modeled as currents but can be easily adapted to a variety of other data and metrics. Future work will focus on the interpretation of the estimated acceleration in terms of external forces exerted on the biological tissue. This will enable the addition of more biological and mechanical priors.

A Differentiation of the Regression Criterion

Using matrix notation, we denote the current state of the system of shape points by the vector X(t) = (x(t), ẋ(t))^t concatenating position and velocity of every point. The state of the system is evolved by the following differential equation:

$$\stackrel{.}{\mathbf{X}}(t)=F(\mathbf{X}(t),\mathit{\alpha }(t))=\left(\begin{array}{c}\stackrel{.}{\mathbf{x}}(t)\\ \ddot{\mathbf{x}}(t)=\mathbf{K}(\mathbf{x}(t),\mathbf{x}(t))\mathit{\alpha }(t)\end{array}\right)$$ (4)

with initial condition X(0) = X₀ = (x₀, ẋ₀)^t.

We now rewrite (2) as $E(\mathbf{X}(t))={\sum }_{t_i}A(\mathbf{X}(t_i))+\gamma {\int }_0^{T}L(\mathbf{X}(t),\alpha (t))dt$. Let δE be a variation of the criterion E with respect to a variation δα(t) of the impulse vectors α(t), which induces a variation of the state variable X(t):

$$\delta E=\sum _{t_i}(d_{\mathbf{X}(t_i)}{A}_i)\delta \mathbf{X}(t_i)+\gamma {\int }_0^T({\partial }_{\mathbf{X}(t)}L(t))\delta \mathbf{X}(t)+({\partial }_{\mathit{\alpha }(t)}L(t))\delta \mathit{\alpha }(t)dt$$ (5)

The ODE in (4) shows that these variations δX(t) satisfy a linear inhomogeneous ODE. The method of variation of parameters gives the solution

$$\delta \mathbf{X}(t)=R_{0t}\delta {\mathbf{X}}_0+{\int }_0^T{R}_{ut}{\partial }_{\mathit{\alpha }(u)}F(u)\delta \mathit{\alpha }(u){\mathbf{1}}_{\{u<t_i\}}du$$ (6)

where $R_{ut}=exp\left({\int }_u^t{\partial }_{\mathbf{X}(s)}F(s)ds\right)$ and 1_{t≤ti} = 1 if ≤ t_i and 0 otherwise.

Plugging this equation into (5) leads to:

$${\nabla }_{\mathit{\alpha }}E(t)={\partial }_{\mathit{\alpha }(t)}L{(t)}^t+{\partial }_{\mathit{\alpha }(t)}F{(t)}^t\mathit{\eta }(t)\text{and}{\nabla }_{{\mathbf{X}}_0}E=\mathit{\eta }(0)$$ (7)

where we denote the auxiliary variable η(t) as

$$\mathit{\eta }(t)=\sum _i{\nabla }_{{\mathbf{X}}_{t_i}}{A}_i{\mathbf{1}}_{\{t\le t_i\}}+{\int }_t^T{\partial }_{\mathbf{X}}L{(u)}^t+{\partial }_{\mathbf{X}}F{(u)}^t\mathit{\eta }(u)du$$ (8)

From now on, we decompose the vectors into 2 blocks (the x-component and the ẋ-component). Due to the definition of A, L and F, we have ∇_X(ti) A_i = (

∇_xi A_i 0)^t, ∂_XL = (γα^t(∂₁ + ∂₁)(K(x, x)α) 0)^t, ∂_αL = 2γα^tK(x, x), ${\partial }_{\mathbf{X}}F=\left(\begin{array}{cc}\mathbf{0}& \mathbf{1}\\ ({\partial }_1+{\partial }_2)\mathbf{K}(\mathbf{x},\mathbf{x})\mathit{\alpha }& \mathbf{0}\end{array}\right)$ and ${\partial }_{\mathit{\alpha }}{F}^x=(\begin{array}{ll}\mathbf{0}\hfill & \mathbf{K}(\mathbf{x},\mathbf{x})\hfill \end{array})$.

Therefore, the gradient of the regression criterion with respect to the L² metric given in (7) is now equal to: ∇_αE(t) = K(x(t), x(t)) (2γα(t) + η^ẋ(t)), where we have decomposed the auxiliary variable η into η = (η^x, η^ẋ).

The matrix K(x(t), x(t)) is precisely the Sobolev metric induced by the kernel on the set of L² functions, so the gradient is given in coordinates as in (3).