Evaluation of removable statistical interaction for binary traits

Abstract

This paper is concerned with evaluating whether an interaction between two sets of risk factors for a binary trait is removable and fitting a parsimonious additive model using a suitable link function to estimate the disease odds (on the natural logarithm scale) when an interaction is removable. Statisticians define the term “interaction” as a departure from additivity in a linear model on a specific scale on which the data are measured. Certain interactions may be eliminated via a transformation of the outcome such that the relationship between the risk factors and the outcome is additive on the transformed scale. Such interactions are known as removable interactions. We develop a novel test statistic for detecting the presence a removable interaction in case-control studies. We consider the Guerrero and Johnson family of transformations and show that this family constitutes an appropriate link function for fitting an additive model when an interaction is removable. We use simulation studies to examine the type I error and power of the proposed test and to show that an additive model based on the Guerrero and Johnson link function leads to more precise estimates of the disease odds parameters and a better fit when an interaction is removable. The proposed test and use of the transformation are illustrated using case-control data from three published studies. Finally, we indicate how one can check that, after transformation, no further interaction is significant.

Introduction

There is a long-standing interest in the evaluation of interactions in genetic and epidemiology studies. The ability to conduct candidate-gene and high-throughput association studies has accelerated the efforts to examine gene-gene and gene-environment interactions in relation to disease risk using a variety of statistical models (see [1 – 6] and several other works reviewed in [7 – 9]). The interest in interactions is also stimulated by the hope that significant interaction effects identified using statistical models can provide insights into biological interactions that underpin the disease [7, 10]. This has also caused some confusion regarding the very meaning of the term “interaction” and substantial confusion as to what is actually being estimated or tested from a biological viewpoint [11, 12].

The term “interaction” is defined in statistical analyses as a departure from additivity in a linear model on a selected scale of measurement [13, 14]. This departure, also referred to as “statistical interaction”, measures the change in the effect on the outcome of one risk factor when the values(s) of another risk factor(s) is (are) altered. Public health burden and policy implications are generally assessed on the scale of risk. A departure from additivity on this scale is an interaction that is often denoted as “synergy” in the epidemiology literature [15]. The term “biological interaction” refers to the joint action of two or more risk factors, which can occur even when there is no statistical interaction [12]. Consider, for example, the etiology of cancer. A normal cell undergoes a malignant transformation through a process termed tumor progression, which is driven by a succession of cellular abnormalities (for example, somatic mutations) that accumulate over multiple stages [16, 17]. Under this paradigm, the risk factors associated with disease must be involved at the biological level. This can occur even in the absence of a statistical interaction. Thus, a simple additive statistical model can still provide useful insights about the joint role of risk factors that are putative contributors to underlying biological interactions. The specific biological interactions, however, may only be understood by conducting additional molecular experiments using human biospecimens or animal models [18, 19].

The term “epistasis”, defined as a masking effect that occurs when one genetic factor prevents another from manifesting its effect [19], is also used to refer to different types of interactions [20]: physical interaction between genes (functional epistasis), masking effect (compositional epistasis), and departure from additivity i.e., statistical interaction (statistical epistasis). Functional epistasis can occur even in the absence of a statistical interaction and may be best understood using laboratory experiments. It has been argued recently that compositional epistasis is a more biological notion than statistical epistasis, in the sense that, under compositional epistasis, the disease risk of some individuals in the population is associated with the simultaneous presence of all the risk factors under consideration [21]. This notion has been used to derive lower bounds for the magnitudes of the interaction parameters in a statistical model, which are used as a non-standard test for compositional epistasis [22].

Statistical interactions (henceforth, simply referred to as “interactions”) correspond to higher order effects. Including interaction terms in a model is equivalent to including higher degree polynomial terms, and the resulting model is non-additive in the risk factors. Large interactions may induce curvature effects [23]. On a selected scale of observation, interaction terms may be required to obtain the best fitting model that can explain the curvature effects. Certain types of interactions may be eliminated by a transformation of the outcome so that the resulting model is additive in the risk factors [24, 25]. Such interactions are referred to as removable interactions. When the disease trait (or outcome) is binary, the transformation corresponds to specifying a link function that is additive in the risk factors. The transformation must be invertible so that the results can be back-transformed for clinical interpretation on the original scale, but the removed interactions will reappear in the model on the original scale [12]. When a removable interaction exists, it is pragmatic to eliminate it, whenever it is possible do so, and fit an additive model on the transformed scale to attain model parsimony and a more precise fit to the data [12].

The ultimate objective of this paper is efficient estimation of disease odds (say, on the natural logarithm scale) using a parsimonious additive model, once we have decided that two factors (for example, single nucleotide polymorphisms and/or environmental exposures) are involved in disease risk. Our objective here is not in detecting interaction once main effects of two risk factors are known to exist since, as noted above, the existence of main effects automatically implies that there is a biological interaction (see also [11, 12]). We focus on case-control studies where the outcome is binary. We first develop a one degree-of-freedom score test for the null hypothesis that there is no interaction on the logistic scale or that it is not removable. The alternative hypothesis is that there is a removable interaction. Once the existence of a removable interaction on the logistic scale is established, we use the Guerrero and Johnson family of transformations [26] for fitting an additive model to the data and estimate the log disease odds. Our focus here is thus on removable interaction, because if there is no removable interaction there is no point in seeking a change of scale to obtain additivity. In the Discussion, we indicate a test for non-removable interaction; unless this is non-significant, we cannot expect an additive model to fit the data well.

This paper is organized as follows. In Section 2 we describe a novel test statistic for removable interactions and describe its asymptotic distribution. In Section 3 we describe different types of interactions. In Section 4 we use simulations to evaluate the type I error and power of the proposed test statistic under the various types of interactions. In Section 5 we illustrate the proposed test using published data from case-control studies of advanced colorectal adenoma [27], bladder cancer [28], and endometrial cancer [29]. In Section 6 we describe the Guerrero and Johnson [26] transformation. In Section 7, we conduct simulation studies to examine the estimation and model fitting properties of this transformation under various types of interaction. In Section 8 we apply this transformation to the case-control studies described in Section 5 to fit additive models, and examine the properties of these models. We conclude the paper with a discussion in Section 9, including a test to verify that after transformation no significant interaction remains.

2. Methods

2.1 Preliminaries

Consider a case-control study where the cases are affected with a disease of interest and the controls do not have that disease. Two risk factors X and Z having L₁ and L₂ levels, respectively, are measured on each individual. Let N_ij and M_ij denote the number of cases and controls, respectively, having the i-th level of X and the j-th level of Z (i = 1, 2, …, L₁; j = 1, 2, …, L₂). Given the total number of individuals N_ij + M_ij in the (i,j)-th risk factor sub-class, N_ij is distributed as a binomial random variable with disease probability p_ijgiven by:

$$\mathrm{P}\left({\mathrm{N}}_{\text{ij}}\right|{\mathrm{N}}_{\text{ij}}+{\mathrm{M}}_{\text{ij}})=(\begin{array}{c}{\text{N}}_{\text{ij}}+{\mathrm{M}}_{\text{ij}}\\ {\text{N}}_{\text{ij}}\end{array})\times {\mathrm{p}}_{\text{ij}}^{{\text{N}}_{\text{ij}}}\times {(1-{\mathrm{p}}_{\text{ij}})}^{{\mathrm{M}}_{\text{ij}}}$$ (Equation 1)

It is assumed that the disease probability p_ij depends upon X and Z, and is modeled as follows. We assume that there are no empty sub-classes i.e., N_ij ≠ 0 and M_ij ≠ 0 for all i,j. Let g₀{.} denote the logit link function i.e., given a real number x ∈ (0,1), ${\mathrm{g}}_0(\mathrm{x})=\text{logit}(\mathrm{x})=\text{log}\left\{\frac{\mathrm{x}}{1-\mathrm{x}}\right\}$. Thus g₀(p_ij) is the log disease odds in the (i,j)-th risk factor sub-class. We model p_ij as:

$${\mathrm{g}}_0({\mathrm{p}}_{\text{ij}})=\mu +{\alpha }_{\mathrm{i}}+{\beta }_{\mathrm{j}}+{\gamma }_{\text{ij}},$$ (Equation 2)

where µ is the baseline risk, α_i is the main effect of the i-th level of X (i = 1, …, L₁), β_j is the main effect of the j-th level of Z (j = 1, …, L₂), and γ_ij is the effect of the interaction between the i-th level of X and the j-th level of Z, subject to the constraints $\sum _{\mathrm{i}=1}^{{\mathrm{L}}_1}{\alpha }_{\mathrm{i}}=0$, $\sum _{\mathrm{j}=1}^{{\mathrm{L}}_2}{\beta }_{\mathrm{j}}=0$, $\sum _{\mathrm{i}=1}^{{\mathrm{L}}_1}{\gamma }_{\text{ij}}=0$ for j = 1, …, L₂, and $\sum _{\mathrm{j}=1}^{{\mathrm{L}}_2}{\gamma }_{\text{ij}}=0$ for i = 1, …, L₁. In vector notation we write α = (α₁, α₂, …, α_L1), β = (β₁, β₂, …, β_L2), γ = (γ₁₁, γ₁₂, …, γ_L1L2).

To estimate the logarithm of disease odds, we can estimate the parameters μ, α, β, and γ and plug these into the right hand side of Equation (2). To obtain the parameter estimates, we can define the design matrix, denoted W₁, for the above model (Equation 2) by specifying orthogonal contrasts corresponding to the main and interaction effects. The unknown parameters μ, α, β, and γ can be estimated using the iteratively reweighted least squares (IRLS) approach for a generalized linear model [30]. An asymptotically equivalent approach is the weighted least squares (WLS) method for logistic regression analysis of contingency tables. The WLS method considers outcomes ξ_ij that are estimated as ${\widehat{\xi }}_{\text{ij}}=\text{log}\left(\frac{{\mathrm{N}}_{\text{ij}}}{{\mathrm{M}}_{\text{ij}}}\right)$ for the (i,j)-th risk factor sub-class, where “log” is the natural logarithm. In vector notation, we write ξ̂ = (ξ̂₁₁, ξ̂₁₂,…, ξ̂_L1L2). The WLS estimates are given by ${({\mathbf{W}}_1^{\mathbf{T}}{\mathbf{A}}_1^{-1}{\mathbf{W}}_1)}^{-1}{\mathbf{W}}_1^{\mathbf{T}}{\mathbf{A}}_1^{-1}\widehat{\xi }$, where ${\mathbf{A}}_1=\text{diag}\{\frac{1}{{\mathrm{N}}_{\text{ij}}}+\frac{1}{{\mathrm{M}}_{\text{ij}}}\}$ denotes the asymptotic variance of ξ̂ [31, 32] and the notation diag{s_ij} denotes a diagonal matrix with diagonal entries equal to s_ij, i = 1, 2, …, L₁ and j = 1, 2, …, L₂. Both the IRLS and WLS estimates can be obtained using standard statistical software packages.

The definition of an interaction depends upon the definition of what constitutes a main effect, and the interaction terms must be interpreted along with the corresponding main effect terms [12, 33]. Therefore, when a term γ_ij is included in the model, the corresponding α_i and β_j terms should also be included in the model. When there is no interaction i.e., when γ_ij = 0 for all i = 1, …, L₁ and j = 1, …, L₂, the right hand side of Equation (2) becomes μ + α_i + β_j. This is a parsimonious additive model that requires estimation of fewer parameters to estimate the log disease odds relative to a model that includes interaction terms. We can test the null hypothesis H₀: γ_ij = 0 for all i = 1, …, L₁ and j = 1, …, L₂ against the alternative H_A: γ_ij ≠ 0 for some (i, j) using a likelihood ratio statistic to determine whether a parsimonious model may be applicable to the data. Here H_A is a general family of alternatives. The likelihood ratio test statistic, denoted Λ_Ghas an asymptotic central chi-squared distribution with (L₁ – 1) × (L₂ – 1) degrees of freedom under H₀ when all the required regularity conditions hold [30]. The subscript “G” is used in Λ_G to indicate that that this test statistic corresponds to the general family of alternatives.

2.2 Removable interaction

Equation (2) states that, under the known link function g₀{.}, disease risk is a non-additive function of the risk factors. Suppose there is an alternative link function f{.} under which disease risk is additive in the risk factors:

$$\mathrm{f}\left\{{\mathrm{p}}_{\mathrm{i}\mathrm{j}}\right\}={\mu }_0+{\alpha }_{\mathrm{i}0}+{\beta }_{\mathrm{j}0}\mathrm{,}$$ (Equation 3)

where μ₀, the α_i0, and the β_j0 are unknown parameters. If f{.} is known, then we may fit Equation (3) to attain model parsimony and possibly a more precise fit. However, f{.} is generally unknown in practice. Hence, we may fit a model using g₀{.}. If g₀{.} is linear in f{.}, then g₀{p_ij} is additive in the risk factors, and we may replace f{.} with g₀{.} on the left hand side of Equation (3). If g₀{.} is a non-linear function of f{.} then a quadratic approximation may provide a better fit than an additive model when the data are fitted using the link function g₀{.} [24]:

$${\mathrm{g}}_0\left\{{\mathrm{p}}_{\text{ij}}\right\}\approx {\eta }_0+{\eta }_1\mathrm{f}\left\{{\mathrm{p}}_{\text{ij}}\right\}+{\eta }_{\text{2}}{\left[\mathrm{f}\right\{{\mathrm{p}}_{\text{ij}}\left\}\right]}^2,$$ (Equation 4)

where η₀, η₁, and η₂ are unknown parameters. Suppose Equation (4) indeed provides a better fit than an additive model. Further, suppose the right hand side is a strictly monotonic function of f{p_ij} in the range (min[f{p_ij}], max[f{p_ij}]), where the minimum and maximum are taken over the values of f{p_ij} estimated for each risk factor sub-class. Then there exists a transformation of the outcome such that the model is additive on the transformed scale [24].

Assuming that the monotonicity condition holds, we may further approximate Equation (4) as [24]:

$${\mathrm{g}}_0\left\{{\mathrm{p}}_{\text{ij}}\right\}\approx \mu +{\alpha }_{\mathrm{i}}+{\beta }_{\mathrm{j}}+\theta \times {\alpha }_{\mathrm{i}}\times {\beta }_{\mathrm{j}},$$ (Equation 5)

The last term on the right hand side of Equation (5) is a quadratic term taking the form γ_ij = θ×α_i×β_j that characterizes the interaction effects. The parameter θ is a scalar that quantifies non-additivity. When there are main effects (i.e., α_i ≠ 0 and β_j ≠ 0 for at least one i and j), there is no interaction (i.e., all estimable γ_ij = 0) if and only if θ = 0, and Equation (5) becomes an additive model. When θ ≠ 0, the model is non-additive. In this case, since monotonicity holds, the model is intrinsically linear, and we may empirically look for a transformation of the outcome to identify a link function f{.} and then fit an additive model on the transformed scale [33].

Monotonicity induces a useful class of alternatives for evaluating interactions – namely, removable interactions. Under the assumption of monotonicity, we can test the null hypothesis of no interaction against the alternative that an interaction exists and is removable, instead of considering the general family of alternatives; i.e., we can test γ_ij = 0 for all i and j against the alternative γ_ij ≠ 0 for some (i,j) and that it takes the form γ_ij = θ×α_i×β_j. When we assume that the main effects are not all 0, this is equivalent to testing H₀: θ = 0 against the alternative H_A: θ ≠ 0. When H₀ is rejected, this would be an indication that there is removable interaction, suggesting that it may be sufficient to fit an additive model to the data under an alternative link function in order to estimate the log disease odds in the various risk factor sub-classes. However, when H₀ is not rejected, this would mean that there is no removable interaction: either there is no interaction at all or there is only non-removable interaction (possibly because the monotonicity assumption fails). In this paper, we focus on the evaluation of removable interaction, but this may need to be complemented by a test for significant non-removable interaction (see Discussion). When there is evidence for a removable interaction, it is pragmatic to eliminate it via a transformation of the outcome to attain model parsimony and a precise fit, especially if all the interactions are removable [12]. In the following subsections, we develop a score test for removable interaction.

2.2.1 Score statistic for evaluating removable interaction

The score function for θ, evaluated at H₀, is denoted U. It can be obtained using Equation (5) (see Appendix A). The estimate of U, denoted Û, is given by:

$$\widehat{\mathrm{U}}={\mathbf{1}}^{\mathrm{T}}\widehat{\mathbf{D}}\mathbf{A}\widehat{\mathbf{\gamma }}=\sum _{\mathrm{i}=1}^{{\mathrm{L}}_1}\sum _{\mathrm{j}{=}_1}^{{\mathrm{L}}_{\text{2}}}{\widehat{\alpha }}_{\mathrm{i}}\times {\widehat{\beta }}_{\mathrm{j}}\times {(\frac{1}{{\mathrm{N}}_{\text{ij}}}+\frac{1}{{\mathrm{M}}_{\text{ij}}})}^{-1}\times {\widehat{\gamma }}_{\text{ij}},$$ (Equation 6)

where

• 1 is a column vector of unities of length L₁×L₂;

• D̂ = diag{α̂_i × β̂_i} is a diagonal matrix of dimension L₁×L₂, where α̂_i (i = 1, 2, …, L₁) and β̂_j (j = 1, 2, …, L₂) are the estimated main effects of X and Z obtained from an additive model (by setting θ = 0 in Equation 5);

• γ̂ are the estimated residuals of the additive model, and provide an estimate of the interaction effects γ;

• A is a diagonal matrix of dimension L₁×L₂, where the diagonal elements represent the inverse of the variance of g₀{p_ij}. When the sample size is large, A is equivalent to ${\mathbf{A}}_1^{-1}$, where A₁ is given in Section 2.1.

2.2.2 Estimating the main effects and residuals from an additive model

Data from a case-control study are unbalanced since all the N_ij + M_ij are not the same. Therefore, the main effects must be defined appropriately to obtain orthogonal estimates of the residuals, as described below.

The elements of γ̂ are of the form γ̂_ij = ξ̂_ij − μ̂ − α̂_i − β̂_j, where μ̂, α̂_i, β̂_j are estimates of the baseline risk and the main effects of the i-th level of X and j-th level of Z, respectively, and ξ̂_ij are defined in Section 2.1. Denoting v_ij as weights for the (i,j)-th subclass, these estimates are, in general, given by Scheffé [14] as:

$$\widehat{\mu }=\frac{\sum _{\mathrm{i}=1}^{{\mathrm{L}}_1}\sum _{\mathrm{j}=1}^{{\mathrm{L}}_2}{\mathrm{v}}_{\text{ij}}{\widehat{\xi }}_{\text{ij}}}{\sum _{\mathrm{i}=1}^{{\mathrm{L}}_1}\sum _{\mathrm{j}=1}^{{\mathrm{L}}_2}{\mathrm{v}}_{\text{ij}}},{\widehat{\alpha }}_{\mathrm{i}}=\frac{\sum _{\mathrm{j}=1}^{{\mathrm{L}}_2}{\mathrm{v}}_{\text{ij}}{\widehat{\xi }}_{\text{ij}}}{\sum _{\mathrm{j}=1}^{{\mathrm{L}}_2}{\mathrm{v}}_{\text{ij}}}-\widehat{\mu },{\widehat{\beta }}_{\mathrm{j}}=\frac{\sum _{\mathrm{i}=1}^{{\mathrm{L}}_1}{\mathrm{v}}_{\text{ij}}{\widehat{\xi }}_{\text{ij}}}{\sum _{\mathrm{i}=1}^{{\mathrm{L}}_1}{\mathrm{v}}_{\text{ij}}}-\widehat{\mu }.$$ (Equation 7)

The standard approach for estimating the parameters of the additive model weights all the study subjects equally. The resulting estimates are the WLS estimates given by (W^TAW)⁻¹ W^T Aξ̂, where W is the design matrix of the additive model with L₁×L₂ rows and L₁+L₂-1 columns. The first column of W is a vector of unities corresponding to the baseline risk, and the next L₁-1 and L₂-1 columns are orthogonal contrasts corresponding to the main effects of X and Z, respectively. When the parameter estimates of Equation (7) are obtained by weighting all the study subjects equally, we have E(γ̂_ij) ≠ 0 even when there is no interaction, i.e., even when γ_ij = 0 for all i and j [11]. [To see this, note that E(ξ̂_ij) = μ + α_i + β_j when there is no interaction.] This suggests that γ̂_ij does not provide an appropriate estimate of the error term under the null hypothesis of no interaction. This issue can be resolved when the weights v_ij are chosen to be proportional (or when they occur in proportional frequencies) i.e., when v_ij = v_i.×v_.j, where v_i. does not depend upon j and v_.j does not depend upon i. A special case of proportional frequencies is the case of equal weights i.e., v_ij = v for all i and j, where v is an arbitrary non-zero real number. When the weights are proportional, it follows from Equation (7) that and $\sum _{\mathrm{i}}{\mathrm{v}}_{\mathrm{i}.}{\widehat{\alpha }}_{\mathrm{i}}=0$ and $\sum _{\mathrm{j}}{\mathrm{v}}_{.\mathrm{j}}{\widehat{\beta }}_{\mathrm{j}}=0$. The following results apply for proportional (and, hence, for equal) weights (see Appendix B):

• Result 1: When the weights are proportional, we have E(γ̂_ij) = 0 in the absence of an interaction, regardless of the choice of v_i. and v_.j.

• Result 2: The expected value of any contrast in α̂_i (or β̂_j) is independent of the weights when there is no interaction.

It then follows that the spaces of dimension L₁ – 1, L₂ – 1, and 1, spanned by α̂_i, β̂_j, and μ̂_j, respectively, are mutually orthogonal. These results suggest that, without loss of generality, we can obtain the parameter estimates of the additive model using equal weights by considering v_i. = 1 for all i = 1, …, L₁ and v_.j = 1 for all j = 1, …, L₂. The parameter estimates can be obtained as (W^TW)⁻¹W^Tξ̂. The estimated residuals are, therefore, given by γ̂ = (I–H)ξ̂, where H = W(W^TW)⁻¹W^T is a symmetric and idempotent matrix.

2.2.3 Test statistic

We can calculate Û (Equation 6) using the parameter estimates obtained as described above. We propose the following statistic, denoted Λ_R, for testing H₀: θ = 0 against H_A: θ ≠ 0:

$${\mathrm{\Lambda }}_{\mathrm{R}}=\frac{{\widehat{\mathrm{U}}}^2}{\mathrm{V}\mathrm{a}\mathrm{r}\left(\widehat{\mathrm{U}}\right|\widehat{\alpha },\widehat{\beta })},$$ (Equation 8)

where Var(Û|α̂,β̂)=1^TD̂A(I−H)A⁻¹ (I−H)AD̂ 1 is the conditional variance of Û. The subscript “R” is used in Λ_R to emphasize that the alternative hypothesis represents a family of removable interactions. This statistic has parallels to Tukey’s one-degree of freedom test for interaction in a balanced two-way analysis of variance with one observation per cell [34]. Here Λ_R is a test statistic for evaluating removable interactions in unbalanced data.

2.2.4 Asymptotic distribution of Λ_R

Distribution under the alternative hypothesis

Since the main effects and interactions are defined using orthogonal contrasts, γ̂ is independent of α̂ and β̂. Suppose the null hypothesis of no interaction does not hold. Under the alternative family of removable interactions; given α̂ and β̂, Û has conditional mean $\mathrm{E}\left(\widehat{\mathrm{U}}\right|\widehat{\mathbf{\alpha }},\widehat{\mathbf{\beta }})=\theta \times \sum _{\mathrm{i}=1}^{{\mathrm{L}}_1}\sum _{\mathrm{j}=1}^{{\mathrm{L}}_2}{\widehat{\alpha }}_{\mathrm{i}}\times {\widehat{\beta }}_{\mathrm{j}}\times {(\frac{1}{{\mathrm{N}}_{\mathrm{i}\mathrm{j}}}+\frac{1}{{\mathrm{M}}_{\mathrm{i}\mathrm{j}}})}^{-1}\times {\alpha }_{\mathrm{i}}\times {\beta }_{\mathrm{j}}$ (see Appendix C). The conditional variance of Û is Var(Û|α̂, β̂) given above. Given α̂ and β̂, each component of γ̂ has an asymptotic normal distribution with mean γ_ij = θ × α_i × β_j under the alternative hypothesis of a removable interaction. Thus, Û (Equation 6) is a weighted sum of asymptotically normally distributed random variables, where the weights α̂_i and β̂_j (and N_ij and M_ij) are known. Hence, Û has an asymptotic normal distribution with mean and variance given above. Therefore, the conditional distribution of Λ_R, given α̂ and β̂, is chi-squared with 1 degree of freedom and non-centrality parameter $\mathrm{\Delta }(\widehat{\mathbf{\alpha }},\widehat{\mathbf{\beta }})=\frac{{\left\{\mathrm{E}\right(\widehat{\mathrm{U}}|\widehat{\mathbf{\alpha }},\widehat{\mathbf{\beta }})\}}^2}{\text{Var}\left(\widehat{\mathrm{U}}\right|\widehat{\mathbf{\alpha }},\widehat{\mathbf{\beta }})}$, which depends on the estimated main effects. Obtaining the unconditional distribution (and, hence, the power of Λ_R) involves obtaining expectations of the form E{Δ^t(α̂, β̂)} for various values of t. Since the numerator and denominator of Δ involve terms of the form ${(\frac{1}{{\mathrm{N}}_{\mathrm{i}\mathrm{j}}}+\frac{1}{{\mathrm{M}}_{\mathrm{i}\mathrm{j}}})}^{-1}$, evaluating these expectations, and hence obtaining a closed form for Δ, is not straightforward. We use simulations to evaluate the power of Λ_R under different parametric configurations in Section 4.

Null distribution

To obtain the asymptotic null distribution of Λ_R, we first assume that main effects exist i.e., α_i ≠ 0 and β_j ≠ 0 for at least one (i,j). Under H₀: θ = 0, the non-centrality parameter is 0. Therefore, the conditional null distribution of Λ_R, given α̂ and β̂, is a central chi-squared distribution with 1 degree of freedom, which is also its unconditional null distribution. Suppose at least one of the risk factors under consideration does not have an effect on the outcome i.e., the true model is g₀(p_ij) = μ (when neither X nor Z has an effect), or μ + α_i (when Z has no effect), or μ + β_j (when X has no effect). Then the interaction effect is not estimable. Suppose, however, we fit the additive model g₀(p_ij) = μ + α_i + β_j, and test for the presence of a removable interaction. In Appendix C we show that, in this case, the asymptotic null distribution of Λ_R has a non-standard form. This non-standard distribution has a slightly heavier tail than a central chi-squared distribution with 1 degree of freedom, resulting in a small inflation in the type I error – particularly when neither risk factor has a main effect and the two risk factors are independent. We observe this phenomenon in our simulations. We also observe that, although the asymptotic null distribution of Λ_R departs from a central chi-squared distribution with 1 degree of freedom, the departure is not severe in our case, suggesting that we may use this distribution as a benchmark for assessing the statistical significance of Λ_R in practical settings.

3. Types of interactions

To evaluate the type I error and power of Λ_R, we simulated risk factors X and Z for cases and controls. We assumed thresholds C₁ and C₂ for the levels of X and Z, respectively, for disease risk through the following model:

$$\text{Logit}\{\mathrm{P}(\text{disease}|\mathrm{X},\mathrm{Z})\}=\mu +{\alpha }_1\times \mathrm{I}(\mathrm{X}\ge {\mathrm{C}}_1)+{\beta }_1\times \mathrm{I}(\mathrm{Z}\ge {\mathrm{C}}_2)+{\gamma }_{11}\times \mathrm{I}(\mathrm{X}\ge {\mathrm{C}}_1)\times \mathrm{I}(\mathrm{Z}\ge {\mathrm{C}}_2),$$ (Equation 9)

where I(.) denotes the indicator function. Before proceeding further, it will be useful to understand the different types of interactions that can result from this model. In this model, X and Z contribute to disease risk only when X ≥ C₁ and Z ≥ C₂. Therefore, the disease risk factors are intrinsically binary. Denote I_X = I(X ≥ C₁) and I_Z = I(Z ≥ C₂). The outcome summaries are ξ_ij = logit{ P(disease | X, Z) } = logit{ P(disease | I_X=i, I_Z=j) }, where (i,j) = (0,0), (0,1), (1,0), or (1,1). The ordering of the ξ_ij induces different types of interactions [34]. Without loss of generality, we assume that the sub-class (I_X,I_Z) = (0,0) has the smallest disease risk. There are 6 possible orderings of the ξ_ij, providing 4 major types of interactions, denoted Type A, Type B, Type C, and Type D ([35]; see Table 1 of Haldane’s paper or Figure 1 of this paper); Types A and D each contain two subtypes. These interactions can be interpreted as given below. Although we consider these four types of interactions here, additional types may be obtained by allowing some of the inequalities to be equalities (for example, [36]).

Table 1.

Empirical type I errors of Λ_R and Λ_G based on 1000 simulations under each parametric configuration. Here α₁ and β₁ are the main effects of the two risk factors, and ρ is the correlation between the risk factors.

ρ	α1	β1	ΛR	ΛG
0	log(1) = 0	0	0.100	0.047
	log(2) = 0.6931	log(2)	0.031	0.048
	log(3) = 1.0986	log(3)	0.042	0.055
0.50	log(1) = 0	0	0.049	0.045
	log(2) = 0.6931	log(2)	0.056	0.048
	log(3) = 1.0986	log(3)	0.050	0.057
0.80	log(1) = 0	0	0.035	0.046
	log(2) = 0.6931	log(2)	0.071	0.049
	log(3) = 1.0986	log(3)	0.067	0.046

Figure 1.

The different types of interactions as classified by Haldane [34]. I_X and I_Z are two binary risk factors. ξ₀₀, ξ₀₁, ξ₁₀, and ξ₁₁ are the outcomes in the four risk factor sub-classes. In each panel, the horizontal axis shows the two values of I_X, and the vertical axis shows the ξ_ij values, ordered differently under the different types of Interactions. The black and red lines show the outcomes as a function of I_X when I_Z = 0 and I_Z = 1, respectively. Type A interaction has two subtypes – one of them is shown in the top left panel, and the second subtype can be obtained by switching the ordering of ξ₁₀ and ξ₀₁, which will not alter the shape of the figure. Type D interaction has two subtypes in a similar manner.

Type A interaction

The outcome summary under condition I_X=1 is as large or larger than that under I_X=0 for both levels of I_Z, and similarly for the summary under the two conditions for I_Z i.e., ξ₀₀ ≤ ξ₁₀, ξ₀₁ ≤ ξ₁₁, ξ₀₀ ≤ ξ₀₁, ξ₁₀ ≤ ξ₁₁. This is equivalent to: (i) μ ≤ μ + α₁; (ii) μ ≤ μ+β₁; (iii) μ+α₁ ≤ μ+α₁+β₁+γ₁₁; (iv) μ+β₁ ≤ μ+α₁+β₁+γ₁₁. Therefore, α₁ ≥ 0, β₁ ≥ 0, and γ₁₁ ≥ max{−α₁, −β₁ }.

Type B interaction

The condition I_X=1 has outcome summary as large as or larger than that under I_X=0 when I_Z=0. The ordering is reversed when I_Z=1. In contrast, the condition I_Z=1 has summary as large as or larger than that under I_Z=0 for both levels of I_X, i.e, ξ₀₀ ≤ ξ₁₀, ξ₀₁ ≥ ξ₁₁, ξ₀₀ ≤ ξ₀₁, ξ₁₀ ≤ ξ₁₁. Therefore, α₁ ≥ 0, β₁ ≥ 0, and −β₁ ≤ γ₁₁ ≤ −α₁ when β₁ ≥ α₁.

Type C interaction

The condition I_X=1 has outcome summary as large as or larger than that under I_X=0 for both levels of I_Z. However, the condition I_Z=1 has summary as large as or larger than that under I_Z=0 when I_X=0, and the ordering is reversed when I_X=1, i.e, ξ₀₀ ≤ ξ₁₀, ξ₀₁ ≤ ξ₁₁, ξ₀₀ ≤ ξ₀₁, ξ₁₀ ≥ ξ₁₁. Therefore, α₁ ≥ 0, β₁ ≥ 0, and −α₁ ≤ γ₁₁ ≤ − β₁ when α₁ ≥ β₁. Type C interaction is similar to Type B interaction, with the roles of I_X and I_Z reversed.

Type D interaction

This interaction does not preserve any specific ordering of the outcome summaries, but rather defines a cross-over effect i.e., ξ₀₀ ≤ ξ₁₀, ξ₀₁ ≥ ξ₁₁, ξ₀₀ ≤ ξ₀₁, ξ₁₀ ≥ ξ₁₁. This leads to the following conditions: α₁ ≥ 0, β₁ ≥ 0, and γ₁₁ ≤ min{−α₁, −β₁}.

Chatterjee et al [37] developed a one-degree of freedom test for detecting a causal allele when there is an interaction between two alleles, and demonstrated the properties of their test statistic for a binary trait and two binary risk factors, using the odds ratio as outcome. Of the interaction models considered by these authors, the multiplicative model is equivalent to a Type A interaction, and all their other interaction models can be written as Type A, B, or C, depending upon the odds ratios assumed for the four cells. Their “cross-over” effect gives the smallest odds ratio (<1) to the cell (I_X=0,I_Z=0), the cells (I_X=0,I_Z=1) and (I_X=1,I_Z=0) have odds ratios equal to 1, and the cell (I_X=1,I_Z=1) has an odds ratio greater than 1. Thus, the “cross-over” effect of Chatterjee et al [37] is not a cross-over effect in the sense of a Type D interaction, but can be written as an interaction of Type A, B, or C, depending upon the magnitudes of the cell values.

Cordell [19] and VanderWeele [21, 22] considered compositional epistasis that is quantified as follows: the presence of at most one risk factor does not result in any change in disease risk, while the simultaneous presence of both the risk factors changes (for example, increases) risk. In our notation, assuming γ₁₁ > 0, the compositional epistasis considered by these authors can be quantified as: ξ₀₀ = ξ₁₀ = ξ₀₁ = μ, and ξ₁₁ = μ + γ₁₁ > μ. This comes under the rubric of Haldane’s Type A interaction since ξ₀₀ ≤ ξ₀₁, ξ₁₀ ≤ ξ₁₁, ξ₀₀ ≤ ξ₁₀ and ξ₀₁ ≤ ξ₁₁.

In Appendix D we use the example of two independent binary risk factors to show that Type A, but not Type D interaction, generally satisfies the monotonicity condition. Indeed, Type A would satisfy strict monotonicity when α₁ > 0, β₁ > 0, and γ₁₁ > max{−α₁, −β₁}. We also show that certain kinds of Type B and Type C interactions satisfy the monotonicity condition. Therefore, the test under removable alternatives, Λ_R, is likely to be a powerful approach for identifying interactions of Types A, and certain kinds of interactions of Types B and C, but not interactions of Type D. The test under the general alternatives, Λ_G, is likely to be beneficial mainly for identifying interactions of Type D.

For simplicity and for ease of explanation, we have described the four types of interactions using 2×2 contingency tables. For this setting, since Type A interaction generally obeys the monotonicity condition and is, hence, removable, compositional epistasis may also be largely removable. However, for larger contingency tables, an interaction term may be needed to obtain a better fit to the data even after a transformation in the presence of compositional epistasis.

4. Simulation

We first conducted a simulation study to establish that Λ_R has adequate power to detect a removable interaction.

4.1 Set up

We simulated data for 1000 cases and 1000 controls by considering two risk factors – X having L₁ = 3 levels with marginal frequencies P(X = 1) = 0.70, P(X = 2) = 0.20, and P(X = 3) = 0.10, and Z having L₂ = 2 levels with marginal frequencies P(Z = 1) = 0.9 = 1 – P(Z = 0). For each person, we generated X and Z using these marginal probabilities and setting the correlation between I_X and I_Z to be ρ ∈ {0, 0.50, 0.80}, where ρ = 0 implies that the risk factors are independent. The baseline parameter μ was chosen by setting the marginal disease probability to be 10%. Given X and Z, the binary disease status for each individual was generated using the model given by Equation (9) with C₁ = 3 and C₂ = 2. To calculate type I error, we set γ₁₁ = 0 and {α₁, β₁} ∈ {0, log(2)=0.6931, log(3)=1.0986}. There are no main effects when α₁ = β₁ = 0. In this case we anticipate Λ_R to have a non-standard null distribution, which would impact the type I error. To calculate power, we set α₁ = β₁ = log(2) = 0.6931, and set values of γ₁₁ in the relevant ranges to represent Type A and D interactions (see Section 3). Note that when α₁ = β₁, interactions of Types B and C are essentially subsumed under Type A interaction. Therefore, we present results for power under Type A and D interactions. We also generated data under compositional epistasis by setting α₁ = β₁ = 0 and γ₁₁ ≠ 0.

A total of 1000 data sets were generated under each parametric configuration. Each data set was analyzed using logistic regression for contingency tables by defining orthogonal contrasts for the main and interaction effects. We tested for removable interaction using Λ_R, and evaluated its significance at the 5% level by using the central chi-squared distribution with one degree of freedom as the null distribution. As a benchmark, we also tested the null hypothesis of no interaction against the family of general alternatives using the test statistic Λ_G, and evaluated its significance using a central chi-squared distribution with (L₁–1) × (L₂–1) degrees of freedom as the null distribution. Under each parametric configuration, the empirical type I error and power of each test statistic are defined as the fraction of data sets out of 1000 where that test statistic is significant.

4.2 Results

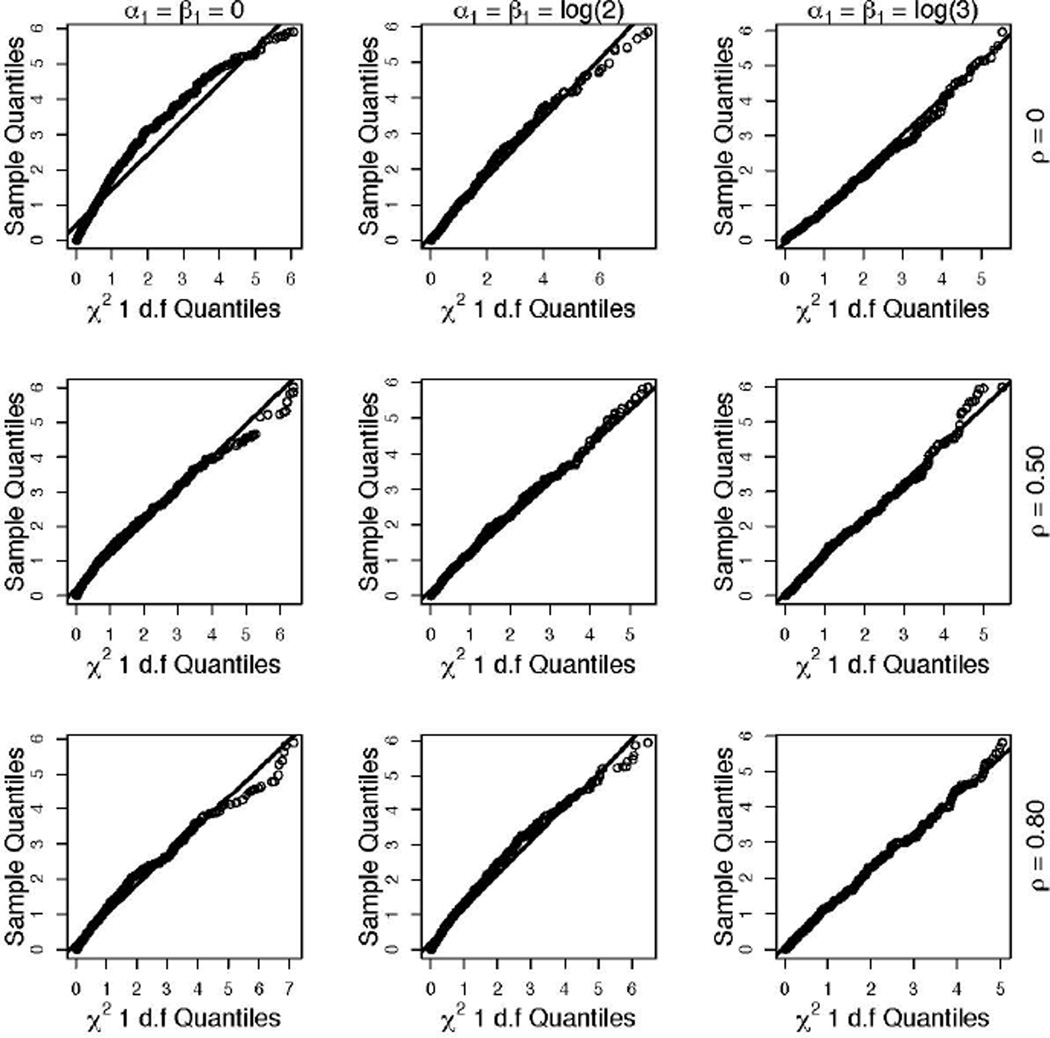
Table 1 shows the empirical type I error rates at the nominal significance level of 0.05. As expected, Λ_G had a nominal type I error rate. When α₁ ≠ 0 and β₁ ≠ 0, Λ_R had type I error close to the nominal rate under all the parametric configurations considered. Any departure of these type I errors from the nominal rate of 5% may be attributed to random variation. This can be seen in Figure 2, which shows the quantile-quantile plots of the empirical distribution of Λ_R versus the quantiles of a central chi-squared distribution with 1 degree of freedom. Figure 2 shows that when α₁ = 0, β₁ = 0, and ρ = 0, the values of Λ_R are slightly larger than expected, resulting in an empirical type I error of 0.10. Otherwise, in general, the empirical null distribution of Λ_R is remarkably close to a central chi-squared distribution with 1 degree of freedom.

Figure 2.

Quantile-quantile plots of the empirical values of Λ_R obtained under the null hypothesis of no interaction and expected values under a central chi-squared distribution with one degree of freedom under various parametric configurations. The 3 rows correspond to data generated with correlation between the risk factors as ρ = 0 (uncorrelated), 0.50, and 0.80. The columns correspond to null simulations with different magnitudes of the main effects.

Table 1 also shows the intriguing result that when the risk factors are correlated (ρ = 0.50 and 0.80) and there are no main effects (α₁ = 0 = β₁), the type I error of Λ_R is close to the nominal level (i.e., similar to a setting where the main effects are non-zero). On reflection, this phenomenon may be explained by considering parameter estimation under a generalized linear regression model with the logit link function. For this explanation, let X and Z denote matrices of dimension N × (L₁-1) and N × (L₂-1), respectively, corresponding to the two risk factors, whose columns indicate the levels of the risk factors in each individual. Here N denotes the total number of cases and controls. Further suppose that X and Z are of full rank, where rank (X) ≥ rank(Z). Let X⊗Z denote a matrix of dimension N × (L₁-1)(L₂-1) whose columns are the product of every column of X with every column of Z. Then, the main effects of the risk factors may be estimated under the Fisher scoring approach, using the working likelihood for the model y = Xα + Zβ + X⊗Zγ + error. In this notation, α, β, and γ are parameter vectors of lengths L₁-1, L₂-1, and (L₁-1)(L₂-1), respectively, quantifying the main effects and the interaction effects, and y is the vector of working responses of length N. Suppose the true value of β is 0. Denote H₁ = X(X^TX)⁻¹X^T. Note that H₁ is a symmetric and idempotent matrix and (I – H₁)X = 0, where I is the identity matrix of dimension equal to the total number of cases and controls. Then β may be estimated from the model (I-H₁)y = (I – H₁)Zβ + (I – H₁)X⊗Zγ + (I – H₁)error. When ρ = 0, the columns of X and Z are orthogonal. Hence, we have (I – H₁)Z = Z. However, when ρ ≠ 0, X and Z span the same vector space. Hence, we have (I – H₁)Z ≈ 0, regardless of the value of β. Consequently, we may consider some arbitrary non-zero value for β even when its true value is 0, so that even when X and Z are correlated, the type I error of L_R is similar to when the main effects are non-zero.

Figure 3 shows the empirical power of Λ_R and Λ_G under Type A and Type D interactions and under compositional epistasis. As expected, Λ_R has remarkably good power to detect both Type A interaction and compositional epistasis as being removable. Further, as expected, Λ_R is much less powerful than Λ_G when the interaction is of Type D.

Figure 3.

Empirical power of Λ_R and Λ_G obtained with α₁ = β₂ = log(2) under Type A interaction (Column 1) and Type D interaction (Column 2) under different levels of correlations between the risk factors (Rows 1, 2, and 3). Empirical power under compositional epistasis is shown in Column 3. In each panel, the horizontal axis represents the magnitude of the interaction parameter γ₁₁ used in the simulations. The black lines denote the empirical power of Λ_R and the red lines are the empirical power of Λ_G.

5. Three illustrative examples

Here we illustrate the proposed test using published data from three case-control studies.

5.1 Advanced colorectal adenoma, smoking, and NAT2 acetylation

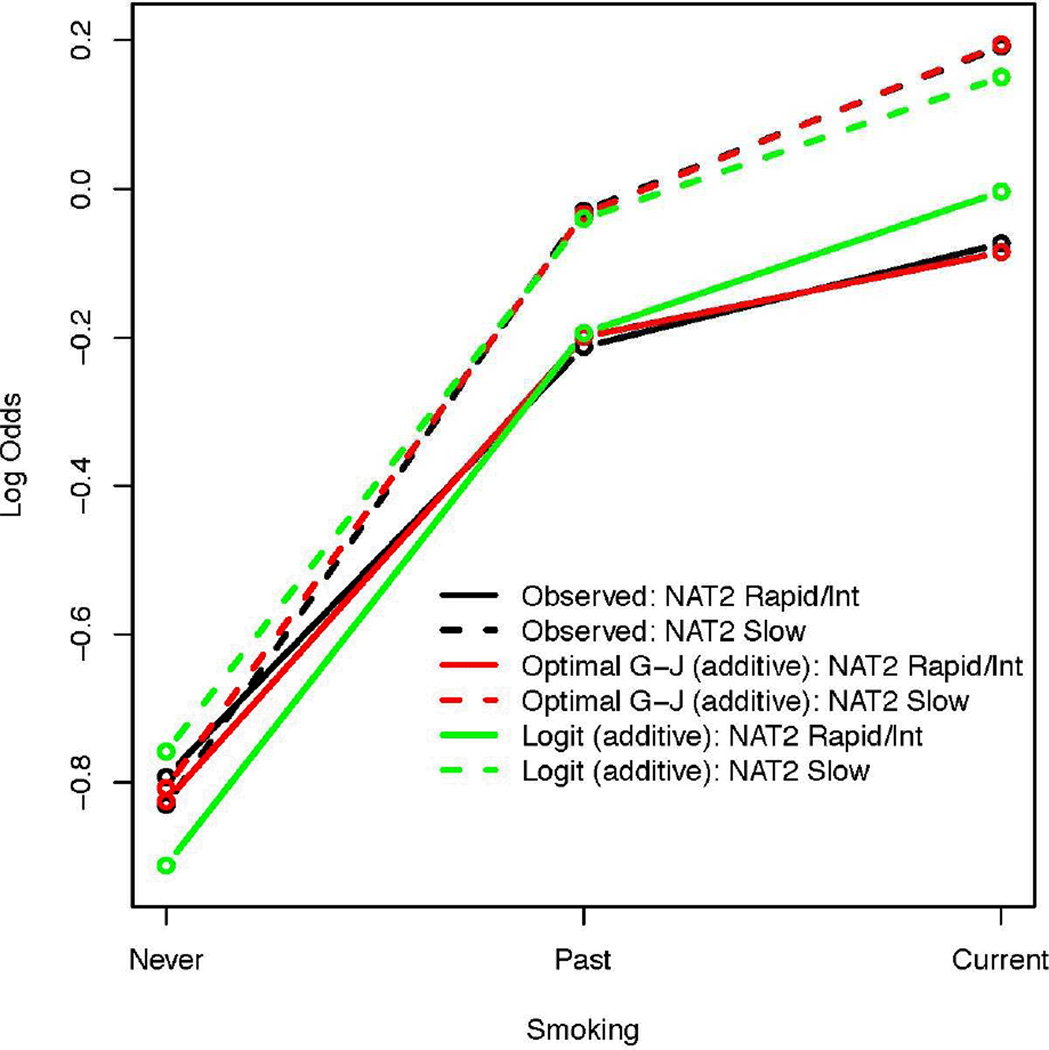
Table 2 gives the number of cases with advanced colorectal adenoma and number of disease-free controls, their smoking status and NAT2 acetylation from a published case-control study reported by Moslehi et al [27]. Smoking has L₁ = 3 levels (never, past, current smoker) and NAT2 acetylation is considered to have L₂ = 2 levels (rapid/intermediate and slow acetylation). The observed log odds values of the 6 risk factor sub-classes are also shown in Table 2 and graphically represented in Figure 4 using bold and dashed black lines. For both never and current smokers, the log odds of NAT2 rapid/intermediate acetylators is smaller than that of the slow acetylators. Although there is a reversal of this trend among past smokers, the difference between the log odds of NAT2 slow versus rapid/intermediate acetylators among past smokers appears to be small. Ignoring this reversal of trend, this figure suggests that an interaction, if it exists, may be of Type A, which is removable.

Table 2.

Case-control data from the advanced colorectal adenoma study of Moslehi et al [27]. Columns 1 and 2 show the levels of smoking and NAT2 acetylation (based on SNP rs1495741). Columns 5, 6, and 7 show the estimated log odds and the standard errors in parentheses based on three models. Note that the full logistic model is a saturated model. Therefore, for this model, the estimated log odds is equal to the observed log odds, and the estimtated standard error is the square root of the sum of the inverse of the number of cases and the number of controls. We refer to these standard errors as the “within class” standard errors. The value of λ used to fit the additive GJ model is shown in parentheses in the last column. The last three rows of the table show the maximum log-likelihood, mean squared error (MSE), Akaike’s AIC, and the Bayes information criterion for the three models.

1	2	3	4	5–7 Estimated log odds (std error) from three models
Smoking	NAT2 acetylation	Case	Control	Full logistic	Additive logistic	Optimal additive GJ (λ = −4.62)
Never	Rapid/Intermediate	92	124	−0.298 (0.138)	−0.319 (0.111)	−0.197 (0.078)
Never	Slow	140	158	−0.121 (0.116)	−0.106 (0.101)	−0.153 (0.095)
Past	Rapid/Intermediate	108	116	−0.071 (0.134)	−0.226 (0.109)	−0.132 (0.080)
Past	Slow	134	153	−0.133 (0.118)	−0.013 (0.102)	−0.070 (0.094)
Current	Rapid/Intermediate	60	52	0.143 (0.189)	0.499 (0.143)	0.163 (0.172)
Current	Slow	115	42	1.007 (0.180)	0.712 (0.137)	1.007 (0.180)
Maximum log-likelihood				−875.308	−879.646	−875.868
MSE				0.0221	0.0561	0.0186
AIC				1762.617	1767.293	1761.735
BIC				1793.61	1787.955	1787.563

Figure 4.

Estimated log odds ratios for the advanced colorectal adenoma study. The horizontal axis shows the three levels of smoking. The vertical axis shows the log odds. The observed log odds for NAT2 rapid/intermediate acetylators and slow acetylators are shown in black bold and dashed lines, respectively. The estimated log odds under the full logistic model coincide with the observed values. The estimates obtained under the additive logistic model for NAT2 rapid/intermediate acetylators and slow acetylators are shown in green bold and dashed lines, respectively. The estimates based on the optimal additive GJ model for NAT2 rapid/intermediate and slow acetylators are shown in red bold and dashed lines, respectively.

Moslehi et al [27] showed a significant evidence for an interaction between current smoking and NAT2 acetylation in this study. We tested the null hypothesis of no interaction against the general family of alternatives as follows. A generalized linear model with a logit link function (Equation 2) was considered by defining the main and interaction effects contrasts using an orthogonal design matrix, and the parameter estimates were obtained using the IRLS approach. The test statistic for interaction was Λ_G = 8.68 (d.f = 2, p-value = 0.01), suggesting significant evidence for an interaction under the general family of alternatives.

In order to determine whether this interaction is removable, we calculated the proposed test statistic Λ_R by estimating the main effects using the equally weighted approach described in Section 2.2.2. The value of the test statistic was Λ_R = 6.77 (d.f = 1, p-value = 0.01), suggesting significant evidence for a removable interaction. Therefore, we may be able transform the outcome to fit an additive model on the transformed scale, which will be pursued in Section 8.

5.2 Bladder cancer, smoking, and NAT2 acetylation

In a published genome-wide association case-control study of bladder cancer, Rothman et al [28] found significant evidence for an interaction between smoking (consisting of three levels as before – never, past and current smokers) and the NAT2 gene (single nucleotide polymorphism rs1495741 consisting of two levels – AA/AG genotypes representing rapid/intermediate acetylators, and GG genotype representing slow acetylators). The case-control data for smoking and NAT2 gene are shown in Table 3. Figure 5 shows the observed log odds in the 6 risk factor sub-classes using bold and black dashed lines. This figure suggests that an interaction, if it exists, may be of Type A, which is removable. We tested for the presence of a removable interaction. The value of the test statistic was Λ_R = 16.82 (d.f = 1, p-value < 0.001), which is significant and suggests the possibility of transforming the outcome to fit an additive model.

Table 3.

Case-control data from the bladder cancer study of Rothman et al [28]. Columns 1 and 2 show the levels of smoking and NAT2 acetylation(based on SNP rs1495741). Columns 5, 6, and 7 show the estimated log odds and the standard errors in parentheses based on three models. Note that the full logistic model is a saturated model. Therefore, for this model, the estimated log odds is equal to the observed log odds, and the estimtated standard error is the square root of the sum of the inverse of the number of cases and the number of controls. We refer to these standard errors as the “within class” standard errors. The value of λ used to fit the additive GJ model is shown in parentheses in the last column. The last three rows of the table show the maximum log-likelihood, mean squared error(MSE), Akaike’s AIC, and the Bayes information criterion for the three models.

1	2	3	4	5–7 Estimated log odds (std error) from three models
Smoking	NAT2 acetylation	Case	Control	Full logistic	Additive logistic	Optimal additive GJ(λ = −3.2)
Never	Rapid/Intermediate	760	1679	−0.793 (0.044)	−0.912 (0.032)	−0.825 (0.027)
Never	Slow	1202	2758	−0.831 (0.035)	−0.756 (0.029)	−0.808 (0.028)
Past	Rapid/Intermediate	1859	2300	−0.213 (0.031)	−0.194 (0.026)	−0.199 (0.023)
Past	Slow	3455	3559	−0.030 (0.024)	−0.041 (0.021)	−0.034 (0.023)
Current	Rapid/Intermediate	1165	1254	−0.074 (0.041)	−0.004 (0.030)	−0.086 (0.033)
Current	Slow	2258	1865	0.191 (0.031)	0.150 (0.027)	0.194 (0.031)
Maximum log-likelihood				−16178.38	−16186.88	−16179.04
MSE				0.0012	0.0052	0.0011
AIC				32368.76	32381.76	32368.08
BIC				32417.30	32414.12	32408.52

Figure 5.

Estimated log odds ratios for the bladder cancer study. The horizontal axis shows the three levels of smoking. The vertical axis shows the log odds. The observed log odds for NAT2 rapid/intermediate acetylators and slow acetylators are shown in black bold and dashed lines, respectively. The estimated log odds under the full logistic model coincide with the observed values. The estimates obtained under the additive logistic model for NAT2 rapid/intermediate acetylators and slow acetylators are shown in green bold and dashed lines, respectively. The estimates based on the optimal additive GJ model for NAT2 rapid/intermediate and slow acetylators are shown in red bold and dashed lines, respectively.

5.3 Endometrial cancer, tea intake and CYP19A1 genotype

In an analysis of case-control data from the Shanghai Endometrial Cancer Study, Xu et al [29] reported a significant interaction between tea intake (two levels: low and high intake) and CYP19A1 genotype based on the single nucleotide polymorphism rs1065779 (three levels: GG, GT, and TT genotypes). These data are shown in Table 4. Column 5 of the table suggests that the log odds decrease monotonically as the number of copies of the T allele increases among individuals having high tea intake. In contrast, there is a lack of monotonic trend among individuals having low tea intake, suggesting that an interaction (if any) may be of Type D, which is not removable. Thus, as expected, the test for removable interaction was not significant at the 5% level (Λ_R = 1.02, d.f = 1, p-value = 0.31). However, the test under the general alternative suggested a significant interaction (Λ_G = 9.10, d.f = 2, p-value = 0.01). These results suggest that a transformation to additivity is not appropriate for these data.

Table 4.

Case-control data from the endometrial cancer study of Xu et al [29]. Columns 1 and 2 show the CYP19A1 genotypes based on rs**** and the levels of tea intake. Columns 5, 6, and 7 show the estimated log odds and the standard errors in parentheses based on three models. Note that the full logistic model is a saturated model. Therefore, for this model, the estimated log odds is equal to the observed log odds, and the estimtated standard error is the square root of the sum of the inverse of the number of cases and the number of controls. We refer to these standard errors as the “within class” standard errors. The value of λ used to fit the additive GJ model is shown in parentheses in the last column. The last three rows of the table show the maximum log-likelihood, mean squared error(MSE), Akaike’s AIC, and the Bayes information criterion for the three models.

1	2	3	4	5–7 Estimated log odds (std error) from three models
CYP19A1	Tea Intake	Case	Control	Full logistic	Additive logistic	Optimal additive GJ (λ = 0.01)
GG	Low	211	226	−0.069 (0.096)	0.064 (0.085)	0.064 (0.085)
GG	High	117	90	0.262 (0.140)	−0.019 (0.102)	−0.020 (0.102)
GT	Low	382	322	0.171 (0.076)	0.098 (0.069)	0.098 (0.069)
GT	High	148	171	−0.144 (0.112)	0.015 (0.091)	0.015 (0.091)
TT	Low	126	153	−0.194 (0.120)	−0.220 (0.106)	−0.219 (0.106)
TT	High	45	65	−0.368 (0.194)	−0.302 (0.123)	−0.303 (0.123)
Maximum log-likelihood				−1416.561	−1421.109	−1421.109
MSE				0.016	0.032	0.032
AIC				2845.121	2850.217	2852.217
BIC				2878.892	2872.731	2880.36

6. Transformation of the outcome

Several methods are available for transforming binary outcomes [26, 37–39]. In this paper, we consider the Guerrero and Johnson [26] family of power transformations, henceforth abbreviated GJ. The GJ transformation of the outcome for the (i,j)-th risk factor subclass is given in terms of the disease risk, p_ij. Denoting λ as the transformation parameter, the transformation, denoted g(p_ij,λ), is given by:

$$\mathrm{g}({\mathrm{p}}_{\mathrm{i}\mathrm{j}},\lambda )=\{\begin{array}{ll}\frac{1}{\lambda }({\left[\frac{{\mathrm{p}}_{\mathrm{i}\mathrm{j}}}{1-{\mathrm{p}}_{\mathrm{i}\mathrm{j}}}\right]}^{\lambda }-1)& \text{when}\lambda \ne 0\\ \text{log}\left(\frac{{\mathrm{p}}_{\mathrm{i}\mathrm{j}}}{1-{\mathrm{p}}_{\mathrm{i}\mathrm{j}}}\right)& \text{when}\lambda =0\end{array}$$ (Equation 10)

6.1 Properties of the GJ transformation

The GJ transformation has similarities to the Box-Cox family of power transformations for continuous outcomes [25]. The logit link function is a member of the GJ family since g(p_ij,λ) approaches the logit link function as λ approaches 0. This transformation is invertible using the identity $\frac{{\mathrm{p}}_{\mathrm{i}\mathrm{j}}}{1-{\mathrm{p}}_{\mathrm{i}\mathrm{j}}}={\{1+\lambda \times \mathrm{g}({\mathrm{p}}_{\mathrm{i}\mathrm{j}},\lambda \left)\right\}}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$\lambda $}\right.}$ when λ ≠0 and $\frac{{\mathrm{p}}_{\mathrm{i}\mathrm{j}}}{1-{\mathrm{p}}_{\mathrm{i}\mathrm{j}}}=\text{exp}\left\{\mathrm{g}\right({\mathrm{p}}_{\mathrm{i}\mathrm{j}},0\left)\right\}$ when λ = 0. However, there is no λ for which g(p_ij, λ) = p_ij.

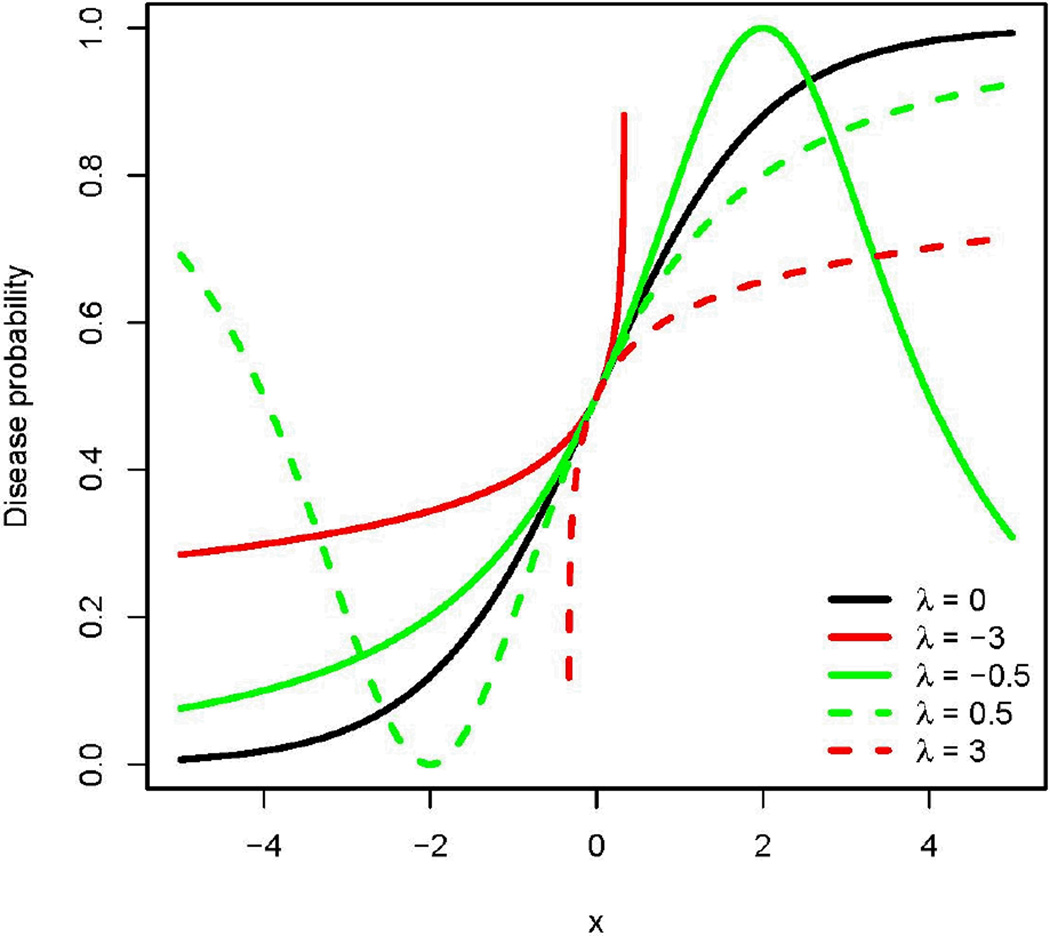
Under the logit transformation, the disease probability is given by $\frac{\text{exp}\left(\mathrm{x}\right)}{1+\text{exp}\left(\mathrm{x}\right)}$, where x is a real number. As a function of x, the disease probability is an “S”-shaped curve, and is symmetric around ½ (see Figure 6). For a given λ, the disease probability under the GJ transformation is given by $\frac{{(1+\lambda \mathrm{x})}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$\lambda $}\right.}}{1+{(1+\lambda \mathrm{x})}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$\lambda $}\right.}}$. This probability is not symmetric, and its shape is governed by the magnitude of λ (see Figure 6). For some values of λ, the probability is finite only when x falls in a certain range. For example, when λ = 3, the disease probability is defined when x > −1/3. When λ≠0, the probability is attenuated (or inflated) relative to the logit transformation for large positive (or negative) values of x (if the probability is defined for these values of x). This tail behavior may help characterize certain curvature effects exhibited by disease probabilities.

Figure 6.

Shape of the logit and GJ transformations. The horizontal axis shows a real number x. The vertical axis shows the disease probability as a function of × (see Equation 10). Setting λ = 0 in Equation 10 gives the logit function, shown as a black curve. The red (green) bold and dashed curves show the disease probability as a function of × based on the GJ transformation with λ = −3 (−0.5) and 3 (0.5), respectively.

6.2 Parameter estimation under the GJ transformation

The additive model on the transformed scale is given by:

$$\mathrm{g}({\mathrm{p}}_{\mathrm{i}\mathrm{j}},\lambda )=\mu +{\alpha }_{\mathrm{i}}+{\beta }_{\mathrm{j}},$$ (Equation 11)

where g(p_ij, λ) is given by Equation (10). The model parameters μ, α_i (i = 1, …, L₁), and β_j (j = 1, …, L₂) and the transformation parameter λ are unknown. For a given λ, the maximum likelihood estimates (MLE) of the model parameters can be obtained using an iterative procedure, as described in Appendix E. We can use these MLEs in Equation (11) to obtain the estimated values of g(p_ij, λ), then plug these into Equation (10) to obtain the estimated value of p_ij, and then, using Equation (1), obtain the maximum log-likelihood of the binomial distribution.

The MLE of the transformation parameter λ can be obtained using a profile log-likelihood approach as follows [25]. Consider various values for λ. For each value, obtain the MLEs of the model parameters and the maximum log-likelihood values, and identify the value of λ that maximizes these maximum log-likelihoods. Denote L_max(λ) as the maximum log-likelihood of the binomial distribution (Equation 1 with probabilities given by Equations 10 and 11) for a given λ and λ̂ as the MLE of λ. Following Box and Cox [25], we can obtain a 95% confidence interval of the form:

$$2\times \left\{{\mathrm{L}}_{\text{max}}\right(\widehat{\lambda })-{\mathrm{L}}_{\text{max}}(\lambda \left)\right\}<3.84$$ (Inequality 12)

From Equation (10), the relationship between the logit and GJ transformations is given by:

$$\text{log}\left(\frac{{\mathrm{p}}_{\mathrm{i}\mathrm{j}}}{1-{\mathrm{p}}_{\mathrm{i}\mathrm{j}}}\right)=\frac{1}{\lambda }\times \text{log}\{1+\lambda \times \mathrm{g}({\mathrm{p}}_{\mathrm{i}\mathrm{j}},\lambda \left)\right\}.$$ (Equation 13)

Consider the MLEs of the model parameters of Equation (11), calculated at the MLE of λ. The MLEs of the parameters can be plugged into Equation (13) to obtain the MLE of the log odds, and their standard errors can be obtained using the delta method by accounting for the fact that λ is unknown and is estimated from the observed data (see Appendix E)

6.3 Relationship between the GJ link and removable interaction

Using a Taylor’s series expansion of the natural logarithm up to the quadratic term, the right hand side of Equation (13) can be written as:

$$\text{log}\left(\frac{{\mathrm{p}}_{\mathrm{i}\mathrm{j}}}{1-{\mathrm{p}}_{\mathrm{i}\mathrm{j}}}\right)\approx \mathrm{g}({\mathrm{p}}_{\mathrm{i}\mathrm{j}},\lambda )-\frac{\lambda }{2}\times {\{\mathrm{g}({\mathrm{p}}_{\mathrm{i}\mathrm{j}},\lambda )\}}^2.$$ (Equation 14)

When the model is additive under the GJ link and when disease risk is a strictly monotonic function of the additive effects of the risk factors, the right hand side of Equation (14) may be further approximated as follows (see also [24]):

$$\text{log}\left(\frac{{\mathrm{p}}_{\mathrm{i}\mathrm{j}}}{1-{\mathrm{p}}_{\mathrm{i}\mathrm{j}}}\right)\approx \mu +{\alpha }_{\mathrm{i}}+{\beta }_{\mathrm{j}}-\frac{\lambda }{2}\times {\{\mu +{\alpha }_{\mathrm{i}}+{\beta }_{\mathrm{j}}\}}^2\approx \mu +{\alpha }_{\mathrm{i}}+{\beta }_{\mathrm{j}}-\frac{\lambda }{2}\times \text{2}\times {\alpha }_{\mathrm{i}}\times {\beta }_{\mathrm{j}}=\mu +{\alpha }_{\mathrm{i}}+{\beta }_{\mathrm{j}}-\lambda \times {\alpha }_{\mathrm{i}}\times {\beta }_{\mathrm{j}}$$ (Equation 15)

Comparing Equations (5) and (15) suggests that the GJ transformation is appropriate for fitting an additive model when the interaction is removable (i.e., of the form given by Equation 5) and that the transformation parameter is λ ≈ − θ. In general, when writing the approximation in the second step of Equation (15), the squared terms such as α_i² and β_j² may be absorbed into the main effects [24, 34]. However, when the interaction is entirely removable, the term −λ/2 × (μ + α_i + β_j}² is the interaction term γ_ij, and the approximations in Equation (15) will be equalities. In particular, using the identifiability conditions given below Equation (2), we can write {μ + α_i + β_j}² = 2×α_i×β_j to obtain the second step (see, for example, Chapter 4 of [14]).

7. Simulation

We conducted simulation studies to investigate the properties of the following three models: (i) the full logistic regression model (i.e., a logistic regression model that includes main effects and interaction terms); (ii) the additive logistic regression model (i.e., a logistic regression model that does not include any interaction term); and the optimal additive GJ model (i.e., an additive model based on the GJ link using the MLE of λ).

We simulated case-control data with 1000 cases and 1000 controls. Two risk factors, X having L₁ levels and Z having L₂ levels, were simulated for each person. We considered simulations with (L₁, L₂) = (3, 2) and (5, 5), which correspond to 2×3 and 5×5 contingency tables. The binary disease trait was simulated using Equation (9) with (C₁, C₂) = (3, 2) and (4, 4) for 2×3 tables and 5×5 tables, respectively. We simulated data under interactions of Types A and D and compositional epistasis, and the simulation parameters were chosen as described in Section 4. When simulating data with 5×5 tables, we considered the prevalence of each level of the risk factors to be 20%. We simulated 1000 data sets under each parametric configuration.

The full logistic model contained (L₁-1)×(L₂-1) interaction terms. Thus, the total number of interaction terms was 2 and 16 for the 2×3 and the 5×5 contingency tables, respectively. We obtained the MLEs and standard errors of the log odds of the three models, and evaluated the estimation properties of the models using their mean squared error (MSE), Akaike’s AIC, and the BIC (Schwartz criterion). The MSE was calculated as the square of the difference between the observed and estimated log odds plus the square of the standard error, averaged over all the risk factor sub-classes. The AIC and BIC were calculated as −2 × maximum log-likelihood + 2P, and −2 × maximum log-likelihood + P×log(N), respectively, where P denotes the number of unknown parameters in the model and N is the total sample size. Thus, P = L₁ × L₂ for the full logistic model, P = L₁ + L₂ – 1 for the additive logistic model, and P = L₁ + L₂ for the optimal additive GJ model (since λ was estimated under this model).

Figures 7 and 8 shows the results, averaged over the 1000 simulated data sets, with ρ = 0.50, γ₁₁ = 2 for Type A interaction and compositional epistasis and γ₁₁ = −2 for Type D interaction. The values of MSE, AIC, and BIC are shown on the natural logarithm scale for ease of visual inspection. The optimal additive GJ model performs similar to the full logistic model and performs better than the additive logistic model under Type A interaction and compositional epistasis. As expected, the optimal additive GJ model performs worse than the full logistic model under Type D interaction. Further, under Type D interaction, the optimal additive GJ model performs similar to the additive logistic model since the MLE of λ is generally close to 0 in this setting. The results for the 5×5 contingency tables under compositional epistasis suggest that the optimal additive GJ model also performs better than the logistic models in terms of AIC and BIC, but its MSE is larger than that of the full logistic model (average MSEs: 0.114 and 0.073 for the optimal additive GJ and the full logistic models, respectively). Note that, while compositional epistasis satisfies the monotonicity condition, the underlying curvature is not strictly monotonic. This lack of strict monotonicity impacts the bias-variance trade-off (quantified by the MSE) when the number of risk factor sub-classes becomes large, but it does not impact the overall quality of the fit (quantified by AIC and BIC). Similar results were obtained under all the other parametric configurations.

Figure 7.

Smoothed kernel density plots of MSE (row 1), AIC (row 2) and BIC (row 3) for data simulated based on a 2×3 contingency table under interactions of Type A (left column), Type D (middle column) and compositional epistasis (right column). These results correspond to the parametric configuration where β = log(2) = 0.6931 = δ (Type A and Type D interactions), β = 0 = δ (compositional epistasis), θ₁₁ = 2 (Type A interaction and compositional epistasis), θ₁₁ = −2 (Type D interaction), and ρ = 0.50. The smoothed kernel density estimates were obtained using the density function in the R programming language with the default settings for bandwidth. Under Type D interaction, the MSEs of the optimal additive GJ model and the additive logistic model are similar. Hence, the two curves overlap. In order to distinguish the two colors (green and red), we have shown these two curves using dashed lines for ease of visualization. Similar approach is used to show the AIC curves for the full logistic and the optimal additive GJ models under Type A interaction and compositional epistasis.

Figure 8.

Smoothed kernel density plots of MSE (row 1), AIC (row 2) and BIC (row 3) for data simulated based on a 5×5 contingency table under interactions of Type A (left column), Type D (middle column) and compositional epistasis (right column). These results correspond to the parametric configuration where β = log(2) = 0.6931 = δ (Type A and Type D interactions), β = 0 = δ (compositional epistasis), θ₁₁ = 2 (Type A interaction and compositional epistasis), θ₁₁ = −2 (Type D interaction), and ρ = 0.50. The smoothed kernel density estimates were obtained using the density function in the R programming language with the default settings for bandwidth. Under Type D interaction, the MSEs of the optimal additive GJ model and the additive logistic model are similar. Hence, the two curves overlap. In order to distinguish the two colors (green and red), we have shown these two curves using dashed lines for ease of visualization.

Taken together, the above results suggest that the optimal additive GJ model is a parsimonious approach for obtaining precise estimates of the disease odds and for obtaining a good fit to the observed data when the interactions are removable.

8. Illustrative examples - revisited

We now illustrate the GJ transformation using the example data sets of Section 5. We provide a detailed illustration for the advanced colorectal adenoma and bladder cancer data, and only a brief summary of the method for the endometrial cancer data.

8.1 Advanced colorectal adenoma, smoking, and NAT2 acetylation

Table 2 shows the estimated log odds and their standard errors under the three models. The additive model provided a poor fit to the data relative to the full logistic model. In particular, the log odds for the current smokers were poorly estimated (see Figure 4).

For the GJ link, the profile MLE of λ was −4.62 (95% CI: −12.50 – −1.02, which excludes λ=0, the logit transformation). The optimal additive GJ model provided a better fit to the data than the additive logistic model (Table 2 and Figure 4). In particular, the log odds of the current smokers was remarkably well estimated relative to the additive logistic model. The log odds of the past smokers was not well estimated, because of a slight lack of monotonic trend in the log odds for this group, as noted in Section 5.1. For the current smokers, the standard errors of the estimated log odds were similar to the within class standard errors, suggesting a remarkably good information recovery for these sub-classes even without considering interactions in the model. For the remaining sub-classes, the standard errors of the estimated log odds were smaller than the within class standard errors. The optimal GJ model had the smallest MSE, AIC, and BIC, suggesting that it provides the best fit to the data among the three models considered (see Table 2), and its 95% confidence intervals for the log odds covered the observed values (Table 5).

Table 5.

95% confidence intervals for the log odds estimated under the additive logistic model and the optimal additive GJ model for two example data sets.

Smoking	NAT2	Observed log odds	95% confidence interval
			Additive logit model	Optimal additive GJ model
ADVANCED COLORECTAL ADENOMA STUDY
Never	Rapid/Intermediate	−0.298	−0.537, −0.102	−0.352, −0.042
Never	Slow	−0.121	−0.303, 0.091	−0.339, 0.033
Past	Rapid/Intermediate	−0.071	−0.441, −0.011	−0.289, 0.024
Past	Slow	−0.133	−0.212, 0.187	−0.254, 0.115
Current	Rapid/Intermediate	0.143	0.218, 0.780	−0.174, 0.499
Current	Slow	1.007	0.443, 0.981	0.653, 1.361
BLADDER CANCER STUDY
Never	Rapid/Intermediate	−0.793	−0.975, −0.849	−0.879, −0.772
Never	Slow	−0.831	−0.815, −0.702	−0.862, −0.753
Past	Rapid/Intermediate	−0.213	−0.245, −0.144	−0.245, −0.154
Past	Slow	−0.030	−0.083, 0.002	−0.079, 0.010
Current	Rapid/Intermediate	−0.074	−0.063, −0.055	−0.150, −0.021
Current	Slow	0.191	0.098, 0.202	0.134, 0.254

Table 6 shows the parameter estimates, standard errors, and p-values under the three models. NAT2 acetylation was significant under the full logistic model. It had marginal significance under the additive logistic model, but was not significant under the optimal additive GJ model. This raises the question as to whether NAT2 has a significant effect on the risk of advanced colorectal adenoma. To investigate this, we considered a GJ model that included smoking, but not NAT2 acetylation, as the risk factor. The profile MLE of λ was 0. Therefore, we considered a logistic regression model with smoking alone as the risk factor in the model and estimated the log odds summaries. The MSE, AIC, and BIC of this model were 0.077, 1770.793, and 1791.455, respectively, which were substantially larger than those of the optimal additive GJ model, suggesting that there may be a small, though non-significant, additive effect of NAT2.

Table 6.

Maximum likelihood estimates (MLE), standard errors (Std. Err), and p-values of the parameters of three models for the two example data sets.

	Full Logistic Model		Additive Logistic Model		Optimal Additive GJ Model
Parameter	MLE (Std. Err)	p-value	MLE (Std. Err)	p-value	MLE (Std. Err)	p-value
ADVANCED COLORECTAL ADENOMA STUDY
Intercept	0.088 (0.061)	0.148	0.091 (0.060)	0.131	−0.080 (0.081)	0.332
Main Effects
Smoking: Past vs Never	0.054 (0.063)	0.396	0.047 (0.063)	0.456	0.070 (0.115)	0.543
Smoking: Current vs Never	0.244 (0.048)	4.9e−07	0.257 (0.048)	6.3e−08	0.122 (0.039)	0.002
NAT2: Slow vs Rapid/Intermediate	0.163 (0.061)	0.007	0.107 (0.057)	0.062	0.050 (0.042)	0.240
Interaction
Past Smoking × Slow NAT2	−0.059 (0.063)	0.347	-	-	-	-
Current Smoking × Slow NAT2	0.134 (0.048)	0.006	-	-	-	-
BLADDER CANCER STUDY
Intercept	−0.291 (0.014)	< 0.001	−0.293 (0.014)	< 0.001	−1.362 (0.516)	0.008
Main Effects
Smoking: Past vs Never	0.345 (0.017)	< 0.001	0.359 (0.017)	< 0.001	1.896 (0.763)	0.013
Smoking: Current vs Never	0.175 (0.010)	< 0.001	0.183 (0.009)	< 0.001	0.693 (0.253)	0.006
NAT2: Slow vs Rapid/Intermediate	0.068 (0.014)	< 0.001	0.077 (0.014)	< 0.001	0.121 (0.021)	< 0.001
Interaction
Past Smoking × Slow NAT2	0.055 (0.017)	0.001	-	-	-	-
Current Smoking × Slow NAT2	0.032 (0.010)	0.002	-	-	-	-

These results suggest that the seemingly significant interaction between smoking and NAT2 observed under the full logistic model reflects non-additivity or curvature effect that cannot be adequately accounted for by an additive logistic model, but one that can be accounted for by modeling the disease risk through an additive model under the GJ link. NAT2 slow acetylators who are current smokers have much larger log odds relative to the other risk factor sub-classes (Table 2). This large log odds is a result of not using a scale that can remove most of the statistical interaction. Although the main effect of NAT2 is not statistically significant under the optimal additive GJ model (p-value = 0.24; Table 6), it does not preclude such an effect. Cigarette smoking results in exposure to aryl and heterocyclic amines. The NAT2 enzyme plays an important role in the metabolism of aromatic and heterocyclic amines. NAT2 may not be a primary contributor to disease risk at a biological level, but it may increase risk solely based on its ability to detoxify herterocyclic and aromatic amines when a person is exposed to these amines. Ochs-Balcom et al [39], who provide a detailed evaluation of NAT2 acetylation in breast cancer, suggest that such molecular explanation may be an important reason for the lack of significant main effect of the NAT2 phenotype in relation to certain diseases.

8.2 Bladder cancer, smoking, and NAT2 acetylation

The profile MLE of λ for the bladder cancer data was −3.2 (95% CI: −8.62 – −1.15). Table 3 shows the estimated log odds for the full logistic model, additive logistic model, and the optimal additive GJ model, the standard errors, MSE, AIC, and BIC. The optimal additive GJ model had the smallest MSE, AIC, and BIC and, thus, provided the best fit among the three models considered.

Under the optimal additive GJ model, the 95% CIs for the log odds included the observed log odds values in all the risk factor sub-classes (Table 5). In contrast, under the additive logistic model, the confidence intervals for never smokers and current smokers who were rapid/intermediate NAT2 acetylators did not include the observed values. Table 6 shows the parameter estimates, standard errors, and p-values under the three models. Both smoking and NAT2 acetylation were significantly associated with the risk of bladder cancer under all the models considered. As in the previous example, we note that the optimal additive GJ model provided log odds estimates that are close to the observed values (Figure 5) and standard errors that were generally close to the within class standard errors.

8.3 Endometrial cancer, tea intake and CYP19A1 genotype

Although the endometrial data do not show significant evidence for a removable interaction (Section 5.3), we briefly summarize the properties of an additive GJ model for these data without providing a detailed analysis. The profile MLE of λ was 0.01 (95% CI: −3.01 – 4.50). Since λ was near 0, the MSE, AIC, and BIC of the additive GJ model were similar to those of an additive logistic model (see Table 4). As expected, the full logistic model had an overall better performance than the additive GJ and the additive logistic models. These results are also consistent with the simulation findings of Section 7 for Type D interaction.

9. Discussion

The primary objective of this paper is to demonstrate that fitting an additive model to the data by eliminating a removable interaction via a transformation of the outcome may provide more precise estimates of the disease odds and a better fit to the data. To demonstrate this, we first developed a test statistic for evaluating whether an interaction is removable, and used the Guerrero and Johnson family of transformation to eliminate a removable interaction.

In developing the test for a removable interaction, we have assumed that there are no empty risk factor sub-classes. This is an important assumption since complete testing for interactions is not possible when there are empty sub-classes. To see this, consider X and Z to be just two binary risk factors. The interaction effect is defined as ξ₀₀ + ξ₁₁ − ξ₀₁ − ξ₁₀. Suppose we do not have observations (neither cases nor controls) in the (0,0) sub-class in the observed data, but these may occur in the population. Then the summary ξ₀₀ is not observed, and we cannot estimate the interaction effect. When X and Z have more than two levels, there are several γ_ij terms representing interactions. We need the relevant risk factor sub-classes to be non-empty in order to be able to estimate these γ_ij terms. Although we cannot estimate interaction effects for empty cells, it is perhaps reasonable to assume that they would be non-significant if the majority of (estimable) interactions are non-significant. Here “significance” relates more to finding a parsimonious model that leads to good estimates of main effects than to statistical significance. When there are empty risk factor sub-classes, we cannot estimate the main effects unless we assume that some of the interactions do not exist [42], which may be an unwarranted assumption. Elston and Bush [43] discuss in some detail what hypotheses can be tested in this situation when the outcome is continuous. Alternatively, when there are empty sub-classes it may be pragmatic to remove the estimable interactions through a transformation of the outcome to estimate the main effects. When some cells are small, but not empty, we may add and one-half to the cells as an adjustment factor to account for small sample size and test for removable interactions. However, the circumstances under which this approach is adequate for the asymptotic distribution of the test to hold require further investigations.

Figures 7 and 8 suggest that the efficiency gains of the additive GJ model (in terms of minimum MSE, AIC, and BIC) may be better for large contingency tables. Testing the null hypothesis of no interaction under the full logistic model involves (L₁-1)×(L₂-1) degrees of freedom. The test for removable interaction has one degree of freedom, which leaves (L₁-1)×(L₂-1) – 1 degrees of freedom for non-removable interaction. There is no point in trying to find a transformation in the case of a 2×2 table since the full logistic model has (L₁-1)×(L₂-1) = 1 degrees of freedom, precluding a separation of the interaction into removable and non-removable components.

Once evidence for a removable interaction is obtained, it is generally useful to establish that there is no non-removable interaction i.e., there is no further interaction after transformation. In this paper we have focused solely on removable interaction. In practice, it may be fairly obvious that the interaction is largely removable (see Figure 4) or non-removable (see Table 4). But if there is any doubt, a complementary step would be to test for significant non-removable interaction after finding a parsimonious additive model for estimation. This amounts to testing the null hypothesis that γ_ij = θα_iβ_j (i = 1, …, L₁; j = 1, …, L₂) against the alternative γ_ij ≠ θα_iβ_j for some (i,j). Variance components method may be used to develop this test by first viewing e_ij = γ_ij - θα_iβ_j as having a priori i.i.d N(0, δ²) distribution and then testing whether σ² = 0 (see, for example [44]). Alternatively and as also noted by a reviewer, a likelihood ratio test may be used. A detailed evaluation of these tests is outside the scope of this paper.

There is also an increasing interest in testing for the presence of interactions or in identifying disease risk factors by incorporating interactions into relevant models in genome-wide association studies (GWAS). While our proposed method is not initially suitable for use in GWAS, it may be used to determine whether a statistical interaction, once it is found, is removable.

In this paper, we have considered the Guerrero and Johnson family of transformations. Using a Taylor’s series expansion, we have shown in Section 6 that this is an appropriate family of transformation for fitting an additive model when the interaction is removable in the sense of Equation (5). Several alternative transformations such as the Aranda-Ordaz family, Burr’s transformation, the identity transformation, and non-parametric link functions are available for fitting binary data [37, 38, 45–47]. A detailed evaluation of alternative transformations to additivity for our illustrative examples is outside the scope of this paper.

The importance of evaluating interactions has been discussed extensively in the literature [7]. One of the stimulating factors for considering interactions is the belief that interactions can provide useful insights about biological mechanisms underlying the disease. However, biological interactions can arguably occur regardless of whether or not there is a statistical interaction [12, 18]. Statistical models, on the other hand, can provide useful ways for fitting data to estimate the roles of risk factors on the outcome. In this work we have shown that model parsimony can be attained via transformation when the risk factors exhibit a curvature effect that obeys certain monotonicity properties, resulting in precise estimation and better fit. It has been argued that transformations must not be pursued because eliminating interactions may limit our ability to obtain biological insights about the risk factors [48]. However, while interaction is eliminated under the transformed scale to attain parsimony, the curvature (i.e., interaction) is indeed retained on the original scale and can be obtained via back-transformation. This is demonstrated in our illustrative examples, where the curvature-type effects are re-found via back transformation after estimating the log odds summaries using the parameter estimates of the additive model under the GJ transformation.

Our illustrative examples show that an additive model on the transformed scale is parsimonious and can provide a precise fit when an interaction is removable, making this an appealing model fitting approach. Our proposed method can be applied to data from a variety of application settings for evaluating removable statistical interactions. We hope that our work will contribute to further research in the area of fitting parsimonious models by removing interactions via a transformation of the outcome.

APPENDIX A. Derivation of the score statistic U

The log-likelihood of the binomial distribution (Equation 1) is given by :

$$\mathrm{L}=\sum _{\mathrm{i}=1}^{{\mathrm{L}}_1}\sum _{\mathrm{j}=1}^{{\mathrm{L}}_2}{\mathrm{N}}_{\mathrm{i}\mathrm{j}}\times \text{log}\left({\mathrm{p}}_{\mathrm{i}\mathrm{j}}\right)+{\mathrm{M}}_{\mathrm{i}\mathrm{j}}\times \text{log}(1-{\mathrm{p}}_{\mathrm{i}\mathrm{j}}),$$

, where p_ij is given by Equation (5). Denote the linear predictor as η_ij = μ + α_i + β_j + θα_iβ_j. Let y_ij denote the first derivative of L with respect to η_ij. In vector notation, write η = (η₁₁, η₁₂, …, η_L1,L2) and y = (y₁₁, y₁₂, …, y_L1,L2). Let v_ij be the negative second derivative of L with respect to η_ij. Let A⁻¹ = diag{v_ij}. The parameters μ, α, β, and θ are estimated via the Fisher scoring approach in an iteratively reweighted least squares manner by considering the working model: y_ij = μ + α_i + β_j + θα_iβ_j + error, where Var(y_ij) = v_ij. The working likelihood function is −1/2 × (y - η)^TA(y - η). The normal equations for estimating the unknown parameters are obtained by taking the derivative of this working likelihood with respect to the parameters. The score function for θ, evaluated at the null hypothesis, is obtained by taking the derivative of this working likelihood with respect to θ and evaluating it at θ = 0. The resulting score function, denote U, is given by U = 1^TDA(y - μ1 - α - β), where 1 is a vector of unities and D is a diagonal matrix with elements α_iβ_j. The term y - μ1 - α - β is the vector of residuals. All these quantities can be estimated using the observed data via an additive model (i.e., a model devoid of any interaction terms) as part of the iterative procedure.

APPENDIX B. Proof of Results 1 and 2

In the absence of an interactions, we have E(ξ̂_ij) = ξ_ij = μ + α_i + β_j. When the weights are proportional and when there is no interaction, it follows from Equation 7 that E(μ̂) = μ, E(α̂_i) = α_i, and E(β̂_j) = β_j. Therefore, we have for E(γ̂_ij) = 0 Result 1.

To obtain Result 2, note that a contrast in α̂_i is given by $\sum _{\mathrm{i}=1}^{{\mathrm{L}}_1}{\mathrm{c}}_{\mathrm{i}}{\widehat{\alpha }}_{\mathrm{i}}$ where c_i are real numbers such that not all c_i are zero and $\sum _{\mathrm{i}=1}^{{\mathrm{L}}_1}{\mathrm{c}}_{\mathrm{i}}=0$. When there is no interaction, the expected value of this contrast is obtained from Equation 7 as: $\mathrm{E}\left(\sum _{\mathrm{i}=1}^{{\mathrm{L}}_1}{\mathrm{c}}_{\mathrm{i}}{\widehat{\alpha }}_{\mathrm{i}}\right)=\sum _{\mathrm{i}=1}^{{\mathrm{L}}_1}{\mathrm{c}}_{\mathrm{i}}\times \frac{\sum _{\mathrm{j}=1}^{{\mathrm{L}}_2}{\mathrm{v}}_{\text{.j}}\times \mathrm{E}\left({\widehat{\xi }}_{\mathrm{i}\mathrm{j}}\right)}{\sum _{\mathrm{j}=1}^{{\mathrm{L}}_2}{\mathrm{v}}_{\text{.j}}}=\sum _{\mathrm{i}=1}^{{\mathrm{L}}_1}{\mathrm{c}}_{\mathrm{i}}\times \frac{\sum _{\mathrm{j}=1}^{{\mathrm{L}}_2}{\mathrm{v}}_{\text{.j}}\times (\mu +{\alpha }_{\mathrm{i}}+{\beta }_{\mathrm{j}})}{\sum _{\mathrm{j}=1}^{{\mathrm{L}}_2}{\mathrm{v}}_{\text{.j}}}=\sum _{\mathrm{i}=1}^{{\mathrm{L}}_1}{\mathrm{c}}_{\mathrm{i}}{\alpha }_{\mathrm{i}}$, which does not depend upon the weights. Similarly, the expected value of any contrast in β̂_j can be shown to be independent of the choice of the weights. Scheffé [14] has derived similar results for two-way analysis of variance for balanced data. Our focus is on unbalanced data, but assuming that the risk factors arise in proportional frequencies.

APPENDIX C. Conditonal expectation of the score under the alternative hypothesis, and the asymptotic null distribution of Λ_R when at least one of the risk factors is not associated with the outcome

Under the alternative hypothesis, the conditional expectation of the score is given by:

$$\mathrm{E}\left(\widehat{\mathrm{U}}\right|\widehat{\mathbf{\alpha }},\widehat{\mathbf{\beta }})=\sum _{\mathrm{i}=1}^{{\mathrm{L}}_1}\sum _{j=1}^{L_2}E\{{\widehat{\alpha }}_i\times {\widehat{\beta }}_j\times {(\frac{1}{N_{ij}}+\frac{1}{M_{ij}})}^{-1}\times {\widehat{\gamma }}_{ij}|\widehat{\mathbf{\alpha }},\widehat{\mathbf{\beta }}\}=\sum _{\mathrm{i}=1}^{{\mathrm{L}}_1}\sum _{j=1}^{L_2}{\widehat{\alpha }}_j\times {\widehat{\beta }}_j\times {(\frac{1}{{\mathrm{N}}_{ij}}+\frac{1}{{\mathrm{M}}_{ij}})}^{-1}\times \mathrm{E}\left({\widehat{\gamma }}_{ij}\right|\widehat{\mathbf{\alpha }},\widehat{\mathbf{\beta }})=\theta \times \sum _{i=1}^{{\mathrm{L}}_1}\sum _{j=1}^{L_2}{\widehat{\alpha }}_i\times {\widehat{\beta }}_j\times {(\frac{1}{N_{ij}}+\frac{1}{M_{ij}})}^{-1}\times {\alpha }_i\times {\beta }_j.$$

The first equality follows from Equation 6. The second equality is obtained by taking the expectation within the summation. The third equality follows from the assumption of removable interaction under the alternative hypothesis, under which γ_ij = θ × α_i × β_j.

The required asymptotic null distribution is obtained as follows (also see [47]). Suppose both the risk factors exhibit a main effect. Then, under the null hypothesis of no interaction, we have γ = 0. The MLE γ̂ then satisfies $\sqrt{\mathrm{N}}\widehat{\gamma }={\mathrm{P}}_0^{-1}{\mathrm{S}}_0$, where N is the total sample size, P₀ is the matrix of second derivatives of the log-likelihood with respect to the interaction effects γ_ij (keeping the main effects fixed at their values estimated under the additive model), and S₀ is the vector of first derivatives of the log-likelihood with respect to the γ_ij (keeping the main effects fixed as above), and both P₀ and S₀ are evaluated under the null, i.e., at γ_ij = 0 (for all i = 1, …, L₁ and j = 1, …, L₂). ${\mathbf{P}}_0^{-1}{\mathbf{S}}_0$ is a normal random variable with mean 0 under the null hypothesis of no interaction.

Suppose the risk factors X and Z are independent and neither is associated with the outcome. Then we have α_i = 0 for all i = 1, …, L₁ and β_j = 0 for all j = 1, 2, …, L₂. Let ε₁ and ε₂ denote vectors of arbitrary real numbers of length L₁ and L₂respectively. Now suppose we fit an additive model and examine evidence for the presence of an interaction - assuming that, perhaps, an interaction indeed exists. Thus, we assume that γ is not actually equal to zero. Now suppose the true value of γ is γ₀, and it is near a boundary of 0 such that the null hypothesis of no interaction does not hold. Following Sen [45], we can conceive of sequences of the form $\frac{{\epsilon }_1}{{\mathrm{N}}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$4$}\right.}}$ corresponding to α and $\frac{{\epsilon }_2}{{\mathrm{N}}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$4$}\right.}}$ corresponding to β and a real number θ₀ ≠ 0 such that ${\gamma }_0=\frac{{\theta }_0\times {\epsilon }_1\times {\epsilon }_2}{\sqrt{\mathrm{N}}}$, where ε₁ × ε₂ denotes a vector of length L₁×L₂ consisting of the product of every element of ε₁ with every element of ε₂.

Therefore, when the true value of γ is on a boundary of 0, we have:

$$\sqrt{\mathbf{N}}(\widehat{\mathbf{\gamma }}-{\mathbf{\gamma }}_0)=\sqrt{\mathbf{N}}\times \widehat{\mathbf{\gamma }}-\sqrt{\mathbf{N}}\times {\mathbf{\gamma }}_0={\mathbf{P}}_0^{-1}{\mathbf{S}}_0-{\theta }_0\times {\mathbf{\epsilon }}_1\times {\mathbf{\epsilon }}_2.$$

suggesting that the asymptotic distribution of γ̂ takes the form of a normal random variable plus a real number. Hence, given the estimated parameters of the additive model, the asymptotic distribution of Û takes the form of a normal variate plus a real number when the true value of γ is γ₀, which may be on a boundary of 0 when neither risk factor is associated with the outcome. Therefore, the null distribution of Λ_R will take the form of a central (one d.f) chi-squared random variable plus a positive constant, resulting in an inflation in the type I error.

APPENDIX D. Monotonicity properties of the different types of interactions – illustrated for two independent binary risk factors

Suppose we have two independent binary risk factors X and Z. Let π_1. = P(X=1) and π_.1 = P(Z=1). The model relating X and Z is given by g{E(Y|X,Z)} = μ + βX + δZ + θ₁₁XZ. Suppose we fit an additive model, ignoring the interaction term. The main effects of X and Z, obtained by weighting the study subjects equally, are β + π_.1θ₁₁ and δ + π_1.θ₁₁, respectively. Our goal is to determine whether g{E(Y|X,Z)} is a monotonic function of C = X(β+π_.1θ₁₁) + Z(δ+π_1.θ₁₁) in the observed range of C. Without loss of generality, we assume that β ≥ 0 and δ ≥ 0. The table below gives the expected values of C and g{E(Y|X,Z)} for all the (X,Z) combinations.

(X,Z)	(0,0)	(1,0)	(0,1)	(1,1)
C	0	β+π.1θ11	δ+π1.θ11	β+δ+(π1.+ π.1)θ11
g{E(Y|X,Z)}	0	β	δ	β+δ+θ11

When β = 0 = δ and θ₁₁ ≠ 0, we have one form of compositional epistasis. This table shows that, under this setting, g{E(Y|X,Z)} is a monotonic function of C.

Type A interaction

Suppose β > 0 and δ = 0. Then, under Type A interaction, we have θ₁₁ > 0. Since β > δ in this scenario, we have g{E(Y|X=1,Z=0)} > g{E(Y|X=0,Z=1)}. Then, monotonicity occurs when β+π_.1θ₁₁ ≥ β+π_1.θ₁₁ i.e., when π_.1 ≥ π_1..

Suppose β = δ > 0. Under Type A interaction, we have θ₁₁ > −β. In this scenario, we have g{E(Y|X=1,Z=0)}=g{E(Y|X=0,Z=1)} and g{E(Y|X=1,Z=1)}>g{E(Y|X=1,Z=0)}. Monotonicity clearly holds in this case since π_1. and π_.1 are between 0 and 1.

Type B (or C) interaction

Consider the scenario where β > 0 and δ = 0. Under Type B interaction, we have −β ≤ θ₁₁ ≤ 0. When θ₁₁ = −β, monotonicity clearly holds. This is also true when θ₁₁ = 0. Hence, monotonicity is applicable in this scenario.

Suppose β = δ > 0. For Type B interaction, we have θ₁₁ = −β. Monotonicity is clearly applicable in this case.

Type D interaction

Suppose β > 0 and δ = 0. Under Type D interaction, we have θ₁₁ ≤ −β. Suppose θ₁₁ = −τβ, where τ ≥ 1. The expected values of C are 0, β (1–τπ_.1), -τβπ_1., and β(1–τπ_1.–τπ_.1) when (X,Z) = (0,0), (1,0), (0,1), and (1,1), respectively. The corresponding values of g{E(Y|X,Z)} are 0, β, 0, and β(1–τ), respectively. Clearly, monotonicity holds when τ = 1. When τ > 1, monotonicity holds only when β(1-τ_1.-τπ_.1) < -τβπ_1. i.e., only when τ > 1/π_.1, and not otherwise.

Suppose β = δ > 0. Under Type D interaction, we have θ₁₁ ≤ −β. As above, let θ₁₁ = −τβ, where τ ≥ 1. The expected values of C are 0, β(1–τπ_.1), β(1–τπ_1.), and β(2–τπ_1.–τπ_.1) when (X,Z) = (0,0,), (1,0), (0,1), and (1,1), respectively. The corresponding values of g{E(Y|X,Z)} are 0, β, β, and β×(2-τ), respectively. Monotonicity holds when τ = 1. Suppose 1 < τ ≤ 2. Then, monotonicity holds only when τ > max{1/π_1., 1/π_.1}, and not otherwise. Suppose τ > 2. In this case, monotonicity holds only when τ > 2/(π_1.+π_.1), and not otherwise.

APPENDIX E. Parameter estimation and standard errors under the GJ transformation

For a given λ let Ω_λ denote the parameters of the model given by Equation (11). Thus, Ω_λ is a column vector of length L₁+L₂-1, consisting of the baseline effect and the main effect contrasts. Let W denote the design matrix of the additive model of Equation 11. Let W_ij denote the row of W corresponding to the (i,j)-th risk factor sub-class. Denote ${\pi }_{\mathrm{i}\mathrm{j}}=1-{\{1+{(1+\lambda {\mathbf{W}}_{\mathrm{i}\mathrm{j}}{\mathbf{\Omega }}_{\lambda })}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$\lambda $}\right.}\}}^{-1}$ and let Σ denote a diagonal matrix of dimension L₁×L₂ with diagonal elements of the form ${\mathrm{\Sigma }}_{\mathrm{i}\mathrm{j}}={\left(\frac{{\mathrm{M}}_{\mathrm{i}\mathrm{j}}}{{\mathrm{N}}_{\mathrm{i}\mathrm{j}}}\right)}^{2\lambda }\times ({\mathrm{N}}_{\mathrm{i}\mathrm{j}}+{\mathrm{M}}_{\mathrm{i}\mathrm{j}})\times {\pi }_{\mathrm{i}\mathrm{j}}\times \left(1{\pi }_{\mathrm{i}\mathrm{j}}\right)$. Finally, let y be a column vector of length L₁×L₂ with elements of the form ${\mathbf{W}}_{\mathrm{i}\mathrm{j}}{\mathbf{\Omega }}_{\lambda }+{\left(\frac{{\mathrm{M}}_{\mathrm{i}\mathrm{j}}}{{\mathrm{N}}_{\mathrm{i}\mathrm{j}}}\right)}^{\lambda }\times \{{\mathrm{N}}_{\mathrm{i}\mathrm{j}}-({\mathrm{N}}_{\mathrm{i}\mathrm{j}}+{\mathrm{M}}_{\mathrm{i}\mathrm{j}}\left){\pi }_{\mathrm{i}\mathrm{j}}\right\}\times {\Sigma }_{\mathrm{i}\mathrm{j}}^{-1}$.

For a given λ, the MLEs of the unknown parameters Ω_λ can be obtained via the following iteratively reweighted least squares procedure. Let ${\mathbf{\Omega }}_{\lambda }^{\left(\mathrm{t}\right)}$ denote the estimates in the t-th iteration. In the (t+1)-th iteration, the updated value of the parameters is given by:

$${\mathbf{\Omega }}_{\lambda }^{(\mathrm{t}+1)}=\left({\mathbf{W}}^{\mathrm{T}}{\mathbf{\Sigma }}^{\left(\mathrm{t}\right)}\mathbf{W}\right){\mathbf{W}}^{\mathrm{T}}{\mathbf{\Sigma }}^{\left(\mathrm{t}\right)}\mathbf{y},$$

where the superscript ^(t) for Σ and y on the right hand side indicates that these quantities are calculated by plugging in the value of Let ${\mathbf{\Omega }}_{\lambda }^{\left(\mathrm{t}\right)}$ for Ω_λ. These calculations are repeated until convergence of the log-likelihood function. In practice, we have found this approach to be quite rapid, with convergence occurring within 5 iterations.

We obtain the variance of the MLEs by inverting the information matrix, which is calculated as the negative second derivative of the log-likelihood function with respect to the parameters Ω_λ and λ. The information matrix is given by $\Im =\left(\begin{array}{ll}{\Im }_{\mathrm{\Omega }\mathrm{\Omega }}& {\Im }_{\mathrm{\Omega }\lambda }\\ {\Im }_{\mathrm{\Omega }\lambda }^{\mathrm{T}}& {\Im }_{\lambda \lambda }\end{array}\right)$, where ${\Im }_{\mathrm{\Omega }\mathrm{\Omega }}={\mathbf{W}}^{\mathrm{T}}\mathbf{\Sigma }\mathbf{W}+\lambda \times {\mathbf{W}}^{\mathrm{T}}\text{diag}\left\{\frac{{\mathrm{N}}_{\mathrm{i}\mathrm{j}}-({\mathrm{N}}_{\mathrm{i}\mathrm{j}}+{\mathrm{M}}_{\mathrm{i}\mathrm{j}}){\pi }_{\mathrm{i}\mathrm{j}}}{{(1+\lambda {\mathbf{W}}_{\mathrm{i}\mathrm{j}}{\mathbf{\Omega }}_{\lambda })}^2}\right\}\mathbf{W}$ is a square matrix of dimension L₁+L₂-1, 𝔍_Ωλ is a column vector of length L₁+L₂-1 with elements of the form:

$$\sum _{\mathrm{i}=1}^{{\mathrm{L}}_1}\sum _{\mathrm{j}=1}^{{\mathrm{L}}_2}{\mathbf{W}}_{\mathrm{i}\mathrm{j}}^{\mathrm{T}}\{\frac{{\mathbf{W}}_{\mathrm{i}\mathrm{j}}{\mathbf{\Omega }}_{\lambda }\times \{{\mathrm{N}}_{\mathrm{i}\mathrm{j}}-({\mathrm{N}}_{\mathrm{i}\mathrm{j}}+{\mathrm{M}}_{\mathrm{i}\mathrm{j}}\left){\pi }_{\mathrm{i}\mathrm{j}}\right\}}{{(1+\lambda {\mathbf{W}}_{\mathrm{i}\mathrm{j}}{\mathbf{\Omega }}_{\lambda })}^2}+\frac{({\mathrm{N}}_{\mathrm{i}\mathrm{j}}+{\mathrm{M}}_{\mathrm{i}\mathrm{j}})\times {\pi }_{\mathrm{i}\mathrm{j}}\times (1-{\pi }_{\mathrm{i}\mathrm{j}})}{1+\lambda {\mathbf{W}}_{\mathrm{i}\mathrm{j}}{\mathbf{\Omega }}_{\lambda }}\times (\frac{-1}{{\lambda }^2}\text{log}(1+\lambda {\mathbf{W}}_{\mathrm{i}\mathrm{j}}{\mathbf{\Omega }}_{\lambda })+\frac{1}{\lambda }\times \frac{{\mathbf{W}}_{\mathrm{i}\mathrm{j}}{\mathbf{\Omega }}_{\lambda }}{1+\lambda {\mathbf{W}}_{\mathrm{i}\mathrm{j}}{\mathbf{\Omega }}_{\lambda }}\left)\right\},$$

and

$${\Im }_{\lambda \lambda }=\sum _{\mathrm{i}=1}^{{\mathrm{L}}_1}\sum _{\mathrm{j}=1}^{{\mathrm{L}}_2}({\mathrm{N}}_{\mathrm{i}\mathrm{j}}+{\mathrm{M}}_{\mathrm{i}\mathrm{j}})\times {\pi }_{\mathrm{i}\mathrm{j}}\times (1-{\pi }_{\mathrm{i}\mathrm{j}})\times {\left(\frac{-1}{{\lambda }^2}\text{log}\right(1+\lambda {\mathbf{W}}_{\mathrm{i}\mathrm{j}}{\mathbf{\Omega }}_{\lambda })+\frac{1}{\lambda }\times \frac{{\mathbf{W}}_{\mathrm{i}\mathrm{j}}{\mathbf{\Omega }}_{\lambda }}{1+\lambda {\mathbf{W}}_{\mathrm{i}\mathrm{j}}{\mathbf{\Omega }}_{\lambda }})}^2-\{{\mathrm{N}}_{\mathrm{i}\mathrm{j}}-({\mathrm{N}}_{\mathrm{i}\mathrm{j}}+{\mathrm{M}}_{\mathrm{i}\mathrm{j}}\left){\pi }_{\mathrm{i}\mathrm{j}}\right\}\times \left\{\frac{2}{{\lambda }^3}\text{log}\right(1+\lambda {\mathbf{W}}_{\mathrm{i}\mathrm{j}}{\mathbf{\Omega }}_{\lambda })-\frac{2}{{\lambda }^2}\times \frac{{\mathbf{W}}_{\mathrm{i}\mathrm{j}}{\mathbf{\Omega }}_{\lambda }}{1+\lambda {\mathbf{W}}_{\mathrm{i}\mathrm{j}}{\mathbf{\Omega }}_{\lambda }}-\frac{1}{\lambda }\times {\left(\frac{{\mathbf{W}}_{\mathrm{i}\mathrm{j}}{\mathbf{\Omega }}_{\lambda }}{1+\lambda {\mathbf{W}}_{\mathrm{i}\mathrm{j}}{\mathbf{\Omega }}_{\lambda }}\right)}^2\}$$

is a scalar. Further, the components of the information matrix are calculated by plugging in the MLE of Ω_λ in the above quantities. The covariance matrix of the MLE of Ω_λ is obtained by inverting the information matrix and is given by $\text{Var}\left({\widehat{\mathbf{\Omega }}}_{\lambda }\right)={({\Im }_{\mathrm{\Omega }\mathrm{\Omega }}-\frac{{\Im }_{\mathrm{\Omega }\lambda }{\Im }_{\mathrm{\Omega }\lambda }^{\mathrm{T}}}{{\Im }_{\lambda \lambda }})}^{-1}$. The variances of the parameter estimates are obtained as the diagonal elements of this matrix.

Let $\mathrm{f}(\mathbf{\Omega },\lambda )=\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$\lambda $}\right.\times \text{log}(1+\lambda \mathbf{W}{\mathbf{\Omega }}_{\lambda })$ denote the log odds values, estimated by plugging in the MLE of Ω_λ. Note that f(.) is a column vector of length L₁×L₂. Using the delta method, the covariance matrix of the estimated log odds is given by $\text{Var}\left(\mathrm{f}\right)=\left(\frac{\partial \mathrm{f}}{\partial {\mathbf{\Omega }}_{\lambda }}\frac{\partial \mathrm{f}}{\partial \lambda }\right)\text{Var}\left({\widehat{\mathbf{\Omega }}}_{\lambda }\right){\left(\frac{\partial \mathrm{f}}{\partial {\mathbf{\Omega }}_{\lambda }}\frac{\partial \mathrm{f}}{\partial \lambda }\right)}^{\mathrm{T}}$, where the derivatives are evaluated at the MLEs of the respective parameters. The variance of the log odds estimate for the (i,j)-th risk factor sub-class is then obtained as the relevant diagonal element of this matrix.