Abstract
This paper proposes an original approach for the statistical analysis of longitudinal shape data. The proposed method allows the characterization of typical growth patterns and subject-specific shape changes in repeated time-series observations of several subjects. This can be seen as the extension of usual longitudinal statistics of scalar measurements to high-dimensional shape or image data.
The method is based on the estimation of continuous subject-specific growth trajectories and the comparison of such temporal shape changes across subjects. Differences between growth trajectories are decomposed into morphological deformations, which account for shape changes independent of the time, and time warps, which account for different rates of shape changes over time.
Given a longitudinal shape data set, we estimate a mean growth scenario representative of the population, and the variations of this scenario both in terms of shape changes and in terms of change in growth speed. Then, intrinsic statistics are derived in the space of spatiotemporal deformations, which characterize the typical variations in shape and in growth speed within the studied population. They can be used to detect systematic developmental delays across subjects.
In the context of neuroscience, we apply this method to analyze the differences in the growth of the hippocampus in children diagnosed with autism, developmental delays and in controls. Result suggest that group differences may be better characterized by a different speed of maturation rather than shape differences at a given age. In the context of anthropology, we assess the differences in the typical growth of the endocranium between chimpanzees and bonobos. We take advantage of this study to show the robustness of the method with respect to change of parameters and perturbation of the age estimates.
Keywords: longitudinal data, statistics, shape regression, growth, spatiotemporal registration, time warp
1 Spatiotemporal variability of longitudinal data
Many scientific questions can be expressed in terms of changes or alterations of a dynamical process. In camera surveillance, one aims at distinguishing normal from abnormal behaviors in video sequences. In clinical studies, one wants to characterize anatomical or functional changes due to disease progression, clinical intervention or therapy. In neuroscience, one studies the neurodevelopment or the neurodegeneration of the brain and its related structures. In cardiac imaging, one looks for abnormal patterns in the heart motion. What make these questions so challenging is that the evolving object of interest changes in appearance in different situations. In video sequences for instance, we want to distinguish a normal from an abnormal behavior behind the large variety of the shapes and the motions of the silhouettes. Similarly, every brain has a different shape, whereas its maturation may follow some common patterns that we would like precisely to describe and quantify.
From the point of view of data analysis and pattern theory, these problems can be addressed by the statistical analysis of longitudinal data sets. A longitudinal data set consists of the observation of a set of homologous objects (such as silhouettes of people or anatomical structures), each object being observed repeatedly at several time points. An abstract example of such a data set is given in Fig. 1, which illustrates the sampling of individual growth trajectories of different subjects. The analysis of such longitudinal data sets should lead to the qualitative and quantitative assessment of change trajectories, to the detection of common growth patterns shared in a population, and to the characterization of their appearances in different subjects.
Fig. 1.
Synthetic example of a longitudinal data set with 3 subjects. Each subject has been observed a few times and at different time-points. The aim of the spatiotemporal variability analysis is to describe the variability of this population in two ways: the geometrical variability (there is a circle, a square and a triangle), and the variability in terms of change of dynamics of evolution (for instance, the square grows first at a faster rate than the circle and then slows down.)
Longitudinal analysis differs from the usual cross-sectional variability analysis in that it takes into account the inherent correlation of repeated measurements of the same individuals. It must also provide a model of how an individual subject’s trajectory changes relative to another subject. At the population level, we typically analyze how the subjects are distributed within a group by estimating a mean configuration and its variance. For longitudinal data, the mean configuration may be a “mean growth scenario”, which averages the growth patterns in the population. The analysis of its variance explains how each subject’s trajectory differs from the mean growth scenario. Such a statistical approach based on mean and variance is well-known for scalar measurements and for analysis of cross-sectional shape data, for which the mean is usually called “template” or “atlas”. The extension of these concepts for longitudinal shape data is challenging, as no consensus has emerged about how to combine shape changes over time and shape changes across subjects.
In this paper, we propose a consistent conceptual and computational framework to address these questions: (i) the estimation of subject-specific trajectories via the introduction of a growth model as a smooth deformation of the baseline shape, (ii) the comparison of different trajectories via spatiotemporal mappings which align both the shape of different subjects and the tempo of their respective evolution, (iii) the estimation of a “mean growth scenario” representative of a given population, and (iv) the statistical analysis of the typical variations of this mean scenario in the studied population. The proposed methodology does not require that the subjects are observed with the same number of samples or at the same time-points.
One of the main contributions of this methodology is that it models the changes in individual trajectories both as morphological changes, which account for the different appearances of the object, and as dynamical changes, which account for different paces of evolution. At the population level, this assumes that the development of different subjects shares the same growth patterns, up to changes in shape and changes in the tempo of the development. This enables in particular the characterization of the effect of a pathology as a systematic developmental delays in the growth of a given organ.
The detailed explanation of the method and its related algorithms is given in Sec. 3. Sec. 2 explains how the proposed framework consistently embeds different concepts introduced in the literature and highlights different possible modeling choices. In Sec. 4, we show how the method can be used to characterize the effect of autism and developmental delay in the growth speed of the hippocampus. In Sec. 5, the method will be used to quantitatively assess the relative developmental delay of the endocranial growth between bonobos and chimpanzees. We will show that this estimation is robust to parameter changes and changes in the age estimates of the samples.
2 An emerging framework for the analysis of longitudinal shape data
This section presents a survey of the literature on the topic of longitudinal analysis of shape data. This will highlight which tools and concepts need to be linked into a common statistical framework. We will also make clear that different modeling choices are possible. We will propose to follow the approach that seems the more adapted to the targeted applications.
2.1 Previous research to design 4D statistical analysis
2.1.1 4D analysis meant as regression or tracking
The first kind of so-called 4D-analysis proposes to estimate a continuous sequence from a set of time-indexed shapes or images of the same subject. In Mansi et al (2009), one estimates a cross-sectional atlas from time series data and then analyzes the correlations between the modes of variability and the age of the subject, considered as an explanatory variable. These correlations may be used to estimate a synthetic growth scenario for a given individual. Other approaches, which do not rely on a cross-sectional atlas, include work by de Craene et al (2009), in which the authors use Large Diffeomorphic Free Form Deformations to estimate time-varying deformations between the first and the last sample of a sequence of images. In the same spirit, Davis et al (2007) propose to perform the regression of a sequence of images via a generalization of the kernel regression method to Riemannian manifolds. Growth scenarios could also be estimated based on stochastic growth models as in Grenander et al (2007); Trouvé and Vialard (2010) or on twice differentiable flows of deformations as in Fishbaugh et al (2011).
These methods are pure regression methods. If they are used with several subjects scanned several times, these regression methods return a single evolution, the most probable evolution in some sense. They do not take into account that data at different time points may come from the same subject or from different subjects. It averages shape evolutions without discarding the inter-subject variability, which leads to “fuzzy” estimation like the average of a set of non-registered images. By contrast, in Thompson et al (2000); Gogtay et al (2008), registrations between baseline and follow-up scans of the same subject are performed and the evolutions of scalar measurements extracted from the registration are compared across subjects. A main contribution of our paper will be to extend this framework for scalar measurements to the high-dimensional space of shapes. In Khan and Beg (2008), the authors propose to perform a regression of the image sequence of every subject separately and then to average the time dependent velocity field of each regression to estimate a typical scenario of evolution. This approach is limited to situations where each sequence is registered in the same reference frame, but no details of how to perform registration of time-indexed sequences of images is given.
2.1.2 3D-registration of 4D-sequences
The problem of registering individual trajectories has been investigated in different communities. In Chandrashekara et al (2003), the motion of the heart of each subject is tracked through time. Then the registration between the baseline image of two subjects is used to transport the velocity field of the tracking from one subject’s space to the other. This approach could also include the estimation of a template image at the baseline time-point using usual cross-sectional atlas construction methods, like in Ehrhardt et al (2008); Qiu et al (2008, 2009). All these methods assume that the inter-subject variability can be captured considering only the baseline images. Using these deformations for registering the whole time-indexed sequence of images is arguable, since they do not take into account anatomical features which may appear later in the sequence.
This issue has been addressed in Peyrat et al (2008) who proposed to register a time-indexed sequence by computing deformations between any pair of successive scans of the same subject and between any pair of scans of two different subjects at the same time-point. Such an approach takes all temporal information into account and therefore leads to a much more robust registration scheme. However, this method assumes that every time-indexed sequence has exactly the same number of images, which are acquired at time points which correspond across subjects. By contrast, in longitudinal studies, only a few scans per subject are available, and the number of scans may vary for different subjects. This issue has been addressed in Hart et al (2010), who proposed an interpolation scheme to average individual trajectories at every time-point independently. However, none of these approaches take into account the inherent temporal correlations between successive inter-subject registration. From a statistical point of view, this means that the inter-subject variability at two different time points are considered as independent variables. As the sampling of the image sequence becomes finer and finer, the number of variables to estimate becomes larger and larger. A main contribution of this paper will be precisely to define a generative statistical model, which takes into account the temporal correlations between inter-subject registrations at different time points, and to provide a way to estimate these correlations from a finite set of observations.
In Gerig et al (2006), a template image is built at every time-point independently. Then, the deformations between the baseline scan and the follow-up of any subjects are compared to the deformation between the baseline atlas and the follow-up atlas. This approach focuses on the analysis of the cross-sectional variability over time. However, since the template image is built at each time point independently, it is not clear whether the difference between the baseline atlas and the follow-up atlas is the average of every subject’s evolution. Moreover, such a method requires that the distribution of age in the longitudinal data set is clustered at two distinct ages, which is a special case. A similar approach has also been proposed in Aljabar et al (2008).
2.1.3 Taking into account temporal re-alignment
The methods cited previously propose a way to combine the subject-specific growth with the inter-subject variability: time-series image sequence are processed by a combination of 3D deformations. In particular, the age at which the subjects are scanned is considered an absolute time which corresponds across subjects. This assumes that at a given age, every subject is at the same development stage and that their anatomy can be compared. Such procedures neglect possible developmental delays between subjects, or some pathology affecting the cardiac pace, for instance, a key feature that we precisely want to detect. A spatiotemporal registration scheme should register individual growth scenarios both in space (usual geometrical variations of the anatomy) and in time (change of the speed of evolution). Time changes should put the ages of the subjects into correspondence, which represents the same developmental stage.
In Declerck et al (1998), a deformation of the 4D domain is provided via 4D planispheric transformations for the registration of the heart motion. In Perperidis et al (2005), spatiotemporal deformations are computed. The temporal part is a 1D function showing the change of cardiac dynamics between the source and the target subject. This temporal alignment is performed jointly with the registration of the anatomy. These methods focus on the registration between a pair of individual trajectories, and requires a fine temporal sampling of the trajectories. A main contribution of our paper will be to use such spatiotemporal deformations for the inference of statistical properties at the population level, via the estimation of spatiotemporal atlases.
2.1.4 Ingredients for a spatiotemporal statistical model
This review of the literature shows that several aspects of the design of a 4D statistical analysis have been addressed separately by different authors, in different contexts and with different tools. There is a lack of a consistent framework to embed these concepts together, covering the estimation of individual trajectories and the inference of population statistics.
In light of this review, a statistical framework for longitudinal data analysis might include:
-
-
The estimation of a continuous shape evolution from a set of observations sparsely distributed in time. These individual trajectories could be used to compare the anatomy of two subjects, who have not been scanned at the same age. They could also be used to analyze the speed of evolution of a given subject at any time-point.
-
-
The comparison between individual trajectories, which should measure not only morphological differences (commonly described by 3D deformations) but also the temporal re-alignment which put the developmental stages of different subject into correspondence. This temporal re-alignment will detect different speeds of evolution and therefore possible developmental delays between subjects.
-
-
A generative statistical model, which combines the two previous concepts to estimate evolution patterns that are shared among a given population. The estimated statistics should include a mean (a growth scenario representative of the population) and variance (the typical variations of this mean growth scenario evident in the population).
2.1.5 Terminology
The survey of the current literature also raises the problem of terminology: there is no consensus among authors about which words refer to which concepts. In this paper, we will use the following definitions:
Data:
-
-
cross-sectional data is a set of samples, which are supposed to be comparable, or homologous (like samples drawn from a healthy adult population, for instance). No notion of time is involved, or equivalently, the effect of time or age on the data can be neglected.
-
-
time-series data is a set of data that are indexed by any temporal marker like age, indicator of developmental stage, disease progression or index of a frame in a movie, for instance. No assumption is made that a sub-set of the samples correspond to the same object seen at different time-points.
-
-
longitudinal data is a time-series data set, which contains repeated observations of individual subjects over a period of time. As a consequence, each subject in the data set should have been observed more than once at different time-points.
Methods:
-
-
shape/image regression, also called tracking, refers to the estimation of a continuous evolution model from a time-series data set. This tool estimates shape changes between discrete temporal observations or averages time-indexed observations into a single evolution.
-
-
spatiotemporal registration puts two individual trajectories into correspondence. This involves the notion of correspondence between shapes and between time-points.
-
-
spatiotemporal or longitudinal data analysis measures the similarities and the differences between individual trajectories. It takes into account the fact that individual subjects were observed several times, which makes it more constrained than the analysis of the effect of time on the observations.
According to these definitions, shape or image regression may be performed on time-series data, whereas spatiotemporal analysis can only be performed on longitudinal data.
2.2 Two possible generative models for longitudinal data
2.2.1 Spatiotemporal variations of a typical growth model
A generative statistical model is a set of hypotheses, which explain how individual trajectories could be derived one from the others. In other words, it should provide an answer to the two fundamental questions: given the anatomy of one subject at time t,
-
-
how can we predict the anatomy of this subject at a later time t′ > t?
-
-
how can we derive the typical anatomy of another subject at the same time-point?
Once these answers are provided, we can easily define a generative statistical model at the population level. This model will assume the existence of a mean growth scenario representative of the population, such that the individual trajectories can be seen as a derivation of this mean scenario. The mean scenario captures the invariants in the population and detects the growth patterns, which are shared among the subjects. The derivation of the mean scenario captures the variance of this mean configuration within the population.
In light of the literature survey, there are at least two different ways to answer these questions. We refer to these two paradigms as a “subject-specific approach” and a “time-specific approach”.
2.2.2 Subject-specific approach
In the subject-specific approach, a specific reference frame is attached to each subject. The whole evolution of each subject is described within the same reference frame: the reference frames are atemporal. We assume that there is a template reference frame in which the evolution is written by a time-varying shape M(t): the prototype scenario of evolution in the population, which can be seen as the 4D analog to the template shape in 3D. We usually assume that the time-varying shape derives continuously from a template shape M0 at a reference time point t0. This is written as:M(t)= χt (M0), where χt is a smoothly varying 3D deformation called the growth function (χt0 = id so that M(t0) = M0).
Change of coordinates from the template reference frame to each subject’s reference frame is modeled by 3D deformations ϕs. Since these reference frames are atemporal, the deformations ϕs do not depend on time. As a consequence, the evolution function M(t) has a different expression in each coordinate system: the evolution of a subject S is given as S(t)=ϕ(M(t)), also written as S(t)=ϕ(χt (M0)). It is as if a single object (M(t)) is seen by different observers in different coordinate systems. As illustrated in Fig. 2a, the change of co-ordinates ϕs transports the evolution function χ(t) from the template frame to the subject’s frame: , so that . The evolution mapping is therefore specific to each subject.
Fig. 2.
Illustration of the hypotheses underlying the subject- and time-specific approaches. In the subject-specific approach (left), one considers that one subject is “circle” and the other is “square”: the difference is described by a single function ϕ, which maps circles to squares. The evolution of the first subject is described by a function χ which maps a small circle to big circle. As a consequence, the evolution of the second subject is described by another function χϕ which maps a small square to a big square. In the time-specific approach (right), one describes the evolution by a universal function χ, which tends to scale the shapes. At the first-time point, the difference between subjects is described by a function ϕ which maps the small circle to the small square. At a later time, the inter-subject variability has changed according to χ: now the difference between subjects is described by ϕt which maps a big circle to a big square.
In this modeling, we can include time as an additional variable, so that the reference frame of each subject is described by 3 spatial coordinates and 1 temporal coordinate. This means that both the anatomy and the age is relative to the subject. This specific time variable can be called the “physiological age” of the subject, as if each subject has their own biological clock. In the reference frame of the prototype, the time would be the absolute age, computed from the date of birth. Then, the 3D warp ϕ(x, y, z) needs to be generalized to a deformation of the underlying 4D space: Φ(x, y, z, t).
The most general form of a 4D-deformation is Φ(x, y, z, t)= (ϕ(x, y, z, t), ψ(x, y, z, t)), where ϕ(x, y, z, t) denotes the 3 spatial coordinates of Φ(x, y, z, t) (the morphological deformation) and ψ(x, y, z, t) its temporal coordinate (the time warp).
Assuming that ψ(x, y, z, t) depends on the spatial variables (x, y, z) means that different parts of the anatomy of a given subject would evolve at different speeds. This is definitely possible in applications involving multi-shape comparisons. However, in this paper, we will assume that all points of the anatomy of a given subject have always the same physiological age over time. In this case, ψ depends only on the time variable t: ψ(t). This assumption is likely to be valid in most longitudinal studies, focusing on one specific structure. The time warp ψ(t) maps the absolute age in the reference frame of the prototype to the physiological age of a given subject. Note that this function should be monotonic, assuming that the sequence of events in every individual trajectory occur in the same order (from birth onwards) but at a different pace.
Since the change of coordinate maps ϕ are independent of time, they are of the form: ϕ(x, y, z). Therefore, in the subject-specific setting, the 4D deformations are written as:
The morphological deformation ϕ is used to measure the geometrical variability. The time warp ψ is used to detect possible developmental delays between subjects.
Note that the most general form of 4D deformations, without any assumptions on the temporal dependency of the spatial part ϕ(x, y, z, t), cannot be used in a statistical model. Indeed, such models will be not identifiable, as there would be an infinite number of different spatial/temporal combinations to explain the same data set.
2.2.3 Time-specific approach
In the time-specific approach, every subject is embedded into the same reference frame, which transports everyone over time. It is as if different objects are seen by a single observer. More precisely, there is a common reference frame at reference time t =0 (the “origin of the world”) in which the anatomy of every subject is described. The evolution function χt changes the geometry of this reference frame over time. At each time t, there is one single reference frame which embeds the anatomy of every subject: this frame is universal. The same function χt applies for each subject, so that the evolution of any subject is given by S(t) = χt (S0), where S0 represents the anatomy of the subject at the reference time t0.
In the common reference frame at t = 0, we assume that each subject’s anatomy S0 results from a deformation of the prototype anatomy M0: S0 = ϕs(M0). The deformations ϕs describe the inter-subject variability at time t = 0. In this framework, the mapping between the template and the subject shape changes over time according to the evolution function χt. At a later time t, the template has evolved as M(t) = χt (M0) and the subject shape has evolved as S(t) = χt (S0). This shows that the template-to-subject registration has become: S(t) = ϕ(M(t)) where , as illustrated in Fig. 2b. Whereas the evolution function is independent of the subject, the inter-subject variability is specific to time.
We can also include possible developmental delays in this framework. If χt is a universal function which carries the anatomies over time, we can imagine that every subject follow this universal scenario at its own pace. There is a subject specific time warp ψ, so that the evolution of this subject is given by χψ(t). However, we must admit that this time-realignment fits less naturally into this time-specific framework than for the subject-specific framework. In particular, it is not clear how to distinguish a developmental delay from a variation of the inter-subject variability in this setting.
This time-specific approach also defines a deformation of the underlying 4D-space Φ(x, y, z, t). The morphological deformations ϕ now depend on time according to the evolution function χt. This leads to the particular form of the 4D mapping:
where the geometrical part has the form:
This last equation is the constraint, which eventually makes the statistical model identifiable.
2.2.4 Which method for which problem?
The subject-specific approach focuses on the variations of a growth scenario from subjects to subjects. One is interested in analyzing how individual trajectories vary across subjects. The time-specific approach focuses on the evolution of the inter-subject variability over time. One is more interested in the evolution of the statistical properties (mean and variance) of the population over time, as illustrated in Fig. 3. Theses two approaches are based on different assumptions and lead to different statistical estimations.
Fig. 3.
Subject- versus time-specific approach. In the subject-specific approach (left) the mean scenario averages the individual trajectories. The inter-subject variability is supposed to be constant over time. In the time-specific approach (right), every subject is supposed to follow the same mean scenario of evolution, up to a change of the initial conditions. The mean scenario describes how the inter-subject variability evolves over time.
The subject-specific approach is the only one to take into account change of coordinates between subjects, and therefore the only one to accommodate for scaling effects across subjects. The time-specific paradigm uses a single diffeomorphic deformation to describe the evolution of every subject. This assumes that the structure of two different subjects, which are superimposed at one time, will remain superimposed in the future. Such topological constraints are often unrealistic. Moreover, the statistical estimations in the subject-specific paradigm are more robust when the number of subjects is greater than the number of observations per subjects, which is the case with the longitudinal data set on which we aim at applying this methodology in Sec. 4 and 5. For these reasons, the presented work will focus on the subject-specific paradigm.
3 A subject-specific approach using 3D diffeomorphisms and 1D time warps
In this section, we propose an instance of the subject-specific paradigm for the analysis of longitudinal shape data, given as point sets, curves or surfaces. Among several other possible choices, we will build our methodology on the large diffeomorphic deformations setting for defining the registration between shapes. This setting is particularly adapted to define statistical models using deformations due to the metric properties of the considered space of diffeomorphisms (Vaillant et al, 2004; Durrleman et al, 2009a). In particular, we will propose an extension of this framework to construct monotonic 1D functions for our “time warp” in a very generic way. We will also consider the geometrical shape like curves and surfaces as currents (Glaunès, 2005). This allows us to inherit from the statistical and computational tools introduced in Durrleman et al (2009a); Durrleman (2010) for the estimation of representative shapes, called templates.
We follow the approach in three steps outlined in the Introduction: (i) the estimation of individual growth trajectories via the inference of a growth model, (ii) the comparison of individual trajectories based on a morphological map and a time warp, (iii) the estimation of statistics from a set of individual trajectories: mean scenario of evolution and analysis of the spatiotemporal variability.
3.1 Sketch of the method
3.1.1 Growth model for individual shape evolution
Our purpose is to fit a continuous shape evolution to a discrete set of shapes (Si) of the same subject acquired at different time points (ti). To infer such a continuous shape evolution, we need a prior on the growth of the shape, called a “growth model”. Here, we hypothesize that the baseline shape S0 observed at time t = 0 continuously and smoothly deforms over time. To be more precise, our growth model assumes that the evolution of the shape S0 can be described by a continuous flow of diffeomorphisms χt. This means that for each t varying in the interval of interest [0,T], χt is a diffeomorphism of the underlying 2D or 3D space, which models the smooth and invertible deformation which maps the baseline at t = 0 to its actual shape at time t. The diffeomorphisms vary continuously over time (the deformation χt+δt is close to χt ). Mapping the baseline shape S0 with the time-varying functions χt leads to a continuously deforming shape S(t) = χt (S0): the individual trajectory of the considered subject. Note that this imposes that χ0 = Id, the identity map, so that S(0) = S0.
Given the set of discrete observations (Si) at time-points ti, one needs to estimate the flow of diffeomorphisms χt, which may have led to these observations. A Maximum A Posteriori (MAP) estimation, in the same framework as in Durrleman (2010)[Chap. 5] leads the minimization of the discrepancy between the growth model at time ti (S(ti) = χti (S0)) at the actual observation Si, up to a regularity constraint on the smoothness of the flow of diffeomorphisms (χt)t∈[0, T]:
| (1) |
where d is a similarity measure between shapes, which will be the distance on currents in the following, Reg(χ) a regularity term, which will be the total kinetic energy of the deformation, and γχ a scalar parameter quantifying the tradeoff between regularity and fidelity to data. The optimization of this criterion will be explained in Section 3.2.2.
As an illustrative example, we used five 2D profiles of hominid skulls which consist of six lines each1, as shown in Fig. 4. Each profile correspond to a hominid (Australopithecus, Homo Habilis, Homo Erectus, Homo Neandertalensis and Homo sapiens sapiens) and is associated to an age (in millions of years). The regression infers a continuous evolution from the Australopithecus to the Homo sapiens sapiens which matches the intermediate stages of evolution.
Fig. 4.
Shape regression of a set of five 2D profiles of hominid skulls (in red). The Australopithecus profile is chosen as the baseline S0. The temporal regression computes a continuous flow of shapes S(t) (here in blue) such that the deforming shape matches the observations at the corresponding time-points. It is estimated by fitting a growth model, which assumes a diffeomorphic correspondence between the baseline and every stage of evolution (S(t) = χt (S0)), with the diffeomorphism χt varying continuously in time.
If there is only one data S1 at time t1 =T, the criterion (1) defines the registration of S0 to S1. In the LDDMM frame-work, the result of such a registration is a geodesic flow of diffeomorphism between t = 0 and t = T that maps S0 close to S1 (Miller et al, 2002). With several data at successive time points, we will show in Sec. 3.2.2 that the result is a flow of diffeomorphism which is geodesic only between successive time points (i.e. piecewise geodesic). We will also show that the computation of the regression functions χt takes into account all the observations Si in the past and future simultaneously. Therefore, it differs from pairwise registration between consecutive shapes. For instance, if the trade-off γχ tends to infinity (no fidelity-to-data term) the regression is a constant map χt = Id for all t. As γχ decreases, the piecewise geodesic regression matches the data with increasing “goodness of fit”. This framework allows us also to perform the regression even if several data are associated to the same time-point. This will be used in Sec. 5 to estimate a mean growth scenario of a time-series cross-sectional data set.
Note that if T is greater than the latest time-point of the data tmax, then the regression function χ is constant over the interval: [tmax, T]. Therefore, the method extrapolates with constant shape outside the time interval [0, tmax]. Such an extrapolation will be needed to compare the evolution of two subjects, whose latest observation correspond to different time-points. Similarly, we can also extrapolate the evolution function at time earlier than 0 with a constant map, so that the evolution function can be defined on any arbitrary time interval.
3.1.2 Spatiotemporal registration between pairs of growth scenarios
We suppose now that we have two subjects S and U which have been scanned several times each (but not necessarily the same number of times and possibly at different ages). Let Sti (resp. Utj) be the shapes of subject S (resp. U) at ages ti (resp. tj). We define a time-interval of interest which contains every ti’s and tj’s. Without loss of generality, we can assume that this time interval of interest is of the form [0, T].
We infer an individual growth model S(t) from the data of the source subject {Sti}, using the procedure of the previous section. As a result, the continuous shape evolution S(t) is of the form: S(t) = χt (S0) for t ∈ [0, 1].
Our goal is to define a spatiotemporal deformation of the continuous evolution S(t) into S′(t) so that the deformed shapes S′(tj) at the time-points of the target tj match the shape Utj (thanks to the continuous regression, we can define S(tj) for the target time point tj even if the source has not been observed at this age.) For this purpose, we introduce two functions (using the subject-specific paradigm in Sec. 2): the 3D morphological deformation ϕ and the 1D time warp ψ. The morphological deformation is a 3D-function, which maps the geometry of the source to the geometry of the target (change of reference frame). Every frame of the source sequence S(t) is deformed using the same function. The time warp ψ maps the time-points t within the time interval [0, T] to ψ(t). This function does not change the frames of the sequence S(t) but change the speed at which the frames are displayed. It models the change of the dynamics of the evolution of the source with respect to the evolution of the target. We impose this 1D function to be monotonic, assuming that the shape changes occur in the same order, even if at a different pace between source and target. The combination of these two functions gives the spatiotemporal deformation of the continuous evolution S(t), defined as:
| (2) |
Using the fact that S(t) = χt (S0), this becomes2:
| (3) |
In a MAP setting, the estimation of the best possible spatiotemporal deformation (ϕ, ψ) of the source evolution which fits the the target observations, leads to the minimization of the discrepancy between the deformed source at target’s time-points S′ (tj) = ϕ(S(ψ(tj)) and the target’s shape Utj :
| (4) |
where d is a distance between shapes, Reg(ϕ) and Reg(ψ) the measure of regularity of the deformation ϕ and ψ and γϕ, γψ the usual scalar trade-offs between regularity and fidelity to data.
An illustration of spatiotemporal registration is shown in Fig. 5, 6 and 7. We use the same set of profiles of 2D hominids skulls as in Fig. 4. Here we want to compare the evolution {Homo habilis-Homo erectus-Homo neandertalensis} (called earlier evolution) with the evolution {Homo erectus-Homo sapiens sapiens} (called later evolution). The differences may be due to a change of the shape of the skull, as well as a change of the dynamics of evolution between the earlier and the later evolution. Therefore, we divide the database into two groups, considered as two different subjects, and translate the target back four million years, so that both evolutions start at the same time (this can be seen as a “rigid” temporal alignment as a pre-processing). See Fig. 5.
Fig. 5.
Illustrative pairwise registration: data preparation. The database is cut in two to compare the evolution {Homo habilis-erectus-neandertalensis} (red shapes) to the evolution {Homo erectus-sapiens sapiens} (green shapes). The later evolution is translated in time, so that both evolutions start at the same time. Then, one performs a shape regression of the source shapes (blue shapes). The spatiotemporal registration of this continuous source evolution to the target shapes is shown in Fig. 6 and 7.
Fig. 6.
Illustrative pairwise registration: morphological deformation and time warp. Top row: The input data as prepared in Fig. 5 with the continuous source evolution (blue) superimposed with the target shapes (green). Middle row: The morphological deformation ϕ is applied to each frame of the source evolution. It shows that, independently of time, the skull is larger, rounder and the jaw less prominent during the later evolution relative to the earlier evolution. Bottom row: The time warp ψ is applied to the evolution of the second row. The blue shapes are moved along the time axis (as shown by dashed black lines), but they are not deformed. This change of the speed of evolution shows an acceleration of the later evolution relative to the earlier evolution. Taking this time warp into account enables a better alignment of the source to the target shapes than only the morphological deformation. Note that the morphological deformation and the time warp are estimated simultaneously, as the minimizers of a combined cost function.
Fig. 7.
Illustrative pairwise registration: analysis of the time warp. Top: plot of the 1D time warp ψ(t) putting into correspondence the time-points of the target shapes with that of the source. The x = y line (dashed in black) would correspond to no dynamical change between source and target (ψ(t) = t). The slope indicates that the shape changes between target data occur 1.66 times faster than the changes in the source evolution, once morphological differences has been discarded. Right: the graph of the skull volume over the human evolution as found in the literature (source: www.bordalierinstitute.com). This curve shows that the increase in skull volume between Homo erectus and Homo sapiens sapiens was 1.62 times faster than between Homo habilis and Homo neandertalensis (ratio between the slope of the two straight lines). This value is compatible with the acceleration measured by the time warp: 1.66.
The regression of the source data leads to a continuous source evolution S(t) shown in blue in the first row of Fig. 5. The estimation of the spatiotemporal deformation between the source and the target results in a morphological deformation ϕ and a time warp ψ, see Fig. 6. The morphological deformation shows that the jaw is less prominent and the skull larger and rounder during the later evolution than during the earlier evolution (second row in Fig. 6). The effect of the time warp is to accelerate the source evolution to adjust to the rate of shape change between the target shapes (third row in Fig. 6). The graph of the time warp is plotted in Fig. 7a. It shows an almost linear increase in speed. The slope of the curve is of 1.66, thus meaning that the later evolution evolves 1.66 times faster than the earlier evolution. This value is compatible with the growth speed of the skull during this period according to the values reported in the literature and in Fig. 7b: between Homo erectus and Homo sapiens sapiens the skull volume had grown at a rate of (1500–900)/0.7 = 860cm3 per millions of years, whereas between Homo habilis and Homo neandertalensis, it had grown at (1500–600)/1.7 = 530cm3 per millions of years, namely 1.62 times faster.
3.1.3 Atlas estimation from longitudinal data sets
In this section, we want to combine the previously introduced growth model and spatiotemporal deformations to estimate statistics from a longitudinal database. Given the repeated observations of a group of subjects, we assume that each subject’s evolution derives from the same proto-type evolution, called a “mean scenario of evolution”. Each subject-specific evolution is derived from the mean scenario via its own spatiotemporal deformation. The analysis of the set of all the spatiotemporal deformations in the population will lead to the estimation of the typical variations of the mean scenario in the population (the variance of the population in a sense to be defined). We assume that the mean scenario of evolution is given by the growth model of an unknown prototype shape M0, called template in the sequel.
Formally, this means that there is a growth function χt for t ∈ [0, T] and a template shape M0, so that the mean scenario of evolution is written as: M(t) = χt (M0) with M(0) = M0. For each subject s (s = 1, …, Nsubj), the subject-specific spatiotemporal deformation of the mean scenario is written as: Ss(t) = ϕs (M(ψs(t))) for all t ∈ [0, T]. ϕs is the morphological deformation for subject s and ψs its time warp. These two functions model how the anatomy of the subject and the dynamics of evolution can be derived from the prototype scenario of evolution. Eventually, we suppose that the observation of the subject s at time-point , denoted , is the temporal sample from Ss(t) at time point , up to a random Gaussian noise: :
| (5) |
where the Gaussian variables are independent and identically distributed over the subject-index s and the time-index j.
This equation is our generative statistical model, which explains how the observations can be seen as instances of a random process. The fixed parameters are the prototype shape M0 and the growth function χt. The random parameters are the spatiotemporal deformations (ϕ, ψ) (each estimated (ϕs, ψs) is an instance of these random deformations). Both the fixed and the random parameters are unknown and should be estimated given the actual observations.
In the same MAP setting as in the previous section, the estimation of the unknown parameters can be done by minimizing the following combined cost function:
| (6) |
The output is the prototype shape M0, the growth function χt and the set of spatiotemporal deformations ϕs, ψs for every subject s. These variables are called a “spatiotemporal atlas”. In Sec. 3.3, we will show how we can perform statistics on the estimated deformations (ϕs, ψs), like Principal Component Analysis for instance. Such statistics will describe the changes in shape and the variations of the speed of evolution across subjects.
To illustrate the method, we run the atlas estimation given the two “subjects” in Fig. 5: the first subject (in red) consists of three shapes, the second subject (in green) consists of two shapes. From these five shapes, the method returns the estimated template, the mean scenario and the two spatiotemporal registrations of this mean scenario to each subject. The estimated template M0 is given as a current, which does not form a set of curves anymore Durrleman et al (2009a). To give an illustration of the atlas, we map the youngest shape of each subject to this current and pick the deformed shape that is the closest to the estimated template. Then, one runs one more iteration of the atlas algorithm, to show the mean scenario and the spatiotemporal registrations as deformations of this template shape. This is shown in Fig. 8. In particular, the two time warps which put into correspondence the evolution stages of each subject to the ones of the estimated mean scenario are shown in Fig. 9-b.
Fig. 8.
Spatiotemporal atlas estimation given the two “subjects” in Fig. 5. On the middle row is shown the estimated mean scenario of evolution. The first frame of this scenario (far left) is the estimated template shape. Two upper rows represents the morphological deformation and then the time warp, which jointly maps the mean scenario to the shapes of the first subject (red shapes). Tow lower rows represents the spatiotemporal deformation of the mean scenario to the shapes of the second subject (green shapes). Black arrows indicate areas where the most important shape deformations occur.
Fig. 9.
Spatiotemporal atlas estimation: template and time warp. (a) the template and its morphological deformation to the first subject (red) and the second subject (green). This corresponds to the far left frames in the second, third and fourth row in Fig. 8. (b) The graphs of the two time warps, mapping the subjects’ growth speed to that of the mean scenario. When the curve is above x = y axis, the subject’s evolution is in advance relative to the rate of shape changes given by the mean scenario. (c) Graph of the function: (in blue), which maps the dynamics of the two subjects. The dashed red curve is the time warp given by the pairwise registration as shown in Fig. 7-a.
Let us denote S1(t) the spatiotemporal deformation of the mean scenario, which is supposed to match the shape of the first subject: S1(t) = ϕ1(M(ψ1(t))). Similarly, S2(t) = ϕ2(M(ψ2(t))) matches the shapes of the second subject. Then, by definition, we have: . At the first glance, this suggests that () corresponds to the spatiotemporal registration between the first subject (considered then as the source) to the second subject (considered as the target). We superimposed in Fig. 9-c the graph of with the graph of the time warp estimated in the previous section and shown in Fig. 7-a. As expected, the two curves show a similar pattern, namely the overall acceleration of the source relative to the target. However, noticeable differences appear, in particular in the slope of the curves. This can be explained by at least two reasons. First, what we called here S1(t) is not the same shape evolution as the one computed in the pairwise registration case (first row in Fig. 5): the regression of the source subject in the registration case did not take into account any information about the target shapes, whereas the mean scenario M(t) (and consequently its deformation S1(t)) averages the growth patterns of both subjects. Second, the reasoning above does not take into account the residual errors into account: assuming that S̃1(t) and S̃2(t) are the true evolution of each subject, then we have: S̃1(t)=ϕ1(M(ψ1(t)))+ε1(t) and S̃2(t) = ϕ2(M(ψ2(t)))+ε2(t), where ε1(t) and ε2(t) models the residuals shape which contains noise, small-scale variations and everything else, which cannot be explained by the model. The squared norm in the criterion to be optimized shows that we assume these residuals to be Gaussian random variables (see Durrleman (2010) for more details). This shows therefore that , meaning that the residual error between the two scenarios S̃1(t) and S̃2(t) is no more Gaussian. Therefore, to retrieve the same deformations and time warps, one would need to change the squared norm in the registration criterion to take into account the distortion in the distribution of the residuals induced by the deformations.
The discussion above highlights the main features of the atlas construction method. The main assumption is that the different subjects derive from the same prototype scenario, and therefore share common growth patterns even if altered in their shape and timing. The atlas aims precisely at detecting these common features and the variations of their shape and pace in the population. Every pattern, which is specific to a given individual, is discarded from the atlas and remains in the residuals. In this sense, the atlas is a statistical tool, which detects the reproducible patterns in the population. Compared to pairwise registration, the advantages of the atlas construction is that it can be applied to more than two subjects and that it does not favor any particular subject in the population.
Remark 1 (On the assumption of diffeomorphic maps) In this modeling, we suppose that the evolution function χ and the morphological deformations ϕ are 3D diffeomorphisms and that the time warps ψ are 1D diffeomorphisms. The motivation and consequences of choosing diffeomorphic maps are different in each case.
The evolution function χ maps the anatomy of a subject over time. Setting χ as a diffeomorphism assumes a smooth one-to-one correspondence between any observed shapes of the same subject. This includes modes of growth like atrophy, dilatation, torque, etc. However, this cannot model a tearing of the shape, its division or the creation of another disconnected component over time. This assumption is realistic in many practical case, like for the heart over a cycle or the macroscopic observation of a brain structure during infancy.
The morphological deformations ϕ model the geometrical inter-subject variability. Assuming a smooth one-to-one correspondence between the anatomies of two different subjects is more questionable. As highlighted in Durrleman et al (2011) and Durrleman (2010)[Chap. 5], the diffeomorphism is used to decompose the inter-subject variability into two terms: the diffeomorphic geometrical variability captured in the deformations and the non-diffeomorphic variability in terms of “texture” captured in the residuals (modeled by the random Gaussian variables). Both terms can be used for the statistical analysis, whereas in this work we will focus only on the geometric variability captured by the deformations. Extending the work of Durrleman et al (2011) to analyze the non-diffeomorphic variations would be possible but out of the scope of this paper.
The time warp ψ model the change of speed of evolution between subjects. The diffeomorphic assumption in 1D implies that the function is smooth and monotonic. The monotonic property assumes that the sequence of the events during evolution occur in the same order for every subject (from birth to death). This is a very realistic (if not desirable) hypothesis, at least from a biological point of view. Moreover, assuming the evolution of a structure is smooth (at least differentiable) like its inverse is also very realistic, so that one can speak about the speed of an evolution. Therefore, the time warps ψ are intrinsically diffeomorphic.
3.2 Computational framework and algorithms
3.2.1 A generic way to build diffeomorphisms
In this section, we explain a way to build generic 3D and 1D flows of diffeomorphisms which will be used as a model for the deformations χt, ϕ and ψ in the following. We use here the LDDMM framework (Trouvé, 1998; Dupuis et al, 1998; Miller et al, 2002) for constructing 3D diffeomorphisms. We propose to adapt this framework to the construction of 1D diffeomorphisms.
3D diffeomorphisms In the LDDMM framework, 3D diffeomorphisms are generated by integrating time-varying vector fields. Let vt (x) be a time-varying speed vector field which gives the velocity of a particle which is at position x at time t. A particle which is at position x at time t = 0 moves to the position ϕt (x) at time t. The function ϕt (x) follows the differential equation for t ≥ 0:
| (7) |
Under some conditions on the regularity of the speed vector field explained in Trouvé (1998), the set of deformation ϕt is a flow of diffeomorphisms of the 3D domain. Following this theory, we assume that the speed vector field belongs to a reproducible kernel Hilbert space (RKHS), meaning the speed vector fields result from the convolution between a square integrable vector field and a smoothing kernel K, which plays the role of a low-pass filter. In our applications, we will use a Gaussian kernel, which writes K(x, y) = σ2 exp (−|x−y|2/λ2) I for any points (x, y) in space and I the identity matrix. The spatial scale λ determines the typical scale at which points in space have a correlated speed, and therefore move in a consistent way. It determines the degree of smoothness of the deformations. Large scale means almost rigid deformations. Small scales favor deformations with many small-scale local variations. The parameter is σ a scaling factor, which in some cases cancels out with the trade-offs in the criterion, as we will discuss later.
In this setting, we define the measure of regularity of the flow of diffeomorphisms as the total kinetic energy of the flow between t = 0 and t = T:
| (8) |
where ‖·‖V denotes the RKHS norm associated to the kernel K.
An important property, (proven in Joshi and Miller (2000); Glaunès (2005) and extended in Durrleman (2010)[Chap.4] in case of the matching term involves several time-points), states that the vector field in the RKHS V which achieves the best trade-off between this regularity term and a fidelity-to-data term has a finite-dimensional parameterization, if the fidelity-to-data term depends only on a finite number of points:
Proposition 1 (Finite dimensional parameterization of minimizing vector field) Let E be a criterion of the form:
| (9) |
where vt denotes a time-varying speed vector field, the flow generated by this vector field in the sense of (7), S a discrete set of N points xi in the 3D domain and Ai a set of positive and continuous functions from ℝ3N to ℝ.
Then, the criterion E admits at least one minimum and the vector field which minimizes E over all possible vector field in the RKHS V is parameterized by a set of N time-varying vectors (αi(t)), such that:
| (10) |
for any points x, where satisfies the flow equations:
| (11) |
The couples (xi(t), αi(t)) are called momenta.
The norm of the minimizing vector field in the RKHS V is given as:
| (12) |
The criterion depends therefore only on the set of L2 functions αi(t). Given these functions and the initial positions xi, one can integrate (11) to generate the trajectories xi(t). Then the criterion E involves only the couples (xi(t), αi(t).
1D diffeomorphisms We can adapt this framework to the construction of 1D diffeomorphisms, which will be used as time warps in our method. Let the variable t ∈ ℝ play the role of the spatial variable x in the construction of 3D diffeomorphisms. We can build a flow of 1D diffeomorphisms ψu(t) for the parameter u in [0, 1] (here u plays the previous role of t, since now t denotes a ‘real’ time and not the integration variable) by integrating the flow equation:
| (13) |
where vu is now a scalar function, which gives the speed at which the time ψu(t) evolves. If it is positive, time tends to accelerate. If it is negative, time tends to slow down. We impose that vu is in 1D RKHS, determined by the kernel K(t, t′) = σ2 exp (−|t−t′|2/λ2). The scalar parameter λ determine the typical time-length at which two time-points t and t′ are changed in a correlated manner. An illustration of the construction of such 1D diffeomorphism is given in Fig. 10.
Fig. 10.
Construction of 1D diffeomorphisms by integration of speed functions. In this illustration, we suppose the speed function to be constant (v independent of u): . Left: The speed profile v is set as the convolution of 3 constant momenta (βi) with a Gaussian kernel with standard deviation λψ = 4 (in red). The integration of the flow equation with the initial condition ψ0(t) = t is shown in blue: the bold blue curve corresponds to the final diffeomorphism at u = 1, light blue curves correspond to ψ1/6(t), ψ1/3(t), ψ1/2(t), ψ2/3(t) and ψ5/6(t). Right: Illustration of the numerical integration of the flow: ψun+1 (t) = ψun (t)+τv (ψun (t)). The speed profile in red is shown along the y-axis. One can show easily that this scheme produces only increasing function (invertible 1D function), when τ is chosen small enough.
Then, the same property as Prop. 1 applies. If E is a criterion of the form:
| (14) |
where t denotes a vector of time-points t1, …, tN and A a positive and continuous scalar function, then the minimum of E over the RKHS exists and is achieved for a speed function vu of the form:
| (15) |
where the time-varying scalars βi(u) are L2 functions from [0, 1] to ℝ. The norm of the speed function vu in the RKHS is given by:
| (16) |
3.2.2 Optimization of the regression criterion
We optimize the regression criterion (1) assuming that the regression function χt is generated by a time-varying velocity field vχ, which belongs to the RKHS Vχ determined by the 3D Gaussian kernel Kχ with standard deviation λχ. Defining the regularity criterion as , the criterion to be minimized becomes:
| (17) |
where d is a similarity measure between shapes. Here we assume that the baseline S0 and the shape Si are sets of points, polygonal lines or meshes. We denote (x1, …, xN) the vertices of the baseline S0. Would d be either the sum of squared differences between point positions or the distance on currents in absence of point correspondence, the conditions of Proposition 1 are satisfied Glaunès (2005): the minimizing vector field vt is parameterized by the momenta
As noticed in Sec. 3.2.1, the regression criterion E is a function of the N L2 functions αp(t). We provide this set of N functions with the metric induced by the kernel Kχ, meaning that the inner-product between two sets of L2 functions αp(t) and is given by:
The gradient of E with respect to the pth function αp(t) is an L2 function denoted ∇αpE(t), which is such that for all:
In Appendix A, we show that this gradient is equal to:
| (18) |
where is the solution of the linear set of backward integral equations for all p:
| (19) |
where 1{t≤ti} =1 if t ≤ ti and 0 otherwise, Ai =d(χti (S0), Si)2 seen as a function of the points positions .
The gradient descent scheme for the computation of the regression S(t) = χt (S0) is summarized in Algorithm 1. We start the gradient descent by setting αp(t) = 0 for all t and p (χt = Id and S(t) = S0, for all t). Computing the gradient requires first to integrate of the flow equation (Eq. (11)) forward in time and then to compute the auxiliary variable ηχ (Eq. (19)) backward in time. In this last case, the initial conditions at t =T is given by ∇xp(T)AT. Then the ODE is integrated for decreasing time t. As soon as a new time point ti is reached, a new contribution ∇xp(ti) Ai is added to ηχ (t). As a consequence, ∇αp E(t) (and therefore the momenta αp(t) and the vector field ) at time t depend on all the data which appear later than t. Once the momenta are updated, the new positions xp(t) are computed by the integration of the flow equation (11) forward in time (the initial condition is given at time t = 0 by xp(0) = xp). These positions at time t depend on the vector field for all time earlier than t. As a result, the positions xp(t) depend on all the data in past and future. This regression fits the best trajectory (χt (S0)) to all the data globally. This differs, for instance, from pairwise registrations between consecutive time-points, although both techniques result in a piecewise geodesic flow.
For better numerical accuracy, we replace the Euler scheme in Algorithm 1 to integrate ODEs by a Euler scheme with prediction/ correction, which has the same accuracy as a Runge-Kutta method of order 2. The computational bottleneck of this algorithm is the computation of every sum of the form αp that need to be computed for all q. These computations of complexity N2 (where N is number of points in the baseline shape) can be efficiently approximated using a linearly spaced grid and FFT (Durrleman, 2010), or Fast Multipole Approximations (Glaunès, 2005), with a nearly linear complexity.
The computation of the gradient requires to compute the differentiation of the fidelity-to-data term: ∇xp(ti) d(ϕti (S0)−Si)2. If Si have the same number of points as S0 (i.e. N points), then d can be defined as the sum of squared differences: , where denotes the points of Si. In this case, . In absence of point correspondence, the distance on currents is used, which can be differentiated as explained in Glaunès (2005); Durrleman (2010).
3.2.3 Optimization of the spatiotemporal registration criterion
As explained in Sec. 3.2.1, the morphological deformation ϕ and the time warp ψ are generated by the integration of flows of 3D and 1D velocity fields respectively. This means that they are the end-points ϕ = ϕ1 and ψ = ψ1 of the differential equations:
| (20) |
with the initial conditions: ϕ0(x) = x and ψ0(t) = t.
Now, we assume that for every parameter u, the 3D velocity fields and 1D velocity profile belong to a RKHS with Gaussian kernel Kϕ and Kψ, with standard deviation λϕ and λψ respectively. We denote {xp}p=1, …, N the set of points of the discrete shape S0. The source trajectory S(t) = χt (S0) is described by the moving points xp(t). Let {tj}j=1, …, Ntarget be the time-points associated to target shapes.
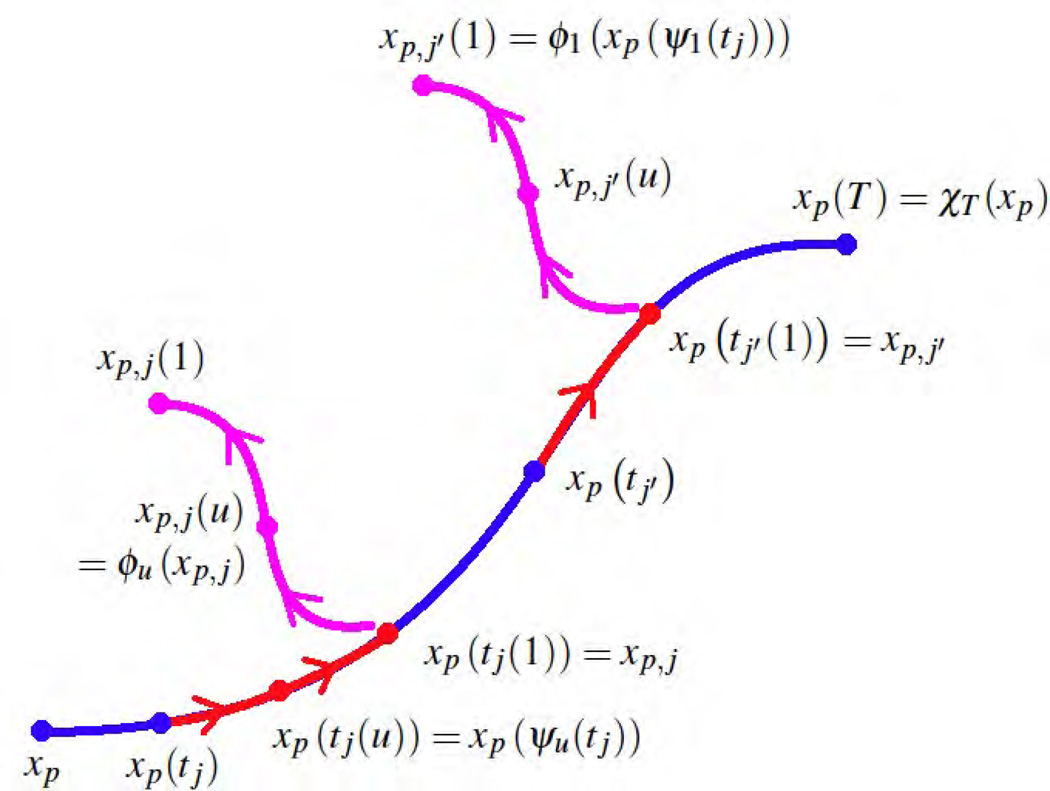
The fidelity-to-data term in (4) depends on the variables ϕ1 (xp(ψ1(tj))) = ϕ1(xp, j), where we denote (see Fig. 11 for an illustrative scheme):
| (21) |
Fig. 11.
Illustrative scheme for the notations: xp denotes a generic point of the source shape, xp(t) = χt (x) the continuous evolution of the source point, (ψu)u∈[0, 1] is a flow of 1D-diffeomorphism which moves the time-labels along the time-axis (in red), (ϕu)u∈[0, 1] is a flow of 3D-diffeomorphism which moves the points of the source evolution (in magenta), independently at each time-point.
Therefore, the application of Proposition 1 leads to the following parameterization of the minimizing velocity fields:
| (22) |
and
| (23) |
Algorithm 1.
Temporal shape regression
| 1: | Input: |
| 2: | A set of time-indexed shapes {(Sj, tj)} |
| 3: | A baseline S0 = {xp}p=1, …, N |
| 4: | A discretization of the interval [0, T]: t0= 0, …, tNtime= T |
| 5: | |
| 6: | Initialization: |
| 7: | for all p = 1, …, N, for all n = 0, …, Ntime, αp(tn) ← 0 |
| 8: | |
| 9: | {Gradient descent} |
| 10: | repeat |
| 11: | {Compute positions of the moving baseline (forward integration)} |
| 12: | xp(t0) ← xp |
| 13: | for n = 0, …, Ntime −1 do |
| 14: | for i = 1, …, N do |
| 15: | |
| 16: | xp(tn+1) ← xp (tn)+v |
| 17: | end for |
| 18: | end for |
| 19: | |
| 20: | {Compute Gradient (backward integration)} |
| 21: | ηp(tNtime) ← 0 |
| 22: | for n = Ntime, …, 1 do |
| 23: | if tn is one of the tj (time-points associated to the shape Sj) then |
| 24: | for p = 1, …, N do |
| 25: | ηp(tn) ← ηp(tn) + ∇pAn(gradient of the matching term) |
| 26: | end for |
| 27: | end if |
| 28: | for p = 1, …, N do |
| 29: | |
| 30: | +2γχ αp(tn)t αq(tn))∇1kχ(xp(tn), xq(tn)) |
| 31: | ηp(tn−1) ← ηp(tn)+vη |
| 32: | end for |
| 33: | end for |
| 34: | |
| 35: | {Update momenta α according to the gradient} |
| 36: | for n = 0, …, Ntime do |
| 37: | for p = 1, …, N do |
| 38: | αp(tn) ← αp(tn)−τ (2γχ αp(tn)+ηp(tn)) |
| 39: | end for |
| 40: | end for |
| 41: | until convergence |
| 42: | |
| 43: | Output: the shape evolution xp(tn). |
The criterion (4) is a function of the N × Ntarget L2 functions αp, j and the Ntarget L2 functions βj. Like for the regression case, we provide this set of functions with the metric induced by the kernel Kϕ and Kψ.
For the sake of simplicity, we introduce the notations xp, t (u) and tj(u) such that:
| (24) |
The regularity parameters in (4) are given by:
| (25) |
and
| (26) |
As shown in Appendix B, the gradient of the criterion with respect to the functions αp, j(u) (denoted ∇αp, j E(u)) and to the functions βj(u) (denoted ∇βj E(u)) is given by:
| (27) |
where ηi, p(u) satisfies the backward integral equation:
| (28) |
where A denotes the matching term which is a function of the variables ϕ1(xp(ψ1(tj))) = xp, j (1). and where ξj(u) satisfies the backward integral equation:
| (29) |
The auxiliary space variable η(u) pulls the gr adient ofthe matching term from u = 1 back to u = 0 along the space axis. Then, the value η(0) is used in the final conditions of the auxiliary time variable ξ (u) in combination with the local speed of the source growth scenario, thus showing the spatiotemporal coupling. The variable ξ (u) pulls back this condition at u = 1 back to u = 0 along the time axis. The gradient transports the driving force in the target space, namely the gradient of the data term, back to source space along the spatiotemporal deformation. This transport is used to update the momenta αp, j(u) and βj(u), which parameterize the spatiotemporal deformation.
In (28), the gradient of the matching term is computed as for the regression function. For instance, if the distance between source and target is the sum of squared differences: , then the gradient is simply ∇xp, i(1) A =2 (xp, j (1)–Up, j).
In (29), one needs to compute the speed of the source growth scenario: . If one has stored the parameterization of the regression function (i.e. the momenta (xp(t), ), then one can compute explicitly:
| (30) |
In our implementation, we only stored samples of the trajectories xp(t) and not the vectors αχ (t). So, we estimate this speed by a finite difference scheme: . This allows us to still use this spatiotemporal registration even if the source evolution has been computed with another regression method than the one presented in Sec. 3.2.2.
The sketch of the gradient descent for this spatiotemporal registration scheme is given in Algorithm 2. Note that we minimize the criterion with respect to the geometrical and the temporal parameters jointly, thus avoiding alternated minimization. The differentiation of the criterion proposed here is here, whereas an approximation was involved in Durrleman et al (2009b); Durrleman (2010). In practice, both differentiations leads to similar results.
Remark 2 Note that since the growth model χt is piecewise geodesic, the evolution S(t) generated by χt is not differentiable at the time-points tj: the continuous S(t) may have different left and right derivatives. This point is discussed in depth in Durrleman (2010)[Chap. 9], where an alternative optimization procedure is proposed, which ensures that an extremum of the registration criterion is achieved at convergence, even in presence of discontinuous velocities. Another way to address the problem is to use the twice-differentiable growth model proposed in Fishbaugh et al (2011).
3.2.4 Optimization of the criterion for atlas construction
The estimation of the 4D-atlas relies on one regression function χt and Nsubj spatiotemporal deformations (ϕs, ψs) for s = 1, …, Nsubj, where Nsubj is the number of subjects. We use the framework of Sec. 3.2.1 to construct the 3D diffeomorphisms χ and ϕs and the 1D diffeomorphisms ψs. As a consequence, every deformation satisfies a flow equation as follows:
| (31) |
where we suppose that the velocity fields vχ (resp. vϕs and vψs) belong to a RKHS Vχ (resp. Vϕ and Vψ) determined by the Gaussian kernel Kχ (resp. Kϕ and Kψ) with standard deviation λχ (resp. λϕ and λψ).
We suppose that the prototype shape M0 (to be estimated) is given by a finite set of points {xp}. In this case, the application of Proposition 1 leads to the parameterization of the time-varying velocity fields by momenta as follows:
| (32) |
where we denote:
| (33) |
for all t ∈ [0, T] and u ∈ [0, 1]. denotes the time-points at which the sth subject has been observed, which might be different for every subject.
The criterion for atlas estimation depends therefore on the N points of the template M0 = {xp} p=1, …, N, the Ntime t-varying vectors αp(t) for the regression function, the u-varying vectors for the morphological deformations and the u-varying vectors )for the time warps. This criterion can be written now as:
| (34) |
where the matching term depends on the positions .
To minimize this criterion, we adopt a 3-step alternating minimization procedure:
-
-
If the template M0 and the growth function χt are fixed, the criterion is divided into Nsubj independent functions. Their minimum is achieved for the spatiotemporal deformations (ϕs, ψs), which maps the mean scenario χt (M0) to the set of data for each subject s. These Nsubj spatiotemporal registrations are computed using Algorithm 2.
-
-If the Nsubj spatiotemporal deformations (ϕs, ψs) and the growth function χt are fixed, the criterion to be minimized with respect to M0 is reduced to:
where we denote . These deformations are 3D-diffeomorphisms. This criterion has exactly the form of the criterion for usual 3D template estimation. If d is the distance on currents, a solution for the minimization of this convex criterion has been proposed in Durrleman et al (2009a) and Durrleman (2010)[Chap. 5, Algorithm 4]. As a consequence, the template M0 is always given as a finite set of points {xp}p=1, …, N. -
-If the template M0 and the Nsubj spatiotemporal deformations (ϕs, ψs) are fixed, the criterion to be minimized becomes:
This is not exactly the regression problem stated in Section 3.1.1 because of the deformation ϕs in the matching term. To turn it into a regression problem, we approximate the matching term by , meaning that the shapes of each subject are matched back to the mean anatomy. This approximation is valid only for diffeomorphisms ϕs whose Jacobian is close to the identity, since the usual metrics d are not left-invariant. As a result, the evolution function χt performs the temporal regression of the set of shapes located at time-points . This regression problem can now be solved using Algorithm 1. Further investigations are needed in order to perform this regression without this approximation, so that we can be consistent throughout the minimization procedure.
To initialize the minimization, we set M0 as the mean current of the earliest data (() for every subject s) and set all the momenta to zeros (χ, ϕs, ψs equal identity map). The whole minimization procedure is summarized in Algorithm 3.
3.2.5 Parameters
The overall framework depends on several parameters. There are 3 kernels of 3 distinct RKHS: Kχ, Kϕ and Kψ. We use Gaussian kernels determined by their standard deviations: λχ, λϕ and λψ respectively. They determine the degree of smoothness (i.e. the scale at which points have a correlated speed) of the mean scenario of evolution, the morphological deformations and the time warp. The first one compares with the scale of the geometrical variations of the structure over time for a typical subject (scale of the intra-subject variability). The second one compares with the scale of geometrical variations between different subjects (geometrical inter-subject variability). The third one compares with the typical time-scale at which the dynamics of evolution changes from subject to subject.
The user must also set the 3 trade-offs between regularity and fidelity to data: γχ, γϕ, γψ. In addition, one needs to set the metric d between shapes. In the framework of currents, this metric depends on a kernel KW. We choose a Gaussian kernel with standard deviation λW. This parameter sets the typical scale at which shape variations are smoothed (see Durrleman (2010)).
The dimension of the trade-off γχ, γϕ and γψ depends on the kinds of data that we deal with. The dimension of the data term in the criterions is L2 (i.e. squared length) for curves and L4 (i.e. squared area) for surfaces, where L denotes the dimension of a length. The parameter t has the dimension of time (denoted T) and the parameter u is an integration parameter, which is normalized to fall in the unit interval [0, 1] and therefore has no physical dimension. Therefore, the velocities are of dimension LT−1, L and T respectively and the regularity terms (integral of the squared norm of the velocities) Reg(χ), Reg(ϕ) and Reg(ψ) are of dimension: L2T−1, L2 and T2 respectively. Eventually, the dimension of the trade-off γ is that of the ratio between the data term and the regularity terms:
| curves | surfaces | |
|---|---|---|
| γχ | T | L2T |
| γϕ | none | L2 |
| γψ | L2T−2 | L4T−2 |
In the future, we plan to normalize these constants so that their values can be compared for different applications. More generally, one needs to better understand the balance between the spatial and temporal constraints and to find an automatic way to estimate this parameters (which could be considered as fixed effects in a Bayesian framework along the lines of Allassonnière and Kuhn (2009)).
3.3 Statistical measures of spatiotemporal variability
The construction of the spatiotemporal atlas leads to the mean scenario M(t), which gives a representative mean of the studied population, and the spatiotemporal deformations of this mean scenario to each subject, which estimates the variance within the population. The criterion for the atlas construction is not unlike the estimation of a Fréchet mean on the “manifold” of the individual trajectories, the distance between two individual trajectories being given by the cost of the spatiotemporal deformation which connects them (see Miller et al (2002) for this interpretation in the 3D case). In this section, we explain how one can compute intrinsic statistics on the spatiotemporal deformations: the mean and the principal modes of the morphological deformations and the time warps are defined as 3D and 1D diffeomorphisms themselves. Due to the definition of the mean scenario, the mean of all deformations vanishes. Nevertheless, one can compute the means of population sub-groups to detect significant differences between them. The modes show the typical variations of the mean scenario within the population or within one sub-group. They can be used to drive the search for anatomical characterization of sub-groups. Besides the quantification of group differences and the usual hypothesis testing, one important aspect of intrinsic statistics is that means and modes can be displayed as movies of shape evolutions, which is crucial for qualitative interpretation purposes. This can be used to better understand the effect of a pathology and drive the search for bio-markers.
3.3.1 Statistics on initial momenta
As shown in Miller et al (2002), the flow of diffeomorphisms which minimize the registration criterion (4) or the atlas construction criterion (6) are geodesic: they are the ones which minimize the length of the path (ϕu, ψu)u∈[0, 1] between the identity map Id and the actual diffeomorphisms (ϕ1, ψ1). These initial velocity plays the role of a tangent-space representation as in finite-dimensional Riemannian geometry (Pennec et al, 2006): they are the equivalent of the logarithm of the deformations. Since we perform template-to-subjects registration (and not subjects-to-template), every flows of diffeomorphisms ϕs ( resp. ψs) starts from the same space, the one of the mean scenario, and therefore share the same tangent-space Vϕ (resp. Vψ). As a consequence, one can perform intrinsic statistics on these common vector spaces. Since the initial velocities are parameterized by a finite number of momenta, the statistics on deformations reduces to statistics in an Euclidean space.
For each subject s, the 3D diffeomorphisms ϕs are parameterized by momenta located at the points , which is a subset of the whole point set xp, k (the trajectories of every template point). Using zero-padding, every ϕs is parameterized by a vector of the same dimension . Similarly, each 1D diffeomorphism ψs is characterized by momenta located at time-points , which is a subset of the set of all time-points {tk}. Using zero-padding, every 1D diffeomorphism is characterized by a vector of the same dimension: .
One can compute a Principal Component Analysis (PCA) on the vectors αs and βs according to the metric on the RKHS Vϕ and Vψ as follows (see Durrleman (2010)[Chap. 5] for more details). One builds the mean vectors α̅ = ∑s αs/Nsubj and β̅ = ∑s βs/Nsubj and the centered vectors α̃s = αs − α̅ and β̃s = βs − β̅. Then, one builds the empirical matrices Σϕ and Σψ of size Nsubj × Nsubj whose term s, s′ is given by:
| (35) |
Let the eigenvectors of the matrices Σϕ and Σψ associated to the mth largest eigenvalues (these are vectors of dimension Nsubj). Then, as shown in Durrleman (2010)[Chap. 5], the mth eigenmode is given by:
| (36) |
such that .
3.3.2 Geodesic shooting for computing intrinsic means and modes
Once one has computed the statistics on the tangent-spaces Vϕ and Vψ, one needs to use the geodesic shooting equations (the equivalent of the exponential map in Riemannian manifold) to generate the 3D and 1D diffeomorphisms, whose initial velocities are parameterized by the computed mean or modes. The computed diffeomorphisms are called the mean or the modes of the deformations.
Given vectors α and β (located at the points {xp, k}p, k and {tk}), the diffeomorphisms, whose initial velocities are parameterized by these vectors, are re-constructed by integrating over the interval u ∈ [0, 1]:
| (37) |
where (see Miller et al (2006) for the proof). The positions of the points xp, k(1) = ϕ1(xp, k) builds a movie, which shows the mean (if α̅ is used as initial conditions) or the mth mode (if ±αm is used as initial conditions) of the morphological deformations within the population or one of its sub-group.
The equivalent equations for 1D diffeomorphisms are given as:
| (38) |
where . The integration of this set of ODEs leads to the 1D diffeomorphism tk(1) = ψ1(tk), called the mean time warp (if the mean vector β̅ is used as initial conditions) or the mth mode of the time warps (if the mth mode ±βm is used as initial conditions).
The geodesic shooting of the mean and the principal modes of the momenta leads to diffeomorphisms. In this sense, they are “intrinsic” statistics on an infinite-dimensional “manifold” of diffeomorphisms. In particular, the mean or the modes of the time warps are all smooth monotonic functions. This differs from computing the point-by-point mean of the real-values functions ψs(t). Examples will be shown in the next sections.
Algorithm 2.
Spatiotemporal Registration
| 1: | Input: |
| 2: | A source growth scenario xp (tn) for p = 1, …, N and n = 1, …, Ntime |
| 3: | Target shapes Uj associated to time-points tj, j = 1, …, Ntarget |
| 4: | Discretization of the interval [0, 1]: u0 = 0, …, uNu= 1 |
| 5: | |
| 6: | Initialization: |
| 7: | for p = 1, …, N, for j = 1, …, Ntarget do αp, j ← 0 end for end for |
| 8: | for j = 1, …, Ntarget do βj ← 0 end for |
| 9: | |
| 10: | {Gradient descent} |
| 11: | repeat |
| 12: | {Compute spatiotemporal deformation of the source (forward integration: time then space)} |
| 13: | tj (u0) ← tj |
| 14: | for k = 0, …, Nu −1 do |
| 15: | for j = 1, …, Ntarget do |
| 16: | |
| 17: | tj (uk+1) ← tj(uk)+v |
| 18: | end for |
| 19: | end for |
| 20: | xp, j(u0) ← xp(tj(uNu)) |
| 21: | for k = 0, …, Nu −1 do |
| 22: | for j = 1, …, Ntarget, p = 1, …, N do |
| 23: | |
| 24: | xp, j (uk+1) ← xp, j (uk)+v |
| 25: | end for |
| 26: | end for |
| 27: | |
| 28: | {Compute Gradient (backward integration: space then time)} |
| 29: | ηi, p (uNu) ← ∇xp, i(1)A {Gradient of the matching term} |
| 30: | for k = Nu, …, 1 do |
| 31: | for p = 1, …, N, i = 1, …, Ntarget do |
| 32: | |
| 33: | +2γϕ αp, i(uk)t αq, j(uk))∇1kϕ(xp, i(uk), xq, j(uk)) |
| 34: | ηi, p (uk−1) ← ηi, p(uk)+vη |
| 35: | end for |
| 36: | end for |
| 37: | |
| 38: | for k = Nu, …, 1 do |
| 39: | for j = 1, …, Ntarget do |
| 40: | |
| 41: | +2γψ βj (uk)t βi(uk))∇1 kψ(tj(uk), ti (uk)) |
| 42: | ξj (uk−1) ← ξj(uk)+vξ |
| 43: | end for |
| 44: | end for |
| 45: | |
| 46: | {Update momenta α and β according to the gradient} |
| 47: | for k = 0, …, Nu do |
| 48: | for p = 1, …, N, j = 1, …, Ntarget do |
| 49: | αp, j (uk) ← αp, j(uk)−τ(2γϕ αp, j (uk) + ηp, j(uk)) |
| 50: | βj (uk) ← βj(uk)−τ (2γψ βj(uk)+ξj(uk)) |
| 51: | end for |
| 52: | end for |
| 53: | until convergence |
| 54: | |
| 55: | Output: |
| 56: | the registered source shapes ϕ(xp (ψ(tj))) = xp, j (uNu) |
| 57: | the parameterization of the morphological deformation (xp, j (uk), αp, j(uk)) |
| 58: | the parameterization of the time warp (tj (uk), βj(uk)) |
Algorithm 3.
Spatiotemporal Atlas Construction
| 1: | Input: A set of time-indexed shapes , where is the jth scan (out of ) of the sth subject (out of Nsubj) at age . |
| 2: | |
| 3: | |
| 4: | M(t) ← χt (M0) the regression of every shapes at time points (using Algorithm 1) |
| 5: | repeat |
| 6: | {Template-to-subject registration} |
| 7: | for s = 1…Nsubj do |
| 8: | (ϕs, ψs) ← spatiotemporal registration of M(t) to for j = 1, …, (using Algorithm 2) |
| 9: | end for |
| 10: | |
| 11: | {Center the template} |
| 12: | for all s = 1, …, Nsubj and |
| 13: | M0 ← Center Template(M0, {Φs, j}, {}) (Algorithm 4 of Durrleman (2010)) |
| 14: | |
| 15: | {Update the mean scenario} |
| 16: | M(t) ← χt (M0) the regression of every shapes (ϕs)−1() at time points ψs() (using Algorithm 1) |
| 17: | until convergence |
| 18: | |
| 19: | Output: |
| 20: | One mean scenario M(t) = χt (M0) |
| 21: | Nsubj spatiotemporal deformations (ϕs, ψs) |
4 Measures of developmental delays of deep brain structures in autism
In this section, we apply the tools introduced in Sec. 3 to analyze a longitudinal database of deep brain structures segmented from images of autistic, developmental delayed and control children (Hazlett et al, 2005). Each child has been scanned twice: a baseline at about age 3 years and a follow-up at about age 5 years. The segmentation provides a set of 24 meshes for each structure: 12 subjects divided on 3 groups of 4 subjects (autistics, developmental delays and controls), each subject having two meshes (a baseline and a follow-up). As a pre-processing, all the meshes were co-registered via rigid transformations using gmmreg (Jian and Vemuri, 2005).
Our purpose is to show how our methodology can be used to give a description of the effect of the pathology on the maturation of the hippocampus and the amygdala of the right hemisphere. Due to the limited number of subjects involved, this study is mostly a proof of concept, aiming at showing the strengths and the limitations of our approach.
4.1 Spatiotemporal atlas estimation
We estimate a spatiotemporal atlas by minimizing the criterion in (6) using the algorithms described in Sec. 3.2.4. We set the time-interval of interest to [0.5, 7.1] years with a time-step of 0.2 years. The parameters of the Gaussian kernels were set to λχ = 10 mm for the regression function, λϕ = 10 mm and σϕ = 1 for the morphological deformation and λψ = 1.5 years and σψ = 1 for the time warp. The typical scale on currents λW is set to 5 mm. The trade-offs were set to γχ = 10−4 mm2 year, γϕ = 10−4 mm2 and γψ = 10−6 mm4 year−2. The diameter of the hippocampus is about 25 mm. We refer the reader to Sec. 3.2.5 for a discussion about the parameters used (an empirical study of the impact of these parameters will be presented in the next section about endocranial data).
The output of the algorithm is a prototype shape, a mean scenario of evolution of this prototype shape, and 12 spatiotemporal deformations of this mean scenario to the pair of meshes of each subject. The analysis of the value of the criterion at the minimum shows that one autistic patient has a residual significantly larger than the other subject. This subject can be considered as an outlier, as will discuss later on. As shown in Durrleman et al (2009a), the prototype shape is given as a current, which does not correspond to a mesh. For visualization purposes, and for the following volume computations, we mapped one instance of the data to the prototype shape and used it as a template. As a consequence, the mean scenario and its spatiotemporal deformations can be seen as the continuous evolution of a mesh.
Significant samples of the estimated mean growth scenario are shown in Fig. 12. The complete scenario can be seen in the companion movie (See Online Resource 1). This mean scenario of evolution shows that the prototype growth of the structure is much more complex than a pure volume scaling over time, and involves several non-linear growth patterns. The visual inspection of the companion movie shows mainly 3 phases of growth: from 1.5 to 2.5 years, the hippocampus tends to “unfold” giving it less curved aspect; from 2.5 to 4.5 years, the hippocampus strongly elongates in the antero/posterior direction; from 4.5 to 6 years, the extremities of the hippocampus tends to bend: the head toward the bottom and the tail toward the top, thus stretching the body of the hippocampus (red blob in the third frame in Fig. 12).
Fig. 12.
Mean growth scenario of the hippocampus. Four significant frames are shown (lateral view). Color indicates the instantaneous speed of the surface deformation (best seen as a movie: see Online Resource 1)
This mean scenario of evolution has been estimated along with its spatiotemporal deformation to each subject. The spatiotemporal deformation takes into account all the shape information and not only the size. Nevertheless, to illustrate the method, we compute the volume of the original meshes, of the template mesh and the deformed meshes. The evolution of the volume of the mean hippocampal growth is shown in Fig. 13-a. Although the growth involves different non-linear patterns in shape as highlighted in Fig. 12, the volume extracted from this mean scenario evolves quite linearly between age 2 and 6 years. Outside this interval, the volume remains constant due to the boundary conditions (the growth function χt equals identity). In Fig. 13-b, c, d, we plot the volume evolution of the mean scenario, once it has been registered to each subject, taking into account both the morphological deformation and the time warp: the morphological deformation changes the values of the curve in Fig. 13a, whereas the time warp stretches or shortens the curve along the time axis. We superimpose the volume of the original pairs of data for each subject, as well as the volume evolution computed from the pairwise registration between these pairs of surfaces.
Fig. 13.
Evolution of the volume of the hippocampus. a- Volume evolution of the mean scenario. b-to d-: Volume of the mean scenario, after it has been registered to each subject (magenta curves). Black asterisks indicate the volume of the original data. Red, green and blue curves indicate the volume evolution given by the pairwise registration between each subject’s data pair. The autistic outlier corresponds to the decreasing red curve in b- (decrease of volume between the two observations of this subject)
Note that there is no reason that the volume of the registered mean scenario corresponds to the volume evolution computed from the pairwise registration. Indeed, the pairwise registration take into account only a pair of data, whereas the mean scenario integrates the information of the whole database: the mean scenario may contain growth patterns which are not present in a given subject’s evolution. Moreover, the pairwise registration aims at minimizing the discrepancy between the two surfaces, whereas the deformed mean scenario is more constrained by the fact that we assume each subject’s pair of surfaces to result from a smooth deformation of a mean scenario.
Having said that, we notice that volume evolution of the deformed scenario does not deviate too much from the volume evolution computed from pairwise registration. This means that the morphological deformation accounts well for the different sizes of the structures and that the time warp enables to adjust the slope of the curves to the different growth speed of each subject.
We notice that the curves for one autistic patient are not properly aligned (the patient for which the the volume decreases between the two observations in Fig. 13-b). This is the patient detected as an outlier. With the current set of parameters, it was too costly to deform the mean scenario to this subject, which present a unique pattern of size reduction over time (this volume reduction might be real or might be due to a segmentation inaccuracy as well). We run the atlas estimation with a more important weight for the time warp than for the morphological deformation (σψ/σϕ up to 10 instead of 1) and for larger scales for the time warps (λψ =1.5 to 2.5), which reduces the cost of time warps of large amplitude. We observe that the estimated mean scenario tends to show a volume reduction near age 6 years (after a phase of volume increase from 2 to nearly 6 years) and the outlier is registered to the later part of the mean growth scenario: its time warp shows a strong advance in development of this subject relative to the mean scenario. Nevertheless, this was done at the cost of less accurate registration of all other subjects and the atlas with such parameters was not optimal. Our statistical model prefers to treat this particular subject as an outlier. However, would more subjects be available showing a decreasing volume over time, the atlas would be likely to take this into account by estimating a growth scenario decomposed into a first phase of increasing volume and a second phase of decreasing volume. Then, the subject with decreasing volume would be systematically considered as delayed with respect to the subject with increasing volume at the same age. Such a population, however, would probably violate our main assumption that the growth of the subjects are homologous, in the sense that they derive from a common prototype scenario. It would be better to consider the two sub-groups as two different populations.
4.2 Analysis of the spatiotemporal variability
Now, we analyze the spatiotemporal variability of the mean scenario in the population, and not only its effect on the volume distribution. This variability is decomposed into a geometrical part captured by the morphological deformations ϕs and a temporal part captured by the time warps ψs. Preliminary tests performed on the initial momenta of the 3D diffeomorphisms ϕs (see Sec. 3.3) do not show any correlations between the morphological deformations and the class of the subject (autistics, developmental delays and controls). The mean initial momenta of the morphological deformations of each group do not differ significantly from zero. The direction of the first mode of deformation is similar for each group, but the variance is larger for the autistics and developmental delays than for the controls. This mode essentially shows important variations in the elongation of the hippocampus along with an enlargement of the body. By contrast, the depth of the hippocampus almost does not vary.
The time warps are plotted in Fig. 14-a for every subject. When the curve is above the y = x axis (resp. below the y = x axis), the evolution of the subject is in advance (resp. is delayed) relatively to the mean scenario. A slope greater than 1 (resp. smaller than 1) denotes an acceleration (resp. a speed reduction) of the evolution of the subject compared to the evolution of the mean scenario. The mean of the curves for each group is plotted in Fig. 14-b. Although the mean of all curves seem to be biased (overall over the x = y axis), this bias is not proven to be statistically significant (ratio of mean over standard deviation being equal to 1.21). We compute the intrinsic first mode of variations in the space of smooth monotonic functions (see Sec. 3.3) in Fig. 14-c, and in Fig. 14-d by excluding the autistic outlier. From these results, we cannot conclude that an autistic or a developmental delayed patient is systematically delayed or in advance compared to controls, even at a given age. However, both the autistics and the controls has a much narrower variability interval than the developmental delays. It seems also that the autistic on average are more advanced than the control at the earlier stages of growth (between 2 and 3 years of age). This suggests that the hippocampus develops faster among autistic children.
Fig. 14.
Estimated time warps from the hippocampus database. a- The monotonic curves indicates how the real age of each subject maps to the virtual physiological stage estimated in the mean growth scenario. When curves are above the x = y axis, the subject is in advance with respect to the mean scenario. The dashed red curve corresponds to the outlier. b- Intrinsic means of each group (also monotonic functions). c- Limits of the first mode of variation at ± one standard deviation. d- Same as c, but excluding the outlier. It shows that autistics tend to be in advance with respect to the control and that the developmental delays have a much greater variance than the other two groups.
To investigate this more in depth, we also compute the spatiotemporal atlas for the amygdala of the right hemisphere (using the the parameters λχ = 15 mm, λϕ = 15 mm, σϕ = 1, λψ = 1 year, σψ = 1, λW = 3 mm, γχ = 10−3 mm2 year, γϕ = 10−3 mm2 and γψ = 10−6 mm4 year−2). Again, the analysis of the morphological deformations does not high-light informative patterns. By contrast, the analysis of the time warps shown in Fig. 15 reveals that the autistics and the controls share a similar pattern, namely a strong acceleration of the growth with respect to the mean scenario, but at a different age. The acceleration occurs between age 2.5 and 3.5 years for the autistics and between age 4 and age 5 years for the controls. The developmental delays also display a similar pattern, but it occurs at a more variable age. This confirms the hypothesis of an over-growth of the autistics compared to the controls at the earlier stages of development. This also confirms that fact that the developmental delays do not build a very homogeneous group because of much more variable patterns.
Fig. 15.
Estimated time warps from the amygdala database a- time warps for the 12 subjects, b- limits of the first mode of variation at ± 1 standard deviation for each group. Autistics and controls show the same evolution pattern, namely a reduction of speed with respect to the mean scenario (slope smaller than 1) and then a quick acceleration (slope greater than 1). This pattern for the autistics group seems to occur later than for the control group. The developmental delays presents also such pattern but at an arbitrary age. Mean and modes are computed as monotonic functions within the space of 1D diffeomorphisms.
These preliminary results on both the geometrical and temporal parts of the variability suggest that the discriminative information between classes might not be inferred from the anatomical variability at a given age, but rather from variations of the growth process. It suggests that autism may more strongly affect the growth speed of the deep brain structures rather than its shape. Note that the hypothesis of an over-growth of the brain of autistic patient has been reported in the literature, for instance in Courchesne et al (2011). We believe that this new methodology is well adapted to test this hypothesis thanks to the introduction of the time warps, which models explicitly the possible developmental delays between subjects both in shape and in size. Of course, one would need to test it on much larger database: the more time-points per subjects, the more constrained the mean scenario estimation; the more subjects, the more robust the statistics.
5 Comparison of the endocast growth between chimpanzees and bonobos
5.1 Framework of the study
In this section, we aim at using our methodology to characterize the differences of growth patterns between the two closest human relatives: the bonobo (Pan paniscus) and the chimpanzee (Pan troglodytes). We will also assess the robustness of the method with respect to parameter changes and changes in age labels.
Since bonobos were discovered to science in 1929, the analysis of what distinguishes them from the common chimpanzee has been controversial. After several morphological and behavioral studies (Kuroda, 1989; Shea, 1989; Kano, 1992; de Waal, 1995), the hypothesis has emerged that the bonobos may be a “juvenilized” version of the chimpanzee, in the sense that the growth of the bonobos may share common patterns with the one the chimpanzees but with a different tempo. The tools that we have developed, and in particular the introduction of the time warps, seem to be well adapted to test this hypothesis.
For this purpose, we will use one the largest collections of endocasts available for the two species, which comes from the collection of the “Musée de l’Afrique centrale” in Tervuren, Belgium. The endocast is a mold of the endocranium, which provides a replica of the inner surface of the skull and therefore has often played an important role for the analysis of the evolution of the brain in fossil mammals. This data set consists of samples from wild-shot animals: 59 chimpanzees and 60 bonobos, with approximately equal numbers of male and female. They have been scanned with slice thickness between 0.33 and 0.50 mm. The segmentation of the endocasts using itkSNAP (Yushkevich et al, 2006) leads to surface meshes. These surfaces have been rigidly co-registered using gmmreg (Jian and Vemuri, 2005).
It has been observed in Kinzey (1984) that the sequences of teeth emergence in bonobos and chimpanzees are essentially identical. This gives a way to estimate the “dental age” of each skull. We will use this dental age as a common proxy of growth, and not the true age of the specimen, which is not available. As a consequence, each skull has been associated to one the 6 dental ages defined in Shea (1989): infant, child, young juvenile, old juvenile, sub-adult and adult. To refine the classification, we associated some skulls with the intermediate class ‘child/young juvenile’. Age distribution is shown in Fig 1. Without loss of generality, we assume that each dental development stage lasts the same amount of time, namely 1 unit of time. Each unit of time has been discretized with 5 time-points, so that the samples are associated to the time-points ti = 5, 10, 15, 20, 25, 30 according to the dental development of the specimen. The age child/young juvenile has been associated to the time-point 13.
Obviously, this database is cross-sectional by nature. It is unthinkable to have several observations of the same wild animals over time. To make the best of this situation, we choose to estimate first a typical growth scenario for each species independently, applying the regression tool to the cross-sectional data. Second, we analyze the differences between the two growth scenarios using the spatiotemporal registration to measure both morphological differences and possible developmental delays, a key feature we aim at detecting in regards to the bonobos hypothesis.
An alternative approach would consist in using the spatiotemporal atlas construction to estimate an hybrid growth scenario and its deformations to each species, considered as 2 subjects. One the one hand, this would prevent biasing the analysis by choosing a reference species and the inter-species comparison would take into account the fact that the different age groups have a different number of samples. On the other hand, the methodology we choose enables a more direct comparison between species. In particular, the estimation of the species’ specific growth scenario, which is done independently for each species, is not constrained by the assumption that the two growth scenarios should derived from the same hybrid scenario.
5.2 Typical growth scenario estimation for each species
We choose the smallest endocast within the child class as the baseline S0 and associate it to the time point t = 2. Then, we perform a temporal shape regression of the endocasts (independently for each species), as explained in Sec. 3.1.1 and Algorithm 1. We set the typical spatial interaction between currents λW =10 mm, the spatial scale of deformation consistency λ χ = 20mm and the trade-off between fidelity-to-data and regularity γχ = 10−3 mm2(unit of time). The diameter of the endocasts are typically between 60 and 70 mm.
Significant samples of the species specific growth scenarios are shown in Figure 16. The complete scenarios can be seen in the companion movies (see Online Resource 2 (chimpanzees) and 3 (bonobos)). Besides the increase of volume, the most salient effect in both scenarios is an elongation along the posterior/anterior axis and a slight contraction along the superior/inferior axis. As a consequence, the endocast which has an almost spherical geometry at birth has an increasingly ellipsoidal geometry. However, it seems that the chimpanzee endocasts have a stronger anisotropy and that this anisotropy increases faster in time. The subsequent spatiotemporal registration will measure the differences in both scenarios more precisely.
Fig. 16.
Temporal shape regression of endocast of the chimpanzees (top) and the bonobos (bottom) estimated from the original endocasts. In each species, the endocast seems to evolve from a spherical geometry at infancy to an ellipsoidal one at adulthood. However, the dynamics of such changes seem to differ for both species. The quite unrealistic evolution of the chimpanzee endocast at infancy is due to the small amount of data at this age (2). Here, only 6 stages of the growth are shown, although the estimated scenario is continuous. Best seen as movies: see Online Resource 2 (chimpanzees) and 3 (bonobos)
The two growth scenarios differ considerably during infancy and childhood, mainly because of the small amount of data in infancy. The two infant chimpanzees have a larger endocasts compared to both the infant bonobos and the children chimpanzees. To have a more relevant estimation of the growth in infancy, we expect to scan more infant chimpanzees skulls in the future. Note that in the next section we will not take the infancy data into account and will consider the growth scenarios starting at childhood.
We can deduce from the growth scenario an estimation of the evolution of the endocranial volume across ages, as shown in Fig. 17 (Note that we have not performed a regression of the volume but of the shapes instead). Besides the evolution in infancy, one intriguing feature is the apparent decrease in endocranial volume of bonobos at sub-adulthood. This feature is also present in the endocranial volume distribution in the original endocasts (mean and standard deviation are shown in Fig. 17): the mean of the volume at sub-adulthood is smaller than the one of old juveniles. However, the Mann-Whitney U test gives a p-value of 0.47 when comparing the volume distribution of old juveniles and sub-adults: the median of the two distributions are not proved to be statistically different. The test run for every pair of consecutive distributions shows a significant increase of volume in only three occasions: (i) between infancy and childhood for the bonobos (p-value: 9 10−3); (ii) between childhood and young juvenility for the chimpanzees (p-value: 0.07); (iii) and between old-juvenility and sub-adulthood for the chimpanzees (p-value: 0.02).
Fig. 17.
From the continuous shape regression shown in Fig. 16, we deduce an estimation of the evolution of the endocast volume during growth. Mean and standard deviation of the volume of the original endocasts are superimposed. The intriguing decrease of volume of bonobos at sub-adulthood is not shown to be statistically significant. The unrealistic regression at infancy of chimpanzees is due to the very small number of samples at this age (2).
5.3 Spatiotemporal registration between the two growth scenarios
We perform a spatiotemporal registration between the two estimated growth scenarios as explained in Sec. 3.1.2 and Algorithm 2. For the reasons explained in the previous section, we consider the part of these scenarios – between childhood and adulthood - discarding the portion between infancy and childhood. We consider the chimpanzee growth scenario as the reference scenario (i.e. the source). The bonobo scenario is sampled every 2 time-steps. These samples play the role of the target shapes. We set the scale of currents to λW = 10mm as for the regression estimation. We run the registration for different sets of parameters and pick the ones which enable to achieve the smallest discrepancy term in (4). This gives the scale of the morphological deformation: λϕ = 10mm, the scale of the time warp λψ = 1 unit of time (i.e. duration of one time-point), the spatial power σϕ = 40, the temporal power σψ = 5, the morphological trade-off γϕ = 10−5 mm2 and the temporal trade-off γψ = 10−5 mm4=(unit of time).
The morphological deformation changes the shape of each frame of the chimpanzee growth as shown in Fig. 18 (this is the equivalent figure to the first and second row in Fig. 6, although we plot here an intermediate step of the deformation). It shows that, independently of the age, the bonobos endocasts are rounder than the chimpanzees. The movie of this deformation clearly shows a twist at the anterior and posterior part of the endocast (see companion movie: Online Resource 4).
Fig. 18.
Morphological part of the spatiotemporal registration between chimpanzees and bonobos growth scenarios. The morphological deformation maps the morphological space of the chimpanzees to that of the bonobos, independently of the age. It is applied here to the chimpanzees endocasts at old juvenility: endocasts from the chimpanzees growth scenario (top row), their deformation to the bonobos space (bottom row) with an intermediate stage of deformation (middle row). This shows that, on average, the endocast of a chimpanzee is more elongated and less round than the one of a bonobo. Note that the deformed endocasts do not match the ones of the bonobo growth at the same age, but at the age given by the correspondence graph shown in Fig. 19. Best seen as a movie: see Online Resource 4
The graph of the estimated time warp is shown in Fig. 19. This plot shows the correspondence between the ages of the bonobos and the chimpanzees. It mostly shows an important speed reduction of the growth of the bonobos with respect to the chimpanzees between old-juvenility and sub-adulthood. The almost constant slope of the curve during this period of time indicates that the bonobos growth speed is 0.25 times that of the chimpanzees. The graph shows also that the bonobos seem to be slightly in advance with respect to the chimpanzees at childhood and that the delay of the bonobos growth at sub-adulthood seems to be reduced at adulthood.
Fig. 19.
Time warp between chimpanzee and bonobo growth. It shows that the growth of the bonobos is in advance with respect to the chimpanzees at childhood and then that it drastically slows down during juvenility (almost linearly by a factor 0.24 between old-juvenility and sub-adulthood). This delay seems to decrease at adulthood. Dashed magenta lines indicate the limits of the 90% confidence interval estimated by bootstrap. Dashed cyan lines indicate the limits of the 90% variation intervals due to random age shifts.
We show the effect of this spatiotemporal registration on the evolution of endocast volume of the chimpanzees in Fig. 20(left). It shows that the spatiotemporal warping enables to match the volume evolution of the chimpanzees endo-cast closer to that of the bonobos endocast. Besides volume, we also analyze the differences of a measure of the shape, namely the ratio between the height (in the superior-inferior direction) and the width (in the anteroposterior direction) of the endocast. Ratio close to 1 indicates a rounded endocast in the sagittal plane. The evolution of the ratio computed from the species specific scenario is shown in Fig. 20(right): the decrease of the curves indicates that the endocast become more and more asymmetric (ellipsoidal) during growth. This ratio is always smaller for the chimpanzees than for the bonobos, thus showing a stronger asymmetry for the chimpanzees. As expected, the morphological deformation moves the curves of the chimpanzees closer to the one of the bonobos, except between sub-adulthood and adulthood. Indeed, we have shown in Fig. 18 that the morphological deformation tends give the endocast a more ellipsoidal aspect. The time warp tends to align the slope of the chimpanzee curve to the slope of the bonobos curve. However, we notice that the spatiotemporal warping aligns the evolution of this ratio with less accuracy than that of the volume (see Fig. 20(left)). It is likely that the registration is primarily driven by the volume information, which may act as a stronger constraint than the shape asymmetries. Multi-scale approaches, with decreasing rigidity scale of the morphological deformation λϕ for instance, should be able to achieve a better matching, which would show an alignment of the measures of shape asymmetries with the same accuracy as the volume.
Fig. 20.
Effects of the spatiotemporal deformation on the evolution of the volume and the geometry of the endocasts. Top: Evolution of the endocast volume for the original growth scenarios of both species starting at childhood (in red and blue as in Fig. 17). Dashed cyan curve correspond to the volume of the chimpanzee growth scenario after the morphological deformation. Magenta curve is derived from the cyan curve by applying the time warp. The combination of the morphological deformation and the time warp approximate the volume evolution of the bonobos. Bottom: Same experiments but for the evolution of the ratio between the elongation in superior-inferior direction and that in the anteroposterior direction, which gives an indication of how the endocast deviates from a circular shape in the sagittal plane. The closer the ratio to 1, the “rounder” the endocast.
5.4 Impact of the temporal scale
Here, we analyze the variability of the spatiotemporal registration with respect to variations of the temporal scale λψ, while keeping the other parameters fixed. This parameter determines the scale at which the time warp may vary. A large scale means a nearly rigid time warp with very slow variations. A small scale allows quick variations of the time warp during small time intervals.
Fig. 21 shows the different values of the data term obtained for different values of the temporal scale λψ. It shows that the optimal value is for λψ = 1 unit of time, namely the the duration of one age group. This is the value chosen in this study. Fig. 22 shows the impact of this temporal scale on the profile of the time warp. The larger the scale, the more rigid the time warp, the less its ability to capture highly non-linear variations. The smaller the scale, the more expensive the cost of a regular deformation.
Fig. 21.
Effect of the temporal scale λψ on the registration accuracy. Value of the residual data term after registration for different values of the temporal scale λψ (the other parameters being fixed to λϕ = 10mm, σϕ = 40, σψ = 5, γϕ = 10−5 and γψ = 10−5). It indicates the optimal value of λψ = 1 unit of time.
Fig. 22.
Effect of the temporal scale λψ on the time warp. If λψ is too large, it cannot capture fast variations in the dynamics of growth of both species. If λψ is too small, it costs more to capture the large-scaled variations. Optimal solution is for λψ = 1 unit of time.
5.5 Estimation of confidence intervals via bootstrap
In this section, we aim at studying the robustness of the estimation of the growth scenario with respect to the samples we have. We use here a bootstrap procedure: a resampling with replacement procedure is applied within each age group of each species, yielding a new data set of the same size as the original. Then, we estimate the two growth scenarios using this new set of data.We repeat the procedure 100 times, so that we end up with 100 growth scenarios for each species, which simulates the variability of these scenarios with respect to the choice of the samples.
For each simulation, we compute the evolution of the endocranial volume given by the estimated growth scenario. Fig 23(top, left) shows the 90% confidence interval of the volume evolutions. It shows that the variability of the volume estimation is relatively small, in particular with respect to the difference in volume between the two species at adulthood.
Fig. 23.
Bootstrap confidence intervals due to resampling (top) and due to random age shifts (bottom). Left: Evolution of the endocranial volume given by the reference growth scenario (bold line) and its 90%-confidence interval estimated via a bootstrap procedure. Right: Discrepancy between the reference growth scenario and the ones estimated by bootstrap, measured as the current norm between the frames. 90% confidence interval is shown at every time-step. On average, the bootstrap makes the frames to vary in the space of currents within a neighborhood of radius 10% the norm of the reference frames.
To gain more insight into the variability of the geometry of the growth scenario, we compute the distance between the endocast of a simulated growth scenario and the reference one at each time-step, using the norm on currents. In Fig. 23(top, right), we show the 90% confidence interval of this difference expressed in terms of percentage of the norm of the endocast of the reference scenario. It shows a large deviation in bonobos infancy and chimpanzees childhood. This large variability is expected due to the small number and the large variability of data at those ages. This confirms that more data are needed for a more robust estimation of the endocranial growth at these ages. The variance of the endocranial geometry during old-juvenility and sub-adulthood is much larger for the bonobos than for the chimpanzees. This may explain the decrease of volume at bonobos sub-adulthood, as many more samples would be needed to converge to the “true” mean. This might also indicate a bi-modal distribution for male and female.
Eventually, we notice that the estimation of the volume seems much less variable than the estimation of the geometry. This is not surprising since one needs much more data to robustly estimate the whole geometry (which has potentially an infinite number of degrees of freedom) than the scalar measure of volume.
Then, we compute the spatiotemporal registration between every pair of growth scenarios. The estimation of the 90% confidence interval of the time warp is shown in Fig. 19. These experiments allow us to give also a confidence interval of the developmental delay between the bonobos and the chimpanzees: the slope of the time warp at old juvenility falls into the interval [0.14, 0.34] in 90% of the cases.
5.6 Estimation of variability intervals via random age shifts
Here, we study the robustness of our estimations to perturbations of the age estimates. For this purpose, we simulate age perturbations by adding a zero-mean Gaussian variable with standard deviation 1 time-point to the dental age of each sample. This means that in 50% of the cases the dental ages have been shifted by +1 or −1 time-point, in 10% of the cases they have been shifted by more than one time-point, and in 40% of the cases they have not moved. We recall that the duration of every dental age group was of five time-points (i.e. 1 unit of time) in the original experiments, which means that in 10% of the cases, the age estimate was shifted at or beyond the boundaries its group. Given these new age estimates, we compute two growth scenarios and then the spatiotemporal deformations between the portion of the scenarios between childhood and adulthood. We repeat this procedure 100 times. We define a 90% variability interval by discarding the five largest and five smallest values of any scalar measurements taken out of these simulations.
In Fig. 23(bottom, left), we show the limits of the 90% variability interval of the volume evolution measured from the growth scenario. In Fig. 23(bottom, right), we show the 90% variability interval of the distance between the perturbed growth scenario and the reference one.
We compute the spatiotemporal registration between every pair of perturbed growth scenarios. The 90% variability interval of the estimated time warp is shown in Fig. 19.
All these experiments show that the perturbations induced by randomly shifting the age estimates are always smaller than the perturbations due to the bootstrap resampling. Therefore, these perturbations are not statistically significant, thus illustrating the robustness of our method to the uncertainty of the age estimates.
6 Conclusion
In this paper, we introduced a new growth model for shape evolution, as a continuous diffeomorphic deformation of a baseline shape over time. Its estimation allows us to infer a continuous shape trajectory from few observations sparsely distributed in time.
We introduced a new registration scheme for the comparison of individual growth trajectories. We proposed to model the differences between individual trajectories as a combination of time-independent shape differences and a difference in the pace of shape changes over time. For this purpose, we introduced the generic construction of 1D diffeomorphisms: smooth and monotonic functions called time warps. This model supposes that the individual trajectories are comparable, in the sense that they contain the same growth patterns, but with a different appearance and a different timing. The presence of new growth patterns in one of the trajectories would not be considered by the registration and would lead to a large residual misalignment after the registration.
Eventually, we introduced an original statistical model for the study of longitudinal databases. This model assumes that the consecutive observations of different subjects derive from a spatiotemporal deformation of an unknown prototype scenario of evolution. The estimation of this models leads to an atlas, which consists of (i) a prototype shape called the template, (ii) the continuous diffeomorphic deformation of this prototype shape over time, called the mean scenario of evolution and (iii) the spatiotemporal deformations of this mean scenario, which map the set of time-dependent observations of each subject. The template shape and the mean scenario of evolution captures the invariants in the population: common shape features and common growth patterns. The spatiotemporal deformations summarize the variations of these invariants in terms of various appearances and various paces of shape change. The characteristics, which are specific to a given individual, are not taken into account and are considered as outliers since it does not comply with the hypotheses of the model.
In addition, we provided a statistical framework to compute intrinsic statistics in the space of spatiotemporal deformations (space of 3D diffeomorphisms for the morphological deformation and space of smooth monotonic functions for the time warp). Mean and modes of deformations are computed as deformations themselves. This is not only useful to perform statistical processing like hypothesis testing or classification for instance, but also gives a way to visualize and interpret the geometrical features captured by the model.
We illustrated our approach with two biological examples. The study of a longitudinal database of deep brain structures from autistic, developmental delays, and controls, shows that a given pathology might be characterized more by the differences in the pace of maturation of a structure, rather than the differences in shapes at a given age. The study of a time-series data set of endocast of bonobos and chimpanzees allows us to give new insights into the differences in terms of development of the endocranium between these genetically very close species. In particular, we were able to give an estimate of the expected developmental delay of bonobos relative to chimpanzees at juvenility. Moreover, we show the robustness of this estimation with respect to variations in the age estimates.
The principle approach that we proposed leads to the definition of new objective functions, for which we proposed efficient algorithms. The shape regression and the spatiotemporal registration are solved using a single gradient descent scheme. The estimation of the spatiotemporal atlas relies on an alternated minimization procedure. Future work will investigate the possibility to derive a single gradient scheme for the estimation of the whole atlas. This should lead to a faster and more controllable procedure. Another important direction of research is to include the residuals into the statistical analysis in the spirit of Durrleman et al (2009a, 2011), in order to better characterize possible outliers, or to detect consistent subgroups in the population.
We emphasized that our approach relies on a set of explicit hypotheses and that alternatives models are also worth investigating. We hope that this approach, which has been driven more by methodological considerations than by the applications, will help to better appreciate the challenges, which are inherent to the joint modeling of time and shape variations. This might contribute to the emergence of an axiomatic approach for the statistical analysis of longitudinal shape data.
Table 1.
Distribution of the dental ages across samples for both species: chimpanzee and bonobo.
| # samples | infant | child | child/young juvenile |
|---|---|---|---|
| Bonobos | 4 | 8 | 3 |
| Chimpanzees | 2 | 6 | 4 |
| Young juvenile |
old juvenile |
sub- adult |
adult | TOTAL |
|---|---|---|---|---|
| 11 | 7 | 9 | 18 | 60 |
| 10 | 13 | 10 | 14 | 59 |
Acknowledgements
We would like to thank B. Combès for preprocessing the endocast data and M. Styner for processing the subcortical structures. We thank W. Van Neer and E. Gilissen the previous and current curator of the “Musée de l’Afrique Centrale” at Tervuren (Belgium).We are indebted to Chems Touati for his help for creating figures and movies and James Fishbaugh for his kind proofreading of the manuscript. This work has been funded in part by the INRIA ARC 3D-Morphine (PI: Sylvain Prima), the European IP Project Health-e-child (IST-2004-027749) and Microsoft Research.
Appendix
A Differentiation of the temporal shape regression criterion
A.1 Matrix notations
For the sake of simplicity, we introduce matrix notations: x0 = {xp}p=1, …, N denotes the 3N vector which is the concatenation of the coordinates of N vertices of the baseline shape M0. Using the notations of Sec. 3.2.2, we denote the moving points x(t) (resp. the parameterizing vectors α(t)) the 3N vector: (xp(t))p=1, …, N (resp. (αp(t))p=1, …, N). We denote also Kχ (x(t), x(t)) the 3N-by-3N block matrix whose block p, q is given by the 3-by-3 matrix (Kχ (xp(t), xq(t))). This matrix is symmetric, positive definite by definition of the kernel Kχ.
Thanks to these notations, the norm of the speed vector vt is written: . For A, a function from ℝ3 to ℝ, we denote by dxA its Jacobian matrix at point x, so that for any vector V: (dxA)V = (∇xA)tV. By extension, ∇xA denotes the 3N vector (∇x1A, …, ∇xNA).
With these notations, the regression criterion (17) becomes:
| (39) |
subject that:
| (40) |
where we denote:
| (41) |
For the sake of simplicity, we will denote in the sequel, f(t) and Lχ (t) instead of f (x(t), α(t)) and Lχ (x(t), α(t)).
A.2 Gradient in a matrix form
Let δE be a variation of the criterion E with respect to a variation δα(t) of the momenta α(t):
| (42) |
where δx(t) denotes the variations of the positions x(t) with respect to the variations of the momenta α(t). The differentiation of the flow equation (40) shows that these variations δx(t) satisfy a linear ODE with source term:
| (43) |
We introduce the flow Rut for u, t ∈ [0, T] which is solution of the homogeneous equation:
| (44) |
The method of the variations of the parameters leads to the following solution of the ODE:
| (45) |
In particular, this shows that we can write the variations δx(ti) as:
| (46) |
where 1{t≤ti} = 1 if t ≤ ti and 0 otherwise.
Now, we can plug these last two equations into (42). Using Fubini’s theorem, which implies that for any L2 function F(u, t), this leads to:
| (47) |
This gives the gradient of E with respect to the L2 metric as:
| (48) |
where we denote the auxiliary variable η(t):
| (49) |
The auxiliary variable η(u) depends on the flows Rut and therefore satisfies an ODE. To make this ODE explicit, we write the inverse flow Rut in integral form. Noticing that RtuRut = Id, we have , which gives in integral form (noticing that Rut and f commute):
| (50) |
Now, we can plug this equation into the definition of η(t) in (49). Writing and noticing that for any L2 function F(u, s), the Fubini’s theorem implies that , this leads to:
| (51) |
Now, we notice that t ≤ u within the integral, which implies that 1{t≤ti} 1{u≤ti} = 1{u≤ti}. Hence, (★) is exactly equal to ηu. Therefore, ηt is the solution of the integral equation (integrated upstream in time):
| (52) |
A.3 Gradient in coordinates
Due to the definition of the functions f and Lχ in (41), we have:
| (53) |
Therefore, the gradient of the regression criterion with respect to the L2 metric given in (48) is now equal to:
The matrix Kχ (x(t), x(t)) is precisely the Sobolev metric induced by the kernel on the set of L2 functions (see Sec. 3.2.2), so that the gradient with respect to this metric is given by:
| (54) |
The auxiliary variable η(t) satisfies the ODE (52), now written as:
| (55) |
The 3N vector ∇xti Ai is equal to (∇x1(ti) Ai, …, ∇xN(ti)Ai). For generic 3N vectors x, y and α, the kth coordinate of the 3N-vector Kχ (x, y)α is given as: . The kernel Kχ is scalar, namely of the form Kχ (x, y) = kχ (x, y)Id for a scalar function kχ. We have therefore for every i, j = 1, …, N:
| (56) |
Therefore, for a generic 3N-vector β, we have:
| (57) |
Now, we can apply this equation with y = x and β = γχα + η and combine it with (55). Noticing that for a symmetric kernel, we have ∇1k(x, y) = ∇2k(y, x), we get eventually the set of ODEs satisfied by the functions ηp(t) as given in (19).
Appendix
B Differentiation of the spatiotemporal matching criterion
B.1 Matrix notations
Let t0 = {tj}j=1, …, Ntarget be the vector of time-points associated to the target shapes. The 1D diffeomorphism ψu changes t0 into t(u) = {tj(u)}j=1, …, Ntarget for u ∈ [0, 1]. This vector satisfies the , with t(0)=t0, where β(u) is the concatenation of the vectors βj(u) defined in (23), Kψ (β(u), β(u)) is the block matrix whose block (i, j) is given by: Kψ(βi(u), βj(u)).
Similarly, we denote x0(t) = {xp(t)}p=1, …, N be the concatenation of the positions of all the points of the source evolution S(t) for any time-point t and x0(t(1)) the concatenation of the x0(tj(1)) for j = 1, …, Ntarget. The diffeomorphism ϕu maps this vector to x(u), which satisfies the with initial condition: x(0) = x0(t(1)) (which depends on the final time-points t(1)), where α(u) is the concatenation of the vectors αp, j(u) defined in (22) for p = 1, …, N and j = 1, …, Ntarget.
Therefore, we can write the matching criterion (4) as:
| (58) |
subject to:
| (59) |
where we denote:
| (60) |
For the sake of simplicity, we will write in the sequel f (u), g(u), Lϕ (u) and Lψ(u) instead of f (x(u), α(u)), g(t(u), β(u)), Lϕ (x(u), α(u)) and Lψ(t(u), β(u)) respectively.
B.2 Gradient in a matrix form
Now, let δE be a variation of the criterion E induced by a variation of the momenta δα(u) and δβ(u):
| (61) |
where we denote δx(u) and δt(u) the variations of the path x(u) and t(u) induced by the variations of the momenta δα(u) and δβ(u). These vectors satisfy the linear ODEs with source term derived from (59):
| (62) |
We introduce the flows Psu and Rsu for all s, u ∈ [0, 1], which are solution of the homogeneous equations:
| (63) |
The method of variations of the parameters leads to the following solution of the ODEs:
| (64) |
where the variations of the initial condition δx(0) = δx0(t(1))equals:
| (65) |
according to (64).
Plugging (64) into (61) leads to the variation of the criterion (noticing that for any L2 function F(s, u) we have that ):
| (66) |
Now, we denote,
| (67) |
which appears twice in (66) as η(0) and η(u). Given the expression of δx(0) in (65), we have:
| (68) |
Denoting
| (69) |
we end up with the gradient of the criterion with respect to the L2 metric written as:
| (70) |
The auxiliary variables η(u) and ξ (u) depend on the flows Rus and Pus. Therefore they satisfy a ODE, which we need to make explicit now. The inverse flows are written in integral form as:
| (71) |
so that the auxiliary variable η(u) satisfies:
| (72) |
where we denote ∇xA = (dxA)t for any scalar function A.
Since we have for any L2 functions F (r,s), by permuting the two integrals, we have:
| (73) |
The term in the brackets is exactly η(s), so that the integral equation satisfied by η(u) is eventually given by:
| (74) |
Similar computations using the integral form of the flow Rus leads to the integral equation satisfied by ξ (u):
| (75) |
B.3 Gradient in coordinates
Given the definition of the functions f, g, Lϕ and Lψ, we have:
| (76) |
so that the gradient with respect to the Sobolev metric (the matrices Kϕ (x, x) and Kψ(t, t) factorize in (70)) is given as:
| (77) |
where
| (78) |
and
| (79) |
The 3NNtarget vector ∇x(1)A is the concatenation of the vectors ∇xp(tj(1)) A for p=1, …, N and j=1, …, Ntarget. Similarly, the 3NNtarget vector is the concatenation of the vectors {xp(tj(1))}p=1, …, N, j=1, …, Ntarget · dt(1)x0 is the 3NNtarget-by-Ntarget matrix: (dt1(1)x0, …, dtNtarget x0). In the vector dtj (1)x0 almost every coordinate vanishes except the ones corresponding at the jth block of size 3N: (dtj (1) x1(tj(1)), …, dtj (1) xN(tj(1))) (since dtj (1)xp(ti(1))=0 when i ≠ j). Therefore, we have: , which is the jth coordinate of the Ntarget vector (dt(1)x0)tη.
Eventually, using the generic expression (57) for scalar kernels Kϕ (x, y) = kϕ (x, y)Id and Kψ(x, y) = kψ(x, y)Id, the evolution of η(u) and ξ(u) in (78) are written in coordinates as in (28) and (29).
Footnotes
source: www.bordalierinstitute.com
We notice that in the time-specific paradigm, this would be S″(t) = χψ(t)(ϕ(S0)) (see Sec. 2)
Contributor Information
S. Durrleman, Scientific Computing and Imaging (SCI) Institute, 72 S. Central Drive, Salt Lake City, UT 84112, USA Asclepios team-project, INRIA Sophia Antipolis, 2004 route des Lucioles, 06902 Sophia Antipolis, France; Centre de Mathématiques et Leurs Applications (CMLA), CNRS-ENS Cachan, 61 avenue du Président Wilson, 94235 Cachan, France.
X. Pennec, Asclepios team-project, INRIA Sophia Antipolis, 2004 route des Lucioles, 06902 Sophia Antipolis, France
A. Trouvé, Centre de Mathématiques et Leurs Applications (CMLA), CNRS-ENS Cachan, 61 avenue du Président Wilson, 94235 Cachan, France
J. Braga, Laboratoire de paléoanthropologie assistée par ordinateur, CNRS-Université de Toulouse (Paul Sabatier), 37 allées Jules Guesde, 37073 Toulouse, France
G. Gerig, Scientific Computing and Imaging (SCI) Institute, 72 S. Central Drive, Salt Lake City, UT 84112, USA
N. Ayache, Asclepios team-project, INRIA Sophia Antipolis, 2004 route des Lucioles, 06902 Sophia Antipolis, France
References
- Aljabar P, Bhatia K, Murgasova M, Hajnal J, Boardman J, Srinivasan L, Rutherford M, Dyet L, Edwards A, Rueckert D. Assessment of brain growth in early childhood using deformation-based morphometry. NeuroImage. 2008;39(1):348–358. doi: 10.1016/j.neuroimage.2007.07.067. [DOI] [PubMed] [Google Scholar]
- Allassonnière S, Kuhn E. Stochastic algorithm for bayesian mixture effect template estimation. ESAIM Probability and Statistics. 2009 In Press. [Google Scholar]
- Chandrashekara R, Rao A, Sanchez-Ortiz G, Mohiaddin RH, Rueckert D. Construction of a statistical model for cardiac motion analysis using nonrigid image registration. Information Processing in Medical Imaging, Springer, Lecture Notes in Computer Science. 2003;vol 2732:599–610. doi: 10.1007/978-3-540-45087-0_50. [DOI] [PubMed] [Google Scholar]
- Courchesne E, Campbell K, Solso S. Brain growth across the life span in autism: Age-specific changes in anatomical pathology. Brain Research. 2011;1380:138–145. doi: 10.1016/j.brainres.2010.09.101. the Emerging Neuroscience of Autism Spectrum Disorders. [DOI] [PMC free article] [PubMed] [Google Scholar]
- de Craene M, Camara O, Bijnens BH, Frangi AF. Large diffeomorphic FFD registration for motion and strain quantification from 3D-US sequences. Proc. of Functional Imaging and Modeling of the Heart, Spinger, LNCS. 2009;vol 5528:437–446. [Google Scholar]
- Davis B, Fletcher P, Bullitt E, Joshi S. Population shape regression from random design data. Proc of International Conference on Computer Vision (ICCV) 2007:1–7. [Google Scholar]
- Declerck J, Feldman J, Ayache N. Definition of a 4D continuous planispheric transformation for the tracking and the analysis of LV motion. Medical Image Analysis. 1998;4(1):1–17. doi: 10.1016/s1361-8415(98)80011-x. [DOI] [PubMed] [Google Scholar]
- Dupuis P, Grenander U, Miller M. Variational problems on flows of diffeomorphisms for image matching. Quaterly of Applied Mathematics. 1998;56(3):587–600. [Google Scholar]
- Durrleman S. Thèse de sciences (phd thesis) Université de Nice-Sophia Antipolis; 2010. Statistical models of currents for measuring the variability of anatomical curves, surfaces and their evolution. [Google Scholar]
- Durrleman S, Pennec X, Trouvé A, Ayache N. Statistical models of sets of curves and surfaces based on currents. Medical Image Analysis. 2009a;13(5):793–808. doi: 10.1016/j.media.2009.07.007. [DOI] [PubMed] [Google Scholar]
- Durrleman S, Pennec X, Trouvé A, Gerig G, Ayache N. Spatiotemporal atlas estimation for developmental delay detection in longitudinal datasets. Medical Image Computing and Computer-Assisted Intervention - MICCAI, Springer, LNCS. 2009b;vol 5761:297–304. doi: 10.1007/978-3-642-04268-3_37. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Durrleman S, Fillard P, Pennec X, Trouvé A, Ayache N. Registration, atlas estimation and variability analysis of white matter fiber bundles modeled as currents. NeuroImage. 2011;55(3):1073–1090. doi: 10.1016/j.neuroimage.2010.11.056. [DOI] [PubMed] [Google Scholar]
- Ehrhardt J, Werner R, Schmidt-Richberg A, Schulz B, Handels H. Generation of a mean motion model of the lung using 4D-CT image data. Proc. of Eurographics Workshop on Visual Computing for Biomedicine, Eurographics Association. 2008:69–76. [Google Scholar]
- Fishbaugh J, Durrleman S, Gerig G. Estimation of smooth growth trajectories with controlled acceleration from time series shape data. Medical Image Computing and Computer-Assisted Intervention - MICCAI, Springer, LNCS. 2011 doi: 10.1007/978-3-642-23629-7_49. to appear. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gerig G, Davis B, Lorenzen P, Xu S, Jomier M, Piven J, Joshi S. Computational anatomy to assess longitudinal trajectory of brain growth. Third International Symposium on 3D Data Processing, Visualization, and Transmission. 2006:1041–1047. [Google Scholar]
- Glaunès J. PhD thesis. Université Paris 13; 2005. Transport par difféomorphismes de points, de mesures et de courants pour la comparaison de formes et l’anatomie numérique. http://cis.jhu.edu/joan/TheseGlaunes.pdf. [Google Scholar]
- Gogtay N, Lu A, Leow A, Klunder A, Lee A, Chavez A, Greenstein D, Giedd J, Toga A, Rapoport J, Thompson P. 3D growth pattern abnormalities visualized in childhood-onset schizophrenia using tensor-based morphometry. Proceedings of the National Academy of Sciences. 2008;105(41):15, 979–15, 984. doi: 10.1073/pnas.0806485105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Grenander U, Srivastava A, Saini S. A pattern-theoretic characterization of biological growth. Medical Imaging, IEEE Transactions on. 2007;26(5):648–659. doi: 10.1109/TMI.2006.891500. [DOI] [PubMed] [Google Scholar]
- Hart G, Shi Y, Zhu H, Sanchez M, Styner M, Niethammer M. DTI longitudinal atlas construction as an average of growth models. Proc. of International Workshop on Spatio-Temporal Image Analysis for Longitudinal and Time-Series Image Data. 2010 [Google Scholar]
- Hazlett H, Poe M, Gerig G, Smith R, Provenzale J, Ross A, Gilmore J, Piven J. Magnetic resonance imaging and head circumference study of brain size in autism. The Archives of General Psychiatry. 2005;62:1366–1376. doi: 10.1001/archpsyc.62.12.1366. [DOI] [PubMed] [Google Scholar]
- Jian B, Vemuri BC. A robust algorithm for point set registration using mixture of Gaussians. 10th IEEE International Conference on Computer Vision (ICCV 2005); 17–20 October 2005; Beijing, China. 2005. pp. 1246–1251. URL http://gmmreg.googlecode.com. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Joshi S, Miller M. Landmark matching via large deformation diffeomorphisms. IEEE Transaction on Image Processing. 2000;9(8):1357–1370. doi: 10.1109/83.855431. [DOI] [PubMed] [Google Scholar]
- Kano T. The last ape: pygmy chimpanzee behavior and ecology. Stanford University Press; 1992. [Google Scholar]
- Khan A, Beg M. Representation of time-varying shapes in the large deformation diffeomorphic framework. 5th IEEE International Symposium on Biomedical Imaging ISBI. 2008:1521–1524. [Google Scholar]
- Kinzey WG. The dentition of the pygmy chimpanzee, Pan paniscus. New York: Plenum; 1984. pp. 65–88. [Google Scholar]
- Kuroda S. Developmental retardation and behavioural characteristics of pygmy chimpanzees. Harvard University Press; 1989. pp. 184–193. [Google Scholar]
- Mansi T, Durrleman S, Bernhardt B, Sermesant M, Delingette H, Voigt I, Lurz P, Taylor AM, Blanc J, Boudjemline Y, Pennec X, Ayache N. A statistical model of right ventricle in tetralogy of fallot for prediction of remodelling and therapy planning. Proc. Medical Image Computing and Computer Assisted Intervention (MICCAI), Springer, LNCS. 2009;vol 5761:214–221. doi: 10.1007/978-3-642-04268-3_27. [DOI] [PubMed] [Google Scholar]
- Miller IM, Trouvé A, Younes L. On the metrics and eulerlagrange equations of computational anatomy. Annual Review of Biomedical Engineering. 2002;4:375–405. doi: 10.1146/annurev.bioeng.4.092101.125733. [DOI] [PubMed] [Google Scholar]
- Miller M, Trouvé A, Younes L. Geodesic shooting for computational anatomy. Journal of Mathematical Imaging and Vision. 2006;24(2):209–228. doi: 10.1007/s10851-005-3624-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pennec X, Fillard P, Ayache N. A Riemannian framework for tensor computing. International Journal of Computer Vision. 2006;66(1):41–66. [Google Scholar]
- Perperidis D, Mohiaddin RH, Rueckert D. Spatio-temporal freeform registration of cardiac MRI sequences. Medical Image Analysis. 2005;9(5):441–456. doi: 10.1016/j.media.2005.05.004. [DOI] [PubMed] [Google Scholar]
- Peyrat JM, Delingette H, Sermesant M, Pennec X, Xu C, Ayache N. Registration of 4D Time-Series of Cardiac Images with Multichannel Diffeomorphic Demons. Proc. Medical Image Computing and Computer Assisted Intervention (MICCAI), Springer, LNCS. 2008;vol 5242:972–979. doi: 10.1007/978-3-540-85990-1_117. [DOI] [PubMed] [Google Scholar]
- Qiu A, Younes L, Miller M, Csernansky J. Parallel transport in diffeomorphisms distinguishes the time-dependent pattern of hippocampal surface deformation due to healthy aging and the dementia of the Alzheimer’s type. NeuroImage. 2008;40:68–76. doi: 10.1016/j.neuroimage.2007.11.041. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Qiu A, Albert M, Younes L, Miller MI. Time sequence diffeomorphic metric mapping and parallel transport track time-dependent shape changes. NeuroImage. 2009;45(1, Supplement 1):S51–S60. doi: 10.1016/j.neuroimage.2008.10.039. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shea B. Heterochrony in human evolution: The case for neoteny reconsidered. Yearb Phys Anthropol. 1989;32:69–101. [Google Scholar]
- Thompson PM, Giedd JN, Woods RP, MacDonald D, Evans AC, Toga AW. Growth patterns in the developing human brain detected by using continuum-mechanical tensor maps. Nature. 2000;404(6774) doi: 10.1038/35004593. [DOI] [PubMed] [Google Scholar]
- Trouvé A. Diffeomorphisms groups and pattern matching in image analysis. International Journal of Computer Vision. 1998;28:213–221. [Google Scholar]
- Trouvé A, Vialard FX. Shape splines and stochastic shape evolutions: A second order point of view. Quaterly of Applied Mathematics. 2010 URL http://arxiv.org/abs/1003.3895, to appear.
- Vaillant M, Miller M, Younes L, Trouvé A. Statistics on diffeomorphisms via tangent space representations. NeuroImage. 2004;23:161–169. doi: 10.1016/j.neuroimage.2004.07.023. [DOI] [PubMed] [Google Scholar]
- de Waal FBM. Bonobo sex and society. Scientific American. 1995;272:82–88. doi: 10.1038/scientificamerican0395-82. [DOI] [PubMed] [Google Scholar]
- Yushkevich PA, Piven J, Cody Hazlett H, Gimpel Smith R, Ho S, Gee JC, Gerig G. User-guided 3D active contour segmentation of anatomical structures: Significantly improved efficiency and reliability. Neuroimage. 2006;31(3):1116–1128. doi: 10.1016/j.neuroimage.2006.01.015. [DOI] [PubMed] [Google Scholar]