Computational strategies for the automated design of RNA nanoscale structures from building blocks using NanoTiler

Abstract

One approach to designing RNA nanoscale structures is to use known RNA structural motifs such as junctions, kissing loops or bulges and to construct a molecular model by connecting these building blocks with helical struts. We previously developed an algorithm for detecting internal loops, junctions and kissing loops in RNA structures.

Here we present algorithms for automating or assisting many of the steps that are involved in creating RNA structures from building blocks: (1) assembling building blocks into nanostructures using either a combinatorial search or constraint satisfaction; (2) optimizing RNA 3D ring structures to improve ring closure; (3) sequence optimisation; (4) creating a unique non-degenerate RNA topology descriptor. This effectively creates a computational pipeline for generating molecular models of RNA nanostructures and more specifically RNA ring structures with optimized sequences from RNA building blocks. We show several examples of how the algorithms can be utilized to generate RNA tecto-shapes.

1. Background

It has been shown that RNA sequences can be designed to self-assemble into a variety of three-dimensional structures, resembling squares, ladders or grids [1,2]. The design approach for these structures was to use elements of known RNA structures (like kissing loops or corner elements) and to connect these molecular building blocks with “struts” consisting of double helices. This approach is rooted in the observation that RNA structure is modular [3–5]. Computational tools for the analysis, prediction and design of RNA structures have been developed that work on the primary-, secondary- or tertiary-structure level [6–8]. There are many analogies between RNA and the DNA design; because of this we also mention, for selected cases, computer programs for designing DNA structures and sequences [9–12].

3DNA is a software package that allows analyzing, visualizing and rebuilding of nucleic acid tertiary structures [13]. NAB is a computer language for the description and automatic model generation of nucleic acid structures. It includes the use of distance geometry in order to build structures fulfilling distance constraints; the software also contains the AMBER force field, which facilitates the minimization and normal-mode analysis of generated models [14]. The program NAMOT is an interactive graphical software package for the generation and molecular modeling of nucleic acid structures [15]. Using a set of reduced coordinates, the program can alter a structure (by bending, stretching, compressing, etc.) while maintaining base pairing.

RNA2D3D [16] is a program for the fast generation of RNA 3D models from RNA secondary structure. It provides a wide spectrum of molecular modeling manipulations; among other things it can launch Tinker minimization and dynamics simulations from its graphical user interface. The software can also build exploratory tectoRNA structures.

MC-Sym is a program that can generate RNA 3D models that are compatible with constraints (such as base pairing interactions) [17]. It has been used for generating many published computational RNA models [18,19]. In combination with the MC-Fold program it was shown to be capable of predicting RNA secondary and tertiary structure with surprisingly high accuracy [20]. The program FARNA developed by Das and Baker [21] uses a fragment assembly approach in combination with a scoring function for de novo RNA tertiary structure prediction. The program S2S provides a framework for integrating the tertiary structure of an RNA with sequence alignment information [22]. The MANIP software allows the rapid assembly of RNA motifs into larger three-dimensional structures using a graphical interface [23]. The program ERNA-3D is a molecular modeling program that allows one to interactively manipulate RNA 3D structures [24]. Specifically for DNA, a graphical molecular modeling program called Gideon has been developed [9]. The program TileSoft provides a graphical interface for designing DNA structures [10].

While the modeled tertiary structure is important for understanding properties of designed RNA structures as well as for applying atom-level simulation methods, it is the set of designed sequences that is potentially passed on to an experiment. Several programs have been developed to address the inverse secondary structure prediction problem (given an RNA (or DNA) secondary structure template, what set of sequences, if any, will fold accordingly?). In particular the programs RNAInverse [25], INFO-RNA [26,27] and RNA-SSD [28], or for DNA NANEV [11] and SEQUIN [12] have been developed for this purpose. Many methods for the prediction of secondary structures from a given sequence have been described elsewhere [6,7].

We previously developed the RNAJunction database which provides a large set of available RNA junctions, internal loops, bulges and kissing loops [29]. Building on this capability we present here a novel combinatorial approach for designing self-assembling RNA structures. In addition, we present several algorithms for the refinement of such combinatorially generated structures. Taken together, the algorithms form a computational pipeline for the automated generation of RNA nanostructures, in particular rings. The algorithms are implemented within the NanoTiler software. This program is a molecular modeling tool that among other things can use sets of RNA junction and kissing loop structures to generate RNA nanostructure models into which these building blocks can potentially self-assemble. While some of the ideas have been outlined in [8,30], we present here for the first time details of the algorithms and provide several examples of how this new approach can be used to generate novel structures from building blocks.

It should be mentioned that the NanoTiler software possesses or has in development many functionalities not mentioned here due to space and scope constraints. Examples are elastic network model capabilities, manual placement of structural elements and the automated placement of single- and double-stranded RNA fragments that bridge structural gaps.

2. Algorithms

In this section we describe the algorithms that constitute the computational pipeline for RNA ring and nanostructure design. The basic idea is to first obtain a set of candidate structures by performing a combinatorial search, trying out all allowed building block combinations and connectivities (algorithms A1 and A2). If the desired RNA structure contains cycles, these obtained candidate structures need to be refined by optimizing their ring closure (algorithms A3 and A4). Lastly the RNA sequences have to be fused (algorithm A5) and optimized (algorithms A6 and A7).

2.1. Topology classification

Using a combinatorial approach for the design of nucleic acid structures can lead to a large number of novel structural models that are only specified by their assembly rules and not by their final shape. How can one classify, compare and “manage” the plethora of structures generated in this fashion? One approach is to abstract the problem of nucleic acid structure comparison to the problem of comparing graphs (graph matching). Our approach is to represent RNA structural elements (junctions, kissing loops, internal loops, etc.) as graph vertices, the connecting helices as graph edges. Similar structure-to-graph mappings have been used by others ([31–33], however we are using a rigorous method [34] in order to map an RNA topology graph to a unique descriptor. Faulon et al. show that their topological descriptor is (unlike many other topological descriptors proposed in the literature) unique in the sense that two graphs have the same descriptor if and only if they are isomorphic. In order to use the computational chemistry software described in Ref. [34] without changes, we map RNA building blocks to pseudo-atoms and RNA helices to covalent bonds connecting these pseudo-atoms. An example of the flow from a 3D structure to a topology descriptor is shown in Fig. 1. The theory behind the topology descriptor is described in Ref. [34]. Important for the use as RNA descriptors is the concept that the topology descriptors of two graphs are identical if and only if the graphs are equivalent.

Fig. 1.

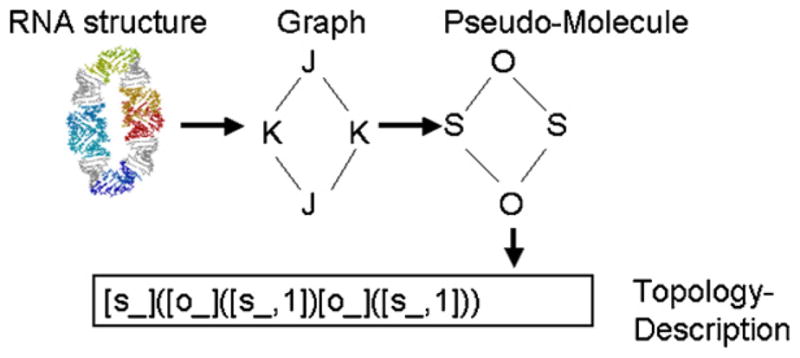
Information flow of topology descriptor generation. We use an external computational chemistry program that computes a unique signature for a molecule [34]. In order to use this program, we use a mapping from building block type to a chemical element character (internal loops and bulges are mapped to “O”, kissing loops are mapped to “S”, three-way junctions are mapped to “N”, four-way junctions are mapped to “C”). The signature is in short a representation of a tree or trees originating from different atoms of the molecule. In this case the signature consists of one tree starting at “S” (represented as “[s]”). Atoms appearing twice in the tree are indicated with a “,1”, in this case “[s,1]”. The generation of the signature is described in detail in Ref. [34].

2.2. Simulated self-assembly for known connectivity and helix lengths: algorithm A1

Let us assume one wants to assemble a complex RNA nanostructure from a set of motifs or building blocks, much like the paradigm described by Jaeger and Chworos [35]. Using a conventional molecular modeling approach, the user has to know in advance which positions of the building blocks and which helix connectivities will lead to the desired 3D structure. What if the user is interested in the question “given these building blocks, what different types of structures can be achieved with self-assembly”? Because of this, we allow the user to simply specify the connectivity rules (like “connect helix 2 of building block type 3 with helix 1 of building block type 1, using a spacer of 5 base pairs”), and simulate a geometry-based self-assembly process starting from a seed building block for a specified number of generations. The algorithm immediately removes placed building blocks that would lead to severe steric clashes. In addition, the method detects the formation of cyclic structures and, if desired, exports structures containing cycles such as ring structures.

We define building block connectivity as a set of building blocks and a set of helix connection rules. A helix connection rule specifies which two helices of two building blocks are to be connected as well as the number of base pairs to be incorporated into a helix spacer that will connect the two helices. For a given building block connectivity and a specified initial building block we use the generational growth procedure outlined in Fig. 2, which depicts pseudocode for algorithm A1.

Fig. 2.

Pseudocode of algorithm A1: growing of RNA structures using a set of building blocks and connectivity rules.

2.3. Simulated self-assembly for specified topology: algorithm A2

Oftentimes one does not know what combination of building blocks and what spacer helix lengths will lead to a desired nanostructure. In this case it would be desirable to iterate over different helix connectivities and spacer helix lengths, potentially constraining the number of generated structures by topology. Using the NanoTiler scripting language, it is possible to loop over different helix connection rules and helix spacer lengths and apply algorithm A1 described in the previous section, thus scanning the space of structures self-assembling using the specified set of building blocks. To simplify the usage as well as constrain the search by RNA topology we developed algorithm A2, outlined as pseudocode in Fig. 3. The basic idea is that algorithm A2 iterates over different connectivities (different helix connections and helix spacer lengths), generates a structure for each connectivity and saves each generated structure that is compatible with the user-specified topology (see Section 2.1).

Fig. 3.

Pseudocode of algorithm A2: Automated search of building block connectivities.

2.4. Constraint satisfaction: algorithms 3a and b

Structures that were found using the combinatorial search often contain either a gap or small collisions (see for example Fig. 4 top). Our approach for rapid ring closure of such structures is to optimize the positions and orientations of the involved building blocks simultaneously in order minimize the strain on the connecting helical struts. This is achieved by specifying constraints describing which helix ends should be connected as well as the number of base pairs that are to be inserted as spacer elements. Examples of the constraint satisfaction algorithm applied to the assembly of three three-way junctions are shown in Figs. 5a and 6. For each helix constraint a constraint violation score is computed; this is described in more detail in the caption of Fig. 5.

Fig. 4.

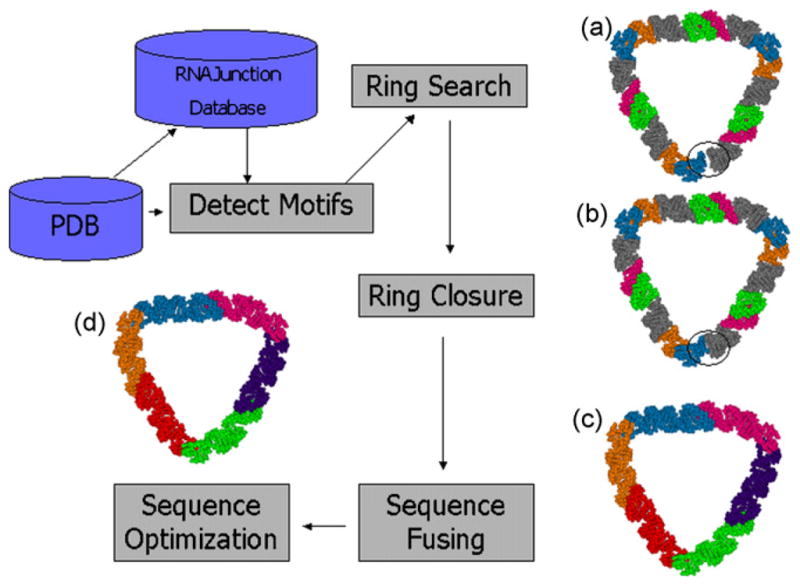
Pipeline for generation of RNA ring structures. Detect motifs: automatic (or manual) extraction of RNA structural elements from coordinate files; ring search: combinatorial search for closed RNA ring structures trying different RNA building blocks and helix length combinations (blue/orange are two strands of one kissing loop type, green/red are strands of another kissing loop type, gray indicate linker helices); ring closure: using constraint satisfaction to reduce the space gap often contained in structures obtained from the combinatorial search algorithm (colors as in the previous step); sequence fusing: automatic or manual fusing of sequence fragments (the six colors indicate six strands each forming an assembly unit); sequence design: automatic optimization of set of RNA sequences to improve RNA folding stability (colors as in the previous step).

Fig. 5.

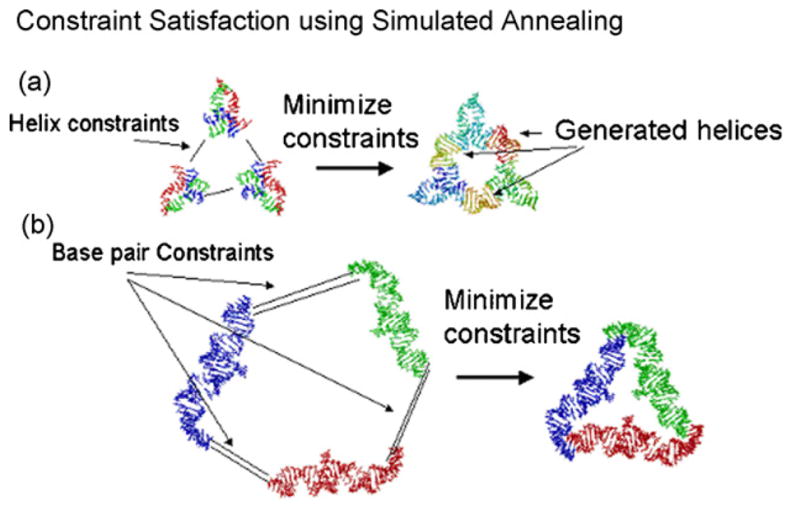
(a) Structure assembly using constraint satisfaction for helix-constraints. Assuming that the 3 three-way junctions have been placed with the names j1, j2 and j3 under the root node “root”, the ring can be assembled with the commands: genhelixconstraint root.j1.(hxend)1 root.j2.(hxend)2 bp = 10; genhelixconstraint root.j2.(hxend)1 root.j3.(hxend)2 bp = 10; genhelixconstraint root.j3.(hxend)1 root.j1.(hxend)2 bp = 10; opthelices steps = 1,000,000. The genhelixconstraint commands requires the specification of two helix ends by their name in the scene graph; optionally a length of a spacer helix can be specified (in this case a spacer helix of length 10 is being used because of the option bp = 10). Each helix constraint describes which two helix ends are to be connected as well as the number n of base pairs that are to be inserted as spacer elements. The constraint score is the maximum of four distances. Two distances arise by extending the first helix by n + 1 base pairs and computing the distances between the two ending C4′ atom positions from both strands with the corresponding C4′ atoms positions of the end of the second helix. Two more distances arise by the reverse procedure of extending the second helix by n + 1 base pairs and comparing the C4′ atom positions of the first helix with the end positions of the extended helix. The command opthelices moves the building blocks in order to minimize the constraint violation score. (b) In this example, the user has specified base-pairing interactions (using the command genbpconstraint or the GUI equivalent thereof) between three building blocks that are supposed to form a triangular structure. The command optbasepairs optimizes the structure with respect to base pair constraints using a simulated annealing algorithm, moving the building blocks as rigid bodies in order to minimize constraint violations. If a base pair constraint is specified between two bases that are each present in the two different building blocks, the error is the distance root mean square between the structure of the given two bases and a reference base pair derived from a 16S ribosome structure. The distance root mean square computation compares distances between eight reference atoms of the first base and eight reference atoms of the second base. This results in 64 inter-base distances. The square root of the sum of the differences between the 64 distances of the reference structure and the corresponding 64 distances of the structure to be optimized is the resulting error score. As reference atoms we use atom names that occur in all four bases, their PDB names are: P, O3*, O5*, C1, C5, N3, N1, C4. Assuming that the three RNA strands have been placed with names A, B and C under the root node “root”, the ring can be assembled with the commands: genbpconstraint root.A.11 root.B.47 2; genbpconstraint root.B.11 root.C.47 2; genbpconstraint root.C.11 root.A.47 2; optbasepairs blocks = root.A; root.B; root.C steps = 10,000. The genbpconstraint command requires the specification of two nucleotides by their name in the scene graph. For example “root.A.11” stands for nucleotide 11 of strand A. Optionally, the length of a helix can be specified as a third parameter (in this case 2); for a helix of length n specified in this way, n individual base pair constraints will be generated corresponding to the n different base pairs of the helix.

Fig. 6.

Pseudocode of algorithm A4: automated generation of constraints to improve closure of RNA ring structures.

A simulated annealing algorithm using a Metropolis criterion is employed to minimize the total score related to the helix constraints [36]. This algorithm moves the different parts of the structure (treated as rigid bodies) in order to minimize the constraint violations. Each rigid body is represented by a local coordinate system; no atom coordinates have to be moved during the optimization. The user can specify the number of optimization steps as well as the starting “temperature” (the temperature is decreased every 10,000 steps by a factor 0.985).

Similar to connecting helix ends it is possible to specify constraints for base pairs. This can be useful to bring two strands involved in a kissing loop interaction together. These constraints can also be optimized by simulated annealing (see Fig. 5b).

2.5. Automated generation of helix constraints for optimizing ring-closure: algorithm A4

As described in the previous section, the definition of helix-constraints can be used to optimize ring closure. Defining all constraints for a ring structure can be cumbersome, however. For this reason we provide an algorithm to automatically generate helix constraints. algorithm A4 is described as pseudocode in Fig. 6. The basic strategy of the algorithm is to generate constraints that lead to a quaternary structure with high symmetry. In the first stage, the placed building blocks are classified into different types, thus generating equivalence classes. Building block equivalence is established with the same method that is used to group the entries of the RNAJunction database into clusters of structural elements with identical sequence and not more than 3 Å nearest neighbor DRMS [29]. Next, the algorithm generates a sorted list of the connectability scores of all pairs of building block helix ends. The connectability score indicates how well a pair of helix ends could potentially be connected by a linker helix (corresponding to least amount of spacer helix distortion using a scoring function described in the caption of Fig. 5). While there are unconnected helices in the system, the algorithm obtains the next top-ranking helix-pair from the list of scores, removes that entry from the list and generates a constraint indicating that the two specific helix ends corresponding to this entry are to be connected by a linker helix. For each constraint generated in this manner, the system also generates all constraints that connect the equivalent building blocks in the structure. If, for example, helix end 1 of building block 3 (which belongs to, for example, class A) and helix end 2 of building block 7 (which belongs to, for example, class C) are considered to be connectable by a linker helix, then all constraints linking helix ends 1 and 2 of building blocks of classes A and C are generated in the order of the connectability score (not allowing any helix to be connected to more than one other helix).

2.6. Sequence fusing: algorithm A5

The ring structure models obtained after optimizing the ring closure contain fragments that are not connected by covalent bonds along the backbone (Fig. 4b). Using NanoTiler it is possible to interactively specify which sequence should be fused or split, thus defining the topology of the RNA structure. For larger complexes, this is a potentially cumbersome process. We developed algorithm A5 for automatically suggesting a sequence-fusing pattern, described in Fig. 7. The basic idea is to generate sequences that are composed of parts of one or several building blocks, however, each building block type is allowed to occur no more than once in each sequence. This is accomplished by first classifying the building blocks in the system into different equivalence classes as described in the previous section. The algorithm then chooses a strand to start a “path” in the structure by consecutively following strands in the 5′ to 3′ direction, “hopping” at the 3′ end of a strand to the closest available 5′ end of another strand and so forth. Strands are eligible to be part of a “path” if they have not been used in a previous path and if they are not associated with building blocks that have already been visited in the current path. If no suitable new strand can be found, the strands participating in the current path are fused and a new path is then started. Please consult for more details the pseudocode shown in Fig. 7. This suggested sequence fusing pattern is just one of many possibilities and it might be necessary for the user to interactively refine the sequence connectivities. We found, however, that for the RNA ring structures we worked with, the algorithm reduced or eliminated the need for interactively refining the sequence connectivity.

Fig. 7.

Pseudocode of algorithm A5: automated fusing of RNA sequences.

2.7. Sequence optimization: algorithm A6

The goal of sequence optimization is to determine a set of RNA sequences that will fold into the desired target structure with minimal amount of misfolded structures. The building block approach taken here is characterized by the fact that oftentimes one wants to keep the parts of the sequences corresponding to known RNA motifs constant while varying the sequences of the introduced spacer helices.

The approach for RNA sequence design is based on the program RNAcofold. RNAcofold uses a pair of sequences as input, and computes intra- and inter-sequence base pairs. We have n sequences each representing a component for self-assembly and each having a target secondary structure to design. We use a Monte Carlo approach for optimizing the sequences. The score assigned to the set of n sequences measures how many desired versus undesired base pairs are predicted by RNAcofold with respect to the target secondary structure. More specifically, the score is the sum of the scores assigned to all sequence pairs. A sequence pair score is computed by counting the number of desired base pairs, subtracting (with a weight factor) the number of undesired base pairs, subtracting the weighted number of instances of consecutive nucleotide repeats (more than four instances of the same nucleotide in a row is penalized) and subtracting an error term dependent on the deviation of desired G + C content from actual G + C content of the current sequences. The mutation step mutates sequences, preserving user-specified regions (typically 3D building blocks derived from known structures will be left unchanged). The mutation step also only explores canonical base pairing (and optionally GU base pairs) for pairs of nucleotides that correspond to base pairs in the target secondary structure.

The advantage of this approach is that RNAcofold is specifically taking into account the balance between intra- and inter-sequence base pairs. Unlike other sequence optimization algorithms it is not restricted to single sequences. It should be noted that RNAcofold does not take pseudoknots into account; this might be an area for future improvement of the method.

2.8. 3D base substitution: algorithm A7

After the sequences have been optimized, the corresponding changed bases are automatically substituted in the 3D model. The approach is to remove the current base and replace it with the reference 3D coordinates of the new base. If the base to be substituted (or “mutated”) is part of a base pair, then the base pair is substituted. The coordinate data of the new base or base pair is determined by searching a reference 3D structure (we currently use a 16S rRNA structure) for bases or base pairs with backbone and base orientations that are most similar to the original base or base pair and do not lead to severe steric clashes in the new structure.

3. Implementation

The algorithms presented here are implemented as part of the program NanoTiler.¹ The NanoTiler software is a stand-alone application written in the Java programming language and has been tested on Linux systems. Certain specialized functionality is obtained by calls to additional programs. Currently the RNAview software [37] is used to identify and classify base pairs in PDB structures, the RNAcofold program [38] is used as part of the sequence design approach. For topology classification a rigorous graph-signature generation program is used [34]. The software can be used via a command line interface, batch scripts or a graphical user interface. Not all capabilities of the software are presented here because in this paper we focus specifically on the pipeline for combinatorially generating RNA nanostructures from building blocks.

3.1. Modeling of molecular structures using a scene graph

Like other object-oriented molecular modeling systems, we exploit the logic hierarchy of bio-molecules by mapping molecular or logical entities (atoms, nucleotides, RNA strands, Junctions) to objects in a tree structure that acts as a scene graph. An RNA strand for example is modeled as an RNA strand object in the tree, which in turn has “child nodes” that represent nucleotides. The nucleotides in turn have child nodes representing their respective atoms. A different data structure (a list of “links”) represents relationships (like base pair interactions or constraints) between pairs of 3D entities. This is important, because we allow the user to manipulate the scene graph using script commands. The scene graph name (a dot-separated list of object-child identifiers) of an object is used to specify any placed 3D object.

3.2. Script language

The NanoTiler software has its own script language. The script language makes manipulation steps reproducible, facilitates communication and allows automation of repetitive tasks. A list of important high-level commands is given in Table 1. The script language provides a mechanism for handling string variables and contains control structures like a foreach command. Other commands that query the current structure or allow simple structure manipulations are not listed.

Table 1.

Non-exhaustive list of NanoTiler script commands

Name	Comment
clone	Copy substructure
dist	Distance between two objects
exportpdb	Save structure in PDB format
foreach	Loop command
fusestrands	Fuses 2 RNA strands
genbpconstraint	Generate base pair constraint
genhelix	Generate double-helix structure bridging to opposing helix ends
genhelixconstraint	Generate helix constraint connecting two opposing helix ends
genshape	Fast generation of rings or polyhedra as graphs
grow	Simulated self-assembly of blocks
growgraph	Combinatorial tracing of graph
import	Read PDB file or graph
loadjunctions	Read junction database
move	Move substructure to different location in tree
mutate	Mutate a residue in 3D
optbasepairs	Constraint satisfaction for base pairs
opthelices	Constraint satisfaction for helices
optsequences	Sequence optimization
place	Place a certain building block at a position
rename	Rename object
ringfixconstraints	Generate helix constraints for ring closure
ringfuse	Heuristic for fusing adjacent sequences
rotate	Rotate selected substructure in space
select	Select substructure
shift	Move selected substructure in space
signature	Generate topology descriptor for structure
splitstrand	Split RNA strand into two strands

3.3. Graphical user interface

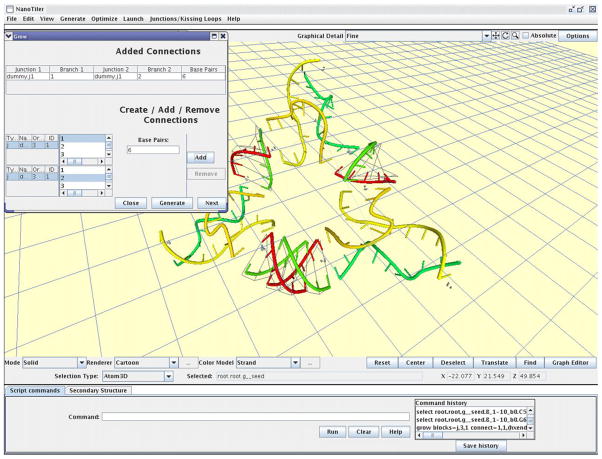
The graphical display is based on the OpenGL graphics architecture in the form of the Java/Jogl OpenGL binding. The user can specify the level of rendering detail and choose between different coloring options and a cartoon or stick representation of the molecular structures. A screenshot is shown in Fig. 8. The graphics also shows non-molecular entities like 3D graphs, which can be important when using the graph-based junction placement algorithm. The program offers optionally an alternative 3D graphics representation that does not depend on the OpenGL binding (not shown). Many script commands have an equivalent GUI element in the form of a button or a pull-down menu item. Conversely, most GUI commands work by internally issuing a script command. This increases the reproducibility of the work by allowing the user to store a command history.

Fig. 8.

Screenshot of the NanoTiler program. The Figure shows the 3D graphics window as well as a mask that is used for specifying building block connectivities and for starting the simulated self-assembly algorithm.

3.4. Detection of junctions and kissing loops

Central to the NanoTiler software is the concept of structural elements that are extracted from known RNA structures and used as building blocks for the assembly of designed structures. As structural elements we currently use RNA junctions, kissing loops, internal loops and bulges. The definition of these structural elements as well as a discussion of the algorithm for detecting them can be found in the description of the RNAJunction database [29].

4. Results and discussion

We illustrate the utility of the computational pipeline for RNA nanostructure design by showing how an RNA ring structure can be designed using kissing loops and three-way junctions as building blocks.

4.1. Example 1: ring structure grown using specified building blocks and connectivity or shape

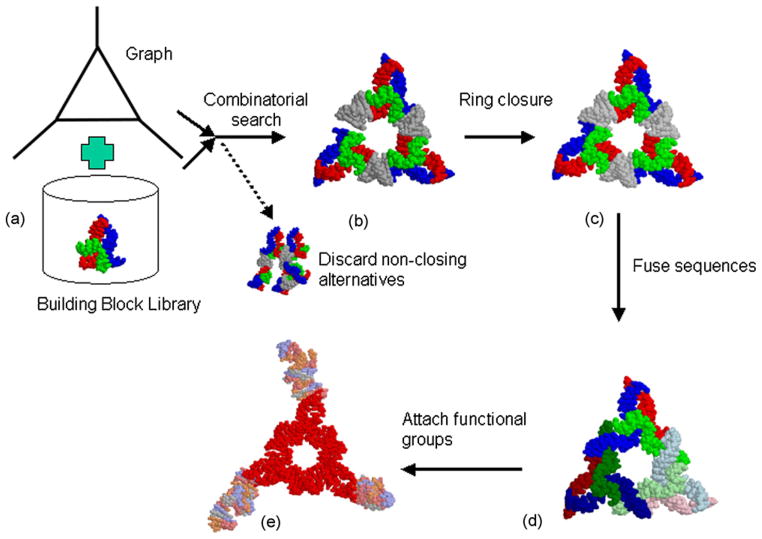
Using this approach, we have taken structural elements from the RNAJunction database and performed a quasi-exhaustive search for generated ring structures (manuscript in preparation). An example is shown in Fig. 4a) of an almost closed ring found through the combinatorial search approach. The “almost closed ring” is an interesting case because it reflects how the structure is generated. Given the fact that many structural elements are flexible, it would be advantageous if one could now modify this structure to produce a closed ring. This can be accomplished using the constraint satisfaction optimization in combination with algorithm A4 for the automated generation of helix constraints mentioned in Section 2. The result of these two steps is shown in Fig. 4b. Applying the sequence-fusing algorithm A5, results in a structure with fused RNA sequences (Fig. 4c). Sequence optimization finally leads to the structure shown in Fig. 4d.

These steps taken together can be used for an automated pipeline that starts with a set of specified building blocks and generates a set of structures that have sufficient quality to be refined without manual intervention by all-atom simulation programs such as AMBER [14]. Only the step involving the sequence optimization currently involves some manual intervention that requires the user to specify which nucleotides should be kept constant during the sequence optimization.

4.2. Example 2: towards a functionalized RNA nanoparticle

Another example showing the capabilities of the approach is shown in Fig. 9. Here we use as a building block a three-way junction (Fig. 9a). Connecting two of its helices with six base pair helical spacer elements results in a triangular RNA structure (Fig. 9b). The number of base pairs leading to ring-closure is found by combinatorial search constrained by the triangular 3D graph shown in Fig. 9a). Applying constraint-satisfaction leads to a structure with improved ring-closure (Fig. 9c). The sequences of the different building blocks are fused with one command (Fig. 9d). Three functional groups were added: an RNA aptamer capable of binding to the HIV tat protein [39], an RNA aptamer capable of binding to the chromophore Malachite Green [40] as well as a ribozyme exemplifying catalytic functionality [41]. Applying three commands for importing the different functional groups, three commands for specifying the helices to be connected and one command for starting the constraint satisfaction algorithm results in Fig. 9e. This demonstrates the flexibility and scope of the presented approach for RNA nanostructure design. We envision the NanoTiler software to be instrumental for designing novel self-assembling RNA structures as well as for exploring RNA structure spaces.

Fig. 9.

An example of the design steps of a multi-functional RNA nanoparticle. In the first step (a) an RNA building block is extracted from coordinate data and is (together with a 3D graph representation of the target structure) imported into the program. (b) The result of 3D structure found by combinatorial search using input data provided in previous step. Structural alternatives that have a different topology compared to the 3D graph are discarded. (c) Structure with improved ring-closure using constraint satisfaction. (d) Automatic fusing of sequences. The strands are again shown in blue, green and red, however these colors are medium for the assembly unit shown at the top corner, dark for the corner unit shown at the lower left and light for the assembly unit shown at the lower right of the triangular structure. (e) Final result depicting triangular nanoparticle with HIV Tat aptamer (top corner), malachite green aptamer (left corner) and lead dependent ribozyme (right corner) attached. The triangular scaffold obtained from the previous step is shown in red and the new functional groups are multi-colored. This step was accomplished using four commands corresponding to importing the triangular scaffold and the three functional groups, three commands specifying the helices to be connected and one command for starting the constraint satisfaction algorithm results.

5. Conclusion

We have presented a set of algorithms geared towards the automated design of RNA nanostructures from building blocks. The involved steps of automatically detecting junction and kissing loop elements, combinatorial search of structural elements, optimizing ring closure, sequence fusing and sequence optimization offer a coherent suite of methods for generating RNA nanostructures.