Abstract
Integrative genomics predictors, which score highly in predicting bacterial essential genes, would be unfeasible in most species because the data sources are limited. We developed a universal approach and tool designated Geptop, based on orthology and phylogeny, to offer gene essentiality annotations. In a series of tests, our Geptop method yielded higher area under curve (AUC) scores in the receiver operating curves than the integrative approaches. In the ten-fold cross-validations among randomly upset samples, Geptop yielded an AUC of 0.918, and in the cross-organism predictions for 19 organisms Geptop yielded AUC scores between 0.569 and 0.959. A test applied to the very recently determined essential gene dataset from the Porphyromonas gingivalis, which belongs to a phylum different with all of the above 19 bacterial genomes, gave an AUC of 0.77. Therefore, Geptop can be applied to any bacterial species whose genome has been sequenced. Compared with the essential genes uniquely identified by the lethal screening, the essential genes predicted only by Gepop are associated with more protein-protein interactions, especially in the three bacteria with lower AUC scores (<0.7). This may further illustrate the reliability and feasibility of our method in some sense. The web server and standalone version of Geptop are available at http://cefg.uestc.edu.cn/geptop/ free of charge. The tool has been run on 968 bacterial genomes and the results are accessible at the website.
Introduction
Essential genes are the genes which are “essential” for survival of an organism [1], [2]. Therefore, identification of gene essentiality is important in understanding the minimal requirements for cell survival and functionality [3], [4]. The study of essential genes is an important step towards understanding the evolution of microbes [5]. Systematic genome-wide interrogations, such as single-gene knockouts [6], [7], transposon mutagenesis [8], [9], [10] and RNA interference [11], [12], have been used to identify essential genes. However, such experiential techniques are challenging and time-consuming. High-efficiency computational methods offer an appealing alternative for predicting essential genes without the expense and difficulty of an experimental screen.
An initial computational approach, by comparing the genomes of Haemophilus influenzae and Mycoplasma genitalium, identified approximately 250 candidate essential genes as the minimal gene set [3]. These genes were considered necessary for the survival of H. influenzae and M. genitalium. Bacterial essential gene products are often attractive drug targets in the development of antibiotics. Several previous studies relied upon homology mapping against an experimentally determined set of essential genes to identify drug targets [13], [14], [15], [16], [17], [18], [19]. The evolutionary distance between genomes can have a significant impact on the outcome of comparative genomic analyses [20]. On the other hand, orthologs of essential genes do not always carry out essential functions among those closely related organisms, and may even be absent in certain situations [21]. When an essential gene is lost, it is possible for a living cell to be rescued through the over-expression of a non-homologous and non-essential gene [5]. Consequently, the number of genes identified in the minimal set using comparative genomics across many bacterial species decreased significantly from comparing of H. influenzae and M. genitalium [20], [22].
Flux balance analysis is a constraint-based modeling technique used to simulate fluxes of metabolic networks at the steady-state. It can be used to identify minimal gene requirements. The essential genes in several bacteria have been predicted based on this method [23], [24], [25]. An accuracy of 85% was obtained in predicting yeast essential genes [26]. Flux balance analysis is a powerful approach for predicting essential genes. However, it is strongly dependent on the knowledge of metabolic networks.
It has been found that several classes of biological features are correlated with gene essentiality and they are used to predict essential genes. As an example, a gene with an essential function is likely to use optimal codons, to be located on the leading strand, and to be with a high centrality [27], [28], [29], [30], [31]. In general, genomic features fall into three categories: intrinsic features based on sequences, those derived from sequences, and data from functional genomics experiments. Machine learning systems based on integrative features have been trained to identify essential genes in Saccharomyces cerevisiae [32], [33], [34]. Chen et al. investaged the relationship between the gene fitness of S. cerevisiae gene and the features derived from the high-throughput data [32]. They selected the fitness associated factors to predict the fitness of individual protein by machine learning methods. Seringhaus et al. [34] used only sequence dependent features to estimate essentiality for yeast proteins. The study showed excellent performance: a ten-fold cross-validation in yeast with a probability threshold of 0.5 correctly classified over 80% of a total of 4648 genes. The organism-wise cross-validation between Escherichia coli and Pseudomonas aeruginosa yielded the area under curve (AUC) scores of 0.75–0.81 in the receiver operating curves (ROC) using 33 broad variables [35]. Cross-organism prediction on four bacteria yielded AUC scores between 0.69 and 0.89, based on 13 integrative biological features [36]. Of the 13 features, the protein domain enrichment is the strongest predictor of essential genes [36].
However, the machine learning method cannot be used universally because of the lack of available experimental data in most genomes. Thus, a black box gene essentiality prediction algorithm, independent of experimental data, has been developed, which incorporates information on the biased gene strand distribution, the homologous search and the codon adaptation index (CAI) [37]. The algorithm achieved an AUC score of 0.81 when applied to the Mycoplasma pulmonis genome. It also achieved an accuracy of 78.9% and 78.1% in predicting essential genes in Staphylococcus aureus and Bacillus subtilis genomes, respectively.
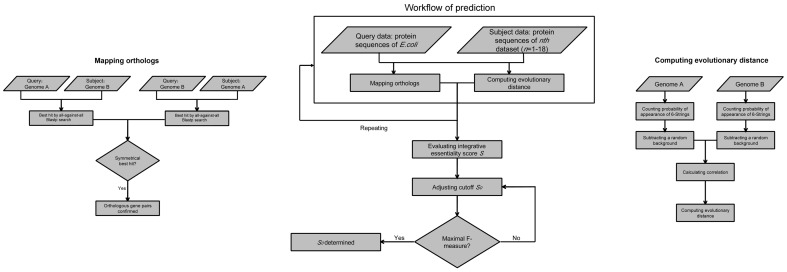
Essential genes should be persistent during the long-term evolution [2]. Based on this idea, we developed a universal tool to offer gene essentiality annotations only via evolutionary information. Therefore, we apply phylogeny weighted orthology variable to reflect evolutionary information in searching essential genes. In this work, we used a workflow similar with that developed by [37] given that its outstanding performance. A gene is considered essential if its essential orthologs are persistent, especially in similar species. For estimating orthology, we used the reciprocal best hit (RBH) method, which was widely and effectively applied to map orthologs [38], [39], [40], [41]. The distance of phylogeny between species was computed using the Composition Vector (CV) method [42]. The tool is called as gene essentiality prediction tool based on orthology and phylogeny (Geptop). The web server and open source standalone package implementing our method are freely available at http://cefg.uestc.edu.cn/geptop/.
Materials and Methods
Data sets
Database of essential genes (DEG) hosts essential genes identified by experimental techniques across a wide range of organisms [43]. The current version (6.8) contains 19 bacterial strains and 8 eukaryotes. The annotations of gene essentiality were obtained from the DEG database and the complete coding sequences of all 19 bacteria were taken from GenBank. We then classified genes into the essential set and the non-essential set according to gene annotations in GenBank for each genome. As a result, 19 essential sets and their corresponding non-essential sets were obtained.
Searching orthologs and estimating phylogeny distance
The orthologous gene pairs between each pair of genomes were identified based on the reciprocal best hit (RBH) method. For two given genomes, one genome was used as the query and the other as the subject. A query-subject gene pair was confirmed if it was found that a gene in the query matches another gene in the subject by all-against-all Blastp search with a default E-value cutoff of 10. If there were multiple hits with the E values lower than the cutoff for a given query gene, the hit with the lowest E-value was masked as the best hit. Then, the query and subject was switched to confirm the subject-query gene pairs using the same procedure. The symmetrical hits between query-subject gene pairs and subject-query gene pairs were identified as orthologous gene pairs.
The composition vector (CV) method is used to estimate evolutionary distance [42]. To calculate the CV distance between two species, we first collected amino acid sequence data. Second, we computed the frequencies of six-peptides. Thirdly, a composition vector of dimension 206 was obtained for each species by putting the ‘normalized’ frequencies in a fixed order. Fourthly, the correlation C between two species was determined by the cosine function of the angle between the two normalized vectors. Finally, the normalized distance D between them is defined to be:
Training workflow
Our method was based on phylogeny weighted orthology to predict the gene essentiality. To determine the optimal cutoff S0 of identifying essential genes, we used E. coli as the test set, and the other 18 proteomes were used as the training set. The homology mappings were performed by RBH between E. coli and each of the proteomes. We identified the mapping score (M) as 1 if an E. coli gene was homologous and essential in the multiple genomes set during the homology mapping procedure. Meanwhile, the CV distance (D) between E. coli and each proteome was also computed. After mapping all 18 genomes, we defined the gene essentiality score Si for ith E. coli gene:
where j denotes the jth proteome in the multiple genomes set, N denotes the count of proteome and the range of S was between 0 and 1. In this training procedure, N equals 18. Finally, we looked for the optimal cutoff, S0, using a greed search method. If S>S0, the gene is predicted to be essential, otherwise, the gene is predicted to be non-essential.
Performance assessment of method
The following parameters were measured in this study to assess the performance of the predictor:
 |
where TP, FN, FP and TN denote the true positives, false negatives, false positives and true negatives, respectively. The sensitivity parameter measures the proportion of essential genes that have been correctly identified. The specificity parameter represents the proportion of negatives that have been correctly predicted. The precision parameter is the probability that the essential genes were predicted as essential. The accuracy is the proportion of overall samples that have been correctly identified. The F-measure represents the harmonic mean of precision and sensitivity.
Gene phyletic ages
We used the method described in [44], [45] to determine the phyletic ages for the genes in E. coli. For mapping orthologs, we applied RBH with E-value >10. We randomly collected 43, 68, 71, 75, 143 and 40 genomes from Archaea, Bacteria, Proteobacteria, Gammaproteobacteria, Enterobacteriaceae and E. coli, respectively. The number of hits required to assign a protein to the given age class was determined as half of the effective number of genomes. Consequently, the genome of E. coli was divided into six broad taxonomic classes. The unassigned genes were classified as strain-specific class.
Results
Homology mapping of essential E. coli genes to other organisms
We used a RBH method to search for orthologs of essential E. coli genes in 18 bacterial species. All bacteria had well-characterized essential genes determined by experimental techniques, and the annotations were extracted from DEG (Table 1). The evolutionary distance between each of the 18 bacterial genomes and E. coli was calculated with the CV method. The numbers of shared essential genes among E. coli and other genomes were correlated to their evolutionary distances (Spearman's r = −0.576, p<0.01). As an example, Salmonella typhimurium Ty2 is phylogenetically related to E. coli, sharing 283 E. coli essential genes (Ecol), of which 256 also show essentiality in S. typhimurium Ty2. B. subtilis shares 221 Ecol genes, of which 149 are consistent with B. subtilis essential genes (Bsub). With respect to the more distinct genomes such as Mycoplasma only share about 120 essential genes when compared with the Ecol dataset. Therefore the evolutionary distance between genomes does indeed have a significant impact on the outcome of homology mapping. Moreover, essential genes are not always conserved in similar species. There are 256 essential genes in S. typhimurium Ty2 closely related to essential E. coli genes, but only 84 Ecol orthologs also perform essential functions in the closely related S. typhimurium LT2. It is confusing when choosing the reference organism for homology mapping by essential function because essential genes do not always transfer across organisms regardless of the evolutionary distance. That is why we performed homology mapping using multiple genomes rather than a single genome.
Table 1. Detailed information regarding the 19 bacterial species investigated.
| Organism | Abbreviation | Number of genes | Phylum | |
| Essential | Total | |||
| Acinetobacter baylyiADP1 | Abay | 499 | 3307 | Proteobacteria |
| Bacillus subtilis 168 | Bsub | 271 | 4176 | Firmicutes |
| Caulobacter crescentus NA1000 | Ccre | 480 | 3878 | Proteobacteria |
| Escherichia coli MG1655 | Ecol | 296 | 4146 | Proteobacteria |
| Francisella novicida U112 | Fnov | 390 | 1719 | Proteobacteria |
| Haemophilus influenzae Rd KW20 | Hinf | 642 | 1657 | Proteobacteria |
| Helicobacter pylori 26695 | Hpyl | 322 | 1573 | Proteobacteria |
| Mycobacterium tuberculosis H37Rv | Mtub | 614 | 4003 | Actinobacteria |
| Mycoplasma genitalium G37 | Mgen | 378 | 475 | Tenericutes |
| Mycoplasma pulmonisUAB CTIP | Mpul | 310 | 782 | Tenericutes |
| Pseudomonas aeruginosa UCBPP-PA14 | Paer | 335 | 5892 | Proteobacteria |
| Salmonella typhi Ty2 | StypT | 352 | 4313 | Proteobacteria |
| Salmonella typhimurium LT2 | StypL | 230 | 4423 | Proteobacteria |
| Staphylococcus aureus N315 | SaurN | 302 | 2583 | Firmicutes |
| Staphylococcus aureus NCTC 8325 | SaurC | 351 | 2891 | Firmicutes |
| Streptococcus pneumonia TIGR4 | SpneT | 111 | 2105 | Firmicutes |
| Streptococcus pneumonia R6 | SpneR | 133 | 2042 | Firmicutes |
| Streptococcus sanguinis SK36 | Ssan | 218 | 2270 | Firmicutes |
| Vibrio cholerae N16961 | Vcho | 779 | 3834 | Proteobacteria |
Classifier training on the 18 bacterial genomes and cross-organism validation in E. coli
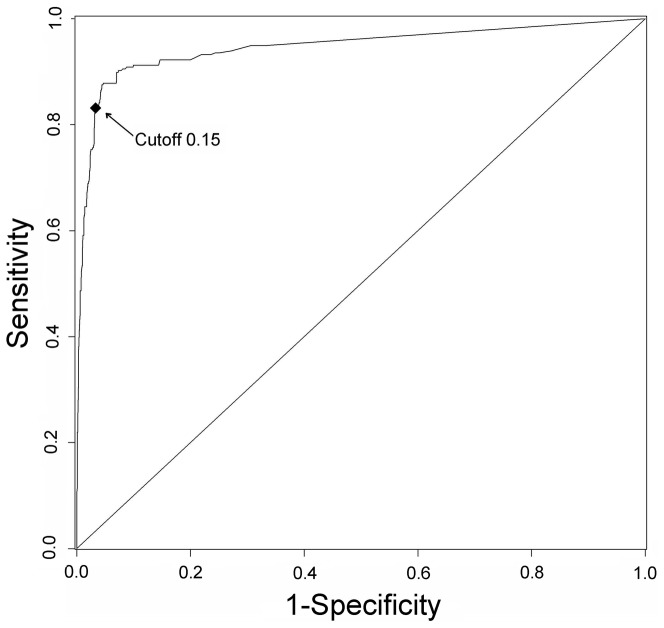
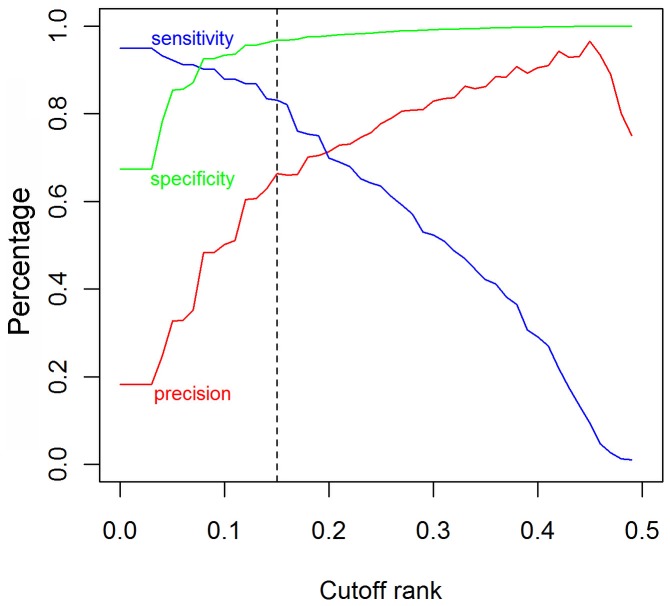
To determine the cutoff of identifying essential genes, we used 18 proteomes as searchable databank and then E. coli was applied to test; a detailed workflow is shown in Figure 1. Validation test of the classifier yielded an AUC score of 0.947 using Ecol (Figure 2). The changes in precision, sensitivity and specificity along with that of predicted essentiality score cutoff are illustrated in Figure 3. The number of non-essential genes was almost eight times greater than that of essential genes. To avoid the bias caused by excessive number of false essential genes and insufficient number of true essential genes, we used the harmonic mean of precision and sensitivity (F-measure) to determinate the threshold of classifying essential genes. This indicator is widely used for assessing the performance of various kinds of classifiers [46], [47], [48]. The classifier identified 371 essential genes in E. coli at (S0 = 0.15) with the maximal F-measure. Of these predicted essential genes, 246 were true positives; however, 50 real essential genes were lost. Therefore, we were able to achieve a sensitivity of 83.1% and specificity of 96.8%.
Figure 1. Training workflow based on 18 groups of essential genes and using Ecol as test.
Figure 2. ROC curve of cross-organism validating for Ecol.
Black diamond denotes the default cutoff of 0.15.
Figure 3. The precision, sensitivity and specificity in relation to the cutoff rank.
The vertical dashed line represents the default cutoff of 0.15.
The other broadly used essential dataset (EcolP) was downloaded from the PEC database [49]. These essential genes were also used as a validation set and the classifier yielded an AUC score of 0.978. This score is much better than the result of a recent study using the integrative machine learning systems [36] (AUC = 0.82–0.89). With the maximal F-measure, the classifier predicted 261 essential genes in EcolP (S0 = 0.15) and achieved an accuracy of 96.7%. Because the cutoff of S determined byEcolP is as the same as by Ecol, we therefore determined S0 to be 0.15.
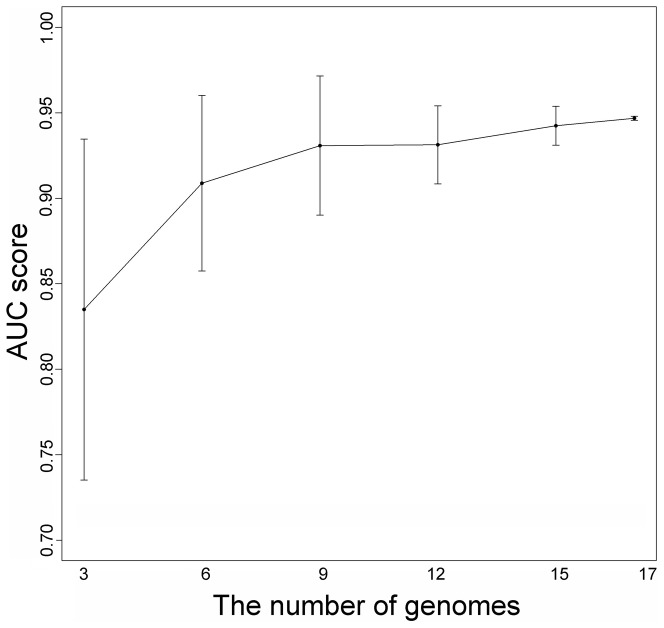
For evaluating the effect of using different multiple genomes, we randomly picked 3, 6, 9, 12, 15 and 17 genomes, for 10 times of each case, from the remaining 18 genomes and computed the AUC scores of predicting Ecol. As can be seen from Figure 4, the application of more genomes indeed made the results of prediction better and more stable. Thus, the application of multiple genomes in the classifier can improve the power of prediction.
Figure 4. AUC scores of jackknife test.
We randomly picked 10 times of 3, 6, 9, 12, 15, 17 genomes from the remaining 18 genomes and computed the AUC scores of predicting Ecol. Error bars are representing 90% confidence intervals on the estimates of the means.
Cross-validations of classifier
The proteins of the 19 collected organisms were randomly upset and then partitioned into ten samples. Of the ten newly generated proteomes, one proteome was used as the test set, and the remaining proteomes were used as the training set. We repeated this ten times, thus each of the ten proteomes was used once as the validation data. This ten-fold cross-validations in the random samples yielded an AUC score of 0.918. The results balanced between precision (0.512) and sensitivity (0.581) with the S0 set at 0.05–0.07 and yielded an accuracy of 0.916.
Considering that the distinct evolutionary information was discarded during the random sampling, cross-organism validation was adopted to re-estimate the classifier. One of the 19 collected organisms was used as the test set, and the other ones were trained. Validation was repeated 18 times with each of the organisms being used exactly once as the validation data (For Ecol dataset, we have already performed this validation test above). Cross-organism predictions yielded AUC scores between 0.569 and 0.959 (Figure 5).
Figure 5. AUC scores from cross-organism Geptop prediction.
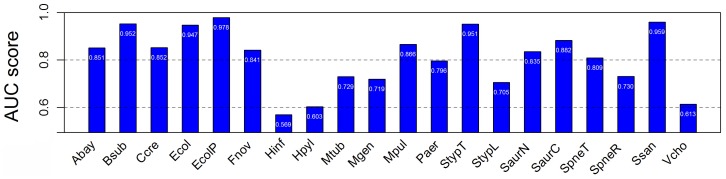
The range of AUC is from 0.5 to 1.
For overall predictions, 52.6% of their AUC scores were greater than 0.8, which indicated that classifier was significant and efficient. For example, the model Gram-positive bacterium Bsub yielded a high AUC score of 0.952. From all predictions, five yielded acceptable AUC scores between 0.7 and 0.8, while the other three predictions tended to be randomized. We applied the cutoff of 0.15 on the classifier to predict essential genes in 18 organisms and 15 of them exceeded an accuracy of 0.8 (Table 2).
Table 2. Cross-organism test accuracies of the Geptop.
| Dataset | Precision | Sensitivity | Specificity | Accuracy |
| Abay | 0.810 | 0.511 | 0.979 | 0.908 |
| Bsub | 0.665 | 0.753 | 0.974 | 0.959 |
| Ccre | 0.824 | 0.527 | 0.984 | 0.928 |
| Ecol | 0.663 | 0.831 | 0.968 | 0.958 |
| EcolP | 0.704 | 0.909 | 0.971 | 0.967 |
| Fnov | 0.787 | 0.633 | 0.950 | 0.878 |
| Hinf | 0.550 | 0.268 | 0.861 | 0.631 |
| Hpyl | 0.343 | 0.308 | 0.848 | 0.737 |
| Mtub | 0.686 | 0.316 | 0.974 | 0.873 |
| Mgen | 0.941 | 0.460 | 0.887 | 0.547 |
| Mpul | 0.914 | 0.581 | 0.964 | 0.812 |
| Paer | 0.503 | 0.496 | 0.971 | 0.944 |
| StypT | 0.734 | 0.793 | 0.975 | 0.960 |
| StypL | 0.254 | 0.444 | 0.929 | 0.903 |
| SaurN | 0.488 | 0.613 | 0.915 | 0.880 |
| SaurC | 0.620 | 0.650 | 0.945 | 0.909 |
| SpneT | 0.199 | 0.532 | 0.881 | 0.862 |
| SpneR | 0.232 | 0.541 | 0.875 | 0.854 |
| Ssan | 0.639 | 0.844 | 0.949 | 0.939 |
| Vcho | 0.675 | 0.285 | 0.965 | 0.827 |
Geptop
Taking all the 19 bacteria as the multiple genomes set and adopting the same model and the threshold, we formed an online and also a standalone tool designated as Geptop. The Geptop web server first provided an online platform to detect essential gene sets across bacterial species using our classifier (http://cefg.uestc.edu.cn/geptop/). After a user submits the whole-proteome for a bacterial species in the FASTA format, the web server will automatically compute the essentiality score for each gene by comparing the orthology and phylogeny information for the 19 genome datasets (from DEG). The default cutoff is set at 0.15. The result will be automatically sent to the user via e-mail when the prediction is completed. Alternatively, a standalone version Geptop is also available. This package is dependent on Python, Biopython and BLAST+.
Application of Geptop: predicting essential genes in sequenced bacterial genomes
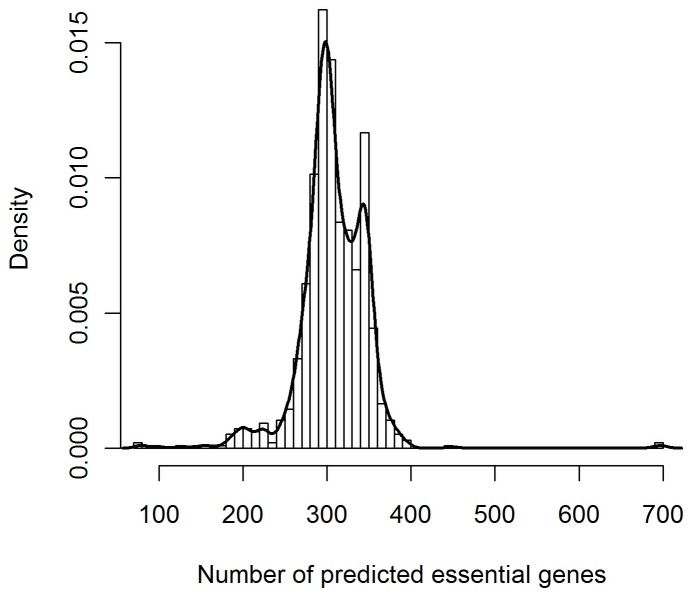
We predicted essential genes in 968 sequenced bacteria, which are from 26 different phyla, using our Geptop method. Our webserver provides the details of these predictions at http://cefg.uestc.edu.cn/geptop/list.html. With the default cutoff (S = 0.15), most predictions identified 250–350 essential genes (Figure 6). Previously, the minimal gene set of cellular life has estimated approximately 250 candidates [3], [21]. Our result provides a piece of evidence for supporting this estimation.
Figure 6. The distribution of predicted essential gene numbers.
A newly experimentally identified essential gene dataset from Porphyromonas gingivalis was also collected [50], which could be used to assess the performance of Geptop since this species belongs to a different phylum comparing the bacteria included in Geptop. As expected, 281 essential genes were predicted by our websever (Table S1 in File S1), 80% of them are experimentally identified. This prediction yields an AUC score of 0.77. We thus confirm that the method of Geptop does predict essential genes effectively even when applied in distantly organisms and most estimations could yield an AUC score exceed 0.70.
Since our method aims to find essential genes by evolutionary information, it might lose the species-specific essential genes. However, the species-specific genes (young genes) were found less likely essential than older genes [45]. As mentioned above, we lost 50 real essential genes for Ecol by the cross-organism prediction. We investigated the phyletic ages of these 50 genes and found 12 of them belong to strain-specific or E. coli-specific. That is to say, only 4% (12/296) essential genes were mistakenly classified because they are species-specific. Therefore, the performance of Geptop is acceptable if we do not specially focus on those species-specific essential genes.
Discussions
Geptop advantages
Cross-organism predictions yielded AUC scores between 0.69 and 0.89 using another integrative genomics method [36]. Acinetobacter baylyi, P. aeruginosa and B. subtilis was used to predict EcolP, and the AUC scores were between 0.82 and 0.89. When using EcolP to predict essential genes in A. baylyi (Abay) and B. subtilis (Bsub), the AUC scores were 0.80. The authors [36] did not use EcolP to carry out prediction for the essential set of Paer for the strain UCBPP-PA14, which is involved in our work. The study used only one genome for cross-validation. As mentioned in [36], RBH did not work well using only one genome. However, our tool consider putting in the phylogeny information (CV), could effectively work dependent of multiple genomes. We here used three of EcolP, Bsub, Abay and Paer for training, and the rest one for testing. The AUC scores of cross-organism predictions of EcolP and Bsub by Geptop are 0.91 and 0.85, respectively, which are slightly better when comparing with the integrative method. However, the AUC of Abay (0.77) shows a little weaker. When using 18 genomes for training, the power of method is improved, even Abay (AUC = 0.85) is better than the integrative method (Figure 5). Another machine learning system based on the integrative features was trained to identify Ecol using Pseudomonas aeruginosa, and to identify essential genes in P. aeruginosa (Paer) using E. coli [35]. It yielded an AUC of 0.81 and 0.80 in predicting Ecol and Paer, respectively. We also used Bsub, Abay and Paer to predict Ecol by Geptop then yielded an AUC of 0.88, simultaneously, adopted Bsub, Abay and Ecol to predict Paer then yielded an AUC of 0.77. Generally, our method is competitive with the integrative method when using only three genomes as training set.
Although integrative genomics predictors scored highly in predicting bacterial essential genes, these classifiers usually rely on several biological features. The lack of functional experimental resources blocked the application of those algorithms. We investigated a different integrative genomics predictor based only on sequence compositional information, with 158 features considered. These features were amino acid usage (20 features), codon usage (64 features), codon position-specific nucleotide usage (12 features), 2-tuple codon position-specific nucleotide usage (48 features), and 14 features from CodonW (http://codonw.sourceforge.net). Details are listed in Table S2 (File S1). Genes were classified as essential or non-essential as given by the DEG annotations. We then used CD-HIT (http://www.bioinformatics.org/cd-hit/) to remove the redundant data. Because of the asymmetric numbers between the essential and non-essential sets, the negative sample set was randomly chosen from the non-essential set to have evenly sized groups. The six prediction models were obtained after the support vector machine training for the six groups of samples. The average prediction score of models for each bacterial genome was computed and this prediction yielded an AUC score (Figure 7). The Geptop predictor improved AUC scores when compared with this compositional bias based classifier by focusing on higher scoring groups that had an AUC higher than 0.8 yielded by the Geptop. However, most low AUC scoring bacteria showed a limited change. For example, the Geptop yielded a maximum AUC score of 0.959 when predicting the Streptococcus sanguinis essential set, which was significantly higher than the integrative compositional information predictor (AUC score of 0.751). For the lowest Geptop AUC score of 0.569 in Haemophilus influenzae, the compositional classifier yielded a similar score of 0.587.
Figure 7. AUC scores from cross-organism tests using the integrative compositional information predictor.
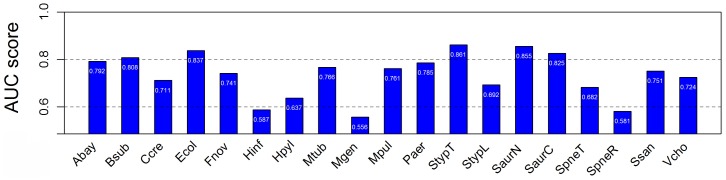
The range of AUC is from 0.5 to 1.
The Geptop is partly based on homology mapping. Similarly, a recently study has also performed Blast searching as a feature of the prediction [37]. This algorithm integrated the homology searching (one-way alignment), the codon adaptation index and the biased distribution of essential genes in leading and lagging strands. This study provided accuracy of about 80% when combined using the essential dataset in the Mycoplasma genitalium (Mgen) and the essential genes for Mycoplasma pulmonis (Mpul) to predict essentiality in genomes of B. subtilis and S. aureus. In our study, we improved the performance of predicting B. subtilis (accuracy = 92%) and S. aureus (accuracy = 87%) by equally using Mgen and Mpul.
The T-iDT finds essential genes by comparing a bacterial gene set against the DEG [51]. This tool matches potential essential genes in the DEG database using Blastp with an E-value cutoff of 10−10 and bit score greater than 100. The tool is based only on homology mapping to search for essential sets, which differs in two aspects when compared with the Geptop. First, we performed homology mapping by RBH to search for optimally matched genes in each bacterial genome; second, evolutionary distance was considered when searching orthologs among distinct genomes. Additionally, we also identified the essential genes in 19 bacterial species using cross-organism T-iDT predictions. Because the aim of the T-iDT is to identify drug targets, the essentiality prediction results showed high average specificity of 0.759 and low average sensitivity of 0.316 (Table S3 in File S1). However, our cross-organism Geptop prediction improved both the average specificity of 17.8% and sensitivity of 23.1% by at the default cutoff of 0.15 compared with the T-iDT. On the other hand, Holman et al. [17] defined a Multiple Hit Score (MHS) to predict essential genes based on the top alignments to essential genes for each bacterial strain in the DEG. Their cross-organism test showed scaled AUC scores between 0.137 and 0.742 among 14 strains. B. subtilis matched the highest score, which was still significantly lower than that predicted by the Geptop (scaled AUC score of 0.904). Our method adopted a different discriminatory function with better results.
Generally, the effectiveness of our method is similar to those method integrating functional genomics data and sequence-related features when only adopting three genomes to train the model. Moreover, with the expansion of training genomes, we can obtain better prediction. On the other hand, although using the multiple genomes, the power of one-way alignment is much weaker than that of combined evolutionary features (RBH/CV) in the field of predicting essential genes. Since our prediction only use protein sequence, we believe that the Geptop could be widely applied in most bacteria rather than only in specific species.
Features of predicted essential genes
Gene essentiality always correlates to codon bias [31]. Therefore, we investigated the difference of codon usage between essential genes predicted by Geptop across organisms and those identified by experimental techniques. The CAI is a species-dependent codon bias measure, and has been widely used as an empirical measure for gene expression, particularly in microbial genomes [52]. With this methodology, the collection of several ribosomal protein genes are chosen as a reference set of highly expressed genes for each genome. All genes for a given genome were classified into four groups: essential genes uniquely identified by experimental disruptions (experimental group); essential genes uniquely predicted by the Geptop (Geptop group); common essential genes; and common non-essential genes. As shown in Table 3, codon bias of the Geptop group was greater than that of the experimental group in 11 of 19 genomes (Mann-Whitney test, p<0.05). Seven genomes had a similar codon bias between the two groups. Only in Francisella novicida does the experimental group show a greater codon bias.
Table 3. Comparison of features between the experimental and the Geptop groups.
| CAI | The percentage of leading genes | Connectivity | |||||||
| Experimental | Geptop | Experimental | Geptop | Experimental | Geptop | ||||
| Abay | 0.553±0.064 | = a | 0.565±0.093 | 56.1% | <<b | 70.0% | 54±49 | <<a | 99±50 |
| Bsub | 0.522±0.071 | << | 0.544±0.076 | 83.6% | << | 97.1% | 54±47 | << | 111±59 |
| Ccre | 0.593±0.124 | << | 0.634±0.099 | 66.1% | >> | 55.6% | 45±37 | << | 103±53 |
| Ecol | 0.481±0.100 | << | 0.589±0.129 | 60.0% | << | 72.8% | 52±40 | << | 114±54 |
| Fnov | 0.646±0.056 | >> | 0.633±0.047 | 65.0% | = | 67.2% | 27±26 | << | 85±40 |
| Hinf | 0.520±0.064 | << | 0.601±0.097 | 52.8% | << | 62.4% | 36±38 | << | 114±50 |
| Hpyl | 0.698±0.036 | << | 0.709±0.024 | 57.4% | = | 58.4% | 35±30 | << | 105±41 |
| Mtub | 0.619±0.067 | = | 0.624±0.069 | 64.8% | << | 86.5% | 47±41 | << | 85±49 |
| Mgen | 0.715±0.041 | = | 0.715±0.029 | 83.3% | >> | 63.6% | 25±23 | << | 55±26 |
| Mpul | 0.679±0.048 | = | 0.679±0.050 | 66.9% | >> | 58.8% | 21±19 | << | 40±25 |
| Paer | 0.634±0.099 | << | 0.692±0.102 | 58.6% | << | 72.6% | 28±32 | << | 100±45 |
| StypT | 0.491±0.116 | << | 0.532±0.112 | 61.6% | = | 66.3% | 46±34 | << | 77±47 |
| StypL | 0.454±0.086 | << | 0.551±0.119 | 64.8% | << | 70.7% | 26±26 | << | 89±46 |
| SaurN | 0.580±0.086 | = | 0.585±0.088 | 80.3% | << | 90.2% | 44±41 | << | 65±44 |
| SaurC | 0.579±0.094 | = | 0.586±0.083 | 82.1% | << | 87.2% | 28±26 | << | 68±45 |
| SpneT | 0.388±0.081 | << | 0.506±0.170 | 84.6% | = | 88.2% | 48±39 | << | 106±49 |
| SpneR | 0.375±0.073 | << | 0.492±0.167 | 90.2% | = | 89.9% | 23±23 | << | 85±41 |
| Ssan | 0.416±0.114 | = | 0.447±0.141 | 76.5% | << | 91.3% | 27±18 | << | 88±41 |
| Vcho | 0.418±0.079 | << | 0.507±0.112 | 58.3% | << | 65.4% | 22±33 | << | 113±57 |
“ = ” denotes significance of the Mann-Whitney test was within 5%; “>>” denotes that the experimental group was greater than the Geptop group using the Mann-Whitney test at a 5% level; “<<” denotes converse case.
“ = ” denotes that the difference between two groups was within 5%; “>>” denotes that the difference at a significance level of 5% for the experimental group was greater than that for the Geptop group; “<<” denotes converse case.
Essential genes are asymmetrically distributed in leading and lagging strands [27], [28]. We extracted positions of replication origin and terminus for each bacterium from the DoriC database [53], and then genes were assigned to the two replication strand types. In 11 genomes the Geptop group shows more uneven strand distribution (the difference exceeds 5%). Only three genomes with leading strand bias in the experimental group were greater than 5% of the Geptop group. There are still five genomes showing the difference within the 5% level.
Connectivity refers to the number of directly-interacting partners of a protein in protein-protein links [29]. Essential genes are likely to link higher connectivity and to be hubs. Interaction data were obtained from the STRING9 database [54], with a default confidence score cutoff of 0.4. The comparison result illustrated the identical extreme preference of the Geptop essential genes (Mann-Whitney test, p = 10−4–10−47). Average numbers of the protein-protein interaction for the Geptop groups were almost two- to five-fold greater than the average connectivity in the experimental groups. We obtained a very low AUC score when predicting Vibrio cholerae by cross-organism Geptop, but the average connectivity of Geptop group was five-fold higher than experimental group. On the other hand, connectivity of the Geptop group was only twice of that of the other group for another high scoring set of Ecol.
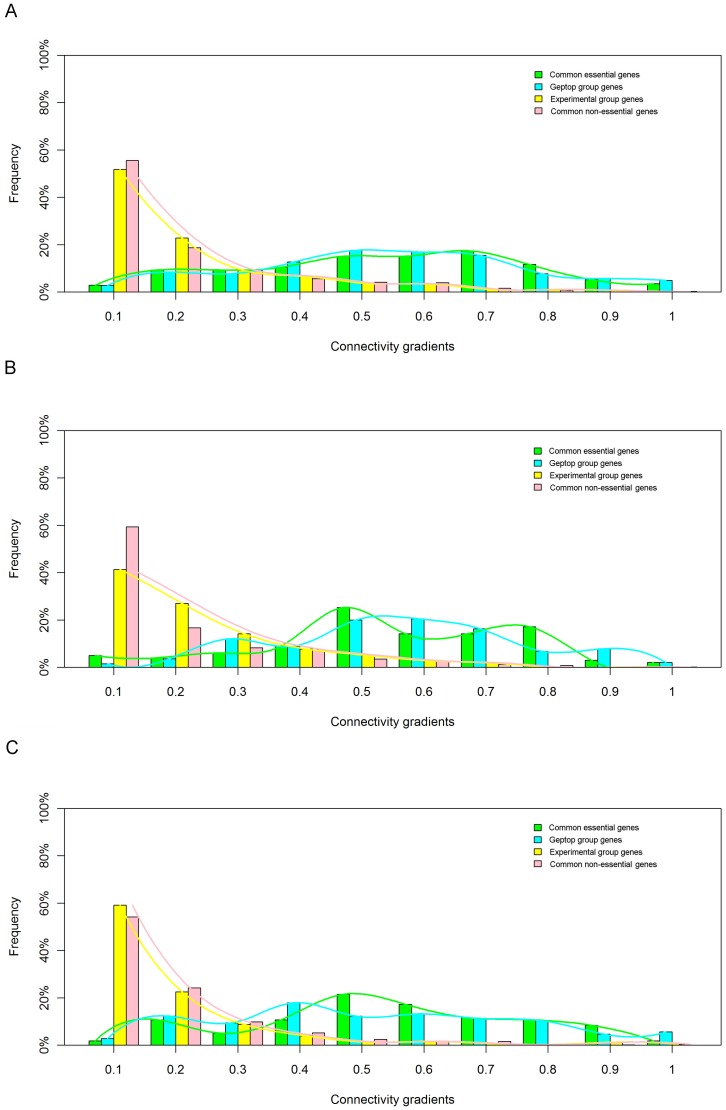
We analyzed the correlation between AUC scores and the multiples of Geptop features over experimental features. Among the above three features, stepwise regression results showed that the AUC scores only related to the feature of connectivity difference (r = −0.533, p = 0.018). Therefore, if a prediction yields a lower AUC score it means that the numbers of protein-protein interactions for the Geptop groups could be significantly greater than the average connectivity of the experimental groups. There were three organisms, (H. influenzae, Helicobacter pylori and V. cholerae), that yielded very low AUC scores of 0.569–0.613. The three predictions lacked lots of essential genes identified by experimental techniques, however, these lacked genes show limited protein-protein interactions. As shown in Figure 8, the distribution of connectivity for the Geptop group was more similar to that for genes identified by both the Geptop and experimental techniques. However, the connectivity distribution of the experimental group was consistent with that of common non-essential genes.
Figure 8. The connectivity distributions of four classes of genes in three bacteria with AUC lower than 0.7.
(a) H. influenza; (b) H. pylori; (c) V. cholera.
Large-scale systematic experiments have provided important information about essential genes in many bacteria. Transposon mutagenesis technique, as the major experimental approach, is likely to mislabel short genes as essential, if insertions have been avoided by chance [9], [55]. The RNAi technique may not silence the expression of an essential gene entirely, but rather “knock down” its expression level [56]. The gene knockout method is the least error-prone approach for identifying essential genes; but this is expensive and time-consuming. The comparison of connectivity between the experimental and the Geptop groups suggested that genes uniquely predicted by the Geptop are more likely to be in protein-protein interaction network hubs, especially in the three organisms with low AUC scores. Moreover, another distinct classifier based on compositional bias also yielded low AUC scores (between 0.587 and 0.724) when predicting the three essential groups whose essential genes had been identified by transposon mutagenesis. In sum, we consider that the experimental identifications of essential genes for these bacteria were not quite accurate, or these genomes have so complex genomic architectures and evolutionary process that those simplistic features (compositional or evolutionary information) did not work well for predicting their essential genes.
In conclusion, our method yielded good AUC scores that are higher than integrative approaches and is expected to be applied widely in every species whose genome has been sequenced. Moreover, the essential genes predicted by the Geptop have more codon bias, distribution bias and abundant protein-protein interactions, which provide further evidence for the reliability of our method. With the availability of more reliable experimental essential sets potentially representing major phylogenetic lineages, the accuracy of our predicting method could be further improved.
Supporting Information
Table S1, Geptop predicted essential genes in Porphyromonas gingivalis. Table S2, Features used in the integrative compositional information predictor. Table S3, Cross-organism test accuracy of the T-iDT.
(DOC)
Acknowledgments
We are indebted to Ms. Dan Lin for critical examining of our results, and to Dr. Xianlong Wang and Dr. Huixiong Zhang for proofing of our manuscript.
Funding Statement
This study was supported by the program for New Century Excellent Talents in University (NCET-11-0059, http://www.moe.gov.cn/), National Natural Science Foundation of China (grant 31071109 and 60801058, http://www.nsfc.gov.cn/), and the special fund of the China Postdoctoral Science Foundation (Grant 201104687, http://res.chinapostdoctor.org.cn/). The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.
References
- 1. Juhas M, Eberl L, Church GM (2012) Essential genes as antimicrobial targets and cornerstones of synthetic biology. Trends Biotechnol 30: 601–607. [DOI] [PubMed] [Google Scholar]
- 2.Acevedo-Rocha CG, Fang G, Schmidt M, Ussery DW, Danchin A (2012) From essential to persistent genes: a functional approach to constructing synthetic life. Trends Genet. [DOI] [PMC free article] [PubMed]
- 3. Mushegian AR, Koonin EV (1996) A minimal gene set for cellular life derived by comparison of complete bacterial genomes. Proc Natl Acad Sci U S A 93: 10268–10273. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4. Shuler ML, Foley P, Atlas J (2012) Modeling a minimal cell. Methods Mol Biol 881: 573–610. [DOI] [PubMed] [Google Scholar]
- 5. Bergmiller T, Ackermann M, Silander OK (2012) Patterns of evolutionary conservation of essential genes correlate with their compensability. PLoS Genet 8: e1002803. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Baba T, Ara T, Hasegawa M, Takai Y, Okumura Y, et al.. (2006) Construction of Escherichia coli K-12 in-frame, single-gene knockout mutants: the Keio collection. Mol Syst Biol 2: 2006 0008. [DOI] [PMC free article] [PubMed]
- 7. de Berardinis V, Vallenet D, Castelli V, Besnard M, Pinet A, et al. (2008) A complete collection of single-gene deletion mutants of Acinetobacter baylyi ADP1. Mol Syst Biol 4: 174. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8. Akerley BJ, Rubin EJ, Novick VL, Amaya K, Judson N, et al. (2002) A genome-scale analysis for identification of genes required for growth or survival of Haemophilus influenzae. Proc Natl Acad Sci U S A 99: 966–971. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9. Liberati NT, Urbach JM, Miyata S, Lee DG, Drenkard E, et al. (2006) An ordered, nonredundant library of Pseudomonas aeruginosa strain PA14 transposon insertion mutants. Proc Natl Acad Sci U S A 103: 2833–2838. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10. Gallagher LA, Ramage E, Jacobs MA, Kaul R, Brittnacher M, et al. (2007) A comprehensive transposon mutant library of Francisella novicida, a bioweapon surrogate. Proc Natl Acad Sci U S A 104: 1009–1014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11. Ji Y, Zhang B, Van SF, Horn, Warren P, et al. (2001) Identification of critical staphylococcal genes using conditional phenotypes generated by antisense RNA. Science 293: 2266–2269. [DOI] [PubMed] [Google Scholar]
- 12. Forsyth RA, Haselbeck RJ, Ohlsen KL, Yamamoto RT, Xu H, et al. (2002) A genome-wide strategy for the identification of essential genes in Staphylococcus aureus. Mol Microbiol 43: 1387–1400. [DOI] [PubMed] [Google Scholar]
- 13. Sakharkar KR, Sakharkar MK, Chow VT (2004) A novel genomics approach for the identification of drug targets in pathogens, with special reference to Pseudomonas aeruginosa. In Silico Biol 4: 355–360. [PubMed] [Google Scholar]
- 14. Dutta A, Singh SK, Ghosh P, Mukherjee R, Mitter S, et al. (2006) In silico identification of potential therapeutic targets in the human pathogen Helicobacter pylori. In Silico Biol 6: 43–47. [PubMed] [Google Scholar]
- 15. Sharma V, Gupta P, Dixit A (2008) In silico identification of putative drug targets from different metabolic pathways of Aeromonas hydrophila. In Silico Biol 8: 331–338. [PubMed] [Google Scholar]
- 16. Barh D, Kumar A (2009) In silico identification of candidate drug and vaccine targets from various pathways in Neisseria gonorrhoeae. In Silico Biol 9: 225–231. [PubMed] [Google Scholar]
- 17. Holman AG, Davis PJ, Foster JM, Carlow CK, Kumar S (2009) Computational prediction of essential genes in an unculturable endosymbiotic bacterium, Wolbachia of Brugia malayi. BMC Microbiol 9: 243. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18. Duffield M, Cooper I, McAlister E, Bayliss M, Ford D, et al. (2010) Predicting conserved essential genes in bacteria: in silico identification of putative drug targets. Mol Biosyst 6: 2482–2489. [DOI] [PubMed] [Google Scholar]
- 19. Juhas M, Stark M, von Mering C, Lumjiaktase P, Crook DW, et al. (2012) High confidence prediction of essential genes in Burkholderia cenocepacia. PLoS One 7: e40064. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20. Juhas M, Eberl L, Glass JI (2011) Essence of life: essential genes of minimal genomes. Trends Cell Biol 21: 562–568. [DOI] [PubMed] [Google Scholar]
- 21. Koonin EV (2003) Comparative genomics, minimal gene-sets and the last universal common ancestor. Nat Rev Microbiol 1: 127–136. [DOI] [PubMed] [Google Scholar]
- 22.Gil R, Silva FJ, Pereto J, Moya A (2004) Determination of the core of a minimal bacterial gene set. Microbiol Mol Biol Rev 68: 518–537, table of contents. [DOI] [PMC free article] [PubMed]
- 23. Edwards JS, Palsson BO (2000) Metabolic flux balance analysis and the in silico analysis of Escherichia coli K-12 gene deletions. BMC Bioinformatics 1: 1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24. Kuepfer L, Sauer U, Blank LM (2005) Metabolic functions of duplicate genes in Saccharomyces cerevisiae. Genome Res 15: 1421–1430. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25. Perumal D, Samal A, Sakharkar KR, Sakharkar MK (2011) Targeting multiple targets in Pseudomonas aeruginosa PAO1 using flux balance analysis of a reconstructed genome-scale metabolic network. J Drug Target 19: 1–13. [DOI] [PubMed] [Google Scholar]
- 26. del Rio G, Koschutzki D, Coello G (2009) How to identify essential genes from molecular networks? BMC Syst Biol 3: 102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27. Rocha EP, Danchin A (2003) Essentiality, not expressiveness, drives gene-strand bias in bacteria. Nat Genet 34: 377–378. [DOI] [PubMed] [Google Scholar]
- 28. Rocha EP, Danchin A (2003) Gene essentiality determines chromosome organisation in bacteria. Nucleic Acids Res 31: 6570–6577. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29. Yu H, Greenbaum D, Xin Lu H, Zhu X, Gerstein M (2004) Genomic analysis of essentiality within protein networks. Trends Genet 20: 227–231. [DOI] [PubMed] [Google Scholar]
- 30. Yu H, Kim PM, Sprecher E, Trifonov V, Gerstein M (2007) The importance of bottlenecks in protein networks: correlation with gene essentiality and expression dynamics. PLoS Comput Biol 3: e59. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31. Gong X, Fan S, Bilderbeck A, Li M, Pang H, et al. (2008) Comparative analysis of essential genes and nonessential genes in Escherichia coli K12. Mol Genet Genomics 279: 87–94. [DOI] [PubMed] [Google Scholar]
- 32. Chen Y, Xu D (2005) Understanding protein dispensability through machine-learning analysis of high-throughput data. Bioinformatics 21: 575–581. [DOI] [PubMed] [Google Scholar]
- 33. Saha S, Heber S (2006) In silico prediction of yeast deletion phenotypes. Genet Mol Res 5: 224–232. [PubMed] [Google Scholar]
- 34. Seringhaus M, Paccanaro A, Borneman A, Snyder M, Gerstein M (2006) Predicting essential genes in fungal genomes. Genome Res 16: 1126–1135. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35. Plaimas K, Eils R, Konig R (2010) Identifying essential genes in bacterial metabolic networks with machine learning methods. BMC Syst Biol 4: 56. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36. Deng J, Deng L, Su S, Zhang M, Lin X, et al. (2011) Investigating the predictability of essential genes across distantly related organisms using an integrative approach. Nucleic Acids Res 39: 795–807. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37. Lin Y, Zhang RR (2011) Putative essential and core-essential genes in Mycoplasma genomes. Sci Rep 1: 53. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38. Tatusov RL, Koonin EV, Lipman DJ (1997) A genomic perspective on protein families. Science 278: 631–637. [DOI] [PubMed] [Google Scholar]
- 39. Rocha EP, Danchin A (2004) An analysis of determinants of amino acids substitution rates in bacterial proteins. Mol Biol Evol 21: 108–116. [DOI] [PubMed] [Google Scholar]
- 40. Drummond DA, Wilke CO (2008) Mistranslation-induced protein misfolding as a dominant constraint on coding-sequence evolution. Cell 134: 341–352. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Chen X, Zhang J (2013) No Gene-Specific Optimization of Mutation Rate in Escherichia coli. Mol Biol Evol. [DOI] [PMC free article] [PubMed]
- 42. Xu Z, Hao B (2009) CVTree update: a newly designed phylogenetic study platform using composition vectors and whole genomes. Nucleic Acids Res 37: W174–178. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43. Zhang R, Lin Y (2009) DEG 5.0, a database of essential genes in both prokaryotes and eukaryotes. Nucleic Acids Res 37: D455–458. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44. Wolf YI, Novichkov PS, Karev GP, Koonin EV, Lipman DJ (2009) The universal distribution of evolutionary rates of genes and distinct characteristics of eukaryotic genes of different apparent ages. Proc Natl Acad Sci U S A 106: 7273–7280. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45. Chen WH, Trachana K, Lercher MJ, Bork P (2012) Younger genes are less likely to be essential than older genes, and duplicates are less likely to be essential than singletons of the same age. Mol Biol Evol 29: 1703–1706. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46. Hwang YC, Lin CC, Chang JY, Mori H, Juan HF, et al. (2009) Predicting essential genes based on network and sequence analysis. Mol Biosyst 5: 1672–1678. [DOI] [PubMed] [Google Scholar]
- 47. Shatkay H, Pan F, Rzhetsky A, Wilbur WJ (2008) Multi-dimensional classification of biomedical text: toward automated, practical provision of high-utility text to diverse users. Bioinformatics 24: 2086–2093. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48. Radivojac P, Clark WT, Oron TR, Schnoes AM, Wittkop T, et al. (2013) A large-scale evaluation of computational protein function prediction. Nat Methods 10: 221–227. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49. Kato J, Hashimoto M (2007) Construction of consecutive deletions of the Escherichia coli chromosome. Mol Syst Biol 3: 132. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50. Klein BA, Tenorio EL, Lazinski DW, Camilli A, Duncan MJ, et al. (2012) Identification of essential genes of the periodontal pathogen Porphyromonas gingivalis. BMC Genomics 13: 578. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51. Singh NK, Selvam SM, Chakravarthy P (2006) T-iDT: tool for identification of drug target in bacteria and validation by Mycobacterium tuberculosis. In Silico Biol 6: 485–493. [PubMed] [Google Scholar]
- 52. Sharp PM, Li WH (1987) The codon Adaptation Index–a measure of directional synonymous codon usage bias, and its potential applications. Nucleic Acids Res 15: 1281–1295. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53. Gao F, Zhang CT (2007) DoriC: a database of oriC regions in bacterial genomes. Bioinformatics 23: 1866–1867. [DOI] [PubMed] [Google Scholar]
- 54. Szklarczyk D, Franceschini A, Kuhn M, Simonovic M, Roth A, et al. (2011) The STRING database in 2011: functional interaction networks of proteins, globally integrated and scored. Nucleic Acids Res 39: D561–568. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55. Gerdes SY, Scholle MD, Campbell JW, Balazsi G, Ravasz E, et al. (2003) Experimental determination and system level analysis of essential genes in Escherichia coli MG1655. J Bacteriol 185: 5673–5684. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56. Elbashir SM, Harborth J, Weber K, Tuschl T (2002) Analysis of gene function in somatic mammalian cells using small interfering RNAs. Methods 26: 199–213. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Table S1, Geptop predicted essential genes in Porphyromonas gingivalis. Table S2, Features used in the integrative compositional information predictor. Table S3, Cross-organism test accuracy of the T-iDT.
(DOC)