Attributable fraction functions for censored event times

Summary

Attributable fractions are commonly used to measure the impact of risk factors on disease incidence in the population. These static measures can be extended to functions of time when the time to disease occurrence or event time is of interest. The present paper deals with nonparametric and semiparametric estimation of attributable fraction functions for cohort studies with potentially censored event time data. The semiparametric models include the familiar proportional hazards model and a broad class of transformation models. The proposed estimators are shown to be consistent, asymptotically normal and asymptotically efficient. Extensive simulation studies demonstrate that the proposed methods perform well in practical situations. A cardiovascular health study is provided. Connections to causal inference are discussed.

1. Introduction

An important task in public health research is to evaluate the impact of risk factors on the occurrence of disease in the population. The population attributable fraction is commonly used for this purpose. First proposed by Levin (1953), the population attributable fraction is defined as ‘the reduction in incidence that would be achieved if the population had been entirely unexposed, compared with its current (actual) exposure pattern’ (Rothman & Greenland, 1998). Unlike relative risk, the population attributable fraction takes into account the prevalence of risk factors in the population and thus quantifies the population impact of risk factors. A related concept is the adjusted attributable fraction, which is the reduction in incidence if a subset of risk factors is eliminated from the population while the other risk factors retain their actual levels. These measures have received considerable attention in recent years (e.g. Benichou, 2001; Greenland, 2001; Silverberg et al., 2004; Graubard & Fears, 2005).

Let D be a binary disease status and Z be a binary exposure indicator. The population attributable fraction is defined as (Levin, 1953)

$$A=\frac{\text{pr}(D=1)-\text{pr}(D=1|Z=0)}{\text{pr}(D=1)}.$$

In the presence of confounding by other risk factors, say W, it is more appropriate to use the adjusted attributable fraction

$$A_{\text{adj}}=\frac{\text{pr}(D=1)-{\sum }_{k=1}^m\text{pr}(W=w_k)\text{pr}(D=1|Z=0,W=w_k),}{\text{pr}(D=1)}$$

where w₁, . . . , w_m are the m levels of W (Whittemore, 1982; Bruzzi et al., 1985).

The aforementioned measures are defined for binary outcomes with time-independent risk factors. Such measures are inadequate for cohort studies that record potentially censored event times and possibly time-dependent risk factors. Chen et al. (2006) extended the population attributable fraction to a population attributable fraction function for event time data by replacing the disease incidence rate with the cumulative distribution function of the event time. They approximated the population attributable fraction function with the so-called attributable hazard function and proposed an estimator for the latter under the proportional hazards model. The two functions can be quite different when the disease is not rare, and the work requires that the censoring time is independent of both the event time and the risk factors.

In the present paper, we study nonparametric and semiparametric estimation of the population attributable fraction function, allowing censoring to depend on the risk factors. The semiparametric estimators are very general in that the model can be proportional hazards or nonproportional hazards and the risk factors can be discrete or continuous and possibly time-dependent. We also extend the adjusted attributable fraction to event time data and develop semiparametric estimators.

2. Inference procedures

2.1. The population attributable fraction function

The population attributable fraction function is defined as

$$A(t)\frac{\text{pr}(T⩽t)-\text{pr}(T⩽t|X=0}{\text{pr}(T⩽t)},$$

where T denotes the time to disease or event time, and X denotes a p-vector of risk factors (Chen et al., 2006). It is convenient to express A(t) in terms of survival functions,

$$A(t)=\frac{S_0(t)-S(t)}{1-S(t)},$$

where S(t) = pr(T > t) and S₀(t) = pr(T > t | X = 0). If S₀(t) and S(t) are estimated by Ŝ₀(t) and Ŝ(t), respectively, then A(t) is naturally estimated by

$$\widehat{A}(t)=\frac{{\widehat{S}}_0(t)-\widehat{S}(t)}{1-\widehat{S}(t)}.$$

Below, we describe various nonparametric and semiparametric estimators for S₀(·) and S(·). In Appendix A, we show that n^1/2{Â(t) – A(t)} converges weakly to a zero-mean Gaussian process with covariance function E{ξ(t)ξ^T(s)} between time-points t and s, where

$$\xi (t)=\frac{1}{1-S(t)}\left\{{\eta }_1(t)-\frac{1-S_0(t)}{1-S(t)}{\eta }_2(t)\right\},$$ (1)

and η₁(t) and η₂(t) depend on the estimation methods for S₀(t) and S(t), respectively. The covariance function can be consistently estimated by $n^{-1}{\sum }_{i=1}^n{\widehat{\xi }}_i(t){\widehat{\xi }}_i^{\text{T}}(s)$, where

$${\widehat{\xi }}_i(t)=\frac{1}{1-\widehat{S}(t)}\left\{{\widehat{\eta }}_{1i}(t)-\frac{1-{\widehat{S}}_0(t)}{1-\widehat{S}(t)}{\widehat{\eta }}_{2i}(t)\right\},$$ (2)

and η̂_1i (t) and η̂_2i (t) are the sample versions of η₁(t) and η₂(t), respectively, for the i th subject.

The above results enable one to construct confidence intervals for A(t). We recommend using the log-transformation log{1 – A(t)}, which not only ensures that the resulting intervals lie in the range (–∞, 1), but also improves the coverage probabilities in small samples.

It is useful to adopt counting process notation. Let N (t) = I {T ⩽ min(C, t)}, and Y (t) = I{min(T, C) ⩾ t}, where C denotes the censoring time, and I(·) is the indicator function. The data consist of n independent replicates {N_i (t), Y_i (t), X_i (t); t ∈ [0, τ]}, where τ is the endpoint of the study. We consider the situation that C is independent of T and X as well as the situation that C is independent of T conditional on X, which are referred to as independent censoring and covariate-dependent censoring, respectively.

When X includes only time-independent categorical covariates, we can estimate S₀(·) by the Kaplan–Meier estimator using the data from the subjects with the baseline covariate values, i.e. X = 0. Then η₁(t) in (1) is given by $-S_0(t){\int }_0^{t}d{M}_0(u)/E\{I(X=0)Y(u)\}$, where $M_0(t)=I(X=0)\{N(t)-{\int }_0^{t}Y(u)d{\mathrm{\Lambda }}_0(u)\}$ and Λ₀(·) = – log{S₀(·)}. The Kaplan–Meier estimator of S₀(·) can be unstable and inefficient if the number of subjects with X = 0 is small.

When X contains continuous or time-dependent covariates, we estimate S₀(·) under a semi-parametric regression model. The familiar proportional hazards model (Cox, 1972) specifies that the cumulative hazard function of T conditional on X takes the form

$$\mathrm{\Lambda }(t|X)={\int }_0^t\text{exp}\{{\beta }^{\text{T}}X(s)\}d{\mathrm{\Lambda }}_0(s),$$

where β is a p-vector of unknown regression parameters and Λ₀(·) is an arbitrary cumulative baseline hazard function. The covariates are assumed to be external in the sense of Kalbfleisch & Prentice (2002, p. 197). We estimate S₀(t) by exp{–Λ̂₀(t)}, where Λ̂₀(t) is the Breslow (1972) estimator of Λ₀(t). Then

$${\eta }_1(t)=-S_0(t)\left[{\int }_0^t\frac{dM(u,\beta )}{E[Y(u)\text{exp}\{{\beta }^{\text{T}}X(u)\}]}-{\int }_0^t{e}^{\text{T}}(u,\beta )d{\mathrm{\Lambda }}_0(u){ℐ}^{-1}(\beta )U(\beta )\right],$$ (3)

where $M(t,\beta )=N(t)-{\int }_0^{t}Y(u)\text{exp}\{{\beta }^{\text{T}}X(u)\}d{\mathrm{\Lambda }}_0(u)$, $U(\beta )={\int }_0^{\tau }\{X(u)-e(u,\beta )\}dM(u,\beta )$, e(t, β) = E[Y (t) exp{β^TX(t)}X(t)]/E[Y (t) exp{β^TX(t)}] and ℐ(β) is the information matrix for β.

Because the proportional hazards assumption may be inappropriate in certain applications, we explore the following class of transformation models:

$$\mathrm{\Lambda }(t|X)=G\left\{{\int }_0^t\text{exp}\{{\beta }^{\text{T}}X(s)\}d{\mathrm{\Lambda }}_0(s)\right\},$$ (4)

where G is a strictly increasing function, β is a vector of unknown regression parameters and Λ₀(·) is an arbitrary increasing function (Zeng & Lin, 2006). If X is time-independent, then (4) reduces to the class of linear transformation models

$$H(T)=-{\beta }^{\text{T}}X+∊,$$

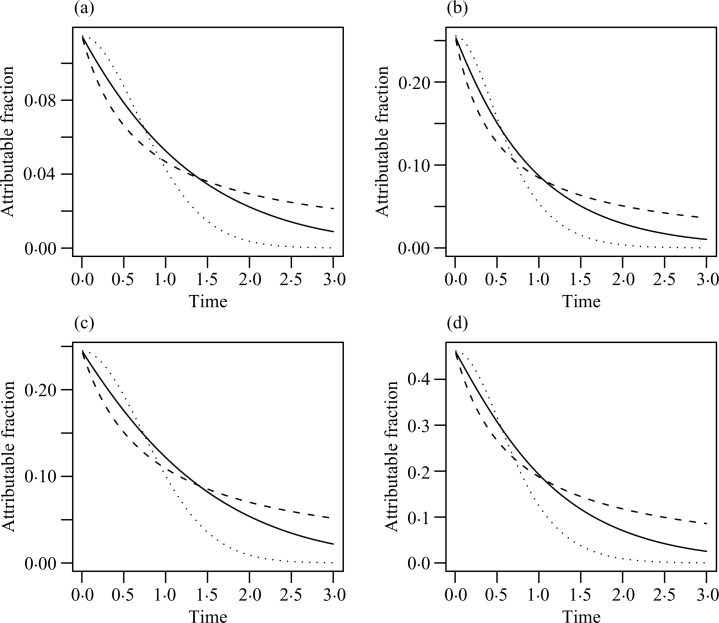
where H is an arbitrary increasing function and ∊ is a random error with a parametric distribution (Dabrowska & Doksum, 1988; Kalbfleisch & Prentice, 2002, p. 241). We consider the class of Box–Cox transformations G(x) = {(1 + x)^ρ– 1}/ρ (ρ ⩾ 0) with ρ = 0 corresponding to G(x) = log(1 + x) and the class of logarithmic transformations G(x) = log(1 + rx)/r (r ⩾ 0) with r = 0 corresponding to G(x) = x. The choice of ρ = 1 or r = 0 yields the proportional hazards model while the choice of ρ = 0 or r = 1 yields the proportional odds model. Figure 1 displays the patterns of the population attributable fraction functions under three transformation models. Not surprisingly, the population attributable fraction increases as the effect of the exposure becomes larger and as the exposure becomes more prevalent.

Fig. 1.

Population attributable fraction functions under transformation models Λ(t | X) = G{t exp(β X)}, where X is Bernoulli with success probability p. (a) corresponds to p = 0.2 and β = 0.5, (b) p = 0.2 and β = 1.0, (c) p = 0.5 and β = 0.5, and (d) p = 0.5 and β = 1.0. The solid, dashed and dotted curves pertain to the proportional hazards model, the proportional odds model and the Box–Cox transformation with ρ = 2, respectively.

Under the transformation models in (4), S₀(t) can be estimated by exp[–G{Λ̂₀(t)}], where Λ̂₀(t) is the nonparametric maximum likelihood estimator of Λ₀(t) (Zeng & Lin, 2006). Then

$${\eta }_1(t)=-S_0(t)G^{\prime }\{{\mathrm{\Lambda }}_0(t)\}({𝒮}_{\beta },{𝒮}_{{\mathrm{\Lambda }}_0}){ℐ}_{\beta ,{\mathrm{\Lambda }}_0}^{-1}\{0,h(\cdot ;t)\},$$ (5)

where (𝒮_β, 𝒮_Λ0) is the score operator for β and Λ₀, ℐ_β,Λ0 is the information operator for β and Λ₀ and h(v; t) = I (v ⩽ t). Here and in the sequel, g^′(x) = dg(x)/dx. In the special case of the proportional hazards model, (5) reduces to (3). We obtain the η̂_1i (t) in (2) as follows. Let t₁ < · · · < t_k be the distinct observed event times. We treat β and the jump sizes of Λ₀ (·) at (t₁, . . . , t_k) as parameters. We calculate the score vector of those parameters for the i th subject, denoted by U_i, and the observed information matrix for those parameters, denoted by ℐ_n. Then η̂_1i is given by $-{\widehat{S}}_0(t)G^{\prime }\{{\widehat{\mathrm{\Lambda }}}_0(t)\}\{0_{p\times 1}^{\text{T}},{\widehat{h}}^{\text{T}}(t)\}{ℐ}_n^{-1}{U}_i$, where ĥ(t) is the vector of indicators I (t_j ⩽ t) (j = 1, . . . , k).

Under the independent censoring assumption, it is natural and simple to estimate S(·) by the Kaplan–Meier method. Then η₂(t) in (1) is given by $-S(t){\int }_0^{t}dM(u)/E\{Y(u)\}$, where $M(t)=N(t)-{\int }_0^{t}Y(u)d\mathrm{\Lambda }(u)$, and Λ(·) = –log{S(·)}. When the independent censoring assumption is violated, the Kaplan–Meier estimator for S(·) is no longer consistent.

Under the covariate-dependent censoring condition, we estimate S(t) by $\widehat{S}(t)=n^{-1}{\sum }_{i=1}^n\widehat{S}(t|X_i)$, where Ŝ (t | x) is a nonparametric or semiparametric estimator of S(t | x) = pr(T > t | X = x). When X only consists of time-independent categorical covariates, S(·| x) can be estimated by the Kaplan–Meier estimator among the subjects with X = x and the corresponding Ŝ(·) is a weighted Kaplan–Meier estimator (Murray & Tsiatis, 1996). Then η₂ (t) = S(t | X) – S(t) + ψ (t; X), where

$$\psi (t;x)=-\text{pr}(X=x)S(t|x){\int }_0^t\frac{dN(u)-Y(u)d\mathrm{\Lambda }(u|x)}{E\{I(X=x)Y(u)\}}.$$

For the general type of X, we adopt the class of transformation models given in (4) and estimate S(t) by $n^{-1}{\sum }_{i=1}^n\text{exp}\left(-G\left[{\int }_0^t\text{exp}\{{\widehat{\beta }}^{\text{T}}{x}_i(u)\}d{\widehat{\mathrm{\Lambda }}}_0(u)\right]\right)$, where β̂ and Λ̂₀(·) are the nonparametric maximum likelihood estimators of β and Λ₀(·). Then

$${\eta }_2(t)=S(t|X)-S(t)+({𝒮}_{\beta },{𝒮}_{{\mathrm{\Lambda }}_0}){ℐ}_{\beta ,{\mathrm{\Lambda }}_0}^{-1}[E\{h_1(t,X)\},[E\{h_2(\cdot ;t,X)\}],$$ (6)

where $h_1(t,x)=-S(t|x)G^{\prime }[{\int }_0^t\text{exp}\{{\beta }^{\text{T}}x(u)\}d{\mathrm{\Lambda }}_0(u)]{\int }_0^t\text{exp}\{{\beta }^{\text{T}}x(u)\}x(u)d{\mathrm{\Lambda }}_0(u)$ and $h_2(\upsilon ;t,x)=-S(t|x)G^{\prime }[{\int }_0^t\text{exp}\{{\beta }^{\text{T}}x(u)\}d{\mathrm{\Lambda }}_0(u)]\text{exp}\{{\beta }^{\text{T}}x(\upsilon )\}I(\upsilon ⩽t)$.

We obtain various estimators of A(·) by combining specific estimators of S₀(·) and S(·). If S₀(·) and S(·) are estimated by the Kaplan–Meier and weighted Kaplan–Meier estimators, respectively, then the resulting estimator of A(·) is referred to as the Kaplan–Meier × weighted Kaplan–Meier estimator; if S₀(·) and S(·) are both estimated under a transformation model, then the resulting estimator of A(·) is referred to as the transformation model × transformation model estimator; other combinations are named in the same way. In Appendix B, we show that the Kaplan–Meier × weighted Kaplan–Meier estimator is asymptotically efficient for the model space satisfying the independent or covariate-dependent censoring assumption and the transformation model × transformation model estimator is asymptotically efficient under model (4).

2.2. Adjusted attributable fraction function

In some applications, the attributable fraction of a particular subset of risk factors is of interest. Suppose that the entire set of risk factors X is decomposed into subsets Z and W, where Z denotes the risk factors of main interest and W denotes the remaining risk factors. For notational simplicity, we assume that the dimensions of Z and W are both 1. We define the adjusted attributable fraction function of Z in the presence of W as

$$A_{\text{adj}}(t)\frac{\text{pr}(T⩽t)-E[\text{pr}\{T⩽t|X={(0,W)}^{\text{T}}\}]}{\text{pr}(T⩽t)},$$

which can also be expressed as

$$A_{\text{adj}}(t)\frac{E[S\{t|{(0,W)}^{\text{T}}\}]-S(t)}{1-S(t)}=\frac{\int S\left\{t\right|{(0,w)}^{\text{T}}\}d{F}_W(w)-S(t)}{1-S(t)},$$

where F_W (·) is the marginal distribution of W . Under model (4), S(t | x) can be estimated by $\widehat{S}(t|x)=\text{exp}(-G[{\int }_0^t\text{exp}\{{\widehat{\beta }}^{\text{T}}x(u)\}d{\widehat{\mathrm{\Lambda }}}_0(u)])$. Then A_adj(t) can be estimated by

$${\widehat{A}}_{\text{adj}}(t)=\frac{n^{-1}{\sum }_{i=1}^n\widehat{S}\left\{t\right|{(0,W_i)}^{\text{T}}\}-\widehat{S}(t)}{1-\widehat{S}(t)},$$

where W_i is the observation of W on the i th subject. In Appendix A, we show that n^1/2{Â_adj(t) – A_adj(t)} converges weakly to a zero-mean Gaussian process with covariance function E{ξ(t) ξ^T(s)} at (t, s), where

$$\xi (t)=\frac{1}{1-S(t)}\left\{{\eta }_1(t)-\frac{1-E[S\{t\left|{(0,W)}^{\text{T}}\right\}]}{1-S(t)}{\eta }_2(t)\right\},$$ (7)

η₁(t) is expression (6) with X = (0, W)^T, and η₂(t) is determined by the estimation method for S(·). Under independent censoring, S(·) can simply be estimated by the Kaplan–Meier method and η₂(t) is equal to $-S(t){\int }_0^{t}dM(u)/E\{Y(u)\}$. In the case of covariate-dependent censoring, S(t) can be estimated by $n^{-1}{\sum }_{i=1}^n\text{exp}(-G[{\int }_0^t\text{exp}\{{\widehat{\beta }}^{\text{T}}{X}_i(u)\}d{\widehat{\mathrm{\Lambda }}}_0(u)])$ under model (4), and η₂(t) is given in (6). The variance estimator for Â_adj(·) and the confidence intervals for A_adj(·) can be obtained in the same manner as in the case of A(·).

2.3. Causal interpretation

Let T be the observed event time, and let T (z) be the potential event time if the exposure Z has value z. We define the function

$$A(t)\frac{\text{pr}(T⩽t)-\text{pr}\{T(0)⩽t\}}{\text{pr}(T⩽t)},$$

which is the proportionate reduction of the incidence by t if the entire population were unexposed, i.e. Z = 0. To connect pr{T (0) ⩽ t} to the observed outcome T, we make the following two assumptions.

Assumption 1. No unobserved confounders: conditional on all observed confounders W, Z is independent of {T (z)}.

Assumption 2. Stable unit treatment value assumption: T = ∑_z T (z)I (Z = z).

These assumptions are standard in causal inference (e.g. Rubin, 1978; Pearl, 2000, pp. 98–103). Under Assumption 1, pr{T (0) ⩽ t} = E_W [pr{T (0) ⩽ t | W }] = E_W [pr{T (0) ⩽ t | Z = 0, W}]. It follows from Assumption 2 that pr{T (0) ⩽ t} = E_W {pr(T ⩽ t | Z = 0, W)}. Thus, A(t) becomes the adjusted attributable fraction function of § 2.2:

$$A_{\text{adj}}(t)\frac{\text{pr}(T⩽t)-E_W\{\text{pr}(T⩽t|Z=0,W)\}}{\text{pr}(T⩽t)}.$$

If the marginal distribution of W is the same as the conditional distribution of W under Z = 0 or, more specifically, Z is independent of W, then E_W {pr(T ⩽ t | Z = 0, W)} = pr(T ⩽ t | Z = 0). Consequently,

$$A(t)\frac{\text{pr}(T⩽t)-\text{pr}(T⩽t|Z=0)}{\text{pr}(T⩽t)},$$

which is the population attributable fraction function of § 2.1 upon setting Z to X.

3. Simulation studies

To assess the performance of the proposed estimators for the population attributable fraction function under independent censoring, we generated event times from the transformation model Λ(t | X) = G{0.1t exp(β X)}, where X is Bernoulli with success probability 0.4, and G is the Box–Cox transformation with ρ =1, 2 or the logarithmic transformation with r =1, 2. We generated censoring times from the Un(0, τ) distribution, where t was chosen to yield a censoring rate of approximately 70%. We generated 10 000 replicates with n =1000. Since censoring is independent and X is binary, all four estimators of A(·) can be used. Table 1 summarizes the results for the Kaplan–Meier × weighted Kaplan–Meier and transformation model × transformation model estimators of A(t) at t = τ/4, τ/2, 3τ/4 and t under β = 1.0. The transformation model × transformation model estimator performs very well: the estimator is virtually unbiased, its variance estimator accurately reflects the true variation and the confidence intervals have proper coverage probabilities. The Kaplan–Meier × weighted Kaplan–Meier estimator performs very well when t is not near τ . As expected, the former estimator is more efficient than the latter. The results for the Kaplan–Meier × Kaplan–Meier and transformation model × Kaplan–Meier estimators are almost the same as those of the Kaplan–Meier × weighted Kaplan–Meier and transformation model × transformation model estimators, respectively, and are thus omitted.

Table 1.

Simulation results for the estimation of A(·) with independently censored data

		Kaplan–Meier × weighted Kaplan–Meier				transformation model × transformation model
Model	Parameter	Bias	sse	see	cp(%)	Bias	sse	see	cp(%)
ρ= 2	A(τ/4)	0.000	0.063	0.062	94.3	0.000	0.040	0.040	94.7
	A(τ/2)	0.000	0.046	0.046	95.1	0.000	0.039	0.038	94.7
	A(3τ/4)	0.001	0.042	0.041	94.4	0.000	0.037	0.036	94.7
	A(τ)	0.001	0.063	0.050	89.6	0.000	0.038	0.036	94.2
ρ= 1	A(τ/4)	0.000	0.060	0.059	94.7	−0.000	0.043	0.042	94.6
	A(τ/2)	0.000	0.046	0.045	95.0	−0.000	0.040	0.039	94.5
	A(3τ/4)	0.000	0.043	0.042	94.4	0.000	0.036	0.036	94.5
	A(τ)	0.001	0.062	0.050	89.9	0.001	0.036	0.035	94.6
r = 1	A(τ/4)	0.000	0.056	0.055	94.3	−0.001	0.047	0.046	94.5
	A(τ/2)	0.000	0.044	0.044	94.6	−0.000	0.040	0.039	94.5
	A(3τ/4)	0.001	0.043	0.042	94.6	0.000	0.034	0.034	94.4
	A(τ)	0.001	0.061	0.050	91.4	0.001	0.033	0.032	94.4
r = 2	A(τ/4)	0.000	0.054	0.053	94.5	−0.000	0.048	0.047	94.4
	A(τ/2)	0.000	0.044	0.044	94.7	0.000	0.038	0.038	94.6
	A(3τ/4)	0.001	0.043	0.042	94.7	0.000	0.033	0.032	94.4
	A(τ)	0.002	0.059	0.050	92.1	0.001	0.031	0.030	94.4

Bias, the sampling bias; sse, the sampling standard error; see, the sampling mean of the standard error estimator; cp, the coverage probability of the 95% Wald confidence interval.

To evaluate the performance of the estimators for the population attributable fraction function under covariate-dependent censoring, we modified the above set-up by generating censoring times from the proportional hazards model Λ(t | X) = 0.1t exp(1.5X). Table 2 shows the results based on 10 000 replicates under the proportional hazards model for the event time with β = 1.0 and n = 1000. The Kaplan–Meier × weighted Kaplan–Meier and transformation model × transformation model estimators have excellent performance. The Kaplan–Meier × Kaplan–Meier and transformation model × Kaplan–Meier estimators, which require independent censoring, are severely biased.

Table 2.

Simulation results for the estimation of A(·) with dependently censored data

	Kaplan–Meier × weighted Kaplan–Meier				Kaplan–Meier × Kaplan–Meier
Parameter	Bias	sse	see	cp(%)	Bias	sse	see	cp(%)
A(τ/4)	−0.000	0.067	0.066	94.8	−0.023	0.065	0.064	91.3
A(τ/2)	0.000	0.049	0.049	94.9	−0.043	0.046	0.045	80.3
A(3τ/4)	0.000	0.042	0.042	95.0	−0.060	0.037	0.036	57.5
A(τ)	−0.000	0.039	0.038	94.8	−0.073	0.031	0.031	31.7
	transformation model × transformation model				transformation model × Kaplan–Meier
Parameter	Bias	sse	see	cp(%)	Bias	sse	see	cp(%)
A(τ/4)	−0.000	0.044	0.044	94.8	−0.023	0.043	0.043	91.8
A(τ/2)	0.000	0.041	0.041	94.8	−0.043	0.039	0.039	78.7
A(3τ/4)	0.000	0.038	0.038	94.9	−0.060	0.034	0.034	56.9
A(τ)	−0.000	0.035	0.034	95.0	−0.072	0.030	0.030	32.4

Bias, the sampling bias; sse, the sampling standard error; see, the sampling mean of the standard error estimator; cp, the coverage probability of the 95% Wald confidence interval.

To evaluate the performance of the proposed estimators for the adjusted attributable fraction function, we generated event times from the transformation model Λ(t | X) = G{0.1t exp(β₁ X₁ + β₂ X₂)}, where X₁ is Bernoulli with success probability 0.4, and X₂ is normal with mean X₁ and variance 1. We generated censoring times from the Un(0, τ) distribution to create censoring rates of approximately 70%. The goal was to estimate the adjusted attributable fraction function of X₁ in the presence of X₂. Table 3 provides the summary statistics for the transformation model × transformation model estimator based on 10 000 replicates with (β₁, β₂) = (1.0, 0.5) and n = 1000. The estimator performs very well. The results for the transformation model × Kaplan–Meier estimator are almost the same and are thus omitted.

Table 3.

Simulation results for the transformation model × transformation model estimator of A_adj(·)

	Box–Cox transformation models
	ρ = 2				ρ = 1
Parameter	Bias	sse	see	cp(%)	Bias	sse	see	cp(%)
Aadj(τ/4)	−0.001	0.046	0.046	94.9	−0.001	0.050	0.049	94.9
Aadj(τ/2)	−0.001	0.045	0.045	95.0	−0.001	0.047	0.046	94.7
Aadj(3τ/4)	−0.000	0.044	0.044	94.7	−0.001	0.043	0.043	94.6
Aadj(τ)	0.001	0.046	0.043	94.0	0.001	0.043	0.041	94.2
	Logarithmic transformation models
	r = 2				r = 1
Parameter	Bias	sse	see	cp(%)	Bias	sse	see	cp(%)
Aadj(τ/4)	−0.002	0.054	0.053	94.6	−0.002	0.053	0.052	94.7
Aadj(τ/2)	−0.001	0.043	0.043	94.9	−0.001	0.045	0.044	94.8
Aadj(3τ/4)	−0.000	0.037	0.037	95.0	−0.000	0.039	0.039	95.0
Aadj(τ)	0.001	0.034	0.034	94.5	0.001	0.037	0.036	94.1

Bias, the sampling bias; sse, the sampling standard error; see, the sampling mean of the standard error estimator; cp, the coverage probability of the 95% Wald confidence interval.

4. Example

We consider the Cardiovascular Health Study (Fried et al., 1991), which is a population-based cohort study of cardiovascular diseases in adults aged 65 years and older. The subjects were recruited from four US field centres. The major events of interest include myocardial infarction, stroke and cardiovascular disease mortality. A key objective of this study was to determine the importance of conventional cardiovascular disease risk factors on the time to the first occurrence of the major events in the Caucasian population. There are 3907 Caucasian subjects in the study, 27% of whom have experienced at least one of the three major events. We consider ten baseline covariates: age, sex, hypertension, body mass index, systolic blood pressure, smoking status, diabetes status and three dummy variables comparing the four field centres, and estimate the attributable fraction functions for hypertension and diabetes.

To assess the independent censoring assumption, we fit a proportional hazards model for the censoring time with the aforementioned ten baseline covariates. Censoring appears to be strongly associated with covariates, the standard-normal test statistics being 14.42, 2.76, 4.29 and 4.48 for age, systolic blood pressure, smoking status and diabetes, respectively. Thus, we allow censoring to depend on covariates in our analysis.

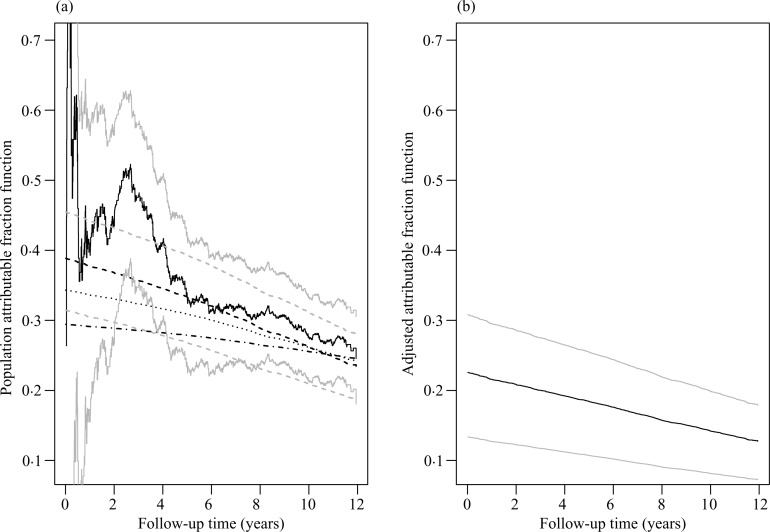
First, we estimate the population attributable fraction function of hypertension without adjusting for any other covariates. We try the proportional hazards model with hypertension as the only covariate. The proportional hazards assumption does not seem appropriate, the test of proportionality based on the score process (Lin et al., 1993) having a p-value of 0.038. We fit the Box–Cox transformation models with ρ = 2, 1, 0.5 and the logarithmic transformation models with r = 0.5, 1, 2. Using the Akaike information criterion (Akaike, 1985), we select the logarithmic transformation model with r = 2. Under this model, the regression coefficient for hypertension is estimated at 0.436 with an estimated standard error of 0.045. Figure 2(a) compares the estimates of the population attributable fraction function based on the nonparametric and semiparametric methods. The estimated population attributable fraction curve under the selected transformation model agrees well with the nonparametric curve, but with narrower confidence intervals. The estimated population attributable fraction curves under the proportional hazards and proportional odds models, especially the former, are considerably lower than those of the selected transformation model and the nonparametric method.

Fig. 2.

Estimation of attributable fraction functions for hypertension in the Cardiovascular Health Study. Panel (a) shows the estimates of the population attributable fraction function: the dark solid and dark dashed curves pertain to the point estimates by the nonparametric method and under the selected transformation model, respectively; the light solid and light dashed curves show the corresponding 95% confidence limits; the dotted and dash-dotted curves pertain to the point estimates under the proportional odds and proportional hazards models, respectively. Panel (b) shows the point estimate of the adjusted attributable fraction function and the corresponding 95% confidence limits.

Next, we estimate the adjusted attributable fraction function of hypertension. We include all ten baseline covariates in the Box–Cox transformation models with ρ = 2, 1, 0.5 and the logarithmic transformation models with r = 0.5, 1, 2. The Akaike information criterion selects the logarithmic transformation model with r = 1, i.e. the proportional odds model. The estimates of regression coefficients under the selected model are shown in Table 4. The corresponding estimate of the adjusted attributable fraction function is shown in Fig. 2(b). The adjusted attributable fraction curve is considerably lower than the population attributable fraction curve. The difference is mainly due to the high correlation between hypertension and systolic blood pressure and the strong effect of systolic blood pressure on the event time.

Table 4.

Analysis of time to the first major event in the Cardiovascular Health Study under the proportional odds model

Parameter	Estimate	se	Estimate/se	p-value
Age	0.103	0.007	15.247	<0.0001
Gender	0.512	0.075	6.840	<0.0001
Hypertension	0.215	0.045	4.732	<0.0001
Body mass index	0.007	0.009	0.833	0.405
Blood pressure > 128	0.496	0.089	5.579	<0.0001
Smoking	0.553	0.118	4.679	<0.0001
Diabetes	0.657	0.102	6.458	<0.0001
Centres 2 vs. 1	−0.051	0.104	−0.491	0.623
Centres 3 vs. 1	0.051	0.103	0.496	0.620
Centres 4 vs. 1	−0.218	0.111	−1.961	0.050

se, standard error.

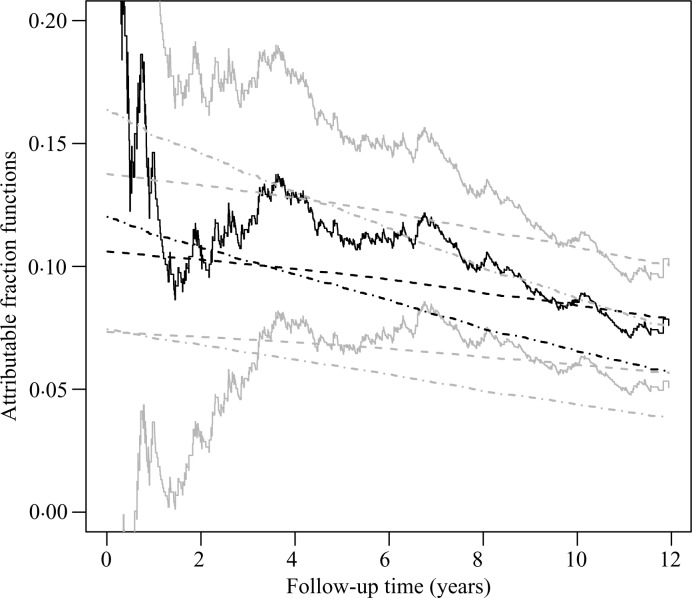
To estimate the population attributable fraction function of diabetes, we fit the proportional hazards model with diabetes as the only covariate. The proportional hazards assumption appears reasonable: the test of proportionality based on the score process (Lin et al., 1993) has a p-value of 0.092, and the Breslow estimate of the baseline survival function is very close to its Kaplan–Meier counterpart. The estimate of the regression coefficient under the proportional hazards model is 0.642, with an estimated standard error of 0.079. As shown in Fig. 3, the estimated population attributable fraction curve under the proportional hazards model agrees well with its Kaplan–Meier counterpart but is less variable.

Fig. 3.

Estimation of attributable fraction functions for diabetes in the Cardiovascular Health Study. The dark solid and dark dashed curves pertain to the point estimates of the population attributable fraction function by the nonparametric method and under the proportional hazards model, respectively; the dark dash-dotted curve pertains to the point estimate of the adjusted attributable fraction function; the light curves show the 95% confidence limits.

To estimate the adjusted attributable fraction function of diabetes, we adopt the proportional odds model shown in Table 4. As evident from Fig. 3, the adjusted attributable fraction curve for diabetes starts higher than its unadjusted counterpart and decreases more rapidly over time.

It is interesting to compare the attributable fraction functions of hypertension and diabetes. Diabetes has a stronger effect on the event time, and yet hypertension has much higher population attributable fraction values than diabetes at all time-points. The reason is that hypertension is much more prevalent than diabetes: the proportions of subjects with 0, 1 and 2 levels of hypertension are 0.453, 0.150 and 0.398, respectively, whereas the prevalence of diabetes is 0.132.

5. Discussion

The assumption on the censoring mechanism is critical to the estimation of attributable fraction functions because the Kaplan–Meier estimator for the marginal survival function is inconsistent when censoring depends on covariates. To deal with covariate-dependent censoring, we construct new estimators for the marginal survival function under a broad class of semiparametric transformation models and establish their asymptotic properties. These estimators are useful beyond the context of attributable fraction functions. Shen & Fleming (1997) studied an estimator for the special case of the proportional hazards model with time-independent covariates.

There has been a tremendous recent interest in transformation models with censored data. These models can greatly improve the accuracy of prediction over the proportional hazards model, but the regression parameters do not have simple interpretations outside the proportional hazards and proportional odds models. In the context of attributable fraction functions, the primary interest lies in the prediction rather than the regression parameters. Thus, transformation models are particularly attractive in our setting.

We have confined our attention to pointwise confidence limits for A(·) and A_adj(·), as opposed to confidence bands. Because the proposed estimators can be expressed as sums of independent terms at each time-point in the form of (1) or (7), the Monte Carlo approach of Lin et al. (1994) can be used to construct confidence bands. Unfortunately, attributable fraction functions involve ratios of probabilities and are thus intrinsically difficult to estimate well, even with large cohorts. Thus, the confidence bands would be too wide to be practically useful.

When X contains only categorical variables, one can estimate the baseline survival function S₀(·) by the Kaplan–Meier estimator or under a semiparametric regression model. The former estimator is model-free, but can be highly unstable and inefficient when the number of subjects with X = 0 is small. The latter is more efficient, but less robust. Because of the intrinsic difficulties in estimating attributable fraction functions, it is generally preferable to adopt a semiparametric estimator for S₀(·). The use of transformation models entails greater robustness of inference, as opposed to indiscriminate application of the proportional hazards model.

We have assumed implicitly that the data come from a random sample of the underlying population. If the sampling depends on the exposure level, then the baseline survival function S₀(·) can still be estimated in the same manner as before, but the estimation of the marginal survival function S(·) needs to be adjusted. Specifically, we can estimate S(t) by ${\sum }_{i=1}^n{p}_i^{-1}\widehat{S}(t|X_i)/{\sum }_{i=1}^n{p}_i^{-1}$, where p_i is the selection probability for the i th study subject. The variance estimators can be modified accordingly.

Appendix A

Weak convergence of n^1/2 {Â(·) – A(·)} and n^1/2 {Â_adj(·) – A_adj(·)}

We prove the weak convergence of n^1/2{Â(·) – A(·)} through modern empirical process theory. The proof for n^1/2{Â_adj(·) – A_adj(·)} is similar and thus omitted. Let 𝒫_n and P denote the empirical measure and the distribution under the true model, respectively. For a measurable function f and measure Q, the integral ∫ f d Q is abbreviated as Q f . We impose the following regularity conditions.

Condition A1. The function Λ₀(·) is strictly increasing and continuously differentiable, and β lies in the interior of a compact set 𝒞.

Condition A2. With probability 1, X(·) is bounded and has uniformly bounded total variation in [0, τ ]. In addition, if there exist a vector γ and a deterministic function γ₀(t) such that γ₀(t) + γ ^TX(t) = 0 with probability 1, then γ = 0 and γ₀(t) = 0.

Condition A3. With probability 1, there exists a positive constant d such that pr(C ⩾t | X) > δ and pr{Y (t) = 1 | X} >δ.

Condition A4. For any sequence 0 < x₁ < · · · < x_m ⩽y, ${\prod }_{l=1}^m\{(1+x_l)G^{\prime }(x_l)\}\text{exp}\{-G(y)\}<{\mu }_0^m{(1+y)}^{-\infty }$, where α₀ and μ₀ are positive constants. This condition is satisfied by the classes of Box–Cox transformations and logarithmic transformations.

Clearly,

$$n^{1/2}\{\widehat{A}(t)-A(t)\}=\frac{n^{1/2}\{{\widehat{S}}_0(t)-S_0(t)\}}{1-\widehat{S}(t)}-\frac{1-S_0(t)}{\{1-S(t)\}\{1-\widehat{S}(t)\}}{n}^{1/2}\{\widehat{S}(t)-S(t)\}.$$

We shall show that n^1/2{ Ŝ(t) – S₀(t) and n^1/2{Ŝ(t) – S(t)} are asymptotically equivalent to n^1/2(𝒫_n – P)η₁(t) and n^1/2 (𝒫_n – P)η₂(t), respectively, where η₁(t) and η₂(t) depend on the estimation methods for S₀(·) and S(·), respectively. It will then follow that n^1/2{Â(t) – A(t)} converges weakly to a zero-mean Gaussian process and is asymptotically equivalent to

$$n^{1/2}({𝒫}_n-P)\frac{1}{1-S(t)}\left\{{\eta }_1(t)-\frac{1-S_0(t)}{1-S(t)}{\eta }_2(t)\right\}.$$

The asymptotic equivalence is defined in the metric space l^∞ [0, τ].

The main task is to establish the weak convergence of n^1/2{Ŝ(·) – S(·)}. Under independent censoring, Ŝ(·) is the Kaplan–Meier estimator. Then n^1/2{Ŝ(t) – S(t)} is asymptotically equivalent to

$$-n^{1/2}({𝒫}_n-P)S(t){\int }_0^t\frac{dM(u)}{E\{Y(u)\}}.$$

Under covariate-dependent censoring, $\widehat{S}(t)=n^{-1}{\sum }_{i=1}^n\widehat{S}(t|X_i)$, where Ŝ(t | x) is an estimator of S(t | x), which can be obtained by the Kaplan–Meier method or under the class of transformation models given in (4). We make use of the following representation:

$$\begin{array}{ll}{n}^{1/2}\{\widehat{S}(t)-S(t)\}=\hfill & n^{1/2}({𝒫}_n-P)\{S(t|X)-PS(t|X)\}\hfill \\ \hfill & +P{n}^{1/2}\widehat{S}(t|X)-S(t|X)\}+n^{1/2}({𝒫}_n-P)\{\widehat{S}(t|X)-S(t|X)\},\hfill \end{array}$$ (A1)

where the expectations 𝒫_n Ŝ(t | X) and P Ŝ(t | X) are taken with respect to X.

If Ŝ(t | x) is the Kaplan–Meier estimator of the survival function among the subjects with X = x, then n^1/2{Ŝ(t | x) – S(t | x)} is asymptotically equivalent to

$$-n^{1/2}({𝒫}_n-P)S(t|x)I(X=x){\int }_0^t\frac{dN(u)-Y(u)d\mathrm{\Lambda }(u|x)}{E\{I(X=x)Y(u)\}}.$$

This result, together with the fact that X has a finite number of categories, implies that the second term on the right-hand side of (A1) is asymptotically equivalent to

$$\begin{array}{l}{E}_X{\left[-n^{1/2}({𝒫}_n-P)S(t|x)I(X=x){\int }_0^t\frac{dN(u)-Y(u)d\mathrm{\Lambda }(u|x)}{E\{I(X=x)Y(u)\}}\right]|}_{x=X}\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}={n^{1/2}({𝒫}_n-P)\left(-E_X{\left[S(t|x)I(y=x){\int }_0^t\frac{dN(u)-Y(u)d\mathrm{\Lambda }(u|x)}{E\{I(X=y)Y(u)\}}\right]|}_{x=X}\right)|}_{y=X}\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}={n^{1/2}({𝒫}_n-P)\left[-\text{pr}(X=y)S(t|y){\int }_0^t\frac{dN(u)-Y(u)d\mathrm{\Lambda }(u|y)}{E\{I(X=x)Y(u)\}}\right]|}_{y=X},\end{array}$$

where E_X denotes expectation with respect to X.

Under the class of transformation models given in (4), $S(t|x)=\text{exp}(-G[{\int }_0^t\text{exp}\{{\beta }^{\text{T}}x(u)\}d{\mathrm{\Lambda }}_0(u)])$ and $\widehat{S}(t|x)=\text{exp}(-G[{\int }_0^t\text{exp}\{{\widehat{\beta }}^{\text{T}}x(u)\}{\widehat{\mathrm{\Lambda }}}_0(u)])$. It can be shown that for any x (·) with bounded total variation, S(·| x) is Hadamard-differentiable with respect to β and Λ₀(·). It then follows from simple algebraic manipulations that n^1/2{Ŝ(t | x) – S(t | x)} is asymptotically equivalent to

$$n^{1/2}{(\widehat{\beta }-\beta )}^{\text{T}}{h}_1(t,x)+n^{1/2}{\int }_0^{\infty }{h}_2(u;t,x)d({\widehat{\mathrm{\Lambda }}}_0-{\mathrm{\Lambda }}_0)(u),$$

which in turn is asymptotically equivalent to $n^{1/2}({𝒫}_n-P)({𝒮}_{\beta },{𝒮}_{{\mathrm{\Lambda }}_0}){ℐ}_{\beta ,{\mathrm{\Lambda }}_0}^{-1}\{h_1(t,x),h_2(\cdot ;t,x)\}$. Since X(·) has uniformly bounded total variation, this asymptotic equivalence is uniform for X(·). Thus, the second term on the right-hand side of (A1) is asymptotically equivalent to

$$n^{1/2}({𝒫}_n-P)({𝒮}_{\beta },{𝒮}_{{\mathrm{\Lambda }}_0})I_{\beta ,{\mathrm{\Lambda }}_0}^{-I}\{E{h}_1(t,X),E{h}_2(\cdot ;t,X)\}.$$

We can verify that P{Ŝ(t | X) – S(t | X)}² →_p 0 uniformly for t ∈ [0, t ] and that Ŝ(t | X) and S(t | X) belong to a P-Donsker class (van der Vaart & Wellner, 1996, § 2.10). It then follows that the third term on the right-hand side of (A1) converges uniformly to zero in probability by Lemma 19.24 of van der Vaart (1998).

Combining the results of the above five paragraphs, we conclude that n^1/2{Ŝ(t) – S(t)} is asymptotically equivalent to n^1/2(𝒫_n – P) η₂(t), where η₂(t) is given in § 2.1. Since n^1/2 {Ŝ₀(t) – S₀(t)} is a special case of n^1/2{Ŝ(t | x) – S(t | x)} with x = 0, the weak convergence of the former follows from that of the latter.

Appendix B

Asymptotic efficiency of the Kaplan–Meier × weighted Kaplan–Meier and transformation model × transformation model estimators

We first establish the asymptotic efficiency of the Kaplan–Meier × weighted Kaplan–Meier estimator. Suppose that X contains only categorical covariates with possible values x₁, . . . , x _J . Let F (·) denote the distribution function of X. We consider the model space 𝒫 = {P: C is independent of T and X } or 𝒫 = {P: C is independent of T given X}. The likelihood is the product of three terms: the first term pertains to the likelihood for the conditional distribution of T given X, the second term to the likelihood for the conditional distribution of C given X and the third term to the likelihood for the distribution of X. Thus, the empirical distribution function of X is an efficient estimator of F(·). Because the first term can be written as the product of the likelihoods for the conditional survival functions of T given X = x _j (j = 1, · · ·, J), the Kaplan–Meier estimator among the subjects with X = x _j is an efficient estimator for S(· | x _j). It can be shown that A(t) is Hadamard-differentiable with respect to S(t | x) and F(x). Hence, the Kaplan–Meier × weighted Kaplan–Meier estimator for A(·) is asymptotically efficient by Theorem 25.47 of van der Vaart (1998).

We now establish the asymptotic efficiency of the transformation model × transformation model estimator. We consider the model space 𝒫 = {P: C is independent of T and X, and the transformation model (4) holds} or 𝒫 = {P: C is independent of T given X, and the transformation model (4) holds}. The likelihood is the product of three terms: the first term pertains to the likelihood for the parameters (β, Λ₀), the second term to the likelihood for the distribution of C given X and the third term to the likelihood for the distribution of X. This implies that the empirical distribution function of X is asymptotically efficient. The maximization of the first term yields the nonparametric maximum likelihood estimators β̂ and Λ^₀. The asymptotic efficiency of β̂₀, was proved in Zeng & Lin (2006). To establish the asymptotic efficiency of Λ^_0, we define ℱ = {w(t) : ||w||_{BV [0τ]} ⩽ 1}, where ||w||_{BV [0,t]} denotes the total variation of w(·) in [0, τ ]. For any t, there exists {w(·), β} ∈ ℱ × ℛ^p such that

$$n^{1/2}\{{\widehat{\mathrm{\Lambda }}}_0(t)-{\mathrm{\Lambda }}_0(t)\}=n^{1/2}{𝒫}_n\left[l_{{\mathrm{\Lambda }}_0}\left\{\int w(s)d{\mathrm{\Lambda }}_0(s)\right\}+l_{\beta }^{\text{T}}b\right],$$

where $l_{{\mathrm{\Lambda }}_0}\{\int w(s)d{\mathrm{\Lambda }}_0(s)\}+l_{\beta }^{\text{T}}b$ is the score function along the path {Λ₀+ ∊ ∫ w(s)dΛ₀(s), β + ∊b} (Zeng & Lin, 2006). In addition, {I (· ⩽ t) : t ∈ [0, τ ]} is a Donsker class. It then follows from Theorem 18.9 of Kosorok (2008) that Λ̂₀(·) is asymptotically efficient. Because A(·) is a function of β, Λ₀(·) and F(·) and is Hadamard-differentiable, the transformation model × transformation model estimator for A(·) is asymptotically efficient by Theorem 25.47 of van der Vaart (1998).