Youth Aggressive/Disruptive Behavior Trajectories and subsequent Gambling among Urban Male Youth

Abstract

Objective

This study examines the association between aggressive/disruptive behavior development in two distinct developmental periods, childhood (i.e., grades 1–3) and early adolescence (i.e., grades 6–10) and subsequent gambling behavior in late adolescence up to age 20.

Method

The sample consists of 310 urban males of predominately minority and low socioeconomic status followed from first grade to late adolescence. Separate general growth mixture models (GGMM) were estimated to explore the heterogeneity in aggressive/disruptive behavior development in the above-mentioned two time periods.

Results

Three distinct behavior trajectories were identified for each time period: a chronic high, a moderate increasing and a low increasing class for childhood, and a chronic high, a moderate increasing followed by decreasing and a low stable class for early adolescence. There was no association between childhood behavior trajectories and gambling involvement. Males with a moderate behavior trajectory in adolescence where two times more likely to gamble compared to those in the low stable class (OR=1.89, 95% CI=1.11, 3.24). Those with chronic high trajectories during either childhood or early adolescence (OR=2.60, 95% CI=1.06, 6.38; OR=3.19, 95% CI=1.18, 8.64, respectively) were more likely to be at-risk/problem gamblers than those in the low class.

Conclusions

Aggressive/disruptive behavior development in childhood and early adolescence is associated with gambling and gambling problems in late adolescence among urban male youth. Preventing childhood and youth aggressive/disruptive behavior may be effective to prevent youth problem gambling.

Youth problem gambling is widespread and associated with a broad range of high-risk behaviors such as delinquency and substance use (Barnes, Welte, Hoffman, & Dintcheff, 2005; Barnes, Welte, Hoffman, & Tidwell, 2009; Winters, Stinchfield, & Fulkerson, 1993), and thus is of high public health concern. Past literature has evidenced a cross-sectional association between aggressive/disruptive behavior and gambling/problem gambling among youth and adults (Goldstein, Walton, Cunningham, Resko, & Duan, 2009; Korman et al., 2007; Liao, 2008; McCormick, 1993; Mishra, Lalumiére, Morgan, & Williams, 2011; Parke & Griffiths, 2004; Slutske, Caspi, Moffitt, & Poulton, 2005; Stinchfield, 2000; Rahman et al., 2012; Yip et al., 2011). Moreover, both gambling (especially problem gambling) and aggressive/disruptive behavior share similar antecedents such as limited decision-making and low behavioral control (Martin-Storey, Serbin, Slack, Ledingham, & Schwartzman, 2011; Slutske, Moffit, Poulton & Caspi, 2012), which makes the gambling- aggressive/disruptive behavior association plausible. While the above body of literature is informative in understanding the aggressive/disruptive behavior-gambling relationship, two research gaps are identified: First, with the exception of study by Slutske and colleagues (2005)- which measured aggressive/disruptive behavior at an earlier time point (at age 18) than the assessment of gambling (at age 21)-, most of these studies have measured aggressive/disruptive behavior and gambling concurrently at a single point-intime. The longitudinal link between the development of aggressive/disruptive behavior and late adolescent gambling has not been adequately explored. Second, most of the studies were based on samples of mainly White respondents. African Americans’ elevated risk of problem gambling evidenced in previous studies (Goldstein et al., 2009; Hardoon, Gupta, & Derevensky, 2004; Morasco, von Eigen, & Petry, 2006; Yip et al., 2011), together with the harmful effect of adolescent problem gambling, has led researchers (e.g., Blinn-Pike et al., 2010; Stinchfield, 2000) to call for more research to study gambling and gambling problems among racial/ethnic minority groups during adolescence.

The importance of studying gambling and gambling problems among adolescents

According to Derevensky & Gupta (2007), the majority of North American adolescents have engaged in some gambling activities in their lifetime. The prevalence of problem gambling among adolescents (3–8%) is significantly higher than that among adults (1–3%; Derevensky & Gupta, 2007; Derevensky & Gupta, 2004; Shaffer & Hall, 1996; Wood & Griffiths, 1998). The higher rates of gambling problems exhibited by African American youths as compared to the general adolescent population are particularly concerning (Alegria et al., 2009; Cunningham-Williams, Cottler, Compton, & Spitznagel, 1998; Lee et al., 2011; Martins, Storr, Ialongo, & Chilcoat, 2008; Wickwire, Whelan, Meyers, & Murray (2007).

Conceptually, it has been argued that the developmental imbalance between a relatively-well-developed reward/punishment processing system and an underdeveloped impulse control system will make adolescents particularly vulnerable to a series of risk taking behaviors including problem gambling (Casey, Jones, & Hare 2008; Chambers, Taylor, & Potenza 2003). Studies have found considerable continuity in problem/pathological gambling: those who meet criteria for problem gambling in adolescence are more likely to be pathological gamblers in adulthood (Winters, Stinchfield, Botzet, & Anderson, 2002). Moreover, problem gambling in adolescence co-occurs with numerous other problem behaviors such as delinquency and substance abuse (Barnes et al., 2005, 2009; Winters et al., 1993), and may share a common etiology with these behaviors. Research on the developmental progression of these factors associated with problem gambling may improve the understanding and prevention of other problem behaviors.

Theoretical explanation for the aggressive/disruptive behavior-gambling association

Several theories provide a plausible explanation for the aggressive/disruptive behavior-gambling association: the Problem Behavior Theory (Jessor, 1987, 1998; Jessor & Jessor, 1977), Hirschi and Gottfredson’s generality of deviance theory (1994), and life-course theories of aggressive/disruptive behavior (Moffitt, 1993, 2006; Patterson, DeBaryshe, & Ramsey, 1989). Jessor and Jessor (1977) proposed that a number of problem behaviors such as drug use and aggressive, disruptive behaviors share a common etiology. In Jessor’s (1998) model, problem/pathological gambling can be best understood as a form of adolescent risky behavior with potential health and life-compromising outcomes. Accordingly, childhood and adolescent aggressive/disruptive behavior could potentially be risk factors for problem/pathological gambling in late adolescence and young adulthood. Based on this conceptual framework, Dickson, Derevensky, and Gupta (2002) described a model in which risk and protective factors for youth and young adult problem/pathological gambling operate interactively in several domains (e.g., behavior, personality, biology, social and perceived environment).

Hirschi and Gottfredson’s generality of deviance theory (1994) also suggests that all deviance occurs in individuals who lack self-control and seek immediate pleasure without thinking about the risk of long-term consequences. This theory fits with the hypothesis that most, if not all, problem behaviors share a common etiology (Jessor, 1998). Life-course theory (Elder 1994; Moffitt, 2006) suggests that chronically displaying aggressive/disruptive behavior during childhood poses a developmental risk, which renders youth vulnerable to maladjustment in multiple domains of development (Bradshaw, Schaeffer, Petras, & Ialongo, 2010). Consistent with the life-course theory, the display of aggressive/disruptive behavior during childhood may elicit negative social interactions with peers, parents, and teachers (Patterson et al., 1989; Moffit, 1993, 2006; Patterson et al., 1989). These children might drift into a deviant peer group in which risk behaviors such as gambling are encouraged and reinforced.

Aggressive/disruptive behavior as a risk factor for a series of problem behaviors

Despite the relative sparse research on the aggressive/disruptive behavior-gambling association, aggressive/disruptive behavior has been linked to a number of other problem behaviors such as later substance use, delinquent behavior, school dropout, unemployment, and mental health problems (Liu, Lynne-Landsmann, Maryn, Petras, & Ialongo., in press; Liu in press; Bradshaw et al., 2010; Huesmann, Dubow, & Boxer, 2009; Moffitt, Caspi, Harrignton, & Milne, 2002; Ostrov & Godleski, 2009; Petras, Chilcoat, Leaf, Ialongo, & Kellam, 2004; Schaeffer, Petras, Ialongo, Poduska, & Kellam, 2003). Another body of research has focused on the developmental progression of aggressive/disruptive behavior in childhood and early adolescence. A general upward trend has been observed in childhood (Liu et al, in press) and a downward trend occurring in early adolescence (Petras, Masyn, & Ialongo, 2011). The development of aggressive/disruptive behavior is also characterized by interindividual heterogeneity (Bradshaw et al., 2010; Côte, Vaillancourt, LeBlanc, Nagin, & Tremblay, 2006; Huesmann et al., 2009; Moffitt, 1993; Petras et al., 2004, 2011). To our knowledge, no study has related the longitudinal development of aggressive/disruptive behavior to future involvement in gambling/problem gambling.

Study Aims

The present study aims to explore whether childhood (grades 1 to 3, e.g., on average ages 6 to 8) and adolescent aggressive/disruptive behavior (grades 6–10, e.g., on average ages 11–15) is associated with late adolescent (when youth were on average 16–20 years of age) gambling and gambling problems in an urban sample of mainly African-American (AA) male adolescents. Specifically, we are interested in: a) whether we can identify different trajectories of aggressive disruptive behavior during early childhood and adolescence; b) whether we can identify gamblers and problem gamblers based on aggressive disruptive behavior trajectories in these two distinct periods of time. Findings have the potential to: 1) enhance our understanding of gambling involvement and of the distinct etiology of gambling and gambling problems in this understudied subpopulation of urban youth and; 2) empirically inform much needed prevention and intervention strategies that target inner-city youths’ gambling problems.

Methods

Sample

In fall 1993, 678 urban first-graders from 27 classrooms in nine elementary schools in western Baltimore, Maryland participated in the Johns Hopkins University Preventive Intervention Research Center (PIRC) Second Generation Intervention Trial (Ialongo, Poduska, Werthamer, & Kellam, 2001). Details about the sample design and the trial are described elsewhere (Ialongo et al., 2001). Of the 362 males enrolled, we selected a sample of 310 males (average age upon entering school is 6.2) according to the following criteria: a) the individual had a valid aggressive/disruptive behavior assessment upon entering school (i.e., fall of first grade), b) the individual had at least one of the five aggressive/disruptive behavior assessments from grades 6 to 10 and c) the individual had valid information on all covariates included in the analyses. Criteria a) and b) were selected to ensure that the period specific analyses were conducted on the same sample of youth. As shown in Table 1, attrition analysis showed that the selected cases (i.e., N=310) resembled the unselected cases (i.e., N=52) on all variables included with the exception of aggressive/disruptive behavior in grade 2 spring (where the selected sample is slightly more aggressive/disruptive than the unselected sample with a difference of less than half of a standard deviation). Among the 310 selected males, the vast majority (87%) was African American, and the remaining 13% were Caucasian. Over 70% originated from low socio-economic status (SES) families (see Table 1 for sample descriptive statistics).

Table 1.

Attrition Analysis and Descriptive Statistics for Males

Variable	Mean (Std. deviation) % of selected sample (310)	Mean (Std. deviation) % of unselected sample (52)	P-value
	Childhood Aggressive/disruptive behavior*
Grade 1 Fall	1.80 (0.96)	1.69 (0.93)	0.419
Grade 1 Spring	1.87 (0.98)	1.77 (1.00)	0.524
Grade 2 Spring	2.11 (1.13)	1.71 (0.89)	0.019
Grade 3 Spring	2.17 (1.02)	1.80 (1.05)	0.083
	Early Adolescent Aggressive/disruptive behavior*
Grade 6 Spring	1.99 (0.86)	1.71 (0.81)	0.614
Grade 7 Spring	1.87 (0.72)	1.87 (0.78)	0.998
Grade 8 Spring	1.91 (0.72)	1.66 (0.78)	0.509
Grade 9 Spring	1.81 (0.76)	1.68 (0.75)	0.745
Grade 10 Spring	1.64 (0.61)	1.83 (1.02)	0.769
	Covariates
SES (1=lower SES)	70.3%	70.2%	1.000
Race (1=African American)	86.5%	78.8%	0.201
Age in Grade 1 Fall (1=Older than 7)	3.5%	5.8%	0.434
Classroom Centered intervention	33.9%	30.8%	0.752
Family School Partnership intervention	33.9%	46.2%	0.117
	Gambling**
Any Gambling	67.0%	57.6%	0.514
At-Risk or Problem Gambling	20.7%	15.2%

^*Assessed via TOCA-R Aggressive/Disruptive Behavior Subscale & TRCB-CF Conduct Disorder Subscale

^**Assessed via SOGS-RA

Measures

Childhood aggressive behaviors

The Teacher observation of classroom adaptation-revised (TOCA-R; grades 1–3) measures child’s performance on classroom core tasks defined by the teacher (Werthamer-Larsson, Kellam, & Wheeler, 1991). Through structured interviews, teachers evaluated each child’s performance on a six-point scale (“never true” to “always true”). The authority acceptance subscale, also known as the aggressive/disruptive behavior subscale, included ten items that measure different aspects of aggressive/disruptive behavior (Bjorvquist, Lagerspetz, & Kaukanien, 1992; Murray-Close, Ostrov, & Crick, 2007), i.e., “breaks rules,” “harms others and property,” “breaks things,” “takes others’ property,” “fights,” “lies,” “trouble accepting authority,” “yells at others,” “stubborn,” and “teases classmates.” The Cronbach’s alpha coefficient for reliability of the scale for each year was above 0.90. The TOCA-R was assessed in fall and spring of first grade and then in spring of second and third grade. The total item average scores were used as continuous indicators.

Early adolescent aggressive behaviors

The Teacher Report of Classroom Behavior-Checklist Form (TRCB-CF; Grades 6–10), an age-appropriate adaptation of the TOCA-R, is designed to obtain teacher reports of child conduct problems. It was based on the standardized teacher interview developed by Werthamer-Larsson et al. (1991) and described above. With respect to the conduct disorder subscale, teachers respond to seven items corresponding to Diagnostic and Statistical Manual of Mental Disorders-IV (American Psychiatric Association 1994) criteria for conduct disorder (i.e., starts physical fights with classmates, lies, hurts others physically, steals, damages other people’s property on purpose, skips school, and bullies classmates into getting his own way). Coefficient alpha for the TRCB-CF Conduct Problems scale in grades 6–10 was .88 or higher. The TRCB-CF was assessed in the spring of each year from grade 6 to grade 10.The total item average scores were used as continuous indicators.

Covariates

Socio-economic status (SES), Race (African-Americans and Caucasians), Age in fall of first grade (categorized as 7 years or younger and older than 7 years), and aggressive/disruptive behavior in fall of first grade (from the TOCA-R aggressive/disruptive behavior subscale used only in the analysis for the second process 6–10^th grades), were included in the models as covariates. Respondents receiving free or reduced-cost lunch were classified as low-SES and those not receiving free or reduced-cost lunch as high-SES (reference category, Sirin, 2005). Intervention Status in first grade (defined as one of three statuses: classroom centered [CC] intervention, family school partnership [FSP] intervention, and control group) was also included as a covariate in the models.

Gambling in late adolescence

The South Oaks Gambling Screen-Revised for Adolescents (SOGS-RA; Winters et al., 1993), an instrument adopted from the adult- oriented SOGS (Lesieur & Blume, 1987) with wording of questions and responses modified to reflect age-appropriate adolescent gambling behavior (Stinchfield, Govoni, & Frisch, 2004) assessed gambling involvement over three waves of data collection (mean ages 17–20 years). Respondents were first asked about their involvement in gambling in the 12 months preceding the interview. Specifically, these questions inquire about the frequency of being involved in gambling behaviors (e.g., slots, lottery, betting) which allowed us to distinguish whether participants had gambled in any of the prior years or not (nongambler vs. gambler). For those who reported involvement, a list of 12 yes/no questions (e.g., whether respondents played cards for money, bet on sports games, played on slot machines) were asked based on the DSM-III-R criteria for pathological gambling, and a SOGS-RA score was created as the sum of these above listed12 items, ranging from 0 to 12, with higher scores indicating more gambling problems. The internal consistency reliability was satisfactory (alpha=0.71).

A score of 0 or 1 indicates participation in social gambling, a score of 2 or 3 indicates meeting criteria for at-risk gambling and a score of 4 or more indicates meeting criteria for problem gambling (Winters, Stinchfield, & Kim, 1995). Guided by the literature that adolescents ‘at-risk’ and those with problems tend to have similar profiles (Hardoon et al., 2004; Wickwire et al., 2007), we combined these two categories in the analysis. As shown in Table 1, two thirds of the sample (67%) has engaged in any gambling, slightly over 20% met criteria for at- risk gambling or problem gambling combined.

Analytic Plan

General growth mixture modeling (GGMM; Muthén, 2004) was used to empirically identify developmental trajectories of aggressive/disruptive behavior in the two developmental periods (i.e., grades 1–3 and grades 6–10). Separate analyses were carried out for the two processes. Unlike conventional growth models, which estimate a single developmental trajectory of aggressive/disruptive behavior while allowing for individual variation around the estimated mean trajectory, GGMM explores population heterogeneity, i.e., whether the study population consists of two or more discrete classes of individuals with varying growth trajectories. The goal of GGMM is to determine the optimal class membership for each individual and to empirically classify individual aggressive/disruptive behavior profiles, such as “high” and “low” rather than relying on expert knowledge or information from previous studies. Moreover, GGMM specifies class membership in a probabilistic fashion, i.e., it allows for the uncertainty of individuals being in each of the latent classes.

Model building proceeded in a systematic and stepwise fashion (Petras & Masyn, 2010). The functional form for individual change in aggressive/disruptive behavior was examined by plotting means and observed individual growth trajectories and then assessing descriptive statistics of aggressive/disruptive behavior over time. Nested models with fixed and random intercept, linear and nonlinear slopes were compared using a Likelihood Ratio Test and other structural equation model selection criteria, including the Comparative Fit Index (CFI), Tucker-Lewis Index (TLI), Root Mean Square Error of Approximation (RMSEA), as well as Standardized Root Mean Square Residual (SRMR).

Heterogeneity in the longitudinal development of aggressive/disruptive behavior was explored by estimating models with increasing numbers of classes. Model selections was done using theoretical reasoning as well as fit statistics appropriate for non-nested models, e.g., the Bayesian Information Criterion (BIC) and the Lo-Mendell-Rubin likelihood ratio chi-square test (LMR; Lo, Mendell, & Rubin, 2001). The model that achieved an optimal balance between fit and parsimony was selected as the best GGMM model. Several modifications of the best-fitting GGMM model were explored to improve fit, such as freeing intercept and residual variances to be different across classes. Once the best GGMM model was chosen, class membership was regressed on covariates, such as race and SES, via categorical logistic regression (Long & Cheng, 2004).

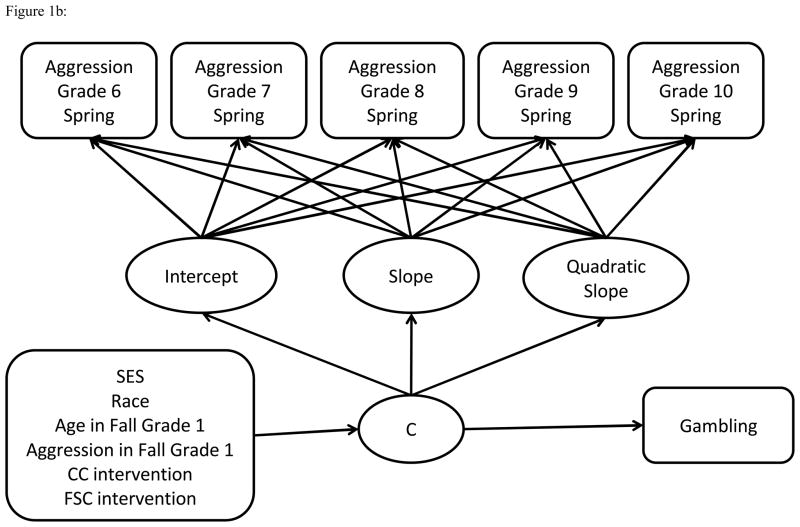
To demonstrate the effects of aggressive/disruptive behavior class membership on gambling, the three-level categorical gambling variable was regressed on class membership via ordered logistic regression (Long & Cheng, 2004). The predicted probabilities of meeting each threshold in the three-level gambling variable, that is, the predicted probabilities of engaging in any gambling (i.e., Pr (SG/AG/PG)) versus no-gambling, and meeting criteria for at-risk/problem gambling (i.e., Pr (AG/PG)) versus no and social gambling, are presented for each class. The analytical models are shown in Figure 1. All analyses were conducted using Mplus version 6.12 (Muthén & Muthén, 1998–2011), and the clustering of students within classrooms was accounted for by computing robust standard errors using a sandwich estimator (White, 1980).

Figure 1.

Figure 1a: Analytical Model for Aggressive/disruptive behavior (Grades 1–3)

Figure 1b: Analytical Model for Aggressive/Disruptive Behavior (Grades 6–10)

Missing data on aggressive/disruptive behavior trajectories over time were accounted for using the full information maximum likelihood (FIML) estimation available in Mplus 6.12. FIML assumes that data are missing at random (i.e., either random or conditional on other measured variables in the study; Arbuckle, 1996; Schafer & Graham, 2002). This method is widely accepted as a form of estimation for longitudinal data with attrition and will produce unbiased and efficient estimates (Muthen & Shedden, 1999; Schafer & Graham, 2002). For the first process (grades 1–3), 72% of the 310 males had valid information on all four measures of aggressive/disruptive behavior, 12% missed only one measure, and the remaining 16% missed two or more measures. For the second process (grades 6–10), 59% had valid information on all five measures of aggressive/disruptive behavior, 22% missed only one measure, and the remaining 19% missed two or more measures. The bivariate coverage ranged from 0.73 to 0.94 for grades 1–3 and .70 to .89 for grades 6–10, well exceeding the required minimum of 0.1.

Results

Functional Form

For grades 1–3, nested model comparisons suggested that a functional form with a random intercept and slope (with the covariance between them fixed at 0) fit the data reasonably well (LL= −1439.37 (8), CFI= 0.996, TLI= 0.996, RMSEA= 0.02 [0.00, 0.08)], SRMR=0.09). For grades 6–10, a functional form with a random intercept and slope and a fixed quadratic slope achieved optimal fit (LL= −1267.99 (11), CFI= 0.98, TLI= 0.98, RMSEA= 0.04 [0.00, 0.08)], SRMR=.04). Overall an increasing trend of aggressive/disruptive behavior was seen in childhood and a slightly increasing followed by a decreasing trend was observed in early adolescence (see Table 3 for the mean and variance of growth factors).

Table 3.

Mean and Variance of Growth Factors for Each of the Three aggressive/disruptive behavior Trajectories (Grades 1–3 and Grades 6–10)

	Overall Sample		High		Moderate		Low
	Mean	Variance	Mean	Variance	Mean	Variance	Mean	Variance
	Childhood Aggressive/disruptive behavior (Grades 1–3)
Intercept	1.894**	0.510**	3.47**	0.01#	1.93**	0.01#	1.18**	0.01#
Slope	0.163**	0.110**	−0.16	0.01#	0.26**	0.01#	0.14**	0.01#
	Early Adolescent Aggressive/disruptive behavior (Grades 6–10)
Intercept	1.956**	0.425**	3.40**	0.02**	2.02**	0.02**	1.34**	0.02**
Slope	0.015	0.007	−0.19	0.03*	0.06	NA	0.02	NA
Quadratic Slope	−0.021**	NA	−0.00	NA	−0.03*	NA	−0.01	NA

NA: fixed to 0

^*significant at 0.05 level

^**significant at 0.01 level

^#borderline significant (p-value<0.10)

GGMM and Covariate Effects

Class enumeration was performed based on the above selected single class models to explore the heterogeneity in development patterns of aggressive/disruptive behavior for both processes. Fit indices for these models are presented in Table 2. For grades 1–3, a 3-class model with residual variances freed to be different for the low class (i.e., 3-class (V1) was chosen to best represent the data (LL= −1175.54, BIC= 2454.33). For grades 6–10, a 3-class model with slope variance fixed to 0 for the middle and low (to avoid negative slope variance estimation) and residual variances freed to be different for the stable low class (i.e., 3-class (V1, V4)) achieved optimal fit (LL= −1088.00 (23), BIC= 2307.94).

Table 2.

Model Fit Statistics for Fitting a Growth Mixture Model for Aggressive/disruptive behavior (Grades 1–3 and Grades 6–10)

Model	Log Likelihood	# of free parameters	BIC a	LMR-LRT b
	Childhood Aggressive/disruptive behavior (Grades 1–3) #
1 class	−1439.372	8	2924.636	NA
2-class	−1381.497	11	2826.096	0.0745
3-class	−1360.855	14	2802.022	0.4465
4-class	−1337.004	17	2771.531	0.1310
5-class	−1319.977	20	2754.685	0.3478
2-class, V1	−1208.434	15	2502.918	NA
2-class, V1 V2	−1198.621	16	2489.028	NA
3-class, V1	−1175.538	18	2454.334	NA
3-class, V1 V2	−1175.378	19	2459.751	NA
	Early Adolescent Aggressive/disruptive behavior (Grades 6–10) #
1 class	−1276.613	10	2610.592	NA
2-class	−1234.927	14	2550.165	0.0170
3-class	−1203.991	18	2511.240	0.0188
4-class	−1185.929	22	2498.062	0.0050
5-class	−1177.911	26	2504.972	0.0243
2-class, V3	−1220.725	14	2521.763	NA
2-class, V1 V3	−1121.684	19	2352.364	NA
2-class, V1 V2 V3	−1113.060	19	2335.114	NA
3-class, V4	−1205.845	18	2514.949	NA
3-class, V1 V4	−1088.000	23	2307.942	NA
3-class, V1 V2 V4	−1085.877	24	2309.432	NA

NA: non-applicable;

^aBayesian Information Criterion;

^bLo-Mendell-Rubin Likelihood Ratio Test p-valueV1: Allowing the residual variances to be different for the low class; V2: Allowing the intercept variance to be different for the low class; V3: Fixing slope variance for the low class to 0 due to a negative estimated slope variance; V4: Fixing slope variance for the middle and low class to 0 due to negative estimated slope variances;

^# Starting from the 1-class model, BIC decreases (indicating better fit). For periods, evidence suggests that both the 2-class and the 3-class model provide reasonable fit. Although BIC continues to decrease for the 4-class and 5-class models, these models are highly unstable, and the smallest class only contains less than ten percent the sample making it difficult to draw meaningful inferences. Therefore, further modification was performed on both the 2-class and the 3-class models to improve model fit. According to BIC, the 3-class, V1 model achieved a reasonable balance between fit and parsimony for Grade 1–3 and the 3-class, V1 V4 model achieved such a balance for Grade 6–10.

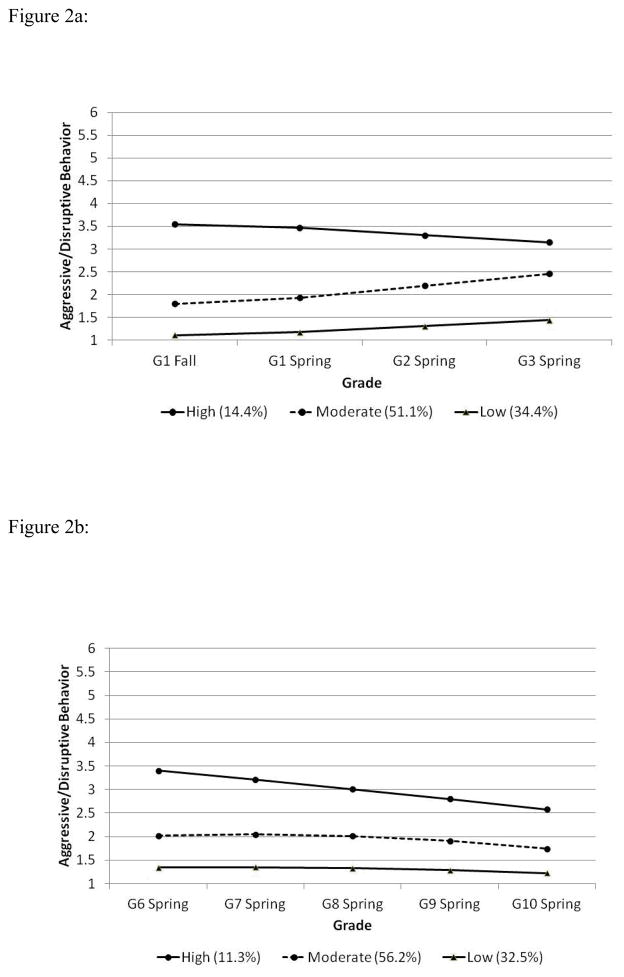
Three distinct aggressive/disruptive behavior trajectories were identified in early childhood: a chronic high class that consists of 14.4% of the sample, a moderate increasing class which consists of 51.3% of the sample, and a low increasing class that consists of 34.4% of the sample (Figure 2a). Similarly, three distinct aggressive/disruptive behavior trajectories were identified in adolescence: a chronic high class that consists of 11.3% of the sample, a moderate increasing and then decreasing class that consists of 56.2% of the sample, and a low stable class that consists of 32.5% of the sample (Figure 2b). Table 3 presents the mean and variance of growth factors (i.e. intercept and slope) for each of the three classes in early childhood and adolescence respectively. As shown in Table 3, the differences between these classes are substantively meaningful.

Figure 2.

Figure 2a: Development of Aggressive/Disruptive Behavior (Grades 1–3)

Figure 2b: Development of Aggressive/Disruptive Behavior (Grades 6–10)

As shown in Table 4, some covariates significantly differentiate these classes. In childhood, both SES and age at first grade were significantly associated with class membership. In adolescence, SES, age at first grade and aggressive/disruptive behavior at 1^st grade were significantly associated with class membership (see ORs and 95%CIs in Table 4).

Table 4.

The Effects of Covariates on Aggressive/Disruptive Behavior Trajectory Class Membership (Grades 1–3 and Grades 6–10)

Covariates	High versus low		High versus moderate		Moderate versus low
	OR	95% CI#	OR	95% CI	OR	95% CI
	Childhood Aggressive/disruptive behavior (Grades 1–3)
Lower SES	4.69	(1.62, 13.54)	2.66	(1.10, 6.45)	1.76	(0.89, 3.49)
African American	2.39	(0.35, 16.46)	1.42	(0.56, 3.61)	1.68	(0.78, 3.65)
Age >7 at fall of 1st grade	5.17	(1.23, 21.77)	13.53	(2.70, 67.90)	0.38	(0.04, 3.95)
CC intervention	1.01	(0.29, 3.48)	0.90	(0.09, 9.50)	1.12	(0.56, 2.24)
FSP intervention	1.53	(0.60, 3.87)	1.20	(0.58, 2.49)	1.27	(0.61, 2.65)
	Early Adolescent Aggressive/disruptive behavior (Grades 6–10)
Lower SES	13.09	(1.70, 100.72)	5.88	(1.56, 8.42)	2.22	(1.08, 4.59)
African American	0.78	(0.21, 2.81)	1.54	(0.51, 4.63)	0.50	(0.22, 1.17)
Age >7 at fall of first grade	1.64	(0.08, 35.17)	3.96	(2.70, 5.81)	0.42	(0.04, 3.89)
1st grade aggressive/disruptive behavior	4.88	(2.24, 10.65)	1.47	(0.34, 6.26)	3.33	(1.56, 7.10)
CC intervention	0.58	(0.19, 1.74)	0.98	(0.40, 2.41)	0.59	(0.33, 1.04)
FSP intervention	0.39	(0.10, 1.64)	0.50	(0.06, 4.43)	0.78	(0.39, 1.59)

^# When 95% CI of an OR includes 1.0, the corresponding OR should be interpreted as non-significant.

The Association between Class Membership and Late-Adolescent Gambling

We investigated the extent to which subsequent gambling in late adolescence varied as a function of childhood and early adolescence aggressive/disruptive behavior trajectories by regressing gambling on aggressive/disruptive behavior class membership separately for each developmental period. Cumulative probabilities Pr (SG/AG/PG), and Pr (AG/PG), for both classes as well as odds ratios with 95% confidence intervals representing the effect of class membership on gambling (any gambling and at risk/problem gambling combined) are presented in Table 5¹.

Table 5.

The Association between Aggressive/disruptive Behavior Trajectory Class Membership (Grades 1–3 and Grades 6–10) and Subsequent Gambling

	Target aggressive/disruptive behavior class	Reference aggressive/disruptive behavior class	Probability	ORa	95% CI#
	Childhood Aggressive/disruptive behavior (Grades 1–3)
Any gambling	High	Moderate	.58	0.57	(0.19, 1.74)
	Moderate	Low	.71	1.32	(0.70, 2.52)
	Low	--	.65	--	--
	High	Low	--	0.76	(0.33, 1.73)
At-risk/problem gambling	High	Moderate	.31	1.60	(0.64, 4.01)
	Moderate	Low	.22	1.63	(0.64, 4.12)
	Low	--	.15	--	--
	High	Low	--	2.60	(1.06, 6.38)
	Early Adolescent Aggressive/disruptive behavior (Grades 6–10)
Any gambling	High	Moderate	.48	0.31	(0.11, 0.89)
	Moderate	Low	.75	1.89	(1.11, 3.24)
	Low	--	.61	--	--
	High	Low		0.58	(0.22, 1.57)
At-risk/problem gambling	High	Moderate	.34	1.88	(0.77, 4.61)
	Moderate	Low	.22	1.70	(0.74, 3.92)
	Low	--	.14	--	--
	High	Low	--	3.19	(1.18, 8.64)

^aOdds (gambling | membership in the high class)/Odds (gambling | membership in the low class).

^#When 95% CI of an OR includes 1.0, the corresponding OR should be interpreted as non-significant.

For early childhood, while class membership in the different childhood aggressive/disruptive behavior trajectories was not significantly associated with engaging in any gambling activities, it was significantly associated with meeting criteria for at-risk/problem gambling. Compared to the low increasing class, those who followed the chronic high trajectory in childhood were almost three times (OR=2.60 [1.06, 6.38]) more likely to meet criteria for at-risk or problem gambling.

Significant differences in gambling probabilities were also observed across the early adolescent aggressive/disruptive behavior classes and such differences in these probabilities between classes vary by gambling categories. Specifically, those in the chronic high class were significantly less likely to engage in any gambling activities than those in the moderate class (OR=0.31 [0.11, 0.89] and those in the moderate class were significantly more likely to engage in any gambling activities than those in the low stable class (OR=1.89 [1.11, 3.24]). However, when it comes to meeting criteria for at-risk/problem gambling, compared to those in the low stable class, those in the chronic high class were over three times as likely to meet such criteria (OR=3.19 [1.18, 8.64].

Discussion

Applying growth mixture modeling to the development of childhood (grades 1–3) and adolescent (grades 6–10) aggressive behavior in boys revealed three distinct trajectories of aggressive/disruptive behavior in each developmental period: a chronic high, a moderate increasing and a low increasing trajectory class in childhood, and a chronic high, a moderate increasing and then decreasing, and a low stable class in early adolescence. First-grade aggressive/disruptive behavior, age in fall of first grade and lower SES had significant influence on class membership for the early adolescence (grades 6–10) developmental period (e.g. lower SES increases the likelihood of being in the high trajectories versus the moderate and low trajectory and first grade aggressive/disruptive behavior increases the likelihood of being in the high trajectory versus the low trajectory). These above findings provide evidence for the construct validity of the latent classes.

Being in a chronic high trajectory of aggressive/disruptive behavior in childhood was not associated with any gambling, but was significantly associated with at-risk/problem gambling in late adolescence. In addition, the adolescent trajectory of aggressive/disruptive behavior was associated with late-adolescent gambling outcomes. The finding that adolescents in the moderate trajectory of aggressive/disruptive behavior are more likely than those in the low aggressive/disruptive behavior trajectory to engage in any gambling might be due to the fact that most of adolescents gamble at one point in adolescence and also because most of them belong to the moderate class. Most importantly, boys in a high aggressive/disruptive behavior class in childhood (grades 1–3) were nearly three times more likely than boys in the low class in childhood to meet criteria for at-risk/problem gambling in late adolescence. Similarly, boys in a high aggressive/disruptive behavior class in adolescence (grades 6–10) were 3.2 times more likely to meet criteria for at-risk/problem gambling in late adolescence. This shows that there is an important relationship between at-risk/problem gambling (the problematic forms of gambling) and childhood as well as adolescent aggressive/disruptive behavior. As such, aggressive/disruptive behavior manifested early in ones development maybe a predictor of future development of gambling problems. Our findings further substantiate those from cross-sectional studies that investigated the relationship between aggressive/disruptive behavior and gambling behaviors conducted among youth and adults (Goldstein et al., 2009; Korman et al., 2008; Liao, 2008; McCormick, 1993; Mishra et al., 2011; Parke & Griffiths, 2004; Stinchfield, 2000; Yip et al., 2011) and findings from Slutske et al. (2005) that explored the role of aggressive personality traits at age 18 and gambling behavior at age 21.

Some limitations must be acknowledged. First, the study sample consisted primarily of urban, minority participants. While this may be viewed as strength of the study given the relative lack of research on aggressive/disruptive behavior-gambling association among urban minority populations, the findings of this study may not be generalizable to the general population and thus should be extrapolated with caution. Findings should be replicated with different longitudinal samples. Second, we caution that the results are based on a specific measure of aggressive/disruptive behavior (the authority acceptance subscale of the TOCA-R, Werthamer-Larsson et al., 1991) which might not generalize to all measures of aggression (e.g., Child Behavior Checklist; Achenbach, 1991). Third, while we have ensured the logical temporal order of events, the observed significant association between heterogeneity in aggressive/disruptive behavior development and gambling behavior does not necessarily indicate a causal relationship. Future studies should further explore the causal relationship using appropriate methods. Fourth, given that only an extremely small percentage (less than 1%) of females in this sample met the criteria of problem gambling, we could not study the aggressive/disruptive behavior-problem gambling association among females. Future studies with larger samples should replicate the findings of this study using a female sample.

The study has important implications for the prevention of problem gambling. First, it is based upon an epidemiologic-defined sample that includes early and continuing measurement of aggressive/disruptive behavior through elementary, middle and into high school, and measures of gambling behaviors in adolescence, which enables us to use growth trajectories to examine the relationship between aggressive/disruptive behaviors and gambling in a unique fashion. The finding that both childhood and early adolescent trajectories of aggressive/disruptive behavior are significantly associated with subsequent gambling in late adolescence suggest that preventing childhood and youth aggressive/disruptive behavior as well as other adolescent risk and maladaptive behaviors may be effective to prevent youth problem gambling. Derevensky and Gupta (2011) have shown that there are several pathways that can lead to youth problem gambling, and that coping and adaptive strategies to enhance resilience are indeed important components in gambling prevention initiatives. Past studies have found evidence that lowering impulsivity may have a promising impact on reducing positive attitudes toward gambling (Williams, 2002), however, currently prevention programs that have specifically targeted adolescent aggressive/disruptive behavior have not been evaluated with respect to reducing positive attitudes towards gambling. In addition, we found that not only childhood trajectories of high aggressive/disruptive behaviors predict later at-risk/problem gambling, but also that first grade aggressive/disruptive behavior was significantly associated with aggressive/disruptive behavior trajectory in adolescence, which is significantly associated with gambling in late adolescence, suggesting a possible indirect effect of first grade aggressive/disruptive behavior on later gambling. Interventions aimed to decrease aggressive/disruptive behavior as early as elementary school may have long term benefit in decreasing the likelihood of youth following an elevated trajectory of aggressive/disruptive behavior and later engaging in gambling activities and developing gambling problems. We found that high levels childhood aggressive/disruptive behavior was related only to gambling problems but not to any gambling. We also found that the association between adolescence aggressive/disruptive behavior trajectories and gambling in late adolescence differs by gambling categories. This suggests that evaluations of intervention trials aimed at reducing youth gambling problems through reducing aggressive/disruptive behavior should distinguish gambling problems (i.e., at-risk and problem gambling) from any gambling.