Bayesian geostatistical modelling with informative sampling locations

Summary

We consider geostatistical models that allow the locations at which data are collected to be informative about the outcomes. A Bayesian approach is proposed, which models the locations using a log Gaussian Cox process, while modelling the outcomes conditionally on the locations as Gaussian with a Gaussian process spatial random effect and adjustment for the location intensity process. We prove posterior propriety under an improper prior on the parameter controlling the degree of informative sampling, demonstrating that the data are informative. In addition, we show that the density of the locations and mean function of the outcome process can be estimated consistently under mild assumptions. The methods show significant evidence of informative sampling when applied to ozone data over Eastern U.S.A.

1. Introduction

Geostatistical models focus on inferring a continuous spatial process based on data observed at finitely many locations, with the locations typically assumed to be noninformative. As noted by Diggle et al. (2010), this assumption is commonly violated in point-referenced spatial data, as it is not unusual to collect data at locations thought to have a large or small value for the outcome. For example, in monitoring of air pollution, one may place more monitors at locations believed to have a high value of ozone or another pollutant, while in studying distribution of animal species one may systematically look in locations thought to commonly contain the species of interest. Diggle et al. (2010) proposed a shared latent process model to adjust for bias due to informative sampling locations. Their analysis was implemented using a Monte Carlo approach for maximum likelihood estimation.

We follow a Bayesian approach using a model related to those described by R. Menezes in an unpublished 2005 Ph.D thesis from Universidad de Santiago de Compostela, Ho & Stoyan (2008) and Diggle et al. (2010). The locations are modelled using a log Gaussian Cox process (Møller et al., 2001), with the intensity function included as a spatially varying predictor in the outcome model, which also includes spatial random effects drawn from a Gaussian process. A parameter a controls the degree of informative sampling, and the sampling locations are ignorable in the special case in which a = 0, while a > 0 implies a tendency to take more observations at spatial locations having relatively high outcome values. This model modifies shared random effects models for joint modelling of longitudinal and event time data (Radcliffe et al., 2004) and for accommodating informative missingness (Wu & Follmann, 1999).

To our knowledge, we are the first to develop a Bayesian approach to the informative locations problem in geostatistical modelling. However, adapting recently proposed models to the Bayesian paradigm is relatively straightforward, and our primary contribution is studying the theoretical properties of the model. In particular, it is not obvious that the data contain information about the informativeness of the sampling locations, and one may wonder to what extent the prior is driving the results even in large samples. We address this concern by proving that the posterior is proper under a noninformative prior on a. In addition, one can consistently estimate a, the density of the sampling locations and the mean function of the outcome process. This result extends recent work showing posterior consistency in Gaussian process regression models (Choi & Schervish, 2007; Choi, 2007). Proofs are provided in the Appendix.

2. Model for spatial data with informative sampling

Our objective is to estimate the spatial surface μ(s) ∈ 𝕉, for all s ∈ 𝒟 ⊂ 𝕉², based on observations y₁, . . . , y_n at locations s₁, . . . , s_n ∈ 𝒟. We propose the joint model

$$y_i|s_i\sim N\{\eta (s_i)+a\xi (s_i),{\sigma }^2\},\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}p(s_i)=\frac{\text{exp}\{\xi (s_i)\}}{{\int }_{𝒟}\text{exp}\{\xi (s)\}ds}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}(i=1,\dots ,n),$$ (1)

where the observations are independent across locations s_i given ξ(s) and η(s), and p(s) is the location density. Assuming the locations are a realization of an inhomogeneous Poisson process with log intensity ξ(s), the mean surface is characterized as μ(s) = η(s) + aξ(s), where η(s) is a baseline surface and aξ(s) is an adjustment due to informative sampling. Letting x(s) denote a vector of spatial covariates, ξ(s) = x(s)^T β_ξ + ξ_r (s) and η(s) = x(s)^T β_η + η_r (s), where β_ξ and β_η are regression coefficients and ξ_r (s) and η_r (s) are zero-mean residual processes.

The log sampling density is treated as a latent covariate to adjust for informative sampling, with a > 0 implying that samples are more likely to be taken in areas with a large response. Setting the coefficient in β_ξ corresponding to the intercept to zero for identifiability,

$$E(y_i|s_i)=x{(s_i)}^{\text{T}}\beta *+a{\xi }_r(s_i)+{\eta }_r(s_i)\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}(i=1,\dots ,n),$$ (2)

where β* = aβ_ξ + β_η. Therefore, accounting for informative sampling is only necessary when there is an association between the spatial surface of interest and the sampling density that cannot be explained by the shared spatial covariates x(s).

The residuals ξ_r (s) ∼ Π_ξr and η_r(s) ∼ Π_ηr are assigned independent zero-mean Gaussian process priors with Matérn covariance functions (Stein, 1999),

$$c(h|\psi )=\frac{{\tau }^2}{2^{\nu -1}\mathrm{\Gamma }(\nu )}{\left(\frac{2{\nu }^{1/2}h}{\rho }\right)}^{\nu }{𝒦}_{\nu }\left(\frac{2{\nu }^{1/2}h}{\rho }\right),\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}h=\Vert s-s^{\prime }\Vert ,$$ (3)

where ψ = (τ², ρ, ν) and 𝒦 denotes the modified Bessel function of the second kind. The Matérn covariance has three parameters: τ² > 0 controls the variance, ρ > 0 controls the spatial range of the correlation and ν > 0 controls the smoothness of the process. Special cases include the exponential c(h | ψ) = τ² exp(−2^1/2h/ρ) with ν = 1/2, and the squared exponential c(h | ψ) = τ² exp(−2h²/ρ²) with ν = ∞.

3. Theoretical properties

3.1. Weak posterior consistency

In this section, we obtain posterior consistency of the parameters of our model under fixed-domain asymptotics. Consider the joint model defined in §2, with 𝒟 = [0, 1]² without loss of generality and Π_ξr, Π_ηr Gaussian processes on 𝒞(𝒟), the space of continuous functions on 𝒟. Letting c(h | ψ_ξ) and c(h | ψ_η) denote the covariance functions for ξ_r and η_r, respectively, we choose independent bounded hyperpriors for ${\tau }_{\xi }^2$, ${\tau }_{\eta }^2$, ν_ξ and ν_η while letting ρ_ξ ∼ π_ξ and ρ_η ∼ π_η, where the supports of both π_η and π_ξ are 𝕉⁺. We choose a proper prior on 𝕉 for a, β_ξ ∼ N(β_0ξ, Σ_0ξ), β_η ∼ N(β_0η, Σ_0η) and σ² ∼ Inv-Ga (α_σ, β_σ).

Assumption 1. The prior ζ ∼ Π satisfies the prior positivity condition Π(ζ : ‖ζ − ζ₀‖_∞ < ∊) > 0 for all ∊ > 0 and for any ζ₀ ∈ 𝒞(𝒟).

van der Vaart & van Zanten (2009) showed that Assumption 1 holds for Gaussian process priors with squared exponential covariance under mild conditions and, in an unpublished 2005 Ph.D thesis from Carnegie Mellon University, T. Choi provided a set of sufficient conditions on the Matéern covariance kernel for the same setting.

Assumption 2. The covariates are uniformly bounded, so there exists an M > 0 such that ‖x(s)‖ ⩽ M for all s ∈ 𝒟.

Theorem 1. Under models (1)–(2) with priors chosen as described in §3 and Assumptions 1–2, the posterior distribution Π[ξ_r, η_r, a, β_ξ, β_η, σ | {(y_i, s_i), i = 1, . . . , n}] is weakly consistent.

Theorem 1 does not imply that the hyperparameters in the covariance kernel are consistently estimated, though we do take into account uncertainty in these parameters and do not assume that the priors are well specified. It is typically not possible to consistently estimate all the parameters in the Matérn covariance (Zhang, 2004).

3.2. Posterior propriety of a

Under models (1)–(2), the parameter a controls the degree of informative sampling. The uniform improper prior, π_a(a) ∝ 1, provides a noninformative choice. Theorem 2 shows that this prior leads to a proper posterior, implying that the data are informative about a.

Letting s = (s₁, . . . , s_n), y = (y₁, . . . , y_n)^T, ${\xi }_r^n$ = {ξ_r (s₁), . . . , ξ_r (s_n)}^T, and ${\eta }_r^n$ = {η_r(s₁), . . . , η_r (s_n)}^T, we have ${\xi }_r^n$ ∼ N(0, ${\mathrm{\Sigma }}_{\xi }^n$) and ${\eta }_r^n$ ∼ N(0, ${\mathrm{\Sigma }}_{\eta }^n$), where ${\mathrm{\Sigma }}_{\xi }^n$(s, s^′) = c(‖s − s^′‖|ψ_ξ) and ${\mathrm{\Sigma }}_{\eta }^n$ (s, s^′) = c(‖s − s^′‖ |ψ_η) for s, s^′ ∈ 𝒟. Let c(h |ψ_ξ) = ${\tau }_{\xi }^2$ exp(−2^1/2h^p/ρ_ξ) and c(h |ψ_η) = ${\tau }_{\eta }^2$ exp(−2^1/2h^p/ρ_η) for 0 < p ⩽ 2. We assume independent bounded priors on τ_ξ and τ_η and independent discrete uniform priors on ρ_ξ and ρ_η. Let β_ξ ∼ N(β_0ξ, Σ_0ξ), β_η ∼ N(β_0η, Σ_0η) and σ² ∼ π(σ²). Here we focus on powered exponential covariance functions rather than Matérn to simplify calculations. A similar result should hold for Matérn covariance functions if the priors on the hyperparameters have a bounded support.

Theorem 2. With the above prior specifications, the marginal posterior distribution of a, p(a | y, s) is proper, provided n ⩾ 2 and E_π (σ) < ∞.

When the conditions of Theorem 2 are satisfied, the joint posterior is also proper.

4. Computational details

The exact density for the sample locations in (1) is not available analytically, so an approximation is required. In point process modelling, the integral is often approximated as the sum over a fine grid. Letting t₁, . . . , t_M ∈ 𝒟 be a rectangular grid covering 𝒟 with cell area Δ, we have

$${\int }_{𝒟}\text{exp}\{\xi (s)\}ds\approx \mathrm{\Delta }\sum _{j=1}^M\text{exp}\{\xi (t_j)\}.$$ (4)

This approximation yields a tractable posterior, but requires computationally expensive matrix inversions, which we limit using a kernel convolution approximation to the process.

Let δ(s) be a zero-mean Gaussian process with covariance c(h | ψ). A process convolution (Higdon, 2002) lets

$$\delta (s)={\int }_{𝒟}{K}_{\psi }(s-u)dW(u),$$ (5)

where W is the Brownian motion and K_ψ is a kernel with parameters ψ. The kernel corresponding to the Matérn covariance is

$$K_{\psi }(u)=\tau \frac{\mathrm{\Gamma }{(\nu +1)}^{1/2}{\nu }^{\nu /4+1/4}|u{|}^{\nu /2-1/2}}{{\pi }^{1/2}\mathrm{\Gamma }(\nu /2+1/2)\mathrm{\Gamma }{(\nu )}^{1/2}{\rho }^{\nu /2+1/2}}{𝒦}_{\nu /2+1/2}\left(\frac{2{\nu }^{1/2}\left|u\right|}{\rho }\right).$$

The kernel convolution representation of the Gaussian process in (5) is often used to motivate dimension reduction for the spatial process. Let ϕ₁, . . . , ϕ_N be a grid of spatial knots. Then, for large N,

$$\delta (s)\approx \sum _{j=1}^N{K}_{\psi }(s-{\phi }_j)w_j,$$ (6)

where w_j ∼ N(0, 1). Applying kernel convolution to ξ(s) and η(s) yields

$$\begin{array}{c}{y}_i|s_i\sim N\left\{x{(s_i)}^{\text{T}}\beta *+\sum _{j=1}^N{K}_{{\psi }_{\eta }}(s_i-{\phi }_j)u_j+a\sum _{j=1}^N{K}_{{\psi }_{\xi }}(s_i-{\phi }_j){\upsilon }_j+{\sigma }^2\right\},\\ p(s_i)=\frac{\text{exp}\{x{(s_i)}^{\text{T}}{\beta }_{\xi }+{\sum }_{j=1}^N{K}_{{\psi }_{\xi }}(s_i-{\phi }_j){\upsilon }_j\}}{{\sum }_{l=1}^M\text{exp}\{x{(t_l)}^{\text{T}}{\beta }_{\xi }+{\sum }_{j=1}^N{K}_{{\psi }_{\xi }}(t_l-{\phi }_j){\upsilon }_j\}},\end{array}$$ (7)

where u_j, υ_j ∼ N(0, 1). Selecting the number of grid points M and knots N is discussed in §5 and §6.

We use a combination of Gibbs and Metropolis sampling for posterior computation. Assuming conjugate normal and inverse gamma priors, and reparameterization so that u_j ∼ N(0, ${\tau }_{\eta }^2$) and υ_j ∼ N(0, ${{\tau }_{\xi }}^2$), the full conditionals for β^*, a, ${\tau }_{\eta }^2$, ${\tau }_{\xi }^2$ and the vector (u₁, . . . , u_N)^T are conjugate and we use Gibbs sampling. The correlation parameters ρ_η and ρ_ξ and the smoothness parameters ν_η and ν_ξ are updated with Metropolis sampling, tuned to have an acceptance ratio near 0.4. The sampling density parameters υ_j are updated using blocked Metropolis sampling to account for posterior correlation between coefficients for nearby knots. We used 10 blocks, with knots allocated to blocks using k-means clustering implemented by the kmeans package in R. For the simulation study in §5, we generated 5000 samples and discarded the first 1000 as burn-in. For the analysis of the ozone data in §6, we generated 20 000 samples and discarded the first 5000. Convergence was monitored using trace plots of the deviance as well as several parameters.

5. Simulation study

We conduct a simulation study to illustrate the effect of failing to account for informative sampling on spatial interpolation, and determine the amount of data needed to reliably identify informative sampling. We assume 𝒟 = [0, 1]² and no spatial covariates, x(s) = 1 for all s. We generate data using model (7) with an equally spaced grid of N = 225 knots on [−0.2, 1.2]² and a Matérn kernel. We generate S = 50 datasets from each of four simulation scenarios: (i) n = 250, a = 0, ρ = 0.2; (ii) n = 250, a = 1, ρ = 0.2; (iii) n = 250, a = 1, ρ = 0.5 and (iv) n = 500, a = 1, ρ = 0.2, with σ = 1, E{μ(s)} = 0, ν = 2.0 and τ = 0.1 under all scenarios. For each simulated dataset, we fit three models. The noninformative sampling model sets a = 0, the plug-in model sets ξ(s) = ξ̂(s) to account for informative locations and the full model implements the approach of §4. In the plug-in analysis, the location density is estimated using kernel density estimation in R’s KernSur function in the GenKern package with default settings. GenKern gives a bivariate kernel density estimate that uses Gaussian kernels with bandwidth chosen using a direct plug-in approach to approximate the asymptotically optimal bandwidth.

We use the same grid of N = 225 knots for generating the data in the kernel convolution model, and approximate the integral using a square grid of M = 900 points t₁, . . . , t_M covering [0, 1]. Motivated by Rodrigues & Diggle (2010), we used an equally spaced grid of 225 knots on [−0.2, 1.2]². The simulation study results show that irrespective of the number and position of the sampling locations, the Gaussian process can be well approximated with 225 knots. Following Lee et al. (2005), the grid spacings are chosen to be no larger than the standard deviation of the kernel in the convolution representation. We use diffuse normal priors for β^* and a and the covariance parameters have priors σ², ${\tau }_{\xi }^2$, ${\tau }_{\eta }^2$ ∼ Inv-Ga(0.01, 0.01), ${\rho }_{\xi }^2$, ${\rho }_{\eta }^2$ ∼ U(0, 2), and ${\nu }_{\xi }^2$, ${\nu }_{\eta }^2$ ∼ U(0, 30).

Table 1 reports bias, mean-squared error, mean absolute deviation, and coverage probability, each averaged over the grid of M spatial locations t₁, . . . , t_M. The coverage probability is the proportion of the M grid locations for which the posterior 95% interval for μ(t_j) covers the true value. For the plug-in model and the full model, we also report the power for a in Table 1 which is defined to be the proportion of datasets for which the posterior 95% credible interval for a excludes zero.

Table 1.

Simulation study results

Design	Model	mse (×102)	mad (×102)	Bias (×102)	cp (×102)	Power for a (×102)
(i)	nis	33.1 (2.8)	41.3 (0.6)	2.0 (1.3)	93.0 (1.0)	–
	Plug-in	32.2 (1.7)	41.3 (0)	2.5 (1.3)	93.0 (1.0)	10.0
	Full	31.9 (1.2)	41.5 (0.7)	2.5 (1.3)	93.0 (1.0)	10.0
(ii)	nis	49.4 (5.0)	50.0 (1.1)	−25.8 (1.3)	90.0 (1.0)	–
	Plug-in	39.2 (5.5)	44.8 (0.9)	−13.9 (1.3)	91.0 (1.0)	74.0
	Full	32.9 (2.8)	43.2 (0.8)	−7.5 (1.6)	93.0 (1.0)	80.0
(iii)	nis	13.2 (1.1)	28.1 (1.8)	−8.3 (1.4)	94.0 (1.0)	–
	Plug-in	12.1 (0.8)	27.1 (1.8)	−3.1 (1.4)	94.0 (1.0)	40.0
	Full	10.8 (0.7)	25.3 (1.4)	−2.0 (1.3)	95.0 (1.0)	50.0
(iv)	nis	25.6 (1.1)	36.9 (0.7)	−15.3 (1.2)	92.0 (1.0)	–
	Plug-in	20.9 (0.8)	33.9 (0.5)	−7.2 (1.1)	92.0 (1.0)	88.0
	Full	19.1 (0.6)	32.6 (0.4)	−0.8 (1.0)	94.0 (1.0)	98.0

nis, noninformative sampling; mse, mean squared error; mad, mean absolute deviation; cp, convergence probability.

All three methods perform similarly, when sampling is not informative. In this case, the informative sampling methods rarely identify a as significant and reduce to the usual geostatisti-cal model. The noninformative sampling model has high mean squared error and negative bias in the remaining designs with informative sampling. The two methods that allow for informative sampling reduce mean squared error compared with the noninformative sampling model. The informative sampling models also reduce bias, although some bias remains, especially for design (ii). In all cases, the full model improves on the plug-in approach. The relative mean squared error of the noninformative sampling model to the full model is smaller for design (iii) (0.132/0.108 = 1.222) with large spatial range and design (iv) (0.256/0.190 = 1.47), a larger sample size than for design (ii) (0.494/0.329 = 1.502), so it seems that accounting for informative sampling is most important for small datasets with considerable spatial variation.

To analyse sensitivity to the prior for a, we redid simulation design (ii) with a = 1 and = 0.2 and used four different priors for a: N(1, 1), N(0, 1), N(0, 10²) and an improper prior. In summary, the mean-squared prediction error and predictive coverage are insensitive to the hyper-parameters of the prior on a for n = 150 and n = 200. Even for a sample size as small as n = 50, differences are small for different priors. However, the N(0, 10²) prior and the informative prior N(1, 1) lead to a better power for a than the others when n = 50 and 100. The minimum sample size needed to swamp out the prior for a is ∼ 150 in this example.

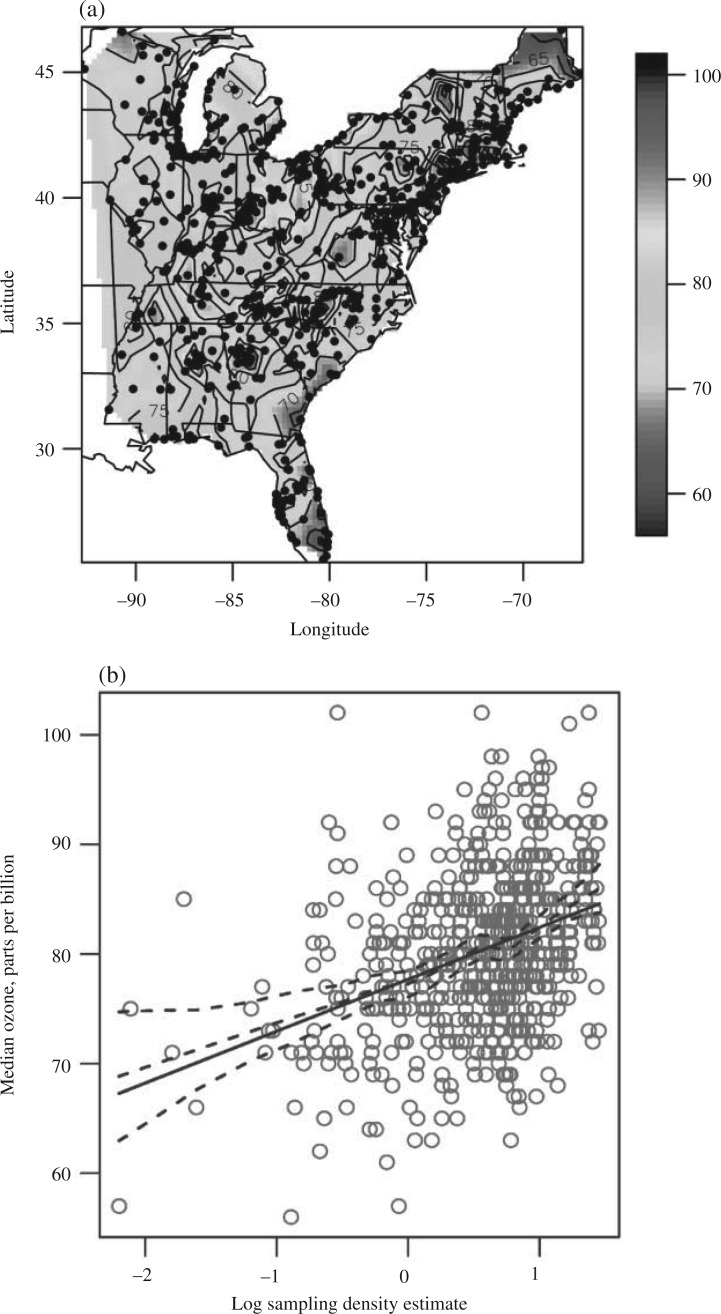
6. Analysis of Eastern United States ozone data

With the increasing concern about air pollution and climate change, building predictive models for ozone is an important area. It is often the case that the monitoring locations are informative about the ozone surface and hence it is important to account for informative sampling. We analyse the median daily ozone for June–August 2007 for n = 631 observations in Eastern U.S.A. The data are plotted in Fig. 1(a). There is a clear association between the sampling density and the response, as there are more monitors placed in areas with high ozone, such as Atlanta and New England, than in areas with low ozone, such as Mississippi and West Virginia. We fit a generalized additive model to the median ozone values and the kernel density estimate of the log sampling density using locally weighted scatterplot smoothing as shown in Fig. 1(b). The linear fit is entirely contained within the generalized additive model 95% confidence intervals for all values of the log sampling density estimate, supporting the log-linear model in (1).

Fig. 1.

Plots of the ozone data. (a) The ozone data in parts per billion and the monitor locations (points). (b) The estimated log sampling density against the response. Log sampling density versus median ozone (circles), gamfit with 95% intervals (dashed line), linear fit (solid line).

To apply a stationary spatial model, we first project the spatial locations to a two-dimensional surface using the Mercator projection, and then scale them to the unit square coordinate-wise by subtracting the minimum and dividing by the range of the observation locations. We fit the informative sampling model with a 30 × 30 grid of knots on [−0.2, 1.2]² in the kernel convolution approximation in (6) and a 50 × 50 grid of points on [0, 1]² in the integral approximation in the sampling density (4). Points outside the convex hull of the observation locations or outside the continental United States were discarded from integral approximation to the sampling density, leaving M = 1077. Kernel convolution knots not within 0.1 of an integral approximation knot were discarded, leaving N = 490.

We include a second-order spatial trend as predictors in x(s), that is, linear and quadratic terms for rescaled latitude and longitude and their interaction. We compare the noninformative sampling, plug-in and full models described in §5. The posteriors for several parameters are summarized in Table 2. The spatial process for both the mean process and sampling density are fairly smooth. The posterior 95% intervals for ν_ξ and ν_η exclude the exponential covariance (ν = 0.5) for all the three models.

Table 2.

Mean and 95% intervals for the ozone data

Parameters	nis	Plug-in	Full
a	–	4.43 (2.16, 6.46)	3.21 (2.12, 4.25)
σ	4.68 (4.37, 5.03)	4.70 (4.38, 5.04)	4.78 (4.47, 5.12)
τg	0.17 (0.14, 0.27)	0.15 (0.13, 0.19)	0.17 (0.13, 0.21)
ρg	0.06 (0.05, 0.16)	0.06 (0.04, 0.10)	0.06 (0.05, 0.10)
νg	3.95 (0.92, 6.42)	3.46 (1.53, 5.52)	12.6 (0.74, 28.8)
τf	–	–	0.05 (0.04, 0.06)
ρf	–	–	0.07 (0.04, 0.13)
νf	–	–	10.7 (0.74, 28.77)

nis, noninformative sampling.

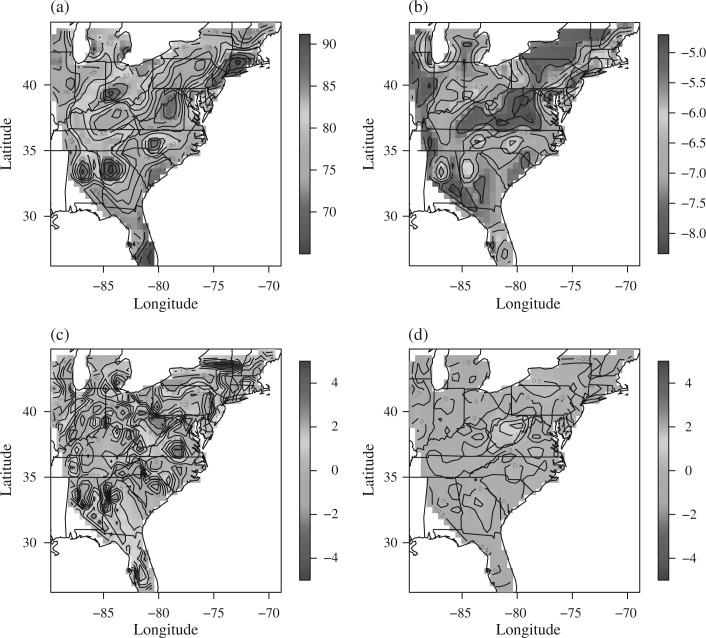
The 95% interval of a for both the plug-in model (2.16, 6.46) and fully Bayesian model (2.12, 4.25) excludes zero, indicating an informative sampling scheme. The scale of a’s posterior is not comparable between the two models, because the plug-in density estimate has been standardized to have zero-mean and variance one. The effect of accounting for informative sampling is illustrated in Fig. 2. The difference in predicted values between the noninformative sampling and full model in Fig. 2(c) is the largest in Northern Pennsylvania and West Virginia. These areas have relatively few monitors and are near areas with high ozone. The difference between the non-informative sampling and plug-in predictions in Fig. 2(d) are also positive in these areas though the differences are not nearly as large in the plug-in analysis. This may be because the plug-in estimates do not appropriately account for uncertainty in estimation, and hence may lead to some attenuation of the estimated surface.

Fig. 2.

The effect of accounting for informative sampling. (a) Posterior mean predicted values; (b) log sampling density from the full model; (c) the difference in posterior mean predicted values of the noninformative sampling model and full model and (d) the plug-in model.

Finally, we refit the model with different priors and different knot locations to test for sensitivity to these assumptions. We fit the model with 20 × 20 and 40 × 40 initial grids of knots in the kernel convolution approximation. After removing knots outside the domain of interest, we obtain N = 206 and N = 876 knots, respectively. The results were fairly similar to the original 30 × 30 grid. In all cases the posterior of a was separated from zero, the posterior median being 3.31 and 2.85 for N = 206 and N = 876 knots, respectively, and the largest difference between the NIS and full model was in the Northern Pennsylvania and West Virginia.

7. Discussion

We have focused on a simple model for informative locations, which assumes that the outcomes are conditionally independent of the locations, given the mean process μ(s) and the spatial location density p(s). In addition, we include a single parameter a controlling the informativeness of the sampling process. These simplifying assumptions certainly make the theory and computation more tractable. However, to characterize the data from a broader variety of applications more realistically, it may be necessary to generalize the models. There are several interesting directions in this regard. First, it is straightforward conceptually to replace the constant a with a spatially varying coefficient a(s), which is assigned a Gaussian process prior. This generalization allows the informativeness of the sampling locations to vary spatially; for example, in certain regions, e.g., near cities, monitors may be placed without regard to the outcome, while in the rural areas, monitors may be placed at sites likely to have high values of ozone. It is an open question whether one can consistently estimate a(s) in this extended model without very restrictive assumptions. However, a simple adjustment for informative sampling may be preferable to more complicated models that require rich datasets for reliable estimation.

Appendix.

Proof of Theorem 1. Let ϕ = (ξ_r, η_r, β_ξ, β_η, a, σ) and ϕ₀ = (ξ_0r, η_0r, β_ξ0, β_η0, a₀, σ₀) be a fixed set of parameters in 𝒞(𝒟) × 𝒞(𝒟) × 𝕉 × 𝕉⁺. Clearly (y_i, s_i) ∼ f (y, s | ϕ), where

$$f(y,s|\phi )=f(y|s,\phi )p(s|\phi )=\frac{1}{\surd (2\pi {\sigma }^2)}\text{exp}\left[-\frac{{\{y-\mu (s)\}}^2}{2{\sigma }^2}\right]\frac{\text{exp}\{x{(s)}^{\text{T}}{\beta }_{\xi }+{\xi }_r(s)\}}{{\int }_{𝒟}\text{exp}\{x{(s)}^{\text{T}}{\beta }_{\xi }+{\xi }_r(s)\}ds}.$$

Here μ(s) = x(s)^T(aβ_ξ + β_η) + aξ_r(s) + η_r(s). Let μ₀(s) = x(s)^T(a₀β_ξ0 + β_η0) + a₀ξ_0r (s) + η_0r(s). Define Λ(ϕ₀, ϕ) = log {f (y, s | ϕ₀)/f (y, s | ϕ)} and K (ϕ₀, ϕ) = E_ϕ0{Λ(ϕ₀, ϕ)}. Then following Schwartz (1965), its enough to show that for all ∊ > 0,

$$({\mathrm{\Pi }}_{{\xi }_r}\times {\mathrm{\Pi }}_{{\eta }_r}\times {\pi }_{{\beta }_{\xi }}\times {\pi }_{{\beta }_{\eta }}\times {\pi }_{\sigma }\times {\pi }_a)\{\varphi :K({\varphi }_0,\varphi )<∊\}>0.$$

We calculate K (ϕ₀, ϕ) using the following equation:

$$\begin{array}{lll}K({\phi }_0,\phi )\hfill & =\hfill & E_{{\phi }_0}\{\mathrm{\Lambda }({\phi }_0,\phi )\}=E_{{\phi }_0}\left\{\text{log}\frac{f(y,s|{\phi }_0)}{f(y,s|\phi )}\right\}\hfill \\ \hfill & =\hfill & \frac{1}{2}\text{log}\frac{{\sigma }^2}{{\sigma }_0^2}+E_{{\phi }_0}\left[-\frac{{\{y-{\mu }_0(s)\}}^2}{2{\sigma }_0^2}\right]-E_{{\phi }_0}\left[-\frac{{\{y-\mu (s)\}}^2}{2{\sigma }^2}\right]\hfill \\ \hfill & \hfill & -E_{{\phi }_0}\{x{(s)}^{\text{T}}({\beta }_{\xi }-{\beta }_{\xi 0})+{\xi }_r(s)-{\xi }_{0r}(s)\}+\text{log}\left[\frac{{\int }_{𝒟}\text{exp}\{x{(s)}^{\text{T}}{\beta }_{\xi }+{\xi }_r(s)\}ds}{{\int }_{𝒟}\text{exp}\{x{(s)}^{\text{T}}{\beta }_{\xi 0}+{\xi }_{0r}(s)\}ds}\right]\hfill \\ \hfill & =\hfill & \frac{1}{2}\text{log}\frac{{\sigma }^2}{{\sigma }_0^2}-\frac{1}{2}\left(1-\frac{{\sigma }_0^2}{{\sigma }^2}\right)+\frac{1}{2{\sigma }^2}{\int }_{𝒟}{\{{\mu }_0(s)-\mu (s)\}}^{2}p(s)ds\hfill \\ \hfill & \hfill & +{\int }_{𝒟}\{x{(s)}^{\text{T}}({\beta }_{\xi }-{\beta }_{\xi 0})+{\xi }_r(s)-{\xi }_{0r}(s)\}p(s)ds\hfill \\ \hfill & \hfill & +\text{log}\left[\frac{{\int }_{𝒟}\text{exp}\{x{(s)}^{\text{T}}{\beta }_{\xi }+{\xi }_r(s)\}ds}{{\int }_{𝒟}\text{exp}\{x{(s)}^{\text{T}}{\beta }_{\xi 0}+{\xi }_{0r}(s)\}ds}\right].\hfill \end{array}$$

For each δ > 0, define

$$\begin{array}{l}{B}_{\delta }=\{\phi :{\Vert {\xi }_r-{\xi }_{0r}\Vert }_{\infty }<\delta ,{\Vert {\eta }_r-{\eta }_{0r}\Vert }_{\infty }<\delta ,\Vert {\beta }_{\xi }-{\beta }_{f0}\Vert <\delta ,\Vert {\beta }_g-{\beta }_{g0}\Vert <\delta ,\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}|a-a_0|<\delta ,|\sigma /{\sigma }_0-1|<\delta \}.\end{array}$$

Take b₁ = ‖μ₀ − μ‖_∞ and b₂ = σ/σ₀. Let g₁(b₁, b₂) = log b₂ − ( $b_2^2$ − 1)/(2 $b_2^2$) + $b_1^2$/(2 ${\sigma }_0^2{b}_2^2$). Clearly g₁(b₁, b₂) is continuous at b₁ = 0 and b₂ = 1 and g₁(0, 1) = 0. We have

$$b_1⩽M\Vert (a{\beta }_{\xi }+{\beta }_{\eta })-(a_0{\beta }_{\xi 0}+{\beta }_{\eta 0})\Vert +\Vert \{a{\xi }_r(s)+{\eta }_r(s)\}-\{a_0{\xi }_{0r}(s)+{\eta }_{0r}(s)\}\Vert$$

and

$$\begin{array}{c}K({\varphi }_0,\varphi )⩽g_1(b_1,b_2)+{\int }_{𝒟}\{x{(s)}^{\text{T}}({\beta }_{\xi }-{\beta }_{\xi 0})+{\xi }_r(s)-{\xi }_{0r}(s)\}p(s)ds\\ +\text{log}\left[\frac{{\int }_{𝒟}\text{exp}\{x{(s)}^{\text{T}}{\beta }_{\xi }+{\xi }_r(s)\}ds}{{\int }_{𝒟}\text{exp}\{x{(s)}^{\text{T}}{\beta }_{\xi 0}+{\xi }_{0r}(s)\}ds}\right].\end{array}$$

For ∊ > 0, there exists a δ₁ > 0 such that for all ϕ ∈ B_δ1,

$$\frac{1}{2}\text{log}\frac{{\sigma }^2}{{\sigma }_0^2}-\frac{1}{2}\left(1-\frac{{\sigma }_0^2}{{\sigma }^2}\right)+\frac{1}{2{\sigma }^2}{\int }_{𝒟}{\{{\mu }_0(s)-\mu (s)\}}^{2}p(s)ds<\frac{∊}{3}.$$

There also exists δ₂ > 0 such that for all ϕ ∈ B_δ2, {x(s)^T(β_ξ − β_ξ0) + ξ_r (s) − ξ_0r(s)} < ∊/3 uniformly for all s ∈ 𝒟. If we define h_ϕ(s) = exp{x(s)^T β_ξ + ξ_r(s)}, then ϕ ↦ ∫_𝒟h_ϕ(s) ds is a continuous function and hence ϕ ↦ log{∫_𝒟 h_ϕ (s) ds} is also a continuous function. So, there exists a δ₃ > 0 such that

$$\varphi \in B_{{\delta }_3}\Rightarrow \text{log}\left\{{\int }_{𝒟}{h}_{\varphi }(s)ds\right\}-\text{log}\left\{{\int }_{𝒟}{h}_{{\varphi }_0}(s)ds\right\}<\frac{∊}{3}.$$

Choosing δ = min{δ₁, δ₂, δ₃}, ϕ ∈ B_δ implies K (ϕ₀, ϕ) < ∊. From T. Choi’s unpublished 2005 Ph.D thesis, it follows that with the priors specified in §3.1

$$({\mathrm{\Pi }}_{{\xi }_r}\times {\mathrm{\Pi }}_{{\eta }_r}\times {\pi }_{{\beta }_{\xi }}\times {\pi }_{{\beta }_{\eta }}\times {\pi }_{\sigma }\times {\pi }_a)(B_{\delta })>0.$$

Hence,

$$({\mathrm{\Pi }}_{{\xi }_r}\times {\mathrm{\Pi }}_{{\eta }_r}\times {\pi }_{{\beta }_{\xi }}\times {\pi }_{{\beta }_{\eta }}\times {\pi }_{\sigma }\times {\pi }_a)\{\varphi :K({\varphi }_0,\varphi )<∊\}>0.$$

Proof of Theorem 2. The prior specifications on ρ_ξ, ρ_η, τ_ξ and τ_η enable one to bound any quadratic forms and determinants involving ${\mathrm{\Sigma }}_{\xi }^n$ and ${\mathrm{\Sigma }}_{\eta }^n$ by fixed quantities. Hence, in showing that the posterior p(a |y, s) is proper, its enough to treat ρ_ξ, ρ_η, τ_ξ and τ_η as constants. Without loss of generality, we can work with 𝒟 = [0, 1]² by the projection argument described in §6. Following Benes et al. (2003), we consider the grid approximation of the infinite dimensional Gaussian process {ξ_r (s) : s ∈ 𝒟}, denoted by ξ_r. Let $𝒟={\cup }_{j=1}^J{I}_j$, with {I_j} denoting a segmentation of 𝒟 into contiguous regions of equal area Δ = J⁻¹ ∫_𝒟ds. Choose J sufficiently large such that at most one s_i lies within any I_j. The infinite-dimensional Gaussian process, ξ_r, can be approximated by a finite dimensional vector ${\xi }_r^J={({\xi }_r^{*1},\dots ,{\xi }_r^{*J})}^{\text{T}}$, corresponding to the choice of arbitrary points $s_1^{*},\dots ,s_J^{*}$ within I₁, . . . , I_J, respectively, such that ξ_r (s_i) = ${\xi }_r^{*j}$ if s_i ∈ I_j. Thus ${\xi }_r^J$ ∼ N(0, ${\mathrm{\Sigma }}_{\xi }^{*J}$), where ${({\mathrm{\Sigma }}_{\xi }^{*J})}_{ij}=c(\Vert s_i^{*}-s_j^{*}\Vert |\psi )$. Define the true posterior p^true( ${\xi }_r^n$|s) and the approximated posterior p^J ( ${\xi }_r^n$|s) as follows:

$$p^{\text{true}}({\xi }_r^n|s)\propto p^{\text{true}}({\xi }_r^n,s)=E{\left\{\int \text{exp}\{x{(s)}^{\text{T}}{\beta }_{\xi }+{\xi }_r(s)\}ds|{\xi }_r^n\right\}}^{-n}\text{exp}\{-0.5{({\xi }_r^n)}^{\text{T}}{({\mathrm{\Sigma }}_{\xi }^n)}^{-1}{({\xi }_r^n)}^{\text{T}}\}$$

and

$$p^J({\xi }_r^n|s)\propto p^J({\xi }_r^n,s)={\left[\mathrm{\Delta }\sum _{j=1}^J\text{exp}\{x{(s_j^{*})}^{\text{T}}{\beta }_{\xi }+{\xi }_r(s_j^{*})\}\right]}^{-n}\text{exp}\{-0.5{({\xi }_r^J)}^{\text{T}}{({\mathrm{\Sigma }}_{\xi }^{*J})}^{-1}{({\xi }_r^J)}^{\text{T}}\}.$$

Marginalizing out ${\eta }_r^n$, we have y|s, ξ_r, a, σ², β_η, β_ξ ∼ N(Xβ* + a ${\xi }_r^n$, σ²I_n + ${\mathrm{\Sigma }}_{\eta }^n$), where X^T = {x(s₁) ⋯ x(s_n)}. The true posterior of ( ${\xi }_r^n$, a, σ², β_ξ, β_η) is

$$p^{\text{true}}({\xi }_r^n,a,{\beta }_{\xi },{\beta }_{\eta },{\sigma }^2|y,s)\propto p(y|s,{\xi }_r,a,{\sigma }^2,{\beta }_{\xi },{\beta }_{\eta })p^{\text{true}}({\xi }_r^n,s)\pi ({\sigma }^2)\pi ({\beta }_{\xi })\pi ({\beta }_{\eta }).$$

Benes et al. (2003) showed that, under these assumptions, for a fixed s ∈ 𝒟ⁿ, the expectation of any bounded function with respect to p^J( ${\xi }_r^n$|s) converges to the corresponding expectation with respect to p^true( ${\xi }_r^n$|s) as J tends to infinity. Hence, there exists a J such that the expectation of the bounded function with respect to p^J ( ${\xi }_r^n$|s) is greater than the corresponding expectation with respect to (1/2) p^true( ${\xi }_r^n$|s). Thus, in order to show propriety of the true posterior of ( ${\xi }_r^n$, a, σ², β_ξ, β_g), which involves p^true( ${\xi }_r^n$|s), it is enough to show the propriety of the approximated posterior p^J ( ${\xi }_r^n$, a, β_ξ, β_η, σ²| y, s). The approximated posterior of ( ${\xi }_r^n$, a, σ², β_ξ, β_η) is

$$\begin{array}{lll}{p}^J({\xi }_r^n,a,{\beta }_{\xi },{\beta }_{\eta },{\sigma }^2|y,s)\hfill & =\hfill & C\text{exp}\{-0.5{(Y-X\beta *-a{\xi }_r^n)}^{\text{T}}{({\sigma }^2{I}_n+{\mathrm{\Sigma }}_{\eta }^n)}^{-1}(Y-X\beta *-a{\xi }_r^n)\}\hfill \\ \hfill & \hfill & \times \text{exp}\{-0.5{({\xi }_r^J)}^{\text{T}}{({\mathrm{\Sigma }}_{\xi }^{{*}^J})}^{-1}({\xi }_r^J)\}\pi ({\beta }_{\xi })\pi ({\beta }_{\eta })\hfill \\ \hfill & \hfill & \times \pi ({\sigma }^2)\frac{\text{exp}\{{\sum }_{i=1}^{n}x{(s_i)}^{\text{T}}{\beta }_{\xi }+{\xi }_r(s_i)\}}{{\mathrm{\Delta }}^n{[{\sum }_{j=1}^J\text{exp}\{x{(s_j^{*})}^{\text{T}}{\beta }_{\xi }+{\xi }_r^{*j}\}]}^n},\hfill \end{array}$$

where C is a constant. As exp{x(s_i)^Tβ_ξ + ξ_r (s_i)} < ${\sum }_{j=1}^J\text{exp}\{x{(s_j^{*})}^{\text{T}}{\beta }_{\xi }+{\xi }_r^{*j}\}$ for all i = 1, . . . , n,

$$\frac{\text{exp}\{{\sum }_{i=1}^{n}x{(s_i)}^{\text{T}}{\beta }_{\xi }+{\xi }_r(s_i)\}}{{[{\sum }_{j=1}^J\text{exp}\{x{(s_j^{*})}^{\text{T}}{\beta }_{\xi }+{\xi }_r^{*j}\}]}^n}<1.$$

After integrating out ${\xi }_r^J$, excluding ${\xi }_r^n$, we are left with

$$\begin{array}{lll}p({\xi }_r^n,a,{\beta }_{\xi },{\beta }_{\eta },{\sigma }^2|Y,s)\hfill & ⩽\hfill & C_1\text{exp}\{-0.5{(Y-X\beta *-a{\xi }_r^n)}^{\text{T}}{({\sigma }^2{I}_n+{\mathrm{\Sigma }}_{\eta }^n)}^{-1}(Y-X\beta *-a{\xi }_r^n)\}\hfill \\ \hfill & \hfill & \times \text{exp}{\{-0.5{({\xi }_r^n)}^{\text{T}}{(\mathrm{\Sigma }}_f^n)}^{-1}({\xi }_r^n)\}\pi ({\beta }_{\xi })\pi ({\beta }_{\eta })\pi ({\sigma }^2),\hfill \end{array}$$

where C₁ > 0 is a constant and ${\mathrm{\Sigma }}_{\xi }^n$ is the variance–covariance matrix of ${\xi }_r^n$ constructed out of ${\mathrm{\Sigma }}_{\xi }^{*J}$. Setting Z = (y − Xβ^*)/a, Σ = ( ${\mathrm{\Sigma }}_{\eta }^n$+ σ²I_n)/a² and Ω_η = {( ${\mathrm{\Sigma }}_{\xi }^n$)⁻¹ + Σ⁻¹}⁻¹ and completing quadratic forms yield

$$\begin{array}{lll}p({\xi }_r^n,a,{\beta }_{\xi },{\beta }_{\eta },{\sigma }^2|y,s)\hfill & ⩽\hfill & C_2\text{exp}\{-0.5{({\xi }_r^n-{\mathrm{\Omega }}_{\eta }{\mathrm{\Sigma }}^{-1}Z)}^{\text{T}}{\mathrm{\Omega }}_{\eta }^{-1}({\xi }_r^n-{\mathrm{\Omega }}_{\eta }{\mathrm{\Sigma }}^{-1}Z)\}\hfill \\ \hfill & \hfill & \times \text{exp}\{-0.5(Z^{\text{T}}{\mathrm{\Sigma }}^{-1}Z-Z^{\text{T}}{\mathrm{\Sigma }}^{-1}{\mathrm{\Omega }}_{\eta }{\mathrm{\Sigma }}^{-1}Z)\}\pi ({\beta }_{\xi })\pi ({\beta }_{\eta })\pi ({\sigma }^2),\hfill \end{array}$$

where C₂ > 0 is another constant. Next we state a useful lemma from matrix algebra.

Lemma 1. If A and B are positive definite square matrices so is A − A(A + B)⁻¹ A.

Proof. We have

$$A-A{(A+B)}^{-1}A=A{(A+B)}^{-1}B={\{B^{-1}(A+B)A^{-1}\}}^{-1}={(B^{-1}+A^{-1})}^{-1}.$$

The conclusion follows from the fact that the sum and inverses of positive definite matrices of the same dimension are also positive definite.

From Lemma 1, we have (Z^TΣ⁻¹Z − Z^TΣ⁻¹Ω_ηΣ⁻¹Z) ⩾ 0, so that

$$\begin{array}{lll}p({\xi }_r^n,a,{\beta }_{\xi },{\beta }_{\eta },{\sigma }^2|y,s)\hfill & ⩽\hfill & C_2\text{exp}\{-0.5{({\xi }_r^n-{\mathrm{\Omega }}_{\eta }{\mathrm{\Sigma }}^{-1}Z)}^{\text{T}}{\mathrm{\Omega }}_{\eta }^{-1}({\xi }_r^n-{\mathrm{\Omega }}_{\eta }{\mathrm{\Sigma }}^{-1}Z)\}\hfill \\ \hfill & \hfill & \times \pi ({\beta }_{\xi })\pi ({\beta }_{\eta })\pi ({\sigma }^2).\hfill \end{array}$$

Integrating out ${\xi }_r^n$first and then β_ξ and β_η,

$$p(a,{\sigma }^2|y,s)⩽C_3|{({\mathrm{\Sigma }}_{\xi }^n)}^{-1}+a^2{({\mathrm{\Sigma }}_{\eta }^n+{\sigma }^2{I}_n)}^{-1}{|}^{-(1/2)}.$$

Call ${\mathrm{\Sigma }}_{\xi }^n$ = A and ${\mathrm{\Sigma }}_{\eta }^n$ = B. Hence

$$|A^{-1}+a^2{(B+{\sigma }^{2}I)}^{-1}|=\frac{|I+a^{2}A{(B+{\sigma }^{2}I)}^{-1}|}{\left|A\right|}=\frac{|a^{2}A+{\sigma }^{2}I+B|}{|{\sigma }^{2}I+B|\left|A\right|}.$$

Now we state a useful result from matrix algebra.

Proposition 1. If A and B and nonnegative definite matrices, then | A + B| ⩾ | A| + |B| with strict inequality holding in case of positive definite matrices.

Using Proposition 1, we get

$$\begin{array}{lll}{\left(\frac{|a^{2}A+{\sigma }^{2}I+B|}{|{\sigma }^{2}I+B|}\right)}^{-(1/2)}\hfill & ⩽\hfill & {\left(\frac{\left|a^{2}A\right|+|{\sigma }^{2}I+B|}{|{\sigma }^{2}I+B|}\right)}^{-(1/2)}\hfill \\ \hfill & =\hfill & {\left\{1+\frac{a^{2n}\left|A\right|}{{\prod }_{i=1}^n({\sigma }^2+b_i)}\right\}}^{-(1/2)}\hfill \\ \hfill & ⩽\hfill & {\left\{1+\frac{a^{2n}\left|A\right|}{{({\sigma }^2+b_n)}^n}\right\}}^{-(1/2)},\hfill \end{array}$$

where 0 < b₁ ⩽ b₂ ⩽ ⋯ ⩽ b_n are the eigen values of B. By Minkowski’s inequality we get

$${\left\{1+\frac{a^{2n}\left|A\right|}{{({\sigma }^2+b_n)}^n}\right\}}^{-(1/2)}⩽\frac{{({\sigma }^2+b_n)}^{n/2}}{c_n{(a^2|A{|}^{(1/n)}+{\sigma }^2+b_n)}^{n/2}}.$$

Set |A|^1/n = k₁ and b_n = k₂. We assume n ⩾ 2. Then ignoring constants

$$\begin{array}{lll}{\int }_{-\infty }^{\infty }\frac{{({\sigma }^2+b_n)}^{n/2}}{{(a^2|A{|}^{1/n}+{\sigma }^2+b_n)}^{n/2}}da\hfill & =\hfill & {\int }_{-\infty }^{\infty }\frac{1}{{\{1+(a^2{k}_1)/({\sigma }^2+k_2)\}}^{n/2}}da\hfill \\ \hfill & ⩽\hfill & {\int }_{-\infty }^{\infty }\frac{1}{\{1+(a^2{k}_1)/({\sigma }^2+k_2)\}}da\hfill \\ \hfill & =\hfill & \pi {\left(\frac{{\sigma }^2+k_2}{k_1}\right)}^{(1/2)}.\hfill \end{array}$$

Now, since E_π (σ) < ∞,

$${\int }_0^{\infty }{\left(\frac{{\sigma }^2+k_2}{k_1}\right)}^{(1/2)}\pi (d{\sigma }^2)<\infty .$$

By Fubini’s Theorem, p(a | Y, s) is integrable.