Design and Coordination Kinematics of an Insertable Robotic Effectors Platform for Single-Port Access Surgery

Abstract

Single port access surgery (SPAS) presents surgeons with added challenges that require new surgical tools and surgical assistance systems with unique capabilities. To address these challenges, we designed and constructed a new insertable robotic end-effectors platform (IREP) for SPAS. The IREP can be inserted through a Ø15 mm trocar into the abdomen and it uses 21 actuated joints for controlling two dexterous arms and a stereo-vision module. Each dexterous arm has a hybrid mechanical architecture comprised of a two-segment continuum robot, a parallelogram mechanism for improved dual-arm triangulation, and a distal wrist for improved dexterity during suturing. The IREP is unique because of the combination of continuum arms with active and passive segments with rigid parallel kinematics mechanisms. This paper presents the clinical motivation, design considerations, kinematics, statics, and mechanical design of the IREP. The kinematics of coordination between the parallelogram mechanisms and the continuum arms is presented using the pseudo-rigid-body model of the beam representing the passive segment of each snake arm. Kinematic and static simulations and preliminary experiment results are presented in support of our design choices.

I. Introduction

Robotic assistance in minimally invasive surgery (MIS) extended the capabilities of surgeons via improved precision, dexterity, and computer assistance [1], [2]. Recently, novel single port access surgery (SPAS) and natural orifice transluminal endoscopic surgery (NOTES) have been investigated by the authors in [3]–[6] for their potential benefits in reducing patient trauma and shortening their recovery time compared to traditional multiport laparoscopic MIS. However, SPAS and NOTES also set strict requirements for instrument miniaturization, dexterity, and collision avoidance between surgical tools operating in confined spaces. Existing surgical robots for MIS cannot satisfy these requirements due to either dexterity deficiency or the size of their actuation mechanisms that prohibit a multitude of arms from operating through a single port. Therefore, to date, SPAS is still limited to a small number of academic centers using instruments that are not clinically proven to be able to facilitate SPAS [7]–[9].

Surgeons and engineers tried to overcome the single-port constraint by using multiport trocars (Triport^® from Advanced Surgical Concepts, Wicklow, Ireland) and single incision laparoscopic surgery port from (Covidien, Inc.), which allow multiple instruments to pass through a single port. Others (Realhand^® from Novare and Cambridge Endo) used instruments which can articulate to avoid the collision between the operator hands [9]. Animal studies of single-port access laparoscopic cholecystectomy have been carried out using these instruments [8]. However, the use of manual instruments requires surgeons to operate with crossed hands and relies on exceptional hand–eye coordination and substantial training.

Other researchers developed robotic assistance tools for NOTES. Abbott [4] developed a wire-actuated dual-arm robotic system for NOTES which has 16 DoF and a diameter larger than 20 mm. Phee et al. [6] presented a 9 DoF Ø22 mm dual-arm robot. Lehman et al. [5] developed NOTES robot that may be inserted into the abdomen via a Ø20 mm overtube. This robot requires surgeon intervention to switch it from a folded configuration to a working configuration. It is also fixed to the abdomen using external magnets. More recently, Harada et al. [10] introduced a novel concept of reconfigurable self-assembling robot for NOTES. This concept has yet to be experimentally proven. Lee et al. [11] presented a stackable four-bar mechanism for single SPAS. Picciagallo et al. [12] presented a dual-arm robot for SPAS. This design used embedded motors inside the links; it has a diameter of 23 mm. Finally, intuitive surgical is developing a dual-arm SPAS system [13] that uses wire-actuated snake-like articulated linkages.

This paper addresses the need for self-deploying robots that provide adequate dexterity in a diameter smaller than 20 mm, while seamlessly supporting 3-D vision feedback during all operation phases (deployment and work). The contributions of this paper are 1) mechanical design of an insertable robotic end-effector platform (IREP) as an enabling technology for SPAS. This novel design incorporates parallel mechanisms and continuum robots with active and passive segments. A unique and novel feature of this design is the improved ability to triangulate the two robotic arms to a surgical site through the use of a hybrid mechanical architecture that incorporates parallel mechanisms and continuum robots with passive and active segments; 2) a kinematic coordination algorithm that coordinates the motion of the parallel mechanisms and the flexible passive segment of each continuum robot; thus, achieving increased workspace while eliminating mechanical overconstraint; and 3) a complete kinematic and static model of the IREP system is used for task-based design and determination of actuator specifications.

II. Clinical Motivation

The clinical rationale for SPAS is based on the principle that reduced abdominal wall trauma results in better outcomes for the patient. As opposed to traditional MIS, SPAS requires a single incision, usually in the umbilicus, rather than multiple incisions. In SPAS, all necessary imaging and instrumentation are inserted through this single incision. In addition to the reduction or the elimination of visible scars, there is potential for less pain and less stress response during and after surgery [3]–[6]. Furthermore, the surgical site infection (SSI) rate is significantly less when using a laparoscopic approach, and a reduction in the number of incisions at risk has the potential to further reduce the incidence of SSI [14]. These benefits suggest that SPAS offers significant benefit to candidates of abdominal surgery.

The hypothesis driving our research is that minimizing the number and size of incisions will lead to patient benefits in recovery time, stress response, SSI incidence, and improved cosmesis. To validate this hypothesis, we designed and constructed the first prototype of the IREP. We believe that successful augmentation of vision feedback combined with telemanipulation assistance will simplify SPAS procedures and increase adoption of this surgical approach in a manner similar to the growth and adoption of MIS supported by the development of MIS instrumentation.

While the IREP prototype is being developed as a SPAS platform for general abdominal procedures, gall bladder removal, termed cholecystectomy, serves as a benchmark procedure because it presents the typical abdominal surgical challenges of suturing, dissection, and specimen extraction.

III. IREP and Its Design Specifications

Fig. 1 shows the first prototype of telerobotic slave of the IREP (this design was first presented in [15]). This prototype has two dexterous arms and a controllable stereo-vision module. Each dexterous arm is comprised from a two-segment continuum snake robot, a parallelogram mechanism, a distal wrist, and a gripper. Each snake arm has two active segments and one passive segment. Each active segment bends in two Degrees-of-Freedom (DoFs) in any direction by using push–pull actuation of NiTi tubes in a manner similar to our previous designs in [16] and [17]. The passive segment is a flexible portion of the snake robot that connects the active segments to the actuation unit. The parallelogram mechanisms serve the purpose of adjusting the location of the base of the proximal¹ active segment of each snake. This functionality increases the workspace of the snake arms and improves dexterity [18].

Fig. 1.

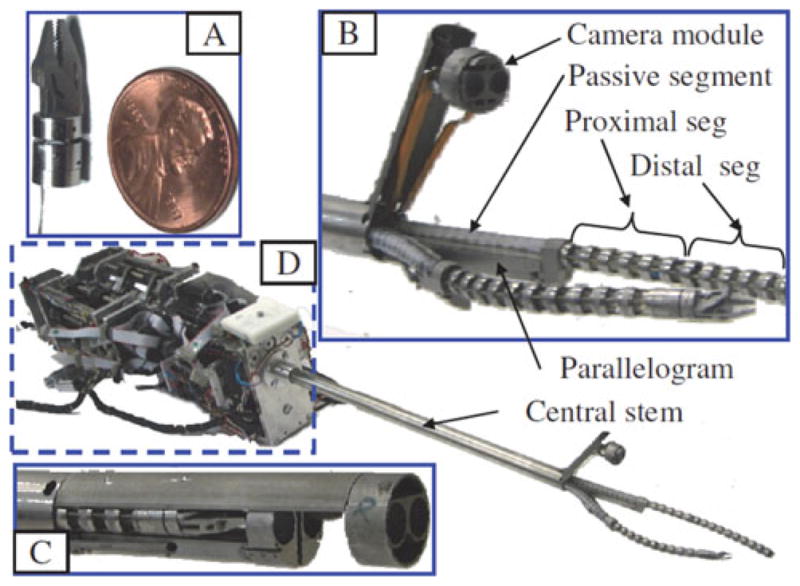
IREP robot has two dexterous arms and a controllable stereo vision module. (a) Gripper and distal wrist. (b) IREP distal end in a working configuration. (c) IREP in a closed configuration (bottom shell cover removed). (d) Modular actuation unit of the IREP.

The workspace of the IREP has been validated through simulation and it was shown in [15] that the proposed design in Fig. 1 is capable of covering a workspace of 50 × 50 × 50 mm as required for typical abdominal procedures such as cholecystectomy. Results in [19] and [20] provide the required force and torques for typical abdominal procedures (see Table I). Other design specifications such as maximal translation velocity and precision were obtained from our surgical team members based on observation of their laparoscopic tool movements in an MIS simulator. Based on kinematics and statics, presented in the following section and the performance specifications of the IREP effectors, the design specifications for the actuation unit are defined, as shown in Table I.

TABLE I.

Design Specifications

Performance Specifications of IREP grippers
Workspace	Speed	Load cap	Precision
50×50×60	30mm/s,60°/s	2N, 60mNm	±0.25mm, ±l°
Actuation Unit Design Specifications
	Travel	Speed	Load
Insertion	±50mm	60mm/s	300N
Parallelogram	±5 mm	5mm/s	100N
Camera	±5mm	5mm/s	20N
Actuation Unit of Snake Module
	Travel	Speed	Load
Snake	±8mm	30mm/s	60N
Wrist	±5mm	5mm/s	30N
Gripper	±5mm	5mm/s	20N

More details on the design specifications are discussed in the following sections after the statics and kinematic models of the IREP are presented.

IV. IREP Kinematics Model

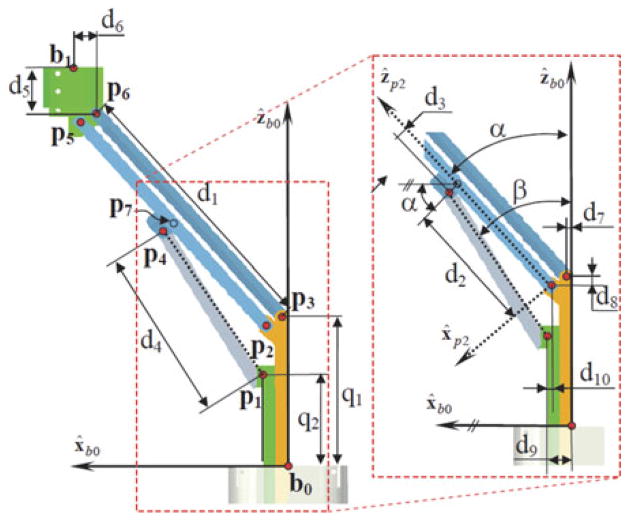
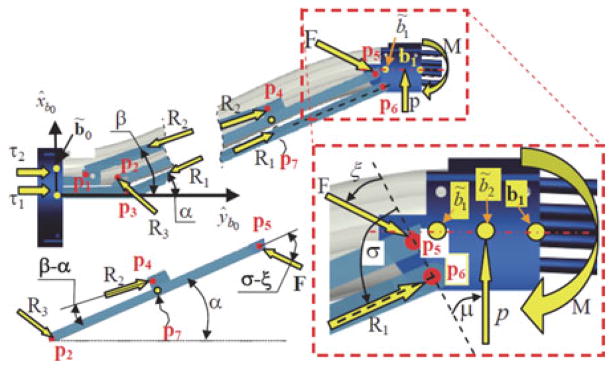
Fig. 2 and Table II define necessary nomenclature for the formulation of the kinematics and statics of the IREP. Since the IREP is symmetric, only the kinematics of one dexterous arm is presented.

Fig. 2.

Dimensions and nomenclature used for forward kinematics.

TABLE II.

Nomenclature Used in This Paper

• {A} - A right handed frame with {x̂a, ŷa, ẑ a} as its axes and point a as its origin.

• Apa/b position vector from point b to a expressed in {A}.

• ARB - orientation of frame {B} relative to {A}

• Cv A/B, CωA/B - linear and angular velocity of frame {A} with respect to frame {B} expressed in frame {C}.

• CtA/B = [CvA/B, CωA/B]-twist of frame {A} with respect to {B} expressed in {C}. Unless otherwise stated, all twists are defined in base frame {B0}.

• [p^] - the skew-symmetric cross product matrix of vector p.

• θi - the angle describing the bending of the ith segment from its straight configuration θi = π/2, Fig. 4(c).

• δi - the angle describing the plane in which the ith segment (i=l, 2) bends. This angle is defined from the bending plane to the first backbone. The direction of δi is defined by the right-hand rule about ẑbi.

• ξ = (b1z, blx, θ1, δ1, θ2, δ2, q7)T - augmented configuration variables vector. The variables b1z and bx represent the coordinates of point b1 in frame {B0},. Variable q7 is the wrist rotation angle measured according to the right-hand rule about ẑt. All joint values are defined with respect to a home configuration in which the dexterous arm is straight and q7=0 as defined in Fig. 4(b).

• Li - Length of the primary backbone of the ith segment.

• Parallelogram lengths di: d1 = ||p5 − p2|| = ||p6 − p3||, d2 = ||p7 − p2||, d3 = (p4−p7)Tx̂p2, d4 = ||p4 − p1||, d5 = (b1 − p6)Tẑb0, d6 = (bl − p6)T x̂b0, d7= (p3−b0)T x̂b0, d8 = (p3 − p2)Tẑb0, d9 = (p1 − b0)T x̂b0, dl0 = (p1 − p2)T x̂b0

In this section, the forward and inverse and the instantaneous inverse kinematics of the parallelogram linkage are first derived. The complete instantaneous kinematics model of the IREP arm is subsequently presented.

A. Forward Kinematics of the Parallelogram Mechanism

The forward kinematics of the parallelogram mechanism provides the position of the moving base ring (point b₁ in Fig. 4) as a function of joint values q₁ and q₂. During our real-time control implementation, we do not use this forward kinematics since we use a resolved-rated solution for the rate kinematics of the dexterous arm as a whole. This solution is used in the initialization step immediately after deployment of the joints q₁ and q₂ to predetermined values that correspond to a defined home position of the robot. To solve the forward kinematics, we define the auxiliary coordinates α and β as shown in Fig. 2. Point b₁ is then given by tracing a path b₀, p₃, p₆, b₁. Using b_1x and b_1z to denote the Cartesian coordinates of b₁ in {B₀}, one obtains these constraint equations

Fig. 4.

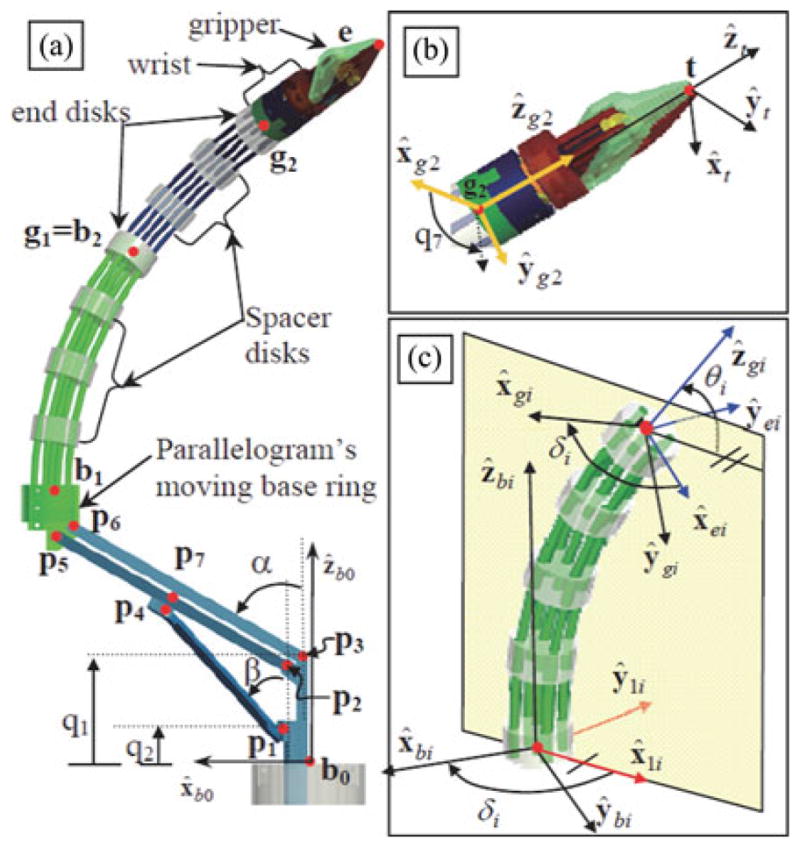
Nomenclature of a single dexterous arm of the IREP: (a) definition of points, (b) definition of the tip frame and the wrist rotation angle q₇, and (c) definition of local frames for the ith segment of the continuum robot.

$$b_{1x}-d_{1}sin(\alpha )-d_6-d_7=0$$ (1)

$$b_{1z}-q_1-d_5-d_{1}cos(\alpha )=0.$$ (2)

The vector loop p₁, p₂, p₇, p₄, p₁ is next used for solving for α while introducing an additional auxiliary unknown β. The vector loop equations are

$$d_{10}-d_{2}sin(\alpha )-d_{3}cos(\alpha )+d_{4}sin(\beta )=0$$ (3)

$$q_1-d_8-q_2+d_{2}cos(\alpha )-d_{3}sin(\alpha )-d_{4}cos(\beta )=0.$$ (4)

Equations (1)–(4) constitute four nonlinear equations with unknowns b_1x, b_1y, α, and β. The trigonometric functions of α and β can be parameterized as a function of t and u, respectively, with the substitution

$$sin(\alpha )=\frac{2t}{1+t^2},cos(\alpha )=\frac{1-t^2}{1+t^2}$$ (5)

$$sin(\beta )=\frac{2u}{1+u^2},cos(\beta )=\frac{1-u^2}{1+u^2}.$$ (6)

After substitution and simplification, β is eliminated by forming the Sylvester resultant (see [21] and [22] for details about resultants) of (3) and (4)

$${\mathbf{R}}_1=\left[\begin{array}{cccc}{\kappa }_1& {\kappa }_2& {\kappa }_1& 0\\ 0& {\kappa }_1& {\kappa }_2& {\kappa }_1\\ {\kappa }_3& 0& {\kappa }_4& 0\\ 0& {\kappa }_3& 0& {\kappa }_4\end{array}\right]$$ (7)

$${\kappa }_1=d_{10}+d_{10}{t}^2-2d_{2}t-d_3+d_3{t}^2$$ (8)

$${\kappa }_2=2d_4{t}^2+2d_4$$ (9)

$${\kappa }_3=q_1+q_1{t}^2-d_8-d_8{t}^2-q_2-q_2{t}^2+d_2-d_2{t}^2-2d_{3}t+d_4+d_4{t}^2$$ (10)

$${\kappa }_4={\kappa }_3-{\kappa }_2.$$ (11)

The vanishing of the determinant of R₁ gives a quadratic equation η₁ t² + η₂t + η₃ = 0 that has two solutions

$$t_1=\frac{-{\eta }_2+\sqrt{{\eta }_2^2-4{\eta }_1{\eta }_3}}{2{\eta }_1},t_2=\frac{-{\eta }_2-\sqrt{{\eta }_2^2-4{\eta }_1{\eta }_3}}{2{\eta }_1}$$ (12)

where the variables η₁ to η₃ are given by

$$\begin{array}{l}{\eta }_1=-2q_1{d}_2+2d_8{d}_2+2q_2{d}_2+2d_8{q}_2-2q_1{d}_8+2d_{10}{d}_3-2q_1{q}_2+q_1^2+d_2^2+d_3^2+d_8^2-d_4^2+q_2^2+d_{10}^2\\ {\eta }_2=4q_2{d}_3-4d_3{q}_1+4d_8{d}_3-4d_2{d}_{10}\\ {\eta }_3=-2q_1{d}_8-2q_1{q}_2+2q_1{d}_2+2d_8{q}_2-2d_{10}{d}_3+d_8^2+d_2^2+q_1^2-2d_8{d}_2-d_4^2+d_3^2+d_{10}^2+q_2^2-2q_2{d}_2.\end{array}$$ (13)

The corresponding values for α are given by α_i = 2 arctan (t_i). We note that t = t₂ is the only physically meaningful solution since it corresponds to the assembly configuration shown in Fig. 2(a). By substituting the result t = t₂ and (5) into (1) and (2), the solutions for b_1x and b_1z are obtained

$$b_{1x}=\frac{d_6{t}^2+d_7+2d_{1}t+d_6+d_7{t}^2}{1+t^2}$$ (14)

$$b_{1z}=\frac{d_1{t}^2-d_5-d_5{t}^2-q_1-q_1{t}^2-d_1}{1+t^2}.$$ (15)

The corresponding value of β are obtained by using (3) and (4) and solving for sin(β) and cos(β) then using Atan2² function

$$\beta =Atan2\left(\begin{array}{c}{d}_{2}sin(\alpha )+d_{3}cos(\alpha )-d_{10},\\ q_1-d_8-q_2+d_{2}cos(\alpha )-d_{3}sin(\alpha )\end{array}\right).$$ (16)

Fig. 3 shows the two assembly modes for q₁ = 20 mm and q₂ = 13.5 mm. The corresponding values for the solution are given in Table III.

Fig. 3.

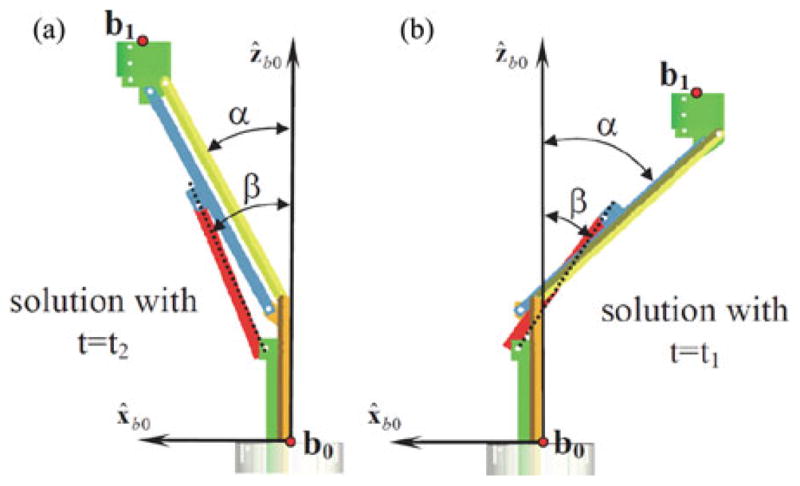
Direct kinematics solutions that correspond to Table III.

TABLE III.

Solutions of the Direct Kinematics Using q₁ = 20 and q₂ = 13.5 mm

b1x [mm]	b1z [mm]	α [degrees]	β [degrees]
−21.8862	49.5743	−47.2136	−33.3805
20.1284	56.7577	27.8091	24.7484

B. Inverse Kinematics of the Parallelogram Mechanism

Noting an explicit closed form of the inverse kinematics of the IREP arm is unavailable, a resolved-rated solution is used to calculate IREP inverse kinematics, whereas the velocity of the snake arm and the velocity ḃ₁ are calculated and integrated to give the desired b₁. This value of b₁ is used to calculate q₁ and q₂ via the parallelogram’s inverse kinematics.

Unlike the direct kinematics, the inverse kinematics of the parallel linkage has only one solution. This solution is obtained first by solving (1) for sin(α) and then calculating α using Atan2 function with two possible solutions for $cos(\alpha )=\sqrt{1-sin{(\alpha )}^2}$

$$\alpha =\text{Atan}2\left(b_{1x}-d_6-d_7,d_1\sqrt{1-{(b_{1x}-d_6-d_7)}^2/d_1^2}\right).$$ (17)

Note that (17) disregards the extraneous solution $cos(\alpha )=-\sqrt{1-sin{(\alpha )}^2}$. Joint value q₁ is then solved from (2)

$$q_1=b_{1z}-d_5-d_{1}cos(\alpha ).$$ (18)

Next, sin(β) is solved from (3) and β is calculated using Atan2 function with two possible solutions for $cos(\beta )=\pm \sqrt{1-sin{(\beta )}^2}$. The extraneous solution with $cos(\beta )=-\sqrt{1-sin{(\beta )}^2}$ is excluded and β is given by

$$\beta =\text{Atan}2\left(\begin{array}{c}{d}_{2}sin(\alpha )d_{3}cos(\alpha )-d_{10},\\ d_4\sqrt{1-(d_{10}-d_{2}sin(\alpha )d_{3}cos{(\alpha )}^2/d_4^2)}\end{array}\right).$$ (19)

q₂ is then found from (4)

$$q_2=q_1-d_8+d_{2}cos(\alpha )-d_{3}sin(\alpha )-d_{4}cos(\beta ).$$ (20)

C. Instantaneous Kinematics of the Parallelogram Linkage

Instantaneous Jacobian was derived to calculate the joint speed for parallelogram to achieve the required end tip velocity as listed in Table I. The parallelogram’s instantaneous inverse kinematics is obtained by taking the time derivative of (1)–(4)

$${\stackrel{.}{b}}_{1_x}-d_{1}cos(\alpha )\stackrel{.}{\alpha }=0$$ (21)

$${\stackrel{.}{b}}_{1_z}-{\stackrel{.}{q}}_1+d_{1}sin(\alpha )\stackrel{.}{\alpha }=0$$ (22)

$$d_{3}sin(\alpha )\stackrel{.}{\alpha }-d_{2}cos(\alpha )\stackrel{.}{\alpha }+d_{4}cos(\beta )\stackrel{.}{\beta }=0$$ (23)

$${\stackrel{.}{q}}_1-{\stackrel{.}{q}}_2-d_{2}sin(\alpha )\stackrel{.}{\alpha }-d_{3}cos(\alpha )\stackrel{.}{\alpha }+d_{4}sin(\beta )\stackrel{.}{\beta }=0.$$ (24)

Using (21) and (22), we solve for α̇ and β̇

$$\left[\begin{array}{c}\stackrel{.}{\alpha }\\ \stackrel{.}{\beta }\end{array}\right]=\left[\begin{array}{cc}1/d_{1}cos(\alpha )& 0\\ tan(\alpha )& 1\end{array}\right]\stackrel{.}{\mathbf{b}}$$ (25)

and using (25) and substituting in (22) and (24), we obtain

$$\stackrel{.}{\mathbf{q}}=\left[\begin{array}{cc}tan(\alpha )& 1\\ tan(\alpha )-\frac{d_2}{d_1}tan(\alpha )-\frac{d_3}{d_1}+tan(\beta )\frac{d_{2}cos(\alpha )-d_{3}sin(\alpha )}{d_{1}cos(\alpha )}& 1\end{array}\right]\stackrel{.}{\mathbf{b}}={\mathbf{J}}_{qb}\stackrel{.}{\mathbf{b}}.$$ (26)

The inverse of J_{q b} is simplified as follows:

$${\mathbf{J}}_{bq}=\left[\begin{array}{cc}\rho & -\rho \\ 1-\rho tan(\alpha )& \rho tan(\alpha )\end{array}\right]$$ (27)

where ρ is given by

$$\rho =\frac{d_1{c}_{\alpha }{c}_{\beta }}{d_2{s}_{\alpha }{c}_{\beta }+d_3{c}_{\alpha }{c}_{\beta }-d_2{s}_{\beta }{c}_{\alpha }+d_3{s}_{\beta }{s}_{\alpha }}$$ (28)

and the shorthand notation c_α, s_α stand for the cosine and sine of α and β, respectively.

D. Direct Kinematics of the IREP

A base frame {B₀} is defined at the tip of the central stem, Fig. 4(a). The position of the gripper described in {B₀} is given by

$${{}^{B_0}\mathbf{p}}_{e/b_0}={{}^{B_0}\mathbf{p}}_{b_1/b_0}+{{}^{B_0}\mathbf{p}}_{g_1/b_1}+{{}^{B_0}\mathbf{R}}_{G_1}{{}^{G_1}\mathbf{p}}_{g_2/b_2}+{{}^{B_0}\mathbf{R}}_{G_2}{{}^{G_2}\mathbf{p}}_{e/g_2}.$$ (29)

The vectors ^B₀p_b1/b0, ^B_op_g1/b1, and ^G₁p_g2/b2 are defined by the direct kinematics of the parallelogram linkage and the individual snake segments. The parallelogram is simplified as two linear joints in order to avoid the calculation of parallelogram Jacobian which is numerically ill-conditioned in real time. The simplified parallelogram’s direct kinematics can be expressed as ^B₀p_b1/b0 = [ê₁ 0 ê₃]^T and ^B₀ R_B1 = I. The direct kinematics of each snake segment subject to circular bending assumption is given by [16]

$${{}^{{\text{B}}_{\text{i}}}\mathbf{p}}_{e_i/b_i}=\frac{L_i}{(\pi /2-{\theta }_i)}{e}^{-{\delta }_i[{\widehat{\mathbf{e}}}_3]}\left[\begin{array}{c}1-sin({\theta }_i)\\ 0\\ cos({\theta }_i)\end{array}\right],i=1,2$$ (30)

$${{}^{{\text{B}}_{\text{i}}}\mathbf{R}}_{G_i}=e^{-{\delta }_i[{\widehat{\mathbf{e}}}_3]}{e}^{\left(\frac{\pi }{2}-{\theta }_i\right)[{\widehat{\mathbf{e}}}_2]}{e}^{{\delta }_i[{\widehat{\mathbf{e}}}_3]},i=1,2$$ (31)

where ê_i (i = 1, 2, 3) are basis unit vectors for ℝ^3×1.

Using the order O = [b0 < b1 < g1 < g2 < e], the rotation matrices in (29) are given by

$${{}^k\mathbf{R}}_j={{}^k\mathbf{R}}_{k+1}{{}^{k+1}\mathbf{R}}_{k+1}\dots .{{}^{j-1}\mathbf{R}}_j\text{where}i,j\in O.$$ (32)

The rotational wrist is accounted for using its direct kinematics

$${{}^{G_2}\mathbf{p}}_{e/g_2}=\left|\right|\mathbf{e}-{\mathbf{g}}_2\left|\right|{\widehat{\mathbf{e}}}_3,{{}^{G_2}\mathbf{R}}_E={\mathbf{e}}^{q_7[{\widehat{\mathbf{e}}}_3]}.$$ (33)

E. Instantaneous Kinematics of the IREP

Let ZtX/Y denote the twist of frame {X} with respect to {Y} expressed in frame {Z}. The absolute twist of the end-effector is given by

$${{}^{{\text{B}}_{\text{0}}}\mathbf{t}}_{E/B_0}={{}^{{\text{B}}_0}\mathbf{t}}_{B_1/B_0}+{\mathbf{S}}_1{{}^{{\text{B}}_1}\mathbf{t}}_{G_1/B_1}+{\mathbf{S}}_2{{}^{{\text{B}}_2}\mathbf{t}}_{G_2/B_2}+{\mathbf{S}}_3{{}^{G_2}\mathbf{t}}_{E/G_2}$$ (34)

where S_j j = 1, 2, 3 are transformations given by

$$\begin{array}{l}{\mathbf{S}}_1=\left[\begin{array}{cc}{\mathbf{I}}_{3\times 3}& [{({\mathbf{g}}_1-\mathbf{e})}^{\wedge }]\\ {\mathbf{0}}_{3\times 3}& {\mathbf{I}}_{3\times 3}\end{array}\right]\\ {\mathbf{S}}_2=\left[\begin{array}{cc}{{}^{{\text{B}}_0}\mathbf{R}}_{B_2}& {[{({\mathbf{g}}_2-\mathbf{e})}^{\wedge }]}^{{\text{B}}_0}{\mathbf{R}}_{B_2}\\ {\mathbf{0}}_{3\times 3}& {{}^{{\text{B}}_0}\mathbf{R}}_{B_2}\end{array}\right]\\ {\mathbf{S}}_3=\left[\begin{array}{cc}{{}^{{\text{B}}_0}\mathbf{R}}_{G_2}& {{}^{{\text{B}}_0}\mathbf{R}}_{G_2}\\ {\mathbf{0}}_{3\times 3}& {{}^{{\text{B}}_0}\mathbf{R}}_{G_2}\end{array}\right].\end{array}$$ (35)

The twist contribution of the parallelogram is given by

$${{}^{{\text{B}}_0}\mathbf{t}}_{B_1/B_0}=\underset{{\mathbf{J}}_p}{\underbrace{\left[\begin{array}{cc}{\widehat{\mathbf{e}}}_1& {\widehat{\mathbf{e}}}_3\\ {\mathbf{0}}_{3\times 1}& {\mathbf{0}}_{3\times 1}\end{array}\right]}}\left[\begin{array}{c}{\stackrel{.}{b}}_{1x}\\ {\stackrel{.}{b}}_{1z}\end{array}\right]={\mathbf{J}}_p{\stackrel{.}{\mathbf{b}}}_1.$$ (36)

Given configuration speeds ψ̇_i = [θ̇_i, δ̇_i]^T for each active segment of the snake, the relative twist of the end disk with respect to the base disk of the segment is calculated through the Jacobian J_xψi as

$${{}^{{\text{B}}_{\text{i}}}\mathbf{t}}_{G_i/B_i}={\mathbf{J}}_{x{\mathit{\psi }}_i}{\stackrel{.}{\mathit{\psi }}}_i\text{where}i=1,2$$ (37)

and the Jacobian J_xψi is given by [23]

$${\mathbf{J}}_{x{\mathit{\psi }}_i}=\left[\begin{array}{cc}{c}_{{\delta }_i}{L}_i\frac{({\theta }_i-{\theta }_0)c_{{\theta }_i}-s_{{\theta }_i}+1}{{({\theta }_i-{\theta }_0)}^2}& -L_i\frac{s_{{\delta }_i}(s_{{\theta }_i}-1)}{{\theta }_i-{\theta }_0}\\ -L_i{s}_{{\delta }_i}\frac{({\theta }_i-{\theta }_0)c_{{\theta }_i}-s_{{\theta }_i}+1}{{({\theta }_i-{\theta }_0)}^2}& -L_i\frac{c_{{\delta }_i}(s_{{\theta }_i}-1)}{{\theta }_i-{\theta }_0}\\ L_i\frac{({\theta }_i-{\theta }_0)s_{{\theta }_i}+c_{{\theta }_i}}{{({\theta }_i-{\theta }_0)}^2}& 0\\ -s_{{\delta }_i}& c_{{\delta }_i}{c}_{{\theta }_i}\\ -c_{{\delta }_i}& -s_{{\delta }_i}{c}_{{\theta }_i}\\ 0& -1+s_{{\theta }_i}\end{array}\right]$$ (38)

where s_θi = sin (θ_i), s_δi = sin (δ_i), c_θi = cos (θ_i), and c_δi = cos (δ_i), i = 1,2.

The twist contribution of the wrist joint is given by

$${{}^{G_2}\mathbf{t}}_{E/G_2}={\mathbf{J}}_w{\stackrel{.}{q}}_7\text{where}{\mathbf{J}}_w=\left[\begin{array}{c}{\mathbf{0}}_{3\times 1}\\ {\widehat{\mathbf{e}}}_3\end{array}\right].$$ (39)

By using the definition of the augmented configuration vector ξ and substituting (36)–(39) into (34), the instantaneous kinematics Jacobian J_tξ is obtained

$$\begin{array}{l}{{}^{{\text{B}}_0}\mathbf{t}}_{E/B_0}={\mathbf{J}}_p{\stackrel{.}{\mathbf{b}}}_1+{\mathbf{S}}_1{\mathbf{J}}_{x{\psi }_1}{\stackrel{.}{\mathit{\psi }}}_1+{\mathbf{S}}_2{\mathbf{J}}_{x{\psi }_2}{\stackrel{.}{\mathit{\psi }}}_2+{\mathbf{S}}_3{\mathbf{J}}_w{\stackrel{.}{\mathbf{q}}}_7\\ =\underset{{\mathbf{J}}_{t\xi }}{\underbrace{[{\mathbf{J}}_p\mid {\mathbf{S}}_1{\mathbf{J}}_{x{\psi }_1}\mid {\mathbf{S}}_2{\mathbf{J}}_{x{\psi }_2}\mid {\mathbf{S}}_3{\mathbf{J}}_w]}}={\mathbf{J}}_{t\xi }\stackrel{.}{\xi }.\end{array}$$ (40)

F. Kinematic Coordination Between the Parallelogram Mechanism and the Passive Segment of the Snake

The continuum robot of each arm has a passive segment that connects the active segments to the external actuation unit. The base disk of the first active segment in each arm is captured in a moving base ring controlled by the parallelogram mechanism (see Fig. 5). Proper control of the IREP robot requires solving the coordination kinematics between the parallelogram and the passive stem.

Fig. 5.

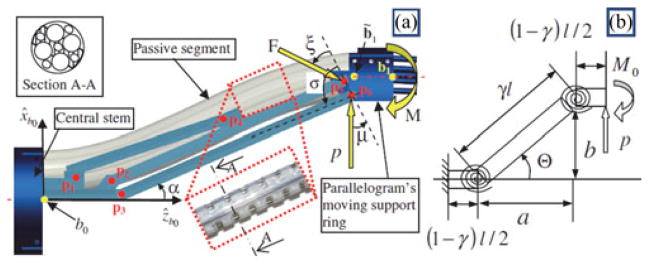
(a) Parallelogram mechanism with the passive snake segment. (b) Corresponding pseudo-rigid-body model (bottom).

The goal of the coordination control is to minimize the tension force along the passive snake segment. The coordination control calculates the required axial insertion length of the passive segment as a function of the position of the parallelogram’s moving base ring and then feed it axially through the IREP central stem. To solve the coordination problem, we use the pseudo-rigid-body approach as developed by Howell [24]. We solve for the required length of the deflected passive stem as a function of a desired position of the parallelogram’s moving base ring. Let (a,b) be the coordinates of point b̃₁ in the xz plane of frame {B₀}, Fig. 5. According to the pseudo-rigid-body model, the coordinates of the beam tip are given as a function of the beam tip deflection angle, a characteristic radius factor γ, and the direction of the external load in xz plane of frame {B₀}. We use parameter n to designate the direction of force that the parallelogram’s moving base ring applies on the passive segment of the snake such that p is the x-component, np is the z–component, and $\sqrt{1+n^2}p$ is the force magnitude. The passive stem is only subjected to x-direction force. The characteristic radius γ = 0.8517 is used in the pseudo-rigid-body model to describe the shape. Therefore, the coordinates of point b̃₁ are given by

$${\stackrel{\sim }{\mathbf{b}}}_1-{\stackrel{\sim }{\mathbf{b}}}_0=\left[\begin{array}{c}a\\ 0\\ b\end{array}\right]=\left[\begin{array}{c}l\gamma sin(\mathrm{\Theta })\\ 0\\ l(1-\gamma (1-cos(\mathrm{\Theta })))\end{array}\right]$$ (41)

where l designates the length of the passive segment of the snake robot measured from point b₀ to b̃₁ and the pseudo-rigid-body beam angle Θ is shown in Fig. 5(b) and defined in [24, eq. (5.58)].

By solving for sin (Θ) and cos (Θ) from the first and third equation in (41) and substituting in the identity cos² (Θ) + sin² (Θ) = 1, a quadratic equation for the length of the passive stem is obtained

$$l^2(1-2\gamma )+l(2a\gamma -2a)+a^2+b^2=0.$$ (42)

The only physically valid solution to this equation leads to a positive length

$$l=\frac{-a+a\gamma +\sqrt{a^2{\gamma }^2-b^2+2\gamma b^2}}{2\gamma -1}.$$ (43)

Equation (43) is used to control the length of the passive stem by feeding the snake actuation unit with the passive stem along the axis of the central stem, as shown in Fig. 14.

Fig. 14.

Actuation unit of the IREP. (a) Actuation elements for the dexterous arms and the camera mechanism. (b) Routing of actuation lines from the actuation unit to the passive stem of each snake arm. (C) Three DoF actuation unit carrying the snake arm actuation unit and actuating the parallelogram linkage.

V. Design Specifications for the Actuation Unit

The dimensions of the IREP snake arms are listed in Table IV. The length of the two active segments of each snake and the travel of the parallelogram mechanism were determined by the required surgical workspace via iterated direct kinematics simulations that validated the coverage of the desired surgical workspace as listed in Table I.

TABLE IV.

Geometric Dimensions of the IREP Snake Arms

Snake geometric dimension (mm)
Distal Seg length	Proximal Seg length		Gripper length	Disk outer diameter	Disk height
35	25		15	6.4	3.2
Ranges of parallelogram joints and snake configuration variables
q1 [mm]	q2 [mm]	θ1,2 [deg]		δ1,2 [deg]	q7 [deg]
0~80	0~30	±90°		±180°	±90°

A. Snake Joint Actuation Speed Requirements

The end-effector of IREP should be able to move fast to provide end-effector speeds congruent with manual surgeon performance in open surgery. Being more conservative in deriving the design requirements for the actuation unit, we calculated the required joint speed by using only four bending joints from the two active segments of snake. The two-stage snake Jacobian can be easily derived by taking columns 3–6 out of (34), thus resulting in

$${{}^{{\text{B}}_1}\mathbf{t}}_{E/B_1}=[{\mathbf{S}}_1{\mathbf{J}}_{x_1{\psi }_1}\mid {\mathbf{S}}_2{\mathbf{J}}_{x_2{\psi }_2}]{\left[\begin{array}{cccc}{\stackrel{.}{\theta }}_1& {\stackrel{.}{\delta }}_1& {\stackrel{.}{\theta }}_2& {\stackrel{.}{\delta }}_2\end{array}\right]}^T.$$ (44)

To calculate the desired joint speeds, we first sample the 4-D space of all possible combinations of configuration space speeds m_i = (θ̇_1i, δ̇_1i, θ̇_2i, δ̇_2i)^T where ||m_i|| = 1. Unit vectors m_i, i = 1, …, n, are parameterized by three angles ν_j ∈ [0, 2π], j = 1,…, 3

$${\mathbf{m}}_i={[c_{{\nu }_{1i}}{s}_{{\nu }_{2i}}{s}_{v_{3i}},s_{{\nu }_{1i}}{s}_{{\nu }_{2i}}{s}_{{\nu }_{3i}},c_{{\nu }_{2i}}{s}_{{\nu }_{3i}},c_{{\nu }_{3i}}]}^{\text{T}}$$ (45)

where c_νj and s_νj stand for cosine and sine of ν_j. These column vectors are augmented in a matrix M_4×n.

The resulting end-effector velocity $\stackrel{.}{\stackrel{\sim }{\mathbf{x}}}$ corresponding to unit vector configuration speeds along each ray in M is given by

$${\stackrel{.}{\stackrel{\sim }{\mathbf{x}}}}_{3\times n}=[{\mathbf{S}}_1{\mathbf{J}}_{x_1{\psi }_1}\mid {\mathbf{S}}_2{\mathbf{J}}_{x_2{\psi }_2}]{\mathbf{M}}_{4\times n}.$$ (46)

Then, the required configuration space speeds that result in maximal desired velocity ||ẋ||_max = 30 mm/s can be calculated by scaling up the column unit vectors in M as ψ̄_4×n = [a₁ m₁ · · ·, a_n m_n] where the scaling factors are calculated by $a_i={\left|\right|\stackrel{.}{x}\left|\right|}_{max}/\left|\right|{\stackrel{\sim }{\stackrel{.}{x}}}_i\left|\right|$, i = 1, …, n.

Given the required configuration speed, the required joint speeds are given by

$$\begin{array}{l}\stackrel{.}{\mathbf{Q}}={\mathbf{J}}_{\psi q}{\overline{\psi }}_{4\times n}\text{where}\\ {\mathbf{J}}_{\psi q}=\left[\begin{array}{cc}\frac{sin(\delta +\beta )}{rsin(\beta )}& -\frac{sin(\delta )}{rsin(\beta )}\\ \frac{cos(\delta )cos(\delta +\beta )}{q_{1}sin(\beta )}& -\frac{{cos}^2(\delta )}{q_{1}sin(\beta )}\end{array}\right].\end{array}$$ (47)

For the minimalistic case, only two secondary backbones are used to control the segment. Fig. 6 shows the maximal required joint speeds for two stages of snake to achieve 30 mm/s and 60 °/s. The simulation sweeps the two-stage snake over its workspace. The x-axis shows the configuration number of the snake. The RMS value of joint speed to provide the desired linear velocity is 10.84 mm/s and the RMS value of joint speed to provide the rotation velocity is 8 mm/s. Although the figure shows high values of instantaneous speeds, we use the RMS value as a more realistic design value since we know that the snake segments are singular at straight configuration and these configurations can be easily avoided using redundancy resolution with maximal joint speed avoidance. Therefore, the value of 30 mm/s (as shown in Table I), which exceeds the RMS value, is chosen as snake actuation speed for motor selection.

Fig. 6.

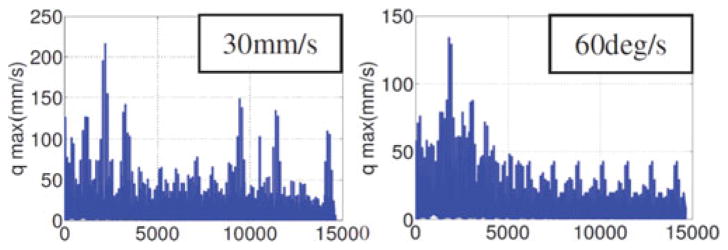
Maximal required joint speed for a two-stage continuum robot.

B. Force Requirements for the Snake Segments

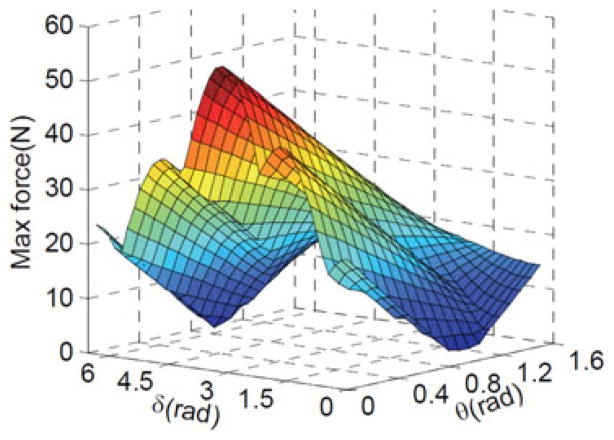
To estimate the required actuation forces, a sweep of the workspace of the IREP arm was conducted in simulation while subjecting the gripper to forces in a plane perpendicular to its longitudinal axis. The norm of these forces was assumed to be 2 N in accordance with our design specifications in Table I. The required actuation forces were estimated using a worst case scenario in which the first segment is bent in the range ψ₁ ∈ ([0, π/2], [−π, π]) while maintaining the second segment fully extended (θ₂ = π/2). Details of the statics calculation were provided in [18]. For brevity, we present the results of our simulation in Fig. 7. The figure shows that a maximal actuation force of 56.2 N is required. Hence, the actuation unit force specification was set to 60 N as shown in Table I.

Fig. 7.

Estimation of the required snake segment actuation force.

C. Parallelogram Joint Speed Estimation

The continuum segments are axially inextensible. Hence, the translational movement along the ẑ_b0 axis is predominantly provided by the parallelogram. Therefore, the parallelogram needs to provide 30-mm/s speed along the z-axis. For each configuration of the parallelogram, we used (26) to calculate the required joint speeds corresponding to sampling of all possible movement directions in a 2-D circle with a speed of 30 mm/s.

Fig. 8 shows the required minimal joint velocity for parallelogram to move its base ring at 30 mm/s. The maximal joint speed is 21.07 mm/s. This value agrees with the design specifications in Table I since the parallelogram actuation unit is built such that the stem insertion speed of 60 mm/s and the parallelogram relative speed of 5 mm/s are combined together.

Fig. 8.

Minimal joint velocity for parallelogram to carry out 30 mm/s velocity.

D. Estimation of the Required Actuation Forces for the Parallelogram Mechanisms

Using the pseudo-rigid-body model in Section IV-F, one may obtain the reaction forces between the passive segment of the snake and the parallelogram’s moving base ring. Using the pseudo-rigid-body static model in [24], the required force P and moment M to bend the passive snake segment is given by

$$p=(2k_{\mathrm{\Theta }}\mathrm{\Theta })/\left(\gamma lsin\left(\frac{\pi }{2}-\mathrm{\Theta }\right)\right)$$ (48)

$$M=pl(1+\gamma (1-cos(\mathrm{\Theta })))$$ (49)

where k_Θ = γk_θ EI/l is the stiffness of the equivalent torsion spring of the pseudo-rigid-body model. We calculated the bending rigidity using an equivalent beam model that represents the five NiTi backbones of the snake and their guiding Teflon tube (passive snake stem) as shown in Fig. 5(a). The Teflon tube was laser cut to create many flexure joints at fixed intervals of 3.5 mm as shown in the inset in Fig. 5. The bending stiffness was calculated using

$$k_{\mathrm{\Theta }}=k_{\mathrm{\Theta }1}+5k_{\mathrm{\Theta }2}+5k_{\mathrm{\Theta }3}$$ (50)

where k_Θ1, k_Θ2, and k_Θ3 are the bending rigidity coefficients of the Teflon passive stem, the five NiTi backbones of the first segment, and the five NiTi backbones of the second segment.

According to our calculations, we found that the maximal required force and moment occurred when the passive segment was at its shortest length and deployed a maximal amount along x̂_b0. Fig. 9 shows the maximal lateral force p was calculated as 2.26 N and the maximal moment M was 69.7 mN·m.).

Fig. 9.

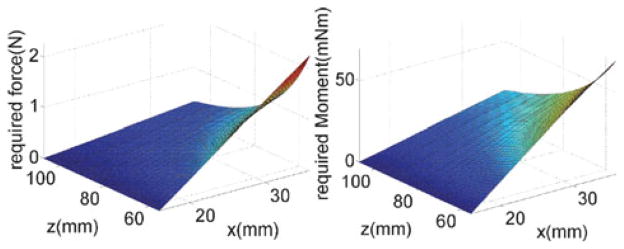
Applied force and moment to bend the passive snake stem.

The required joint forces to actuate the parallelogram were found by solving the static model of the parallelogram while neglecting frictional forces as a first-order simplification. We make the simplifying assumption that the reaction force p applied by the passive stem on the parallelogram’s moving base ring is concentrated at the midpoint b̃₂ = (b₁ + b̃₁)/2. Referring to the inset in Fig. 10, the static equilibrium equations are

Fig. 10.

Free body diagram of the forces acting on the moving base ring of the parallelogram linkage.

$$\{\begin{array}{l}pcos(\mu )-R_{1}cos(\sigma )-Fcos(\xi )=0\hfill \\ R_{1}sin(\sigma )+Fsin(\xi )+psin(\mu )=0\hfill \\ M-R_{1}sin(\sigma )\left|\right|p_5-p_6\left|\right|-p{({\stackrel{\sim }{b}}_2-p_5)}^T{\widehat{y}}_{b0}=0.\hfill \end{array}$$ (51)

Equilibrium conditions on link p₂ p₄ p₅ result in

$$R_{2}cos(\beta )-Fcos(\alpha -(\sigma -\xi ))+R_{3_y}=0$$ (52)

$$R_{2}sin(\beta )+Fsin(\alpha -(\sigma -\xi ))+R_{3x}=0$$ (53)

$$R_{2}sin(\beta -\alpha )\left|\right|p_2-p_7\left|\right|-Fsin(\sigma -\xi )\left|\right|p_2-p_5\left|\right|=0$$ (54)

where R₁, R₂, and F are internal reaction forces and angles μ, ξ, and σ are defined in Fig. 10.

Equations (51)–(54) comprise six linear equations with six unknowns R₁, R₂, F_x = Fcos(ξ), F_y = Fsin(ξ), R_3x, R_3y. The required joint actuation forces τ₁ and τ₂ are found via projection of R₁ and R₂ along the axis of joints q₁ and q₂

$$\begin{array}{l}{\tau }_1=R_{1}cos(\alpha )+R_{3_y}\\ {\tau }_2=R_{2}cos(\beta ).\end{array}$$ (55)

Fig. 11 shows a simulation of (55) throughout the workspace of the parallelogram. The figure shows that the maximal actuation forces are less than 16 N for both joints. To be conservative, we used 100 N as a design specification (as shown in Table I) for the actuation unit in order to account for frictional effects and applied load at the tip of the snake.

Fig. 11.

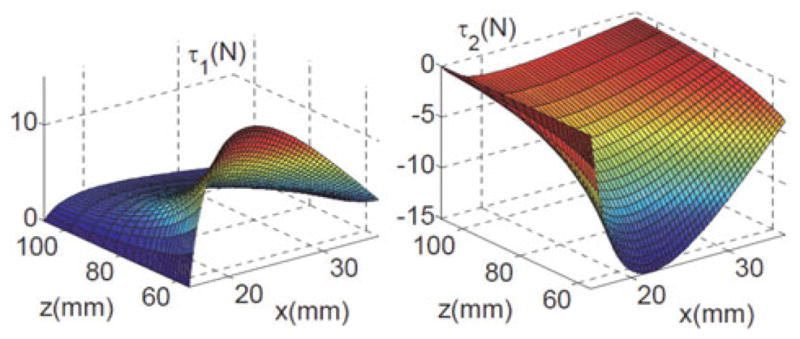
Plot of the required joint forces throughout the workspace of the parallelogram linkage for minimal q₂.

VI. System Design and Development

A. Distal End Design

The IREP arms are equipped with a dexterous wrist and gripper assembly providing fine manipulation capability to the tele-operator. The previously reported prototype wrist and gripper design, [25], has undergone revision to improve performance based on initial testing. The original and modified assemblies are shown in Fig. 12.

Fig. 12.

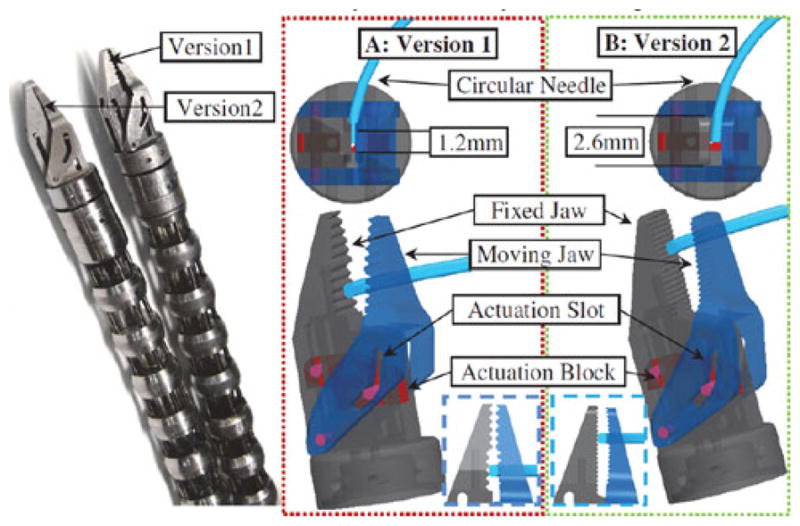
Iterations of the distal wrist-gripper assembly.

1) Gripper

The multifunction IREP gripper serves as a tissue grasper, needle driver, and general manipulator. Referring to Fig. 12, a Ø0.4 mm NiTi wire linearly actuates an actuation block along the longitudinal axis of the fixed jaw. A slot in the moving jaw constrains the motion of the moving jaw. This slot is designed with two inclination angles to provide a large jaw opening angle of 35° while offering y large mechanical advantage for opening angles smaller than 7°. The maximal gripping force for this gripper is 40 N as presented in [15].

The initial proposed gripper design, presented in [25], used a stepped contact area between the gripper halves and an asymmetrical alignment of teeth in order to ensure a stable three-point contact, Fig. 12(a) (inset). Initial testing suggested that the gripper successfully constrained a circular needle with respect to forces in the plane defined by the needle and therefore could be advanced through tissue. However, the design could not constrain the needle when subjected to forces out of the plane of the needle. Also, the small width of gripper tip was deemed not clinically useful by the surgical team.

A second iteration of the gripper was designed and fabricated to address the limitations identified in the initial design. The opposing gripper halves are curved to achieve local parallel faces for needle sizes common to SPAS, Fig. 12(b) (inset) and the distal tip size was increased.

2) Distal Wrist Design

While previous work [26], [27] demonstrated transmission of axial rotation through a continuum robot with proper compensation for model imperfections, a dedicated distal wrist simplifies the design and control of the overall IREP arms. Design considerations and alternatives presented in [18] showed that the use of a distal wrist increases the dexterity compared to using transmission of rotation about the backbone of the continuum robot. This work justified the investment in designing and constructing a miniature wrist.

The wrist mechanism in Fig. 13 is driven by a Ø0.33 mm steel wire rope that is passed through two adjacent backbones of the snake arm. A set of pulleys directs the wire to run around a capstan arranged axially in line with the gripper. The capstan is supported by custom-fabricated integrated thrust bearings that axially and radially constrain the wrist and gripper. The capstan rotates the gripper with respect to the snake-arm end disk, (g₂ in).

Fig. 13.

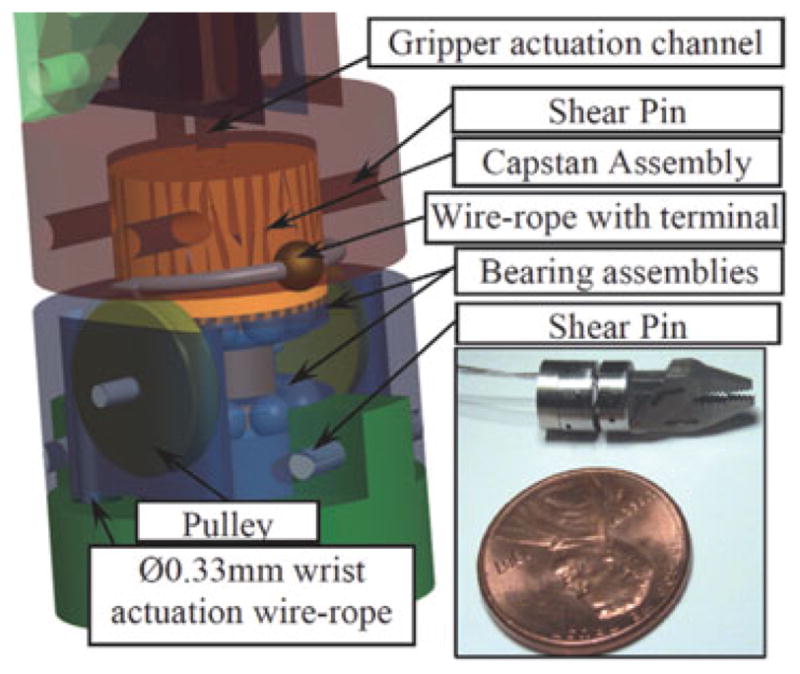
Prototype of wrist and gripper.

It is very difficult to precisely estimate the friction between wrist wire and snake tube from the model since the friction depends on the snake configuration. Therefore, a value of 30 N was selected to actuate wrist joint based on experimental evaluation.

B. Actuation Unit Design

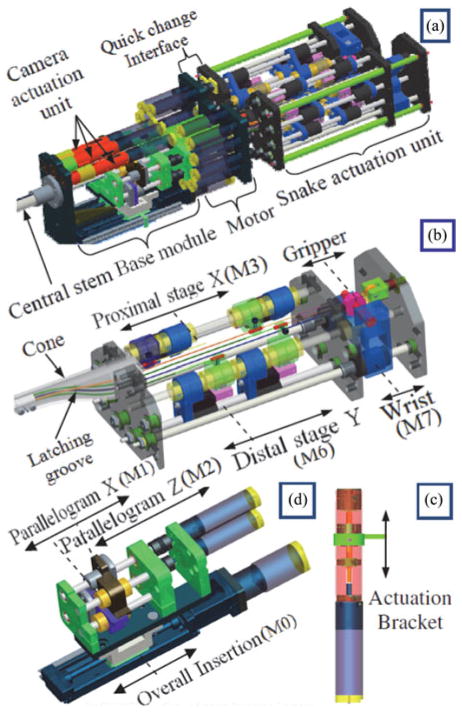
The actuation unit was designed with the aim of achieving modularity. The individual arms are removable and are decoupled from the power electronics [see Fig. 14(a)]. This also simplifies the task of sterilizing the independent arms of the IREP. In order to achieve this goal, all the motors were assembled in a central motor housing module. This module is equipped with a quick-change interface that accepts each arm comprised of a second module (the snake actuation unit and the snake dexterous arm assembled as a unit). The third module (base module) was attached at the bottom of the actuation unit and it was designed to actuate the camera mechanism and the parallelogram mechanisms while offering also translation along the axis of the central stem. The following sections detail our considerations for the design of these actuation modules.

1) Snake Actuation Unit

The design of the continuum robots with four actuation backbones (secondary backbones) that are circumferentially distributed around a central backbone allowed simple mechanical coupling between opposing secondary backbones [see Fig. 14(a)]. For example, any amount of push on the first secondary backbone is matched by an equal amount of pull on the opposing secondary backbone. This mechanical coupling was easily achieved by using a single motor coupled to a twin-lead screw for actuating each pair of opposing secondary backbones in each active snake segment. Therefore, the actuation unit of each snake arm has four twin-lead screws for actuating the snake segments. Fig. 14(b) shows one snake actuation unit with only two twin-lead screws for clarity. An additional two lead screws were used for the wrist and gripper.

The bottom portion of this actuation unit has an assembly [the “cone” in Fig. 14(b)] that routes the NiTi actuation lines of the continuum robots such that they all converge into a flexible Teflon multilumen extrusion that serves as the passive flexible stem of each dexterous continuum robot [see Fig. 5(a)]. The cone in Fig. 14(b) has a feature that allows a quick latch connection into the motor housing module of Fig. 14(a).

The overall weight of the snake actuation unit is 1.85 kg and fits within a 70mm ×140 mm × 220 mm volume (an initial estimate of 2.25 kg was reported in [18] based on a Pro/E model, a conservative estimates of component weights, and including the parallelogram actuation unit weight). This weight and size allow the surgeon or surgical technician to easily pull out the actuation unit and snake if a replacement is needed.

The total weight of the actuation unit shown in Fig. 14(a) is approximately 8.20 kg (18 lb). This small weight enables easy fixation on a surgical bed such that reorientation of the patient during surgery is possible without interrupting the surgical workflow to readjust the robot with respect to the patient.

2) Central Stem

Fig. 15 shows the cross section of the central stem previously shown in Fig. 14(a). Only 15 mm in diameter, this stem provides access to two dexterous arms, the actuation linkages for the camera and the parallelogram mechanisms, and the electronic wiring for light and for the camera module.

Fig. 15.

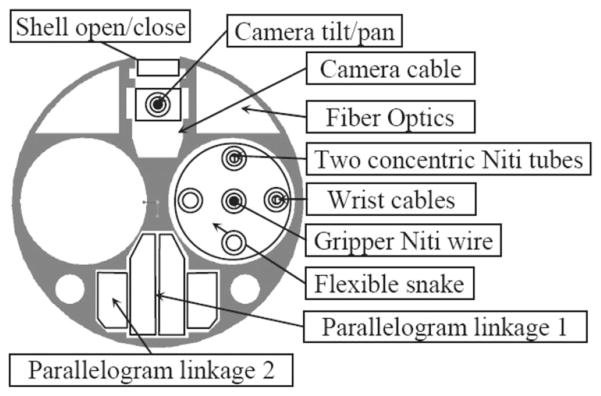
Cross section of the IREP central stem.

3) Component Selection

The actuation components were selected by considering multiple factors such as dimensions, power, stroke, maximal load capacity, and cost. Most of IREP joints are actuated by pushing and pulling. Hence, we chose various linear actuator units to carry out IREP movement. The specifications of these actuators are listed in Table V. The parallelogram joints and central stem insertion axis are actuated by high-efficiency ball screws due to their required high loads. The joints for the snake segments are special, because they require mechanical coupling using twin-lead screws as shown in Fig. 14(b). Customizing a twin-lead ball screw is expensive; therefore, we chose Kerk twin-lead screws with 6.35-mm pitch and an efficiency of 79%.

TABLE V.

Rated Specification of Actuation Components of IREP Actuation Unit

	Parallelogram	Snake segments	Wrist/gripper	Central stem Insertion
Screw Lead (mm)	1	6.35	1.27	2
Max Force (N)	550	81	236	192
Max speed (mm/s)	4.6	29	5.83	9.2

Table V shows the power requirements for each axis. The motor selection was made as uniform as possible for interchangeability and cost reduction. We chose a 4.5 W Maxon motor RE 16, with 29:1 gear reduction for all joints except the central stem insertion axis, which used a 6.5 W RE-max 24 with 4.3:1 gear reduction and ball screw with 2-mm pitch in order to accommodate the gravitation forces due to the weight of the actuation unit.

VII. Stereo Camera System Design

A. Camera and Illumination

Although transferring internal images to an externally mounted charge-coupled device (CCD) camera using fiber optics is a design alternative, the cost of developing custom fiber optics, the problems of routing them through mechanical joints, and the associated resolution loss and image distortion suggested the use of an internally mounted CCD cameras. In the IREP stereo-vision system, we used small pinhole cameras distally, and sent images out through camera cables as in [28]. This inexpensive setup can be improved by new emerging commercial camera chips. We chose NET (CSH-1.4, 6.5 mm in diameter) pinhole camera and used a 7.6-mm baseline.

Providing illumination by fiber optics also introduces routing and fiber-optic bundle flexibility problems. The IREP used Philips lumileds Luxeon c LED (2.04 mm ×1.64 mm × 0.7 mm, 85lumen/350 mA) to provide illumination. As shown in Fig. 16, we constructed an array of 14 LEDs on a printed circuit board that is mounted on the camera head. This design can provide up to 1190 lumens for visualizing the abdominal cavity.

Fig. 16.

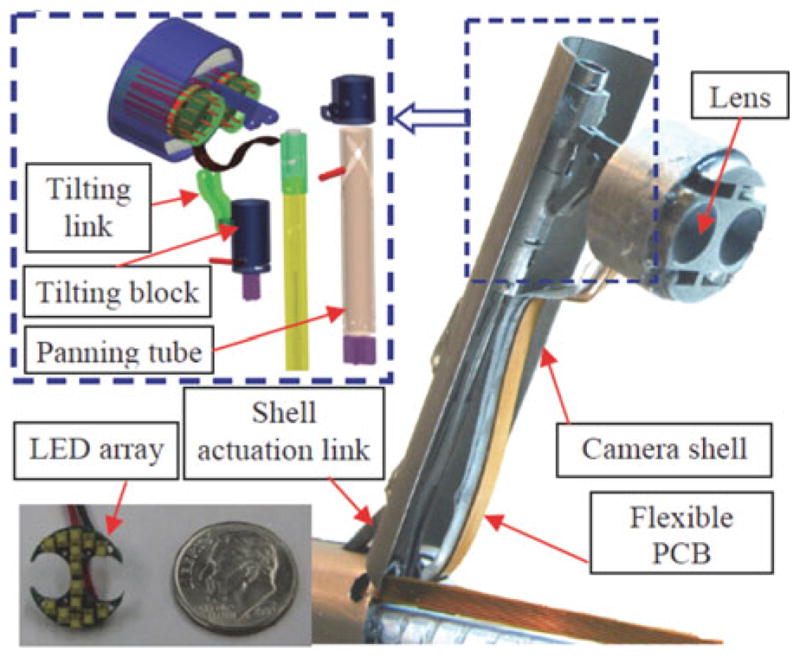
Camera module of the IREP.

B. Camera Mechanism

The mechanism of Fig. 16 controls the zoom, pan, and tilt for increased visual field. The aim of this 3-D vision feedback is to provide depth perception to the surgeon and to provide automatic instrument tracking (e.g., [29]). Other planned applications of this module include online estimation of flexible robot actuation compensation parameters (see, e.g., [26]).

The zoom functionality is achieved by opening and closing the controllable camera shell. Pan is achieved by linear actuation of the panning block to drive the relative movement between the panning tube and the bracket guide. The panning tube can generate panning movement via its helical grooves. The tilting movement is also actuated using push–pull actuation of the tilting block, which drives the tilting linkage to generate camera tilting movement.

VIII. Experimental Evaluation

The experiments reported in this section were used to validate the kinematic models and the control system implementing these models. A decentralized PID controller was implemented using MATLAB xPC with a joint-level control frequency of 1 kHz. The details of telemanipulation control and preliminary evaluation of this system were reported in [30] and additional experimental movies of the system can be found in [31].

Fig. 17 shows an experiment we performed to validate the correctness of our kinematic coordination between the parallelogram linkage and the passive flexible stem. The figure shows that while opening the parallelogram linkage, the flexible stem was advanced axially such that the base disk of the continuum snake robot remained in its position inside the parallelogram’s moving base ring. This coordination is a prerequisite for subsequent telemanipulation of this system.

Fig. 17.

Demonstration of kinematic coordination.

Fig. 18 shows an overlay of several images taken while one snake arm of the IREP was moved in its configuration space. The figure demonstrates the large workspace of the snake arm and its ability to bend more than 90°.

Fig. 18.

Image overlay of the IREP continuum robot reaching configurations throughout the work space.

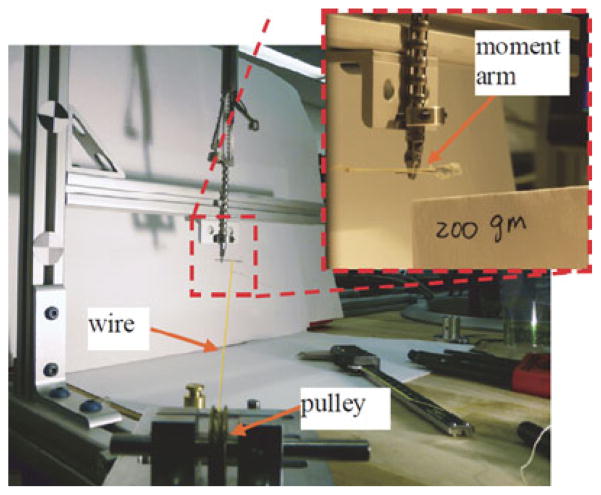
The load carrying capability of the wire-actuated wrist was also validated. The experimental setup for the validation is depicted in Fig. 19. A rigid rod was grasped between the jaws of the gripper and loaded by a wire attached 10 mm from the central axis of the gripper. The experiment showed that the wrist prototype is capable of providing approximately 150° axial rotation and greater than 20 N·mm torque demonstrating suitability SPA surgery.

Fig. 19.

Validation of the IREP wrist load carrying capability.

Fig. 20 shows the experiment we carried out to test the internal camera module of the IREP. The figure shows that the snake is easily visualized using the internal IREP camera module.

Fig. 20.

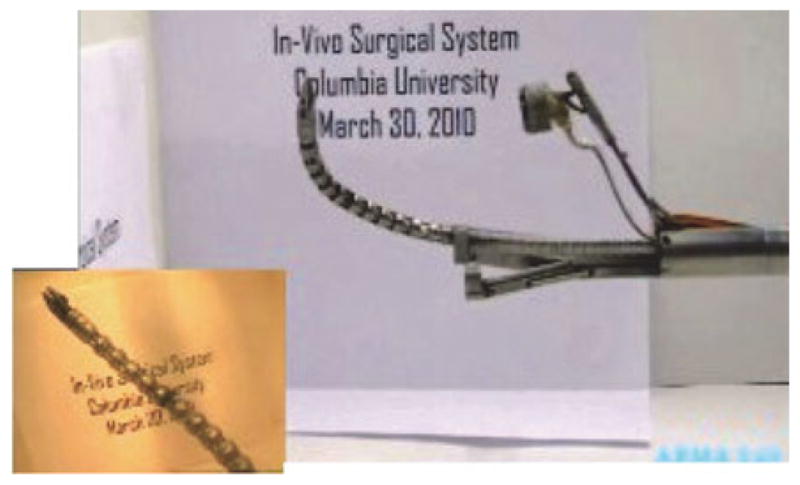
One IREP arm with the camera mechanism deployed. The inset shows the view from the IREP camera.

IX. Conclusion

The emerging surgical paradigms of natural orifice surgery and SPAS require new surgical slaves capable of meeting the challenges of dexterity, size, and sensory feedback. This paper presented our new IREP for surgical assistance and in vivo sensory feedback during SPAS. The robotic slave of this system has a novel design that incorporates parallel mechanisms and continuum robots with active and passive flexible segments. The paper presented the kinematics, statics, and design considerations of the IREP while following a task-based design approach for deriving the required component specifications from kinematic and static simulations of this system. Preliminary verification of this robotic slave demonstrates the validity of the modeling used by our real-time control system and the performance of its subcomponents. We believe that this system offers a major advancement in medical robotics because of its small size and its ability to meet the needs of accessing the internal organs through a single small orifice while providing 3-D vision feedback. The small size of this system overcomes the limitations of existing commercial systems that cannot be mounted on the patient’s bed, thus resulting in limitations of surgical setup time and ability to reorient the patient during surgery. Our future work includes integrating the IREP robotic slave into a telemanipulation system and evaluating its surgical performance.

Biographies

Jienan Ding (M’09) received the B.E., M.E., and Ph.D. degrees in mechatronics from the Department of Mechanical Engineering, Tianjin University, Tianjin, China, in 2002, 2004, and 2008, respectively.

From 2008 to 2010, he was a Postdoctoral Research Scientist at Columbia University, New York, NY. In 2010, he was at Meka Robotic as a Research Engineer. Since 2011, he has been a Senior Control Engineer at Hstar Technologies, Inc., Boston, MA. His research interests include medical applications of robotic technologies which includes surgical robot, rehabilitation robots, and humanoid robots for hospital and home care.

Roger E. Goldman (M’07) received the B.Sc. degree in mechanical engineering from Stanford University, Stanford, CA, in 2002, and the Ph.D. degree in biomedical engineering from Columbia University, New York, NY, in 2012, where he is currently working toward the M.D. degree in the College of Physicians and Surgeons.

In 2003, he joined Foxhollow Technologies, Inc., Redwood City, CA, as a Research and Development Engineer, where he developed catheters for endovascular procedures. He is currently a National Institutes of Health Medical Scientist Training Program Fellow at Columbia University. His current research interests include novel robotic instruments for applications in medical diagnosis and therapy.

Kai Xu (S’06–M’11) received the B.E. and M.S. degrees from the Department of Precision Instruments and Mechanology, Tsinghua University, Beijing, China, in 2001 and 2004, respectively, and the Ph.D. degree (with distinction) from the Department of Mechanical Engineering, Columbia University, New York, NY, in 2009.

Since 2010, he has been with the University of Michigan–Shanghai Jiao Tong University Joint Institute, Shanghai Jiao Tong University, Shanghai, China, where he is currently an Assistant Professor and the Director of the Robotics Innovation and Intervention Laboratory. His research interests include medical and surgical robotics, humanoid and service robotics, production automation, mechanism design, and continuum mechanics.

Peter K. Allen (S’82–M’85) received the A.B. degree in mathematics economics from Brown University, Providence, RI, the M.S. degree in computer science from the University of Oregon, Eugene, and the Ph.D. degree in computer science from the University of Pennsylvania, Philadelphia.

He is currently a Professor of computer science at Columbia University, New York, NY. His current research interests include robotic grasping, 3-D vision and modeling, and medical robotics.

Dr. Allen was the recipient of the CBS Foundation Fellowship, Army Research Office Fellowship, and the Rubinoff Award for innovative uses of computers. In recognition of his research, he has been named a Presidential Young Investigator by the National Science Foundation.

Dennis L. Fowler received the M.D. degree from the University of Kansas School of Medicine, Kansas City, in 1973.

He is currently the Gerald and Janet Carrus Professor of Clinical Surgery and the Director of the Simulation Center, Columbia University Medical Center, and New York Presbyterian Hospital/CU. He is also the Director of the Reemtsma Center for Innovation and Outcomes Research, Department of Surgery, Columbia University. He has recently completed a term on the GI Advisory Council of the American Board of Surgery. As a clinical surgeon, his research is focused on minimally invasive surgery and surgical education and on outcomes research, technology development, and the use of simulation for training and assessment in healthcare.

Dr. Fowler is a Fellow of the American College of Surgeons and a member of the Society of American Gastrointestinal Endoscopic Surgeons.

Nabil Simaan (M’04) received the B.Sc., M.Sc., and Ph.D. degrees in mechanical engineering from the Technion—Israel Institute of Technology, Haifa, Israel, in 1996, 1999, and 2002, respectively.

During 2003, he was a Postdoctoral Research Scientist at The Johns Hopkins University National Science Foundation (NSF) Engineering Research Center for Computer-Integrated Surgical Systems and Technology, where he was involved in research on minimally invasive robotic assistance in confined spaces. In 2005, he joined Columbia University, New York, NY, as an Assistant Professor of mechanical engineering and the Director of the Advanced Robotics and Mechanisms Applications Laboratory, where he became an Associate Professor in 2010. He subsequently joined Vanderbilt University, Nashville, TN, in Fall 2010.

Dr. Simaan received an NSF Career Award for young investigators to design new algorithms and robots for safe interaction with the anatomy in 2009.