Abstract
Using data from South Asia, this article examines how arranged marriage cultivates rivalry among sisters. During marriage search, parents with multiple daughters reduce the reservation quality for an older daughter’s groom, rushing her marriage to allow sufficient time to marry off her younger sisters. Relative to younger brothers, younger sisters increase a girl’s marriage risk; relative to younger singleton sisters, younger twin sisters have the same effect. These effects intensify in marriage markets with lower sex ratios or greater parental involvement in marriage arrangements. In contrast, older sisters delay a girl’s marriage. Because girls leave school when they marry and face limited earning opportunities when they reach adulthood, the number of sisters has well-being consequences over the life cycle. Younger sisters cause earlier school-leaving, lower literacy, a match to a husband with less education and a less skilled occupation, and (marginally) lower adult economic status. Data from a broader set of countries indicate that these cross-sister pressures on marriage age are common throughout the developing world, although the schooling costs vary by setting. JEL Codes: J1, I25, O15.
I. Introduction
Economic, social, and cultural change occur unevenly, with some behaviors and institutions lagging behind technological progress. Social scientists have long been interested in how these slowly evolving traditions interact with the process of development (e.g., Weber 1905; Grief 1994; Guiso, Sapienza, and Zingales 2006). One such tradition is arranged marriage. Although arranged marriage has gradually given way to love-based marriage in some societies over the past millennium, it remains prevalent in many parts of the world (Goode 1970; Goody 1983). For example, among Indian women born in the 1950s, 1960s, and 1970s, only 5% report having arranged their marriages independently of their families (Desai and Andrist 2010). This article uses data from South Asia to study how the family’s continued influence over marriage arrangements creates trade-offs among siblings, such that one sibling’s presence in the family affects another sibling’s marriage and human capital outcomes. The interaction of this tradition with recent expansions in mobility and educational opportunities appears to magnify these trade-offs.
Competition among siblings has received much attention for its potential to have a lasting impact on the outcomes of children, but the typical economic treatment of this issue places little emphasis on institutions like arranged marriage. In the standard framework, siblings compete for limited resources within the household, so that an increase in the number of children decreases average child investment.1 But sibling rivalry also occurs in arenas that are not fully captured by a conventional budget constraint. For instance, siblings of the same gender participate in the same marriage market, sharing a pool of potential spouses. In some ways, they are like any other participants on the same side of the market, but their membership in the same family introduces special constraints on their marriages.
These constraints are particularly severe in societies with arranged marriage, where for a variety of reasons parents seek to marry children of the same sex in order of birth. When search for a suitable spouse takes time, this practice implies that same-sex siblings constrain each other’s marriage arrangements. A girl’s presence in the family leads her parents to hurry the marriage arrangements of her older sisters and delay those of her younger sisters, both at the expense of groom quality. The logic is similar for boys but probably more acute for girls, who in many parts of the world (including South Asia) leave school if they marry young (Field and Ambrus 2008). Because women’s economic status depends heavily on age at marriage, schooling, and spousal attributes, the effect of these sibling effects may be felt well into adulthood.
Although the article focuses on measuring that impact, it begins by describing the practice of marrying daughters in order of birth and outlining a simple marriage search framework. The framework predicts that the presence of older sisters delays the marriages of their younger sisters; the presence of younger sisters hastens the marriages of their older sisters; and the presence of any sisters reduces expected groom quality. Using data from the Demographic and Health Surveys (DHS), the article then analyzes sister effects in South Asia’s four largest countries, comprising a fifth of the world’s population. Much of the analysis centers on a simple natural experiment within the family. If a girl has at least x younger siblings, then in the absence of sex selection, one can treat the gender of her xth-younger sibling as exogenous.2 A comparison of girls with next-born brothers and sisters thus identifies the effect of the next-born sibling’s gender.
The analysis has two parts, the first of which uses data on whether a girl has left her natal home. Home-leaving is tantamount to marriage for South Asian women, so parental coresidence proxies for never-marriage. In Bangladesh, India, Nepal, and Pakistan, teenage girls with next-youngest sisters are roughly 3 percentage points more likely to have left their natal homes than their counterparts with next-youngest brothers. The effects are stronger in rural areas, where marriage markets are thinner; in areas with more parental involvement in marriage arrangements, where cross-sister constraints would be expected to be stronger; and in marriage markets with low ratios of marriageable men to marriageable women, consistent with the idea that a scarcity of grooms intensifies parents’ fear that they will fail to find a husband for their younger daughter. An analysis of twin births, though underpowered due to the rareness of twins, suggests that these patterns solely reflect the effects of sisters. Teenage girls with younger twin sisters are more likely to have left home than their counterparts with younger singleton sisters. But those with younger twin brothers and those with younger singleton brothers have indistinguishable rates of home-leaving. Also, as the search framework predicts, girls with next-oldest sisters marry later than those with next-oldest brothers. Because endogenous fertility confounds comparisons based on the sex composition of older siblings, the article assesses the extent of selection bias using both Heckman’s (1974) selection correction model and Lee’s (2009) nonparametric bounds estimator. Both methods give results consistent with the hypothesis that an older sister’s presence leads a girl to leave home later, although the 95% confidence interval of the bounds estimator includes 0. The data thus suggest that older and younger sisters have opposite effects on home-leaving.
To examine whether these effects have lasting consequences, the second part of the analysis uses data from Nepal in which adult women report all of their siblings ever born. Consistent with the results on home-leaving, women with younger sisters marry and initiate childbearing earlier than women with younger brothers. The earlier transition to married life comes at the expense of human capital and spousal quality. Next-youngest sisters cause lower school attendance among teenagers, as well as lower educational attainment and literacy among adult women. Furthermore, compared to women with next-youngest brothers, those with next-youngest sisters have husbands with less education and lower skill occupations, and they live in marginally poorer households.
How siblings affect adult outcomes is an enduring question in the social sciences, so the results are of interest independent of the mechanism mediating them. Collectively, the results suggest a prominent role for marriage search and are inconsistent with leading alternative theories of the effects of sibling composition on adult well-being. In this respect, the queuing of girls to leave the household is perhaps the most distinguishing result. Neither models in which the gender of a child is a wealth shock, nor models in which parents substitute resources from girls to boys, nor models of son-biased fertility-stopping behavior, nor models of the demand for male and female labor in the household predict on their own that older sisters have the opposite effect of younger sisters. Many of these theories also predict effects of sibling sex composition in earlier childhood, which the data do not show. After these explanations, one prominent alternative remains, also rooted in the marriage market. This theory posits that liquidity-constrained families adjust their daughters’ marriage ages because they cannot afford to pay two dowries in close succession. But the effects of younger sisters on marriage risk are no stronger in regions with high dowry prevalence than in those with small dowry prevalence. Sister effects on age at marriage are also evident in societies outside South Asia, some of which exchange bride price rather than dowry. Limited data on South Asian males suggest that younger brothers increase the marriage risk of young men, for whom net marriage payments are positive. Liquidity constraints are thus unlikely to explain the results.
The results contribute to the literatures on the effects of both sibling sex composition and family size. Much of my empirical work makes comparisons based on the sex of the next-youngest sibling, which speaks most directly to research on sibling sex composition. A few papers in this literature have considered the role of patrilineal and matrilineal inheritance norms (see Fafchamps and Quisumbing 2007), but on the whole, the economics literature has tended to emphasize more generic theories of intrahousehold resource distribution, without regard to specific institutions like arranged marriage.3 However, because an increase in family size tends to raise the number of sisters, the article also relates to research on the effects of family size. Recent results from Norway suggest that although an increase in the number of younger siblings does not affect adult outcomes, an increase in the number of older siblings (i.e., an increase in birth order) reduces educational attainment and adult economic status (Black, Devereux, and Salvanes 2005). These results stand in contrast to South Asia, where older sisters allow a girl to remain in school, whereas younger sisters force her to leave. The mechanisms underlying the Norwegian findings remain unknown, but these differences remind us that varying constraints on household decisions lead to varying forms of sibling competition.
Even so, given the role of families in marriage arrangements in many parts of the world, the cross-sibling marriage pressures documented in South Asia are likely to carry to other settings.4 Indeed, the penultimate section of the article shows that sister effects on age at marriage are evident across much of the developing world, although they are much smaller in world regions with less arranged marriage. Meanwhile, the effects on schooling surface only in societies where marriage occurs sufficiently early and school-leaving occurs sufficiently late. In this sense, the results contribute to the research effort toward understanding the ramifications of various marriage institutions, especially during times of social, economic, and demographic change (e.g., Edlund 1999; Tertilt 2005; Edlund and Lagerlöf 2006; Anderson 2007; Jacoby and Mansuri 2010). More broadly, they relate to recent work on how variation in the cultural importance of family ties shapes both individual and aggregate economic outcomes (Bertrand and Schoar 2006; Alesina and Giuliano 2010).
II. Sex-Specific Birth Order and Marriage
When parents have a say in marriage arrangements, they typically seek to marry children of the same sex in strict order of birth. Historical texts from both inside and outside South Asia contain many references to the practice. In the Hebrew Bible, Laban deceives Jacob into marrying his daughter Leah instead of her younger sister Rachel under the defense, “This is not done in our country—giving the younger before the firstborn” (Gen. 29:26, New Oxford Annotated Bible). The Mahabharata, one of the two major ancient Hindu epics, takes a stronger position, putting the marriage of a younger daughter before her elder sister in the same list of sins as arson, breach of contract, and the murder of a teacher, a woman, or a member of a high caste. Sons, too, often come under the purview of the rule. For example, the Hindu text Laws of Manu states: “The elder brother who marries after the younger, the younger brother who marries before the elder, the female with whom such a marriage is contracted, [the father] who gives her away, and the sacrificing priest … all fall into hell” (Bühler 1886, p. 76). Note the role of parents in enforcing the practice. Indeed, demographers have shown that sisters married disproportionately in order of birth in several historical Western contexts; they have interpreted the decline of this practice as evidence of waning parental authority in marriage decisions (Smith 1973; Dillon 2010).
Several theories could explain this practice, which prevails as a social norm in present-day societies with widespread arranged marriage. For one, it addresses issues of fairness and competition within the family. It equalizes outcomes among siblings of the same sex by ensuring that parents will find a groom for an unattractive elder sibling even if her younger sibling has many suitors, and it minimizes direct competition between siblings over potential spouses. To some extent, the practice may also reflect a family’s optimal consumption or search behavior. In the case of daughters, whose weddings are typically costly, a younger sister’s marriage prevents a liquidity-constrained family from marrying her elder sister for quite some time. As a result, parents who wish to marry all daughters in their youth may feel compelled to marry their daughters in order of birth. Search frictions also create some pressure to prioritize an elder sibling, who faces a shorter horizon on the marriage market.5 Finally, given the equilibrium prevalence of the practice, an out-of-order marriage may send a bad signal about the elder sibling’s desirability.
The importance of marriage by (sex-specific) order of birth in South Asia is apparent in DHS data from Bangladesh, India, Nepal, and Pakistan, which Section IV introduces in greater detail. Specific data on sisters’ marriage ages are not available, but because South Asian newlyweds move in with the groom’s parents, one can gauge the importance of marriage by sex-specific birth order by examining what fraction of girls leave home before their older sisters do. If parents are constrained to marry their daughters in order of birth, then the fraction of girls who leave home out of order will be lower than the fraction predicted based on their ages alone. To implement this test, I restrict the sample to families with exactly x daughters, estimate a regression of parental coresidence on age indicators, and then predict the probability that each daughter lives at home. Among families with two daughters aged 15–24, the predicted probability that the younger daughter has left home but her older sister remains is 12%, but the actual probability is 3%. With three daughters aged 15–24, the predicted probability is 27%, and the actual probability is 7%.
Figure I, which uses the same data to plot rates of parental coresidence by age and sex-specific birth order, gives further evidence that sex-specific birth order matters for marriage. The figure presents graphs for families with two, three, and four girls. At each age, the oldest sister is most likely to have left home, followed by the next-oldest, the third-oldest, and the youngest. The differences are substantial; among families with two daughters, the median younger daughter leaves home roughly two years older than the median older daughter.6
Figure I.
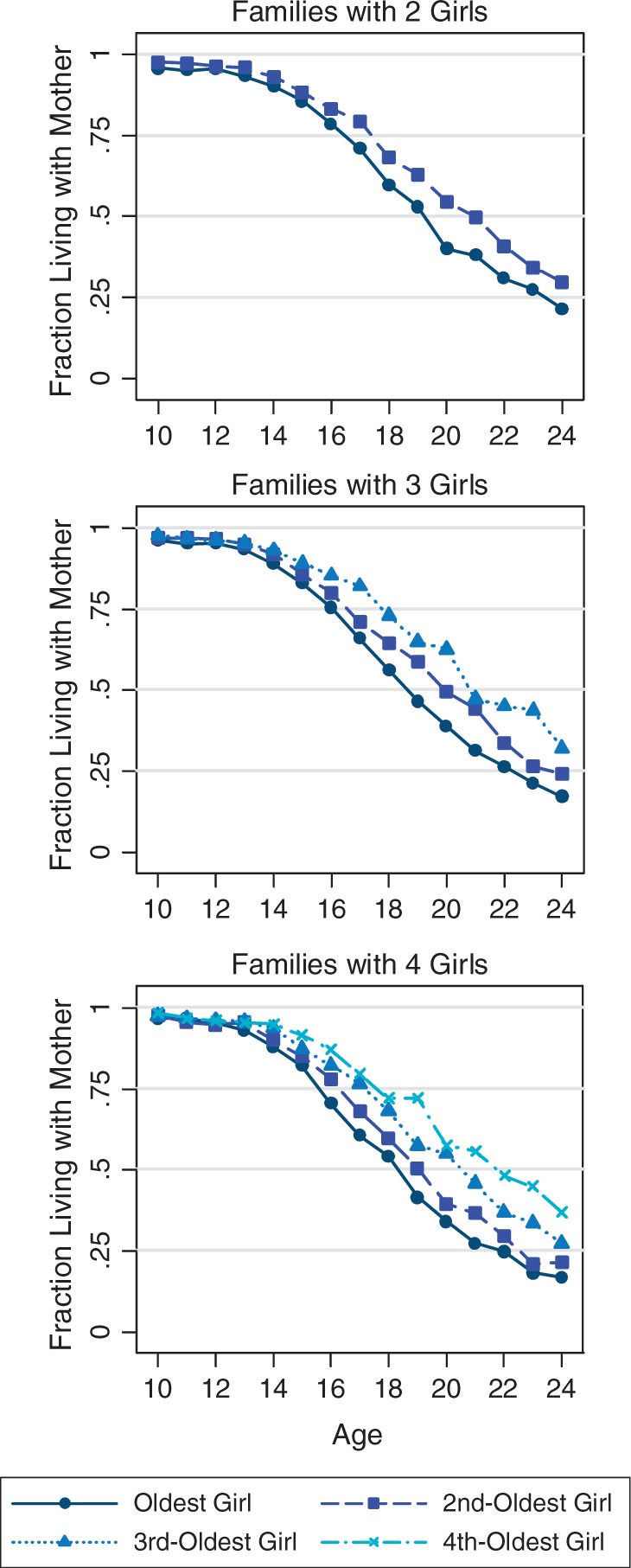
Parental Coresidence by Age and Sex-Specific Birth Order
Number of observations from two-girl families = 66,684; from three-girl families = 53,187; from four-girl families = 31,671. Source: DHS Fertility Histories.
III. Sister Effects in a Model of Search for Grooms
This section develops a simple search framework for understanding how the practice of marrying daughters in order of birth, which features prominently in most systems of arranged marriage, affects marriage timing and spousal choice. The Online Appendix proves all claims.
III.A. Main Model
A family has either one or two daughters, who vary only in age a. In a two-daughter family, the age gap between the elder and younger daughters is denoted Δ. As is typical in South Asia, the family awaits visits from grooms’ families, who travel in search of brides. In each period, representatives from a groom’s family arrive with probability 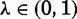 . Each groom is characterized by quality q, drawn from a log-concave distribution F with full support on
. Each groom is characterized by quality q, drawn from a log-concave distribution F with full support on 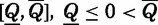 .7
.7
The bridal family obtains payoff q for each period a daughter is married to a husband of quality q and 0 for each period she remains unmarried. If a groom’s representatives arrive, the bridal family decides whether to offer the eldest daughter in the household; by custom, a younger daughter may not marry before her elder sister. For a daughter aged a, the groom’s representatives accept the offer with probability π(a), in which case the couple marries immediately. I choose a general specification for π(a) that is motivated by the widespread demand for young brides.8 A daughter begins her marriageable life at age a with π(a) > 0. Her value then steadily declines, with 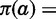
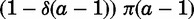 and
and 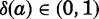 , until she reaches age
, until she reaches age 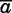 , when
, when 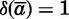 , so that
, so that 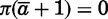 .9 If a groom’s representatives do not arrive, if the bridal family does not offer a bride, or if the groom’s representatives do not accept an offer, the process repeats in the next period.
.9 If a groom’s representatives do not arrive, if the bridal family does not offer a bride, or if the groom’s representatives do not accept an offer, the process repeats in the next period.
As is standard in optimal stopping problems, the parents accept a groom if and only if his quality exceeds a reservation level. Because the problem is nonstationary, reservation quality varies with age. Define q1(a) as the reservation quality at age a for a one-daughter family. At age 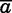 , the parents are indifferent between a spouse of quality zero and a never-married daughter, so
, the parents are indifferent between a spouse of quality zero and a never-married daughter, so 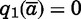 . We solve for earlier ages by backward induction:
. We solve for earlier ages by backward induction:
| (1) |
On the right-hand side of the transition equation, the term 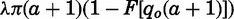 is the probability that a wedding occurs: the product of the probabilities that a groom’s representatives arrive, the groom exceeds the reservation quality, and the representatives accept the daughter as a bride. The term
is the probability that a wedding occurs: the product of the probabilities that a groom’s representatives arrive, the groom exceeds the reservation quality, and the representatives accept the daughter as a bride. The term 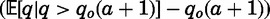 is the expected excess quality of that groom over the reservation quality. Because both terms are positive, reservation quality decreases with age.
is the expected excess quality of that groom over the reservation quality. Because both terms are positive, reservation quality decreases with age.
This solution changes in an intuitive way when the family has two daughters. We again solve by backward induction. Once the elder daughter is out of the way, the younger daughter’s problem reduces to the only-daughter problem. In contrast, the optimal policy for the elder daughter embeds the cost of delay to her younger sister. Define q2(a,Δ) as the reservation quality for an elder daughter aged a who has a younger sister aged a – Δ. Because an unmarried elder daughter prevents her younger sister from ever marrying, 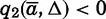 . Before that, during
. Before that, during 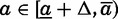 :
:
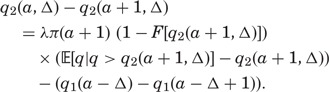 |
(2) |
The term 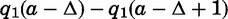 is the cost (in terms of expected spousal quality) of forcing the younger sister to postpone entering the marriage market for another period. This cost is positive, so an elder daughter’s reservation quality is less than a younger daughter’s for all
is the cost (in terms of expected spousal quality) of forcing the younger sister to postpone entering the marriage market for another period. This cost is positive, so an elder daughter’s reservation quality is less than a younger daughter’s for all 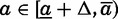 . Before the younger daughter reaches marriageable age, q2(a,Δ) evolves according to the only-daughter transition equation but remains lower than q1(a).
. Before the younger daughter reaches marriageable age, q2(a,Δ) evolves according to the only-daughter transition equation but remains lower than q1(a).
The reservation quality for an elder daughter is always less than that of an only daughter, so she marries earlier than an only daughter and to a lower quality groom. Meanwhile, a younger daughter has the same age-specific reservation quality as an only daughter, but she enters the marriage market at a later age and thus marries later. Because reservation quality declines with age, her late entry implies lower expected spousal quality.
Result —
Compared to a girl with no sisters,
A girl with a younger sister has higher cumulative marriage risk at any age.
A girl with an elder sister has lower cumulative marriage risk at any age.
A girl with either an elder or younger sister has lower expected spousal quality.
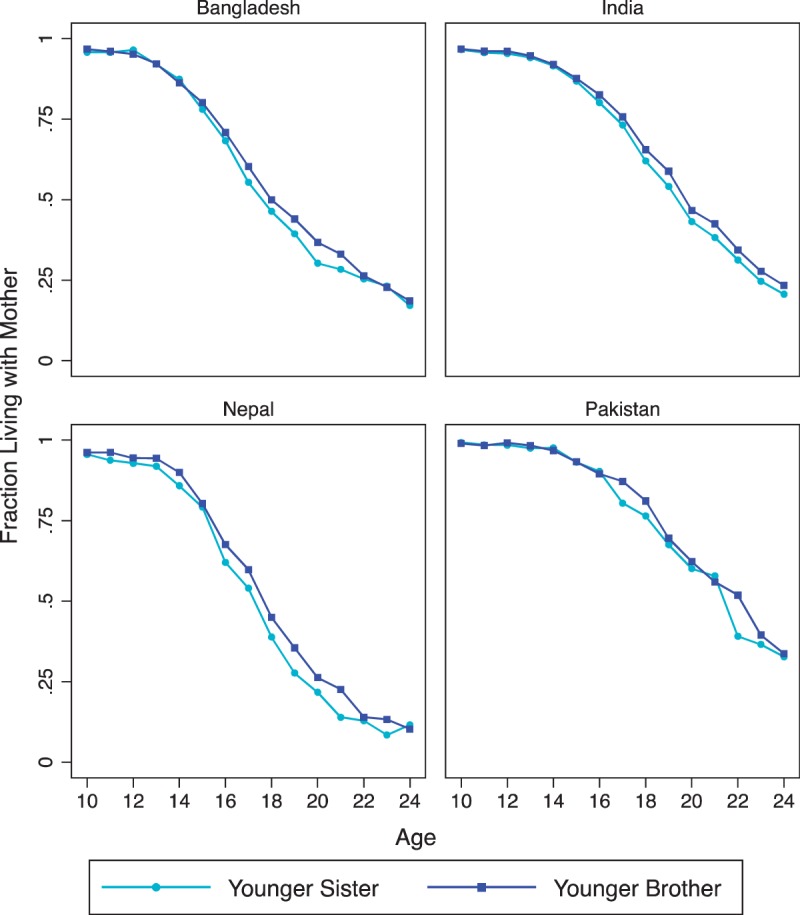
Much of the empirical application focuses on the effect of having a younger sister on marriage outcomes. Because the transition function for an elder daughter differs from that of an only daughter solely through the cost of delaying a younger sister, we gain insight into comparative statics on the younger sister effect by examining the properties of this cost, 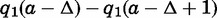 . If the rate of marriage market depreciation δ(a) is sufficiently small, then this quantity decreases in the age gap, so the effect of a younger sister on marriage risk is stronger for closely-spaced sisters.10 The arrival rate also has an ambiguous influence on the younger sister effect. Assume δ(a) is small. Then with high λ, the younger sister’s reservation quality declines slowly for most of her lifetime and then drops precipitously in the last few periods before
. If the rate of marriage market depreciation δ(a) is sufficiently small, then this quantity decreases in the age gap, so the effect of a younger sister on marriage risk is stronger for closely-spaced sisters.10 The arrival rate also has an ambiguous influence on the younger sister effect. Assume δ(a) is small. Then with high λ, the younger sister’s reservation quality declines slowly for most of her lifetime and then drops precipitously in the last few periods before 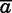 ; with low λ, her reservation quality declines more steadily because her parents expect fewer chances to sample from the groom distribution. If the age gap is sufficiently large, however, then the cost of delaying a younger sister decreases in the arrival rate, so that low arrival rates lead to large sister effects on marriage outcomes.
; with low λ, her reservation quality declines more steadily because her parents expect fewer chances to sample from the groom distribution. If the age gap is sufficiently large, however, then the cost of delaying a younger sister decreases in the arrival rate, so that low arrival rates lead to large sister effects on marriage outcomes.
III.B. Extension: No Marriage-by-Birth-Order Rule
In localized marriage markets, sisters may compete for the same flow of grooms. Implicitly, I have constructed the model so they do, although due to the marriage-by-birth-order rule, identical results would arise if each daughter had her own flow of grooms. But if the family receives only one flow of grooms, is the birth order rule necessary to generate sister effects? As shown in the Online Appendix, in the absence of such a rule, a two-daughter family offers the younger daughter to high-quality grooms, the elder daughter to middle-quality grooms, and neither daughter to low-quality grooms.11 Compared to the profile of reservation quality with respect to age for an only daughter, that for an elder daughter is everywhere lower; that for a younger daughter is everywhere higher. As a result, compared to a girl with no sisters, a girl with an elder sister has lower cumulative marriage risk at any age, and a girl with any sister has lower expected groom quality. However, without a rule, the presence of a younger sister has an ambiguous effect on a girl’s marriage risk.
III.C. Extension: Brothers
Because norms associated with arranged marriage also prohibit the marriage of brothers out of order, one might expect similar brother effects. In the South Asian context, the marriage of a son typically involves more deliberate search effort than the marriage of a daughter. To this end, the Online Appendix endogenizes search intensity in an extension to the model that retains the marriage-by-birth-order assumption. In the optimal policy, the family channels some of the pressure from a younger brother into lower reservation quality and some of it into increased search intensity. Despite this effort adjustment, all same-sex sibling effects in Result 1 are qualitatively unchanged.
III.D. Other Modeling Choices
For parsimony, the model does not include dowries or premarital investments. Dowry could have two offsetting effects. On one hand, as discussed in Section I, it could interact with liquidity constraints to exacerbate the pressure from having two daughters. On the other, it could allow liquid families to alleviate some of the pressure by paying a larger dowry. Dowry was not prevalent in all parts of South Asia in all periods I consider, so the institution is not crucial for understanding the mechanism. Furthermore, Section VIII estimates sister effects on marriage in a wide range of societies outside South Asia, where families do not exchange dowries. By omitting dowry from the model, I provide a framework for a much broader set of societies. In any case, Section VII finds no consistent empirical evidence of a role for dowry in South Asia.
One could also imagine parents adjusting premarital investments under the expectation of cross-sister pressure. But the the most valued bridal traits are beauty, age, and family characteristics, which do not offer much opportunity for differential investment.12 Consistent with this notion, Section VII finds no sister effects on several preadolescent outcomes.
IV. Data and Methods
IV.A. Sibling Data from the Demographic and Health Surveys
To examine how sisters affect one another’s marriage and human capital outcomes, I use data from the Demographic and Health Surveys (DHS) in Bangladesh, India, Nepal, and Pakistan.13 In these settings, marriage is widespread, nonmarriage is a taboo, dowries are common, andpostmarital residence is virilocal—the couple resides with the husband’s extended family.
I analyze two types of data. The first type derives from the DHS fertility history module, in which women list all of their live births. For each live birth, women report on a series of outcomes, including current parental coresidence.14 Because South Asian societies are almost uniformly virilocal, home-leaving is a good proxy for marriage among young women.15 However, these data suffer from the important drawback that they do not track a mother’s children after they have left the household. For more information on teenagers and adult women, I turn to the DHS sibling history module, which asks respondents to list all children ever born to their biological mothers. Nepal’s 2006 DHS is the only survey in South Asia with nationally representative sibling history data on all women of childbearing age (15–49), rather than ever-married women. The absence of adult sibling data for other South Asian countries is unfortunate, but Nepal’s marriage market has a similar structure to those elsewhere in the region, so one might expect to find similar patterns in other countries. I use the Nepal data to analyze the effect of sibling structure on the ages of first marriage and first birth, school enrollment and attainment, literacy, height, weight, and spousal attributes. Because the analysis of spousal attributes necessarily focuses on ever-married women, I minimize selection bias by restricting the sample for this analysis to ever-married women over age 30, who represent over 98% of all women over age 30. For statistical power, I supplement these data with the 30-plus sample from the 1996 Nepal DHS, which interviewed ever-married women.
Although the empirical work relies mainly on South Asian DHS data, supplementary analyses draw on several other data sources, including the 2001 Census of Nepal, the India Human Development Survey, and Demographic and Health Surveys conducted elsewhere in the world.
IV.B. Empirical Strategy
For both the Fertility Histories and the Sibling Histories, the basic estimation strategy takes advantage of variation in younger siblings’ genders. Conditional on a girl having at least x younger siblings, the gender of her xth younger (ever-born) sibling may be taken as random. A comparison of girls with next-born sisters to those with next-born brothers (or of those with second-subsequent sisters and brothers) therefore allows a causal interpretation. Similarly, conditional on a mother having at least x more pregnancies, the occurrence of a twin birth instead of a singleton birth in the xth-subsequent pregnancy may be taken as random. As a result, a comparison of girls with next-born twin sisters to those with next-born singleton sisters (or of those with second-subsequent twins and singletons) also allows a causal interpretation.16 Because twin births are rare (less than 1% of the sample) and thus limit statistical power, most of the analyses focus on the sister–brother comparison rather than the twin–singleton comparison. Additionally, most of the analyses study the outcome of the mother’s next pregnancy (conditional on at least one more pregnancy), but some also show results for second-subsequent pregnancy (conditional on at least two more pregnancies).
Although outcome of a given birth is random in ideal circumstances, it may in reality be correlated with prebirth characteristics. This threat to identification applies mainly to the sister–brother comparison, due to the prevalence of sex-selective abortion in South Asia (Arnold, Kishor, and Roy 2002; Bhalotra and Cochrane 2010).17 Because of the uneven spread of prenatal sex detection technologies, some birth cohorts and countries in this study are subject to concerns about sex-selective abortion, and others are not.18 Nevertheless, respondents may be more likely to remember deceased boys than deceased girls, which may also lead to selection bias. Additionally, the Trivers-Willard hypothesis proposes that a woman’s status affects the sex of her offspring (Trivers and Willard 1973). Section V shows that evidence of sex selection is absent in some estimation samples and quantitatively small in others. Still, I control for the exact permutation of older siblings by sex (e.g., BG, GG, GBG) as well as the birth interval between the individual and her next-youngest sibling. The likelihood of sex selection declines in the number of older brothers due to a demand for sons, and it increases in the birth interval because longer birth intervals allow for more terminated pregnancies between births (Pörtner 2010).19
For a girl of family i and older sibling composition j, I run the following basic regression:20
| (3) |
The central variables are yij, a marriage or human capital outcome, and sistersij, the number of girls born in a subsequent pregnancy (first- or second-subsequent, depending on the analysis). For the sister-brother experiment, sistersij varies between 0 (for a next brother) and 1 (for a next sister). For the twins experiment, sistersij varies between 1 (for a singleton sister) and 2 (for twin sisters). The fixed effect δj is unique to each permutation of older siblings; the covariates in Xij vary by sample.21
V. Sister Effects on Home-Leaving
The analysis first focuses on the process of female home-leaving in the Fertility Histories. The Fertility Histories establish basic patterns across all four countries and allow a detailed examination of how sister effects differ across subsamples and differ between older and younger sisters.
V.A. Younger Sister Effects on Home-Leaving
The basic home-leaving result appears in Figure II, which plots the share of girls living with their parents by age and sex of the next-youngest sibling. Similar patterns emerge in all four countries. Starting in the mid-teenage years, female rates of parental coresidence decline precipitously, as girls leave their natal homes and move in with their husbands’ families. Precisely when rates of parental coresidence begin their steep decline (and rates of marriage increase), a persistent gap emerges between girls with younger brothers and sisters. Compared to girls with next-youngest brothers, girls with next-youngest sisters are a few percentage points less likely to be living with their parents.
Figure II.
Parental Coresidence by Sex of Next-Youngest Sibling
Samples include surviving girls with at least one ever-born younger sibling. Current and next multiple births are excluded. Sample sizes: India = 149,650; Bangladesh = 29,244; Nepal = 15,107; Pakistan = 12,539. Source: DHS Fertility Histories.
Table I places magnitudes on these graphical differences with ordinary least squares (OLS) estimates of the effect of next-youngest sisters on parental coresidence between ages 15 and 24. In each panel, the first row reports the coefficient on the younger sister dummy, and the second row reports the control group mean, or the share of girls with younger brothers who still live with their parents. Relative to their counterparts with next-youngest brothers, girls with next-youngest sisters are roughly 3 percentage points more likely to have left home (Panel A). Additionally, girls with second-youngest sisters are roughly 1.5 percentage points more likely to have left home than those with second-youngest brothers (Panel B). Many of the second-youngest sister coefficients are not statistically significant at the individual country level, but a pooled regression with country-by-year fixed effects yields a significant coefficient of –0.015 (std. err. = 0.003).22 The point estimates in both panels show moderate variation across countries, with Bangladesh and Nepal showing lower average rates of parental coresidence and larger effects.
Table I.
Younger Sister Effects on Parental Coresidence, Women Aged 15–24
| (1) | (2) | (3) | (4) | |
|---|---|---|---|---|
| Bangladesh | India | Nepal | Pakistan | |
| Panel A. First subsequent pregnancy (conditional on ≥ 1 more pregnancy) | ||||
| Younger sister | −0.035 | −0.027 | −0.037 | −0.028 |
| [0.007] | [0.003] | [0.010] | [0.011] | |
| Mean among women w/ a younger brother | 0.49 | 0.59 | 0.44 | 0.73 |
| Number of observations | 14,650 | 77,589 | 7,542 | 6,211 |
| Panel B. Second subsequent pregnancy (conditional on ≥ 2 more pregnancies) | ||||
| Younger sister | −0.015 | −0.014 | −0.015 | −0.010 |
| [0.008] | [0.004] | [0.010] | [0.011] | |
| Mean among women w/ a younger brother | 0.46 | 0.55 | 0.41 | 0.72 |
| Number of observations | 11,881 | 58,647 | 6,453 | 5,677 |
Notes. OLS estimates. Brackets contain standard errors clustered at the PSU level. Only observations with singleton current and subsequent births are included. Each cell reports a coefficient from a separate regression. The dependent variable equals 1 if the woman resides with her mother, 0 otherwise. All regressions include fixed effects for age, mother’s region of residence, survey year, and the exact composition of older siblings by birth order and sex. Regressions also control for spacing from the previous birth, maternal and paternal educational attainment, maternal age, and rural residence.
Source. DHS Fertility Histories.
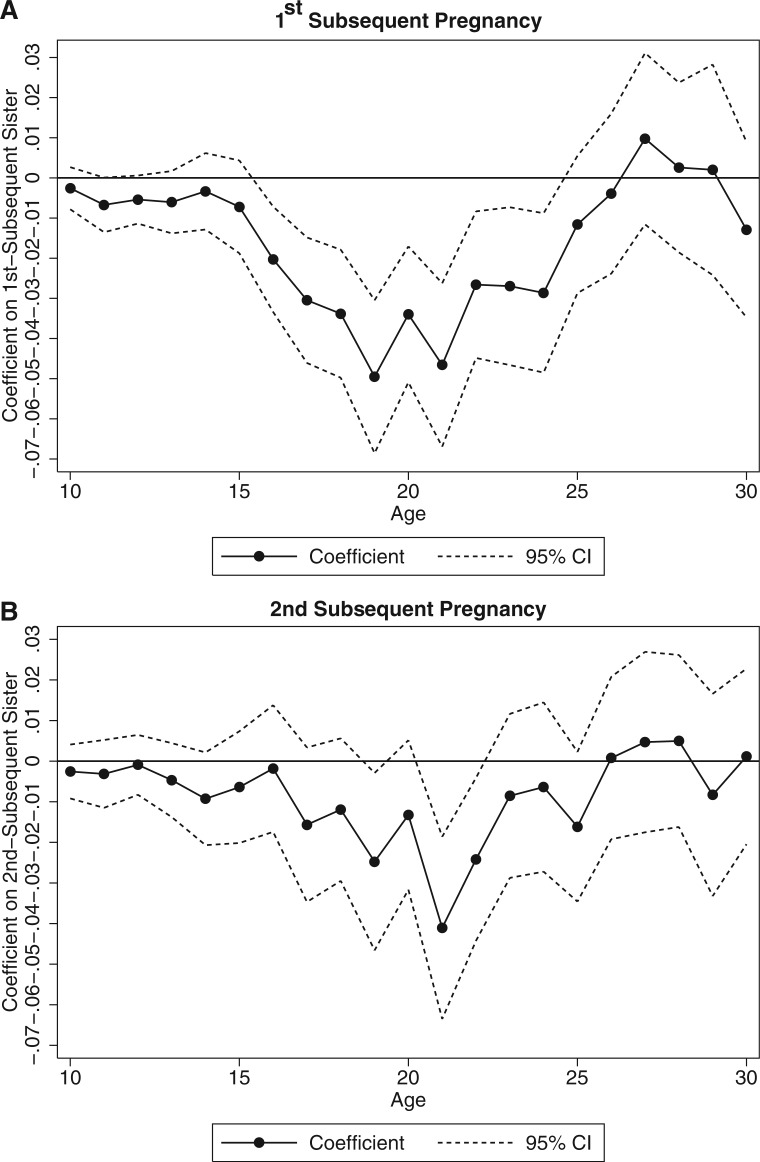
The evolution of these effects across ages emerges in Figure III, which plots younger sister effects from age-specific estimations of equation (3). Panel A graphs the coefficients on the sex of the first-subsequent sibling, and Panel B graphs the coefficients on the sex of the second-subsequent sibling. In Panel A, through roughly age 15, differences between girls with next-youngest sisters and brothers are indistinguishable from zero. The gap then widens until it reaches roughly 5 percentage points at age 19 but then reverses course, so that by the late 20s, when almost all women have left home, next-youngest sisters have negligible effects on parental coresidence. The age patterns in Panel B, for second-subsequent siblings, are similar but closer to zero.
Figure III.
Younger Sister Effects on Parental Coresidence by Age, Pooled Data
The figure plots coefficients from age-specific estimations of equation (3). In Panel A, the sample includes surviving girls with at least one ever-born younger sibling. In Panel B, the sample includes surviving girls with at least two ever-born younger siblings. Current and subsequent multiple births are excluded. Source: DHS Fertility Histories.
Possible threats to causal inference in Table I include sex-selective abortion, recall error, and the Trivers-Willard hypothesis. To investigate these threats, Online Appendix Table III reports regressions of the next-youngest sibling’s gender on the birth interval, the sex composition of older siblings, and several parental characteristics; for an alternative approach to the same issue, Online Appendix Table IV displays covariate means by sex of the next-youngest sibling. The results reveal little reason to believe that sex selection will bias the results. Few coefficients or differences are statistically significant, all are small in magnitude, and all vary in sign across countries. The only country with consistent evidence of sex selection is India, where a one-year increase in the birth interval is associated with a 0.3 percentage point reduction in the probability of a female birth, and an increase in the number of older brothers by one is associated with a 0.9 percentage point rise in this probability. But the effects of younger sisters are just as evident outside India as inside it.
Importantly, the estimates in Table I may reflect a negative effect of a younger sister on parental coresidence, a positive effect of a younger brother on parental coresidence, or some combination of the two. The next segment of the analysis relies on twin births to clarify this ambiguity. With twin girls, one can estimate the effect of having two younger sisters rather than one, which would generate upstream marriage pressure. In contrast, twin younger brothers should not affect home-leaving relative to singleton younger brothers.
Column (1) of Table II carries out this approach using pooled data from all countries. For comparison, Panel A repeats the younger sister–younger brother comparison from Table I, this time pooling countries together. Panel B then compares girls with a younger singleton sister to girls with younger twin sisters. Panel C does the same for pregnancies that only resulted in male births, comparing younger twin brothers with younger singleton brothers.23 Under the assumption that twin births are random, the analyses in Panels B and C measure the effect of an additional younger sister or brother on home-leaving, instead of the difference between a sister and a brother.
Table II.
Effects of Younger Twins, Women Aged 15–24, Pooled Data
| (1) | (2) | |
|---|---|---|
| Parental coresidence | Number of siblings | |
| Panel A. Effect of a singleton sister relative to a singleton brother | ||
| First subsequent pregnancy (N = 105,992) | −0.028 | 0.417 |
| [0.003] | [0.010] | |
| Second subsequent pregnancy (N = 82,658) | −0.015 | 0.355 |
| [0.003] | [0.011] | |
| Panel B. Effect of twin sisters relative to a singleton sister | ||
| First subsequent pregnancy (N = 51,730) | −0.020 | 0.831 |
| [0.028] | [0.097] | |
| Second subsequent pregnancy (N = 39,977) | −0.057 | 0.939 |
| [0.029] | [0.109] | |
| Panel C. Effect of twin brothers relative to singleton brother | ||
| First subsequent pregnancy (N = 54,787) | −0.003 | 0.843 |
| [0.027] | [0.098] | |
| Second subsequent pregnancy (N = 43,115) | 0.005 | 0.857 |
| [0.028] | [0.099] | |
Notes. OLS estimates. Brackets contain standard errors clustered at the PSU level. The sample includes young women whose mothers had at least one or two subsequent pregnancies, depending on the specification. Each cell reports a coefficient from a separate regression. All regressions include fixed effects for age, survey (country-by-year), and the exact composition of older siblings by birth order and sex. Regressions also control for spacing from the previous birth, maternal and paternal educational attainment, maternal age, religion, and rural residence.
Source. DHS Fertility Histories.
In Panel A of Table II, the usual pattern emerges, with younger sisters causing earlier home-leaving relative to younger brothers. As in Table I, next-youngest sisters reduce parental coresidence by 3 percentage points, and second-youngest sisters reduce parental coresidence by half that amount. Panels B and C then give suggestive evidence that the sister–brother difference is due solely to an effect of the number of sisters. Because twin births are rare (200–300 in each regression, or less than 1% of the sample), the standard errors are large and the estimates noisy. Even so, in Panel B, the coefficients on the number of girls born in subsequent pregnancies are both negative and, in one out of two cases, statistically significant. The coefficient is larger for the second subsequent pregnancy than for the first, which is surprising but may be the result of sampling error. Meanwhile, Panel C yields coefficients of 0 for the number of boys born in subsequent pregnancies. An exogenous increase in the number of younger sisters increases marriage risk, whereas an exogenous increase in the number of younger brothers does not. This result suggests that the sister–brother comparison solely reflects the effect of an additional sister, rather than offsetting (nonzero) effects of sisters and brothers.
Throughout South Asia, parents are more likely to continue childbearing after a female birth than after a male birth (Filmer, Friedman, and Schady 2009). As a result of this son-biased fertility-stopping behavior, family size may be an important mediator of the effects of younger sisters. Column (2) of Table II addresses this issue by rerunning both the sister–brother and the twins analyses with the number of siblings as the dependent variable. Panel A confirms that the birth of a younger sister rather than a younger brother increases the number of siblings by 0.4, implying that family size effects may play a role in explaining the results. However, the twins analysis rules out this explanation. Relative to singleton younger siblings, younger twins increase sibship size by 0.9, irrespective of their gender. Meanwhile, in column (1), female twins, not male twins, decrease parental coresidence. The fact that female and male twins have similar effects on family size but different effects on parental coresidence suggests that family size effects do not explain the article’s main results.
V.B. Heterogeneity in Younger Sister Effects on Home-Leaving
A comparison of the next-youngest sister effects across selected subsamples sheds some light on the mechanisms behind the basic result.
1. Younger Sister Effects by Demographic Group
Table III pools data from all four countries and then divides the sample by several relevant characteristics.24 As a basis for comparison, column (1) reports the baseline estimate of the younger sister effect in the pooled data. Because India’s sample is so large relative to other countries, the baseline estimate in the pooled data, –0.028, is very close to the estimate for India in Table I, Panel A.25
Table III.
Next-Youngest Sister Effects on Parental Coresidence, Selected Subsamples, Women Aged 15–24, Pooled Data
| Parents’ sector of res. | Dad’shighest grade | Age gap to next sibling | ||||||
|---|---|---|---|---|---|---|---|---|
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | |
| Baseline estimate | Rural | Urban | < 5 | ≥ 5 | <2 yrs. | 2–3 yrs. | 4+ yrs. | |
| Younger sister | −0.028 | −0.033 | −0.020 | −0.024 | −0.034 | −0.035 | −0.028 | −0.020 |
| [0.003] | [0.003] | [0.004] | [0.004] | [0.004] | [0.005] | [0.004] | [0.007] | |
| Number of Observations | 105,992 | 71,003 | 34,989 | 51,074 | 55,918 | 33,409 | 55,785 | 16,798 |
Notes. OLS estimates. Brackets contain standard errors clustered at the PSU level. The sample includes young women with at least one ever-born younger sibling. Only observations with singleton current and next births are included. Each cell reports a coefficient from a separate regression. The dependent variable equals 1 if the woman resides with her mother and 0 otherwise. All regressions include fixed effects for age, mother’s region of residence, survey (country-by-year), and the exact composition of older siblings by birth order and sex. Regressions also control for spacing from the previous birth, maternal and paternal educational attainment, maternal age, and rural residence.
Source. DHS Fertility Histories.
Columns (2) and (3) of Table III show that the effects are stronger for girls who grew up in rural areas than for their urban counterparts. This result has two interpretations in the context of the search model. The first is that urban families may adhere less to traditional marriage practices. The second is that urban areas are characterized by higher arrival rates than rural areas. In urban areas, marriage markets are thick, matchmakers and newspaper classifieds are easily accessible, and the search process does not involve (sometimes arduous) travel to neighboring villages. The theoretical framework reveals that cross-sister effects on marriage risk vary ambiguously with the arrival rate, so one could interpret the urban/rural difference as preliminary evidence on the sign of this comparative static.
The remainder of Table III examines heterogeneity by parental socioeconomic status and the age gap between sisters. Columns (4) and (5) show that the effects are stronger among girls whose fathers have above-median educational attainment, implying that the effects are not driven by economic constraints affecting only poor families. Finally, columns (6)–(8) subdivide the sample based on the next birth interval. The model predicts stronger effects of younger sisters when the age gap is small. Indeed, the effect estimates decrease with the age gap, but the differences in coefficients are statistically insignificant. Importantly, birth spacing is associated with parental socioeconomic status, so the comparison across subsamples does not isolate the comparative static of interest.
2. Younger Sister Effects and the Arrival Rate of Grooms
Intuition suggests that a younger sister’s effect on marriage risk may be especially strong when grooms arrive at a slow rate because parents fear that they will fail to find their younger daughter a groom while she is still desirable on the marriage market. The model clarifies that this comparative static is ambiguous because the slow arrival rate also decreases the rate at which the younger daughter loses value in her final years of marriageability. How cross-sister effects vary with the arrival rate is an empirical question.
The true arrival rate is unobservable, but one can use marriage market demographics as proxies. The starting point is a meeting function, m(M,F), which gives the number of meetings per unit of time as a function of the number of marriageable men (M) and women (F).26 The literature commonly specifies this function as a Cobb-Douglas technology, so that 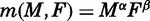 . Then from a female perspective, the arrival rate of grooms is:
. Then from a female perspective, the arrival rate of grooms is:
| (4) |
Equation (5) expresses the arrival rate of grooms as a function of observable features of the marriage market: namely, the sex ratio and the number of women. Research on search in both the labor and marriage markets points to two empirical regularities.27 First, the arrival rate increases in the tightness of the market (here measured by the sex ratio), so that α > 0. Second, the meeting (or matching) function is typically characterized by constant returns to scale, so that α + β = 1. This implies that doubling the size of the market leads to a doubling of the number of meetings.
To use equation (5) in a linear regression, take logs to obtain:
| (5) |
One can implement this specification of the log arrival rate using basic data on the demographics of the marriage market. Not all DHS samples can be linked to data on local marriage markets, but the 2001 and 2006 Nepal DHS samples are geocoded, allowing a merge to district-level information from the 2001 Census of Nepal (Nepal Central Bureau of Statistics 2010). Using this linked Nepal data set, I interact the next-youngest sister dummy with the logarithms of the marriage market sex ratio and the number of women in the marriage market. Most marriages in Nepal take place within district and within caste or ethnicity, so I aggregate marriage markets at the district-by-ethnicity level.28 Men marry at ages 20–24, and women marry at ages 15–19. For each of three five-year female marriage cohorts that were aged 15–19 in 1996, 2001, and 2006, I use the 11% census micro-sample to estimate the number of women in the cohort, as well as the ratio of men in the next-oldest five-year cohort to women in the cohort.29 The resulting marriage market sex ratio has a mean of 0.8 and a standard deviation of 0.26. The mean sex ratio is below 1 because population growth implies that the number of 15–19-year-olds exceeds the number of 20–24-year-olds.
Table IV adds these measures and their interactions with the next-youngest sister dummy to specification (3). The new specification also includes fixed effects at the five-year marriage cohort, district, and caste-ethnicity level. To ease interpretation, I run one regression as specified above, with both marriage market variables in logs, and one regression that uses the level of the sex ratio rather than its logarithm. The dependent variable is an indicator for parental coresidence.
Table IV.
Next-Youngest Sister Effects and Marriage Market Demography, Women Aged 15–24, Nepal
| (1) | (2) | |
|---|---|---|
| Sex ratio in levels | Sex ratio in logs | |
| Younger sister | −0.218 | −0.075 |
| [0.078] | [0.059] | |
| Marriage market sex ratio (M/F) | −0.112 | −0.070 |
| [0.052] | [0.043] | |
| (Younger sister)*(Sex ratio) | 0.138 | 0.109 |
| [0.058] | [0.044] | |
| Log(women in the marriage market) | 0.009 | 0.010 |
| [0.012] | [0.013] | |
| (Next sister)*Log(women) | 0.010 | 0.009 |
| [0.011] | [0.011] | |
| Marriage cohort fixed effects | X | X |
| District & ethnicity fixed effects | X | X |
| Number of observations | 4,859 | 4,859 |
Notes. OLS estimates. Brackets contain standard errors clustered at the district level. The dependent variable is an indicator for parental coresidence. Sample includes women ages 15–24 with at least one ever-born younger sibling. Only observations with singleton current and next births are included. The marriage market sex ratio is the number of men aged 20–24 divided by the number of women aged 15–19. It is calculated using the 11% micro-sample of the 2001 Nepal Census. Women are grouped into five-year birth cohorts (1977–81, 1982–86, 1987–91), and are then matched to their marriage market sex ratios at age 15–19. In addition to the fixed effects reported in the table, all regressions include fixed effects for age, mother’s region of residence, survey year, and the exact composition of older siblings by birth order and sex. Regressions also control for spacing from the previous birth, maternal and paternal educational attainment, maternal age, religion, and rural residence.
Sources. 2001 and 2006 Nepal DHS Fertility Histories, 2001 Nepal Census.
Younger sister effects on home-leaving are stronger when grooms are scarce but do not depend on the scale of the marriage market. The levels and logs specifications of the sex ratio lead to similar estimates, which is unsurprising because sex ratios are on average close to 1, so that 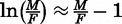 . The coefficient of 0.138 in column (1) implies that a move from the 75th percentile (0.96) to the 25th percentile (0.64) of sex ratio distribution increases the younger sister effect on home-leaving by 4 percentage points. Note also that the probability of parental coresidence tends to decrease in the relative supply of grooms, implying that the risk of nonmarriage is high when grooms are scarce. Interestingly, both specifications indicate little role for the absolute number of women, consistent with constant returns to scale in the meeting function.
. The coefficient of 0.138 in column (1) implies that a move from the 75th percentile (0.96) to the 25th percentile (0.64) of sex ratio distribution increases the younger sister effect on home-leaving by 4 percentage points. Note also that the probability of parental coresidence tends to decrease in the relative supply of grooms, implying that the risk of nonmarriage is high when grooms are scarce. Interestingly, both specifications indicate little role for the absolute number of women, consistent with constant returns to scale in the meeting function.
The preceding analysis is based on cross-sectional variation in marriage market demographics, which may result from population growth, (pre- and postnatal) sex selection, and migration. Unfortunately, no credible instrument exists for marriage market sex ratios in Nepal. Nonetheless, the strength of the association between younger sister effects and the relative supply of grooms reinforces a marriage market interpretation of the results.
3. Younger Sister Effects and the Prevalence of Arranged Marriage
Although sisters may constrain one another’s marriage timing even in the absence of formal arranged marriage, the constraints are likely to be especially important when parents have a strong say in their daughters’ marriages. The DHS contains no information on parental involvement in marriage arrangements, but another survey, the India Human Development Survey (IHDS), does. A nationally representative household survey, the IHDS includes a fertility history module similar to that found in the DHS, a marriage history module asking adult women to report how their marriages were arranged, and a marriage practices module asking women to describe some aspects of marriage practice in their communities. I use the IHDS data to measure whether the next-youngest sister effect varies with the prevalence of arranged marriage.
Because the data on marriage arrangements are self-reported but the data on home-leaving and sibling composition are mother-reported, I cannot estimate individual heterogeneity in sister effects by type of marriage arrangement.30 However, I can aggregate self-reported marriage arrangements of young women at the district level and ask whether sister effects vary with the district-level prevalence of arranged marriage.31 To measure the district-level prevalence of arranged marriage, I calculate the shares of young women age 25–29 who arranged their own marriages, arranged their marriages jointly with their parents, and had no input into their marriage arrangements. I then interact the next-youngest sister dummy in specification (3) with the share self-arranged and the share with no say. Looking across districts, the share self-arranged has a mean of 0.06 and first, second, and third quartiles of 0.00, 0.00, and 0.07, respectively. The share with no say has a mean of 0.36 and first, second, and third quartiles of 0.00, 0.30, and 0.60, respectively.
The results of this exercise, presented in Table V, show that younger sister effects on home leaving are significantly weaker in districts with a greater share of self-arranged marriages.32 At the same time, relative to joint marriage arrangements, parent-only marriage arrangements do not significantly change the magnitude of the younger sister effects. In the full specification in column (4), the coefficient on the interaction of the next-youngest sister dummy with the share self-arranged 0.19 (std. err. = 0.09). A move from the median to the 75th percentile of the share self-arranged shrinks the younger sister effect by 1.3 percentage points, and a move from the 75th percentile to the 90th percentile shrinks it by a further 2.3 percentage points.
Table V.
Next-Youngest Sister Effects and the Prevalence of Arranged Marriage, Women Aged 15–24, India
| (1) | (2) | (3) | (4) | |
|---|---|---|---|---|
| Younger sister | −0.039 | −0.047 | −0.049 | −0.065 |
| [0.011] | [0.012] | [0.017] | [0.020] | |
| District share of women aged 25–29 with self-arranged marriages | 0.056 | −0.041 | ||
| [0.076] | [0.074] | |||
| (Younger sister)*(Share self-arranged) | 0.158 | 0.189 | ||
| [0.086] | [0.093] | |||
| District share of women aged 25–29 with no say in marriage arrangements | −0.113 | −0.118 | ||
| [0.030] | [0.032] | |||
| (Younger sister)*(Share with no say) | 0.028 | 0.048 | ||
| [0.034] | [0.037] | |||
| Number of observations | 16,154 | 16,154 | 16,154 | 16,154 |
Notes. OLS estimates. Brackets contain standard errors clustered at the PSU level. The dependent variable is an indicator for parental coresidence. Sample includes women ages 15–24 with at least one ever-born younger sibling. Only observations with singleton current and next births are included. The district shares are estimated within the same survey data set, based on respondents’ reports of their own marriage arrangements. All regressions include fixed effects for age and the exact composition of older siblings by birth order and sex. Regressions also control for spacing from the previous birth, maternal and paternal educational attainment, maternal age, and religion.
Source. 2005 India Human Development Survey.
These results imply that sister effects intensify with more family involvement in marriage arrangements. But we should note that the prevalence of arranged marriage is likely correlated with social conservatism more generally. If conservatism is associated with strong social norms for marriage by birth order, then arranged marriage may not be the culprit per se. In either case, however, adherence to orthodox marriage practices is key to putting sisters’ interests at odds.
V.C. Older Sister Effects on Home-Leaving
The search framework predicts that the effects of older and younger sisters have opposite sign. However, mean differences between girls with older brothers and girls with older sisters may reflect selective fertility, rather than the effects of older siblings. Because of the demand for sons, parents are far more likely to continue having children after a female birth than after a male birth (Filmer, Friedman, and Schady 2009). For girls with at least one older sibling in the pooled sample, Online Appendix Table V regresses the gender of the next-oldest sibling on family characteristics, and Online Appendix Table VI shows mean family characteristics by sex of the next-oldest sibling. Girls with next-oldest sisters have fewer older brothers (not counting the next-oldest birth), shorter birth intervals, more educated and older mothers, and later birth years than girls with next-oldest brothers. Many more of these differences are statistically significant than in Online Appendix Tables III–IV, which studied the correlates of the next-youngest sibling’s gender. But more important, the magnitudes of the differences are much larger for the gender of the next-oldest sibling. As a result, a mean comparison of girls with next-oldest brothers and sisters may yield a biased estimate of the effect of an older sister.
The selection problem is most intuitive if we view the older sibling as the unit of observation. As before, consider a child from family i with older sibling composition j. Let femaleij, Sij, and Yij be indicators for the child’s gender, the presence of a next-youngest sister, and the presence of a next-youngest sister who lives with her parents, respectively. In more general language, femaleij is the treatment indicator, Sij is the sample selection indicator, and Yij is the outcome. Then:
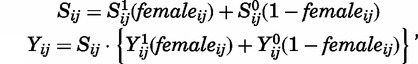 |
(6) |
where 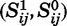 are potential sample selection probabilities and
are potential sample selection probabilities and 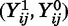 are potential outcomes. We observe only (femaleij,
Sij, Yij) but wish to make inferences about moments of
are potential outcomes. We observe only (femaleij,
Sij, Yij) but wish to make inferences about moments of 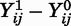 : the effect of a child’s sex on a younger sister’s propensity to live with her parents, were a younger sister to exist.
: the effect of a child’s sex on a younger sister’s propensity to live with her parents, were a younger sister to exist.
The econometrics literature suggests a few ways to estimate treatment effects under endogenous sample selection. Horowitz and Manski (2000) propose making worst-case assumptions about the missing outcomes to generate treatment effect bounds that require no assumptions about the selection process. But if both the treatment and control groups select out of the sample at reasonably high rates, as is the case here, Horowitz-Manski bounds become uninformative.33 However, Heckman (1974, 1979) and Lee (2009) show that added structure on the selection process can improve identification. Both approaches depend heavily on a latent variable threshold-crossing model of sample selection, which is equivalent to the monotonicity condition that 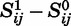 has weakly the same sign for all children (Vytlacil 2002). Heckman’s parametric selection correction model yields a point estimate of the treatment effect but is only robust when an instrument for selection—a variable that affects selection but bears no direct effect on the outcome—exists. In contrast, the procedure of Lee provides nonparametric bounds on the treatment effect without requiring such an exclusion restriction. This procedure involves identifying the excess number of observations in the group with a higher selection rate and then trimming the left and right tails of that group’s outcome distribution by this excess number of observations.
has weakly the same sign for all children (Vytlacil 2002). Heckman’s parametric selection correction model yields a point estimate of the treatment effect but is only robust when an instrument for selection—a variable that affects selection but bears no direct effect on the outcome—exists. In contrast, the procedure of Lee provides nonparametric bounds on the treatment effect without requiring such an exclusion restriction. This procedure involves identifying the excess number of observations in the group with a higher selection rate and then trimming the left and right tails of that group’s outcome distribution by this excess number of observations.
I use the methods of both Heckman (1974) and Lee (2009) to assess the extent of selection bias in OLS estimates of the older sister effect on parental coresidence.34 As a first step to implementing these methods, one must justify the monotonicity assumption. In South Asia, where parents have a demand for sons, the monotonicity condition generally implies that all couples who stopped childbearing after a girl would have also stopped after a boy. This condition may not hold exactly for all families, but because son-biased fertility-stopping behavior is so pervasive in South Asia (Filmer, Friedman, and Schady 2009), it is a reasonable approximation. Nonetheless, if parents also have a demand for gender diversity, a female birth may decrease fertility in families with many boys but without many girls. To account for this possibility, I allow the effect of a girl on fertility continuation to differ by the exact composition of older siblings in both the selection correction and bounds estimations. In the selection correction model estimations, I interact the gender dummy with indicators for the exact composition of older siblings. In the bounds estimations, I compute separate bounds for each composition of older siblings and then average across them, weighting by sample size.
The monotonicity condition requires a careful choice of the analysis sample. One sample of interest is every individual in the fertility histories over age 15, which includes every older sibling of the 15–24 age group. But the inclusion of individuals aged 26 and above may violate the monotonicity condition, since an initial spike in parental fertility following a female birth may then decrease the probability that a younger sibling lands in the 15–24 age group. As a result, I analyze how the genders of individuals aged 16–25 affect rates of parental coresidence among their younger sisters aged 15–24. This approach exacerbates sample selectivity because it leaves a short period for the birth of a younger sibling, but it makes the monotonicity condition plausible.
A second step to implementing the Heckman selection correction model is the choice of an instrument for sample selection. Based on the logic that women become less likely to continue childbearing as they age, I use the mother’s age at the older sibling’s birth as an instrument for whether a younger sibling is born. Because the mother’s age at a given child’s birth is correlated with her age at first birth, I control for her age at first birth in both the selection equation and the outcome equation.35 I also report a specification that controls for the mother’s age at first birth, age at first marriage, and educational attainment, as well as the father’s educational attainment. In both specifications, the exclusion restriction—that absent selection, children born longer after their mothers’ first births would have similar home-leaving propensities to those born sooner after their mothers’ first births—is strong, but the results are nonetheless instructive. The DHS does not offer an obviously superior instrument for selection.
Table VI exhibits the uncorrected OLS estimates, the Heckman selection-corrected estimates, and the Lee bounds. To clarify the procedure, Table VI presents separate estimations for birth orders 1–5. For comparison, column (1) presents estimates the effect of next-youngest sibling gender. Columns (2)–(7) contain estimates of the effect of next-oldest sibling gender. These effects do not apply to first-borns (who have no older siblings); the Heckman models are not estimable for second-borns (for whom the mother’s age at first birth equals her age at the next-oldest sibling’s birth).
Table VI.
Next-Youngest versus Next-Oldest Sister Effects on Parental Coresidence, Women Aged 15–24, Pooled Data
| Effect of older sister |
|||||||
|---|---|---|---|---|---|---|---|
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | |
| Effect of younger sister (OLS) | OLS | Heckman (1974) | Heckman (1974) | Avg. trimming proportion | Lee (2009) lower bound | Lee (2009) upper bound | |
| First birth order | −0.027 | — | — | — | — | — | — |
| [0.004] | |||||||
| Second birth order | −0.029 | 0.013 | — | — | 0.032 | 0.001 | 0.032 |
| [0.005] | [0.004] | [0.010] | [0.007] | [0.009] | |||
| Third birth order | −0.037 | 0.0124 | 0.0143 | 0.0105 | 0.028 | 0.006 | 0.033 |
| [0.006] | [0.0056] | [0.0068] | [0.0066] | [0.012] | [0.008] | [0.010] | |
| Fourth birth order | −0.027 | 0.030 | 0.033 | 0.033 | 0.087 | 0.001 | 0.091 |
| [0.008] | [0.007] | [0.008] | [0.008] | [0.017] | [0.010] | [0.012] | |
| Fifth birth order | −0.019 | 0.020 | 0.030 | 0.028 | 0.110 | −0.023 | 0.102 |
| [0.011] | [0.010] | [0.011] | [0.011] | [0.022] | [0.015] | [0.018] | |
| Own age | 15–24 | 15–24 | 15–24 | 15–24 | 15–24 | 15–24 | 15–24 |
| Older sib’s age | — | Any | 16–25 | 16–25 | 16–25 | 16–25 | 16–25 |
| Younger sib’s age | Any | — | — | — | — | — | — |
| Covariates: | |||||||
| Older sibling comp. | X | X | X | X | X | X | X |
| M’s age at first birth | X | X | X | X | |||
| Other parental vars. | X | X | X | ||||
Notes. Brackets contain standard errors. Other parental variables include the mother’s age at first marriage, the mother’s educational attainment, and the father’s educational attainment. Columns (1) and (2) report OLS estimates of the coefficient on a dummy indicating that the specified (singleton) sibling is female, conditional on that sibling ever being born, with standard errors clustered at the PSU level. Columns (3) and (4) show Heckman selection-corrected coefficients on the next-oldest sister dummy, estimated by maximum likelihood with standard errors clustered at the PSU level. The excluded instrument is the mother’s age at the older sibling’s birth. The Heckman models are not estimable for second-born children because the mother's age at first birth is the same as the mother's age at the older sibling's birth. Columns (5)–(7) implement Lee’s (2009) trimming procedure to estimate nonparametric bounds on older sister effects, which are stratified by the exact composition of older siblings (not counting the next-oldest). Column (5) reports the average trimming proportion across the strata, with standard errors that are computed using the delta method and are clustered at the PSU level. Columns (6) and (7) report the corresponding upper and lower bounds on the effect of a next-oldest sister, with standard errors that are block bootstrapped at the PSU level.
Source. DHS Fertility Histories.
The results support the queuing theory’s prediction that younger and older sisters have opposite effects. Column (1) shows that the presence of a younger sister has a robust negative effect on parental coresidence across all birth orders. In contrast, the results in columns (2)–(7) suggest that the presence of an older sister has a positive effect on parental coresidence. The uncorrected OLS results in column (2), which use the full sample of women aged 15–24 who have at least one older sibling, indicate that women with older sisters exhibit significantly higher rates of parental coresidence than those with older brothers. Selection bias is possible, however, so columns (3)–(7) perform the selection-correction and bounding procedures. The selection-corrected estimates (columns (3)–(4)) are broadly similar to the uncorrected OLS estimates in both magnitude and statistical significance. The nonparametric bounds are necessarily less precise, but they too support the hypothesis that younger and older sisters have opposite effects. Column (5) shows the average proportion of observations trimmed from each older sibling composition stratum, and columns (6) and (7) display the trimmed bounds. Except among fifth-born women, for whom the trimming proportion is 11%, both the lower and upper bounds on the older sister effect are positive. Unfortunately, the lower bound is too close to 0 to statistically reject a zero effect. Coupled with the OLS and Heckman results, however, the results are strongly consistent with positive older sister effects on parental coresidence—providing evidence that girls queue to leave the household.
V.D. Comparison with Boys
As discussed in Section III, the predictions of the theoretical framework apply to boys as much as they do to girls.36 Unfortunately, data constraints prevent a full parallel analysis of boys. Sibling History data, analyzed in Section VI, are unavailable for men. The Fertility Histories do include data on boys, but as shown in Online Appendix Table I, home-leaving is not as closely tied to marriage for boys as it is for girls. Among boys of prime marriageable age (20–29), marriage is associated with a 25 percentage point drop (from 82% to 57%) in the probability of being linked to their mothers through the household roster. Among girls of prime marriageable age (15–24), that reduction is 74 percentage points (from 90% to 16%).37 Boys frequently leave home to study or work. Despite this limitation, an analysis of boys in the Fertility Histories can still be instructive. Table VII estimates equation (3) in a sample of men aged 20–29. Relative to a next-youngest brother, a next-youngest sister significantly increases male parental coresidence by 2.4 percentage points. Furthermore, among coresident boys, those with next-youngest sisters are 2.4 percentage points more likely to be married than those with next-youngest brothers. These results are opposite the patterns for girls (also shown in Table VII), suggesting that the presence of younger brother leads to increased marriage pressure for boys.
Table VII.
Next-Youngest Sister Effects on Parental Coresidence and Marriage, Men and Women of Prime Marriageable Age
| Women aged 15–24 |
Men aged 20–29 |
|||
|---|---|---|---|---|
| (1) | (2) | (3) | (4) | |
| Coresident | Unmarried | coresident | Coresident | Unmarried | coresident | |
| Younger sister | −0.035 | −0.008 | 0.024 | 0.024 |
| [0.004] | [0.003] | [0.005] | [0.006] | |
| Mean among individuals w/ a younger brother | 0.58 | 0.09 | 0.65 | 0.65 |
| Number of observations | 45,123 | 24,867 | 28,141 | 18,402 |
Notes. OLS estimates. Brackets contain standard errors clustered at the PSU level. The sample includes young women and men with at least one ever-born younger sibling. Only observations with singleton current and next births are included. Each cell reports a coefficient from a separate regression. In columns (1) and (3), the dependent variable equals 1 if the individual resides with his or her mother and 0 otherwise. In columns (2) and (4), the sample includes only coresident individuals; the dependent variable equals 1 if the individual has never married. All regressions include fixed effects for age, mother’s region of residence, survey, and the exact composition of older siblings by birth order and sex. Regressions also control for spacing from the previous birth, maternal and paternal educational attainment, maternal age, and rural residence.
Source. DHS Fertility Histories. Pre-1999 surveys are excluded because they do not allow linkage between the household roster (which contains data on marriage) and the individual women’s questionnaire (which contains the respondent’s fertility history). All countries have at least one post-1999 survey.
VI. Sister Effects on Marriage and Human Capital
The Fertility History results establish some compelling facts about how sisters affect each other’s home-leaving. But because the Fertility Histories fail to track these women after they leave home, they cannot provide answers to several key questions. Do the effects of younger sisters on home-leaving indeed correspond to effects on marriage? If so, does the earlier marriage of women with younger sisters come at the expense of their education? And what are the implications for spousal quality? This section explores these questions using women’s Sibling Histories from Nepal. The Sibling History data do not provide enough information to compute selection-corrected estimates of the effects of older sisters, so the section focuses only on the effects of younger sisters.
VI.A. Younger Sister Effects on Marriage Age and Human Capital among Teenagers
Figure IV plots rates of parental coresidence, never-marriage, and school attendance by age and younger sibling gender. The top panel shows rates of parental coresidence in a graph analogous to Figure II, this time focusing only on the 2006 Nepal Fertility History data. The middle panel displays rates of never-marriage among young women in the same survey’s Sibling History data. The bottom panel combines Fertility History data on coresident daughters with self-reported data on women age 15 and older. By combining the samples this way, one can observe precisely when schooling gaps emerge between girls with younger brothers and sisters.38
Figure IV.
Home-Leaving, Marriage, and Schooling by Sex of Next-Youngest Sibling, Nepal
Sample includes females with at least one younger sibling. The top panel is based on Fertility Histories. The middle panel is based on Sibling Histories. The bottom panel is based on Fertility Histories for ages 3–14 and Sibling Histories for ages 15–24. Source: 2006 Nepal DHS.
The patterns in Figure IV match a theory in which same-sex sibling competition emerges only when girls are at risk of marriage. From age 3 to age 15, girls with younger brothers and sisters have identical school attendance rates. This pattern holds both for 10-year-olds, who have high school attendance rates, and for 3- to 5-year-olds, who do not. At age 16, a large gap in school attendance emerges between girls with younger brothers and sisters, only to close at age 19, when school attendance rates become quite low. These are precisely the ages at which girls are most likely to marry.
Based on these patterns, Table VIII estimates younger sister effects on marriage, childbearing, school enrollment, and literacy among women aged 15–19. A younger sister increases a teenage girl’s probability of marriage by 5.5 percentage points and decreases her probability of attending school in the previous year by 6.5 percentage points. Girls often leave school in advance of their weddings, so the larger effect on school attendance does not necessarily imply that nonmarital forces are at work. (In any event, the effects are not statistically distinguishable.) The effects on literacy and fertility are small and insignificant, which may be due to the low rates of illiteracy and maternity in this young sample.
Table VIII.
Next-Youngest Sister Effects on Young Women Aged 15–19, Nepal
| Marriage and fertility |
Human capital |
|||
|---|---|---|---|---|
| (1) | (2) | (3) | (4) | |
| Never married | Childless | Illiterate | In school | |
| Younger sister | −0.055 | −0.022 | 0.012 | −0.067 |
| [0.022] | [0.015] | [0.021] | [0.024] | |
| Mean among women w/ a younger brother | 0.69 | 0.88 | 0.20 | 0.50 |
| Number of observations | 1,945 | 1,945 | 1,945 | 1,944 |
Notes. OLS estimates. Brackets contain standard errors clustered at the PSU level. Women born in the same year as a sibling, women with two next-youngest siblings born in the same year, and women with no younger siblings are excluded. The first row reports the regression results. The independent variable equals 1 for a next-youngest sister and 0 for a next-youngest brother. The second row reports the mean outcome for women with next-youngest brothers. All regressions control for religion, spacing from the respondent’s birth, the year the respondent’s mother initiated childbearing, birth year fixed effects, and fixed effects the exact composition of older siblings by birth order and sex.
Source. 2006 Nepal DHS Sibling Histories.
VI.B. Younger Sister Effects on Marriage Age and Human Capital among Adults
Similar effects on marriage risk and human capital are also evident among women later in the lifecycle. Panel A of Table IX presents analyses based on all women aged 15–49. The first two columns report Cox hazard regressions based on equation (3).39 The presence of a younger sister raises a woman’s risk of marriage and childbearing by slightly over 10%. In the time metric, this represents an average effect of approximately half a year. Younger sisters cause earlier marriage, which also appears to hasten childbearing.
Table IX.
Next-Youngest Sister Effects on Women, Nepal
| Marriage and fertility (Cox hazard ratios) |
Human capital (OLS coefficients) |
Health (OLS coefficients) |
||||
|---|---|---|---|---|---|---|
| (1) | (2) | (3) | (4) | (5) | (6) | |
| Marriage | First birth | Highest grade | Illiterate | Height (cm) | BMI (m/kg2) | |
| Panel A: All women aged 15–49, 2006 DHS | ||||||
| Younger sister | 1.116 | 1.127 | −0.146 | 0.029 | 0.090 | −0.122 |
| [0.025] | [0.027] | [0.078] | [0.010] | [0.129] | [0.071] | |
| Mean among women w/ a younger brother | 0.11 | 0.08 | 3.18 | 0.44 | 150.89 | 20.69 |
| Number of observations | 8,706 | 8,706 | 8,706 | 8,701 | 8,669 | 8,667 |
| Marriage and fertility (Cox hazard ratios) | Own human capital (OLS coefficients) | Match attributes (OLS coefficients) | ||||||
|---|---|---|---|---|---|---|---|---|
| (7) | (8) | (9) | (10) | (11) | (12) | (13) | (14) | |
| Marriage | First birth | Highest grade | Illiterate | H’s grade | H skilled occ. | H’s age | Asset index | |
| Panel B: Ever-married women aged 30–49, 1996 and 2006 DHS | ||||||||
| Younger sister | 1.056 | 1.063 | −0.150 | 0.029 | −0.215 | −0.044 | −0.044 | −0.044 |
| [0.022] | [0.024] | [0.068] | [0.011] | [0.100] | [0.012] | [0.148] | [0.026] | |
| Mean among women w/ a younger brother | 0.15 | 0.09 | 1.09 | 0.73 | 4.03 | 0.40 | 43.06 | 0.02 |
| Number of observations | 6,877 | 6,877 | 6,877 | 6,873 | 6,672 | 6,772 | 6,329 | 6,877 |
Notes. Brackets contain standard errors clustered at the PSU level. Women born in the same year as a sibling, women with two next-youngest siblings born in the same year, and women with no younger siblings are excluded. The first row of each panel reports the regression results. The independent variable equals 1 for a next-youngest sister and 0 for a next-youngest brother. The second row of each panel reports the mean outcome for women with next-youngest brothers; for the Cox models, the row reports the mean hazard during ages 10–30. All regressions control for religion, spacing from the respondent’s birth, the year the respondent’s mother initiated childbearing, and birth and survey year fixed effects. The OLS regressions include fixed effects for the exact composition of older siblings by birth order and sex; the Cox models stratify by this variable (so as not to impose proportionality).
Source. 1996 and 2006 Nepal DHS Sibling Histories.
The remaining columns in Panel A of Table IX examine the effects of younger sisters on other female outcomes in adulthood. Column (3) shows a moderate (but only marginally significant) negative effect on the highest grade completed, and column (4) indicates a large, statistically significant positive effect on illiteracy. Of women with younger brothers, 44% are illiterate, compared to 47% of those with younger sisters. This finding is consistent with the results of Field and Ambrus (2008), who find that early marriage reduces female literacy in Bangladesh.40 Women with younger sisters also display slightly lower body mass indexes (BMIs) than women with younger brothers (p = .08).41 However, younger sisters have no effect on height, an indicator of early childhood conditions. This result supports the hypothesis that the effects of younger sisters emerge only in young adulthood.
VI.C. Younger Sister Effects on Spousal Attributes
Shorter search time implies lower spousal quality. For obvious reasons, data on spousal quality are available only for ever-married women. I thus restrict attention to women over age 30, whose rates of never-marriage are extremely low (less than 2%).42 Because this reduces the sample size substantially, I supplement the 2006 sample with data from the 1996 Nepal DHS. The 1996 survey also included a sibling history module, but it only interviewed ever-married women, making it inappropriate for some of the preceding analyses. Nonetheless, the sample design introduces no new biases for the study of spousal quality.
Panel B of Table IX analyzes this sample of women aged 30–49. For completeness, the table first verifies that younger sisters increase the hazards of marriage and childbirth in this sample of older women. The effects remain positive and statistically significant, although they are smaller than in the 2006 full-sample results.43 The human capital effects are similar to before, and the coefficient for educational attainment is now significant at the 5% level.
Columns (11)–(14) then show that younger sisters also reduce spousal quality and household wealth in adulthood. The husbands of women with younger sisters have completed 0.2 fewer grades and are 4 percentage points less likely to have skilled occupations than their counterparts whose wives have younger brothers. Durable goods ownership, measured in an index normed to have mean 0 and standard deviation 1, is also slightly lower in the households of women with younger sisters. However, although the effects on spousal education and occupation are statistically significant at the 5% level, the effect on household wealth is only statistically significant at the 10% level. Finally, younger sisters do not affect the age of their older sisters’ husbands, a result consistent with the small, insignificant estimates of the value of a groom’s age that arise in hedonic dowry regressions (e.g., Edlund 2000). These results suggest that the constraints younger sisters place on their older sisters’ marriage arrangements lead to reductions in spousal quality.
VI.D. Older Sister Effects on Marriage Age, Human Capital, and Spousal Attributes
Unfortunately, the Sibling Histories do not allow estimation of older sister effects using the same methods as those applied to the Fertility Histories in Section V. The primary reason is that selection probabilities are unobserved for much of the sample.44 In the end, feasible estimates of bounds or selection models would be based on too little data to be informative or yield precise estimates. In addition to this broader problem, a selection correction model would also be difficult to estimate because the Sibling Histories have such limited information on respondents’ parents. In the available data, no variable plausibly satisfies the exclusion restriction of the Heckman selection model.
Uncorrected regressions of marriage and human capital outcomes on the sex of the next-oldest sibling can still be informative, albeit biased. Online Appendix Table VII carries out the older sister equivalents of the analyses in Tables VIII and IX. Compared to women with older brothers, those with older sisters marry later, initiate childbearing later, obtain more schooling, and are more likely to be literate. These results are consistent with the search framework’s prediction that the presence of an older sister delays marriage and school-leaving. On the other hand, the husbands of women with older brothers and older sisters are observably equivalent, counter to the prediction that the presence of any sister, older or younger, lowers spousal quality. The amount of bias in these estimates is unclear. But if we take them at face value, they suggest that in a household with two daughters, the elder daughter loses in both human capital and spousal quality, whereas the younger daughter gains in human capital but not in spousal quality.
VII. Alternative Explanations for Sister Effects
The results in Sections V and VI are strongly consistent with a marriage search framework, but several alternative theories also predict that women’s outcomes vary with the sex composition of their siblings. The leading alternatives focus on marriage costs, the demand for male and female labor, son-biased resource allocation, and son-biased fertility-stopping behavior. This section discusses the alternative mechanisms and explores whether their implications match the data. The basic conclusion is that no single alternative theory can account for all the patterns observed in the data.
VII.A. Dowry and Liquidity Constraints
The first alternative explanation for the patterns in Sections V and VI remains firmly rooted in the marriage market but concentrates on the family consumption problem rather than search. To marry their daughters, South Asian families pay dowries that regularly reach several times their annual income (Anderson 2007). A liquidity-constrained family must delay its younger daughter’s marriage to allow time to accumulate a second dowry. Because dowries increase with bridal age (Field and Ambrus 2008), the delay increases her dowry, which the family may offset by marrying her older sister at a younger age. Like the search framework, this simple theory predicts opposite effects of older and younger sisters on marriage age.
The analysis of sons already provides some evidence against the dowry theory. In Table VII, the presence of a younger brother increases a boy’s home-leaving and marriage risk in much the same way as a younger sister increases a girl’s. This effect is consistent with same-sex marriage queueing but not with the dowry theory. Boys generate positive net marriage transfers for their families, so liquidity constraints should not bind.
The data offer two additional testing grounds for the dowry theory. The first is Nepal, which exhibits significant regional variation in marriage institutions, as discussed by Niraula and Morgan (1996) and Sah (2010). In the terai lowlands, where nearly half of Nepal’s population lives, dowry is a deep-seated institution. Dowries are large and widespread in terai marriages, and parents take on overwhelming debt to marry their daughters. In contrast, dowries are smaller and less common in Nepal’s other two ecological regions, the hills and mountains.45 If the interaction of dowry and liquidity constraints drives the home-leaving patterns, then these patterns should be stronger in the terai than in the hills and mountains. As column (1) of Table X reveals, the opposite is true. In the hills and mountains, younger sisters decrease parental coresidence in early adulthood by over 8 percentage points. This compares with an effect of less than 2 percentage points in the terai.46
Table X.
Next-Youngest Sister Effects and Dowries, Women Aged 15–24, Nepal and India
| (1) | (2) | |
|---|---|---|
| Nepal DHS | India HDS | |
| Younger sister | −0.083 | −0.040 |
| [0.017] | [0.011] | |
| Dowry | −0.033 | 0.009 |
| [0.020] | [0.011] | |
| (Younger sister) x (Dowry) | 0.060 | −0.003 |
| [0.024] | [0.008] | |
| Measure of dowry | Dummy for high- | First PC of mother- |
| dowry region | reported gifts | |
| Number of observations | 5,348 | 15,845 |
Notes. The dependent variable equals 1 if the individual resides with her mother, 0 otherwise. OLS estimates. Brackets contain standard errors clustered at the PSU level. For Nepal, the classification of regions by the prevalence and size of the dowry is based on Niraula and Morgan (1996), Sah (2010), and references therein. For India, the measure of dowry is the first principal component of the vector of mother-reported gifts at the time of a typical wedding; results are similar if a leave-one-out district average is used because of endogeneity concerns. The sample includes girls with at least one ever-born younger sibling. Only observations with singleton current and next births are included. All regressions include fixed effects for age, mother’s region of residence, survey year, and the exact composition of older siblings by birth order and sex. Regressions also control for spacing from the previous birth, maternal and paternal educational attainment, maternal age, and rural residence.
Sources: 2001 and 2006 Nepal DHS Fertility Histories; 2005 India Human Development Survey.
The second testing ground is India, where the IHDS data allow for more precise measurement of dowry. The IHDS features a module on marriage practices, including a series of questions on the types of “gifts” typically transferred during a daughter’s wedding, from precious metals to livestock to cash. I use the responses of the young woman’s mother, although the results are similar if one instead uses a district-level average that leaves out the young woman’s mother due to endogeneity concerns. To aggregate the various gifts, I take the first principal component of the vector of the mother’s responses. I then interact this measure of dowry with the next-youngest sister dummy. The results, in column (2) of Table X, show no evidence that sister effects are more pronounced in communities with larger dowries.47
Local social and economic factors affect the equilibrium size and prevalence of dowry, so the cross-sectional analyses in Table X should be seen as suggestive. Combined with the other evidence in this section, the results suggest no role for the interaction of dowry and liquidity constraints in explaining the article’s findings. Actually, one could interpret the Nepal results as consistent with a model in which dowry mitigates some of the pressure from having two daughters. In that case, the institution of dowry relieves other cultural constraints, rather than adding to them.
VII.B. Household Labor Demand
Apart from the marriage market explanations, sibling sex composition may affect marriage age because of complementarities in household production. If opposite-sex siblings are complements in household production, but same-sex siblings are substitutes, then a sister’s presence in the household decreases the demand for female labor, whereas a brother’s presence increases it. However, while this theory predicts higher home-leaving (and marriage) among young women with sisters, it gives no reason for the opposite effects of older and younger sisters that are suggested by the data. Furthermore, Table III shows that the birth of twin brothers relative to a singleton brother does not affect female home-leaving. Finally, the school attendance differences in Figure IV are also inconsistent with the labor demand theory. Girls with brothers are more likely to attend school than are girls with sisters; the labor demand theory predicts that they should be working rather than studying.48 Household demand for male and female labor is unlikely to account for the patterns in Sections V and VI.
VII.C. Son Bias
The existing literature on the effects of sibling sex composition in resource-poor settings has emphasized yet another mechanism: a bias for sons in both intrahousehold resource allocation and fertility stopping.49 Families may substitute resources from girls to boys, so that a girl benefits from the birth of a sister rather than a brother. However, brothers raise per capita resources in the household, both directly—through productivity—and indirectly—because families are more likely to continue fertility after a girl than after a boy (Filmer, Friedman, and Schady 2009).50 As a result, sibling sex composition may have multiple countervailing effects.
Many results in Section V and VI address these theories. As a starting point, note that women with younger sisters appear to be worse off than women with younger brothers, which makes allocative bias for sons an unlikely explanation for the effects. Son-biased fertility stopping rules, which are evident in Table II, are more likely to play a role. However, several findings suggest that fertility-stopping rules also fail to explain the observed sister effects.51 First, the data suggest that older sisters have opposite effects from younger sisters on home-leaving. The alternative theories in the previous paragraph might predict that only older or younger siblings would matter—for example, because younger siblings do not yet work—but they do not give a natural interpretation for opposite effects.52 Second, the increase in family size due to twin boys is similar to that due to twin girls, but only the latter affect female home-leaving. These results imply that the younger sister effect is due to the presence of a sister rather than the absence of a brother. Third, in Figure IV, the gap in school attendance between girls with younger sisters and brothers emerges only when girls are marriageable. Theories based on the value of sons would predict gaps in earlier childhood as well. For a broader look at this issue, Online Appendix Table VIII considers the effects of next-youngest sibling gender on four outcomes in earlier life: under-five mortality, height and weight for two- to four-year-olds, and school enrollment for five- to nine-year-olds.53 The results reveal little systematic evidence that the gender of a girl’s next-youngest sibling affects her well-being in childhood.54
VIII. Sister Effects on Marriage Outside South Asia
Because the family of origin is involved in marriage arrangements in many parts of the world, younger sisters may affect women’s marriage age more globally. One would expect these sister effects to be strongest in regions with the strictest adherence to parental arranged marriage, such as the Middle East, North Africa, Central Asia, and South Asia. In other world regions—such as Africa, East Asia, and Latin America—where the role of the family in marriage arrangements has declined, the effects may be smaller. Apart from Nepal, 40 other countries in Africa, Asia, and Latin America have conducted DHS surveys with questions on siblings, marriage, and education. Table XI presents estimates of next-youngest sister effects on marriage risk and educational attainment in five world regions other than South Asia, using data on these 40 other countries.55
Table XI.
Next-Youngest Sister Effects on Marriage and Education Outside South Asia
| Age at marriage |
Highest grade |
|||
|---|---|---|---|---|
| (1) | (2) | (3) | (4) | |
| Cox HR | % married by age 16 | OLS coef. | % w/ no school | |
| Southeast Asia/Pacific (N = 116,178) (Cambodia, Indonesia, Philippines) | 1.020 | 20 | −0.021 | 15 |
| [0.0061] | [0.023] | |||
| Central Asia (N = 39,465) (Afghanistan) | 1.083 | 29 | 0.016 | 73 |
| [0.015] | [0.040] | |||
| Middle East and North Africa (N = 22,986) (Jordan, Morocco) | 1.058 | 18 | 0.002 | 53 |
| [0.016] | [0.056] | |||
| Latin America and the Caribbean (N = 167,237) (Bolivia, Dominican Republic, Haiti, Peru) | 1.016 | 19 | −0.004 | 8 |
| [0.0056] | [0.021] | |||
| Sub-Saharan Africa (N = 396,400) (Benin, Burkina Faso, Cameroon, CAR, Chad, DRC, Congo, Côte D’Ivore, Ethiopia, Gabon, Ghana, Guinea, Kenya, Lesotho, Madagascar, Malawi, Mali, Mozambique, Namibia, Nigeria, Rwanda, São Tomé & Príncipe, Senegal, Sierra Leone, South Africa, Swaziland, Tanzania, Togo, Zambia, Zimbabwe) | 1.018 | 32 | −0.028 | 46 |
| [0.0035] | [0.012] | |||
Notes. Brackets contain standard errors clustered at the PSU level. Women born in the same year as a sibling, women with two next-youngest siblings born in the same year, and women with no younger siblings are excluded. The independent variable equals 1 for a next-youngest sister and 0 for a next-youngest brother. The Cox regressions stratify by birth order–by-country interactions, as well as control for spacing from the respondent’s birth, birth year dummies, and survey year dummies. The OLS regressions control for spacing from the respondent’s birth, birth year dummies, survey year dummies, and birth order–by-country interactions. Column (2) reports the fraction of women married before their 17th birthdays. All countries with DHS surveys containing sibling histories and age-at-marriage are included.
Column (1) reveals that younger sister effects on age at marriage are surprisingly prevalent throughout the developing world. As one would expect, in Afghanistan, Jordan, and Morocco, the Cox hazard ratios are similar in magnitude to those found in South Asia, ranging from 1.06 to 1.08. For Latin America, the Pacific, and Sub-Saharan Africa, the hazard ratios remain significantly greater than 1, but they all lie between 1.01 and 1.02. These regional differences are consistent with the global diffusion of liberal attitudes toward marriage. Notably, dowry payments (net transfers from the bride’s family) are extremely rare outside South Asia (Anderson 2007), so the results reinforce the conclusion that dowry does not explain why younger sisters cause earlier marriage.
The table then examines whether these marriage age effects to translate into schooling effects, as they do in South Asia. For the schooling effects to operate, two conditions must be met: (1) marriage must occur at a sufficiently early age, and (2) school-leaving must occur at a sufficiently late age. As such, along with the hazard ratios for marriage and the OLS coefficients for educational attainment, the table reports the fraction of women who were married by age 16 and the fraction of women with no schooling.
Column (3) indicates that younger sisters have significant negative effects on educational attainment only in Sub-Saharan Africa. This result is easily squared with the distributions of marriage age and educational attainment. In Afghanistan, girls marry young but do not attend school for long, with an average of less than the second grade. In the Middle East and North Africa, they obtain more schooling but marry late. Early marriage is also fairly rare in Latin America and the Pacific. But the conditions are right for schooling effects in Sub-Saharan, where both early marriage and adolescent schooling are common. The effects on schooling are small, one-tenth the size of the effects in Nepal, but the effects on marriage risk are also small.
The cross-country comparisons suggest that the timing of institutional change and educational expansion may be key to producing the results obtained in South Asia. Consistent with this notion, Nepal underwent massive increases in female marriage age and female educational attainment during the study period, as shown in Online Appendix Figure II.
IX. Conclusions
Traditional institutions interact in interesting ways with social and economic change. This article studies how traditional marriage practices induce trade-offs among sisters, tradeoffs most intense at intermediate levels of female schooling. Across four large South Asian countries, parents rush a daughter’s marriage search if she has younger sisters and delay her marriage search if she has older sisters, at the expense of spousal quality. These effects are especially strong in settings where grooms are scarce, search frictions are large, and arranged marriage is common. Because girls leave school when they marry and depend on their husbands for economic support in adulthood, the effects have long-term consequences. In Nepal, where data on adult women are available, younger sisters cause earlier school-leaving, lower educational attainment and adult literacy, lower spousal educational attainment and spousal occupational status, and marginally lower adult household economic status. Sibling rivalry over leaving the nest has effects that last long after all siblings have left it.
These findings augment previous research on the life cycle consequences of the marriage decision. In a notable paper on this topic, Field and Ambrus (2008) use age at menarche as an instrument for marriage age in rural Bangladesh, where girls may only enter the marriage market after reaching menarche. They find that women who started menstruating early married young and left school young but saw no change in spousal quality. Their different results on spousal quality highlight an important difference in the variation driving marriage age. In their study, early menarche leads to early marriage by expanding the opportunity set, thus allowing parents to find a weakly better groom. In mine, younger sisters lead to early marriage because they restrict the opportunity set.56
If the results have any policy implications, those implications depend on the nature of the marriage market and the production function. If schooling has decreasing returns, then the cost of an older sister’s lost time in school is greater than the benefit of her younger sister’s gain, so the redistribution of education in the family has negative welfare effects. Perhaps more important, the theory predicts that the presence of any sister, older or younger, decreases expected spousal quality. If grooms’ attributes are equally valuable to all women, then the results imply a transfer of high-quality grooms from large families to small. But if marriages are characterized by match-specific quality, then a large number of daughters per family may cause aggregate mismatch in the marriage market. Along these lines, the findings may provide a new justification for family planning policies (which on average reduce the number of daughters per family and increase the spacing between them), for the promotion of love marriage, or for the development of search technologies (e.g., matchmakers and websites).57
The apparent role of search in explaining the results is surprising because it implies that for a large swath of the world’s population, conventional budget constraint considerations fail to describe a principal cause of sibling rivalry. This finding suggests an interesting direction for future research, concerning how the interaction of persistent institutions with a changing economy shapes the effects of family structure on children’s outcomes. It also calls attention to the question of why some institutions evolve slowly, a topic raised by Roland (2005) and Guiso, Sapienza, and Zingales (2006). A deeper understanding of these institutions and their effects may shed light on a range of social and economic phenomena, both across and within families.
Supplementary Material
An Online Appendix for this article can be found at QJE online (qje.oxfordjournals.org).
Acknowledgments
* I am grateful to Erica Field, Michael Kremer, and especially David Cutler, Claudia Goldin, and Lawrence Katz for their guidance throughout this research project. I thank the editor, Robert Barro; four anonymous referees; Ruchir Agarwal, Anne Case, Amitabh Chandra, Joyce Chen, Tom Cunningham, Janet Currie, Thomas Fujiwara, Supreet Kaur, Michal Kolesar, Ed Glaeser, Seema Jayachandran, Kyle Meng, Sendhil Mullainathan, Daniele Paserman, Nancy Qian, and Monica Singhal; as well as seminar participants at BU, Harvard, Princeton, RAND, Yale, UCLA, UT Austin, and the World Bank for helpful comments and suggestions. Bishnu Thapa provided excellent research assistance and sage insights into Nepali society. This research was supported by the Multidisciplinary Program on Inequality and Social Policy (NSF IGERT Grant 0333403) and the NBER Aging Program (NIA Grant T32-AG000186).
Footnotes
1. The classic model of the trade-off between child quality and quantity is due to Becker and Lewis (1973). Early evidence of the negative association between childhood family size and adult outcomes can be found in Leibowitz (1974) and Blake (1983). Despite this association, Black, Devereux, and Salvanes (2005) and Angrist, Lavy, and Schlosser (2010) find no evidence in data from Norway and Israel that an exogenous increase in the number of younger siblings affects adult outcomes. But Li, Zhang, and Zhu (2008) and Rosenzweig and Zhang (2009) estimate negative family size effects on schooling outcomes in China.
2. The article takes seriously the possibility that the gender of the xth-younger sibling is endogenous. As Section V discusses, the data do not show consistent evidence of sex selection across the four countries.
3. The literature on the effects of sibling sex composition has varied results; see Steelman et al. (2002) for a review. Edmonds (2006), studying child labor in Nepal, finds that girls with younger brothers exhibit slightly higher (market and domestic) labor supply than those with younger sisters, which he interprets through a model of gender- and age-specific skills. Elsewhere in Asia, Parish and Willis (1993) find that oldest daughters in Taiwanese families marry and leave school early, which they interpret through the lens of credit constraints. In Africa, Garg and Morduch (1997) and Morduch (2000) find mixed evidence that girls with a greater share of female siblings display better health and education outcomes.
4. The degree to which the family of origin controls marriage arrangements is continuous, rather than binary. Even in societies that no longer formally adhere to arranged marriage, the family of origin still may influence spouse selection (Goode 1970; Goody 1983; Caldwell et al. 1998).
5. However, the search model that follows clarifies that in the absence of institutional constraints, the family may offer a younger sister first if it encounters a groom of sufficient quality.
6. A regression of parental coresidence on the number of older brothers and sisters, age effects, and mother fixed effects confirms that these patterns reflect sex-specific birth order, rather than birth order generally. The coefficient on the number of older sisters is 0.060 (std. err. = 0.010), whereas the coefficient on the number of older brothers is 0.007 (std. err. = 0.011).
7. A random variable is log-concave if the logarithm of its density function is concave, implying that the distribution is unimodal. Examples include the uniform, normal, logistic, and exponential distributions. Log concavity is key to search theoretic models because it implies that the expectation of a left-truncated distribution increases less than one for one with the truncation point. See Bagnoli and Bergstrom (2005).
8. From an evolutionary perspective, the demand for youth can be seen as reflecting the decline of fecundity with age.
9. Thus, a daughter is marriageable between ages 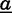 and
and 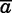 .
.
10. A sufficient condition on the depreciation rate is: δ (a) < 1 − 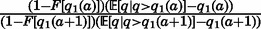 for all a.
for all a.
11. Compared to the elder daughter, the younger has both higher probability of acceptance and higher option value. Hence, the family offers her to high-quality grooms but withholds her from middle-quality grooms.
12. See, for example, Edlund (2000) for hedonic regressions of dowry on bridal traits.
13. The specific survey years are Bangladesh (1993–94, 1996–97, 1999–2000, 2004, 2007), India (1992–93, 1998–99, 2005–6), Nepal (1996, 2001, 2006), and Pakistan (1990–91, 2006–7), representing 13 of the 14 Standard DHS surveys available for South Asia as of January 2012. The only survey I omit is Sri Lanka’s 1987 DHS, a small sample with relatively few variables. Marriage institutions in Sri Lanka differ substantially from those elsewhere in South Asia (Caldwell et al. 1998). Compared to other South Asian societies, the Sinhalese marry much later, have far less parental involvement in spousal choice, and exchange far smaller dowries. The Sinhalese also do not adhere to virilocal postmarital residence.
14. For girls who have left home, the data do not contain the age at home-leaving.
15. Online Appendix Table I shows the relationship between parental coresidence and marriage among women of prime marriageable age (15–24). The DHS does not include data on the full matrix of relationships among household members, so the table uses two proxies for a household member’s parental coresidence status: (1) whether the member’s mother responded to the fertility history—implying that the mother is coresident and younger than 50—and (2) whether the member can be linked to her mother through the household head. Panel A shows that 93% of coresident daughters of survey respondents are unmarried. Panel B shows that 16% of married women can be linked to their mothers through the household head; the same is true for 90% of unmarried women. These differences shrink slightly in models with age effects.
16. Rosenzweig and Wolpin (1980) were the first researchers to use twins to identify family size effects. More recent examples include Black, Devereux, and Salvanes (2005) and Angrist, Lavy, and Schlosser (2010).
17. In theory, threats to identification may also apply to the secondary analysis of twin births. However, the data show no evidence that twinning probabilities are correlated with parental characteristics or the composition of older siblings.
18. Prenatal sex-detection technologies became available in India in the mid-1980s and in Bangladesh and Pakistan somewhat later. Their penetration in Nepal remains low.
19. For all outcomes, Online Appendix Table II reports unadjusted mean differences between women with younger sisters and brothers. The unadjusted estimates are all similar to the regression results that follow.
20. Although serial correlation across households is probably minimal in this natural experiment, I estimate standard errors conservatively by clustering at the primary sampling unit (PSU) level. I weight regressions using survey weights, but unweighted regressions produce identical results. For ease of interpretation, I omit girls who are themselves twins (less than 1% of the sample).
21. For the Fertility Histories, Xij includes the birth interval, mother’s and father’s education, and maternal age, as well as indicators for the girl’s age or birth year, the mother’s place of residence, religion, and survey. The Pakistan DHS surveys do not include a question about religion. Because over 96% of Pakistanis are Muslim (Pew Research Center 2009), I code the entire Pakistan sample as Muslim. For the Sibling Histories, Xij includes the birth interval and indicators for birth year, the decade that the woman’s mother initiated childbearing, religion, and survey.
22. The weaker effects of second-youngest sisters are consistent with the search framework’s prediction that sister effects decline in the age gap between sisters (assuming a sufficiently small depreciation rate). However, because of compositional differences across samples, the results in Panels A and B of Table I are not directly comparable.
23. In Panels B and C of Table II, the analysis focuses on subsequent pregnancies that only resulted in same-sex siblings. As a result, girls with mixed-gender younger twins are excluded from the sample.
24. The search model has no specific predictions for how sister effects vary with religion, so Table II does not report effects by religion. For completeness, I analyzed Hindus and Muslims separately and found no significant difference between the two in the pooled sample. The effects are larger for Hindus than for Muslims in Bangladesh, India, and Nepal, but Pakistan (which is predominantly Muslim) exhibits large effects.
25. One could argue that the coefficient on the gender of the next-youngest ever-born sibling is not the estimand of interest. If the effects operate through a marriage search channel, then one should take interest in the effect of a younger sister who is still alive when her older sister reaches marriageable age. In a a two-stage least squares (2SLS) regression that uses the gender of the next-youngest ever-born sibling as an instrument for a surviving next-youngest sister at age fifteen, the effect estimate is 14 percent larger than OLS estimate. This estimator assumes that the effect of the younger sibling’s gender operates only through circumstances in young adulthood. While this exclusion restriction may not hold exactly, the estimate is nonetheless informative.
26. I refer to 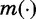 as a “meeting function” rather than a “matching function” to emphasize that a meeting does not necessarily translate to a match.
as a “meeting function” rather than a “matching function” to emphasize that a meeting does not necessarily translate to a match.
27. On labor markets, see the review by Petrongolo and Pissarides (2001). On marriage markets, see Angrist (2002), Botticini and Siow (2009), and Abramitzky, Delavande, and Vasconcelos (2011).
28. I assume that cross-district marriage-related migration is minimal, although I do not have specific data on this issue. Marriage-related migration would tend to bias the coefficients toward zero.
29. Respondents reported their district of residence five years before, so for the 1996 cohort, I use the ratio of men age 20–24 to women 15–19 five years before the census. For the 2001 cohort, I use the current ratio men age 20–24 to women age 15–19. For the 2006 cohort, I use the current ratio of men age 15–19 to girls age 10–14 in the current district of residence. The 1996 and 2006 sex ratio estimates will be accurate if mortality and international emigration are minimal. To avoid bias from a badly measured sex ratio denominator, I omit district/ethnicity-level cohorts with fewer than 15 women in the micro-sample.
30. Individual-level variation in the type of marriage arrangement may also be endogenous to sibling composition.
31. Unlike the 11% census sample from Nepal, the IHDS sample is too small to disaggregate districts by caste.
32. The uninteracted coefficient in column (1) of Table VI may appear large relative to the DHS results for India. However, when the regressions are estimated with sampling weights, the coefficients are much closer. In the India DHS data, the weighted regression coefficient is 0.034. In the IHDS data, the weighed regression coefficient is 0.039. The IHDS survey weights are not representative at the district level, so the weights are not helpful for the analysis in Table VI.
33. Because we only observe outcomes for girls, who represent roughly half of next-born children, the attrition rate would be approximately one-half even in the absence of fertility cessation.
34. In implementing both estimation procedures, I account for clustering in the DHS survey design. The maximum likelihood version of Heckman’s selection correction model is easier to adjust for clustering than the two-step version, so I use the former. For consistency with the other results in the article, I use a linear probability model for the second-stage equation. For the bounds estimator, Lee provides formulas for asymptotic standard errors only in the i.i.d. case, so I block-bootstrap the bounds estimator at the PSU level.
35. The results are also robust to omitting the mother’s age at first birth.
36. The same may not be true in societies in which the groom himself asks the bride’s father for her hand in marriage, as is common in the Middle East.
37. Similarly, only two-thirds of boys not linked to their mothers are married, compared to nine-tenths of such girls. All of these differences shrink slightly in models with age effects. See note 13 for a description of Online Appendix Table I.
38. Changes in sample composition pose a potential problem for this approach. Girls in the Fertility Histories all have mothers younger than 50, whereas those in the Sibling Histories have mothers of any age. However, adjustment for the year of the mother’s first birth does not change the patterns in Figure II. (The year of the mother’s first birth serves as a proxy for her age; her actual age is not available in the Sibling Histories.)
39. To avoid possibly inappropriate proportionality restrictions, the Cox models stratify by the composition of older siblings, instead of including fixed effects. Otherwise, the specification is identical to equation (3).
40. Among women from these cohorts who attended school, many started in late childhood, so it is plausible that early teenage dropout would affect literacy.
41. The standard deviations of BMI and height are 3 and 6, respectively.
42. Nearly all ever-married women in the sample reported their husbands’ characteristics.
43. Online Appendix Figure I shows that secular change across cohorts may account for the different results in the main sample and the over-30 sample. For four decadal birth cohorts, the figure plots the share of women married by ages 14, 15, 16, 17, and 18. Younger sisters increase marriage risk only among cohorts born after 1970. This coincides with population growth, which raised marriage market sex ratios, and also with the rapid growth of the Nepali public school system, which increased the dispersion of groom quality and the value of parental coresidence for teenage daughters.
44. For example, neither selection correction nor bounding is possible for second-borns, who constitute over a quarter of women with at least one older sibling. Because the DHS only interviewed women, one cannot estimate the effect of the first-born child’s gender on parents’ subsequent fertility decisions. As a result, the degree of sample selection is unknown for this large subsample.
45. Nonetheless, arranged marriage and marriage-by-birth-order norms are prevalent in the highlands. See, for example, Macfarlane and Gurung (1992) on the persistence of both customs among the Gurung, a highlands ethnic group.
46. The younger sister effect remains smaller in the terai than in the hills and mountains even if one omits Tharu women from the sample. The Tharu, an ethnic group from the western terai, do not exchange dowries (Gurung and Kittelsen 1996). The size and direction of the regional difference was unexpected, but one can reconcile it with the search framework. First, because of the rugged terrain in the hills and mountains, communities are more isolated than in the terai. Travel to neighboring communities is more cumbersome, which may intensify search frictions. Second, young men migrate from the hills and mountains to the terai for work; as a result, the terai has marriage market sex ratios that are approximately 10 percentage points higher than the hills and mountains. Third, families may use dowry to alleviate some of the pressure from having two daughters, just as they use search effort to alleviate some of the pressure from having two sons in Section III.
47. The size of the dowry may be correlated with household income, which in turn may be inversely related to the incidence of liquidity constraints. In unreported results, I control for the education of the young woman’s father and for the interaction of his education with dowry size. The results still fail to support the dowry theory.
48. Using data from Nepal, Edmonds (2006) finds that both boys’ and girls’ labor supply decreases if the next-youngest sibling is female, with the effect substantially larger among boys. However, this effect is concentrated only among closely spaced children, whereas the effects on marriage risk are evident at wider birth spacing as well. Furthermore, in unreported estimates, teenage boys with younger sisters have lower home-leaving risk than those with younger brothers, which is opposite the result for girls. This difference is at odds with Edmonds’s labor supply estimates.
49. See Garg and Morduch (1998), Morduch (2000), and Chen, Chen, and Liu (2010).
50. The presence of a son may also improve a mother’s bargaining power, with benefits to his sisters. The next paragraph discusses empirical patterns that reject this explanation.
51. In addition to the findings discussed in this paragraph, the inclusion of childhood family size as a covariate did not substantively change the results. I do not report this finding in a table because completed family size is endogenous.
52. The confidence intervals on the nonparametric bounds on older sister effects include 0, but the bounds themselves are both positive, and the OLS and selection-corrected estimates reject 0.
53. Some of these variables do not appear in every survey. I analyze the heights and weights of two- to four year-olds because the DHS only collects anthropometric data on children under age five, and few one-year-olds have a younger sibling. The height and weight z-scores have mean 0 and standard deviation 1 in a “healthy” population.
54. One could argue that forward-looking families might adjust their investments based on their daughters’ marriage market prospects, but apparently they do not, at least along the margins studied in Online Appendix Table VIII.
55. The data from Indonesia and Jordan only include ever-married women, so I restrict both these samples to women over the age of 30. For all other countries, the data include both married and unmarried women.
56. Also consistent with my results, Field and Ambrus (2008) report that age at menarche has smaller effects on marriage age among women with more older sisters. However, their data only include siblings who survived to adulthood and as a result do not allow a more careful examination of sibling effects.
57. Were they enforceable, compulsory schooling and minimum age at marriage laws would have complicated effects on the intrahousehold dynamics studied in this paper. By preventing early marriage, these laws would intensify search constraints, potentially leading to greater groom quality reductions for both sisters and greater marriage delay for younger sisters. However, a full analysis of this problem would need to take into account the general equilibrium effects of these laws in the marriage market.
References
- Abramitzky Ran, Delavande Adeline, Vasconcelos Luís. “Marrying Up: The Role of Sex Ratio in Assortative Matching,”. American Economic Journal: Applied Economics. 2011;3:124–157. [Google Scholar]
- Alesina Alberto, Giuliano Paola. “The Power of the Family,”. Journal of Economic Growth. 2010;15:93–125. [Google Scholar]
- Ambrus Attila, Field Erica, Torero Máximo. “Muslim Family Law, Prenuptial Agreements, and the Emergence of Dowry in Bangladesh,”. Quarterly Journal of Economics. 2010;125:1349–1397. [Google Scholar]
- Anderson Siwan. “The Economics of Dowry and Brideprice,”. Journal of Economic Perspectives. 2007;21:151–174. [Google Scholar]
- Angrist Joshua. “How Do Sex Ratios Affect Marriage and Labor Markets? Evidence from America’s Second Generation,”. Quarterly Journal of Economics. 2002;117:997–1038. [Google Scholar]
- Angrist Joshua, Lavy Victor, Schlosser Analia. “Multiple Experiments for the Causal Link between the Quantity and Quality of Children,”. Journal of Labor Economics. 2010;28:773–824. [Google Scholar]
- Arnold Fred, Kishor Sunita, Roy T K. “Sex-Selective Abortions in India,”. Population and Development Review. 2002;28:759–785. [Google Scholar]
- Bagnoli Mark, Bergstrom Ted. “Log-Concave Probability and its Applications,”. Economic Theory. 2005;26:445–469. [Google Scholar]
- Becker Gary S, Gregg Lewis H. “On the Interaction between the Quantity and Quality of Children,”. Journal of Political Economy. 1973;81:S279–S288. [Google Scholar]
- Bertrand Marianne, Schoar Antoinette. “The Role of Family in Family Firms,”. Journal of Economic Perspectives. 2006;20:73–96. [Google Scholar]
- Bhalotra Sonia, Cochrane Tom. “Where Have All the Young Girls Gone? Identification of Sex Selection in India,”. Mimeo, Bristol University, 2010. [Google Scholar]
- Black Sandra, Devereux Paul J, Salvanes Kjell G. “The More the Merrier? The Effect of Family Composition on Children’s Education,”. Quarterly Journal of Economics. 2005;120:669–700. [Google Scholar]
- Blake Judith. Demography, 18. 18: 1983. “Family Size and the Quality of Children,”; pp. 421–442. [PubMed] [Google Scholar]
- Botticini Maristella, Siow Aloysius. “Are There Increasing Returns to Scale in Marriage Markets?,”. Mimeo, Università Bocconi, 2009. [Google Scholar]
- Bühler, G., ed., The Laws of Manu (1886; Charleston: BiblioBazaar, 2008)
- Butcher Kristin F, Case Anne. “The Effect of Sibling Sex Composition on Women’s Education and Earnings,”. Quarterly Journal of Economics. 1994;109:531–563. [Google Scholar]
- Caldwell John C, Caldwell Pat, Caldwell Bruce K, Pieres Idrani. “The Construction of Adolescence in a Changing World: Implications for Sexuality, Reproduction, and Marriage,”. Studies in Family Planning. 1998;29:137–153. [PubMed] [Google Scholar]
- Chen Stacey H, Chen Yen-Chien, Liu Jin-Tan. “The Effects of Sibling Sex Composition on Child Mortality and Education,”. Mimeo, Royal Holloway, University of London, 2010. [Google Scholar]
- Desai Sonalde, Andrist Lester. “Gender Scripts and Age at Marriage in India,”. Demography. 2010;47:667–687. doi: 10.1353/dem.0.0118. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dillon Lisa. “Parental and Sibling Influences on the Timing of Marriage, 17th and 18th-Century Quebec,”. Annales de Dèmographie Historique. 2010;119:139–180. [Google Scholar]
- Edlund Lena. “Son Preference, Sex Ratios, and Marriage Patterns,”. Journal of Political Economy. 1999;107:1275–1304. [Google Scholar]
- Edlund Lena. “The Marriage Squeeze Interpretation of Dowry Inflation: A Comment,”. Journal of Political Economy. 2000;108:1327–1333. [Google Scholar]
- Edlund Lena, Lagerlöf Nils-Petter. “Individual vs. Parental Consent in Marriage: Implications for Intra-Household Resource Allocation and Growth,”. Mimeo, Columbia University, 2006. [Google Scholar]
- Edmonds Eric. “Understanding Sibling Differences in Child Labor,”. Journal of Population Economics. 2006;19:795–821. [Google Scholar]
- Fafchamps Marcel, Quisumbing Agnes R. “Household Formation and Marriage Markets in Rural Areas,”. in Handbook of Development Economics, vol. 4, T. Paul Schultz, and John A. Strauss, eds. (Amsterdam: Elsevier, 2007), 3187–3247. [Google Scholar]
- Field Erica, Ambrus Attila. “Early Marriage, Age of Menarche, and Female Schooling Attainment in Bangladesh,”. Journal of Political Economy. 2008;116:881–930. [Google Scholar]
- Filmer Deon, Friedman Jed, Schady Norbert. “Development, Modernization, and Childbearing: The Role of Family Sex Composition,”. World Bank Economic Review. 2009;23:371–398. [Google Scholar]
- Garg Ashish, Morduch Jonathan. “Sibling Rivalry and the Gender Gap: Evidence from Child Health Outcomes in Ghana,”. Journal of Population Economics. 1998;11:471–493. doi: 10.1007/s001480050080. [DOI] [PubMed] [Google Scholar]
- Goode William Josiah. World Revolution and Family Patterns. New York: Free Press; 1970. [Google Scholar]
- Goody Jack R. The Development of the Family and Marriage in Europe. New York: Cambridge University Press; 1983. [Google Scholar]
- Greif Avner. “Cultural Beliefs and the Organization of Society: A Historical and Theoretical Reflection on Collectivist and Individualist Societies,”. Journal of Political Economy. 1994;102:912–950. [Google Scholar]
- Guiso Luigi, Sapienza Paola, Zingales Luigi. “Does Culture Affect Economic Outcomes?,”. Journal of Economic Perspectives. 2006;20:23–48. [Google Scholar]
- Gurung Ganesh Man, Kittelsen Tove C. Emerging Ethnicity and Aspects of Community Adaptation. Kathmandu: Central Department of Sociology and Anthropology, Tribhuvan University; 1986. “Kurma, Kola, and Kuli as Community Concepts: Patrilineage, Deities, and Inside-Outside Dichotomy among the Rana Tharus,”; pp. 78–93. [Google Scholar]
- Heckman James. “Shadow Prices, Market Wages and Labor Supply,”. Econometrica. 1974;42:679–694. [Google Scholar]
- Heckman James. “Sample Selection Bias as a Specification Error,”. Econometrica. 1979;47(1):153–162. [Google Scholar]
- Horowitz Joel L, Manski Charles F. “Nonparametric Analysis of Randomized Experiments with Missing Covariate and Outcome Data,”. Journal of the American Statistical Association. 2000;95:77–84. [Google Scholar]
- Jacoby Hanan, Mansuri Ghazala. “Watta Satta: Exchange Marriage and Women’s Welfare in Rural Pakistan,”. American Economic Review. 2010;100:1804–1825. [Google Scholar]
- Lee David S. “Training, Wages, and Sample Selection: Estimating Sharp Bounds on Treatment Effects,”. Review of Economic Studies. 2009;76:1071–1102. [Google Scholar]
- Leibowitz Arlene. “Home Investments in Children,”. Journal of Political Economy. 1974;82:S111–S131. [Google Scholar]
- Li Hongbin, Zhang Junsen, Zhu Yi. “The Quantity-Quality Tradeoff of Children in a Developing Country: Identification Using Chinese Twins,”. Demography. 2008;45:223–243. doi: 10.1353/dem.2008.0006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Macfarlane Alan, Gurung Indrabahadur. Gurungs of Nepal: A Guide to the Gurungs. 2nd ed. (Kathmandu: Ratna Pustak Bhandar, 1992) [Google Scholar]
- Morduch Jonathan. “Sibling Rivalry in Africa,”. American Economic Review. 2000;90:405–409. [Google Scholar]
- Nepal Central Bureau of Statistics. National Population Census 2001, in Minnesota Population Center, Integrated Public Use Microdata Series, International: Version 6.0 [Machine-readable database] Minneapolis: University of Minnesota; 2010. [Google Scholar]
- Niraula Bhanu B, Philip Morgan S. “Marriage Formation, Post-Marital Contact with Natal Kin and Autonomy of Women: Evidence from Two Nepali Settings,”. Population Studies. 1996;50:35–50. [Google Scholar]
- Parish William L, Willis Robert J. “Daughters, Education, and Family Budgets: Taiwan Experiences,”. Journal of Human Resources. 1993;28:863–898. [Google Scholar]
- Petrongolo Barbara, Pissarides Christopher A. “Looking into the Black Box: A Survey of the Matching Function,”. Journal of Economic Literature. 2001;39:390–431. [Google Scholar]
- Pew Research Center. Mapping the Global Muslim Population: A Report on the Size and Distribution of the World’s Muslim Population. Washington, DC: Pew Research Center; 2009. [Google Scholar]
- Pörtner Claus. “Sex-Selective Abortions, Fertility, and Birth Spacing,”. Mimeo, University of Washington, 2010. [Google Scholar]
- Roland Gérard. “Understanding Institutional Change: Fast-Moving and Slow-Moving Institutions,”. Studies in Comparative International Development. 2003;38:109–131. [Google Scholar]
- Rosenzweig Mark R, Wolpin Kenneth I. “Testing the Quantity-Quality Fertility Model: The Use of Twins as a Natural Experiment,”. Econometrica. 1980;48:227–240. [PubMed] [Google Scholar]
- Rosenzweig Mark R, Zhang Junsen. “Do Population Control Policies Induce More Human Capital Investment? Twins, Birth Weight, and China’s ‘One Child’ Policy,”. Review of Economic Studies. 2009;76:1149–1174. [Google Scholar]
- Sah Nepali. Patterns and Determinants of Age at First Marriage of Women in Nepal. Ph.D, dissertation, Australian National University, 2010. [Google Scholar]
- Smith Daniel Scott. “Parental Power and Marriage Patterns: An Analysis of Historical Trends in Hingham, Massachusetts,”. Journal of Marriage and the Family. 1973;35:406–415. [Google Scholar]
- Steelman Lala Carr, Powell Brian, Werum Regina, Carter Scott. “Reconsidering the Effects of Sibling Configuration: Recent Advances and Challenges,”. Annual Review of Sociology. 2002;28:243–269. [Google Scholar]
- Tertilt Michèle. “Polygyny, Fertility, and Savings,”. Journal of Political Economy. 2005;113:1341–1371. [Google Scholar]
- Trivers Robert L, Willard Dan E. “Natural Selection of Parental Ability to Vary the Sex-Ratio of Offspring,”. Science. 1973;179(4068):90–92. doi: 10.1126/science.179.4068.90. [DOI] [PubMed] [Google Scholar]
- Vytlacil Edward. “Independence, Monotonicity, and Latent Index Models: An Equivalence Result,”. Econometrica. 2002;70:331–341. [Google Scholar]
- Weber Max. The Protestant Ethic and the Spirit of Capitalism. London: Routledge Classic; 1905. [Google Scholar]