Gene-Environment Interplay in Twin Models

Abstract

In this article, we respond to Shultziner’s critique that argues that identical twins are more alike not because of genetic similarity, but because they select into more similar environments and respond to stimuli in comparable ways, and that these effects bias twin model estimates to such an extent that they are invalid. The essay further argues that the theory and methods that undergird twin models, as well as the empirical studies which rely upon them, are unaware of these potential biases. We correct this and other misunderstandings in the essay and find that gene-environment (GE) interplay is a well-articulated concept in behavior genetics and political science, operationalized as gene-environment correlation and gene-environment interaction. Both are incorporated into interpretations of the classical twin design (CTD) and estimated in numerous empirical studies through extensions of the CTD. We then conduct simulations to quantify the influence of GE interplay on estimates from the CTD. Due to the criticism’s mischaracterization of the CTD and GE interplay, combined with the absence of any empirical evidence to counter what is presented in the extant literature and this article, we conclude that the critique does not enhance our understanding of the processes that drive political traits, genetic or otherwise.

1 Introduction

In his essay, Doron Shultziner (2013) claims that the larger correlation between monozygotic (MZ), relative to dizygotic (DZ), twins, on political traits, is not due to MZ twins being more genetically similar, but is a result of MZ co-twins selecting into more similar environments, or responding to environments more comparably than DZ co-twins. Although this may not be entirely false, it is extremely far from the whole truth. The essay further claims that this is a novel interpretation of the estimates from twin models and that it invalidates twin model results. This is patently untrue. In our response, we address three of the major problems with the essay’s criticisms. First, the suggestion that individuals are differentially affected by environmental stimuli, which forms the bulk of the criticism’s theoretical justification, is part of twin model interpretations, and is commonly dubbed gene-environment (GE) interplay (Rutter 2006). GE interplay is explicitly integrated into behavioral genetic theory and twin methods and is explored in myriad studies both inside political science (for reviews, see Hatemi, Dawes, et al. 2011; Hatemi and McDermott 2012a) and in the broad behavioral genetics literature (Eaves et al. 1977; Neale and Cardon 1992; Purcell 2002; Rutter and Silberg 2002). Second, whether genetic factors directly influence a trait, or indirectly influence it through the selection into environments that influence the trait, genes play a role in understanding why people differ from one another, and this is the major contribution of twin studies. Third, the criticism ignores the fact that the classical twin design (CTD) is only one empirical tool in a larger toolbox, and that other methods exist that explicitly deal with gene-environment covariation (rGE) and interaction (G × E). Accordingly, the criticism’s unnecessarily narrow focus, incorrect assertions about the method, and neglect of published studies in political science that explore GE interplay result in a criticism that is responding to an inaccurate interpretation of the biometric theory and empirical method that undergirds the twin model.

Specifically, although the criticism purportedly focuses on univariate twin models, it intentionally ignores the various extensions that provide a counterargument to the criticism (p. 3). Furthermore, the essay puts forth a series of statements that it claims are representative of twin studies, and then “responds” to these claims. Yet, most of the essay’s criticisms are based upon a small subset of articles, with a disproportionate emphasis on Alford, Funk, and Hibbing (2005). These articles are not representative of the wider body of literature that includes GE interplay (e.g., Boardman 2011; Hatemi, Dawes, et al. 2011; Boardman et al. 2012; Hatemi 2013). In other places, the critique is built upon a series of individual sentences taken out of context, where the interpretation of the statements does not correspond with the conclusions from the cited studies. This results in a biased review of the literature that ignores relevant research that had previously identified the assumptions and limitations of the CTD or specifically estimated GE interplay. The final product is an impoverished representation of twin methodology and theory.

The critique also reflects a divergence in how science progresses in the social and life sciences by conflating theory and method. Specifically, the essay criticizes univariate twin models for not including interaction terms, and then dismisses G × E models. Such an approach is equivalent to criticizing the method of simple regression because a single study does not include covariates, but then dismissing the ability to use multiple regression. This is analogous to criticizing Alford, Funk, and Hibbing (2005) for not testing specific GE interactions or correlations, but ignoring alternative methods to test these hypotheses. This does not invalidate the univariate twin method. Instead, it implicitly emphasizes the cumulative nature of scientific research.

An example from the political behavior literature illustrates this point. Early research utilized correlations to explore the link between partisanship and attitudes (Campbell et al. 1960). As the theories developed, more innovative statistical approaches were needed for the study of political attitudes, and covariates, interactions, mediators, and moderators were then considered. This natural progression does not invalidate the methods of correlation or simple regression. Instead, as the theories advanced, more complex methods were necessary to test more complex, nuanced hypotheses. The same logic applies to the use of twin models. Study on a given trait begins with a univariate CTD, much like correlations or simple regression. This becomes the base model. As specific theories are developed to further clarify how genetic and environmental factors account for variance on a given trait, more complex models are employed to test those hypotheses (for a review of the progression of the study of genetics and attitudes that began with correlations and progressed to G × E and rGE models, see Hatemi and McDermott 2012a). This is the natural progression of research in science: begin with a simple model and then, using more complex models, test theoretically justified and increasingly complex hypotheses.

The goal of our response, therefore, is to bring some clarity to the use and limitations of twin models as well as the potential for effectively modeling GE interplay within the CTD framework. We first give a brief overview of the twin method and then review the extant literature on GE interplay, emphasizing the theoretical and methodological refinement that is overlooked in the critique, which contradicts the essay’s claims that twin studies do not explicitly consider rGE or G × E. We also recapitulate some of the nuanced features of the CTD that are the source of confusion and misunderstanding in the critique. Following this, we address the argument that differences in co-twin similarity by zygosity are due to twins selecting into different environments that influence the trait, not because they have different genetic dispositions for the trait itself. To do so, we present results from simulations that empirically illustrate the effect of GE interplay on the parameter estimates of the CTD under a wide variety of circumstances, where the independence between genes and the environment is not assumed, as the critic argues is the norm. The simulations quantify the resulting biases in the CTD under the conditions discussed in the critique and further extend them in a variety of directions that are not mentioned in the critique, but are common in the extant literature. The one area of the essay that we do not address is the criticisms of candidate gene studies. A critique on this topic was recently published in the APSR (Charney and English 2012), and responded to by Fowler and Dawes (2013). We conclude by discussing the broader implications of GE interplay for political science and advocate for an empirically based research program that relies upon the scientific method to integrate novel methods into mainstream political science theories.

2 GE Interplay in the CTD

The core claim of the criticism, that it offers a novel explanation of why MZ twins are more similar, is summarized by the following quotation:

The most logical explanation of the results of twin studies is that individuals with identical genomes (e.g., MZ twins) react more similarly to the same particular environmental effects compared to individuals with non-identical genomes (e.g., DZ twins) under equivalent conditions. … While this explanation is new in the twin studies context, the basic notion underpinning it has been part and parcel of biological theory for decades.

The criticism goes on to argue that because the environment is essential for the development of phenotypes, genotypes do not matter and can therefore be ignored. This is not true. More realistically, both an individual’s genotype and their environment matter, and the complex interplay between genes and environment produces enormous amounts of variation in the behaviors individuals engage in across a wide variety of situations. Such a view is explicated in great detail in the extant literature (Plomin 1994; Hatemi, Alford, et al. 2009; Boardman 2011; Eaves et al. 2011; Hatemi, Dawes, et al. 2011; Hatemi, Byrne, and McDermott 2012). This explanation is not new in the context of twin studies as claimed in the essay, but commonly referred to as gene-environment (GE) interplay, which includes gene-environment covariance (rGE) and gene-environment interaction (G×E). Both rGE and G×E are popular topics within behavioral genetics and political science, and as such are often discussed within the method and theory of twin analyses (Eaves et al. 1977; Boomsma et al. 1999; Purcell 2002; Middeldorp et al. 2008; Medland et al. 2009). As is emphasized by Robert Plomin, a leading scholar in behavior genetics, in his contribution to The Annals of the American Academy of Political and Social Science (Plomin and Asbury 2005, 90–92), individuals take an active role in “selecting, modifying, constructing and reconstructing” their experiences, suggesting that “increasing heritability may occur because small genetic differences may snowball as we progress through life, creating environments that are correlated with our genetic propensities.” This implies that due to one’s genotype, some people may get multiple doses of an environmental stimulus, whereas others may receive none at all. In addition, more genetically similar individuals may also react more similarly to certain environments. The genetic influence remains, but the magnitude of the genetic influence depends upon exposure to, or selection into, the environment. This also means that some part of the genetic influence may not directly influence the trait, or may be underestimated or overestimated for the trait (e.g., see Eaves and Hatemi 2008; Hatemi et al. 2010; Verhulst, Eaves, and Hatemi 2012).

It is not possible or appropriate to recapitulate over 100 years of genetic theory and empirical analyses upon which the twin model is based (Mendel 1930; Galton 1869). However, several papers are central to the development and justification of the basic statistical assumptions of the model specifications, and these are critical to correcting the critique’s misunderstandings of the method and warrant inclusion. As a proof of principle, Fisher (1918) convincingly demonstrated that the results presented by Pearson and Lee (1903) for height followed a polygenic additive model (a trait that few people object to having a large genetic component and one that we know has changed over generations), which provided the foundation for the development of the twin and family models broadly. Sewall Wright (1920, 1921, 1934) developed path analysis techniques which, nearly 100 years later, remain essential for modern quantitative genetic modeling. Mather and Jinks (1971) and Jinks and Fulker (1970) provide the conceptual framework and statistical proofs for the detection, analysis, and significance of GE interplay in humans. The modern synthesis of the basic principles of twin modeling by Eaves et al. (2005), combined with Loehlin's (2004) articulate application of structural equation modeling techniques for quantitative genetics and Fulker’s (1979) practical explication of GE interplay to the study of intelligence, a didactic work of art that applies equally well to the analysis of political traits, precludes any possible claim that GE interplay in twin models is a “novel contribution.” Rather, as is evident, GE interplay is clearly ingrained within the theory and statistical model of modern twin analyses (Eaves et al. 2011).¹ Because the critique does not address these works, it does not take into account the conceptual nuances of the twin model or existing GE interplay research, and thus renders itself immaterial.

Today, there are many approaches to analyzing rGE and G × E in humans using twins (Kendler and Eaves 1986; Turkheimer et al. 2003; Eaves et al. 2005). For example, Purcell (2002) and Neale et al. (2002) provide eloquent, cogent expositions for modeling G × E and rGE in twin data, with scripts, data files, and simulations. Middeldorp et al. (2008) provides an accessible example of how to use basic correlation analyses to identify if twins are selecting into specific environments, or differentially influenced by environments.

We reiterate the importance of these contributions not as a history lesson, but to underscore that a wealth of research currently exists that explores GE interplay. Each of these methods simply tests a hypothesis, and if the method does not test the proposed hypothesis, it is incumbent upon the researcher to employ a different method. From this perspective, the fact that the CTD does not estimate GE interplay is not a failure of the model. If GE interplay is suspected, then extensions of the CTD are available and should be utilized. Thus, it is not appropriate to criticize a statistical method because researchers did not test different hypotheses. Rather, this provides opportunities for future researchers to modify, clarify, or extend the current understanding of the topic.

2.1 The Classical Twin Design

Before directly delving into the nuances of GE interplay, it is useful to delineate the basic construction of the CTD and the assumption that is the focus of the critique.² Like any methodological technique, some level of reductionism is required and assumptions must be made to statistically identify the parameters. In the CTD, the total variance (V_t) is decomposed into some combination of three latent variables: additive genetic influences (A) that capture the combined genetic effect of all genes (inherited traits), common environment influences (C) that capture the factors that are perfectly shared between twins such as the effects of other family members or familial socialization, and unique environmental influences (E) that capture all environmental stimuli that are not shared between twins (i.e., personal experiences), including stochastic error (Neale and Cardon 1992; Medland and Hatemi 2009). Thus, assuming no interaction between genes and environment in the operationalization of the CTD is V_t = A + C + E (see supplementary appendix 1 for structural model and matrix algebra). This is analogous to the multiple regression framework where an independent variable (X) is theoretically posited to cause a dependent variable (Y), where the model is operationalized as Y = B₀ + B₁X₁ + e (for a detailed explanation of how to conduct twin models using regression, see Smith and Hatemi 2013). The difference between these two linear models is that the regression model focuses on the mean and the twin model focuses on the variance. Accordingly, the A, C, and E parameters give proportions of variance (similar to R²) rather than marginal effects. Importantly, in both these instances, no covariates or interactions are present.

The univariate twin model is a simple expression of a highly complex process. In behavioral genetics, the CTD is viewed as the baseline model that is explored early in the research trajectory. It allows for the subsequent exploration of more complex possibilities of phenotypic transmission that intentionally relaxes some of the statistical assumptions of the base model (for a description of this progression, see Hatemi, Alford, et al. 2009). Indeed, the prevalence of the CTD as an initial exploration of the data does not imply that tests of GE interplay do not exist, that follow-up studies cannot explore these possibilities, or that scientists who utilize the CTD are unaware of GE interplay, contrary to what the critique claims. Rather, it is understood and well documented that within each of the broad parameters resides the potential for an individual’s genes to be correlated with or conditional upon environmental stimuli that influence the trait. We compare this to the use of interaction terms in multiple regression. In any given study, it is understood that any number of interactions or additional covariates might be significant and alter the parameter estimates. In this way, one would not critique linear regression but the specific use of the regression in the particular study.

Extensions of the CTD that incorporate information from multiple phenotypes (i.e., multivariate genetic analysis; see Martin and Eaves 1977; Neale and Cardon 1992), other types of relatives (i.e., extended pedigree models; see Truett et al. 1994; Eaves et al. 1999; Hatemi et al. 2010), and interactions between relatives (i.e., sibling interaction models; see Eaves 1976; Carey 1986) make it possible to estimate GE interplay. Statistically speaking, when an individual selects into an environment, or responds to environment as a function of their genotype, they induce a correlation between their genotype and the environment (rGE), or an interaction (G × E), or both. The effect of rGE on the CTD estimates is elucidated by Medland and Hatemi (2009, 200):

In effect, one is “choosing” their environment based in part on their genes … . This correlation may be classified as active, where the individual’s own genes influence their exposures to certain environments or passive in which the environment of an individual is influenced by the genes of a relative. Unmodeled rGE may either inflate or deflate the estimates of genetic influences.

Therefore, if one wishes to explore interactions or covariation based upon some theoretical justification or empirical curiosity, the CTD is extended. Delineating the mathematical operationalization of each extension is beyond the scope of any single paper, but has been done in numerous highly cited publications, including one in the current journal, Political Analysis (Medland and Hatemi 2009). Yet, one example should prove sufficient to make this point. Continuing our comparison with regression, extending simple regression to multiple regression with an interaction term can be accomplished simply by adding additional terms: Y = B₀ + B₁X₁ + B₂X₂ + B₃X₁X₂ + e, where B₁ and B₂ capture the main effects of the independent variables, X₁ and X₂, and B₃ captures the interaction between them. Just as the extension of the moderated regression model is only slightly different from the simple regression model, the extension of the twin model to include G × E interactions is only slightly different from the CTD. Hence, rather than using the linear equation V_t = A + C + E, the variance associated with each of the three components is expressed as a linear interaction with the environmental condition of choice: V_t = (a + ß_aX)² + (c + ß_cX)² + (e + ß_eX)². Thus, extending the CTD to estimate G × E interactions simply allows each variance components to have one additional parameter that allows the environmental variable, X, to increase or decrease the amount of variance in the trait that is attributed to the specific variance component (for a full description of G × E models, see Hatemi 2013). As is evident, each term in the G × E model is essentially a linear regression model that predicts the A, C, and E variance components.

If the genetic variance component is significantly correlated with (rGE) or conditional upon (G × E), either the common or the unique environmental variance components of the CTD statistical assumptions are violated. In such situations, the parameter estimates will change, as the critique points out, yet this is not a failure of the CTD, but rather a case where the CTD is not the appropriate model. As is the case with any statistical technique, if you estimate the wrong model, you will get the wrong results. Further, whether genes correlate or interact with environments that are shared or unshared between the twins makes an enormous difference for determining which parameter will be affected. This very important consideration is overlooked in the critique. In some cases, GE interplay will result in overestimates of the genetic effect, as the criticism argues. In other cases, however, common or unique environmental estimates will be inflated (for an example of both conditions, see Hatemi 2013) . Thus, not only is it essential to understand GE interplay from the genetic perspective, but it is also essential to explore it from the environmental perspective, a concern the critique does not consider.

Importantly, there are three primary types of rGE: active, passive, and evocative. The criticism is limited to only considering active rGE, but inclusion of passive and evocative rGE is equally important because the implications for twin models vary as a function of the specific type of rGE. With active rGE, an individual’s genotype motivates him or her to select into, or out of, environments that influence the trait. Passive GE correlation arises because people are often genetically related to individuals in their environments: Parents typically create the environments within which children develop. Evocative GE correlation arises when an individual evokes particular responses from the people who constitute their environment (e.g., Posner et al. 1996). The specific type of rGE or G × E has different implications for the data necessary to test for such interplay, but the impact of unmodeled rGE and G × E on the variance components, when significant, is a function of whether the genotype is interacting or correlated with factors drawn from the shared or unique environment.

2.2 GE Interplay in Political Science

The concept that individuals select into nonrandom environments or react to environments differently as a function of their genotype has been appropriately credited, explained, addressed, or estimated in original studies in the extant political science literature (Eaves et al. 2008; Hatemi, Alford, et al. 2009; Hatemi, Funk, et al. 2009; Medland and Hatemi 2009; Hatemi et al. 2010; Sturgis et al. 2010; Boardman 2011; Boardman et al. 2011; Klemmensen 2011; Boardman et al. 2012; Hatemi, Byrne, and McDermott 2012; Hatemi and McDermott 2012b; Norgaard 2012; Smith et al. 2012; Hatemi 2013). Here we provide some examples of how these types of GE Interplay have been explored for political traits and discuss the empirical implications for the CTD, and place the remainder in supplementary appendix 2. These studies were either ignored or misunderstood in the critique, and we correct some of those omissions here.

Several studies have explored passive rGE using extended family twin designs (Eaves and Hatemi 2008; Hatemi et al. 2010). These studies demonstrate that for the majority of political attitudes, ideology, and party identification, estimates of passive rGE are very small; some are positive, and some are negative. Simply put, inclusion of passive rGE has shown that CTD analyses on political traits both overestimate and underestimate genetic influences, but such biases so far are not significant or substantial. This possibility is also not mentioned in the critique. Rather, the essay portrays rGE as a one-way effect that if not accounted for always results in inflated genetic influences.

The above studies also illustrate a powerful impact of active rGE, based upon the “environmental” choice of spouse, which is possibly the most important element in the transmission of political traits (Martin et al. 1986; Eaves, Eysenck, and Martin 1989). This is important because CTD models assume random mating and due to the very large correlation between spouses (r ≈ 0.6) for attitudes, the CTD actually underestimates the magnitude of genetic influences (Truett et al. 1994; Eaves et al. 1999; Eaves and Hatemi 2008; Hatemi et al. 2010). This finding has led to an entire stream of research exploring the import of mate selection on political phenomena (Alford et al. 2011; Zietsch et al. 2011; Klofstad, McDermott, and Hatemi 2012).

Using an alternative approach to investigate active rGE, Hatemi, Funk, et al. (2009) relied on longitudinal data of attitudes to explore the extent to which individuals select into environments that allow them to express their genotypes. They found that co-twin correlations for attitudes were the same regardless of zygosity while twins lived with their parents. Thus, genetic influence emerged significant only once children left home. The authors offered several explanations:

The evidence for genetic influence starting at about age 21–25 stems mostly from a substantial drop in the attitude concordance between DZ twins while the correlation between MZ pairs remains stable. … One explanation for this pattern is that those pairs who are most discordant in attitudes are the first to leave the nest, and genetic differences are a large contributor for leaving home and each other. … An alternative explanation may be that DZ twin pairs are choosing less similar environments than MZ twin pairs for reasons, which are not influenced by genes, thus influencing MZ twin pairs to be more like each other or become less dissimilar as compared with DZ twin pairs. However, this would run counter to previous analyses of social attitudes. In a longitudinal study Posner et al. (1996) found that attitude similarity was the basis for the amount of contact between twins and not vice versa. … (Hatemi, Funk, et al. 2009, 1152–53).

Given this direct test and explanation, the critique’s claims that rGE and G × E influences are not considered or that twin models present genetic influences as unmalleable are clearly false. This study was highlighted in the criticism, but unfortunately, the criticism described the results with terrific inaccuracy, stating (p. 12):

What Hatemi and his colleagues actually show is that heritability estimates can be produced not because MZ become more similar in time (as they argue) but simply due to the fact that DZ twins show less similarity in a new environment or later in life relative to MZ twins.

As can be seen, the criticism’s interpretation is exactly opposite of what Hatemi, Funk, et al. (2009) state.³

The critique also failed to address several critical contributions that provide didactic explorations of GE interplay specifically tailored for political scientists. Hatemi (2013) tested whether genetic influences are a function of twins selecting into specific life events that influence attitudes, or if twins respond to stimuli based on genetic similarity.⁴ He found no evidence of rGE, but did find and quantify several significant G × E interactions, where the genetic influence diminished in the face of certain life events but increased in others (also see Hatemi, Dawes, et al. 2011). Of critical import, these interaction effects were relatively short lived: Two years after the life event, genetic influences in the affected population were no different from the unaffected population. Boardman (2011) provided a detailed review of GE interplay for political science, including empirical examples, theoretical considerations, and integration with sociological theories. In addition, Smith et al. (2012) tested for GE interplay with regard to childhood and adult environments and political ideology. They found that differences in room sharing, having the same friends, dressing alike, attending the same classes at school, and sibling contact in person, over the phone, and electronically had a trivial influence on the variance components estimates even when the authors included nonsignificant GE interplay estimates in the model.

In summary, the critique of the CTD appears to be misplaced and overstated. The CTD does exactly what it is intended to do, and simple extensions of the CTD address the critique’s main concerns. Indeed, the effects of rGE and G × E are explicitly discussed in hundreds, if not thousands, of behavior genetic, medical, psychological, psychiatric, and social science studies, as well as the core theoretical and methodical literature used to guide those who conduct twin analyses (Neale and Cardon 1992; Purcell 2002; Medland and Hatemi 2009). It is well documented that the additive genetic, common, or unique environmental estimates may be overestimated or underestimated in the presence of rGE and G × E, and the empirical models to test for these effects are increasingly used by political scientists when theory and hypotheses demand such an approach. So far, however, such tests have suggested that the influences of rGE on the CTD estimates are minimal, though the field of research is very recent.

2.3 Other Mischaracterizations of the Twin Model

The critique also contains many claims that do not accurately portray the literature, creating the illusion of controversy where none exists. We do not have space to address all of the critique’s inaccuracies. Instead, we address some of the most central issues here and place more details in supplementary appendix 3.

The first point that warrants attention is the essay’s claim that twin studies present heritability estimates as immutable and do not entertain the possibility that heritability can change between and within populations at different times. This is an incorrect representation of the literature. Heritability estimates vary in different populations and across time, and the malleability of heritability estimates is explicitly discussed in the extant literature (e.g., Hatemi, Alford, et al. 2009; Hatemi et al. 2010; Hatemi, Dawes, et al. 2011; Hatemi and McDermott 2011; Hatemi 2012; Hatemi and McDermott 2012b; Smith et al. 2012; Hatemi 2013). In fact, a series of papers in political science, several of which are cited by the critic, have empirically quantified the malleability of heritability over time, and across cultures, measures, and locations (Eaves et al. 1997; Hatemi, Funk, et al. 2009; Fazekas and Littvay 2011; Klemmensen, Hatemi, Hobolt, Petersen, et al. 2012; Klemmensen, Hatemi, Hobolt, Skytthe, et al. 2012). For a concise review of how political scientists view heritability estimates over time and in different populations and across cultures, see Hatemi, Byrne, and McDermott (2012, 315), presented in full in supplementary appendix 3.

Second, the critique asserts that twin studies claim to provide mean effects and that twin researchers do not understand that variance is different from direction and content. Although undoubtedly erroneous interpretations of twin studies have crept into a few manuscripts, these criticisms should be directed at the interpretation of the results in specific papers and not at the method or literature generally. As Medland and Hatemi’s methodological primer on the topic (2009, 192) states:

The finding that a genetic effect influences a trait does not provide information regarding the number of genes affecting the trait, the direction of these genetic effects (i.e., whether these effects increase or decrease the mean), or the identity of the genes exerting this influence. Rather, they provide evidence that individual differences are genetically influenced and that it is worthwhile to attempt to identify the genes involved.

A review of the literature in political science shows that studies that rely on twin models are concerned with accounting for variation within a population and not that twin studies claim to explain “the specific political content or direction of these traits” (p. 7). Rather than predicting directional effects, as is the goal in regression analysis, the focus of the CTD is on understanding the variation, analogous to analysis of variance (for reviews, see Eaves, Eysenck, and Martin 1989; Hatemi, Byrne, and McDermott 2012; Hatemi and McDermott 2012a, 2012b; Hatemi 2013). In the first thorough review of the literature, Hatemi, Dawes, et al. (2011, 74) also explicitly enumerate this fact (the full quote is in supplementary appendix 3). If genetic influences account for population variation on a trait, then individual genes will operate on the trait direction. Twin studies conceptualize genetic influences as an unobserved latent variable, instead of millions of individual markers or tens of thousands of genes, with some alleles increasing and others decreasing an individual’s phenotype. Accordingly, the CTD cannot be used to disentangle this type of genetic influence, and therefore molecular analyses are required to identify the directional effect of a specific genetic marker on a trait (for discussion of this topic, see Hatemi, Dawes, et al. 2011; Hatemi, Gillespie, et al. 2011; Hatemi, Byrne, and McDermott 2012).

Third, the critique argues that twin studies tell us nothing about the causal flow between traits or between genes and traits. This implies that the CTD claims to offer information on causality. Yet both the foundational and recent literature is clear that the CTD focuses on covariance and not causality (Eaves, Eysenck, and Martin 1989; Plomin 1994; Medland and Hatemi 2009; Hatemi and McDermott 2011; Hatemi, Byrne, and McDermott 2012).

There are several distinct uses of the term causality that may also fuel the critique’s misunderstanding. The first use of the word “cause” in twin studies stems from the factor analysis literature, where latent traits are assumed to “cause” the measured indicators of those traits. For example, if you have a five-item scale for political attitudes, the level of an individual’s latent liberalism is said to “cause” a person to respond to the political attitude items. Because recent incarnations of the CTD rely on factor analytic methods, the same language is used. As is clear, in this context causality does not have the same meaning as is typically used in political science.

However, it may be important to consider that certain extensions of the classic twin model actually can provide some leverage on causal relationships between traits, where the meaning of “cause” is consistent with the intuitive meaning. These models, dubbed direction-of-causation models, provide a statistical estimate of causation (Heath et al. 1993; Duffy and Martin 1994; Neale, Duffy, and Martin 1994; Gillespie and Martin 2005; Ozaki and Ando 2009; Vitaro, Brendgen, and Arseneault 2009; Kohler, Behrman, and Schnittker 2011; Ligthart and Boomsma 2012), analogous to meditational models (Baron and Kenny 1986). Numerous empirical examples of these models exist, including some in political science (Gillespie et al. 2003; De Moor et al. 2008; Gillespie et al. 2012; Verhulst and Estabrook 2012; Verhulst, Eaves, and Hatemi 2012).

The last major concern we address in this section is the disparity between the essay and the language used in empirical science and the principles of basic research. This might best be illustrated by a quote in the essay:

Leading scholars in this field relate to this point and explain that in “a univariate model, additive genetic variance will include all the genetic influence from all covariates, some part of gene-environment covariation if it exists, and some part of gene environment interaction, if it exists” (Hatemi, Dawes, et al. 2011, 74; emphases added). They also admit that this model simplifies a far more complex interaction and reality (ibid.). What they apparently fail to see is that this “covariation” and “interaction” are not minor possibilities (“if”) or mere noise in the measurement of the genetic factor. This covariation, or rather conflation, exists by definition and is built into the model because the genetic factor already includes and measures environmental effects (p. 20).

The logic of hypothesis testing explicitly seeks to reject the null hypothesis. The critique advocates a different position: that it should be assumed that GE interplay exists until proven otherwise. In essence, the critique is highlighting the fact that for most traits, we simply do not know whether GE interplay affects parameter estimates or the direction of the potential bias. An empirical approach assumes that an effect does not exist (the null hypothesis) and attempts to reject that hypothesis. Thus, scholars do not automatically assume that GE interplay exists, but rather point out that “if it exists,” GE interplay could either increase or decrease the magnitude of the genetic estimate. This equivocation is the language used to communicate when presenting empirical analyses. When it comes to the potential for active rGE or G × E, we must test if it exists on every environmental trait of interest. Thus, we cannot say that GE interplay always exists, or never exists; statistically, we must test if it exists on a trait-by-trait basis, preferably with a theoretically driven hypothesis. The essay’s unfamiliarity with this type of academic approach and communication makes it very difficult for scholars to engage in a constructive discourse.

Furthermore, we do not, nor do any authors we are aware of, consider covariation or interaction minor possibilities or noise, as is claimed in the essay. As the first and last authors of the quoted paper, we have documented through numerous publications that the CTD has limitations and that should the independence assumptions be violated, or if that rGE and G × E are estimated and found significant, the CTD estimates may change. Indeed, it is explicated throughout the body of the article that the select quotes were taken from Hatemi, Dawes, et al. (2011). Unfortunately, those portions of the article were not considered. Here again, the criticism’s claims are contradicted by numerous published or forthcoming works that explicitly model rGE and G × E (e.g., Eaves and Hatemi 2008; Settle et al. 2010; Boardman 2011; Boardman et al. 2011; Klemmensen 2011; Boardman et al. 2012; Hatemi 2013).

Essentially, the essay is advocating that every author that explores a main effect or baseline model using any method, twin design or otherwise, implicitly considers interactions “minor” possibilities, unless they test every single possible interaction and trait. The critique also advocates that exploration should start with interactions and multivariate models without having any idea of what the base model looks like. This is not a reasonable suggestion. Accordingly, criticizing scholars for what has not yet appeared in the literature, or for not conducting analyses when no hypothesis is given, or for work they have not done, or for choosing a model to test something different than what the critique would prefer, is not consistent with the scientific method. Rather, research is incremental. It is first necessary to identify main effects, then look for theoretically justified interactions, and then test if specific environments significantly influence our main effects based on data and theory. Regarding twin models, a quote from Hatemi, Alford, et al. (2009, 596) characterizes this nicely:

Twin studies do not pretend to offer an exhaustive analysis of all the potential subtleties of the action and interaction of social and genetic influences. The CTD and associated linear structural models provide an initial decomposition of individual differences into broad genetic, common, and unique environmental components. The genetic and social consequences of assortative mating, genotype x environment interaction (G×E) and genotype–environment correlation (rGE) are confounded with the estimates of the principal variance components. … Any sophisticated behavior is far too complex to fully explain in discrete terms. However, estimates of variance components are no more absolute than estimates of regression coefficients in typical social science models. In the “real” world, behavior is not divided into perfect buckets of genes and environment, nor is a regression coefficient a definitive predictive estimate. Interpretation of results is based on the models employed and covariates used, with accepted limitations. Our univariate and multivariate analyses are based on the initial ACE model widely used across disciplines. They constitute an invitation to explore a paradigm until it fails to account for significant features of future data. Establishing general estimates of genetic and environmental influence … paves the way to consider more complex models and measures, which might yield more specific interpretations and predictions. … The analysis of the roles of genes and environment is progressive. Success is judged by the cumulative weight of coherent findings.

3 Estimating the Impact of Unmodeled rGE on the ACE Estimates

The previous section identified numerous inaccuracies in the critique and briefly sketched extensions to the CTD that are used to estimate GE interplay. In this section, we explore the statistical implications of GE interplay on the variance components estimates from twin models and identify how estimates of the CTD may change under different GE interplay conditions. To be clear, the critic argues that GE interplay uniformly increases the size of the genetic variance component in the CTD. Importantly, in some cases the genetic parameter may increase, as the critic notes, but in other places it decreases, in direct contrast with what the critic claims. What is clear is that GE interplay does not automatically increase the genetic variance component, but rather, whether the genetic variance component increases or decreases depends upon the specific type of GE interplay. We note that although the simulations conducted for this study are original, such explorations have been conducted in detail in the extant literature (Rao, Morton, and Yee 1976; Molenaar et al. 1990; Purcell 2002; Boomsma and Martin 2003; Eaves and Erkanli 2003; Price and Jaffee 2008). Furthermore, the simulation results that are presented can be arrived at analytically.

One of the central assertions in the critique is that real data frequently violate the statistical assumption in the CTD that the genetic and environmental variance components are independent. Accordingly, all of the simulated data we present violate the independence assumption to varying degrees. The question that remains unanswered, however, is to what extent these violations will bias the results. Because the critique offers no empirical evidence or means to estimate the impact of potential biases, we offer such a test here. Specifically, to explore the influence of GE interplay, we conduct a series of simulations to quantify the bias under different circumstances. This approach is ideal in this circumstance, because we can generate data that violates the independence assumption of the CTD, and then evaluate the model using the CTD (which is the wrong model) to explore the impact that it has on the parameter estimates.

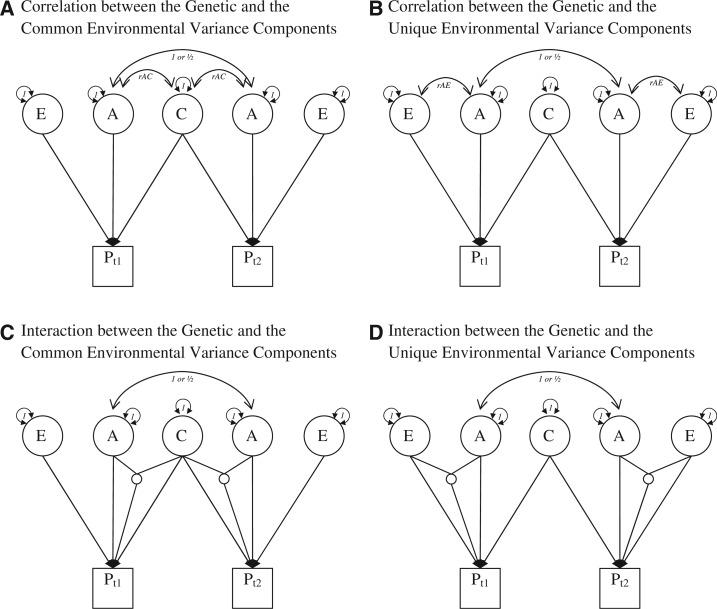
To begin, let us explore the possibility that the latent genetic component is correlated with the common environmental component. A path depiction of this model is presented in Fig. 1A.

Fig. 1.

Path diagrams that violate the independence assumption in the classical twin design. Consistent with conventions of path analysis, squares denote manifest or observed variables, whereas circles denote latent variables. Single-headed arrows indicate causal effects, whereas double-headed arrows indicate correlational effects. Interactions between latent variables are indicated by small circles with no variance. All these models are unidentified.

Note that whereas the correlation between the genetic components for MZ twins is twice the size of that between DZ twins, the correlation between the genetic and common environmental component is equal regardless of zygosity. Accordingly, in direct contrast with what the critique suggests, positive correlations between the A and C variance components would be expected to increase the common environmental variance component and decrease the additive genetic variance component. Negative correlation between A and C would have the opposite effect: It would decrease the size of the common environmental variance component. The extent of this bias, however, is contingent on the sign and magnitude of the correlation between the genetic and common environmental variance components.

To explore the magnitude of the bias as a function of a correlation between A and C, we simulated data for a thousand pairs of MZ twins and a thousand pairs of DZ twins under the rGE model implied by Fig. 1A two hundred thousand times and then evaluated the simulated data using the CTD (ignoring the rGE). Specifically, we simulated genetic, common, and unique environmental scores from a multivariate normal distribution, then aggregated the scores into a single phenotypic score using the linear equation

(1)

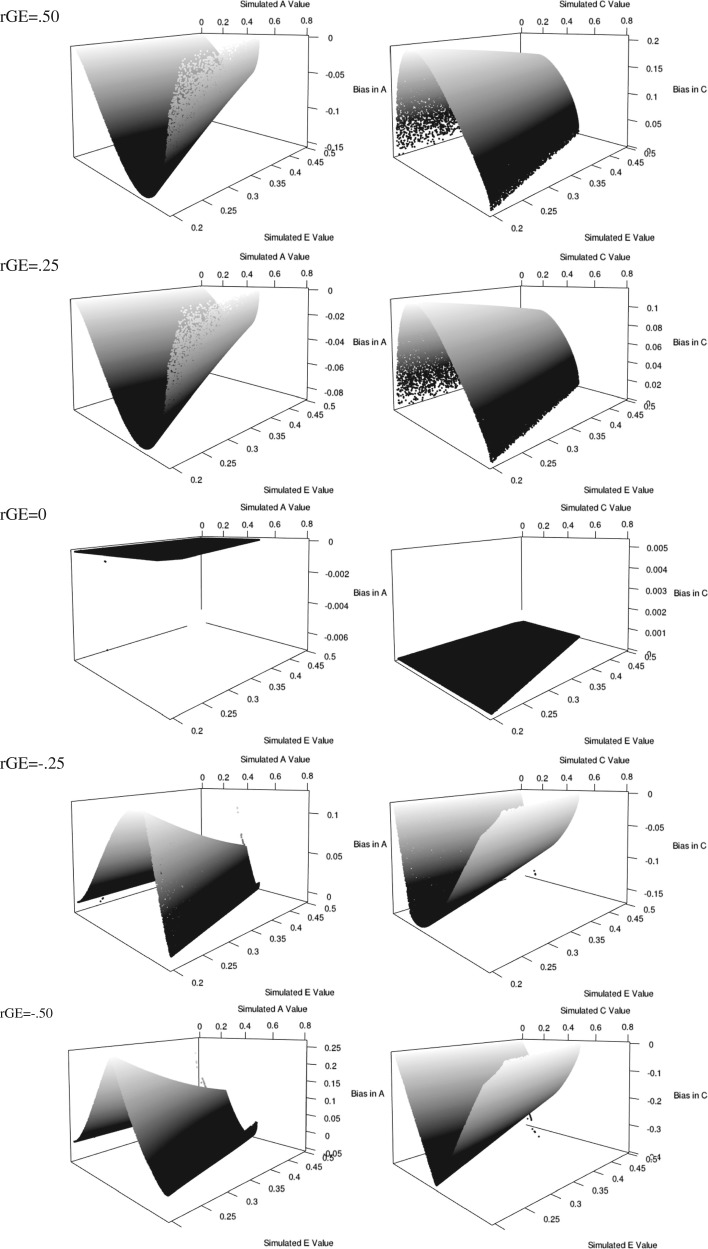
where P_i is the phenotypic score for the ith individual; a, c, and e are the genetic and environmental path coefficients; and A_i, C_i, and E_i are simulated scores for the ith individual for the genetic and environmental latent traits. Further, we then fixed the rGE parameter to five specific values (rGE = −0.50, −0.25, 0.00, 0.25, 0.50) to illustrate the biases when the magnitude of the GE correlation varied. These values correspond with zero, moderate, and extreme violations of the independence assumption.

Figure 2 presents the three-dimensional scatter plot of the biases in the standardized A and C parameters across the continuous range of possible parameter values.

Fig. 2.

Biases in A and C estimates as a function for gene–common environment correlation.

As can be seen in Fig. 2, the bias in the estimate of the genetic parameter as a function of rGE is contingent on four values: the magnitude of rAC and the simulated A, C, and E parameter values. As expected, as the magnitude of the correlation between the genetic and common environmental variance components increases, the bias in both the genetic and environmental estimates increases. Importantly, if rGE is positive, implying that people are selecting into environments (active rGE) or imitating their biological relative (passive rGE), the genetic component is underestimated and the common environmental component is overestimated. If rGE is negative, the converse result is found. Further, as the genetic and common environmental variance components approach the center of the possible parameter space, the amount of bias in both estimates increases. Essentially, as the “a” (or “c”) pathway approaches zero, the correlation between A and C induces less bias in the parameter estimates. Finally, as the amount of variance contributed by the unique environmental variance component decreases, the amount of bias increases. Importantly, within this scenario, in order for the overestimation of the genetic parameter to be noteworthy there must be a moderate to large negative correlation between the A and C factors, which is incredibly rare in real data.

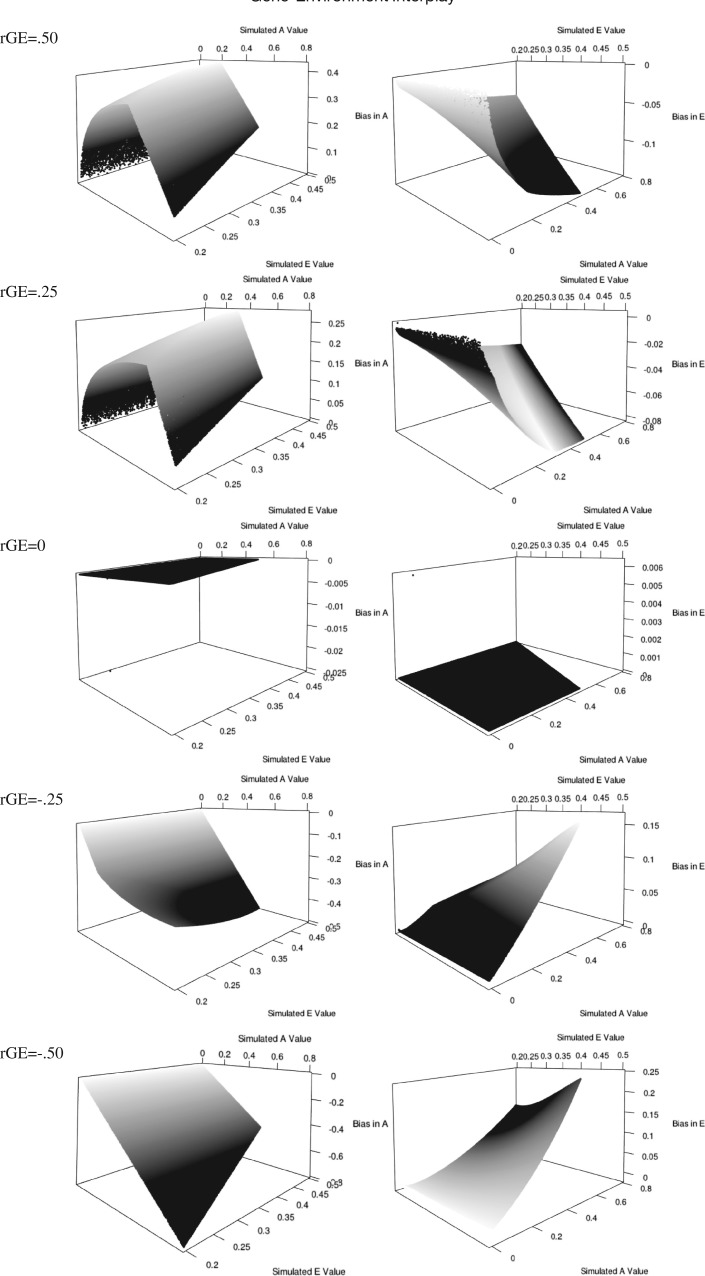
Next, let us explore the possibility that the latent genetic variance component is correlated with the unique environmental variance component. A path depiction of this model is presented in Fig. 1B. Similar to the previous simulation, data were generated for a thousand pairs of MZ and DZ twins under the model presented in Fig. 1B and the phenotypes were constructed using equation (1). The phenotypes were then evaluated with a standard ACE model. Again, we fixed the rGE parameter to the same five values (rAE = −0.50, −0.25, 0.00, 0.25, 0.50).

As can be seen in Fig. 3, the biases derived as a function of rAE are much different from those derived from rAC. Specifically, whereas positive rGE causes a decrease in the estimated genetic parameter if A and C are correlated, positive rGE causes an increase in the estimated genetic parameter if A and E are correlated. This result is expected because E does not contribute to the covariance between twins, and therefore would drive MZ twins to be more similar as a function of them being more genetically related.

Fig. 3.

Biases in A and E estimates as a function for gene–unique environment correlation.

Importantly, the A and E biases are not mirror reflections of each other, nor are the biases inverted as the rAE correlation becomes negative, as was seen in the rAC model. Further, calling this “bias” is misleading. Specifically, if an individual’s genes motivate him or her to seek specific environments that influence the phenotype, the genes are still influencing the phenotype, even though the environment mediates this effect. In this light, the heritability under rAE should be interpreted as the impact of genetic factors on the development of the phenotype. For example, take active rGE, where an individual selects into an environment not shared with his or her twin. As he or she interacts with the world, the genotype motivates him or her to select into the environments that influence the development of the phenotype. Accordingly, these reactions still have a genetic component even though they are also a function of the environment. Importantly, this does not imply rigidity, the lack of efficacy of intervention, or the impossibility of change. If it is possible to intervene in the way that a person interacts with his or her environment, it would be possible to alter the impact of heritability on a trait (Hatemi, Byrne, and McDermott 2012). This heritability estimate, however, remains a function of genetic variability even though the total amount of variability from genetic and environmental sources has changed.

It is important, now, to justify the choice of the magnitude of the correlations between the genotype and the environmental variables in order to compare the current simulation results to statistical theory and real data. Specifically, the critique concludes that “the genetic estimate itself actually consists of a total and complete conflation of an environmental effect on random genomes for which we know nothing about” (p. 20, emphasis in original). This claim of “complete conflation” of the genetic and environmental variance components is impossible because it implies a perfect relationship between genetic influences and the environment. This generates a nonpositive definite matrix for the estimated genetic and environmental components. In fact, the maximum correlation between the genetic and environmental components is 0.7071, which is conveniently the positive square root of the genetic relationship between parents and children, and as such acts as a biological upper bound on the extent of possible rGE. A value of zero indicates that there is no rGE, and as was seen, the model shows absolutely no bias. The value of 0.5 corresponds with a large effect size (Cohen 1988), or something that is obvious to an observer without statistical analysis. The value of 0.25 roughly corresponds with a medium effect size (technically 0.3).

Under the rAC model at this moderate effect size level, with a simulated “e” pathway of 0.2 (or extremely small), the bias in the genetic variance component is about 10%–15% of the total variance when the common environment and the genetic variance components are of equal magnitude (these are well within most confidence intervals in CTD). Importantly, as the “e” pathway increases in magnitude or as the “a” or “c” pathways become more discrepant, the size of the bias drops precipitously. Thus, rather than a complete conflagration, there is a reasonable, though small, amount of bias in the parameter estimates under this condition.

Under the rAE model at this moderate effect size level, with a simulated e pathway of 0.2 (or very small), the bias in the genetic variance component is about 0.25 if the correlation is positive and −0.40 if the correlation is negative. Thus, in this case, there is a substantial amount of bias, though, as noted above, the bias is difficult to interpret. Therefore, in order for rGE to have a substantial influence on variance components estimates in the CTD, the specified environment would have to correlate substantially with the measured trait of interest. Considering that some of the best models of prediction in political science, which include several predictors, rarely account for more than 0.25 of the variance (Matsusaka and Palda 1999; Plutzer 2002), the likelihood of finding a politically relevant environment that correlates at greater than 0.5, is under rGE, and is not tautological is quite small.

3.1 The Implications for G × E Interaction in the CTD

Another argument put forward by the critique is that G × E increases the size of the genetic variance component (p. 15). In both theory and empirical application, this is not accurate. To explore the effect of an interaction between the genetic variance component and the common environmental variance component, we simulated one hundred thousand runs of a simulation at seven specified values of the A, C, and E parameters and varying the interaction pathway by units of 1/2. In these simulations, the unique environmental parameter was always fixed at 0.40, a reasonable parameter value in many twin studies, though lower than is normally found in behavioral data. This allowed us to increase the A variance component by units of 0.10 ranging between 0 and 0.6 while simultaneously decreasing the C variance component to ensure that the sum of the variance contributed by the main effects was fixed at 1.0. The results of the biases in the parameter estimates that result from the simulation can be found in Table 1. A path depiction of this model can be found in Fig. 1C.⁵

Table 1.

Biases in the genetic and environmental variance components as a function of G × E interaction between the genetic and common environmental variance components

		Simulated interaction pathway
		0	0.5	1	1.5	2
Genetic variance component	0	0	0.2	0.5	0.69	0.8
	0.1	0	0.18	0.45	0.62	0.72
	0.2	0	0.16	0.4	0.55	0.64
	0.3	0	0.14	0.35	0.48	0.56
	0.4	0	0.12	0.3	0.41	0.47
	0.5	0	0.1	0.24	0.34	0.38
	0.6	0	0.06	0.18	0.25	0.3
Common environment variance component	0.6	0	−0.12	−0.3	−0.42	−0.48
	0.5	0	−0.1	−0.25	−0.35	−0.4
	0.4	0	−0.08	−0.2	−0.28	−0.32
	0.3	0	−0.06	−0.15	−0.21	−0.24
	0.2	0	−0.04	−0.1	−0.13	−0.15
	0.1	0	−0.02	−0.05	−0.06	−0.06
	0	0	0.01	0.02	0.02	0.02
Unique environment variance component	0.4	0	−0.08	−0.2	−0.28	−0.32

As can be seen in the first column of Table 1, when the interaction between the latent A and C components is fixed at zero, there is no bias in the model. This is consistent with the expectations of the CTD. When the independence assumption is violated due to the G × E interaction, the amount of bias in the A parameter is primarily a function of two factors: the size of the interaction and the size of the simulated “a” pathway. First, as the size of the interaction increases, the bias in the estimated genetic variance component increases. Thus, when there is no main effect of the genetic parameter (because the “a” parameter is fixed to zero), the interaction pathway between A and C is 1, the total variance in the phenotype is 2, and the estimated genetic variance component is 0.5. Accordingly, we would conclude that half of the variance in the phenotype was a function of genetic variance while in truth the main effect of the genetic effect is zero.

Second, as the size of the simulated genetic parameter increases, the bias in the estimated genetic parameter decreases. Essentially, because the total variance is standardized to 1 to give us a proportion, the size of the bias in the genetic parameter cannot increase linearly, but instead increases at a diminishing rate as the true genetic parameter increases.

The standardized estimates of the C and E parameters decrease to compensate for the increase in the variance due to the A × C parameter. Thus, it is not true that “c” or “e” pathways are underestimated, but rather the interaction increases the total amount variance in the phenotype. Therefore, the amount of variance that is a function of C or E decreases proportionally as the magnitude of variance that is directly a function of the interaction increases.

To explore the effect of an interaction between the genetic variance component and the unique environmental variance component, we simulated one hundred thousand runs of a simulation at thirty specified values of the A, C, and E parameters and vary the interaction pathway by units of 1/2. As the unique environmental variance component is of critical interest in this set of simulations, it was fixed at four possible values (e = 0.20, 0.30, 0.40, 0.50). The A and C parameters, then, range across the remaining parameter space from 0.0 to 0.8 at units of 0.1 such that the total variance of the main effects was constrained to equal 1. A path depiction of this model can be found in Fig. 1D. The results of the biases in the parameter estimates that result from the simulation can be found in Table 2.

Table 2.

Biases in the genetic and environmental variance components as a function of G × E interaction between the genetic and unique environmental variance components

	Simulated interaction pathway
	0		1/2		1		1 1/2		2
	Estimates	(Std. Dev)	Estimates	(Std. Dev)	Estimates	(Std. Dev)	Estimates	(Std. Dev)	Estimates	(Std. Dev)
Genetic variance component	0.0	0.00	(0.00)	0.02	(0.04)	0.04	(0.05)	0.04	(0.06)	0.04	(0.06)
	0.1	0.00	(0.00)	−0.02	(0.06)	−0.03	(0.07)	−0.04	(0.07)	−0.05	(0.06)
	0.2	0.00	(0.00)	−0.04	(0.06)	−0.09	(0.08)	−0.12	(0.07)	−0.14	(0.06)
	0.3	0.00	(0.00)	−0.06	(0.06)	−0.15	(0.09)	−0.2	(0.08)	−0.23	(0.06)
	0.4	0.00	(0.00)	−0.08	(0.06)	−0.2	(0.09)	−0.28	(0.08)	−0.32	(0.06)
	0.5	0.00	(0.00)	−0.11	(0.06)	−0.26	(0.08)	−0.36	(0.08)	−0.41	(0.06)
	0.6	0.00	(0.00)	−0.13	(0.05)	−0.32	(0.08)	−0.44	(0.08)	−0.5	(0.06)
	0.7	0.00	(0.00)	−0.15	(0.05)	−0.37	(0.07)	−0.51	(0.07)	−0.59	(0.06)
	0.8	0.00	(0.00)	−0.18	(0.04)	−0.43	(0.06)	−0.59	(0.07)	−0.67	(0.06)
Common environment variance component	0.0	0.00	(0.00)	0.02	(0.03)	0.03	(0.04)	0.03	(0.04)	0.03	(0.04)
	0.1	0.00	(0.00)	−0.02	(0.05)	−0.04	(0.06)	−0.05	(0.05)	−0.06	(0.04)
	0.2	0.00	(0.00)	−0.04	(0.05)	−0.1	(0.06)	−0.13	(0.06)	−0.15	(0.04)
	0.3	0.00	(0.00)	−0.06	(0.05)	−0.15	(0.07)	−0.21	(0.06)	−0.24	(0.05)
	0.4	0.00	(0.00)	−0.08	(0.05)	−0.2	(0.06)	−0.29	(0.06)	−0.33	(0.05)
	0.5	0.00	(0.00)	−0.1	(0.04)	−0.26	(0.06)	−0.36	(0.06)	−0.42	(0.05)
	0.6	0.00	(0.00)	−0.13	(0.04)	−0.31	(0.05)	−0.44	(0.05)	−0.5	(0.05)
	0.7	0.00	(0.00)	−0.15	(0.04)	−0.37	(0.05)	−0.51	(0.05)	−0.59	(0.05)
	0.8	0.00	(0.00)	−0.18	(0.03)	−0.43	(0.04)	−0.58	(0.05)	−0.67	(0.05)
Unique environment variance component	0.2	0.00	(0.00)	0.16	(0.02)	0.4	(0.03)	0.55	(0.04)	0.64	(0.04)
	0.3	0.00	(0.00)	0.14	(0.02)	0.35	(0.03)	0.48	(0.04)	0.56	(0.04)
	0.4	0.00	(0.00)	0.12	(0.02)	0.3	(0.03)	0.41	(0.04)	0.48	(0.04)
	0.5	0.00	(0.00)	0.10	(0.02)	0.25	(0.03)	0.34	(0.04)	0.40	(0.04)

As expected based upon the prior literature, an unmodeled A × E interaction component increases estimates of the unique environmental variance component, again proportional to the increase in the variance in the phenotype that is a function of the interaction component. Furthermore, the negative bias in the genetic and common environmental variance components is symmetrical and proportional to the increase in the variance of the phenotype. Specifically, the increase in the estimated unique environmental variance component will be mirrored by an evenly split decrease in the estimated A and C variance components.

In summary, although the critique argued that the effect of GE interplay would increase the genetic component in the CTD, the results from our simulations do not support this claim. Instead, unmodeled rAC only increases estimates of the genetic variance if the correlation is negative, whereas unmodeled rAE increases estimates of the genetic variance component if the correlation is positive. Alternatively, an A × C interaction increases estimates of the genetic variance component, whereas A × E interactions decrease estimates of the genetic variance component. Thus, rather than GE interplay consistently increasing the amount of variance from genetic causes, its actual impact is dependent on the specific form of the relationship and the magnitude of the specific GE interplay.

4 Integrating Behavioral Genetics into Political Science

Integrating two highly differentiated disciplines is a difficult task. In order to successfully do so, one must develop new methodological skills and learn new theoretical postulates. Effective criticism requires the same skills. The current criticism, however, promotes misunderstandings of the aims of twin studies and ignores the wide variety of models that speak to their limitations. In so doing, it mischaracterizes the extant literature on GE interplay and obfuscates the appropriate use of the CTD as a baseline model. In our response, we have emphasized that empirical models exist that deal with a variety of different mechanisms of GE interplay. In addition, using simulations, we demonstrate that when the effect size of the GE interplay is small or modest, the parameter estimates will change, but these changes will be equally modest.

To conduct empirical research, scholars are forced to make assumptions about the world, and these assumptions shape the interpretation of the results and limit the generalizability of the findings. In some situations, the assumptions will be violated, and new theories and models will be required to replace them. This includes the use of mediators and moderators. Importantly, violations of the assumptions do not necessarily invalidate the results. In some cases, statistical techniques are robust to minor (or even major) violations of the identifying assumptions. Statistical models are intended to simplify the vast complexity of the real world to allow us to test specific hypotheses and do not claim to be perfect representations of reality. As Box and Draper (1987, 74) remind us: “Remember that all models are wrong; the practical question is how wrong do they have to be to not be useful.” All models are simplifications of the real world and are useful as long as they are reasonable approximations of reality. When models fail to approximate observations from the real world, new theories must be constructed, and new methods must be derived that more closely reflect reality. Accordingly, effective tests of the assumptions allow us to refine our understanding of the model, the data, and the underlying processes and mechanisms in the real world.

It is important to reiterate that science is a cumulative exercise and future research must learn from existing knowledge and not base conclusions on conjecture or ideology. Research is incremental. Analyses are done in steps, and discovery is based on the convergence of multiple methods and theoretical approaches, with known and clear limitations. Finally, statistical models test theoretical propositions and it is the researcher’s job to choose the appropriate method. If an individual researcher chooses the wrong method, it does not invalidate the method.

Human behavior is incredibly complex, and in the broad cumulative behavioral genetics research program, CTDs are only a small part of the progression. The CTD should be viewed as an initial, baseline model, akin to correlation or simple regression. The fact that more complicated models exist and that more specific hypotheses can be tested does not make these approaches useless or invalid. Nor are twin analyses intended to be the final word in any discussion. Convergent evidence from extended family models, GE interplay models, molecular designs, hormonal studies, neuroimaging designs, and experimental designs are only some of the complementary and integral approaches required to develop a more complete understanding of the process by which individuals develop, change, and maintain political preferences.

Through decades of refinement and modification, twin studies have demonstrated robustness. This is not to suggest they remain above criticism or the need for further refinement or that we begrudge criticisms of the CTD. Any credible scholar welcomes honest and open discussion about methods and theories and waits in anticipation for model improvements. In fact, the strongest empirical criticisms and best improvements to kinship models have come from finding new ways to test for violated assumptions (Jinks and Fulker 1970; Eaves et al. 1977; Turkheimer et al. 2003; Keller et al. 2009).

The question worth asking in this context is: To what extent do twin models provide useful baseline estimates given the limitations in the data and what direction does this suggest for future research? This is an empirical question. Here we have reviewed the methods needed to test these possibilities and provided empirically supported conditions under which unmodeled rGE and G × E will return different parameter estimates than the CTD. We also reviewed the literature and found that overall, the CTD is robust to moderate violations of the independence assumption. This information, however, has long been available in the literature, but was not addressed in the critique.

A critique that presents an original idea, credits and engages the extant literature to provide an informed contribution, unpacks the methodological shortcomings of the CTD as it applies to GE interplay, accompanied by appropriate statistical methods, simulations, or real-data examples, resulting in an honest, transparent, and valid product that offers a novel approach to address such shortcomings would have made a real contribution to the literature. Unfortunately, we find the critique falls short of this threshold. Yet we remain optimistic because the opportunity to do this still remains. Research exploring GE interplay in the social sciences has only just begun. Thus, we invite the critic and other scholars to challenge the assumptions of the CTD or to extend the baseline models, with the methods that are currently available, or with new methods that they derive themselves, driven by hypotheses, but informed by the extant literature to provide novel information. This type of behavior is healthy for a discipline that is in the process of expanding its theoretical and methodological repertoire. Theorizing without addressing the literature, methods, or theory on the subject, however, is counterproductive.

5 Conclusion

We find the critique to be indicative of a larger problem of integrating novel theoretical approaches and statistical methods into political science. Traditional social science models, molecular designs, evolutionary models, and variance components approaches are not mutually exclusive or even competing. Incorporating both genetic and environmental influences provides a complementary way to study political behaviors, increasing the explanatory power and generalizability of existing political science models. At heart, the twin method is just a linear model based upon correlations between family members, a method that political scientists understand quite well. Integrating new theories and methods that build upon existing knowledge will keep political science vibrant and progressive. Rehashing old debates that have been settled in other disciplines, and selectively choosing what literature to include making one’s point appear more credible than it is, however, does not advance our understanding of the phenomena under examination.

A recent quote by Gary King (2011, 719) in many ways reflects our concerns of a degenerative approach becoming increasingly common in our field:

Fifteen years ago, Science published predictions from each of 60 scientists about the future of their fields. The physical and natural scientists wrote about a succession of breathtaking discoveries to be made, inventions to be constructed, problems to be solved, and policies and engineering changes that might become possible. In sharp contrast, the (smaller number of) social scientists did not mention a single problem they thought might be addressed, much less solved, or any inventions or discoveries on the horizon. Instead, they wrote about social science scholarship—how we once studied this, and in the future we’re going to be studying that.

The critique is an exemplar of why it is difficult to integrate theories and methods from life and social sciences and to enter into an honest discussion about the limitations inherent in genetic work and still employ the methods in a progressive and useful manner. There are major developments in genetics that not only require altering how we interpret twin models, but also advocate increased use of twin models in new ways. Contrary to the critique’s claims about the diminishing use of twins, it is important to remember that there is no better control of gene expression than identical twins, and there are no better controls for both family environments and genotype than identical twins. Indeed, the best models of genetic expression for complex human traits involve identical twins. Current issues in genetics, such as epigenetics, the epigenome, epistasis, GE interactions, problematic genomic regions, proper coverage of small variants, rare mutations and variants, redefining heritability, small effects, tissue-specific expression, trait heterogeneity, undefined genetic pathways, and unresolved functionality of genetic markers, among other concerns, gain additional complexity for the study of humans, who create their own environments and have the ability to transcend their genetic history. Properly capturing the interdependent influence of genes and environment for complex human traits can only be improved by open and honest interdisciplinary research, not a wholesale dismissal of methods or refusal to engage in the literature (for a more detailed discussion of this topic, see Hatemi and McDermott 2012a).

The goal for political science, therefore, is to rise to the challenge: to carefully, thoughtfully, and progressively integrate the useful components of behavioral genetics, as well as other disciplines, into political science and revise the theories and methods that require revision. If genes do affect political traits, future studies using related and unrelated methods will confirm and expand upon what we are currently learning. If false, future research will bring this to light. To paraphrase Shakespeare, the truth will out! If instead critics seek exceptions, ignore the existing literature, and rely on conjecture and misdirection because new approaches are foreign or too difficult to comprehend, the result will be a marginalization of our field.

Funding

B.V. was supported by National Institute on Drug Abuse (NIDA) Grant [5R25DA026119 (PI Neale)].