Pitch- and spectral-based dynamic time warping methods for comparing field recordings of harmonic avian vocalizations

Abstract

Quantitative measures of acoustic similarity can reveal patterns of shared vocal behavior in social species. Many methods for computing similarity have been developed, but their performance has not been extensively characterized in noisy environments and with vocalizations characterized by complex frequency modulations. This paper describes methods of bioacoustic comparison based on dynamic time warping (DTW) of the fundamental frequency or spectrogram. Fundamental frequency is estimated using a Bayesian particle filter adaptation of harmonic template matching. The methods were tested on field recordings of flight calls from superb starlings, Lamprotornis superbus, for how well they could separate distinct categories of call elements (motifs). The fundamental-frequency-based method performed best, but the spectrogram-based method was less sensitive to noise. Both DTW methods provided better separation of categories than spectrographic cross correlation, likely due to substantial variability in the duration of superb starling flight call motifs.

INTRODUCTION

Many species of birds and mammals produce vocalizations that are learned from conspecifics (Janik and Slater, 1997; Williams, 2004). These sounds typically serve social functions such as attracting mates (Searcy and Yasukawa, 1996), repelling intruders (Beecher et al., 1996), and signaling kinship, group membership, or individual identity (Mundinger, 1970; Boughman, 1997). In contrast to innately specified vocalizations, learned calls and songs reflect an individual's experience of a social environment (Beecher and Burt, 2004). Understanding how vocalizations are shared among individuals of the same species requires quantitative methods for measuring how acoustic features vary across groups and individuals.

Automated signal-processing techniques can greatly aid in the analysis of large sets of recordings. One set of methods is based on measuring one or more of the many acoustic features that can be extracted from recordings (Schrader and Hammerschmidt, 1997). Multivariate statistics are then used to determine which features or combinations of features vary across individuals (Mammen and Nowicki, 1981; Freeberg et al., 2003), groups (Boughman, 1997; Townsend et al., 2010), or geographic and genetic distance (Irwin et al., 2008).

Other methods compare recordings directly in a pairwise manner to quantify their acoustic similarity. Recordings are typically represented as univariate or multivariate time series. In the well-established technique of spectrographic cross correlation (SP/CC), the representation is the signal's power in different frequencies (Clark et al., 1987; Baker and Logue, 2003; McDonald and Wright, 2011). Other representations have been used, including cepstral coefficients (Ranjard et al., 2010), peak frequency (Farabaugh et al., 1994), fundamental frequency (or pitch) (Deecke et al., 1999; Smolker and Pepper, 1999; McComb et al., 2003; Shapiro and Wang, 2009), and harmonicity and Wiener entropy (Tchernichovski et al., 2000). The time series are then compared to each other, often using cross correlation. Similar signals will exhibit a peak in the cross correlation, and the height of the peak can be taken as a measure of similarity. Cross correlation can be sensitive to small differences in duration and modulation rate. For example, two tones modulated at slightly different rates will have spectrograms that may overlap at only a few points, resulting in low correlations. Other metrics of similarity, such as piecewise and polynomial fits (Smolker and Pepper, 1999), hidden Markov models (Chen and Maher, 2006) and dynamic and linear time warping (Anderson et al., 1996; Tchernichovski et al., 2000), allow the signals to distort in time and are less sensitive to temporal differences.

The fundamental frequency (F₀) is a particularly useful basis for comparison of vocalizations that are tonal and harmonic. Tonal sounds are perceived by humans and at least some species of birds and mammals as having a defined pitch that corresponds to F₀ (Shofner, 2005). Pitch can be modulated under motor control (Curry, 1937; Goller and Suthers, 1996), and both absolute pitch and pitch modulations can serve as signals in vocalizations (e.g., Christie et al., 2004). Because of the importance of pitch to human perception, there have been countless studies on automated methods of extracting F₀ from human speech and song (Gold et al., 2011), and some of these methods have been applied to studies of non-human mammals (McCowan, 1995; Deecke et al., 1999; McComb et al., 2003; Shapiro and Wang, 2009).

Although many avian songs and calls are tonal, pitch has not been extensively used for acoustic similarity measurements in field studies of birds (Tchernichovski et al., 2000; Ranjard et al., 2010). This paper describes a method for comparing tonal avian vocalizations using dynamic time warping (DTW) of F₀ contours. The F₀ contours were estimated with a pitch-tracking algorithm (Wang and Seneff, 2000) modified for increased robustness to noise in open-air field recordings. This method and a number of similar algorithms were evaluated for how well they separated clusters of similar vocalizations in a library of tonal, harmonic flight calls from superb starlings, Lamprotornis superbus.

METHODS

Recording apparatus

The recordings in this study were collected with a PMD660 or PMD661 digital recorder (Marantz, Mahwah, NJ) and an ME66 or ME62 shotgun microphone (Sennheiser Electronic, Old Lyme, CT) with a foam wind screen (MZW66 or MZW62; Sennheiser Electronic). The recorder digitized the signals at 16-bit resolution and a sampling rate of 44.1 or 48 kHz and stored the data in time-stamped WAVE files.

Study species and acoustic recordings

Superb starlings are cooperative breeders that live primarily in semi-arid savannas in East Africa (Feare and Craig, 1999). The recordings for this study were collected at Mpala Research Centre, Kenya (08.17°N, 378.52°E) from a population of nine geographically isolated social groups all located within 8.7 km of each other. Groups consisted of up to 35 birds at any one time (Rubenstein, 2007a). All the individuals in the population were marked with a unique combination of four color leg bands and a numbered metallic ring (Rubenstein, 2007b).

When taking off or flying over conspecifics, superb starlings often make loud calls (hereafter, flight calls). The data in this study comprised 365 flight calls recorded between May and July in 2008–2010 during daylight hours. Caller identity was established through a spotting scope and was noted vocally on the recordings. In total, 109 banded adults (56 male, 53 female) were recorded. Recording conditions varied with distance from the bird (20–100 m) and the presence of environmental noise, including wind, vocalizations from other species and more distant conspecifics, and human-generated sounds. Signal-to-noise ratio (SNR), measured relative to one or more segments of background from the same recording, ranged between −22 and 28 dB (mean ± SD = 3.3 ± 8.1).

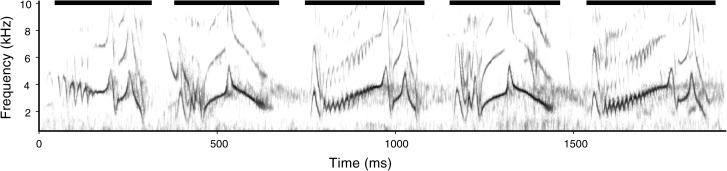
The recorded flight calls were tonal, harmonic, and rapidly modulated in frequency (Fig. 1). Calls consisted of bouts of “motifs” that were separated by intervals of silence (typically 40–100 ms) and that were often used multiple times in the same bout. Some of the same motifs were recorded in other kinds of vocalizations from this population, including songs (Pilowsky and Rubenstein, 2013) and short calls given from elevated perches (S. C. Keen, personal observation), but only motifs from flight calls were included in this study.

Figure 1.

Spectrogram of an exemplar superb starling flight call bout. Darker shades indicate increasing power (log scale). Horizontal black bars above the spectrogram indicate the component motifs.

For analysis, call bouts were segmented into motifs by visual inspection of spectrograms, with a criterion of at least 25 ms of silence or background noise between motifs. Of a total of 2552 motifs, 210 (8%) were excluded because the signal quality was too poor. For another 226 of the motifs (9%), the focal singer could not be positively identified either because more than one bird was singing with similar loudness (at different times) or the colored bands on the bird's leg could not be clearly observed. These motifs were used in testing the F₀-tracking algorithm but excluded from the analysis of call similarity. A total of 2116 motifs were from identified birds (mean ± SD = 5.8 ± 4.1 motifs per bout, N = 365).

F₀ tracking

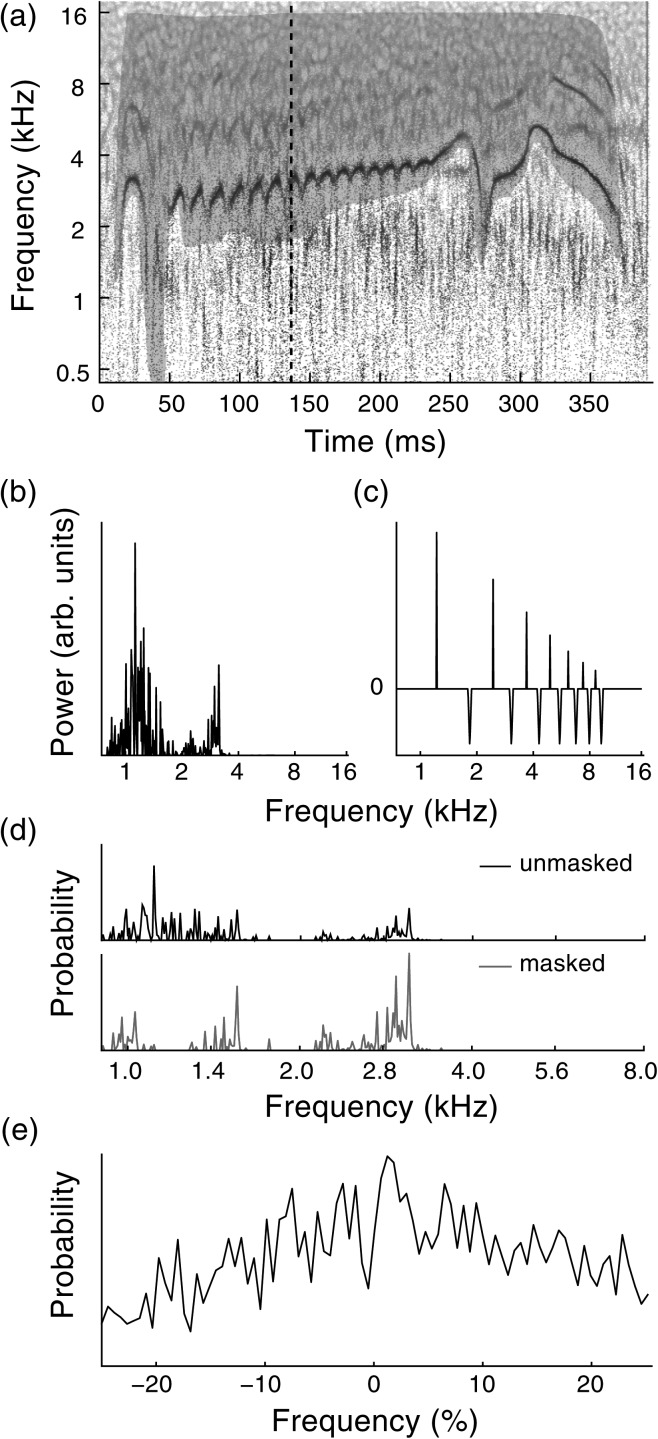
All the recorded flight call motifs were tonal and harmonic with a well-defined F₀ that modulated in time as seen in Figs. 12a. F₀ was estimated from the recordings using a harmonic-template-matching algorithm modified from Wang and Seneff (2000). The modifications include the use of time-frequency reassignment spectrograms to increase resolution, particle filtering to smooth estimates across time, and spectrogram masking to remove noise. Briefly, the harmonic-template algorithm is based on the definition of harmonic sounds as having peaks of spectral entry at integral multiples of F₀. An estimate of F₀ can be obtained by cross correlating the power spectrum on a logarithmic frequency grid [Fig. 2b] with a harmonic template that has peaks at logarithmically-spaced intervals. Following Wang and Seneff (2000), the harmonic template had seven peaks, which were scaled so that the normalized area under each peak decreased exponentially with a decay factor of 0.85. Negative peaks were added between the positive ones, with an amplitude of 0.35 times the amplitude of the main peak in the template. The template is shown in Fig. 2c. These features help to reduce pitch-doubling and halving errors.

Figure 2.

(Color online) Example of F₀ tracking analysis. (a) Time-frequency reassignment spectrogram of a superb starling flight call motif. Shaded region is a manually drawn mask used to reduce influence of low-frequency noise. Dashed line indicates time frame analyzed in subsequent panels. (b) Power spectrum in example time frame. Note the peak corresponding to the fundamental frequency of the vocalization, around 3 kHz, is small relative to the low-frequency noise. (c) Harmonic template, with logarithmically spaced peaks to detect harmonic structure. (d) Cross correlations of spectrum with harmonic template. Masking the spectrogram [shaded polygon in (a)] reduces low-frequency interference so that the highest peak corresponds to the fundamental frequency. (e) Cross correlation between the example frame and the following time point, which is used by the particle filter to smooth estimates. The peak at +2% indicates F₀ is increasing.

To extract F₀ contours (i.e., as a function of time), the harmonic template was cross correlated with spectra calculated in short, overlapping analysis windows. Due to the high rate of frequency modulation in superb starling motifs (as high as 80 Hz in the trills), the analysis windows needed to be short (around 10 ms), which in a standard short-time Fourier transform (STFT) would lead to relatively broad peaks in the frequency domain. Time-frequency reassignment was used to sharpen the peaks (Auger and Flandrin, 1995).

Analysis windows were 12 ms in duration, shifted by 1.5 ms in each frame. A multitaper algorithm was used to produce more stable estimates, with five Hermitian tapers (Xiao and Flandrin, 2007), and spectral energy was “locked” to within 480 Hz and 7.5 ms of its original location, which helps to further reduce noise (Gardner and Magnasco, 2006). Frequency reassignment was on a logarithmically spaced grid to facilitate cross correlation with the template. The code used to calculate the reassigned spectrograms is available at http://www.github.com/dmeliza/libtfr.

Some tracking algorithms for pitch (and peak frequency) impose a continuity constraint to ensure that estimates change smoothly between successive frames and avoid doublings and halvings (Boersma, 1993; Wang and Seneff, 2000; Mallawaarachchi et al., 2008). This constraint can be especially important in field recordings where low-frequency noise (e.g., from wind), vocalizations from other species, and other non-stationary environmental sounds temporarily obscure the main peak in the cross correlation. Particle filtering, a well-established statistical sampling method, was used to smooth estimates of F₀ across time (Liu and Chen, 1998). Following Wang and Seneff (2000), the cross correlation between successive frames [Fig. 2e] of the spectrogram was used as the smoothing constraint (i.e., proposal density). The particle filter generated a distribution of likely contours, which was backtracked using a Viterbi algorithm (Godsill et al., 2001) to find the most likely contour. F₀ was taken as the mean across five runs with different initial conditions.

Start and stop times for tracking were set manually by inspecting the spectrograms. The parameters of the algorithm were optimized heuristically using several exemplar motifs. Plots of the F₀ estimates were overlaid on the spectrograms, and the parameters were adjusted to maximize the degree of overlap of the estimates with the strongest and lowest frequency contour in the spectrogram. The same parameters were used for all motifs.

After an initial run of the algorithm, a polygonal mask was drawn on the spectrogram [Fig. 2a] to exclude interference from wind, other vocalizations, and reverberation. The power for time-frequency points outside the mask was set to zero, effectively restricting the F₀ contours to areas within the mask and preventing the algorithm from treating noise as a possible harmonic [Fig. 2d]. The masks were iteratively refined until the F₀ estimates aligned with the lowest harmonic. These refined estimates were used as the basis for evaluating the performance of the algorithm on unmasked recordings at different SNR. The error in the unmasked F₀ estimate was calculated as the root-mean-square (RMS) of the difference between the unmasked and refined estimates. Recordings where the fundamental frequency was not clearly visible in the spectrogram, or where the F₀ estimate could not be refined to match the spectrogram, were excluded from later analyses. Masking and exclusion were done blindly, with no information about the locations of or individuals in the recordings made available to the operator.

Motif comparisons

A number of different pairwise-comparison methods were tested on two sets of flight call motifs comprising 5–20 exemplars of nine distinct motif types, three types from three different social groups. Each set was chosen by an observer given spectrograms of the motifs and information about which social group they were recorded from but not the F₀ estimates or any information that would identify the singer. Observers were instructed to choose sets of exemplars that looked similar to each other but were distinct from the other eight motif types. One set (hereafter, the test set) was chosen by C.D.M. and was used to tune parameters of the comparison methods to maximize the similarity among exemplars of each motif type and maximize dissimilarity among different motif types. The second set (hereafter, validation set) was chosen from three different social groups by a person familiar with superb starling song but without any prior exposure to this dataset. The comparison procedures were applied to the validation set without further adjusting the parameters. Details of individual comparison algorithms are given in the following text.

To evaluate the performance of each comparison metric, the similarity values within types were compared to the similarity values between types. An ideal comparison metric would yield large within-type similarities compared to between-type similarities. The average silhouette (Rousseeuw, 1987), a nonparametric measure of cluster separation, was used to quantify performance. For each motif i, the silhouette index is defined as s_i = (b_i − a_i)/max(a_i, b_i), where a_i is the average dissimilarity between i and the other motifs of the same type, and b_i is the minimum dissimilarity between i and all the motifs of a different type. Dissimilarity was taken to be the reciprocal of similarity. The average silhouette is the mean of s_i over all motifs, and it ranges between −1 and 1 with larger values indicating better separation among types. Because silhouette is nonparametric it is less likely to be influenced by differences in the scale of similarity scores from different methods. Silhouette was calculated in R with the package cluster (version 2.15.1).

Cross correlation

The peak cross correlation of two time series provides a simple similarity metric. Motifs were compared using cross correlation of the F₀ estimates (F₀/CC) and cross correlation of the spectrograms (SP/CC). SP/CC is identical to standard univariate cross correlation but averaged across multiple frequency bands. In keeping with standard methodology (Charif et al., 2010), spectrograms for SP/CC were calculated using a conventional STFT, a Hanning window of 10.8 ms (518 samples corresponding to a frequency resolution of 93 Hz) and a frame shift of 1.04 ms (50 samples). These values gave the best performance on the test set. Based on visual inspection, the power in superb starling flight calls was restricted to frequencies between 750 Hz and 10 kHz, so only those bands were included in the calculation. To avoid spurious correlations between beginnings and ends of motifs, only lags where the shorter signal overlapped completely with the longer one were used. SP/CC was tested with power on a linear scale and on a log scale, and with and without masking. For log-scale spectrograms and F₀ the mean was subtracted before evaluating the correlation. Similarity was taken to be the peak of the cross correlation.

Dynamic time warping

DTW is similar in principle to cross correlation, but the time series are allowed to compress and expand temporally to find the best alignment (Vintsyuk, 1971; Anderson et al., 1996). DTW consists of two steps. First, all the time points in the two signals A and B are compared in a pairwise manner to generate a difference matrix, ${\Theta }_{i,j}$, where i is a time index in A and j a time index in B. For the F₀ contours, the signals were univariate functions, $F_0^A$(t) and $F_0^B$(t), and the difference was the Euclidean distance, ${\Theta }_{i,j}^2={(F_0^A(t_i)-F_0^B(t_j))}^2$. For spectrograms, each time point was represented by a vector [S_f(t)], and there were multiple options for calculating ${\Theta }_{i,j}$. DTW of spectrograms (SP/DTW) was tested using the Euclidean distance, ${\Theta }_{i,j}^2={\sum }_f{(S_f^A(t_i)-S_f^B(t_j))}^2$, which emphasizes differences in power, and the cosine of the angle between the vectors

$${\Theta }_{i,t}=\frac{S_f^A(t_i)\cdot S_f^B(t_j)}{\Vert S_f^A(t_i)\Vert \Vert S_f^B(t_j)\Vert },$$

which emphasizes differences in shape. As with SP/CC, the spectral DTW algorithm (SP/DTW) was tested on both linear and log-scale spectrograms and with and without masks.

The second step in DTW is finding the optimal path through the difference matrix that minimizes the dissimilarity, subject to a cost function that determines how much warping will be allowed. For this application, to allow some degree of local warping while penalizing large differences in duration, an adaptive Itakura constraint was used (Itakura, 1975)

$$d(k,l)=\{\begin{array}{cc}\max (k,l)& \mathrm{if}k=1,l\le 3\hspace{0.17em}\text{or}\hspace{0.17em}k\le 3,l=1,\\ \exp [\max (k,l)]/3& \mathrm{if}k=1,l\le N\hspace{0.17em}\text{or}\hspace{0.17em}k\le N,l=1,\\ \infty & \text{otherwise}\end{array}$$ (1)

where d(k,l) is the cost of moving k time points in one signal and l in the other, and N is one greater than the minimum factor by which the shorter motif needs to be deformed to be alignable with the longer motif. It can be seen that this cost function allows signals to compress or expand locally by a factor of up to N but with exponentially increasing penalties. The total dissimilarity is defined by the sum of ${\Theta }_{i+k,j+1}d(k,l)$ over the best path, with 0 indicating that the signals are identical and larger numbers indicating greater dissimilarity. Scores were normalized by the average length of the two signals, and similarity was defined as the reciprocal of dissimilarity.

sound analysis pro

sound analysis pro (SAP) is widely used in laboratory studies of song learning and development (Tchernichovski et al., 2000) and in some field studies as well (Baker and Logue, 2003; Brunton and Li, 2006; Ranjard et al., 2010). SAP's symmetric comparison function was used to make pairwise similarity measurements. Out of a range of values for the interval and minimum duration parameters, the best results were observed with an interval of 60 ms and a minimum duration of 26 ms. It was not possible to test masked spectrograms because SAP only takes sound files as inputs.

Software

The F₀ tracking, DTW, and CC algorithms used in this study are available as part of an open-source, freely available software package called chirp (http://github.com/dmeliza/chirp). Version 1.2 was used for analyses in this study. The software includes a graphical interface for inspecting spectrograms and drawing denoising masks and a batch processing interface for calculating F₀ and comparing recordings. Batch analyses take advantage of multi-core processors for substantial improvements in speed with large libraries of recordings. Results can be exported to plain text files or sql databases. Signal comparisons use a modular plugin architecture that allows users to supply additional algorithms.

RESULTS

F₀ tracking

For recordings of superb starling flight calls with high SNR, the estimated F₀ traces reliably tracked the fundamental frequency in the spectrogram. As shown in Fig. 3a, the F₀ contours followed rapid and fine-scale frequency modulations in trilled and “hairpin” sections of the motifs. With increasing noise, the algorithm was increasingly likely to briefly follow ridges in the noise instead of the contour of the vocalization. Nonstationary sounds from other birds, humans, and mechanical devices were the most problematic, but low-frequency noise from wind could also introduce errors when the amplitude was large enough. Reverberation smeared spectral energy across time, as seen in Fig. 3a, and could lead to a failure to track frequency modulations. At high levels of noise, around 0 dB SNR, the algorithm was increasingly unlikely to find the start of the contour.

Figure 3.

F₀ tracking performance on noisy recordings. (a) Spectrograms of six exemplar motifs. Numbers in each panel indicate signal-to-noise ratio (dB RMS). Red traces indicate F₀ estimates without masking; blue traces indicate estimates after masking. In the final panel, the signal is barely visible and the F₀ estimate is extremely noisy. Dynamic range of the spectrograms is 50 dB, and the time and frequency scales are the same for all plots. Arrowheads indicate reverberation. (b) Boxplot of average error (RMS difference between masked and unmasked F₀ estimates) as a function of recording SNR. Thick horizontal lines indicate medians. The upper and lower edges of the boxes indicate upper and lower quartiles, and the vertical lines extend to 1.5 times the interquartile range. Outliers beyond the range of the whiskers are shown as points.

Most of these errors could be corrected by using spectrotemporal masks to eliminate interference from other sources. An example mask is shown in Fig. 2a. Effectively the mask acted as a bandpass filter the passband of which could be controlled on a fine time scale. The F₀ traces extracted after masking were used to assess the performance of the tracker on unmasked signals. Figure 3b shows that the median RMS difference between masked and unmasked estimates and the number of recordings with large errors (>2 kHz RMS) increased with noise. A substantial proportion (11%) of the recordings with SNR below 0 dB were so badly obscured by noise that the F₀ contour could not be seen in the spectrogram. Even with masking, F₀ estimates from these recordings were highly variable, as seen in the last panel of Fig. 3a, and the recordings were not included in further analysis.

Motif-similarity measurements

A subset of the superb starling flight call recordings was used to test several different pairwise-comparison methods. The results from these analyses are shown in Fig. 4 as matrices in which each cell corresponds to a different pair of motifs, and intensity indicates the similarity score. As seen in Fig. 4a, F₀/DTW yielded relatively high similarity scores between motifs of the same type and low similarity scores between motifs of different types. Results for some of the other comparison methods are shown in Fig. 4c. SP/DTW using both masked and unmasked spectrograms gave results comparable to DTW using F₀ estimates refined by masking, but F₀/DTW with unrefined estimates appeared to give lower within-type similarity. F₀/CC gave the lowest between-type scores but also showed low within-type scores for many of the motif types. SP/CC and SAP gave relatively high between-type scores.

Figure 4.

Similarity of superb starling flight calls calculated with different comparison methods. (a) Matrix of similarity scores for each pair of recordings from a test set comprising multiple exemplars of nine different motif types (indicated by brackets below matrix). Scores are calculated using DTW of the F₀ contours with lighter shades indicating higher similarity. Motifs are indexed in the matrix by type so that cells corresponding to within-type comparisons are in blocks along the diagonal and between-type comparisons are off the diagonal. (b) Exemplars of recordings from three of the motif types. Note differences within types in duration, modulation rate, and background noise. (c) Similarity score matrices for some of the other comparison methods. SP/DTW: Dynamic time warping of spectrograms with linear spectrogram scale and cosine distance metric; F₀/CC: Cross correlation of F₀ contours; SP/CC: Spectrographic cross correlation with cosine distance metric; SAP: sound analysis pro. “Masked” indicates that a denoising mask was applied to the spectrograms prior to running the F₀ estimation or spectrographic comparisons. Intensity maps are on a log scale for DTW scores due to their large range and on a linear scale for CC and SAP, which give scores bounded between 0 and 1.

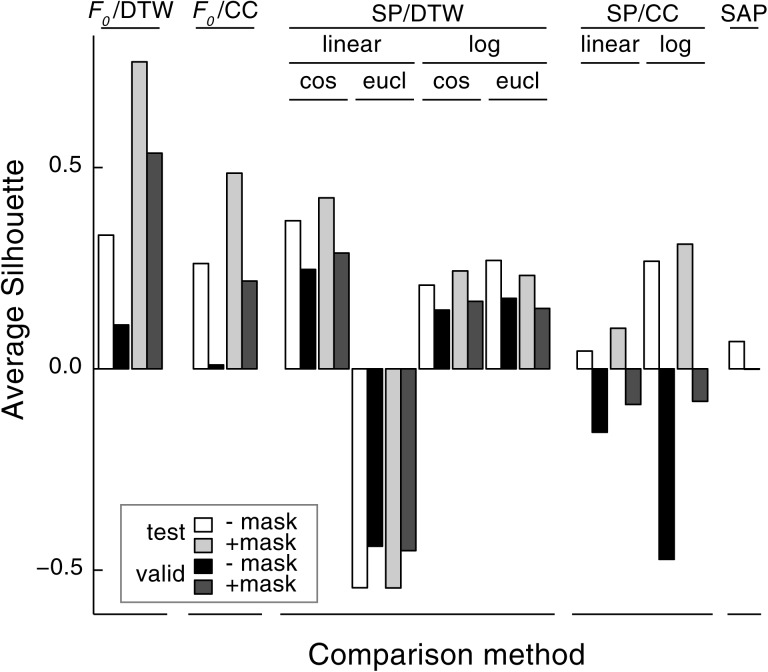
The average silhouette was used to quantify how well each of the comparison methods separated the motif types into distinct clusters. High within-type and low between-type similarity results in silhouette values approaching 1. Silhouette values close to or below 0 indicate overlap between clusters. The same algorithms were also applied to a second set of validation motifs. As seen in Fig. 5, the F₀/DTW algorithm using masked spectrograms gave the best cluster separation on both the test and validation sets, followed by the SP/DTW algorithm using masked spectrograms, a linear power scale, and cosine-based spectrographic distance. However, for unmasked spectrograms, SP/DTW outperformed F₀/DTW. F₀/CC also gave relatively good separation for masked spectrograms. The worst cluster separation was with SP/DTW using a linear power spectrum and a Euclidean spectrographic distance.

Figure 5.

Cluster separation (average silhouette) for pairwise-comparison metrics. Headings in capital letters are the comparison algorithms of which there were one or more variants. For the spectrographic metrics, subheadings indicate whether the power scale was linear or logarithmic, and whether spectrographic distance was calculated using a cosine (cos) or Euclidean (eucl) metric.

DISCUSSION

F₀ tracking

Despite the importance of pitch as a bioacoustic feature, obtaining good pitch estimates from field recordings remains difficult. The most advanced algorithms are specialized for the human vocal system, and more general algorithms can be fairly sensitive to noise. The pitch-tracking algorithm described here is based on harmonic template matching, originally developed for human telephone speech (Wang and Seneff, 2000) but also used with whale vocalizations (Shapiro and Wang, 2009). For these recordings, multitaper reassignment spectrograms increased precision and robustness to unstructured noise, and a Bayesian particle filter improved tracking by smoothing estimates over time. F₀ estimates from this method were reliable if the signal strength was at least 10 dB above background noise. This method could be used without denoising on recordings made in good acoustic conditions, including field sites where the microphone is close to the animal.

For noisier recordings, applying a mask to the spectrogram to eliminate interference from noise sources restricted to specific times and frequencies improved F₀ tracking down to SNR levels around 0 dB. Masking has the potential to introduce bias and operator error, in the extreme reducing the procedure to hand-tracing of contours. Depending on the system, more automated methods of denoising may be preferable (Mallawaarachchi et al., 2008; Johansson and White, 2011). However, it is important to note that most analyses of field recordings involve a heuristic element if only to identify the onsets and offsets of recordings, and all manual steps in acoustic analyses should be conducted blindly with no information about variables of potential interest available to the operator.

Motif comparisons

DTW of F₀ estimates from denoised recordings gave similarity scores that corresponded well with identified motif types, yielding high scores for comparisons between exemplars of the same type and low scores for comparisons between exemplars of different types. These motif types were identified through inspection of spectrograms and are likely to reflect the most visually salient features of the spectrograms, which in these data were the overall shapes of the F₀ modulations. Variations in duration and amplitude modulation, in contrast, were not as visually salient. Thus F₀/DTW accurately quantifies the differences between recordings that are apparent in spectrograms. Using CC to compare F₀ estimates instead of DTW gave worse cluster separation, consistent with the greater sensitivity of CC to differences in temporal structure. Some of these differences may be behaviorally significant (e.g., Nelson and Marler, 1989), and playback studies are necessary to determine whether additional information is carried in the duration of superb starling flight calls.

Cluster separation was also good for DTW of full spectrograms when the spectrograms were calculated on a linear power scale and the comparisons between time points were based on the cosine of the angle between spectra rather than the Euclidean distance. The cosine metric is normalized for the power of the spectra and thus emphasizes differences in shape, whereas the Euclidean metric is also sensitive to differences in total power. Furthermore, a linear scale emphasizes peaks in the power spectrum more than a logarithmic scale. The combination of these choices probably causes the DTW algorithm to find optimal warpings based on the harmonic peaks of the signals. In contrast, the combination of a linear scale and a Euclidean metric led to a complete failure to separate motif types. This combination of parameters is likely to be extremely sensitive to differences in overall power, which is not optimal given the range of recording quality and amplitude in the field recordings used here.

F₀/DTW, SP/DTW, and F₀/CC outperformed SP/CC and SAP, two commonly used methods for pairwise comparisons. The poor performance of SP/CC on this dataset may reflect variability in the temporal structure of the motifs. A comparison of the similarity matrices for SP/CC and F₀/CC [Fig. 4c] suggests that both methods show relatively good clustering for the same subset of motif types. However, SP/CC gives much higher between-type scores than F₀/CC, indicating that the poor cluster separation for SP/CC may also be due to spuriously high correlations between unrelated recordings.

Environmental noise had a clear impact on the performance of the similarity metrics (Fig. 5). For F₀/DTW, noise degraded cluster separation by introducing errors in the F₀ estimates. A similar effect probably accounted for the poor performance of SAP, which is designed for lab recordings and does not have any denoising functionality. Noise also affected the spectral-based comparisons, presumably by introducing spurious correlations, but overall the spectral methods were less sensitive than F₀-based ones. For unmasked spectrograms, SP/DTW outperformed F₀/DTW. Because masking requires significant manual effort and introduces potential biases, SP/DTW is probably a better choice for comparing noisy recordings if the F₀ estimates are not needed for anything else.

CONCLUSIONS

Quantitative, automatic comparisons of acoustic signals offer the possibility of studying large numbers of vocalizations to look for patterns in the development of an individual's repertoire or in cultural transmission of vocal behaviors through populations (Lachlan and Slater, 2003; Runciman et al., 2005; Sewall, 2009). The current results illustrate the importance of choosing comparison metrics that reflect the structure of the vocalizations under study. Superb starling flight call motifs are tonal and harmonic, and F₀ provides a useful low-dimensional representation for making pairwise comparisons. Similar improvements over spectral-based methods are likely to obtain for other species that produce tonal vocalizations and use pitch modulations to convey information. Likewise, superb starling motifs vary substantially in duration while maintaining the same overall shape of F₀ modulation. For such data, time-warping methods provide estimates of similarity that correspond better to visual classification in comparison to cross-correlational methods, which are more sensitive to small differences in temporal structure.