Evaluation of the impact of backscatter intensity variations on ultrasound attenuation estimation

Abstract

Purpose: Quantitative ultrasound based approaches such as attenuation slope estimation can be used to determine underlying tissue properties and eventually used as a supplemental diagnostic technique to B-mode imaging. The authors investigate the impact of backscatter intensity and frequency dependence variations on the attenuation slope estimation accuracy.

Methods: The authors compare three frequency domain based attenuation slope estimation algorithms, namely, a spectral difference method, the reference phantom method, and two spectral shift methods: a hybrid method and centroid downshift method. Both the reference phantom and hybrid method use a tissue-mimicking phantom with well-defined acoustic properties to reduce system dependencies and diffraction effects. The normalized power spectral ratio obtained is then filtered by a Gaussian filter centered at the transmit center frequency in the hybrid method. A spectral shift method is then used to estimate the attenuation coefficient from the normalized and filtered spectrum. The centroid downshift method utilizes the shift in power spectrum toward lower frequencies with depth. Numerical phantoms that incorporate variations in the backscatter intensity from −3 to 3 dB, by varying the scatterer number density and variations in the scatterer diameters ranging from 10 to 100 μm are simulated. Experimental tissue mimicking phantoms with three different scatterer diameter ranges (5–40, 75–90, and 125–150 μm) are also used to evaluate the accuracy of the estimation methods.

Results: The reference phantom method provided accurate results when the acoustical properties of the reference and the sample are well matched. Underestimation occurs when the reference phantom possessed a higher sound speed than the sample, and overestimation occurs when the reference phantom had a lower sound speed than the sample. The centroid downshift method depends significantly on the bandwidth of the power spectrum, which in turn depends on the frequency dependence of the backscattering. The hybrid method was the least susceptible to changes in the sample's acoustic properties and provided the lowest standard deviation in the numerical simulations and experimental evaluations.

Conclusions: No significant variations in the estimation accuracy of the attenuation coefficient were observed with an increase in the scatterer number density in the simulated numerical phantoms for the three methods. Changes in the scatterer diameters, which result in different frequency dependence of backscatter, do not significantly affect attenuation slope estimation with the reference phantom and hybrid approaches. The centroid method is sensitive to variations in the scatterer diameter due to the frequency shift introduced in the power spectrum.

INTRODUCTION

Quantitative ultrasound (QUS) parameters such as the attenuation slope, sound speed, backscatter coefficient, effective scatterer diameter, and spacing have been investigated in order to evaluate the pathological state of tissue.^{1, 2, 3, 4, 5} The ability to estimate the attenuation slope accurately is important for the estimation of many of the other QUS parameters. In addition, the attenuation slope may provide a direct correlation to diagnostic approaches that are used for clinical diagnosis currently.^{6, 7, 8} Attenuation slope estimates may also be important for the eventual differentiation between benign and malignant tumors in many organ systems.

Kiss et al. measured the attenuation coefficient ex vivo of human uterine and cervical tissue and showed variation in the attenuation coefficient values between the normal uterine tissue, leiomyomas, as well as cervical tissue over a frequency range of 5–10 MHz.⁹ Cervical ripening which is related to preterm birth has also been investigated by measuring the attenuation slope, where the attenuation coefficient decreases for a ripened cervix when compared with an unripened cervix.^{10, 11} Human pregnant cervix has been evaluated and it has been shown that ultrasonic attenuation estimates have the potential to be an early and objective noninvasive parameter to detect the interval between examination and delivery.^{12, 13}

Ultrasound attenuation of the liver has also been investigated to detect diffuse diseases such as steatosis, fibrosis, and cirrhosis as well as for evaluating differences between benign and malignant masses. Literature reports show that the attenuation coefficient values of patients with alcoholic cirrhosis are significantly higher than that of the normal liver. ^{2, 14, 15, 16} Dong et al. measured the mean attenuation in hepatic hemangioma, hepatocellular carcinoma, and metastatic liver tumors which presented with a lower attenuation than normal liver tissue.¹⁷

In breast tissue, frequency dependent ultrasonic attenuation mapping has been investigated since the 1980s to determine differences between normal and pathological breast tissue. It has been shown that the attenuation parameter is capable of differentiating breast masses on the basis of the number of cells and collagen fibers they contain.^{18, 19}

Both frequency and time domain approaches for attenuation coefficient estimation have been developed and described in the literature.^{20, 21, 22, 23, 24, 25, 26, 27} In frequency domain approaches the attenuation slope is mainly determined from the amplitude reduction and shift in the power spectrum toward lower frequencies. Time domain approaches, on the other hand, are based on the reduction in amplitude and frequency of the echo signal with depth. The reference phantom method (RPM), a spectral difference method, determines the attenuation from the decay in the power spectral amplitude with depth.²³ This approach uses a reference phantom with well characterized acoustic properties, to reduce ultrasound system dependencies and diffraction effects. A second frequency domain method is the centroid downshift method, a spectral shift method, that estimates the attenuation slope from the signal's power spectrum calculated at each depth by measuring the shift in signal toward lower frequencies with depth.²⁴ The hybrid method was developed to combine the advantages inherent with both the reference phantom and centroid downshift methods, while minimizing their limitations.²⁷ The hybrid method initially uses a reference phantom to reduce system dependencies and diffraction effects. The normalized power spectral ratio is then filtered by a Gaussian filter centered at the transmit center frequency to reintroduce the transfer function of the transmitted pulse. Since the filtered power spectrum is still affected by the potential difference in backscatter between different regions, a spectral shift method is then used to estimate the attenuation coefficient from the normalized and filtered power spectrum.

Attenuation slope estimated using the methods described above should be compared and quantified to determine the precision and accuracy of the different approaches. Dependence on the region of interest (ROI) size, limitations with various techniques, and errors that may result from tissue in-homogeneities have to be investigated.²⁸ We have previously evaluated the impact of sound speed on attenuation slope estimates for simulated and tissue-mimicking (TM) phantoms that have similar acoustic properties other than the sound speed variations.²⁹

In this work we investigate the impact of backscatter intensity variations of the sample with respect to a reference phantom. We investigate backscatter variations introduced by both changes in the scatterer number density by varying the number of scatterers/millimeter cubed and variations in scatterer diameter while maintaining Rayleigh scattering statistics in most situations. Varying scatterer diameters will change the frequency dependence of scattering observed in the power spectrum, while variations in the scatterer number density will not change the underlying frequency dependence of scattering. The accuracy and precision of the attenuation slope estimation are evaluated under both these conditions in this paper.

MATERIALS AND METHODS

Simulated tissue-mimicking phantoms

A frequency domain simulation program was used to generate numerical phantoms and acoustic interaction based on linear diffraction theory of continuous waves.^{30, 31} Li and Zagzebski have described the frequency domain model utilized for generating B-mode images and radiofrequency (RF) echo signals with ultrasound array transducers. The ultrasound simulation model for the beam from a transducer is solved by approximating the integral in the pressure field, taking into account the effects of frequency-dependent attenuation, backscattering, and dispersion.³⁰ The dimensions of the numerical phantoms were 80 mm along the axial, 38 mm in the lateral, and 5 mm in the elevational direction, respectively. A linear-array transducer was modeled with 128 rectangular elements of dimensions 0.15 mm × 10 mm with a center to center element spacing of 0.2 mm. The simulation parameters used produced 190 beam lines over the 38 mm lateral span that was scanned. A fixed elevational focus was applied and set to be equal to the lateral focal point to avoid the impact of different elevational and lateral foci in the analysis. The incident pulse was simulated to be a Gaussian-shaped pulse with center frequency of 6 MHz and 80% bandwidth. A single transmit focus at 40 mm was utilized for all TM numerical phantom simulations. The sampling rate was set to 40 MHz. The ultrasound system beamformer sound speed was set at 1540 m/s and was not altered, while the sample sound speeds, attenuation coefficients, scatterer number density, and/or scatterer diameters were varied. Glass beads were utilized in the model to generate backscattered echo signals with the propagation of the ultrasound pulse.

In this paper, we simulated two groups of uniformly attenuating numerical phantoms to simulate backscatter intensity variations with and without the frequency dependence of backscatter as described previously. The reference phantom used was the same for both sets with a speed of sound (SOS) of 1540 m/s, backscatter intensity level with a scatterer number density of 20 scatterers/mm³, and a 0.5 (dB/cm)/MHz attenuation slope. In medical ultrasound imaging most tissues of interest are within a margin of 2%–3% of the sound speed of 1540 m/s.³² Table 1 shows the acoustical properties of the simulated phantoms used to estimate and compare the performance of the attenuation estimation algorithms.

Table 1.

Acoustical properties of experimental and numerically simulated reference (Ref) and sample (Sam) phantoms.

Acoustical properties			Speed of sound (m/s)		Scatterer diameter (μm)		Scatterer intensity (dB)		Attenuation coefficient [(dB/cm)/MHz)]
Group	Set	Fig.	Ref	Sam	Ref	Sam	Ref	Sample	Ref	Sam	Runs
1	1	2a	1540	1540	50	50	0	−3 −2 −1 0 1 2 3	0.5	0.5	70
		2b	1540	1540	50	50	0	−3 −2 −1 0 1 2 3	0.5	0.3	70
		2c	1540	1540	50	50	0	−3 −2 −1 0 1 2 3	0.5	0.7	70
	2	3a	1540	1540	25	25	0	−3 −2 −1 0 1 2 3	0.5	0.5	70
		3b	1540	1500	25	25	0	−3 −2 −1 0 1 2 3	0.5	0.5	70
		3c	1540	1580	25	25	0	−3 −2 −1 0 1 2 3	0.5	0.5	70
2	1	4a	1540	1540	50	10 20 30 40 50 60 70 80 90 100	−3	−3	0.5	0.5	100
		4b	1540	1500	50	10 20 30 40 50 60 70 80 90 100	−3	−3	0.5	0.5	100
		4b	1540	1580	50	10 20 30 40 50 60 70 80 90 100	−3	−3	0.5	0.5	100
	2	5a	1540	1540	50	10 20 30 40 50 60 70 80 90 100	−3	−3	0.5	0.5	–
		5b	1540	1540	50	10 20 30 40 50 60 70 80 90 100	−3	−3	0.5	0.3	100
		5c	1540	1540	50	10 20 30 40 50 60 70 80 90 100	−3	−3	0.5	0.7	100
		6a	1533	1533	5–40	5–40	264	264	0.58	0.58	45
						75–90		11		0.62
						125–150		2		0.72
		6b	1500	1533	5–40	5–40	264	264	0.58	0.58	15
						75–90		11		0.62
						125–150		2		0.72
		6c	1580	1533	5–40	5–40	264	264	0.58	0.58	15
						75–90		11		0.62
						125–150		2		0.72

The first group of phantoms used incorporated only scatterer number density changes to vary the backscatter intensity without changes in the frequency dependence on the power spectrum for estimating the attenuation slope. This was done in the simulation by varying the number of scatterers per millimeter cubed and keeping the diameters of the scatterers constant in the simulation. Two different sets for this group were simulated as shown in Table 1. The first set represents simulated phantoms that consisted of randomly distributed scatterers in three media with three different attenuation coefficient values of 0.5, 0.3, and 0.7 (dB/cm)/MHz, respectively. The second set represents simulated phantoms that consisted of randomly distributed scatterers in three media with three different SOS, namely, 1500, 1540, and 1580 m/s, respectively. The scatterer intensity in the sample phantoms was varied while keeping the reference phantom properties constant for both sets. The scatterer diameter is kept constant between both the sample and the reference phantoms. Ten independent realizations at each intensity value with the acoustical properties listed in Table 1 were performed (total of 420 runs for group 1). The scatterer intensity for both of these sets was varied from −3 to +3 dB; where −3 dB represents a scatterer number density of 10 scatterers per millimeter cubed (to obtain Rayleigh scattering statistics) and the +3 dB scattering level includes 40 scatterers per millimeter cubed. The following equation was used to determine the scatterer number density at each intensity value:

$$\begin{array}{c}\hfill I\left[\mathrm{dB}\right]=10\times 1{\mathrm{og}}_{10}\frac{I_d\left[\frac{No}{{\mathrm{mm}}^3}\right]}{I_o\left[\frac{No}{{\mathrm{mm}}^3}\right]},\end{array}$$ (1)

where I denotes the intensity value in decibels, I_d is the scatterer number density at which we desire to calculate the dB value, and I_o is the scatterer number density when the scatterer intensity value in dB is the same as that for the reference phantom. I_o in Eq. 1 is set to 20 scatterers/mm³.

In order to study the impact of changes in the frequency dependent backscatter intensity on attenuation slope estimation, we simulated the second group of numerical phantoms with different scatterer diameters. Use of different scatterer diameters should not introduce any variations in the results as long as the reference and sample phantoms were simulated with similar sized scatterers, thereby possessing the same frequency dependence. These simulations are listed under Group 2 in Table 1. Faran's theory on scattering from solid cylinders and spheres³³ was used to calculate the frequency dependent backscatter coefficients in the simulation; with the scattering calculations performed at 180°, i.e., for backscattered echo signals.

The second group also consisted of two sets of simulated TM phantoms. In both sets the reference phantom was the same with an attenuation coefficient of 0.5 (dB/cm)/MHz, SOS of 1540 m/s, and glass bead scatterers with a diameter of 50 μm, that were randomly distributed within the medium for all the simulation experiments. The SOS of the sample phantoms in the first set of Group 2 were set to 1500, 1540, and 1580 m/s, respectively, with an attenuation coefficient of 0.5 (dB/cm)/MHz. For the second set of phantoms in Group 2, the attenuation coefficients were 0.3, 0.5, and 0.7 (dB/cm)/MHz, respectively. The scatterers used in the sample phantoms were spherical glass beads with diameters ranging from 10 to 100 μm at 10 μm increments, for both the phantom sets in Group 2.

Each numerical phantom was independently generated 10 times and the estimated values were averaged over the ten realizations to obtain statistically significant results. A total of 500 independent numerical uniform phantoms were generated for this group.

Experimental TM phantoms

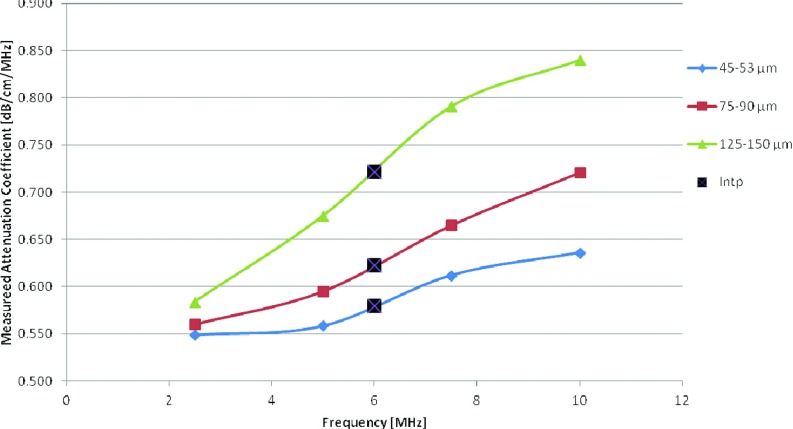
Three uniform TM experimental phantoms with a constant sound speed of 1533 m/s at 22 °C and uniform attenuation coefficient of 0.58 (dB/cm)/MHz were manufactured in our laboratory. These three phantoms consisted of glass beads with diameters in the range of 5–40 μm (Catalog No. 3000E, Potters Industries, 300 Lindenwood Drive Valleybrooke Corporate Center Malvern, PA 19355-1740), 75–90 μm, and 125–150 μm, respectively, that were randomly distributed in an agar background with scatterer concentrations of 264, 11, and 2 beads/mm³, respectively. The glass beads provided the frequency dependence of backscatter, while powdered graphite was utilized to obtain the requisite tissue-like attenuation coefficient. Both the SOS and the attenuation coefficient of the phantoms were measured using narrowband substitution in our laboratory.^{34, 35} The measured SOS was 1533 m/s and the measured attenuation is shown in Fig. 1 for all the phantoms vs frequency. Each phantom is encased within a rectangular plexiglass container of dimensions 15 cm depth, 15 cm width, and 5 cm thickness.

Figure 1.

Attenuation coefficient measurements over a frequency range from 2 to 10 MHz obtained using a narrowband substitution method. The term “Intp” denotes linearly interpolated data for the 6 MHz center frequency.

The phantoms were scanned using a Siemens S2000 clinical ultrasound system (Siemens Medical Systems, Issaquah, WA, USA) using a 9L4 linear array transducer operated at a 6 MHz center frequency with transmit power of 39%, dynamic range of 90 dB, 40 MHz sampling rate, and a constant external TGC setting with all the potentiometer knobs located in the center. The internal TGC of the system was not disabled. The power level was kept low to avoid saturation of the echo-signals which could lead to clipping (truncation) of the time-domain signals during digitization; adversely impacting the computation of the power spectrum. Each RF data loop collected consists of 15 frames acquired at different locations in the uniform phantom to obtain independent uncorrelated frames. The scanning depth for the phantoms was set to 6 cm with a focus at 3 cm. A ROI was selected around the focus and data within a 2 cm depth over all of the lateral width of the transducer was used to estimate the attenuation coefficient. Data acquisitions were also performed using reference phantoms with SOS of 1500 and 1580 m/s to evaluate the variations in the attenuation estimation when the reference SOS was both higher and lower than the sample SOS. These data acquisitions resulted in a total of 75 (15 for each phantom) independent data acquisitions.

Attenuation estimation methods

The three frequency domain estimation methods evaluated in this paper include a spectral difference method, also known as the RPM, a spectral shift method, i.e., the centroid downshift method, and the hybrid method. The RPM measures the intensity decay of the backscattered RF signal with depth. Under the assumption that the tissue can be modeled as a linear system, the ratio of the power spectrum at two different depths is related to the attenuation of the propagating pulse.

Given two backscattered intensity signals one from the unknown sample, I_s(ω, t), and the second from the reference phantom, I_r(ω, t), with known acoustic properties, the spectral ratio between the reference and the sample phantom is given by

$$\begin{array}{ccc}\hfill \frac{I_s\left(\omega ,t\right)}{I_r\left(\omega ,t\right)}& =& \frac{{\mathrm{BSC}}_s\left(\omega \right)·{\mathrm{e}}^{-4{\alpha }_{\mathrm{s}}\left(\omega \right)z}}{{\mathrm{BSC}}_r\left(\omega \right)·{\mathrm{e}}^{-4{\alpha }_r\left(\omega \right)z}}=\frac{I_s\left(\omega ,z\right)}{I_r\left(\omega ,z\right)}\hfill \\ & =& \mathrm{RB}\left(\omega \right){\mathrm{e}}^{-4\Delta \alpha \left(\omega \right)z},\hfill \end{array}$$ (2)

where BSC_s(ω) and BSC_r(ω) denote the backscatter coefficients of the sample and reference, respectively. RB(ω) represents the ratio of the backscattered signals and Δα(ω) is the difference in attenuation coefficients of the sample and the reference phantom. The echo signal at time t is mapped to the signal at depth z by z = c.t/2, where c is the SOS. The RPM assumes a constant SOS between the reference and the sample phantoms.

The second approach discussed represents a spectral shift method, characterized by estimating the centroid downshift of the power spectrum with depth. Soft tissue has the transfer characteristics of a low pass filter since attenuation increases with frequency, the power spectrum generated from the RF data shifts toward lower frequencies at increased depths.³⁶

The pulse width echo transfer function for a sample with attenuation α and thickness D, and the relationship to the power spectrum P_z( f ) at two different depths z₁ and z₂, where z₂> z₁, is given by Eq. 3:

$${\left|H\left(f\right)\right|}^2=e^{-4\alpha fD}=\frac{p_{z_2}\left(f\right)}{p_{z_1}\left(f\right)}.$$ (3)

Assuming that the backscattered signal has a Gaussian shaped power spectrum with bandwidth BW, frequency at depth z of f_z, and C_z which is a constant related to the initial transmit power, the power is given by Eq. 4 which is then substituted into Eq. 3 to give Eq. 5:

$$P_z\left(f\right)=e^{\frac{-{\left(f-f_z\right)}^2}{B{W}^2}}.$$ (4)

Then

$$f_{z_2}=f_{z_1}-2\alpha ·D·BW.$$ (5)

Equation 5 shows that for a Gaussian shaped power spectrum at depth z₁ which maintains its shape at depth z₂, a shift to a lower frequency of the signal at depth z₂ is observed.

The third method compared in this paper combines the advantages of both the spectral difference and spectral shift methods. The hybrid method initially uses the RPM approach to reduce the impact of system dependent parameters such as diffraction effects by taking the power spectral ratio of the reference to the sample, then a Gaussian filter centered at the transmit center frequency (f_c) of the system is used to filter the normalized power spectrum that also includes BSC variations.²⁷ The hybrid method then utilizes a spectral cross-correlation algorithm, i.e., a spectral shift method to calculate the spectral shifts from the filtered power spectra in order to estimate the attenuation coefficient.³⁷

The center frequency of the Gaussian filtered intensity ratio at depth z is expressed in Eq. 6. Where VAR is the variance of the transmit pulse, α_r and α_s are the attenuation coefficients of the reference and the sample, respectively:

$$f_c\left(z\right)\approx -4VAR\left({\alpha }_s-{\alpha }_r\right).$$ (6)

By differentiating Eq. 6 with respect to depth and under the assumption of linear frequency dependence of the attenuation in soft tissue we can calculate attenuation using a linear regression using Eq. 7:

$${\alpha }_s\left[\mathrm{dB}/\mathrm{cm}/\mathrm{MHz}\right]=-4.383\frac{d{f}_c\left(z\right)}{VAR}+{\alpha }_r.$$ (7)

Since the backscattered signal received contains lower frequencies than the center frequency of the transmit pulse, we set the filter center frequency to the center frequency of the received pulse, to obtain improved results. Since the second step uses a spectral shift method, we decided to use the centroid downshift approach to estimate the shift in the center frequency with depth. Table 2 summarizes the three different attenuation estimation methods being used and Sec. 2D describes the data processing and parameters used in the calculation of the attenuation coefficient.

Table 2.

Summary of the three attenuation estimation methods.

Attenuation slope estimation method	Type	Spectral shift estimation	Need for reference phantom
Reference phantom (RPM)	Spectral difference	–	Yes, Basis of the method
Hybrid (HYB)	Spectral shift	Centroid shift	Yes, Remove system dependencies
Centroid downshift (CEN)	Spectral shift	Centroid shift	No, A reference phantom is not used

Data processing

Both the simulated and experimentally acquired data were processed using MATLAB (MathWorks Inc., Natick, MA, USA). RF data was divided into 8 mm segments along the beam direction and 38 A-lines along the lateral direction, and each block was processed separately with a 70% overlap between blocks. The power spectrum was calculated using a chirp z-transform based Fourier analysis for each block using a 3 mm windowed (Hanning window) segment. The gated segment length was chosen based on the full width half maximum (FWHM) criterion, previously described.²⁷ The gated segment was chosen such that it was small enough to satisfy the stationarity assumption and to provide sufficient spatial resolution for the attenuation estimate, but large enough to generate an accurate and robust power spectrum of the backscattered RF signal. A 50% overlap between the gated segments was used to obtain a stable power spectrum based on the Welch method.³⁸

After computation of the power spectrum, attenuation estimation is performed over the same selected bandwidth for the entire dataset, and spectral signals outside this band with poor signal to noise ratio (SNR) were ignored. The power spectral frequency range was set to lie between 2–9 MHz for the simulated data and 2–8 MHz for the experimental data. The power spectrum in the specified frequency range was then used in the implemented frequency domain estimation methods discussed previously, with the results presented in Sec. 3.

The centroid of the power spectrum ( f_c) is calculated by taking the ratio of the first to the zeroth moment, given by Eq. 8:

$$f_c=\frac{m_1}{m_0}=\frac{{\int }_0^{\infty }f\left|X\left(f\right)\right|df}{{\int }_0^{\infty }\left|X\left(f\right)\right|df},$$ (8)

where m₁ and m₀ are the first and zeroth moments, respectively. f is the frequency and X( f ) represents the Fourier transform of the backscattered ultrasound signal in the time domain.

RESULTS

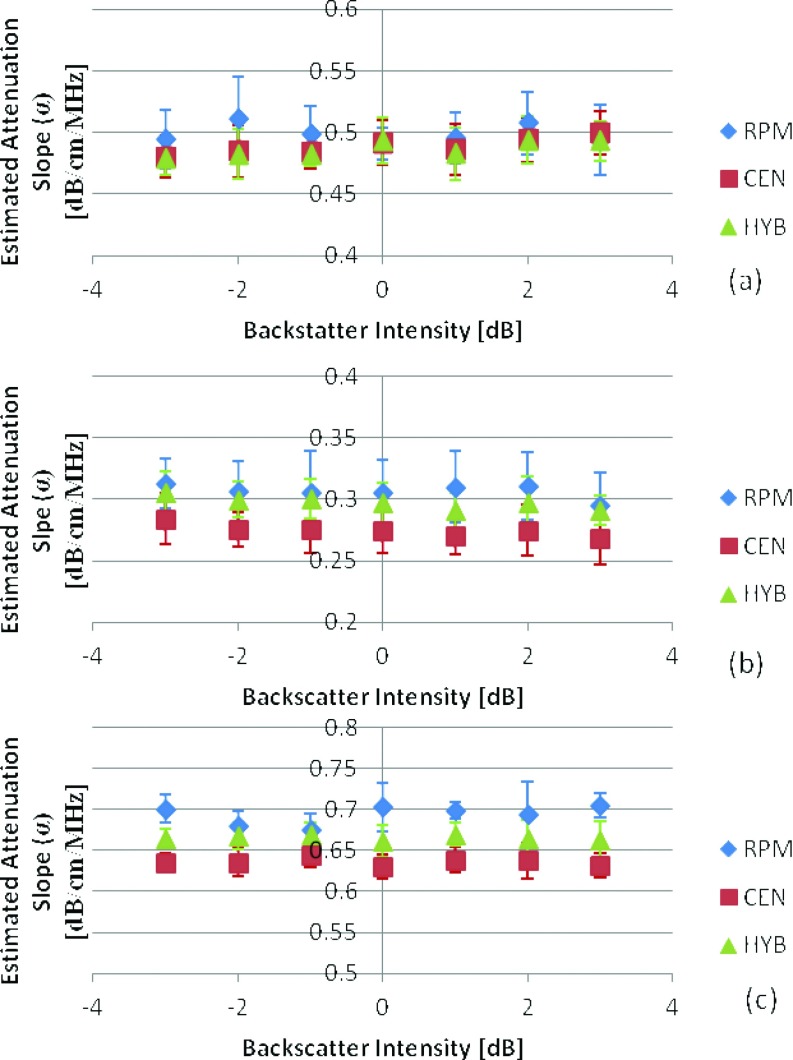
In this paper, we first discuss the impact of variation in the backscatter intensity on attenuation estimation by varying the scatterer number density, while keeping the scatterer diameter the same for the corresponding sample and reference phantoms, respectively. For the first set of numerical phantoms in Group 1 we kept the SOS constant at 1540 m/s and varied the backscatter intensity from −3 to 3dB, for three different attenuation coefficient values (0.3, 0.5, and 0.7 (dB/cm)/MHz). The attenuation coefficient of the reference phantom was 0.5 (dB/cm)/MHz. The results in Fig. 2 show a close estimation of the mean attenuation coefficient for all the three frequency domain estimation techniques with the RPM providing the closest estimate with mean values of 0.49 ± 0.025, 0.306 ± 0.027, and 0.69 ± 0.023 (dB/cm)/MHz, when compared to the actual mean values of 0.5, 0.3, and 0.7 (dB/cm)/MHz, respectively. The hybrid method demonstrates the lowest standard deviation (0.017, 0.018, and 0.015) of the estimated values with respect to both the RPM and centroid downshift methods.

Figure 2.

Attenuation slope estimates for TM phantoms with a SOS of 1540 m/s, with sample attenuation coefficients of (a) 0.5, (b) 0.3, (c) 0.7 (dB/cm)/MHz. In all cases the reference phantom had a 0.5 (dB/cm)/MHz attenuation coefficient, 50 μm scatterer diameter, and 1540 m/s sound speed at 0 dB scatterer intensity. The frequency range is 2–9 MHz. The range of backscatter intensity varies from −3 to 3 dB with respect to the backscatter level of the reference phantom.

For the second set of numerical phantoms in Group 1, we varied the SOS of the sample phantoms verses the reference phantom over the backscatterer intensity range from −3 to 3 dB, when the reference and sample phantoms possessed similar acoustical properties as shown in Fig. 3. Note that in Fig. 3a, all of the methods performed well with low standard deviation over the range of backscatter intensities simulated. Since the centroid downshift method does not depend on a reference phantom, the mean attenuation was estimated accurately over all simulated cases. On the other hand, with the RPM, when the SOS of the sample was lower than that of the reference phantom, as illustrated in Fig. 3b RPM underestimated the attenuation coefficient with a mean value of 0.3 ± 0.028 (dB/cm)/MHz, whereas when the SOS of the sample was higher than that of the reference phantom, as shown in Fig. 3c, the attenuation coefficient was overestimated with a mean value of 0.7 ± 0.025 (dB/cm)/MHz. These results corroborate the previous results reported on attenuation coefficient estimations with SOS variations reported previously.²⁹

Figure 3.

Attenuation coefficient estimates for phantoms with attenuation coefficient of 0.5 dB/cm/MHz, with sample sound speed of (a) 1540, (b)1500, (c) 1580 m/s. In all cases the reference phantom has a 0.5 (dB/cm)/MHz attenuation coefficient, a 25 μm scatterer diameter, 1540 m/s sound speed, and scatterer intensity of 0 dB. The frequency range is 2–9 MHz. The range of backscatter intensity varies from −3 to 3 dB with respect to the backscatter level of the reference phantom.

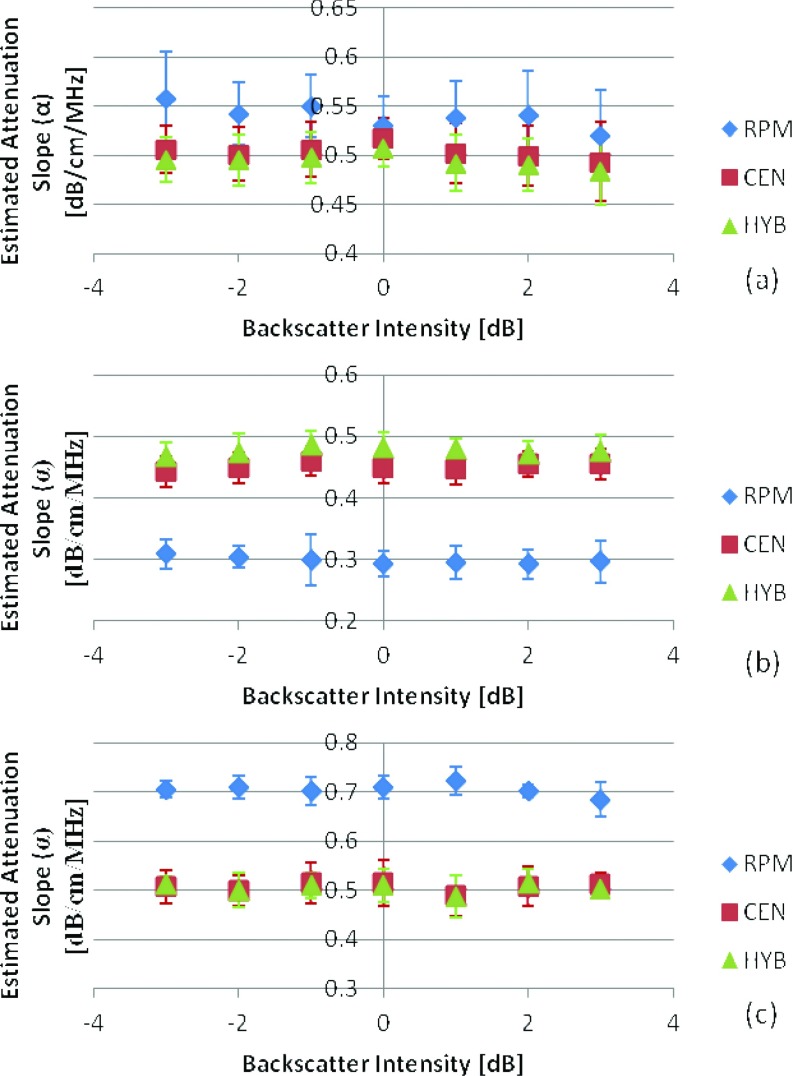
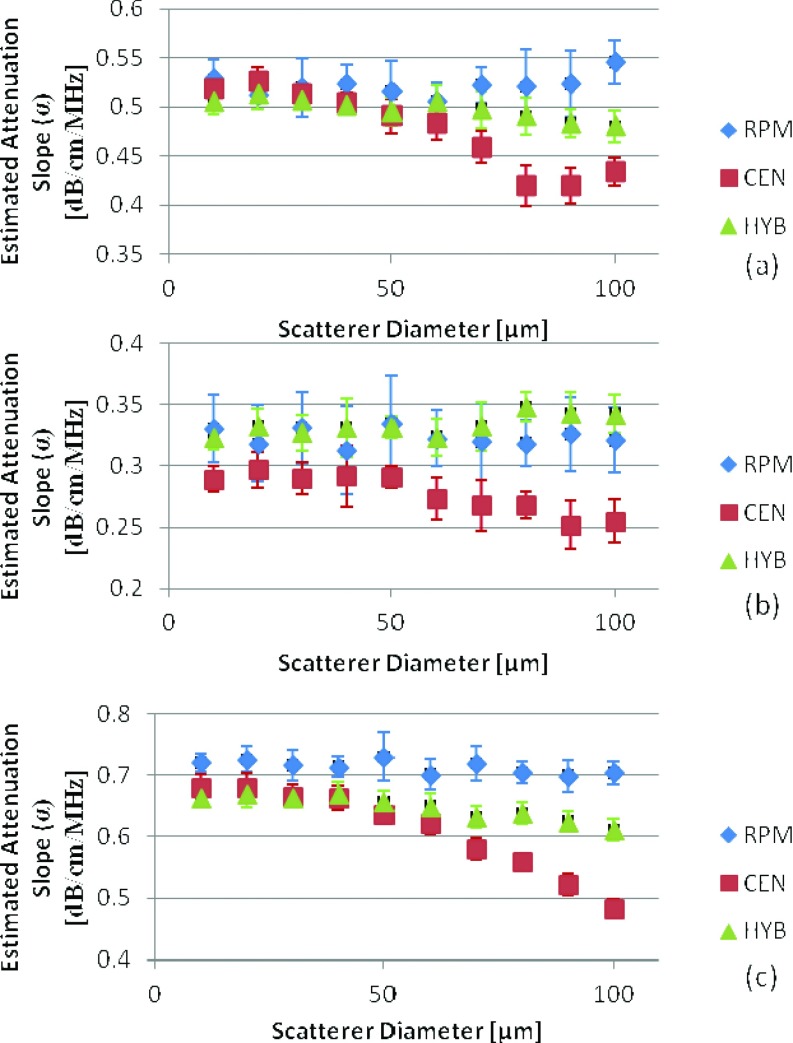
The second part of our study evaluates backscatter intensity variations that also incorporate variations in the frequency dependence of backscatter. This is done by evaluating backscatter from different distributions of scatterer diameters in both numerical and experimental phantoms. For the numerical simulations in Group 2, the investigation included the variation of the scatterer diameter with respect to the backscatter generated from a reference phantom with a fixed scatterer diameter of 50 μm. In the simulation, this is done by varying the frequency dependence of the backscatter coefficient using Faran's scattering theory calculated at the desired sphere diameters.³³ In the first set of phantoms in Group 2, the scatterer diameter in the samples was varied from 10 to 100 μm with a constant diameter size for each simulated phantom while keeping the scattering diameter in the reference phantom at 50 μm. The SOS and attenuation coefficient for the reference phantom were kept at 1540 m/s and 0.5 (dB/cm) /MHz, respectively. Figure 4 shows the estimated attenuation coefficient values when the sample SOS is equal to, higher than, and lower than that of the reference phantom for scatterer diameters in the sample phantoms ranging from 10 to 100 μm. For the RPM an underestimation was observed in Fig. 4b when the sample had a lower SOS than that of the reference and an overestimation is observed in Fig. 4c when the sample had a higher SOS than the reference. This corroborates with results previously reported.²⁹ Both the RPM and hybrid methods were not significantly affected by the variations in the scatterer diameter; however, the standard deviation obtained with the RPM (0.028) is higher than that obtained when compared to the hybrid method (0.017). On the other hand the mean attenuation estimate obtained using centroid downshift method shifts to lower values (increased bias in the estimation) with an increase in the scatterer diameter.

Figure 4.

Attenuation coefficient estimates for phantoms with attenuation coefficient of 0.5 (dB/cm)/MHz, with sample sound speed of (a) 1540, (b) 1500, (c) 1580 m/s. In all cases the reference phantom has a 0.5 (dB/cm)/MHz attenuation coefficient, a 50 μm scatterer diameter, and 1540 m/s sound speed. The frequency range is 2–9 MHz.

Figure 5 shows the results when the attenuation coefficient of the sample was varied with respect to the reference phantom for three different sample attenuation values of 0.5, 0.3, and 0.7 (dB/cm)/MHz, respectively. In all cases the reference phantom's attenuation coefficient was 0.5 (dB/cm)/MHz. The RPM provides the closest mean attenuation slope estimate (0.52 ± 0.026, 0.32 ± 0.03, 0.71 ± 0.023 (dB/cm)/MHz) and the hybrid provides the lowest standard deviation (0.014, 0.015, 0.017) when the acoustic properties of the reference and phantom are matched.

Figure 5.

Attenuation coefficient estimates for phantoms with a SOS of 1540 m/s, with sample attenuation coefficient of (a) 0.5, (b) 0.3, (c) 0.7 (dB/cm)/MHz. In all cases the reference phantom has a 0.5 (dB/cm)/MHz attenuation coefficient, a 50 μm scatterer diameter, and 1540 m/s sound speed. The frequency range is 2–9 MHz.

In order to compare the measured attenuation slope to the estimated results we linearly interpolated the measured data to get an estimate of the attenuation slope at 6 MHz. The values were (0.58, 0.623. 0.72 (dB/cm)/MHz), for the scatterer diameter range of (5–40, 75–90, 125–150 μm), respectively, as shown in Fig. 1.

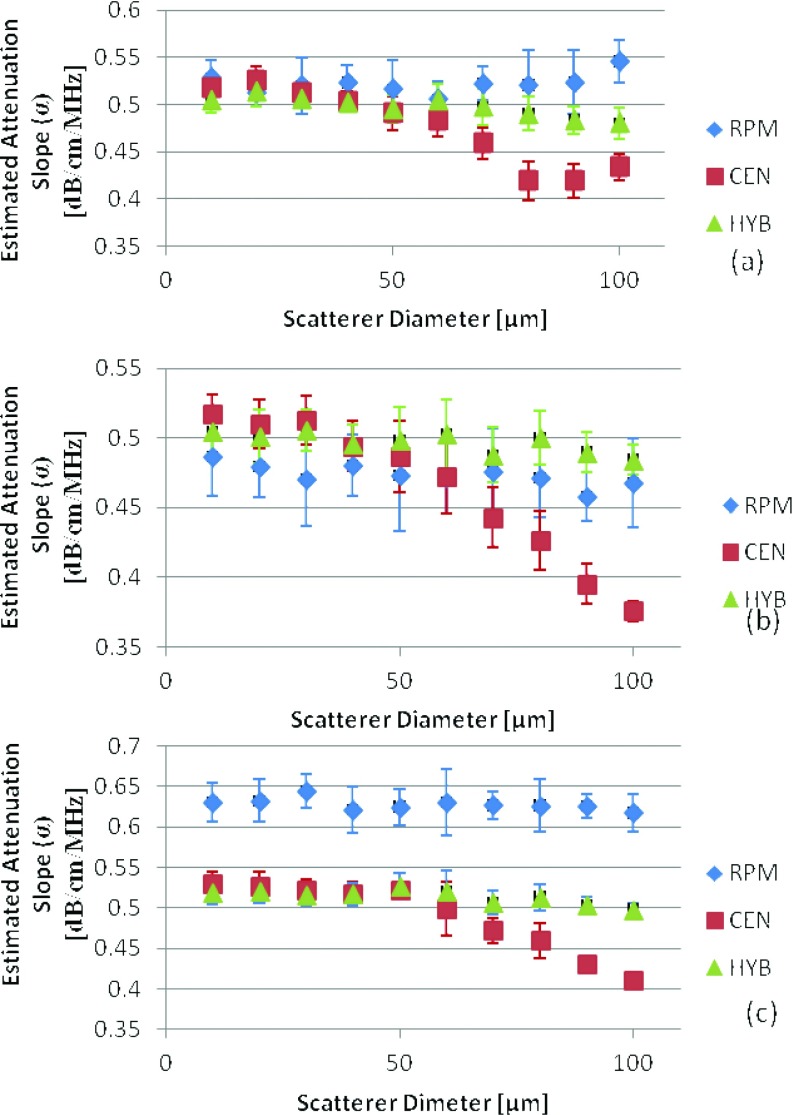
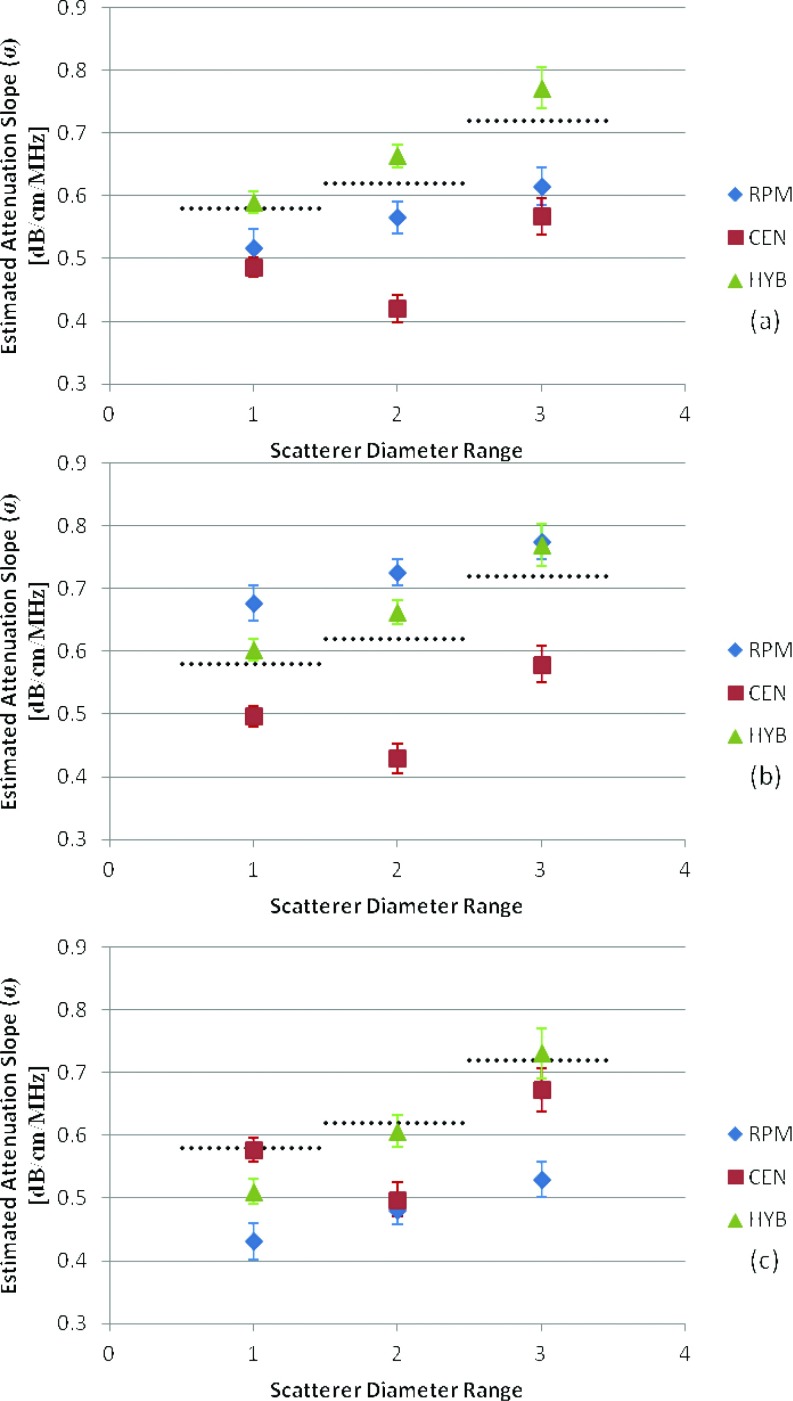
Figure 6 presents the experimental results obtained from the tissue-mimicking phantom where the dotted black dot lines indicate the expected attenuation slope. In Figs. 6b, 6c, the reference phantom method indicates overestimation (0.68 ± 0.028, 0.73 ± 0.021, and 0.78 ± 0.028 (dB/cm)/MHz) and underestimation (0.43 ± 0.029, 0.48 ± 0.023, and 0.53 ± 0.028 (dB/cm)/MHz) errors when the reference phantom had a SOS which is lower than or larger than the sample's SOS, respectively. These results agree with the simulation results reported earlier. In all cases the hybrid method provides the closest results to the actual value of the attenuation coefficient. In the scatterer range of 75–90 μm the centroid downshift method for all cases showed an underestimation similar to the simulated results due to the shift in the power spectrum toward lower frequencies. However, for the phantom with the scatterer range of 125–150 μm the power spectrum was not significantly affected by the scatterer sizes due in part to the low scatterer density per cubic millimeter of 2 beads/mm³ violating the assumption of Rayleigh scattering.

Figure 6.

Experimental attenuation slope estimates for TM phantoms with an attenuation coefficient of 0.58 (dB/cm)/MHz and sound speeds of (a) 1533, (b) 1500, (c) 1580 m/s. Scatterer diameter and attenuation coefficients of the samples are in the range of (1) 5–40, (2) 75–90, and (3) 125–150 μm. The dotted black line represents the actual measured values of the attenuation slope (0.58, 0.62, and 0.72 (dB/cm)/MHz).

DISCUSSION

Quantification of the accuracy and precision of ultrasonic attenuation slope parameter is important for the evaluation of tissue properties. In this paper, we evaluate the contributions of backscatter variations to the three different frequency domain attenuation methods. When the backscatterer intensity was varied by modifying only the scatterer number density for the simulated phantoms, with the rest of the acoustical properties maintained constant, we found no significant difference (p > 0.3) between the estimation performance of the three methods as shown in Figs. 2a, 3a. A single factor analysis of variance (ANOVA) with alpha equal to 0.05 was used for statistical significance. This is expected since the simulation assumes weak scattering using the Born's approximation and the scatterer number density does not significantly impact the estimation process, with no relative shifts in the frequency spectrum expected, since similar scatterer diameters were used in both the sample and the reference phantoms.

Our results in Figs. 2b, 2c indicate that when the SOS between the reference and the sample are similar, the reference phantom approach provides the closest and most accurate estimate of the mean attenuation slope. However, if a higher precision or repeatability is desirable then the hybrid method would be the algorithm to utilize for attenuation slope estimation. The results in Figs. 2b, 2c were statistically significant with p-values lower than 0.008. This aspect is also demonstrated in Fig. 5 where the RPM provides the closest estimate to the expected attenuation coefficient value. On the other hand, when differences between the SOS exist between the sample and the reference, i.e. a sound speed mismatch is present, the reference phantom method collapses since it assumes sound speed similarities between the reference and the sample, as illustrated in Figs. 2b, 2c, 4b, 4c.

In this paper, we also evaluated the impact of varying the frequency dependence of scattering on the accuracy of the attenuation estimation provided by the three methods. Note that changes in the scatterer diameter within the sample did not significantly impact the estimation results obtained using the RPM and the hybrid methods. Under this condition, the centroid downshift method was more sensitive to the variation in the scatterer diameter, especially for larger diameter scatterers. Looking closely at the centroid downshift estimation process which calculates the centroid of the power spectrum, as the power spectrum shifts towards lower frequencies with an increase in the scatterer diameter over the range of frequencies that was selected for the processing, it encounters increased bias. Note that the frequency range was maintained the same to obtain a fair comparison of the three estimation methods. This led to the underestimation with centroid downshift, shown in both Figs. 45. For the centroid downshift approach, this bias in the results can be corrected by choosing a more appropriate frequency range dynamically with the corresponding increase in scatterer diameter. However, this would be eventually limited by the bandwidth of the transducer.

Both the simulation and experimental results show that the hybrid method performs well by estimating the attenuation slope with a high accuracy and even better repeatability (lowest standard deviation or variance along all the independent realizations). The hybrid method appears to be the most robust of the three methods and is not significantly impacted by backscatter or SOS variations. The reference phantom method is significantly impacted by SOS mismatches, while the frequency dependence of backscatter introduces a bias in the centroid downshift results especially for larger scatterer diameters.

These results are important in determining the appropriate method to use when performing an attenuation imaging experiment. For example, if the SOS of the specimen or organ being imaged is already known a priori, a reference phantom with the appropriate acoustical properties would be the best method for determining the attenuation coefficient. On the other hand if the SOS is unknown, the hybrid or centroid downshift methods would be good choices. In most situations under clinical imaging conditions, we do not have a priori information on the SOS or backscatter variations or information on the frequency dependence of the backscatter, leading to the easy choice of using the hybrid method.

CONCLUSION

In this paper we demonstrated that there was no significant impact on the estimation of the attenuation coefficient with the three frequency domain methods, with an increase in the scatterer number density in the simulated numerical phantom. We also showed that variations in the scatterer diameters resulting in different frequency dependence of backscatter did not significantly affect the estimation process for the RPM and the hybrid approaches. The RPM provides accurate results when the SOS is matched between the sample and the reference phantom. Therefore, RPM should be avoided when estimating the attenuation coefficient for tissues with different or unknown SOS properties. Our results show that the centroid method is affected by the frequency band of the power spectrum utilized in the computation, since it affects the location of the centroid and can provide erroneous or biased attenuation estimates. The hybrid method demonstrated the least dependence on the variation in acoustic properties and provides accurate results even with variations between the reference and the sample acoustical properties. The hybrid method also provided the lowest standard deviation or variance over all estimation approaches demonstrating its repeatability or precision.