A comparison of five standard methods for evaluating image intensity uniformity in partially parallel imaging MRI

Abstract

Purpose: To investigate the utility of five different standard measurement methods for determining image uniformity for partially parallel imaging (PPI) acquisitions in terms of consistency across a variety of pulse sequences and reconstruction strategies.

Methods: Images were produced with a phantom using a 12-channel head matrix coil in a 3T MRI system (TIM TRIO, Siemens Medical Solutions, Erlangen, Germany). Images produced using echo-planar, fast spin echo, gradient echo, and balanced steady state free precession pulse sequences were evaluated. Two different PPI reconstruction methods were investigated, generalized autocalibrating partially parallel acquisition algorithm (GRAPPA) and modified sensitivity-encoding (mSENSE) with acceleration factors (R) of 2, 3, and 4. Additionally images were acquired with conventional, two-dimensional Fourier imaging methods (R = 1). Five measurement methods of uniformity, recommended by the American College of Radiology (ACR) and the National Electrical Manufacturers Association (NEMA) were considered. The methods investigated were (1) an ACR method and a (2) NEMA method for calculating the peak deviation nonuniformity, (3) a modification of a NEMA method used to produce a gray scale uniformity map, (4) determining the normalized absolute average deviation uniformity, and (5) a NEMA method that focused on 17 areas of the image to measure uniformity. Changes in uniformity as a function of reconstruction method at the same R-value were also investigated. Two-way analysis of variance (ANOVA) was used to determine whether R-value or reconstruction method had a greater influence on signal intensity uniformity measurements for partially parallel MRI.

Results: Two of the methods studied had consistently negative slopes when signal intensity uniformity was plotted against R-value. The results obtained comparing mSENSE against GRAPPA found no consistent difference between GRAPPA and mSENSE with regard to signal intensity uniformity. The results of the two-way ANOVA analysis suggest that R-value and pulse sequence type produce the largest influences on uniformity and PPI reconstruction method had relatively little effect.

Conclusions: Two of the methods of measuring signal intensity uniformity, described by the (NEMA) MRI standards, consistently indicated a decrease in uniformity with an increase in R-value. Other methods investigated did not demonstrate consistent results for evaluating signal uniformity in MR images obtained by partially parallel methods. However, because the spatial distribution of noise affects uniformity, it is recommended that additional uniformity quality metrics be investigated for partially parallel MR images.

BACKGROUND

Partially parallel imaging (PPI) involves the use of phased array coils and the acquisition of fewer phase encoding (PE) steps in order to reduce scan time.^{1, 2} This reduction in the number of PE steps is often called the reduction factor and denoted as R.¹ The R-value indicates both that the number of PE steps is reduced by the factor 1/R and also that the image acquisition time is reduced by the factor 1/R. In conventional MRI, reducing the number of PE steps would result in aliasing artifact. In the case of PPI, the reconstruction methods utilize calibration scans and/or auto-calibration lines of data to generate signal reception profiles for each coil element, which are then used to unfold or interpolate PPI data in order to avoid aliasing artifacts.

Analysis of signal uniformity in MRI was originally presented in a context that was already familiar to imaging scientists working in nuclear medicine.³ There, the primary source of image nonuniformities was the spatially dependent sensitivity of photomultiplier tubes in Anger camera systems. In conventional MRI, the most significant influence on image intensity uniformity has been the geometry and sensitivity of radio frequency coil configurations.⁴ Additional sources of MR image intensity nonuniformities include the homogeneity of the excitation RF coil (particularly at higher fields),⁵ reconstruction irregularities such as truncation artifacts⁶ and image signal aliasing,⁷ electromagnetic properties of tissues that cause susceptibility⁸ and dielectric effects,⁹ image uniformity corrections and contamination by external noise.

In PPI, aliasing can be substantial because image domain reconstruction algorithms tend to be built with the assumption that signal aliasing is due exclusively to the partially parallel data acquisition strategy. Therefore, it is important to avoid acquiring data from body parts that are larger than the image field of view. An additional important source of image nonuniformities inherent to PPI is spatially heterogeneous noise propagation, which occurs because the encoding functions used to generate parallel images are not orthogonal.¹⁰ In partially parallel images this artifact presents as noisy patchy regions in the image being studied. Thus the noise in partially parallel images is increased beyond the noise increase that can be attributed solely to reducing the number of data points acquired during the image acceleration process. The effect of noise propagation is usually described by the spatially dependent g-factor,^{1, 11} which often is used as a figure of merit for evaluating parallel imaging receiver coils.^{12, 13, 14, 15}

However, the purpose of evaluating image uniformity extends beyond providing a metric of image quality, often being used to provide a basis for undertaking uniformity corrections. Many methods have been proposed to compensate for the sensitivity irregularities in phased array and other coil configurations. Belaroussi et al. reviewed over 40 methods of nonuniformity correction.¹⁶ More recently a number of groups have proposed regularization methods that can potentially be used to reduce the effects of noise propagation in parallel MRI. Regularization algorithms using the Tikhonov method,¹⁷ wavelet basis sets,¹⁸ and an augmented Lagrangian formalism,¹⁹ have been proposed specifically to improve partially parallel MR images. These correction methods are touted to improve both image intensity uniformity and overall image signal-to-noise ratio (SNR) through the compensation of the noise propagation characteristics inherent to parallel imaging.

By their nature PPI MRI protocols¹¹ employ image processing methods, which lead to image quality characteristics that differ fundamentally from conventional MR images. This change in image processing methodology has led to a re-evaluation of how SNR should be measured when PPI is implemented.^{22, 23} However, in the current literature the only investigations of the decrease in image intensity uniformity with parallel imaging have been reported for specific cases.^{14, 20} Uniformity has been formally investigated as a metric for image quality assessment for PPI spine protocols.²⁰ Uniformity has also been calculated using a method requiring raw data in a breast coil study, which did not compare effects of PPI on uniformity but the uniformity differences from three coils.¹⁴ In general, an accurate and simple method for determining image intensity uniformity in PPI has not yet been validated.²¹

The current study examines five standard methods of uniformity measurement to evaluate their adequacy in the context of parallel imaging. The purpose of this study is to determine if any of these standard methods will allow for protocol comparison when PPI is involved so that it could be used as an extension to other routine quality control metrics. The strategy of measuring uniformity changes with R was chosen since both noise propagation and aliasing get worse with increasing R values. It seems reasonable that a necessary requirement for an appropriate uniformity metric in PPI is that it decreases with increasing R values.

MATERIALS AND METHODS

Image acquisition

Images were obtained from a spherical phantom, 17.8 cm in diameter (about the average size of a human head). The phantom was produced by filling a #3 soccer ball with a double bladder (Balden Series Z Soccer Ball PN S130Z-018) with an aqueous solution. The solution consisted of 5.45 g NaCl (99.99% pure) 5.29 ml of Magnevist per 1 l distilled water and had a total volume of 2415 ml. This phantom was used in and described in a previous study²³ and developed by AAPM Task Group #118 on “Parallel Imaging in MRI: Technology, Applications, and Quality Control.” Images were acquired using a 12-channel matrix head coil (Siemens Medical Systems, Erlangen, Germany) on a 3T MRI system (TIM Trio, Software Version VB15A, Siemens Medical Systems, Erlangen, Germany). Images were acquired using echo-planar imaging (EPI), Fast Low Angle SHot (FLASH), balanced steady state free precession (Tru-FISP), and turbo spin echo (TSE) pulse sequences.²⁴ The acquisition parameters for each of the pulse sequences are listed in Table 1.

Table 1.

This table lists the imaging protocols that were used to acquire the images used for the SNR analysis in this study.

Sequence	TR (ms)	TE (ms)	Slice thickness (mm)	BW (Hz/pixel)	Matrix	FOV (mm × mm)	Slice gap (mm)	NEX	ETL
EPI	1840	187	5	752	256 × 256 × 5	220 × 220	1	1	256
FLASH	175	4	5	240	256 × 256 × 5	220 × 220	1	1	N/A
Tru-FISP	6.88	3.44	5	244	256 × 256 × 5	220 × 220	1	1	N/A
TSE	1200	76	5	122	256 × 256 × 5	220 × 220	1	1	16

Note: ETL = echo train length; BW = bandwidth; TR = repetition time; TE = echo time; FOV = field of view (in this case transaxial); and NEX = number of excitations.

The parameters in Table 1 were kept constant throughout image acquisition except for the case of EPI. The EPI sequence does not benefit from PPI protocols unless TE is minimized. In addition to a set of EPI protocols where TR and TE times were held constant, a second set of EPI images was acquired. In this second set of EPI protocols the TE and TR times were minimized at each R-value as shown in Table 2.

Table 2.

List of minimum TE and TR values for the secondary EPI protocol.

R	TE (ms)	TR (ms)
2	98	956
3	69	666
4	54	515

Each pulse sequence was used to acquire images of the phantom first without PPI implementation and then imaging was repeated using the PPI methods, modified sensitivity-encoding (mSENSE) and generalized autocalibrating partially parallel acquisition algorithm (GRAPPA).^{1, 2} Conventional images and PPI images with R values of 2, 3, and 4 were acquired in the axial orientation using two series, with the PE direction both anterior–posterior (AP) and in the right–left (RL) orientation in order to evaluate the differences in noise propagation artifacts.²⁵ With each slice being an image, this procedure resulted in 70 images per pulse sequence with a total of 350 images analyzed for the current study. Image analysis was automated by an algorithm developed in-house using a commercial technical computing environment for data visualization and analysis (MATLAB version 7.2, The Mathworks, Inc, Natick, MA). The measurements performed on the images included the five different standard uniformity measurements, which are described below.

Uniformity measurements

The standard methods of MR image uniformity analysis, published by National Electrical Manufacturers Association (NEMA) and American College of Radiology (ACR), were used.^{26, 27, 28}

NEMA method 1, Peak deviation nonuniformity: UN1

In this method the maximum (S_max) and minimum (S_min) pixel values within a region of interest (ROI) that encompasses 75% of the volume of the phantom were measured and used to calculate the peak deviation nonuniformity (N),

$$N=100·\frac{S_{\max }-S_{\min }}{S_{\max }+S_{\min }}.$$ (1)

The peak deviation nonuniformity measure is sensitive to the SNR of an image. As SNR decreases, S_max and S_min diverge, lowering computed peak deviation uniformity.³

In order to make results from Eq. 1 comparable to other methods it was adjusted and replicates the uniformity equation provided by the ACR (Ref. ²⁶) thus following the percent image uniformity (PIU) definition [Eq. 2]:

$$\mathrm{UN}1=100·\left(1-\frac{S_{\max }-S_{\min }}{S_{\max }+S_{\min }}\right).$$ (2)

NEMA method 2, Gray scale uniformity map: UN2

The second NEMA method was utilized as a precursor to a method that was developed to obtain a new value for uniformity. The original NEMA method creates a gray scale uniformity map using the following procedure.²⁷

A ROI at the center of the image is selected that includes 75% of the signal producing volume. The mean value of this volume is S, each pixel value has an intensity value I, and F is a fraction with a fixed value of 0.1 that specifies the width of a histogram bin where

$$S·(1-F)<I<S·(1+F).$$ (3)

Pixel values of I that fall within the criteria of Eq. 3 are assigned an initial gray level value. Pixels that fall within the range

$$S·(1+F)<I<S·(1+2·F)$$ (4)

are assigned the next brighter gray level value. This process is continued, with each gray level including pixels for which I is

$$\begin{array}{c}\hfill S·(1+n·F)<I<S·(1+(n+1)·F),n=1,2,3...\end{array}$$ (5)

until all pixels that are brighter than S have been assigned a gray level. Pixels in the highest bin are then assigned the highest (white) intensity. Similarly, pixels with intensities less than S × (1 − F) are assigned gray level values, with the lowest intensity bin being assigned to black. Gray level bins in this case are defined by

$$\begin{array}{c}\hfill S·(1-(n+1)·F)<I<S·(1-n·F),n=1,2,3...\end{array}$$ (6)

until each pixel darker than S has been assigned a gray level value.

Alternatively, five gray level representation groups can be created with the following ranges for I:

• A.I ≤ Sx0.8,
• B.Sx0.8 < I ≤ Sx0.9,
• C.Sx0.9 < I ≤ Sx1.1,
• D.Sx1.1 < I ≤ Sx1.2, and
• E.Sx1.2 ≤ I.

In the NEMA standard²⁷ either of these methods utilizes the assigned gray level values to produce an image which gives a contour map of uniformity. This map however does not give a quantitative value to compare against other methods of uniformity or for protocol comparison. To remedy this, an extension of this method was developed to obtain a single value for percent image uniformity.

First, the pixels were binned into five gray level values as described in the alternative method and shown in groups A–E above. These groups were then combined to produce three separate groups 0–2:

• Group 0 is the total number of pixels from group C.

• Group 1 is the total number of pixels from groups B and D.

• Group 2 is the total number of pixels from groups A and E.

Thus three groups containing pixels within 10% of the mean, those between 10% and 20% of the mean and those greater than or less than 20% of the mean were created. The number of pixels in each of these groups was then used to compute a PIU as follows, with group 0 intentionally being omitted:

$$\mathrm{UN}2=100(1-(0.5·\mathrm{group}1+\mathrm{group}2\left)\right).$$ (7)

ACR method: UACR

A ROI that encompasses about 0.15% of the phantom volume is used to measure the areas of greatest intensity and lowest intensity with the average values designated as ACR_max and ACR_min, which are used to compute the PIU from the following formula:

$$\mathrm{UACR}=100\left\{1-\frac{({\mathrm{ACR}}_{\max }-{\mathrm{ACR}}_{\min })}{({\mathrm{ACR}}_{\max }+{\mathrm{ACR}}_{\min })}\right\}.$$ (8)

A larger UACR value indicates a more uniform image.²⁶

Normalized absolute average deviation: UNAAD

The average pixel $\left(\overline{Y}\right)$ intensity within a ROI of 75% of the phantom volume was found and then UNAAD calculated using:²⁷

$$\mathrm{UNAAD}=100\left(1-\frac{1}{N·\overline{Y}}\sum _{i=1}^N\left|Y_i-\overline{Y}\right|\right),$$ (9)

where Y_i is the individual pixel value and N is the total number of pixels within the ROI used for the measure of mean intensity. A larger UNAAD indicates a more uniform image.

NEMA method 3, Tic-Tac-Toe method: UTTT

A circular ROI covering 75% of the phantom volume was used. Then 17 ROIs were placed within this region, nine were evenly spaced in a checkerboard fashion in the center of the image, four at the “corners,” and four in the middle edge of each side. All of the ROIs were 7 × 7 pixels squared. An example of ROI placement is depicted in Fig. 1. The mean of each ROI was found and used to calculate the uniformity using the equation below where S_n is the mean of each small ROI and S18 is the large 75% ROI:²⁸

$$\mathrm{UTTT}=100·\left(1-\frac{\sum _{n=1}^{17}\frac{\left|S_n-S_{18}\right|}{\left|S_n+S_{18}\right|}}{17}\right).$$ (10)

Figure 1.

This figure depicts the placement of ROIs in the UTTT method. Each white square is a 7 × 7 pixel square and the white circle indicates the 75% central ROI used for the overall mean. The scale of this image is not necessarily accurate in terms of pixel numbers. ROI numbers 2, 3, 15, and 16 indicated the “corners” of the circle.

Statistical analysis

All statistical analyses were completed using a biostatistics, curve fitting, and graphing program (Prism 5, Graph Pad Software, Inc, La Jolla, CA). Linear regressions were used to find the average slope of the individual uniformity tests for measured uniformity as a function of R-value. Linear regressions were performed for each pulse sequence and at each reconstruction method. Additionally, the differences in signal intensity uniformity measured for the two methods of reconstruction, GRAPPA and mSENSE with the same R-value and pulse sequence, were investigated.

Three, two-way analysis of variance (ANOVA) were performed to determine (1) the relative effects that R-value and reconstruction method had on PIU values, (2) the effects R-value and phase encode direction (PE) had on PIU values, and (3) the effects of R-value and pulse sequence on PIU value. Percent decrease in uniformity as a function of the increase in R-value for each pulse sequence and reconstruction method was also calculated.

RESULTS

When PPI methods are implemented aliasing as well as noise propagation artifacts are often apparent especially in the case of the image-based reconstruction methods.¹¹ The appearance of this artifact as shown in Fig. 2a increases with R-value, and is also more noticeable in the mSENSE-reconstructed images compared to GRAPPA-reconstructed images in Fig. 2b. Based on this observation it is expected that for most of the pulse sequences the slope from the linear fit of signal intensity uniformity versus R-value should be negative, indicating a decrease in uniformity with increasing R-value. The exception to this rule would be the EPI sequence with minimum TR and TE time for which a positive slope would be possible due to a decrease in susceptibility artifact²⁹ and subsequent increase in uniformity.

Figure 2.

Displayed in (a), noise propagation artifact is evident in this image taken with a TRUFisp pulse sequence using mSENSE reconstruction with an R-value of 4. (b) Images produced by a FLASH pulse sequence demonstrate noise propagation for mSENSE and GRAPPA reconstruction at R values of 2, 3, and 4. Noise propagation artifact increases with increasing R-value and is more visible in mSENSE than in GRAPPA images.

Figures 34567 respectively, display the UN1, UN2, UACR, UNAAD, and UTTT measurement methods including each pulse sequence and each PPI method acquired. The slopes obtained by linear regression from the methods UN1 and UN2 were all negative, except in the case of the EPI sequence used with minimum TR and TE. Method UNAAD had positive slopes in the case of TSE both with GRAPPA and mSENSE reconstruction. Also the slope was positive with FLASH and mSENSE reconstruction. Method UACR had positive slopes with sequence EPI with GRAPPA reconstruction with TE and TR held constant. TRUFisp with mSENSE reconstruction also had a positive slope and FLASH with mSENSE reconstruction also had a positive slope. The UTTT results were positive at EPI GRAPPA with TE and TR held constant and at TSE with both GRAPPA and mSENSE reconstruction.

Figure 3.

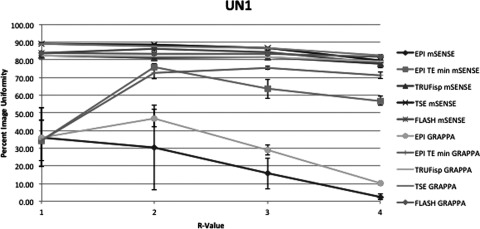
This figure displays the UN1 uniformity measurement method of each pulse sequence and PPI method acquired. The x-axis indicates R-value. At R = 1 there was no parallel imaging implemented. The y-axis indicates PIU where 100 is a perfectly uniform image, i.e., all pixels have the same value.

Figure 4.

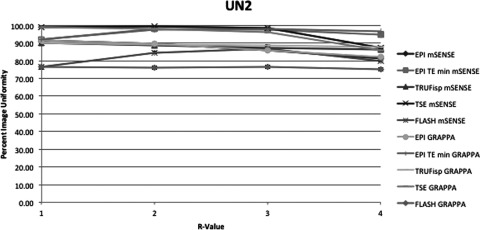
This figure displays the UN2 uniformity measurement method of each pulse sequence and PPI method acquired. The x-axis indicates R-value. At R = 1 there was no parallel imaging implemented. The y-axis indicates PIU where 100 is a perfectly uniform image, i.e., all pixels have the same value.

Figure 5.

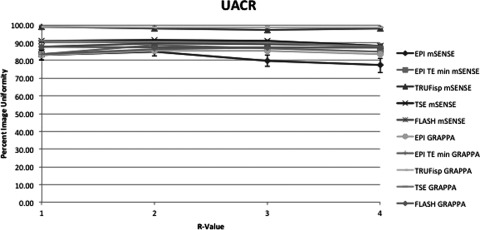
This figure displays the UACR uniformity measurement method of each pulse sequence and PPI method acquired. The x-axis indicates R-value. At R = 1 there was no parallel imaging implemented. The y-axis indicates PIU where 100 is a perfectly uniform image, i.e., all pixels have the same value.

Figure 6.

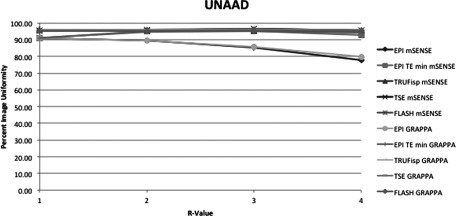
This figure displays the UNAAD uniformity measurement method of each pulse sequence and PPI method acquired. The x-axis indicates R-value. At R = 1 there was no parallel imaging implemented. The y-axis indicates PIU where 100 is a perfectly uniform image, i.e., all pixels have the same value.

Figure 7.

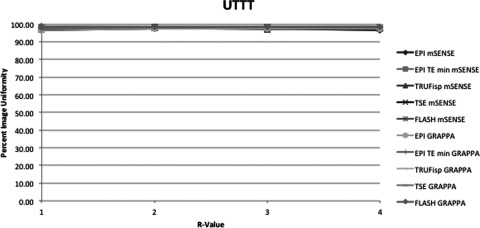
This figure displays the UTTT uniformity measurement method of each pulse sequence and PPI method acquired. The x-axis indicates R-value. At R = 1 there was no parallel imaging implemented. The y-axis indicates PIU where 100 is a perfectly uniform image, i.e., all pixels have the same value.

Average slopes and standard deviations across all pulse sequences and reconstruction methods were calculated with the exclusion of EPI with minimum TR and TE. Of the two methods with all negative slopes UN1 and UN2, UN1 had on average a more negative slope at −4.00 ± 4.2 across all sequences and reconstruction methods. UN2 had an average slope of −1.03 ± 1.4. Additionally UNAAD had an average slope of −1.02 ± 1.8, UACR had an average slope of −0.5 ± 0.82, and UTTT had an average slope of 0.004 ± 0.2. The differences between uniformity with PPI method GRAPPA and the equivalent mSENSE protocol and R-value were also compared. For each pulse sequence measured there were three R values and two PE directions resulting in six comparable mSENSE and GRAPPA values per pulse sequence and uniformity measurement method. To compare the GRAPPA and mSENSE values the GRAPPA uniformity value was subtracted from the mSENSE uniformity value. Table 3 displays the number of times GRAPPA uniformity was greater than mSENSE uniformity. The slopes between equivalent GRAPPA and mSENSE protocols were also compared. The UN1 method was the only method where mSENSE had a more negative slope than GRAPPA. The average mSENSE slope was 1.12 units less than the average GRAPPA slope when the UN1 method was employed with a standard deviation of ±0.6. In the case of the TSE sequence each method of uniformity measurement with the exception of UN1 indicated that GRAPPA images had a more negative slope than mSENSE images. Additionally when the FLASH sequence was used GRAPPA slopes were more negative than mSENSE slopes using all uniformity metrics with the exception of UN1 and UTTT. All other protocols with the exception of TRUFisp with UACR method employed indicated that GRAPPA had a more negative slope than mSENSE. As expected a visual inspection of the images demonstrated more noise propagation with increasing R-value as well as increased residual aliasing. These problems also were more apparent in mSENSE reconstructions than GRAPPA reconstructions.

Table 3.

This table displays the number of measurements that indicated GRAPPA had a higher uniformity than mSENSE with the same R-value and PE direction. The left column indicates the measurement method used and the top row indicates the pulse sequence used. EPI min indicates an EPI sequence where TR and TE were minimized with changes in R-value. The total number of measurements was 6 for each sequence and 30 overall, thus 30 in the total column is the optimal number.

	Total	EPI	EPI min	TRUFisp	TSE	FLASH
UN1	20	6	4	5	3	2
UN2	17	5	4	5	2	1
UACR	11	6	3	0	2	0
UNAAD	18	6	4	5	3	0
UTTT	24	6	5	6	3	4

Three two-way ANOVA tests were performed on each of the five uniformity measurement methods with P-value <0.05 indicating significance. These tests determined how much effect R-value and reconstruction method had on image intensity uniformity, how much effect R-value and phase encode direction had on uniformity, and how much effect R-value and pulse sequence had on uniformity. EPI results with minimum TE and TR were excluded from two-way ANOVA analysis because the TR and TE were different at each R-value and thus a two-way ANOVA analysis would not be appropriate. The results of all the two-ANOVA tests are displayed in Table 4.

Table 4.

This displays the results from all two-way ANOVA tests performed. Three tests were performed on each measurement method and the percent of variation (% of variation) accounted for by the associated variable as well as the P values are displayed. The associated variables studied include: acceleration factor (R-value), reconstruction method (recon), phase encode direction (PE-direction), and the pulse sequence used (pulse sequence).

	Two-way ANOVA results
	R-value and recon method				R-value and PE-direction				R-value and pulse sequence
	R-value		Recon		R-value		PE-direction		R-value		Pulse sequence
Uniformity method	% of variation	P-value	% of variation	P-value	% of variation	P-value	% of variation	P-value	% of variation	P-value	% of variation	P-value
UN1	88	0.0104	8.93	0.06	91.13	0.0216	3.55	0.2515	2.32	0.0796	95.47	<0.0001
UN2	99.11	0.0013	0.05	0.6927	99.64	<0.0001	0.27	0.0539	5.19	0.1963	86.71	<0.0001
UACR	89.02	0.0325	4.01	0.2803	60.75	0.3561	1.06	0.7913	4.01	0.1049	91.62	<0.0001
UNAAD	96.18	0.0112	0.29	0.6559	99.18	<0.0001	0.7	0.0253	7.03	0.2414	80.37	0.0003
UTTT	6.21	0.8532	69.62	0.0605	12.66	0.5495	72.53	0.0313	0.61	0.9363	85.79	0.0003

The results for the two-way ANOVA which involved pulse sequence and R-value were the same for each method of uniformity measurement method. Each method indicated that pulse sequence type significantly affected uniformity (P-value ≤0.0003) with an average effect on variance of 87.92% and a standard deviation of ±5.8%. For reconstruction method and R-value the two-way ANOVA indicated that the effect of reconstruction method was not significant for all of the measurement methods (P values > 0.05), however with the UTTT method it indicated that reconstruction method was responsible for 69.6% of variance. The R-value was found to be significant in all methods of uniformity measurement (P-value < 0.05) except for UTTT where it was responsible for 6.21% of the variance (P-value = 0.85). The two-way ANOVA for phase encode direction and R-value indicated that phase encode was significant in UTTT (P-value = 0.0313) and UNAAD (P-value = 0.0253) tests where it was responsible for 72.53% and 0.7% of variance, respectively. R-value was shown to be significant for methods UN1 (P-value = 0.0216), UN2 (P-value < 0.0001), and UNAAD (P-value <0.0001), with an average variance responsibility of 96.65%. In the case of UACR and UTTT the two-way ANOVA indicated that R-value was not significant with UACR reporting R-value to be responsible for 60.75% (P-value = 0.3561) of variance and UTTT for 12.66% (P-value = 0.5495).

DISCUSSION

The results obtained from this study demonstrated how various methods of uniformity measurement in MRI reflect well-defined uniformity changes in partially parallel MR images. The known changes in image intensity uniformity due to increasing acceleration value, R, were used to evaluate the appropriateness of each metric. In general, those measurement methods that only take into consideration portions of the image, offer less robust and less accurate indications of the true image intensity uniformity. The UN2 method overall was found to be the most consistent metric for describing image uniformity based on the principle that uniformity should decrease with increasing R-value.

All of the investigated methods showed that uniformity increased with increasing R-value in an EPI sequence where TE and TR were minimized at each R interval. This was an expected result since EPI images obtained with PPI methods at minimum TE values have been shown to have better image uniformities.²⁹ The decrease in TE, which PPI allows in EPI sequences, produces an increase SNR (Ref. ²²) and reduces the variability of signal intensity as a function of position that is due to the nonuniform signal intensity profiles obtained from phase array coil elements.

For non-EPI imaging, PPI uniformity should decrease with increasing R-value and a metric that accurately measures uniformity in the case of PPI MRI should decrease with an increase in R-value. The results of this investigation indicated that only two of the measurement methods studied consistently resulted in a decrease in uniformity with increasing R-value. UN1 and UN2 both had negative slopes in every case with the average of the UN1 method being more negative than that of UN2 in every case. When the slopes were averaged over each pulse sequence each metric, with the exception of UACR, resulted in a negative slope. UACR had an average slope of 0.004 and standard deviation of 0.18 so was within one standard deviation of being negative. These results suggest that each metric offers some reasonable insight into the degree of uniformity associated with PPI methods in MRI. However, the UN1 and UN2 methods would likely be the most useful because they consistently offered negative slopes.

It should be considered as well that none of the methods studied failed to have negative slopes in every case. Additionally the UTTT method detected less uniformity in mSENSE than GRAPPA images more often than any other method. The UNAAD also detected less uniformity in mSENSE images compared to GRAPPA more often than the UN2 method. Thus each of the methods of uniformity studied offers some perspective into the effect of PPI on image uniformity. The UACR method gives an indication of the range of pixel intensities, but does not investigate pixels outside the minimal and maximal range. The UNAAD method attempts to measure nonuniformity incorporating all pixels while normalizing for signal intensity. This normalization process likely makes it less sensitive to images with high signal intensities. The UTTT method gives an indication of uniformity in defined regions of an image but leaves out many pixels and regions which could contain artifacts or noise that add or subtract to image uniformity.

The differences in UN1 and UN2 should be closely considered. Of the five uniformity measurement methods studied UN1 has the smallest sample size, using only two data points from the entire MRI image in order to calculate uniformity, which makes it more susceptible to random errors in the image and does not give a full picture of image uniformity since, for example, in the case of a 512 × 512 image containing a circular phantom that spans 400 pixels only 0.0016% of the information is used to quantify uniformity. The method UN2, on the other hand, uses information from each pixel in the image, increasing its power since 100% of the data provided from the signal in the volume imaged is utilized. One possible advantage to the UN1 method is that it is more sensitive to nonuniformities. This sensitivity can be observed when comparing Figs. 34567, which clearly show that the UN1 data have the most dramatic drop off in uniformity with increasing R-value and also produce the most negative slopes on average for each pulse sequence. One could conceive that the calculation of UN2 could be modified by changing the weighting of the pixel categories, the number of categories used, or the amount of deviation from the mean to place pixels in each category. The situations for which these modifications would be beneficial have not yet been investigated.

The two-way ANOVA results indicated that the R-value has the greatest influence on changes in uniformity within a sequence. Additionally the type of sequence used affected uniformity even more dramatically than R-value and this was the case with all uniformity metrics. Also, the two-way ANOVA analysis of the effect of reconstruction method indicated that there was little effect on uniformity due to the method chosen or at least it was not comparable to the effect that R-value had on uniformity.

The current study was limited by the fact that all the measurements were taken on a single scanner, using a particular RF coil and a unique phantom and software release. It must be emphasized that the results presented here are applicable only to this specific environment. Uniformity results are likely to vary from vendor to vendor, software release to software release, and under different reconstruction methods not just limited to PPI. Further investigations need to be undertaken to determine whether the results, reported here, hold for other models of MRI systems, using different RF coil geometries and for phantoms that simulate other body parts. In addition, the FOV values included the whole phantom so that additional aliasing in the images was minimized.

Image intensity uniformity has been investigated previously as a metric for evaluating the quality of image segmentation and thresholding algorithms.^{30, 31, 32} In these formulations the uniformity, U_α, of a feature over a region of area α is defined as being inversely proportional to the variance of the values of the feature being evaluated, at every pixel belonging to that region. In the segmentation problem, multiple features are typically evaluated so that overall uniformity is taken as the average uniformity over all identified features. Typically U_α is normalized so that a feature with all pixels having the same intensity would produce a value of unity. Unlike the general problem of image segmentation, in image quality evaluation the medical physicist has control over the features being evaluated through the design of the phantom. Typically flood phantoms, like the one described for the current project, have been used to analyze image intensity uniformity. In general, the formulation of the definition of uniformity is typically based on a choice between evaluating uniformity for one large ROI or multiple smaller ROIs. This is the same distinction as was found in the present study for the results obtained using the UN1 and UN2 methods. Perhaps a more complete characterization of image intensity uniformity would relate the uniformity metric to the scale at which the measurement is made. An approach based on these speculations could conceivably then allow some form of characterization of the texture of the image. Experiments based on this approach will likely be fertile topics for future investigations. These studies should aim to develop the more promising signal intensity measurement methods with the goal of making them both more sensitive and more robust.

CONCLUSIONS

The only image intensity uniformity measurement method, of those investigated, that uses information from the entire image, and thus takes into account the smaller and larger local and total changes in pixel value was UN2, the gray scale uniformity mapping method. The peak deviation nonuniformity method, UN1, is limited in that it quantifies information from only two of the pixels. Thus for measuring uniformity with PPI in MRI, UN2 offered the most robust and consistent measurement of PPI image uniformity of the standard methods considered. Future investigations should aim to evaluate the utility of the UN2 method and extend its utility for quantifying differences in image uniformity for different RF coil configurations and different partially parallel MR image regularization methods.