Response to “Comments on ‘A theoretical model of the pressure distributions arising from asymmetric intraglottal flows applied to a two-mass model of the vocal folds’” [J. Acoust. Soc. Am. 130, 389–403 (2011)]

Abstract

Hirschberg [J. Acoust. Soc. Am. 134, 9-12 (2013)] presents a commentary and criticisms of the viscous flow model presented by Erath et al. [J. Acoust. Soc. Am. 130, 389–403 (2011)] that solves for the asymmetric pressure loading on the vocal fold walls. This pressure loading arises from asymmetric flow attachment to one vocal fold wall when the glottal channel forms a divergent configuration. Hirschberg proposes an alternative model for the asymmetric loading based upon inviscid flow curvature at the glottal inlet. In this manuscript further evidence is provided in support of the model of Erath et al. and the underlying assumptions, and demonstrates that the primary criticisms presented by Hirschberg are unwarranted. The model presented by Hirschberg is compared with the model from the original paper by Erath et al., and it is shown that each model describes different and complementary aspects of divergent glottal flows.

INTRODUCTION

Hirschberg1 comments on the manuscript by Erath et al.,2 which presents, for the first time, an analytical model of the asymmetric loading experienced by the vocal folds during the divergent phases of the phonatory cycle. The asymmetric pressure loading on the vocal folds is generated by the fluid flow within the glottis that asymmetrically attaches to one wall, while fully-separating from the opposing wall for divergent glottal orientations. Prior to this publication, the majority of numerical studies using reduced-order vocal fold models3 assumed one-dimensional flow within the glottis, despite considerable experimental evidence of the two-dimensionality of the flow.4, 5 The model presented by Erath et al.2 aims to provide a simple, computationally inexpensive method of incorporating asymmetric fluid flow, and consequently asymmetric fluid loading, into reduced-order vocal fold models, which has been found to have a considerable impact on the vocal fold dynamics, particularly when coupled with asymmetric tissue properties.6

The model, termed Boundary Layer Estimation of Asymmetric Pressures (BLEAP), models the viscous flow in the glottis using a boundary layer approach. The model is applied during the divergent phases of the phonatory cycle when the geometry and flow orientation is similar to that of a diffuser in a state of two-dimensional stall.7 At the glottal inlet, which defines the minimal glottal area for a divergent configuration, the flow attaches to one wall (termed the flow wall) and fully separates from the opposing wall (termed the non-flow wall). The pressure along the flow wall slowly recovers from the pressure at the inlet, reaching atmospheric pressure at the glottal exit. Along the non-flow wall the pressure is assumed to be atmospheric along its entire length.

In his Comment, Hirschberg1 questions some of the physical reasoning and assumptions made in the BLEAP model derivation. He proposes an alternate inviscid model based upon the force of the wall on the fluid required to turn the flow such that it attaches to the flow wall; hereafter this model will be referred to as the “flow curvature” model. In this manuscript we specifically address the two major criticisms in the Comment.

RESPONSE TO CRITICISMS

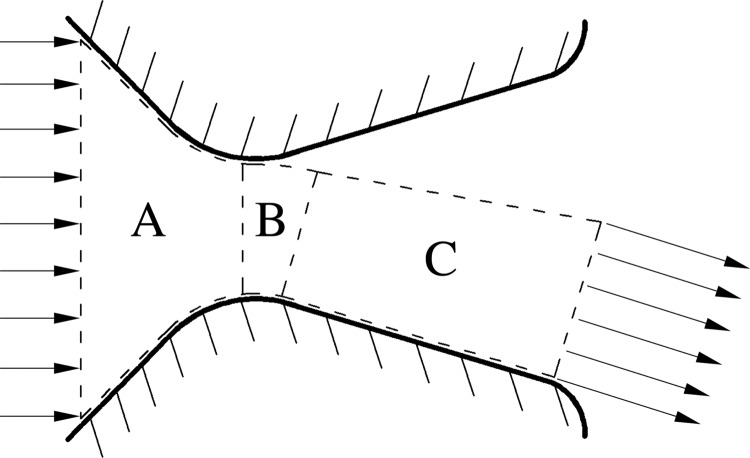
The fluid mechanics of intraglottal flows during divergent glottal phase can be approximately discretized into three regions, as shown in Fig. 1: (A) a convergent inlet section, (B) a flow curvature section, and (C) a divergent section. The convergent inlet section (A) is traditionally modeled using a combination of Bernoulli's equation and the continuity equation to relate pressure, velocity, and area; this is a valid approach due to the strong favorable pressure gradient and thin boundary layers.

Figure 1.

Approximate regions of validity of the (A) Bernoulli flow model, (B) flow curvature model (Ref. 1), and (C) BLEAP model (Ref. 2).

Both the BLEAP model2 and the flow curvature model1 aim to predict the asymmetric pressure loadings that occur during the divergent phase of the phonatory cycle when the glottal flow pattern becomes asymmetric. Hirschberg's flow curvature model accounts for asymmetric pressures arising from streamline curvature at the inlet using an inviscid flow assumption. While valid at the inlet of the glottis (region B) where the boundary layer is very thin, downstream of the inlet this model implies constant wall jet height with equal pressure on both the flow and non-flow walls; this is not supported by experimental observation or physical intuition, since the adverse pressure gradient promotes rapid boundary layer growth in this region (this will be definitively shown in Sec. 2A). Consequently, the flow curvature model proposed by Hirschberg1 is not applicable in region (C). Conversely the viscous BLEAP model accounts for the pressure recovery in the attached wall jet along the straight-walled section of the flow wall due to viscosity, thereby determining the pressure difference that is observed experimentally between the flow and non-flow walls; that is, the flow behavior that occurs in region (C). However, the BLEAP approach, as stated in the original manuscript,2 neglects the flow curvature at the glottal inlet (region B) and the consequential loading on the flow wall that precedes the evolution of the wall jet along the straight-walled section of the diffuser.

In his Comment, Hirschberg1 cites two major criticisms of the physics of the BLEAP model: (1) the pressure gradient across the shear layer in the wall jet and the related use of the Bernoulli equation in the core of the wall jet, and (2) the temporal discontinuity in the force on the flow wall that arises from the lack of dependence of the asymmetric force with the minimum glottal area. In this section we address these two criticisms.

Pressure concerns

The viscous BLEAP model implicitly assumes that the attached wall jet consists of three regions: a boundary layer that grows along the flow wall; an “inviscid jet core;” and a shear layer at the interface of the wall jet and the “dead water” region formed when the flow separates from the non-flow wall at the glottal inlet. The wall jet decelerates as it propagates along the wall due to the action of viscosity, which is primarily relegated to the boundary layer and shear layer regions. In his Comment, Hirschberg notes an apparent contradiction in our model, stating that BLEAP predicts “a transversal pressure discontinuity across the shear layer separating the wall-jet from the dead water region,” which he states “is physically impossible because a shear layer (or streamline in a frictionless model) cannot sustain a pressure difference” unless the flow is inherently viscous. Based on these arguments he concludes that the use of the Bernoulli equation in the wall jet, as applied in the BLEAP model, is invalid. There are two conditions that must be satisfied in order to justify the use of the Bernoulli equation in the BLEAP formulation: (1) the actual flow (and our model of it) is viscous, as opposed to inviscid; and (2) viscous losses in the core of the jet are negligibly small.

As to point (1), glottal flows are a known viscous phenomenon, see for example, the recent review paper by Mittal et al.8 Furthermore, a confined, viscous, asymmetrically separated flow can support a transverse pressure gradient, as evidenced by cross-channel pressure differences in diffuser flows.7, 9 It is clarified, however, that the BLEAP approach does not attempt to model the details of the transverse pressure gradient across the shear layer. Rather, it computes the pressure in the inviscid jet core based on the streamwise velocity decay and imposes it on the flow wall using boundary layer assumptions. Experimental measurements indicate that the pressure on the non-flow wall is approximately atmospheric within the glottis, and thus the BLEAP model makes an ad hoc assignment of atmospheric pressure to this wall. In short, BLEAP models the pressures along the walls, and not in the entirety of the glottis.

The latter point (2) stands in need of more consideration. A derivation of Bernoulli's equation requires the integration of Euler's equations along a streamline. To get from the Navier-Stokes equations to Euler's equations, one generally assumes that the fluid viscosity is zero, and thus the viscous terms are eliminated. However, it is also possible to arrive at Euler's equations in a viscous flow if the viscous stresses are zero due to the behavior of the velocity field. This is the case, for example, in uniform flow, whereby all velocity gradients are zero and the viscous terms vanish identically. Therefore, in order for the viscous terms to be negligible in the wall jet core, and consequently for Bernoulli's equation to be applicable in this region (along a streamline), either the flow must be inviscid, which is not the case as per point (1), or the velocity profile in this region must be uniform and the viscous normal stresses (e.g., μ∂u/∂x) must be small. These conditions should be met if the boundary layer and shear layer growth rates are sufficiently low that these regions do not merge within the glottis and the viscous normal stresses are negligible.

In support of point (2), Fig. 2 shows the phase-averaged velocity profiles obtained used particle image velocimetry at the glottal inlet, midline, and exit for driven vocal fold models at a 20° included glottal angle and a life-sized volumetric flow rate of Q = 159.4 mL/s at a phase of t/T_open = 0.7, where t is time and T_open is the period of the open phase. As the wall jet progresses along the medial surface, the peak velocity decreases and the jet spreads. These profiles emphasize the importance of utilizing a viscous modeling approach in the diffusing portion of the glottis since the boundary layer grows to ∼y/d = 1 (i.e., the initial wall jet height) by the glottal exit, and the velocity magnitude decreases appreciably. These observations confirm that Hirschberg's application of an inviscid flow description downstream of the glottal inlet, which implies negligible boundary layer growth and constant velocity magnitude, is inappropriate. The central core region, however, retains a relatively blunt profile throughout the glottis, suggesting minimal viscous dissipation in this section, which would imply the Bernoulli equation is valid in the jet core, despite nonzero fluid viscosity. Bernoulli's equation is used to relate the wall pressure to the velocity in the core of the wall jet using standard boundary layer arguments. It is emphasized that this relationship is only valid in the inviscid core of the attached wall jet, and that the velocity need not be constant. That is, the velocity decay observed in in vivo and in vitro experiments is captured using our viscous flow approach (see Fig. 2).

Figure 2.

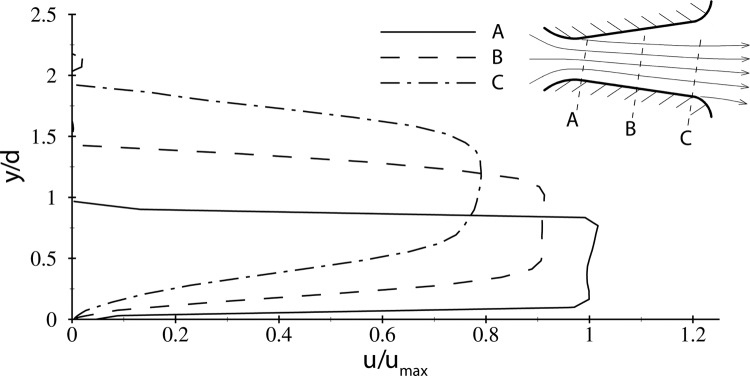
Velocity profiles extracted normal to the wall at the (A) glottal inlet; (B) midpoint of the medial surface; and (C) near the glottal exit, for a life-size flow rate Q = 159.4 mL/s and a total included glottal angle of 20°.

The validity of using Bernoulli's equation to compute the pressure along the wall from the velocity decay in the core of the wall jet is corroborated by Fig. 3, which shows the total pressure along a streamline in the core of the wall jet as it passes through the straight-walled section of the glottis for static vocal fold models with a transglottal pressure drop of 15 cm H₂O and a total included glottal angle of 10°. The data are plotted such that x = 0 corresponds to the location of the minimal glottal area. The pressure along the streamline is assumed equal to the experimentally measured static wall pressure based upon the standard boundary layer argument of ∂p/∂y ≈ 0, where p is the static pressure. The total pressure, computed as p₀ = p + 1/2ρV², where ρ is the fluid density and V is the velocity magnitude, should be constant in the absence of viscous losses, or decrease if the losses are significant. The uncertainty in the total pressure is approximately ±0.25 cm H₂O. We note that within the experimental uncertainty the total pressure does not decrease, confirming that viscous losses in the wall jet core are negligible and validating the use of Bernoulli's equation in the jet core in the BLEAP model. These calculations were repeated using experimental data over a range of glottal angles and transglottal pressure drops,10 with all instances yielding the same result, although they are not shown here for brevity.

Figure 3.

Total pressure along a streamline in the wall jet core for a static vocal fold model with a transglottal pressure drop of 15 cm H₂O and a total included glottal angle of 10°.

Finally, Hirschberg questions the use of Eq. (18) in the BLEAP manuscript2 [Eq. 1 of the Comment] as it does not include the centripetal acceleration term to account for the derivation of the velocity in a non-inertial reference frame. This observation is correct. A typographical error in the original manuscript resulted in an incorrect form of the equation. The correct form of the equation is given as:

$$p\left(x\right)=p_i+1/2\rho \left[U_i^2-U{\left(x\right)}^2\right]+1/2{\mathrm{\Omega }}_z^2[x^2+2x{x}_{\text{off}}+x_{\text{off}}^2],$$ (1)

where all variables are defined as in Erath et al.2

Temporal force discontinuity and a_min dependence

In his Comment, Hirschberg is critical of the fact that the force predicted by the BLEAP model is discontinuous, and independent of the minimum glottal area a_min. The BLEAP model depends on a flow parameter n that is directly related to the streamwise pressure gradient in the wall jet core; for BLEAP, n is negative due to the adverse pressure in the glottis in divergent configurations (a value of n = 0 corresponds to the zero pressure gradient Blasius boundary layer). As discussed in the original manuscript,2 the value of n should be a function of the glottal angle, going from zero when the walls are nearly parallel and becoming more negative as the divergence angle increases. Since the “BLEAP” force is directly proportional to n, it too should go from zero when n = 0 to a maximum value when the adverse pressure gradient is on the verge of causing flow separation. The exact dependence of n on the glottal angle is non-trivial, however, due to the complex nature of the glottal flow field. As such, in the original manuscript we opted to select an “average” n for all glottal angles, with the understanding that more work is required to find the correct function relating n to the divergence angle (this is stated explicitly in the original publication). As will be seen in Sec. 3, when a model incorporating a variable n value is used, the BLEAP force is no longer discontinuous at the onset of the divergent glottal phase.

Similarly, the force predicted by the BLEAP model is independent of a_min because it depends upon the velocity at a_min, which is also constant, and discontinuous at closing. This is a result of the assumption of constant subglottal pressure (that is, the lungs are a constant pressure source) that was utilized in the initial formulation to enable a comparison with existing data. This can be rectified by using an alternate subglottal pressure model; e.g., one that incorporates fluid-structure-acoustic interactions (i.e., “level 2” acoustic interactions),11 meaning the transglottal pressure drop will no longer be independent of area.

COMPARISON BETWEEN BLEAP AND HIRSCHBERG'S MODEL

In summary, it is broadly accepted that Bernoulli's equation is valid in region (A), Hirschberg's flow curvature model1 handily accounts for the flow curvature section in region (B), and the BLEAP model describes the flow development and consequent pressure recovery in the divergent, straight-walled section of region (C). Thus, it is the recommendation of the authors that Hirschberg's flow curvature model and the BLEAP model should be used in conjunction to describe the overall flow physics and fluid loading during divergent phases of the glottal cycle.

The forces predicted by the BLEAP and flow curvature models are compared in Fig. 4 at a constant subglottal pressure of 1.5 kPa to give a sense of relative magnitudes and temporal variations of these forces. Both forces are zero when the glottis is either closed or in a convergent configuration, while both forces are negative, that is, they aid in closing, when the glottis is divergent. Two BLEAP models are presented, one with the constant n simplification originally described in Erath et al.,2 and the other with a variable n that is linearly related to the glottal divergence angle. BLEAP with constant n has a discontinuity in the force at the start of the divergent portions of the phase, and again when the glottis closes, leading to one of Hirschberg's criticisms discussed previously. The magnitude of the BLEAP force in this case is linearly proportional to p_s. Employing a variable n eliminates the discontinuity at the start of the divergent phase. A discontinuity still exists at closing since the glottis closes while still in a divergent configuration. This is a consequence of the subglottal pressure model that is employed, as opposed to the BLEAP method itself. The BLEAP and flow curvature forces are of the same order, demonstrating that both flow turning and pressure recovery along the flow wall are important in determining the overall loadings in the divergent passage, giving credence to the recommendation that both the flow curvature and BLEAP models should be used in conjunction with each other to provide the most accurate description of the pressure loading conditions.

Figure 4.

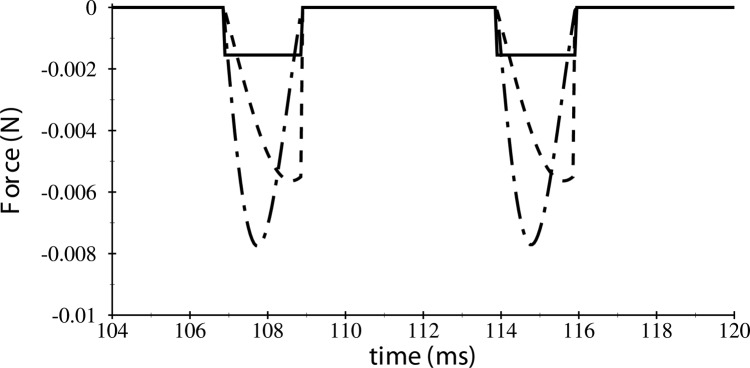
Comparison of the magnitudes of the force due to BLEAP with constant n (—), BLEAP with n as a function of divergence angle (- - -), and the flow curvature model (- · -) for p_s = 1.5 kPa.

CONCLUSIONS

In this Response we have provided further evidence in support of the assumptions explicit and implicit in the BLEAP model, most notably regarding the use of Bernoulli's equation in the core of the wall jet and in the use of a glottal angle dependent n value to eliminate force discontinuities at the inception of glottal divergence. We have also discussed the merits and limitations of both the BLEAP model and the flow curvature model introduced by Hirschberg in his Comment. We have shown that although the flow curvature model predicts the pressure loading due to streamline curvature at the glottal inlet, it is incapable of predicting the viscous pressure recovery that occurs due to the diffusing glottal walls downstream of the inlet. Conversely, the BLEAP model does not account for streamline curvature, although it does capture the viscous pressure recovery. As such, each model has its region of validity and the two regions are, in fact, complementary. Furthermore, we have shown that the magnitudes of the forces predicted by the two models are of the same order and thus neither can nor should be neglected based on relative importance. Rather, it is the recommendation of the authors that both models be used in conjunction by researchers using reduced-order vocal fold models, particularly in studies involving asymmetric tissue properties.