Failure-probability driven dose painting

Abstract

Purpose: To demonstrate a data-driven dose-painting strategy based on the spatial distribution of recurrences in previously treated patients. The result is a quantitative way to define a dose prescription function, optimizing the predicted local control at constant treatment intensity. A dose planning study using the optimized dose prescription in 20 patients is performed.

Methods: Patients treated at our center have five tumor subvolumes from the center of the tumor (PET positive volume) and out delineated. The spatial distribution of 48 failures in patients with complete clinical response after (chemo)radiation is used to derive a model for tumor control probability (TCP). The total TCP is fixed to the clinically observed 70% actuarial TCP at five years. Additionally, the authors match the distribution of failures between the five subvolumes to the observed distribution. The steepness of the dose–response is extracted from the literature and the authors assume 30% and 20% risk of subclinical involvement in the elective volumes. The result is a five-compartment dose response model matching the observed distribution of failures. The model is used to optimize the distribution of dose in individual patients, while keeping the treatment intensity constant and the maximum prescribed dose below 85 Gy.

Results: The vast majority of failures occur centrally despite the small volumes of the central regions. Thus, optimizing the dose prescription yields higher doses to the central target volumes and lower doses to the elective volumes. The dose planning study shows that the modified prescription is clinically feasible. The optimized TCP is 89% (range: 82%–91%) as compared to the observed TCP of 70%.

Conclusions: The observed distribution of locoregional failures was used to derive an objective, data-driven dose prescription function. The optimized dose is predicted to result in a substantial increase in local control without increasing the predicted risk of toxicity.

INTRODUCTION

Locoregional failure after (chemo)radiotherapy for locally advanced head and neck squamous cell carcinoma (HNSCC) remains a major issue. A radiation dose–response relationship has been demonstrated for HNSCC (Ref. ¹) in several studies. However, dose escalation must be balanced against the increased toxicity as the current clinical practice is already close to the tolerance of the normal tissue. Modeling studies suggest that dose-painting approaches may substantially improve locoregional outcome^{2, 3, 4} without the toxicity associated with uniform dose escalation. Most attempts at identifying and validating a dose-painting target have taken a “bottom-up” strategy, typically focusing on a single imaging biomarker thought for mechanistic reasons to be a surrogate of radioresponsiveness.⁵ In the present work, a “top-down” approach is taken to arrive at a data-driven dose-painting strategy based on the analysis of the estimated point of origin of locoregional recurrences in relation to target delineations and pretreatment ¹⁸F-fluorodeoxyglucose positron emission tomography (FDG-PET) uptake.

The approach involves three steps. First, each recurrence in a large clinical series of HNSCC cases is analyzed in order to assign a focal point of origin on the original planning CT scan.^{6, 7} The analysis encompassed 48 local recurrences in 39 patients after complete clinical response at the 2-month follow-up visit after radiotherapy, all with a CT scan at the time of the recurrence. This allows assigning each failure to a single target subvolume or iso-SUV (Standardized uptake value) contour.⁷ Second, the observed distribution of failures is combined with the actuarial rate of local recurrence to obtain a set of control probabilities in each target subvolume. The rates of local control in each subvolume of the target are combined with the total, actuarial rate of local control to yield a tumor control probability in each subtarget fulfilling the following assumptions/criteria: (A) the spatial distribution of failures is equivalent to the observed pattern of failure and (B) the total probability of failing in at least one target volume is equal to the observed actuarial rate of local failure. A dose–response curve is fitted to these observed control rates to provide a model of the expected tumor control in each subvolume as function of prescribed dose, see Sec. 2. The result is a clinically realistic estimate of the change in tumor control when changing the prescription dose. Finally, the radiation dose prescriptions to the different subvolumes are optimized to maximize the total tumor control under the constraint that the integral dose to the whole target volume is kept constant as a surrogate for maintaining constant treatment intensity.

In the present study, we derive such data-driven dose–response models and investigate the potential gains in tumor control from optimizing the dose distribution. Furthermore, a dose planning study in 20 patients is performed to confirm the feasibility of delivering the optimized dose prescription. The dose planning study is also used to investigate the effect on normal tissue complication probability when changing the dose prescription.

METHODS

Patients treated with definite IMRT in the period from 2005–2009 were included in the pattern of failure analysis. All patients received treatment according to national guidelines (DAHANCA) as follows. Five target volumes were delineated for each patient, starting from a FDG PET defined volume, visually delineated by a nuclear medicine physician. Each of the subsequent volumes would then encompass all previous volumes, i.e., the volumes are nested. The gross tumor volume (GTV) was delineated by an oncologist and radiologist in collaboration based on all available scans and clinical information. Subsequently, the clinical target volume of the tumor, CTV-t, was created by an oncologist using a 1 cm margin from the GTV, to account for delineation uncertainty, followed by subtraction of bony structures and other borders of tumor invasion. All of these structures would receive 66 or 68 Gy in 2 Gy fractions depending on tumor size. The high and low risk elective target volumes, CTVE-h and CTVE-l, were defined based on lymph node regions and prescribed a physical dose of 60 and 50 Gy, respectively, given as a simultaneous integrated boost, i.e., in 33 or 34 fractions. A margin of 4 mm was applied between all clinical target volumes and the planning target volumes (PTVs) to which the dose was prescribed. Dose coverage of 95%–107% of the prescription was required according to protocol and the plans would normally be normalized to the mean dose of the high dose volume (66 or 68 Gy). Patients with advanced disease would receive weekly concomitant cisplatinm unless contraindicated. In accordance with national guidelines, all patients received hypoxic cell sensitizer (Nimorazole) daily unless contraindicated.

Of the 357 patients completing IMRT for HNSCC with curative intend, 204 achieved a complete remission with no evidence of disease at the last available follow-up and 53 patients had residual disease after RT. Of the 100 remaining patients, 31 had isolated distant progression. This leaves 69 patients with a “true” local recurrence; albeit 7 did not have a biopsy verified recurrence and 23 did not have a CT scan of the recurrence. In the cohort of patients with no evidence of disease (i.e., complete response) at first follow-up visit 2 month after completion of treatment we calculated the actuarial rate of local recurrence using the Kaplan Meier product limit method with locoregional failure as event and death of any cause as censoring. The five-year local recurrence free rate in this cohort was 70%. Patients with residual disease at first follow-up were excluded from this analysis The follow-up time with respect to local recurrence was defined as the time from start of radiotherapy to local recurrence or last follow up, whichever comes first. With this definition, the median follow-up is 17 months.

Derivation of data-driven dose–response model

The purpose of this section is to derive a clinically realistic dose–response function matching the clinically observed failures, such that the effect of changing the dose prescription can be predicted.

As mentioned above, the actuarial five-year control in patients with clinical complete response is 70%. The 2% of local failures occur outside the treated volume, hence the actuarial local control inside the treated volume is (100%–30%)*(100%–2%) = 70.6%. The empirical tumor control probability (TCP) for each subvolume under the assumption of independence can be estimated by first calculating a crude TCP for each VOI: ${\mathrm{TCP}}_{\mathrm{VOI}}^{\mathrm{crude}}=100\%-f_{\mathrm{VOI}}\times 30\%$, where f_VOI is the proportion of local failures observed to be located specific to the VOI. ${\mathrm{TCP}}_{\mathrm{VOI}}^{\mathrm{crude}}$ does not necessarily match the actuarial estimate of local control under the assumption of independence, so the crude TCP is scaled by a common factor to obtain the estimated TCP: ${\mathrm{TCP}}_{\mathrm{VOI}}=\eta {\mathrm{TCP}}_{\mathrm{VOI}}^{\mathrm{crude}}$ such that ${\prod }_{\mathrm{all}\mathrm{VOI}}{\mathrm{TCP}}_{\mathrm{VOI}}=70.6\%$, where η is 0.993. The current tumor controls estimates based on these derivations are given in Table 1 (Ref. ⁶) and the fitted dose–response functions are shown in Fig. 1.

Table 1.

Calculation of current TCP for each of the five target subvolumes, see text for details. GTV-PET: the ¹⁸F-fluorodeoxyglucose positive gross tumor volume. GTV: gross tumor volume. CTV-t: clinical target volume. CTVE-h: high risk elective clinical target volume. CTVE-l: low risk elective clinical target volume. TCP: tumor control probability.

Target volume	Mean volume (range) of PTV	Proportion of local failures specific to volume (%)	Crude TCP (%)	Estimated TCP with current prescription (%)
GTV-PET	83 cm3 (14–255 cm3)	54	83.9	83.3
GTV	150 cm3 (45–362 cm3)	28	91.5	90.9
CTV-t	439 cm3 (195–894 cm3)	14	95.8	95.1
CTVE-h	861 cm3 (434–1805 cm3)	2	99.4	98.7
CTVE-l	1080 cm3 (646–1972 cm3)	0	100	99.3
Out of field	N/A	2	N/A	N/A

Figure 1.

(Left) Estimated dose–response curves based on the observed recurrence pattern and the actuarial risk of local recurrence following complete clinical response after five years. The circles show the partial control probabilities with the current prescription. (Right) The optimized mean physical doses to the target structures in 20 HNSCC patients versus the current clinical plans.

Once the current TCP for each target volume (denoted partial TCPs below) has been established, a mathematical dose–response relationship for the volumes of interest can be estimated. The central target volumes, CTV-T, GTV, and GTV-PET can be assumed to have near zero probability of local control at zero dose, so TCP is assumed to follow a logistic dose–response model⁸

$${\mathrm{TCP}}_{\mathrm{VOI}}\left(D\right)=\frac{1}{1+\exp \left\{4{\gamma }_{50}\left(1-\frac{D}{D_{50}^{\mathrm{VOI}}}\right)\right\}},$$ (1)

where D is the dose to the VOI, γ₅₀ is the normalized steepness of the dose–response curve, and $D_{50}^{\mathrm{VOI}}$ is the dose resulting in 50% TCP in the VOI. All doses in the models, including D and D₅₀, refer to fractionation corrected dose, here calculated as equivalent dose in 2 Gy fractions (EQD2) using α/β = 10 Gy for the tumor.

The steepness of the dose–response curves, γ₅₀, needs to be extracted from the literature as our outcome data only involve a single dose level. We use the clinically observed ${\gamma }_{50}^{\mathrm{literature}}$ = 1.8¹. However, this value is based on uniform dose escalation. If γ₅₀ = 1.8 was applied in Eq. 1, the steepness of TCP_CTV = TCP_GTV-PET*TCP_GTV*TCP_CTV-t would be overestimated.

Consequently, we find a self-consistent combination of γ₅₀ and $D_{50}^{\mathrm{VOI}}$ fulfilling that

• The steepness of TCP_CTV = TCP_GTV-PET* TCP_GTV*TCP_CTV-t at 68 Gy is the same as the steepness of a single logistic dose–response curve with ${\gamma }_{50}^{\mathrm{literature}}$ = 1.8.

• The estimated TCP at the current prescription in the target-subvolumes is in accordance with the calculated values in Table 1.

Of note, we have implicitly assumed that γ₅₀ is the same for all target subvolumes.

The details of the calculation is given in the Appendix of the supplementary material.²¹ We find a common γ₅₀ = 1. 39 and D₅₀ for CTV, GTV, and GTV-PET are 44, 48.2, and 53.1 Gy, respectively. Once γ₅₀ and D₅₀, are determined, the dose–response curve for the central target volumes is completely defined by Eq. 1.

The dose–response for the elective clinical target volumes needs to be modeled differently as control probability without radiotherapy will be much greater than zero. The risk of subclinical disease in the clinically negative neck varies with stage of disease and subsite within the head and neck region.^{9, 10, 11, 12, 13} However, levels included in the low and high risk elective volumes are those estimated to have a roughly 20% and 30% risk of involvement, respectively, and these probabilities were applied in the modeling. Additionally, the dose–response relationship is modeled as a function of the logarithm of dose⁸ as this ensures a horizontal asymptote as the dose tends to zero at 0 Gy. The dose–response function is then defined as

$$\begin{array}{c}\hfill \mathrm{TCP}\left(D\right)=\left(1-\mathrm{TCP}\left(0\mathrm{Gy}\right)\right)\frac{1}{1+{\left(\frac{D_{50}}{D}\right)}^{4{\gamma }_{50}}}+\mathrm{TCP}\left(0\mathrm{Gy}\right).\end{array}$$ (2)

Here, γ₅₀ is assumed to be 1.8 and D₅₀ is determined from the observed TCP_VOI at the current prescription dose. The dose–response for the elective clinical target volumes are then determined fully from Eq. 2 and shown in Fig. 1.

Optimizing the dose prescription

Once the clinical data-driven model of partial tumor control is specified, it is possible to estimate the effect of a changed dose prescription on the tumor control. In particular, it is possible to optimize the dose prescription in order to maximize the “bottom line,” i.e., the individual patients’ probability of achieving disease control in all the target subvolumes taken together. In doing this, we constrain the total dose. In the present work we focus on dose redistribution, i.e., maintaining the same integral dose (corresponding to a constant absorbed energy in the treated volume), but redistributing the dose between the delineated VOIs. Additional dose volume constraints were applied.

For a given dose prescription to the five delineated structures, $\vec{D}=[D_{\mathrm{CTVE}-\mathrm{l}},D_{\mathrm{CTVE}-\mathrm{h}},D_{\mathrm{CTV}-\mathrm{t}},D_{\mathrm{GTV}},D_{\mathrm{CTV}-\mathrm{PET}}]$, the total tumor control probability can be calculated as the product of the partial TCPs by using the assumption of independence. Hence, the optimal prescription is found as the dose D maximizing the function

$${\mathrm{TCP}}^{\mathrm{total}}\left(\vec{D}\right)=\prod _{\mathrm{all}\mathrm{VOIs}}{\mathrm{TCP}}_{\mathrm{VOI}}\left(D_{\mathrm{VOI}}\right).$$ (3)

However, it will be necessary to constrain the optimization to avoid excessive doses as described in more detail below. Again, all references to doses in the modeling are fraction-size corrected (EQD2).

Optimization was performed by the fminsearch function in MATLAB R2009b (The MathWorks Inc., Natick, MA), minimizing TCP^total with respect to the four first elements of $\vec{D}$ and determining the last element by the requirement of constant integral dose

$$\sum _{\mathrm{all}\mathrm{VOIs}}{v}_{\mathrm{VOI}}{D}_{\mathrm{VOI}}^{\mathrm{Standard}}=\sum _{\mathrm{all}\mathrm{VOIs}}{v}_{\mathrm{VOI}}{D}_{\mathrm{VOI}}^{\mathrm{optimized}}.$$

Here, v_VOI is the volume of the PTV pertaining to the VOI in question minus the volume of more central regions, i.e., the volume specific to the PTV, cf. Table 2. Additionally, we required two constraints to be fulfilled; (1) The maximum dose was limited to EQD₂ = 85.4 Gy_, corresponding to a physical dose of 81 Gy in 32 fractions corrected using α/β = 10 Gy, which was shown acceptable in the Ghent experience.¹⁴ And (2). We required the dose to be monotonically increasing from the outer target (PTVE-l) and inwards to PTV-PET.

Table 2.

After optimization of the dose prescription, cf. Eq. 3, we tested the feasibility of dose planning to the optimized prescription using the following planning acceptance criteria. The normal tissue constraints and priority are the same as for the clinical plans. All doses are physical.

ROI		Acceptance criteria	Hard constraint?	Priority
All PTVs		98% of target must receive at least 45 Gy	Yes	Takes priority over mean prescription doses
PTVE-l\PTVE-h	}
PTVE-h\PTV-T		Mean dose = prescription ± 1 Gy. DVH	Yes	Min dose of 45 Gy takes priority over these
PTV-T\PTV-solid		“As steep as possible.”
PTV-solid\PTV-PET
PTV-PET
Max dose		<88 Gy	Yes	Should not conflict
Medulla		D0.1% < 45 Gy	Yes	Takes priority over PTV coverage
Brainstem		D0.1% < 54 Gy	Yes
Chiasm, N. opticus, inner ear		D0.1% < 54 Gy	Yes	Takes priority over PTV coverage, but not CTV or GTV coverage
Parotids, submandibular, larynx		Mean dose as low as possible	No	PTV coverage takes priority over these

The resulting, optimized dose prescription is patient-specific because the actual volume in the patient, v_VOI, is used in the optimization process.

We performed a separate optimization in the 20 most recent patients from the previously published series while varying the maximum dose constraint from 68 to 120 Gy in order to investigate the optimized TCP dependence on the maximum dose constraint.

After optimization of the dose prescription to the five target volumes, we now turn to a dose planning study on the 20 most recent patients from the previously published series to assess the feasibility of delivering the optimized prescription.

Dose planning

Clinical target volumes were expanded by a 4 mm isotropic margin to account for setup uncertainties. Thus for each delineated target volume, a planning target volume was created. The planning target volumes pertaining to GTV-PET, GTV, CTV-T, CTVE-h, and CTVE-l are named PTV-PET, PTV-solid, PTV-T, PTVE-h, and PTVE-l below. The mean dose to each of those planning target volumes with the standard prescription are estimated by the average of the mean doses to the target volume in the delivered plans of the 20 HNSCC patients from the previously published series. Ideally, these doses should equal the prescribed dose, but in practice, they are often higher due to, e.g., penumbra between regions with two different prescriptions.

Bottom-line optimization was performed on the 20 HNSCC patients. The resulting redistributed dose prescription was dose planned using the planning goals stated in Table 2.

The dose planning was performed in Eclipse version 10 with an intensity modulated arc technique using two 358° arcs on a Varian Trilogy accelerator using 6 MV photons. The optimized dose plan was compared to the clinical delivered plan (Typically, seven field static gantry IMRT technique) with respect to predicted TCP and normal tissue doses. Additionally, the 20 delivered plans were reoptimized with the intensity modulated arc technique to assess if the differences in normal tissue sparing were consistent across the treatment techniques.

RESULTS

Figure 1 shows dose–response functions for the five target subvolumes. The partial control with the current dose prescription is marked on the curves. The mean of the physical doses in the 20 most recent patients from the previously published series are 68.1/67.6/67.4/62.4/54.7 Gy to PTV-PET, PTV-solid, PTV-T, PTVE-h, and PTVE-l, respectively. The physical doses are converted to EQD₂ using α/β = 10 Gy for the tumor.

The product of the control of all subvolumes of the tumor matches the previously derived actuarial estimate of ${\prod }_{\mathrm{all}\mathrm{VOI}}{\mathrm{TCP}}_{\mathrm{VOI}}=70.6\%$ when accounting for the very low observed risk of local failure outside of the delineated target.

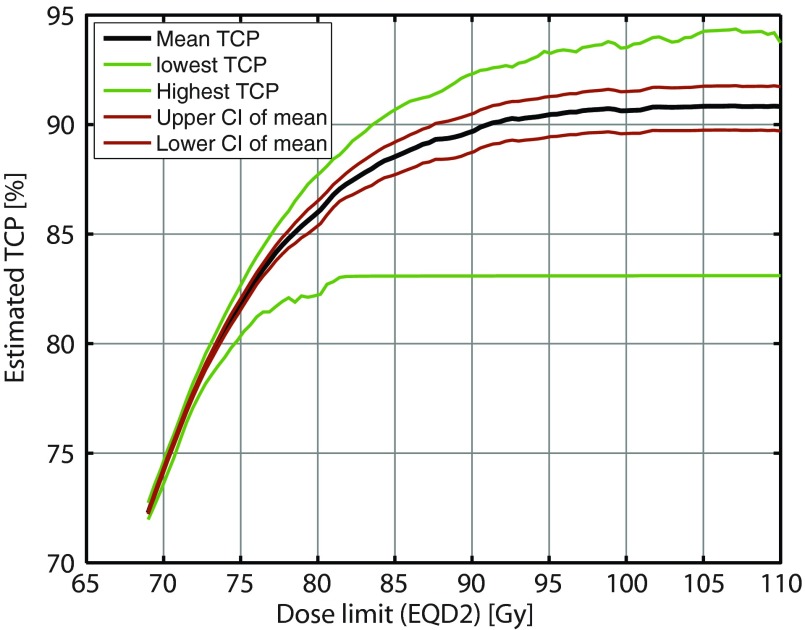
The prescription is modified for each of the 20 HNSCC cases by optimizing the total TCP. The maximum dose constraint of 85.4 Gy EQD₂ to any substructure was reached for in 18 of the 20 patients, cf. Fig. 1 (right). The resulting mean TCP in these patients with the modified prescription is 89% (range: 82.2%–90.9%). Figure 2 presents an analysis of the optimized TCP as function of the maximum dose constraint. The curves flatten at high doses when the requirement of constant integral dose, rather than the maximum dose constraint, limits TCP.

Figure 2.

Optimized tumor control probability vs maximum dose constraint. The 85 Gy maximum tolerated dose from the Ghent experience (Ref. ⁹) capture the vast majority of the potential for improvement in TCP. The curves are smoothed to remove a part of a jitter on the order of 0.5% TCP from the optimizer.

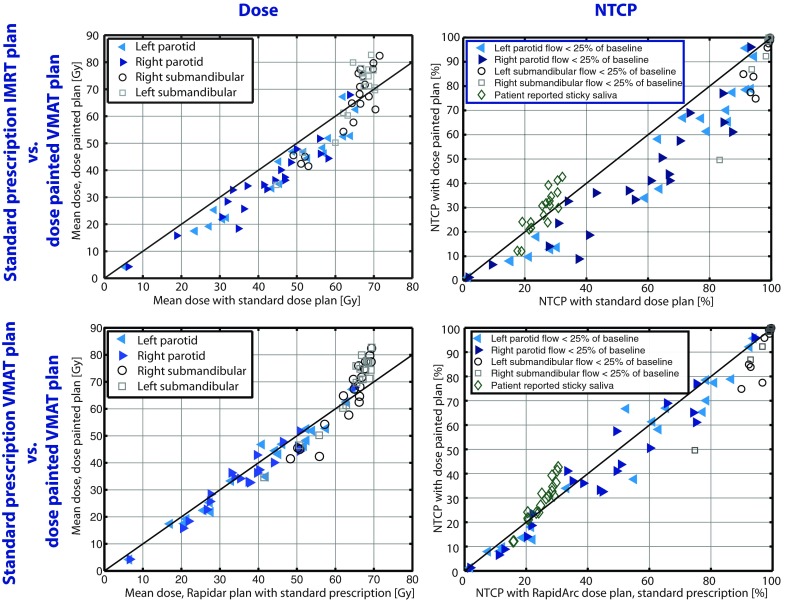
Figure 3 shows a comparison of the mean doses to the targets using the delivered clinical plans and the optimized dose prescription.

Figure 3.

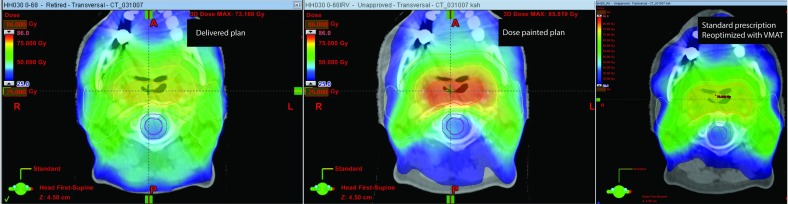
Clinical dose plan (left) and the realization of the optimal dose prescription (middle). The doses to the central target volumes are substantially increased with the optimized prescription. The parotids appear to be better spared with the dose painted plan. This is, however, mostly an effect of the updated technique (VMAT versus IMRT) and largely the same sparing of the parotids can be achieved by replanning the clinically used dose prescription with a VMAT technique (right). See also Fig. 4.

The dose plan using the optimized dose prescription resulted in reduced doses to some of the delineated organs at risk when comparing to the delivered seven-field IMRT plans. However, most of this benefit could be attributed to the change from fixed gantry IMRT to VMAT technique as demonstrated in Fig. 4. Figure 4 shows the mean dose to the salivary gland structures in dose painted versus standard prescription plans and the corresponding plot where the risk of complications has been estimated with a normal tissue complication probability model previously published.^{15, 16}

Figure 4.

(Left) Mean physical doses to the salivary gland structures with the dose painted plans versus the delivered plans (upper) or reoptimized VMAT plans with standard prescription (lower) in 20 patients. (Right) Normal tissue complication probability for the salivary gland structures (Refs. ¹⁵, ¹⁶, ¹⁷). The models presented on submandibular toxicity is for stimulated flow (Ref. ¹⁶) and in the multivariate model of sticky saliva we assumed, for illustration, a patient of age 60 and same dose to sublingual glands as for the submandibular glands (Ref. ¹⁷).

If this strategy is clinically implemented, the cohort of patients achieving complete clinical remission at first follow-up cannot be identified at baseline, thus all cases will need to undergo dose redistribution. Assuming, conservatively, that the rate of persistent disease is not altered by the modified dose prescription, the total probability of local control will change from 60% with the current prescription (70% control in the 85% of patients achieving complete clinical remission) to an estimated 76% (∼89% control in 85% of patients achieving complete clinical remission). Under this assumption, a sample size estimation shows that a hypothetical randomized controlled trial with a 1:1 allocation ratio to the test and control arms should enroll 188 patients in each arm to detect the estimated change in local control using a two-sided test, 90% power and a 5% level of significance.

DISCUSSION

A framework is presented for using clinical outcome data to build a model of dose–response in different target subvolumes and use that model to optimize the prescription dose to future patients. The model predicts substantial improvements in the overall local tumor control resulting from this bottom line optimization. This is in qualitative agreement with earlier mechanistic modeling studies of dose-painting based on heterogeneous tumor radiosensitivity,^{2, 3} but the current estimates rely only on empirical dose–response relationships. The suggested escalation of radiation dose to volumes with high relative FDG uptake on PET supports current clinical studies trying to boost the dose to these regions.^{4, 18} However, the present approach demonstrates a way to quantify the dose distribution in the target that is expected to optimize the local control and can be extended to provide a data driven and objective dose prescription function.

The focus in this study was on patients achieving complete clinical remission at first follow-up, thus implicitly making the assumption that patients with residual disease after radiotherapy are not affected by the dose redistribution. The patients with persistent disease, by definition, fail inside the GTV. The GTV will receive a higher dose with the modified prescription and it is therefore likely that a subset of patients with persistent disease will achieve tumor control or a prolonged time to progression. To avoid speculating on the magnitude of this gain, the very conservative assumption made here is that the rate of persistent disease is unchanged using the optimized dose prescription. As discussed above, TCP estimates in the entire patient cohort is 60% with the current dose prescription changing to 76% with the modified dose prescription. This is a sufficient effect size to be tested in a clinical trial of about 370 patients.

There are some limitations to this approach. The assumptions on the same γ₅₀ for all target subvolumes can be challenged. However, deviating from this assumption would require target subvolume specific failure rate observations at two distinct dose levels. This is not available in the literature and the statistical power of the analysis in the peripheral target subvolumes (even in CTV-t) would almost certainly be very limited as recurrences here are infrequent. In addition, the reliability of the dose–response model will clearly be limited by the precision of the clinically observed failure map. Maintaining the total energy deposited in the treated volume is a simplified measure to balance the treatment intensity to match the current prescription. Yet, the escalated dose to the central target structures may cause a different toxicity profile as seen in a previous phase 1 study.¹⁴ Ideally, the dose prescription should be optimized directly in the treatment planning system to ensure that the total risk of unacceptable toxicity is constant and the total TCP optimized under this constraint. This would require reliable dose–response curves for all suspected toxicities and direct interaction with the dose planning system. More problematically, it will require a trade-off of one type of toxicity against another. If the method was implemented, however, the continual reassessment method may improve the prediction of unacceptable toxicity.¹⁹

Probably, the most important limitation lies in the assumption of independence of failure in each target subvolume. This assumption could break down, for example, if tumors failing centrally were of a more radio-resistant phenotype and therefore prone to fail subsequently elsewhere. Unfortunately, current data do not allow dropping this assumption as this would require extended follow-up of the patients after first failure. If, in a prospective trial, the failure pattern with the optimized dose prescription changes such that more failures are observed in the periphery than centrally, this would most likely be due to such an effect and the dose prescription should be modified accordingly.

At our institution, a relatively large margin is added to the GTV to account for delineation uncertainty and subclinical spread of disease.²⁰ Institutions with less conservative delineation, a different pattern of failure may be seen. However, the current results are in broad agreement with most other studies of pattern of failure in concluding that failures appear inside the high dose volume. Pooling data from institutions with different delineation procedures may further inform the model and increase the generalizability of the results.

In conclusion, a method to generate a data-driven dose–response model has been demonstrated and used to optimize a spatially modulated dose prescription. This constitutes an approach to objectively choose a dose prescription function for dose-painting studies without mechanistic assumptions related to imaging biomarkers.