Empirical Measurements of Biomechanical Anisotropy of the Human Vocal Fold Lamina Propria

Abstract

The vocal folds are known to be mechanically anisotropic due to the microstructural arrangement of fibrous proteins such as collagen and elastin in the lamina propria. Even though this has been known for many years, the biomechanical anisotropic properties have rarely been experimentally studied. We propose that an indentation procedure can be used with uniaxial tension in order to obtain an estimate of the biomechanical anisotropy within a single specimen. Experiments were performed on the lamina propria of three male and three female human vocal folds dissected from excised larynges. Two experiments were conducted: each specimen was subjected to cyclic uniaxial tensile loading in the longitudinal (i.e. anterior-posterior) direction, and then to cyclic indentation loading in the transverse (i.e. medial-lateral) direction. The indentation experiment was modeled as contact on a transversely isotropic half-space using the Barnett-Lothe tensors. The longitudinal elastic modulus E_L was computed from the tensile test, and the transverse elastic modulus E_T and longitudinal shear modulus G_L were obtained by inverse analysis of the indentation force-displacement response. It was discovered that the average of E_L/E_T was 14 for the vocal ligament and 39 for the vocal fold cover specimens. Also, the average of E_L/G_L, a parameter important for models of phonation, was 28 for the vocal ligament and 54 for the vocal fold cover specimens. These measurements of anisotropy could contribute to more accurate models of fundamental frequency regulation and provide potentially better insights into the mechanics of vocal fold vibration.

1 Introduction

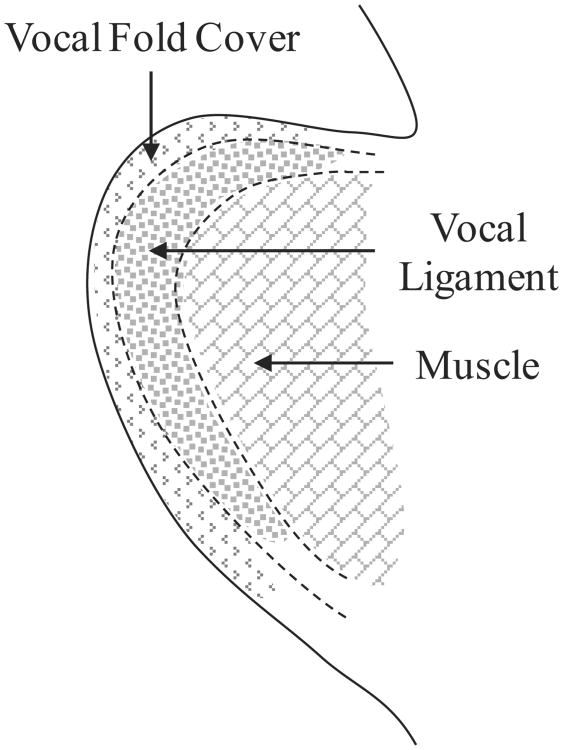
The vocal folds are composed of a layered structure with distinct histologies which play different functional roles in the phonation process. The layers may be classified using a three-layer scheme as: vocal fold cover (epithelium and superficial layer of the lamina propria), vocal ligament (intermediate and deep layers of the lamina propria), and muscle (see Figure 1). The vocal fold cover is the main oscillatory portion during vocal fold vibration. The vocal ligament is the load-bearing portion (Titze, 2000; Gray et al, 2000). The superficial, intermediate, and deep layers are collectively referred to as the lamina propria. The lamina propria is predominantly an extracellular matrix consisting of non-muscular tissues. The two main fibrous proteins in the lamina propria are elastin and collagen fibers. Interstitial proteins (e.g. hyaluronan) surround these fibrous proteins and are largely responsible for the viscosity of the tissue (Butler et al, 2001; Gray, 2000). The elastin fibers and bundles of collagen fibers in the lamina propria are aligned primarily in the anterior-posterior direction (Hirano et al, 1982; Ishii et al, 1996; Gray et al, 2000; Thibeault et al, 2002; Chan et al, 2007; Miri et al, 2012). This microstructural arrangement, which is well established in the literature, would logically lead to anisotropy in tissue mechanical properties. The term “anisotropy” in this study is defined as either the ratio of the longitudinal elastic modulus to the transverse elastic modulus (E_L/E_T) or the ratio of the longitudinal elastic modulus to the longitudinal shear modulus (E_L/G_L). Figure 1 shows a schematic drawing of the relevant anatomical structures.

Fig. 1.

A schematic showing a coronal cross-section of the vocal fold and the thyroarytenoid (vocalis) muscle.

For canine vocal folds, the anisotropic tissue properties (i.e. longitudinal, transverse, and shear elastic moduli) were measured by Hirano et al (1982), assuming transverse isotropy and tissue incompressibility. However, due to the testing procedures employed, all measurements were not made on a single specimen but rather required inter-subject comparisons, which introduced uncertainties due to large inter-subject variations. Measurements on the tensile response of the human vocal fold lamina propria showed that the longitudinal elastic modulus can vary by an order of magnitude (Zhang et al, 2007; Kelleher et al, 2011). The transverse shear modulus of the vocal fold lamina propria can vary by an order of magnitude as well (Chan and Rodriguez, 2008). These large variations between subjects make estimations on the anisotropy dubious. Hence, for such purpose the measurements should be made on a single specimen.

Past finite element modeling and analytical modeling with Timoshenko beam theory of vocal fold specimens revealed that the fundamental frequency of vibration could strongly depend upon the degree of anisotropy (Kelleher et al, 2010, 2011). Also, a sensitivity study ranked the elastic constants, specifically the transverse elastic modulus and the longitudinal shear modulus, as some of the most influential model parameters relating to modal frequencies (Cook et al, 2009). The elastic constants are sometimes inversely predicted using lumped parameter or continuum models (e.g. de Vries et al (1999)), or they are often assumed, particularly the transverse properties, with little justification provided (e.g. Alipour et al (2000); Berry and Titze (1996); Titze (1976)). This could potentially generate model errors that lead to faulty conclusions. Consequently, building accurate models of vocal fold vibration and fundamental frequency prediction is limited by the lack of knowledge on the tissue anisotropy.

To our knowledge, how the anisotropic tissue properties compare within a single specimen has never been quantitatively studied in human vocal folds. Macroscale transverse indentation experiments can be a viable technique for estimating the transverse mechanical properties of human vocal fold tissues (Chhetri et al, 2011). Therefore, it is hypothesized that a mechanical testing protocol including transverse indentation can be used in conjunction with uniaxial tension in order to obtain an estimate of the biomechanical anisotropy within a single specimen. Measurements of the anisotropy as described in this study could contribute to more accurate models of fundamental frequency regulation and provide potentially better insights into vocal fold vibration.

Analyzing the mechanics of indentation in an anisotropic medium requires a much greater deal of complexity than analyzing isotropic indentation. It is partly for this reason that virtually all of the analytical indentation studies on soft tissues have only considered isotropy. There are a few investigations that characterize the anisotropic mechanical properties of soft tissues, but typically by inversely fitting computational models (Cox et al, 2008). For vocal fold tissues, a transverse indentation-type loading has been attempted in vivo in humans (Tran et al, 1993) and in canines (Haji et al, 1992), though the analyses were highly simplified and assumed isotropy. In other biological materials, rarely is an anisotropic contact model used to analyze indentation experiments (e.g. Mattice et al (2006); Gefen and Margulies (2004); Yoo et al (2011)), except for nano-indentation studies on mineralized hard tissues (Fan et al, 2002). However, one does not necessarily know a priori that an isotropic contact model is appropriate for tissues that are anisotropic.

There are a few closed-form analytical solutions available for contact on a transversely isotropic half-space (e.g. Dahan and Zarka (1977); Turner (1980); Yu (2001)). However, all of these solutions are limited to loading in the direction that is parallel to the axis of material symmetry. Only recently has an analytical solution been presented where the loading occurs in a direction orthogonal to the axis of material symmetry (Zhupanska, 2010). Unfortunately, the solution in Zhupanska (2010) is given as complicated functions of stress and strain rather than in the force-displacement form which is more convenient for this investigation. Traditional methods of solving deformations for anisotropic elasticity (e.g. the Stroh formalism) involve solving the eigenvalue problem in terms of the elastic stiffnesses. This approach encounters difficulties for certain cases of material symmetry (e.g. isotropy or transverse isotropy when the axis of material symmetry is not parallel to the loading direction), due to repeated eigenvalues and/or eigenvectors (Ting, 1996). Thus, for the present indentation experiment, the solutions that rely on solving the eigenvalue problem to compute relations for the displacements cannot be implemented (e.g. Willis (1966); Swanson (2004)). An alternative solution procedure that is utilized here to estimate the transverse mechanical properties involves the Barnett-Lothe tensors (Barnett and Lothe, 1975; Lothe and Barnett, 1976). This technique is attractive because it avoids solving the eigenvalue problem and instead computes the necessary functions directly from the elastic stiffnesses. Therefore, cases of mathematical degeneracy due to non-distinct eigenvalues are circumvented.

2 Materials and Methods

2.1 Vocal Fold Specimens

Tissue specimens were isolated from the excised larynges of six human cadaveric subjects, with no known history of smoking, laryngeal or head and neck disease (see Table 1). Three male and three female subjects were included, all of whom were Caucasian except subject E who was African American. All larynges were procured from the Willed Body Program of the University of Texas Southwestern Medical Center and gross examination of the vocal folds revealed no abnormalities or pathologies. For each subject, one vocal fold cover (i.e. epithelium and superficial layer of the lamina propria) specimen and the contralateral vocal ligament (i.e. middle and deep layers of the lamina propria) specimen were dissected from the excised larynx and tested with a tensile cyclic stretch-release paradigm (Chan et al, 2007). The sample preparation and testing protocols were approved by the Institutional Review Board of University of Texas Southwestern Medical Center. The cover and ligament specimens were dissected with instruments for phonomicrosurgery, separated from the underlying vocalis muscle and immediately placed in phosphate buffered saline (PBS). As the tensile stretch test required sections of thyroid and arytenoid cartilages dissected together with a cover or a ligament specimen (to maintain the natural anterior and posterior attachments), it was only possible to dissect the vocal ligament contralateral to the vocal fold cover within any single larynx.

Table 1.

Details on the human vocal fold specimens for this study (L₀ = initial length of the mid-membranous portion of the specimen (see Figure 2), D₀ = initial specimen cross-sectional diameter).

Subject	Gender	Age	Postmortem Hours	Specimen	L0 [mm]	D0 [mm]
A	Male	45	18	Ligament	5.71	2.5
				Cover	6.32	1.5
B	Male	64	19	Ligament	4.86	2.7
				Cover	4.27	1.1
C	Male	57	44	Ligament	4.86	2.7
				Cover	4.04	0.9
D	Female	73	76	Ligament	3.76	1.8
				Cover	3.71	0.8
E	Female	70	65	Ligament	3.51	1.7
				Cover	3.84	0.8
F	Female	97	59	Ligament	3.30	2.3
				Cover	3.11	0.6

2.2 Uniaxial Tension

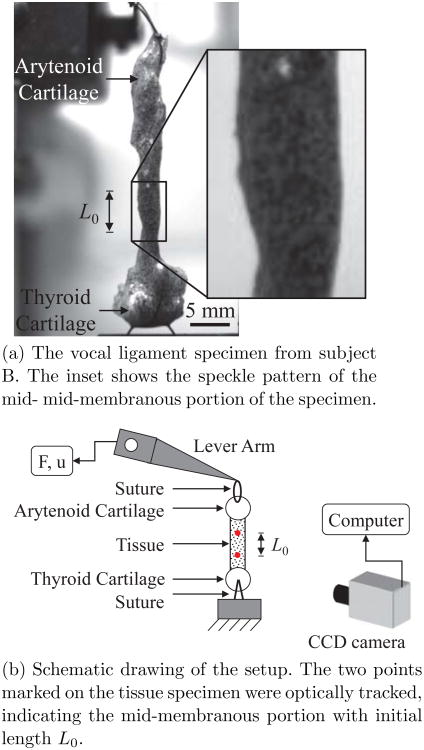
3-0 nylon sutures were inserted through the center of a section of arytenoid cartilage and the center of a section of thyroid cartilage, both remained naturally attached to the vocal ligament or vocal fold cover specimen following dissection. The suture inserted through the arytenoid cartilage section was connected to the actuator (lever arm) of a servo-controlled lever system¹, while the suture in the thyroid cartilage section was connected to the mechanical support at the bottom of the experimental setup.

Figure 2 depicts the tensile experimental setup. The lever system was under displacement feedback control, and was connected to a function generator and an oscilloscope to monitor the displacement input. The tensile force response of the specimen was detected by the lever system, digitized at 500 samples/sec and output for further analysis. A small amount of pre-load (typically 0.01-0.02 N) was applied to the tissue in order to remove any suture slackness. The applied displacement was sinusoidal at 1 Hz with an amplitude of 4.0 to 8.0 mm, depending upon the initial in situ vocal fold length. The length measurements in Table 1 were made after the specimen was dissected. Each tissue was mounted in the tensile testing setup in a manner where the specimen's length was near the in situ measurement in order to closely mimic the physiological state. The uniaxial tensile test was conducted for 180 cycles, similar to previous studies on vocal fold elasticity (Kelleher et al, 2011, 2012).

Fig. 2.

The experimental setup for the cyclic tensile stretch test.

A monochrome CCD camera² (pixel size of 9.9 × 9.9 μm, maximum frame rate of 75 fps) together with a macro-lens³ was used to capture images continuously during the experiment, in order to optically track the specimen displacement at specific points. A spirit level was used to ensure that the optical path of the camera was perpendicular to the specimen axis. A traceable speckle pattern was applied to the surface of the tissue specimen by using black enamel based spray paint. The spray paint produced a fine mist where the sizes of the black spots on the specimen were less than 1 mm. This procedure resulted in a covering of the tissue specimen surface with a discontinuous speckle pattern (see Figure 2(a)) such that specimen stiffness and moisture ingress were not disturbed (Kelleher et al, 2010, 2011). During the experiment, specimens were kept in air at room temperature to avoid optical distortions related to the use of a glass chamber with physiological solution, as well as dissolution or smudging of the spray paint. Instead, specimens were hydrated periodically by dripping PBS onto the tissue.

Optical measurements of tensile deformation have been shown to be crucial for vocal fold tissues (Kelleher et al, 2011). Therefore, displacements of two points on the specimen surface at equidistant longitudinal locations from the anterior commissure and the vocal process were obtained from image sequences via digital image correlation functions of the Image Processing Toolbox™ of Matlab®. The elongation of this mid-membranous portion of the tissue specimen was computed optically. The tensile stretch λ can then be calculated by

$$\lambda =1+\frac{\Delta L}{L_0}$$ (1)

where ΔL is the elongation of the tissue specimen as determined from the displacement data at the two measurement points. The point tracking algorithm used for determining ΔL were confirmed to be accurate within ±1 pixel (approximately ±0.06 mm) by manually tracking the points using NIH ImageJ, as in other studies (Kelleher et al, 2011).

Distance measurements were calibrated by taking the image of an object of known dimensions to establish a pixel-to-mm ratio. The specimen diameter was optically measured at five equidistant locations between the two points defining L₀, and the cross-sectional area was calculated assuming the tissue specimen to be of circular cross-section. A second CCD camera, orthogonal to the first, confirmed the circular cross-section to be a reasonable assumption (the diameter measurements from each camera were generally within 10%) though it is generally more applicable for describing the geometry of the vocal ligament specimens. The circular cross-section approximation is an outcome of the dissection procedure and not necessarily applicable to the in vivo geometry. The five area measurements were averaged to estimate the cross-sectional area A₀. The average cross-sectional diameter D₀ is given in Table 1. Finally, the nominal stress σ = F/A₀ was determined from the force output from the lever arm F and the cross-section area A₀ in the undeformed state. The linear (i.e. small stretch) portion of the loading and unloading curves of the tensile stress-stretch response was characterized by a linear elastic model as

$$\sigma =E_L^i(1+\lambda )$$ (2)

where $E_L^i$ is the longitudinal elastic modulus and i = loading or unloading, respectively. The first few points of the loading (or unloading) curve were fit to Eqn. 2. Each successive point along the curve was added and re-fit until the coefficient of determination (R²) value began to consistently decrease. The stretch level at this instance (typically λ ≈ 1.05) was determined to be the end of the linear regime. The longitudinal elastic modulus E_L was then taken as the average of the modulus of the loading and unloading curves within the linear, small stretch region.

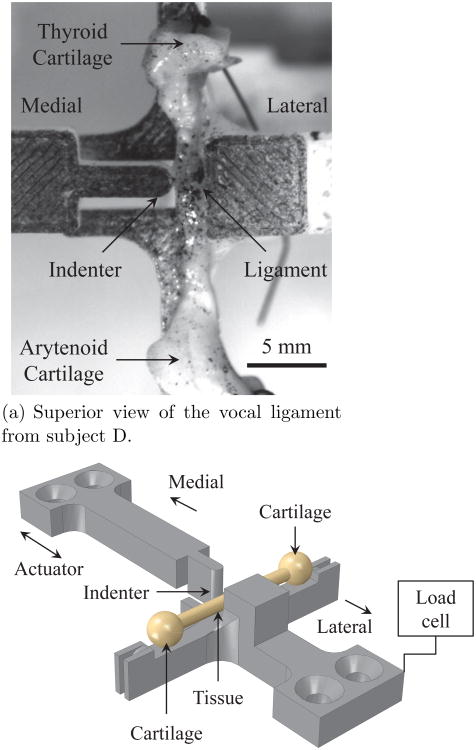
2.3 Transverse Indentation

Immediately following the uniaxial tensile stretch experiment, the specimen was placed in PBS and allowed to rest for at least 75 minutes. As the vocal fold lamina propria is a connective tissue (primarily an extracellular matrix), unlike other tissue types such as muscles, it is not as susceptible to postmortem tissue changes that would significantly affect the mechanical properties. In fact, changes in elastic shear modulus of the vocal fold lamina propria within 24 hours postmortem at room temperature have been shown to be minimal (Chan and Titze, 2003). The specimen was then positioned onto another mechanical testing device⁴ for the transverse indentation experiment. A custom test fixture (see Figure 3) was designed for the Bose ELF 3200 system. The fixture was fabricated using a rapid prototyping system⁵ and made of acrylonitrile butadiene styrene (ABS) which possesses a modulus several orders of magnitude larger than the vocal folds. The moving part of the fixture serves as an indenter (radius of 1.0 mm) and was driven by the linear motor of the system in a sinusoidal fashion at 1 Hz. The stationary part of the fixture provides a rigid support for the specimen to be compressed against, and was connected to a precision miniature strain-gauge load cell with a range of ±2.45 N and a non-repeatability error of ±2.45 mN.⁶ Precise translational oscillatory actuation was enabled by displacement feedback control via a linear variable differential transformer (linearity error of ±16 μm) in the Bose ELF 3200 system. The diameter of the tissue specimen at the location of indentation was measured optically. The applied compressive displacement ranged from 0.12 to 0.48 mm, such that all tissue specimens were indented to approximately 30% of their initial diameter for a total of 60 cycles. The displacement of the indenter and the compressive force response of the specimen were digitized at 5000 samples/sec and output for further analysis. Also, the raw force signal was filtered to remove high frequency noise. The data was filtered with a low-pass Butterworth filter of second order and a cutoff frequency of 10 Hz with the Signal Processing Toolbox™ of Matlab®.

Fig. 3.

The experimental setup for the transverse indentation test.

The indentation setup is shown in Figure 3. Following dissection, the medial surface of the tissue was identified, typically by the vocal process or the thyroid cartilage which was bisected in the mid-sagittal plane at the anterior commissure, such that the orientation of the specimen was always known. The tissue was positioned such that the indentation took place in the medial-to-lateral direction at a frequency of 1 Hz, with no tension applied along the anterior-posterior direction of the specimen. Along the anterior-posterior axis, the specimen was indented at the mid-coronal location so that the tissue was indented within the gauge length of the measurements in the tensile experiment. This is imperative because our previous studies have shown that there is a spatial heterogeneity in the elastic modulus of vocal fold tissues (Kelleher et al, 2010, 2012). Thus, the location of indentation must match the tissue region where the stretch is optically measured from the uniaxial tensile test in order to make an accurate comparison of the longitudinal and transverse properties.

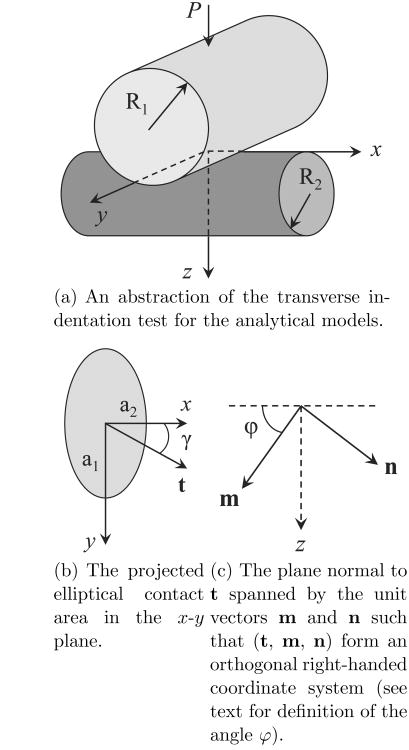
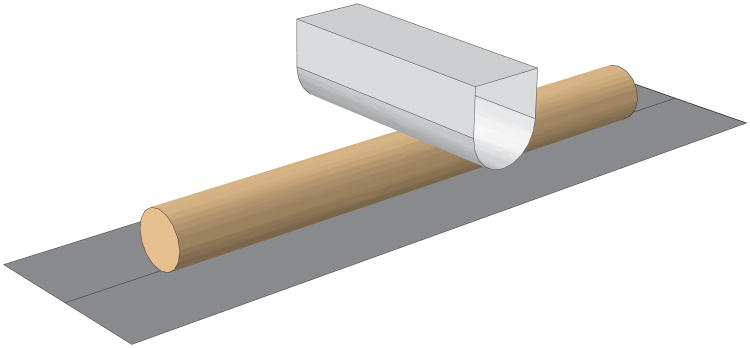
The compressive force-displacement response was evaluated using an anisotropic contact model and considering a transversely isotropic tissue. The transverse indentation experiment was modeled as contact between two cylinders with perpendicular axes, Figure 4(a). The analytical solution for two contacting cylinders with perpendicular axes is equivalent to a sphere contacting an elastic half-space with an effective Gaussian radius of curvature $\stackrel{\sim }{R}=\sqrt{R_1{R}_2}$ (Popov,2010).

Fig. 4.

Model of the indentation experiment.

The analytical solution of the force-indentation depth response accounting for the tissue anisotropy follows from Swadener and Pharr (2001), which was developed for the more general case of complete anisotropy. Now considering a transversely isotropic tissue with the axis of material symmetry being in the x-direction and subjected to an indentation load in the z-direction (as depicted in Figure 4), the stiffness tensor C_ijkl of the stress-strain relationship σ_ij = C_ijkl∊_kl is

$$C_{\mathit{\text{ijkl}}}=\left[\begin{array}{cccccc}{C}_{11}& C_{12}& C_{13}& 0& 0& 0\\ C_{21}& C_{22}& C_{23}& 0& 0& 0\\ C_{31}& C_{32}& C_{33}& 0& 0& 0\\ 0& 0& 0& \frac{E_T}{2(1+{\nu }_{\mathit{\text{TT}}})}& 0& 0\\ 0& 0& 0& 0& G_L& 0\\ 0& 0& 0& 0& 0& G_L\end{array}\right]$$ (3)

$$C_{11}=E_L(1-{\nu }_{\mathit{\text{TT}}}^2)Y$$

$$C_{12}=C_{13}=C_{21}=C_{31}=E_L({\nu }_{\mathit{\text{TL}}}+{\nu }_{\mathrm{TT}}{\nu }_{\mathit{\text{TL}}})Y$$

$$C_{22}=C_{33}=E_T(1-{\nu }_{\mathit{\text{TL}}}{\nu }_{\mathit{\text{LT}}})Y$$

$$C_{23}=C_{32}=E_T({\nu }_{\mathit{\text{TT}}}+{\nu }_{\mathit{\text{TL}}}{\nu }_{\mathit{\text{LT}}})Y$$

$$Y=\frac{1}{1-{\nu }_{\mathit{\text{TT}}}^2-2{\nu }_{\mathit{\text{TL}}}{\nu }_{\mathit{\text{LT}}}-2{\nu }_{\mathit{\text{TT}}}{\nu }_{\mathit{\text{TL}}}{\nu }_{\mathit{\text{LT}}}}$$

The symmetry condition requires that E_Lν_TL = E_Tν_LT, thus reducing the number of elastic constants to five: E_L, E_T, G_L, ν_TT, ν_LT. The P-δ relation for an anisotropic half-space contacted by a rigid frictionless sphere is

$$P=\frac{4M\sqrt{R}}{3}{\delta }^{3/2}$$ (4)

where P is the indentation force, M is the indentation modulus, and δ is the indentation depth. The radius of curvature R should be substituted with R̃ for the case of the contacting cylinders with perpendicular axes. The indentation modulus M is

$$M=\frac{2\pi }{{\int }_0^{\pi }\frac{a_{3i}{B}_{\mathit{\text{ij}}}^{-1}(\gamma )a_{3j}}{{[(a_1/a_2){\text{cos}}^2\gamma +(a_2/a_1){\text{sin}}^2\gamma ]}^{1/2}}d\gamma }$$ (5)

where a_3i are the direction cosines of the indentation load normal to the surface, B is a Barnett-Lothe tensor, a₁ and a₂ are the semiaxes of the contact ellipse, and γ is the angle between t and the x-axis. It was initially assumed that the contact area is circular, a₁/a₂ = 1. Furthermore, since the indentation was occurring orthogonal to the axis of material symmetry and not offset at some angle, then a₁ and a₂ will be aligned with the x and y axes (i.e. the angle φ defined in Swadener and Pharr (2001) is zero). The Barnett-Lothe tensor B is

$$\mathbf{\text{B}}(t)=\frac{-1}{\pi }{\int }_0^{\pi }[(\text{mn}){(\text{nn})}^{-1}(\text{nn})-(\text{mm})]d\phi$$ (6)

with φ being the angle between m and an arbitrary datum in the plane normal to t. The second-order tensors (ab) are defined as (ab)_jk = a_iC_ijklb_l, and the unit vectors with respect to the (x, y, z) coordinate system are m = [−cos φ sin γ cos φ cos γ sin φ]^T and n = [sin φ sin γ − sin φ cos γ cos φ]^T, where T denotes the transpose. The primary equations concerning the anisotropic contact model relevant to this investigation are given above, but readers seeking more details should consult the original article by Swadener and Pharr (2001).

Equations 3–6 were implemented and solved numerically in Matlab®. The integration of B and M were performed using the trapezoidal rule over the open interval from 0 to π (0 < γ, φ < π). The tissue was assumed to be nearly incompressible so ν_LT = 0.45 and ν_TT = 0.95 (though the model was insensitive to these values, see Appendix B), and E_L was known from the uniaxial tensile test. The anisotropic contact model received inputs for the elastic constants E_L, ν_LT, ν_TT and the effective Gaussian radius of curvature R̃. Therefore, two parameters E_T and G_L, remain to be inversely estimated relative to the experimental data.

The anisotropic contact model was fitted to the midline of the hysteresis loop of the filtered P-δ response by a nonlinear least-squares approach. Upper and lower bounds were set on the parametric search space for E_T and G_L. Supposing the extreme case of an isotropic tissue, the upper bounds were [E_LE_L/2] for E_T and G_L, respectively. The lower bounds for E_T and G_L were set to zero. Additionally, a constraint was imposed such that E_T > G_L. An optimization process was executed which solved the least-squares problem for multiple start points for E_T and G_L, in an effort to find the global minimum rather than local minima. The initial start point given was the solution of the classical Hertzian contact law for isotropic materials P = 4Ê_T√R̃δ^3/2 / [3(1 − ν²)], i.e. [Ê_TÊ_T /3] for E_T and G_L, respectively. The set of E_T and G_L that was deemed the optimal solution was one that met the conditions above and minimized the residual sum of squares (RSS). As a measure of the goodness-of-fit, the coefficient of determination R² = 1 − RSS/TSS, where TSS is the total sum of squares, was calculated and provided in Table 2.

Table 2.

The effective radius of curvature and the elastic constants from all subjects. E_L was estimated from the uniaxial tensile test, E_T and G_L from the anisotropic contact model along with R² representing the goodness-of-fit.

			Tension	Anisotropic contact model
Subject	Specimen	R̃ [mm]	EL [kPa]	ET [kPa]	GL [kPa]	R2
A	Ligament	0.87	28.20	2.53	0.91	1.000
	Cover	0.70	196.40	5.18	4.18	0.997
B	Ligament	1.01	29.95	1.18	0.89	0.997
	Cover	0.73	579.20	7.17	6.01	0.978
C	Ligament	1.01	24.32	1.48	0.77	0.997
	Cover	0.54	268.20	8.25	7.50	0.976
D	Ligament	0.96	25.82	1.51	0.78	0.996
	Cover
		0.48	302.25	14.35	6.42	0.999
E	Ligament	0.90	38.56	5.06	1.59	0.999
	Cover	0.49	199.80	4.80	3.24	0.976
F	Ligament	0.85	14.11	3.08	1.03	0.999
	Cover	0.47	253.85	11.93	7.62	0.988

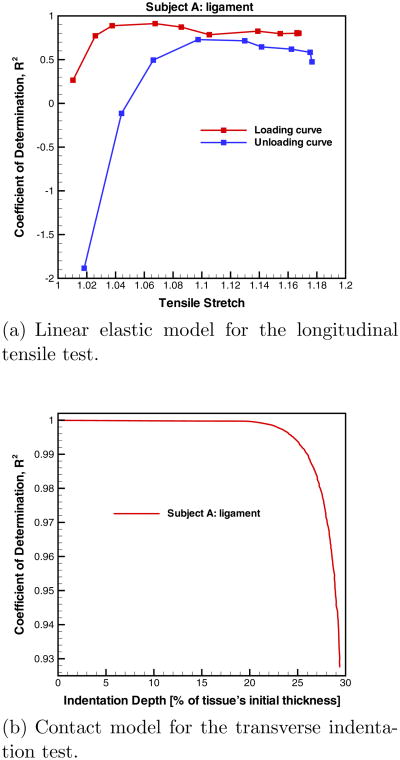
Each tissue specimen was indented to approximately 30% of its initial diameter. However, compressing the tissue to this level may induce substantial nonlinear effects causing the linear contact models (both isotropic and anisotropic) to poorly predict the nonlinear experimental P-δ response. It was observed that the P-δ response begins to exhibit nonlinearity when the indentation exceeds approximately 20% of the specimen's initial thickness, for our indentation setup. As an example, the contact models were fit to the P-δ curve for the vocal ligament of subject A at increasing levels of indentation depth. The goodness-of-fit (i.e. R² value) is very good until an indentation depth of approximately 20%, which can be seen in Appendix A. Therefore, the contact models were fitted to the experimental P-δ response until 20% indentation depth to ensure linearity. This approach was similar to the one described previously (§ 2.2) for curve fitting the tensile data.

3 Results

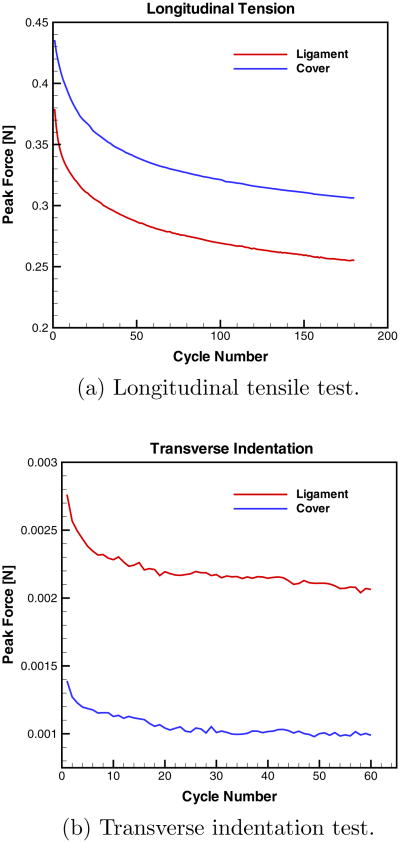
All vocal fold tissue specimens exhibited a time dependent response with the stress at maximum applied stretch/indentation declining continuously with the number of load cycles N, such that no steady state response was reached, consistent with other studies (Chan et al, 2009; Zhang et al, 2009). Thus, the elastic constants E_L, E_T, and G_L were obtained from a representative cycle such that transient effects associated with tissue preconditioning were minimized, following the approach of Kelleher et al (2011). In particular, data are presented for the 55^th loading cycle of both the uniaxial tension and transverse indentation tests. For uniaxial tension, the average in-cycle peak force decayed by 33% from cycles N = 1 to N = 180. The detailed analysis of the tissue specimens was conducted for cycle N = 55 where the peak force had experienced on average 75% of the total decay. For transverse indentation, the average in-cycle peak force decayed by 28% from cycles N = 1 to N = 60. Thus, by cycle N = 55 the peak force had experienced on average 92% of the total decay. An example of the in-cycle peak force decay in dependence of the applied load cycle number for both the tensile and indentation experiments, along with sample longitudinal σ-λ and transverse P-δ curves for subject A are displayed in the Appendix.

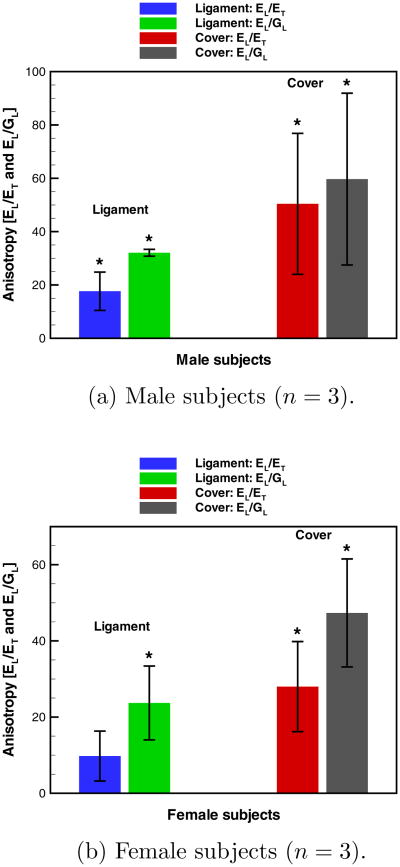
The values of the elastic constants computed for all subjects are given in Table 2. The mean and standard deviation of ratios E_L/E_T and E_L/G_L, commonly employed as measures of the “degree of anisotropy,” are presented in Figure 5 for the cover and ligament specimens from male and female subjects. Ratios E_L/E_T and E_L/G_L were computed within each tissue specimen and then the mean was calculated, rather than taking the population mean of E_L and then dividing it by the population mean of E_T or G_L. The mean and standard deviation of E_L/E_T was 14±8 for the vocal ligament and 39±22 vocal fold cover specimens of all subjects. For E_L/G_L, the mean and standard deviation for all subjects was 28±8 for the vocal ligament and 54±23 for vocal fold cover specimens. Furthermore, on average the male subjects had higher E_L/E_T and E_L/G_L ratios than the female subjects, though it was not statistically significant. For all subjects tested, the vocal fold cover was stiffer in longitudinal tension than its contralateral vocal ligament roughly by a factor of 10, consistent with the findings of Chan et al (2007). Also, the vocal fold cover exhibited a larger E_T and G_L than its contralateral vocal ligament, except for subject E. In order to assess the anisotropic model's sensitivity to assumed values (a₁/a₂, ν_LT, and ν_TT) and material parameters (E_L, E_T, and G_L), a sensitivity study was conducted for one subject and the results are in Appendix B. Additionally, the anisotropic contact model is validated in a numerical experiment with a finite element model given in Appendix C.

Fig. 5.

Mean ± standard deviation of the anisotropy ratios (E_L/E_T and E_L/G_L) for the vocal ligament and vocal fold cover. * denotes that E_L/E_T > 1 or that E_L/G_L > 3 with statistical significance (p < 0.05).

Hypothesis testing of the data was conducted to determine if the anisotropic tissue parameters were different from the isotropic tissue with statistical significance (p < 0.05). The mean anisotropy ratios (E_L/E_T and E_L/G_L) were the test statistics. The null hypotheses were that the mean of E_L/E_T was equal to one, and that the mean of E_L/G_L was equal to three – signifying that the material is isotropic. The alternative hypotheses were that the mean of E_L/E_T and E_L/G_L were greater than one and three, respectively – signifying that the tissue is anisotropic. The hypothesis tests were performed using a one-tailed Student's t-distribution for four cases with n = 3: vocal ligament from male subjects, vocal fold cover from male subjects, vocal ligament from female subjects, and vocal fold cover from female subjects.

It was found that E_L/E_T was greater than one with statistical significance for the vocal ligament (p = 0.028) and vocal fold cover (p = 0.042) from male subjects, but only the vocal fold cover (p = 0.029) from female subjects. Also, the ratio E_L/G_L was greater than three with statistical significance for the vocal ligament (p = 0.0003) and vocal fold cover (p = 0.046) from male subjects, and the vocal ligament (p = 0.033) and vocal fold cover (p = 0.016) from female subjects.

An additional hypothesis test was conducted to determine if the means of E_L/E_T and E_L/G_L of the vocal fold cover were greater than those of the vocal ligament with statistical significance. The null hypotheses were that the mean anisotropy ratios of the cover were equal to those of the ligament. The alternative hypotheses were that the means of E_L/E_T and E_L/G_L of the cover were greater than those of the ligament. The male and female subjects were combined and E_L/E_T and E_L/G_L of the cover (n₁ = 6) were compared to those of the ligament (n₂ = 6) using a two sample Student's t-distribution. It was discovered that E_L/E_T and E_L/G_L of the cover were significantly greater than those of the ligament (p = 0.018 and p = 0.021, respectively) with all subjects combined.

4 Discussion

The results in this investigation reveal that the longitudinal elastic modulus of the vocal fold cover is generally larger than that of the vocal ligament, which is consistent with other studies (Chan et al, 2007; Hirano et al, 1982; Zhang et al, 2007; Kelleher et al, 2011). The transverse elastic modulus results corroborate the findings on canine vocal folds where typically E_L > 10E_T (Hirano et al, 1982). Additionally, the values of E_L reported here for the vocal ligament specimens compare well to those in previous studies where E_L of the ligament was estimated to be near 30 kPa (Min et al, 1995). Measurements of the complete set of transversely isotropic elastic properties of human vocal fold tissue have not been reported so far. In studies concerned solely with measurements of the transverse response of humans and canines, the transverse modulus was typically estimated to be in the range of 1-10 kPa (Chhetri et al, 2011; Hirano et al, 1982; Tran et al, 1993), which is in the range measured in this study. Concerning anisotropy values of other biological samples reported in the literature, the ratio of E_L/E_T common in bone is approximately 2 (Lotz et al, 1991; Dong and Guo, 2004). This ratio is larger in non-mineralized tissue with E_L/E_T ≈ 4 for shoulder ligaments (Moore et al, 2004, 2005) and E_L/E_T ≈ 30 for the knee ligaments (Quapp and Weiss, 1998), indicating that the anisotropy is likely dependent upon the tissue's function. The anisotropy E_L/E_T presented here for the vocal fold lamina propria is near that of other soft tissues, particularly those of the knee. Also, when comparing the transverse elastic modulus E_T with the prediction from an isotropic contact model, it was discovered that there was only a mild difference. Therefore, the isotropic solution may be used to provide a quick initial guess for E_T which has been suggested in similar investigations (Vlassak et al, 2003).

The averages of E_L/E_T and E_L/G_L of the cover were greater than the ligament with statistical significance, indicating that the vocal fold cover is more anisotropic. This outcome seems contradictory to previous histological studies that have reported the vocal ligament (middle and deep layers of the lamina propria) to have more longitudinally aligned fibrous proteins than the vocal fold cover (epithelium and superficial layer of the lamina propria, SLLP, encompassing the basement membrane zone, BMZ) (Gray et al, 2000; Hammond et al, 2000). Nonetheless, some histological examinations have found less type I collagen in the intermediate layer than in the superficial and deep layers (Bühler et al, 2011). It has also been proposed that, “Although the SLLP has been characterized as having sparse and loose fibrous proteins, the SLLP around the BMZ is relatively rich in the deeper part of the SLLP not only in collagen type III, but also in collagen type I and elastin. The SLLP around the BMZ might be regarded as a different layer from that identified as the deeper part of the SLLP” (Tateya et al, 2006). Additionally, there may be age-related aberrations in the microstructure since all the subjects tested in this study, except subject A, were geriatric. Aging has been shown to potentially cause increased cross-linking of fibers (Monniere and Sell, 1994; Sato and Hirano, 1997), increased prevalence of disarray of the microarchitecture (Madruga de Melo et al, 2003), and elastic fibers that are looser and more atrophied in the intermediate layer of the lamina propria (Hirano et al, 1982). Even though the finding that the longitudinal elastic modulus of the cover is generally larger than that of the ligament may seem to disagree with the classical histological findings, this observation has actually been corroborated by some other studies (Chan et al, 2007; Hirano et al, 1982; Zhang et al, 2007; Kelleher et al, 2011). Therefore, our results suggest that the familiar notion that the vocal fold cover is an isotropic tissue layer with a loose fiber architecture may need to be reassessed.

This study quantitatively reports the anisotropic biomechanical properties within a single human vocal fold specimen. As noted earlier, the elastic constants (E_L, E_T, and G_L) are crucial to accurately replicate vibration characteristics in models of phonation (Cook et al, 2009). The biomechanical constants presented in this paper may have significance relating to phonatory processes. The shear mode of deformation is known to be a primary factor contributing to the mucosal wave of vocal fold vibration (Titze, 2006). However, this mode cannot be captured in string or classical (i.e. Euler-Bernoulli) beam models of phonation. It was recently demonstrated in an approximate analytical Timoshenko beam model that the fundamental frequency of vibration would decrease by roughly 30% for E_L/G_L near 40-50 with typical vocal fold length and diameter dimensions (Kelleher et al, 2011). This decrease is not present in models that do not account for rotary inertia nor shear deformation. Based on the current findings continuum models of phonation could now have a realistic range for elastic constants which were previously assumed, even though the sample size in this study is small. Additionally, it is proposed that this transverse indentation approach could be tested in vivo, with an instrument like that described by Tran et al (1993). This could potentially provide data for the transverse stiffness of the vocal folds in an in situ, natural, physiological environment.

In order to accurately model more advanced phonatory processes (e.g. vocal fold posturing) where longitudinal tensile stretch is present with shear deformation, the evolution of E_T and G_L as a function of the longitudinal load will need to be understood. This development of the elastic constants of vocal folds subjected to multi-axial loads is a subject of future research. Also, assessing the anisotropy as modulus ratios, E_L/E_T or E_L/G_L, is a good foundation, but a more detailed understanding of anisotropy could be gained through a multi-scale constitutive model incorporating quantitative histological data on the vocal fold anisotropic microstructure (e.g. the orientation of collagen and elastin fibers). Recent work to study the morphology of vocal fold fibrous proteins with advanced microscopy techniques could be a promising method to obtain such quantitative microstructural data (Miri et al, 2012).

The findings of this study should be regarded as preliminary, as limited by the small sample size, as well as several other limitations. First, only the initial linear response of the σ-λ and P-δ curves were analyzed. This represents a first step towards understanding the biomechanical anisotropy in human vocal folds, yet it is not a complete description. How the nonlinearity of the σ-λ and P-δ curves at larger deformations could change the anisotropy should be addressed in future studies. Another limitation of the current study is the 1 Hz loading rate in the transverse (medial-lateral) direction during indentation. This indentation loading rate was chosen in order to be consistent with the 1 Hz tensile test. However, with regard to phonation, the transverse compressive forces encountered during vocal fold collision occur at phonatory frequencies (roughly 100-250 Hz). Testing the tissue under such high loading rates would likely produce a much stiffer material response due to the viscous nature of the tissue. The transverse shear modulus has been shown to increase substantially as the loading rate is increased to the phonatory range (Chan and Rodriguez, 2008). Estimations of the transverse properties E_T and G_L could potentially be extrapolated to the high frequency regime if the material's time dependence in the transverse direction was known. Therefore, the transverse elastic properties of human vocal folds at higher frequencies should also be examined by further studies.

5 Conclusion

A new protocol has been developed to quantitatively measure the biomechanical anisotropy of vocal fold tissues within a single specimen. The protocol included each specimen being subjected to cyclic uniaxial tensile loading in the longitudinal (i.e. anterior-posterior) direction, and then to cyclic indentation loading in the transverse (i.e. medial-lateral) direction. For this investigation, experiments were performed on the lamina propria of three male and three female human vocal folds dissected from excised larynges. A rigorous analytical treatment of the indentation test was achieved by modeling the contact with a transversely isotropic half-space using the Barnett-Lothe tensors. The longitudinal elastic modulus E_L was computed from the tensile test, whereas the transverse elastic modulus E_T and the longitudinal shear modulus G_L were obtained by inverse analysis of the indentation force-displacement response. E_L/E_T and E_L/G_L ratios were computed as indications of the degree of anisotropy. The tissue specimens exhibited substantial anisotropy. It was found that the average ratios E_L/E_T and E_L/G_L of the vocal fold cover were greater than those of the vocal ligament with statistical significance, signifying that the vocal fold cover is more anisotropic. These measurements of anisotropy could contribute to more accurate models of fundamental frequency regulation and provide potentially better insights into the mechanics of vocal fold vibration.

Fig. 7.

The goodness-of-fit, represented by R², to the experimental data from the vocal ligament of subject A.

Appendix A

As one example of the complete analysis Appendix A provides experimental data details for subject A of this study. Figure 6 depicts the in-cycle peak force decays in the cyclic tensile and indentation experiments.

Fig. 6.

The peak force decay as a function of the cycle number for subject A.

The linear elastic model and contact model were fit to the σ-λ and P-δ curves, respectively, for the vocal ligament of subject A at increasing levels of stretch or indentation depth. The goodness-of-fit (i.e. R² value) begins to decline at an indentation depth of approximately 20% of the tissue's initial diameter due to nonlinear effects in the P-δ curve.

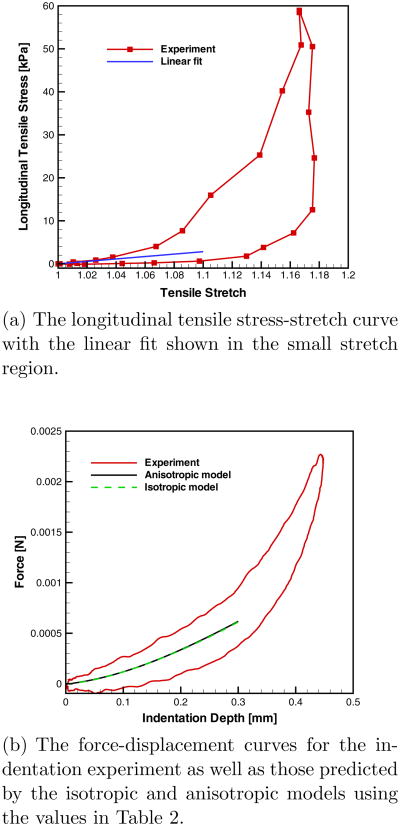
The longitudinal σ-λ and transverse P-δ curves for the vocal ligament of subject A. The linear fit of E_L lies within the small stretch regime of the loading and unloading tensile response in Figure 8(a). For the transverse indentation response, the isotropic and anisotropic contact models yield P-δ curves that are identical in Figure 8(b), but the values of elastic constants (E_T, G_L, and Ê_T) obtained are different (see Table 2).

Fig. 8.

Experimental and model results for the 55^th loading cycles of the vocal ligament of subject A.

Appendix B

A brief sensitivity analysis was performed using subject A in order to assess the anisotropic contact model's sensitivity to certain parameters. First, the assumption of a circular contact area was tested. The ratio of the semiaxes of the contact ellipse a₁/a₂ was increased from 1.0 to 1.5, causing the predicted parameters E_T and G_L to decrease by 0.5%. This reveals that the model is essentially unaffected by a₁/a₂, as supported by another study for a broad range of anisotropic materials (Swadener and Pharr, 2001). Next, the Poisson ratios ν_LT and ν_TT were changed to see their effect on E_T and G_L. When increasing ν_LT from 0.45 to 0.49, the estimations of E_T and G_L decreased by approximately 2%; and increasing ν_TT from 0.95 to 0.99, caused E_T and G_L to increase by almost 1.0%. Once again, the model is relatively insensitive to the choice of the two Poisson's ratios.

Since the model's sensitivity to assumed values has been shown to be minimal, the sensitivity to computed parameters (i.e. elastic constants) was then explored. The longitudinal elastic modulus E_L was varied by ±10% which resulted in E_T and G_L changing by about ±5%, respectively. Holding E_L constant and then varying E_T by ±10% caused the estimated value of G_L to change by approximately ∓4%, respectively. Finally, varying only G_L by ±10% resulted in the estimated value of E_T to change by ∓30%, respectively. Therefore, the most sensitive parameter seemed to be the longitudinal shear modulus.

Appendix C

In order to validate the anisotropic contact model, a finite element model of the indentation experiment was created and analyzed using the commercial software ABAQUS (version 6.11). The finite element model consisted of two cylinders with perpendicular axes contacting each other (see Figure 9). The indenter was modeled as a rigid body. The tissue was modeled as a transversely isotropic linear elastic solid, and discretized using 10 node modified three-dimensional tetrahedron hybrid elements with hourglass control (C3D10MH). The nodes at both ends of the cylinder representing the tissue were fixed in all directions. Additionally, a rigid plane was defined to provide the contact constraint as the indenter compresses the tissue from the medial direction. The cylinder representing the tissue had a diameter of 1.5 mm and a length of 15 mm. The indenter radius was 1 mm. In a numerical experiment, the tissue was assumed to be linear elastic and transversely isotropic with the following material parameters: E_L = 28.2 kPa, E_T = 2.53 kPa, G_L = 0.91 kPa, ν_LT = 0.45, and ν_TT = 0.95. Such values correspond to the properties of the vocal ligament of subject A, which are typical anisotropies for the vocal fold tissue considered here. The force-displacement response was obtained as applied displacements and computed reaction forces at the reference node to the rigid surface representing the indenter. The data was used as input to the anisotropic contact model for inverse parameter estimation, together with E_L . The material parameters obtained as the outcome from the anisotropic contact model were E_T = 2.84 kPa and G_L = 0.88 kPa. This corresponds to errors of 12% for E_T and 3% for G_L.

Fig. 9.

The finite element model of the indentation experiment.