Bayesian Gamma Frailty Models for Survival Data with Semi-Competing Risks and Treatment Switching

Abstract

Motivated from a colorectal cancer study, we propose a class of frailty semi-competing risks survival models to account for the dependence between disease progression time, survival time, and treatment switching. Properties of the proposed models are examined and an efficient Gibbs sampling algorithm using the collapsed Gibbs technique is developed. A Bayesian procedure for assessing the treatment effect is also proposed. The Deviance Information Criterion (DIC) with an appropriate deviance function and Logarithm of the Pseudomarginal Likelihood (LPML) are constructed for model comparison. A simulation study is conducted to examine the empirical performance of DIC and LPML and as well as the posterior estimates. The proposed method is further applied to analyze data from a colorectal cancer study.

1 Introduction

In chronic disease or cancer studies and clinical trials, it is very common to have both terminating events and nonterminating events in the data. This type of situation is referred as semi-competing risks, in which an event time can be censored by another event time but not vice versa. A terminating event potentially censors a nonterminating event, but the nonterminating event does not prevent subsequent observation of the terminating event. An example of this is the colorectal cancer clinical trial that we examine here, called the panitumumab 408 study, which was conducted by Amgen Inc. (see Section 5). In this study, disease progression is a nonterminating event, death is a terminating event, and disease progression can be censored by death but not vice-versa. In addition to semi-competing risks, treatment switching may also occur in clinical trials. In such trials, patients in the control arm who experience an intermediate event, such as disease progression, may begin taking the experimental treatment. In the panitumumab 408 study, there were a substantial proportion of patients in the control arm who switched treatment after disease progression (see Section 5). As discussed in Marcus and Gibbons (2001), an intent-to-treat (ITT) analysis leads to attenuated treatment effect estimates, and thus one must properly model the data accommodating this switching effect and then appropriately estimate the treatment effect.

In semi-competing risks data, there are two major issues: dependent censoring and identifiability. In order to deal with these issues, several modeling and inference approaches have been developed. One major approach is to model the joint distribution of T_D and T_E, where T_D denotes the time to terminating event and T_E denotes the time to nonterminating event. Day and Bryant (1997) used frailty models for the joint survival function using a relevant censoring process. Later, Fine et al. (2001) adopted this model and proposed a novel estimator for the marginal distribution of T_E based on a bivariate location-shift model with a completely unspecified underlying distribution for T_D and T_E. Although this method is appropriate for modeling one recurrent event taking into account dependent censoring, it cannot be applied to more than two recurrent events. Furthermore, various types of copula models have been applied for modeling the joint distribution of (T_E, T_D) (Wang, 2003; Ghosh, 2006; Peng and Fine, 2007). Another approach is to model the gap time T_G between T_D and T_E (Mandel, 2010). Nonparametric estimation of the gap time distribution and regression methods for gap time hazard functions have been developed. A third approach is similar to the above gap time model. In addition to modeling T_E and T_G, another event time $T_D^{*}$ is introduced, which denotes the terminating event that happens without the nonterminating event T_E. Shen and Thall (1998) used such a model for obtaining the marginal distributions of T_E, T_G and $T_D^{*}$. They assumed that the distributions of T_E and $T_D^{*}$ are mutually independent. For the bivariate distribution of T_E and T_G, they used a bivariate generalized von Morgenstern distribution, which characterizes the positive or negative association between these two times using a single parameter. A conditional model is also developed (Zeng et al., 2012). Instead of modeling the joint distribution of T_E and T_G, a conditional model of T_G given T_E is used. Multistate modeling is another approach for survival data with semi-competing risks, in which no event, nonterminating event, and terminating event can be viewed as the three states in a multistate process. The focus of multistate modeling is mainly on the transition probabilities between different states. Aalen-Johansen estimators (Aalen et al., 1978; Andersen et al., 1993) can be used to estimate these transition probabilities. However, this approach does not provide much information on the dependence structure between the time to nonterminating event and the time to terminating event. Except for Zeng et al. (2012), most of the aforementioned articles do not directly deal with both semi-competing risks and treatment switching.

In this paper, we introduce a Bayesian frailty model for survival data with semi-competing risks in the presence of partial treatment switching (i.e., not every subject in the control arm switched to active treatment). In the frequentist inference, the Monte Carlo EM (MCEM) algorithm is often used to obtain the maximum likelihood estimates in the presence of the unobserved frailty variables. However, the MCEM algorithm may fail to converge when fitting a semi-competing risks frailty model with unknown parameters in the frailty distribution since the estimates of these unknown parameters are unstable. To overcome this challenging computational issue, we develop an efficient Gibbs sampling algorithm via the introduction of latent variables, reparameterization, and the collopsed Gibbs sampler. The Bayesian framework also allows us to characterize the conditions for model identifiability by examining posterior propriety. In addition, to appropriately estimate the treatment effect, we extend the method of Zeng et al. (2012) to derive the predictive survival function with partial treatment switching under the semi-competing risks frailty model and carry out Bayesian inference on this quantity without resorting to asymptotics.

The rest of the paper is organized as follows. Section 2 presents a detailed development of the semi-competing risks model via a gamma frailty including explicit expressions for the likelihood function based on the observed data. In Section 3, we characterize posterior propriety conditions under this complex model, provide the Bayesian formulation of the predictive survival function with partial treatment switching, develop an efficient Gibbs sampling algorithm, and introduce two Bayesian model comparison criteria. A simulation study is carried out to examine the empirical performance of the posterior estimates and Bayesian model criteria in Section 4, and a detailed analysis of a subset of the data from the panitumumab 408 study is presented in Section 5. We conclude the paper with a brief discussion in Section 6. The proofs of all theorems and detailed derivations of the computational development are given in the Appendices.

2 The Semi-Competing Risks Frailty Models

2.1 Models

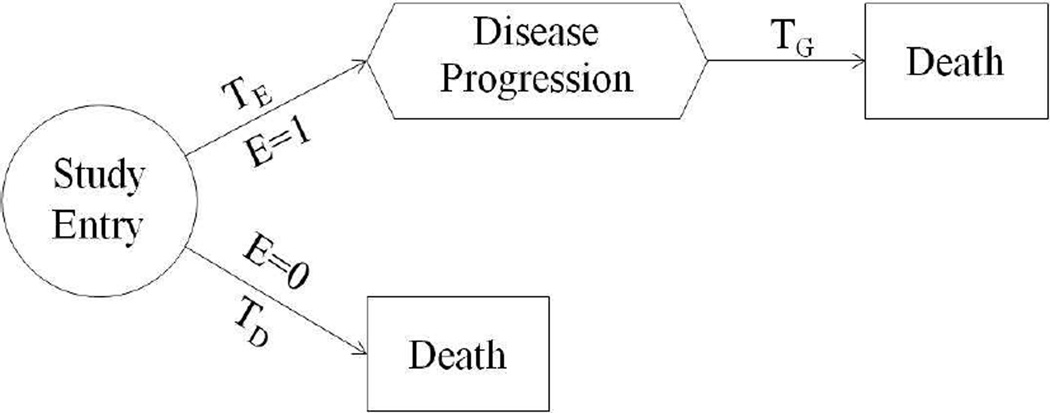
To introduce the proposed model, we use the following notation. As motivated from the panitumumab 408 study, we consider disease progression as a nonterminating event. However, the proposed model can be applied to any other type of nonterminating event. Let E be a dichotomous variable to denote the disease progression status of subjects, where E = 1 if the subject is in the disease progression population, which include subjects who eventually develop disease progression before death, and E = 0 if otherwise. Also let T_D denote the time from study entry to death for subjects with E = 0. For the disease progression population (E = 1), we further let T_E denote the time from study entry to disease progression and let T_G denote the time from disease progression to death. A graphical illustration of these variables is shown in Fig. 1.

Fig. 1.

A graphical illustration of key random variables in the semi-competing risks model.

The proposed statistical model consists of the following three components. The first component is to model the disease progression status E given the baseline covariates x and the treatment indicator A (A = 1 if the subject is on the treatment arm and A = 0 if the subject is on the placebo or control arm). To this end, we assume

$$\text{logit}(P(E=1|A,\mathit{x},\mathit{\alpha }))=\text{log}\{\frac{P(E=1|A,\mathit{x},\mathit{\alpha })}{1-P(E=1|A,\mathit{x},\mathit{\alpha })}\}={\alpha }_0+A{\alpha }_1+\mathit{x}\prime {\mathit{\alpha }}_2,$$ (2.1)

where α₀, α₁, and α₂ are unknown coefficients and $\mathit{\alpha }=({\alpha }_0,{\alpha }_1,{\mathit{\alpha }}_2^{\prime })\prime$. The second component models the survival distribution of the non-progression population given x and A, which is defined by

$$h_D(t|A,\mathit{x},E=0)=h_0(t)\text{exp}\{A{\beta }_0+\mathit{x}\prime {\mathbf{\gamma }}_0\},$$ (2.2)

where h_D(t|A, x, E = 0) is the conditional hazard function of T_D given the covariates, h₀(t) is an unknown baseline hazard function, and (β₀, γ₀) are unknown regression coefficients.

As shown in Fig. 1, T_E and T_G are potentially dependent. To capture this dependence, we assume the frailty model

$$h_E(t|A,\mathit{x},E=1,\omega )=h_1(t)\text{exp}\{A{\beta }_1+\mathit{x}\prime {\gamma }_1\}\omega \text{and}{h}_G(t|A,\mathit{z},V,E=1,\omega )=h_2(t)\text{exp}\{A{\beta }_{21}+V(1-A){\beta }_{22}+\mathit{z}\prime {\mathbf{\gamma }}_2\}\omega ,$$ (2.3)

where h_E(t|A, x, E = 1, ω) is the conditional hazard function for T_E, h_G(t|A, z, E = 1, ω) is the conditional hazard function for T_G, both h₁(t) and h₂(t) are unknown baseline hazard functions, and the β’s and γ’s are regression coefficients. Here, V is the treatment switching indicator (1 = switching; 0 = no switching) and z reflects the covariates collected at baseline or at disease progression, which could be prognostic factors for the treatment switching decision. In (2.3), ω is a latent gamma-frailty, which is assumed to follow a Gamma distribution, Gamma(1/τ, 1/τ ), with mean one, variance τ (τ > 0), and density given by $f(\omega |\tau )=\frac{{(1/\tau )}^{1/\tau }}{\Gamma (1/\tau )}{\omega }^{1/\tau -1}\text{exp}(-\omega /\tau )$. Given ω, T_E and T_G are conditionally independent. Unconditionally, T_E and T_G are dependent and, moreover, the local measure of dependence (Oakes, 1989) between T_E and T_G is ϕ_FM = 1 + τ, indicating a positive association between T_E and T_G. When τ → 0, ϕ_FM → 1 and T_E and T_G become independent. The model defined by (2.1) – (2.3) is thus called the semi-competing risks frailty model abbreviated by FM. As an alternative to (2.3), we may consider the following models for T_E and T_G:

$$h_E(t|A,\mathit{x},E=1)=h_1(t)\text{exp}\{A{\beta }_1+\mathit{x}\prime {\gamma }_1\}\text{and}{h}_G(t|A,\mathit{z},V,T_E,E=1)=h_2(t)\text{exp}\{A{\beta }_{21}+V(1-A){\beta }_{22}+T_E{\gamma }_{21}+\mathit{z}\prime {\gamma }_{22}\},$$ (2.4)

where γ₂₁ is the regression coefficient corresponding to T_E and γ₂₂ is the corresponding vector of regression coefficients associated with z. The model defined by (2.1), (2.2), and (2.4) is called the conditional semi-competing risks model, denoted by CM. After some algebra, we can show that the local measure of dependence between T_E and T_G under CM is given by ϕ_CM =[∫_tE{exp[−H₂(t_G) exp{Aβ₂₁ + V (1 − A)β₂₂ + γ₂₁u + z′γ₂₂}]h₁(u) exp(Aβ₁ + x′γ₁) × exp{−H₁(u) exp(Aβ₁ + x′γ₁)}}du exp(t_E γ₂₁)] × [∫_tE {exp[−H₂(t_G) exp{Aβ₂₁+V (1−A)β₂₂+γ₂₁u+z′γ₂₂}]h₁(u) exp(Aβ₁+x′γ₁)×exp{−H₁(u) exp(Aβ₁+x′γ₁)} exp(uγ₂₁)}du]⁻¹ for t_E > 0 and t_G > 0, where $H_j(t)={\int }_0^t{h}_j(u)du$ for j = 1, 2. Unlike ϕ_FM, ϕ_CM depends on (t_E, t_G). It is easy to see that ϕ_CM > 1 when γ₂₁ < 0, ϕ_CM = 1 when γ₂₁ = 0, and ϕ_CM < 1 when γ₂₁ > 0. This result implies that CM allows a positive or negative association between T_E and T_G. As discussed in Zhao (2009), FM is a homogeneous Markov model when h₂(t) is constant while CM is a homogeneous semi-Markov model since the hazard function for T_G in (2.4) depends on the progression time T_E. On the other hand, the marginal distributions of T_E and T_G after integrating out the gamma frailty belong to the class of generalized odds-rate hazards (GORH) models (see Banerjee et al, 2007). As the GORH model is a non-proportional hazards model, FM is more robust to the proportional hazards assumption than CM.

We further assume piecewise exponential models for the baseline hazard functions h₀(t), h₁(t), and h₂(t). For k = 0, 1, 2, let 0 < s_k1 < s_k2 < … < s_kJ_k be a finite partition of the time axis. Thus, we have the J_k intervals: (0, s_k1], (s_k1, s_k2], … (s_k,Jk−1, s_kJk], where s_kJk = ∞. In the j^th interval, we assume a constant baseline hazard, h_k(y|λ_k) = λ_kj for y ∈ (s_k,j−1, s_kj]. Letting λ_k = (λ_k1, λ_k2, …λ_kJ_k)′, the cumulative baseline hazard function corresponding to h_k(t) is given by

$$H_k(y|{\mathit{\lambda }}_k)={\lambda }_{kj}(y-s_{k,j-1})+\sum _{g=1}^{j-1}{\lambda }_{kg}(s_{kg}-s_{k,g-1})\text{when}{s}_{k,j-1}<y\le s_{kj}$$ (2.6)

for k = 0, 1, 2.

2.2 Likelihood Function

Suppose we have n subjects. Let y_i denote the observed death time or censoring time, x_i is the vector of baseline covariates, A_i is the treatment indicator, y_Ei is the observed disease progression time, z_i is the vector of covariates collected at baseline or at disease progression, and V_i is the indicator for treatment switching for the i^th subject for i = 1,…, n. Also let ν_i be the censoring variable such that ν_i = 1 if y_i is a death time and ν_i = 0 if y_i is a right censoring time, and let d_i be the indicator variable such that d_i = 1 if y_Ei is a disease progression time and 0 if there is no disease progression for the i^th individual. When d_i = 0, y_Ei is assumed to be equal to infinity. Finally, we use E_i to denote the disease progression indicator such that E_i = 1 if subject i is in the disease progression population and 0 otherwise. Let $P(E_i=0|A_i,{\mathit{x}}_i,\mathit{\alpha })=[1+\text{exp}{({\alpha }_0+A_i{\alpha }_1+{\mathit{x}}_i^{\prime }{\mathit{\alpha }}_2)]}^{-1},S_0(y_i|A_i,{\mathit{x}}_i,{\beta }_0,{\gamma }_0,{\mathit{\lambda }}_0)=\text{exp}\{-H_0(y_i|{\mathit{\lambda }}_0)\text{exp}(A_i{\beta }_0+{\mathit{x}}_i^{\prime }{\gamma }_0)\},f_0(y_i|A_i,{\mathit{x}}_i,{\beta }_0,{\gamma }_0,{\mathit{\lambda }}_0)=h_0(y_i|{\mathit{\lambda }}_0)\text{exp}(A_i{\beta }_0+{\mathit{x}}_i^{\prime }{\gamma }_0)S_0(y_i|A_i,{\mathit{x}}_i,{\beta }_0,{\gamma }_0,{\mathit{\lambda }}_0),S_1(y_{Ei}|A_i,{\mathit{x}}_i,{\omega }_i,{\beta }_1,{\gamma }_1,{\mathit{\lambda }}_1)=\text{exp}\{-{\omega }_i{H}_1(y_{Ei}|{\mathit{\lambda }}_1)\text{exp}(A_i{\beta }_1+{\mathit{x}}_i^{\prime }{\gamma }_1)\},f_1(y_{Ei}|A_i,{\mathit{x}}_i,{\omega }_i,{\beta }_1,{\gamma }_1,{\mathit{\lambda }}_1)={\omega }_i{h}_1(y_{Ei}|{\mathit{\lambda }}_1)\text{exp}(A_i{\beta }_1+{\mathit{x}}_i^{\prime }{\gamma }_1)S_1(y_{Ei}|A_i,{\mathit{x}}_i,{\omega }_i,{\beta }_1,{\gamma }_1,{\mathit{\lambda }}_1),S_2(y_{Gi}|A_i,V_i,{\mathit{z}}_i,{\omega }_i,{\beta }_2,{\gamma }_2,{\mathit{\lambda }}_2)=\text{exp}[-{\omega }_i{H}_2(y_{Gi}|{\mathit{\lambda }}_2)\text{exp}\{A_i{\beta }_{21}+V_i\times (1-A_i){\beta }_{22}+{\mathit{z}}_i^{\prime }{\gamma }_2\}]\text{and}{f}_2(y_{Gi}|A_i,V_i,{\mathit{z}}_i,{\omega }_i,{\beta }_2,{\gamma }_2,{\mathit{\lambda }}_2)={\omega }_i{h}_2(y_{Gi}|{\mathit{\lambda }}_2)\text{exp}\{A_i{\beta }_{21}+V_i(1-A_i){\beta }_{22}+{\mathit{z}}_i^{\prime }{\gamma }_2\}{S}_2(y_{Gi}|A_i,V_i,{\mathit{z}}_i,{\omega }_i,{\beta }_2,{\gamma }_2,{\mathit{\lambda }}_2)$, where β₂ = (β₂₁, β₂₂)′ and ω_i is a latent frailty for the i^th subject. Based on the nature of the semi-competing risks, the observations in the observed data can be classified into four different cases. Under FM, the likelihoods for these four cases are derived as follows.

Case 1

Subject died at time y_i and no disease progression was observed. Then we have E_i = 0, d_i = 0 and ν_i = 1 and the observation is D_i = (E_i = 0, y_i, d_i = 0, ν_i = 1, x_i, A_i). The likelihood function is given as follows:

$$L_{1i}(\mathit{\alpha },{\beta }_0,{\gamma }_0,{\mathit{\lambda }}_0|D_i)=P(E_i=0|A_i,{\mathit{x}}_i,\mathit{\alpha })f_0(y_i|A_i,{\mathit{x}}_i,{\beta }_0,{\gamma }_0,{\mathit{\lambda }}_0).$$ (2.5)

Case 2

Subject was observed to have disease progression at y_Ei and died at y_i. Then we have E_i = 1, d_i = 1, and ν_i = 1, and the observation is d_i = (E_i = 1, y_Ei, y_Gi = y_i − y_Ei, d_i = 1, ν_i = 1, x_i, A_i, V_i (1−A_i), z_i) with the likelihood function given by:

$$L_{2i}(\mathit{\alpha },{\beta }_1,{\gamma }_1,{\mathit{\lambda }}_1,{\beta }_2,{\gamma }_2,{\mathit{\lambda }}_2|D_i,{\omega }_i)=P(E_i=1|A_i,{\mathit{x}}_i,\mathit{\alpha })f_1(y_{Ei}|A_i,{\mathit{x}}_i,{\omega }_i,{\beta }_1,{\gamma }_1,{\mathit{\lambda }}_1)\times f_2(y_{Gi}|A_i,V_i,{\mathit{z}}_i,{\omega }_i,{\beta }_2,{\gamma }_2,{\mathit{\lambda }}_2),$$ (2.6)

where P(E_i = 1|A_i, x_i, α) = 1 − P(E_i = 0|A_i, x_i, α).

Case 3

Subject was observed to have disease progression at y_Ei and right censored at y_i. Then we have E_i = 1, d_i = 1, and ν_i = 0, and the observation is D_i = (E_i = 1, y_Ei, y_Gi = y_i − y_Ei, d_i = 1, ν_i = 0, x_i, A_i, V_i(1 − A_i), z_i) with the likelihood function given by

$$L_{3i}(\mathit{\alpha },{\beta }_1,{\gamma }_1,{\mathit{\lambda }}_1,{\beta }_2,{\gamma }_2,{\mathit{\lambda }}_2|D_i,{\omega }_i)=P(E_i=1|A_i,{\mathit{x}}_i,\mathit{\alpha })f_1(y_{Ei}|A_i,{\mathit{x}}_i,{\omega }_i,{\beta }_1,{\gamma }_1,{\mathit{\lambda }}_1)\times S_2(y_{Gi}|A_i,V_i,{\mathit{z}}_i,{\omega }_i,{\beta }_2,{\gamma }_2,{\mathit{\lambda }}_2).$$ (2.7)

Case 4

Subject was only observed to be right censored at y_i and no disease progression occurred before y_i. Then we have d_i = 0 and ν_i = 0 and the observation is D_i = (y_i, d_i = 0, ν_i = 0, x_i, A_i) and for such a subject, it is possible that E_i = 1 or E_i = 0. The likelihood function is given by

$$L_{4i}(\mathit{\alpha },{\beta }_0,{\gamma }_0,{\mathit{\lambda }}_0,{\beta }_1,{\gamma }_1,{\mathit{\lambda }}_1|D_i,{\omega }_i)=P(E_i=1|A_i,{\mathit{x}}_i,\mathit{\alpha })S_1(y_i|A_i,{\mathit{x}}_i,{\omega }_i,{\beta }_1,{\gamma }_1,{\mathit{\lambda }}_1)+P(E_i=0|A_i,{\mathit{x}}_i,\mathit{\alpha })S_0(y_i|A_i,{\mathit{x}}_i,{\beta }_0,{\gamma }_0,{\mathit{\lambda }}_0).$$ (2.8)

Let D_obs = (D_i, i = 1,…, n) denote the observed data, where D_i is defined by (2.5) – (2.8). Then, the observed-data likelihood function under FM is given by

$$L(\mathit{\alpha },{\beta }_0,{\gamma }_0,{\mathit{\lambda }}_0,{\beta }_1,{\gamma }_1,{\mathit{\lambda }}_1,{\beta }_2,{\gamma }_2,{\mathit{\lambda }}_2,\tau |D_{obs})=\prod _{i=1}^n\{{[L_{1i}(\mathit{\alpha },{\beta }_0,{\gamma }_0,{\mathit{\lambda }}_0|D_i)]}^{1\{d_i=0,{\nu }_i=1\}}{[L_{2i}(\mathit{\alpha },{\beta }_1,{\gamma }_1,{\mathit{\lambda }}_1,{\beta }_2,{\gamma }_2,{\mathit{\lambda }}_2|D_i)]}^{1\{d_i=1,{\nu }_i=1\}}\times {[L_{3i}(\mathit{\alpha },{\beta }_1,{\gamma }_1,{\mathit{\lambda }}_1,{\beta }_2,{\gamma }_2,{\mathit{\lambda }}_2|D_i)]}^{1\{d_i=1,{\nu }_i=0\}}{[L_{4i}(\mathit{\alpha },{\beta }_0,{\gamma }_0,{\mathit{\lambda }}_0,{\beta }_1,{\gamma }_1,{\mathit{\lambda }}_1|D_i)]}^{1\{d_i=0,{\nu }_i=0\}}\},$$ (2.9)

where 1{B} denotes the indicator function such that 1{B} = 1 if B is true and 0 otherwise, L_1i(α, β₀, γ₀, λ₀|D_i) is defined by (2.5), L_2i(α, β₁, γ₁,λ₁, β₂, γ₂, λ₂|D_i) = P(E_i = 1|A_i, x_i, α)[(1 + τ) h₁(y_Ei|λ₁) $\text{exp}(A_i{\beta }_1+{\mathit{x}}_i^{\prime }{\gamma }_1)h_2(y_{Gi}|{\mathit{\lambda }}_2)\text{exp}\{A_i{\beta }_{21}+V_i(1-A_i){\beta }_{22}+{\mathit{z}}_i^{\prime }{\gamma }_2)\}\times {\{1+\tau [H_1(y_{Ei}|{\mathit{\lambda }}_1)\text{exp}(A_i{\beta }_1+{\mathit{x}}_i^{\prime }{\gamma }_1)+H_2(y_{Gi}|{\mathit{\lambda }}_2)\text{exp}\{A_i{\beta }_{21}+V_i(1-A_i){\beta }_{22}+{\mathit{z}}_i^{\prime }{\gamma }_2\}]\}}^{-(2+\frac{1}{\tau })},L_{3i}(\mathit{\alpha },{\beta }_1,{\gamma }_1,{\mathit{\lambda }}_1,{\beta }_2,{\gamma }_2,{\mathit{\lambda }}_2|D_i)=P(E_i=1|A_i,{\mathit{x}}_i,\mathit{\alpha })h_1(y_{Ei}|{\mathit{\lambda }}_1)\text{exp}(A_i{\beta }_1+{\mathit{x}}_i^{\prime }{\gamma }_1)\times {\{1+\tau [H_1(y_{Ei}|{\mathit{\lambda }}_1)\text{exp}(A_i{\beta }_1+{\mathit{x}}_i^{\prime }{\lambda }_1)+H_2(y_{Gi}|{\mathit{\lambda }}_2)\text{exp}(A_i{\beta }_{21}+V_i(1-A_i){\beta }_{22}+{\mathit{z}}_i^{\prime }{\gamma }_2\}]\}}^{(1-\frac{1}{\tau })},\text{and}{L}_{4i}(\mathit{\alpha },{\beta }_0,{\gamma }_0,{\mathit{\lambda }}_0,{\beta }_1,{\gamma }_1,{\mathit{\lambda }}_1|D_i)=P(E_i=1|A_i,x_i,\mathit{\alpha }){[1+\tau H_1(y_i|{\mathit{\lambda }}_1)\times \text{exp}(A_i{\beta }_1+{\mathit{x}}_i^{\prime }{\gamma }_1)]}^{-\frac{1}{\tau }}+P(E_i=0|A_i,{\mathit{x}}_i,\mathit{\alpha })S_0(y_i|A_i,{\mathit{x}}_i,{\beta }_0,{\gamma }_0,{\mathit{\lambda }}_0).$

The likelihood under CM can be derived in a similar way. Specifically, under CM, P(E_i = 0|A_i, x_i, α), S₀(y_i|A_i, x_i, β₀, γ₀,λ₀), f₀(y_i|A_i, x_i, β₀, γ₀,λ₀), and (2.5) remain the same while (2.6) – (2.8) are obtained using $S_1(y_{Ei}|A_i,{\mathit{x}}_i,{\beta }_1,{\gamma }_1,{\mathit{\lambda }}_1)=\text{exp}\{-H_1(y_{Ei}|{\mathit{\lambda }}_1)=\text{exp}(A_i{\beta }_1+{\mathit{x}}_i^{\prime }{\gamma }_1)\},f_1(y_{Ei}|A_i,{\mathit{x}}_i,{\beta }_1,{\gamma }_1,{\mathit{\lambda }}_1)=h_1(y_{Ei}|{\mathit{\lambda }}_1)\text{exp}(A_i{\beta }_1+{\mathit{x}}_i^{\prime }{\gamma }_1)S_1(y_{Ei}|A_i,{\mathit{x}}_i,{\beta }_1,{\gamma }_1,{\mathit{\lambda }}_1),S_2(y_{Gi}|A_i,V_i,{\mathit{z}}_i,y_{Ei},{\beta }_2,{\gamma }_2,{\mathit{\lambda }}_2)=\text{exp}[-H_2(y_{Gi}|{\mathit{\lambda }}_2)=\text{exp}(A_i{\beta }_{21}+V_i(1-A_i){\beta }_{22}+y_{Ei}{\gamma }_{21}+{\mathit{z}}_i^{\prime }{\gamma }_{22})\text{and}{f}_2(y_{Gi}|A_i,V_i,{\mathit{z}}_i{y}_{Ei},{\beta }_2,{\gamma }_2,{\mathit{\lambda }}_2)=h_2(y_{Gi}|{\mathit{\lambda }}_2)\text{exp}\{A_i{\beta }_{21}+V_i(1-A_i){\beta }_{22}+y_{Ei}{\gamma }_{21}+{\mathit{z}}_i^{\prime }{\gamma }_2\}{S}_2(y_{Gi}|A_i,V_i,{\mathit{z}}_i,y_{Ei},{\beta }_2,{\gamma }_2,{\mathit{\lambda }}_2)\text{where}{\gamma }_2=({\gamma }_{21},{\gamma }_{22}^{\prime })\prime$

3 Posterior Inference and Computation

3.1 Prior and Posterior Distributions

Let $\mathit{\theta }=({\mathit{\alpha }}^{\prime },{\beta }_0,{\gamma }_0^{\prime },{\mathit{\lambda }}_0^{\prime },{\beta }_1,{\gamma }_1^{\prime },{\mathit{\lambda }}_1^{\prime },{\beta }_2^{\prime },{\gamma }_2^{\prime },{\mathit{\lambda }}_2^{\prime },\tau )$ denote the vector of all the model parameters. To carry out a Bayesian analysis, we need to specify a prior distribution for θ.We assume that α, (β₀, γ₀), (β₁, γ₁), (β₂₁, β₂₂, γ₂), λ₀, λ₁, λ₂ and τ are independent, a priori, and the following priors are specified for these parameters: $\mathit{\alpha }~N_{p_a}(0,{\Sigma }_a),({\beta }_0,{\mathit{\gamma }}_0^{\prime })\prime ~N_{p_0}(0,{\Sigma }_0),({\beta }_1,{\mathit{\gamma }}_1^{\prime })\prime ~N_{p_1}(0,{\Sigma }_1),({\mathit{\beta }}_2^{\prime },{\mathit{\gamma }}_2^{\prime })\prime ~N_{p_2}(0,{\Sigma }_2)$, and τ ~ IG(a_τ, b_τ), which is an inverse Gamma distribution with mean b_τ/(a_τ −1) and variance (b_τ)²/[(a_τ − 1)²(a_τ − 2)], where p_a, p₀, p₁, and p₂ are the dimensions corresponding to the respective vectors of the model parameters, and Σ_a, Σ₀, Σ₁, Σ₂, and (a_τ, b_τ ) are pre-specified hyperparameters. Independently, we assume λ_kj ~ Gamma(a_kj, b_kj) for j = 1,…, J_k and k = 0, 1, 2. Let π_a(α), π₀ (β₀, γ₀), π₁ (β₁, γ₁), π₂ (β₂, γ₂), π(τ |a_τ, b_τ), π_0λ(λ₀), π_1λ (λ₁), and π_2λ(λ₂) denote the above prior distributions, respectively. Then, the joint prior of θ is given by π(θ) ∝ π_a(α)π₀(β₀, γ₀)π₁(β₁, γ₁)π₂(β₂, γ₂)π(τ |a_τ, b_τ) π_0λ(λ₀) π_1λ(λ₁)π_2λ(λ₂). In the simulation study in Section 4 and the analysis of the real data from a colorectal cancer study in Section 5, these hyperparameters were specified as Σ_a = 1000I_pa, Σ₀ = 1000I_p0, Σ₁ = 1000I_p1, Σ₂ = 1000I_p2, a_τ = b_τ = 0.01, and a_kj = b_kj = 0 for j = 1,…, J_k and k = 0, 1, 2, where I_pa, I_p0, I_p1, and I_p2 are the identity matrices. Using (2.9) and π(θ), the posterior distribution of θ given the observed data D_obs under FM is of the form

$$\pi (\mathit{\theta }|D_{obs})\propto L(\mathit{\theta }|D_{obs})\pi (\mathit{\theta }).$$ (3.1)

When π(θ) is proper, the posterior distribution π(θ|D_obs) is also proper. However, even when π(θ) is improper, the posterior distribution can still be proper under certain mild conditions. To formally establish posterior propriety in this case, let 𝒩_j denote the set which consists of subjects who were in Case j and n_j = |𝒩_j|, which is the total number of subjects in Case j for j = 1, …, 4, respectively. Write $X_a=((1-2E_i){\mathit{x}}_{Ei},i\in {\cup }_{j=1}^3{𝒩}_j)\prime$, which is an (n₁ +n₂ +n₃)×p_a matrix with rows $(1-2E_i){\mathit{x}}_{Ei}^{\prime }$, where ${\mathit{x}}_{Ei}=(1,A_i,{\mathit{x}}_i^{\prime })\prime$. Let δ_i0j = 1 if y_i ∈ (s_0,j−1, s_0j] and 0 otherwise for j = 1, 2, …J₀ for i ∈ 𝒚₁; δ_i1j = 1 if y_Ei ∈ (s_1,j−1, s_1j] and 0 otherwise for j = 1, 2, …J₁ and i ∈ 𝒩₂∪𝒩₃; and δ_i2j = 1 if y_i−y_Ei ∈ (s_2,j−1, s_2j] and 0 otherwise for j = 1, 2, …J₂ and i ∈ 𝒩₂ ∪ 𝒩₃. Define X₀ to be an n₁ × (J₀ + p₀) matrix with rows $({\delta }_{i01},\dots ,{\delta }_{i0J_0},A_i,{\mathit{x}}_i^{\prime })$ for i ∈ 𝒩₁, X₁ an (n₂ +n₃) ×(J₁ + p₁) matrix with rows($({\delta }_{i11},\dots ,{\delta }_{i1J_1},A_i,{\mathit{x}}_i^1)$) for i ∈ 𝒩₂, ∪ 𝒩₃ X₂ an n₂ × (J₂ + p₃) matrix with rows $({\delta }_{i21},\dots ,{\delta }_{i2J_2},A_i,V_i(1-A_i),{\mathit{z}}_i^{\prime })$ for i ∈ 𝒩₂ We are led to the following theorem.

Theorem 1

Assume π_a (α) ∝ 1, π₀ (β₀, γ₀) ∝ 1, π₁(β₁, γ₁) ∝ 1, π₂(β₂, γ₂) ∝ 1, and a_kj = b_kj = 0 for j = 1, …, J_k and k = 0, 1, 2. If the following conditions are satisfied: (i) X_a is of full rank; (ii) there exists a positive vector c = (c₁, …, c_n* )′ ∈ R^{n₁+n₂+n₃}, i.e., each component c_i > 0, such that $X_a^{\prime }\mathit{c}=0$; (iii) X₀, X₁, and X₂ are of full rank; and (iv) a_τ > 0 and b_τ > 0, then the joint posterior π(θ|D_obs) in (3.1) is proper, i.e., ∫ L(θ|D_obs)π(θ)dθ < ∞.

The proof of Theorem 1 is given in Appendix A. When a_kj = b_kj = 0 for j = 1, …, J_k and k = 0, 1, 2, we specify improper (Jeffreys’s) priors for all the λ_jk’s, namely, ${\pi }_{k\mathit{\lambda }}({\lambda }_{kj})\propto \frac{1}{{\lambda }_{kj}}$ for j= 1,… J_k and k = 0, 1, 2. Conditions (i) and (ii) ensure posterior propriety for α, Condition (iii) leads to the posterior propriety of (λ₀, β₀, γ₀) and Conditions (iii) and (iv) are required for the posterior propriety of (λ₁, β₁, γ₁, λ₂, β₂, γ₂, τ ). Condition (iii) is quite mild and essentially requires that at least one event (death or disease progression) occurs in each interval (s_k,j−1, s_kj], and the corresponding covariate matrix is of full rank. These conditions are easily satisfied in most applications and are quite easy-to-check.

3.2 The Predictive Survival Function with Partial Treatment Switching

An inferential research goal in this research is to compare the survival function of the death time in the setting when no subjects have switched treatment. Let $T_D^{*}$ (a) denote a potential survival time when a subject receives treatment a at the time of randomization and stays on the same treatment over the entire study duration. Let $S_a(t|\mathit{\theta })=P(T_D^{*}(a)>t|\mathit{\theta })$. Following Zeng et al. (2012), we state the following two assumptions: (i) Treatment A is completely randomized and $T_D^{*}(a)=T_D(a)$ if a subject never switches treatment; and (ii) Given (A = 0, z, T_E = u) or (A = 1, z, T_E = u), V is independent of the potential outcomes $\{T_D^{*}(0),T_D^{*}(1)\}$. We note that these two assumptions are only used to compute S_a(t|θ). Similar to Zeng et al. (2012), under Assumptions (i) and (ii), we have

$$S_a(t|\mathit{\theta })={\int }_{\mathit{x}}P(T_D>t|A=a,\mathit{x},E=0,{\beta }_0,{\gamma }_0,{\mathit{\lambda }}_0)P(E=0|A=a,\mathit{x},\mathit{\alpha })fx(\mathit{x}|A=a)d\mathit{x}+{\int }_{\mathit{x},\mathit{z},\omega ,u}P(T_G>t-u|A=a,\mathit{z},V=0,E=1,{\beta }_2,{\gamma }_2,{\mathit{\lambda }}_2,\omega )\times f_1(u|A=a,\mathit{x},\omega ,{\beta }_1,{\gamma }_1,{\mathit{\lambda }}_1,\omega )duf(\omega |\tau )d\omega \times f_Z(\mathit{z}|A=a,\mathit{x},E=1)P(E=1|A=a,\mathit{x},\mathit{\alpha })f_X(\mathit{x}|A=a)d\mathit{z}d\mathit{x},$$ (3.2)

where f_X(x | A = a) is the conditional density of X given A = a, and f_Z (z | A = a, x, E = 1) is the conditional density of Z given A = a, x, and E = 1. When J₀ = J₁ = J₂ = 1, after some algebra, we obtain

$$S_a(t|\mathit{\theta })={\int }_x\text{exp}\{-t{\mathit{\lambda }}_0\text{exp}(A{\beta }_0+{\mathit{x}}^{\prime }{\gamma }_0)\}P(E=0|A=a,\mathit{x},\mathit{\alpha })f_X(\mathit{x}|A=a)d\mathit{x}+{\int }_{\mathit{x},\mathit{z}}({[\frac{1}{1+{\mathit{\lambda }}_1\text{exp}(A{\beta }_1+\mathit{x}\prime {\gamma }_1)t\tau }]}^{\frac{1}{\tau }}+\frac{{\mathit{\lambda }}_1\text{exp}(A{\beta }_1+\mathit{x}\prime {\gamma }_1)}{{\mathit{\lambda }}_2\text{exp}\{A{\beta }_{21}+V(1-A){\beta }_{22}+\mathit{z}\prime {\gamma }_2\}-{\mathit{\lambda }}_1\text{exp}(A{\beta }_1+\mathit{x}\prime {\gamma }_1)}\times \{{[\frac{1}{1+{\mathit{\lambda }}_1\text{exp}(A{\beta }_1+\mathit{x}\prime {\gamma }_1)t\tau }]}^{\frac{1}{\tau }}-{[\frac{1}{1+{\mathit{\lambda }}_2\text{exp}\{A{\beta }_{21}+V(1-A){\beta }_{22}\mathit{+}\mathit{z}\prime {\gamma }_2\}t\tau }]}^{\frac{1}{\tau }}\})\times f_Z(\mathit{z}|A=a,\mathit{x},E=1)P(E=1|A=a,\mathit{x},\mathit{\alpha })fx(\mathit{x}|A=a)d\mathit{z}d\mathit{x}.$$ (3.3)

A detailed derivation of (3.3) is given in Appendix B. We assume nonparametric distributions for f_X(x | A = a) and f_Z(z | X, A = a, E = 1) as follows: $f_X(\mathit{x}|A=a)={\sum }_{j=1}^{n}I(X_j=x,A_j=a)/{\sum }_{j=1}^{n}I(A_j=a)$ and $f_Z(z|X,A=a,E=1)=\frac{{\mathrm{\Sigma }}_{j\in (\text{Cases}2,3)}\delta (Z_j=z)K_{a_n}(\parallel X_j-X\parallel )I(A_j=a)}{{\mathrm{\Sigma }}_{j\in (\text{Cases}2,3)}{K}_{a_n}(\parallel X_j-X\parallel )I(A_j=a)}.$. Since S_a(t|θ) is a function of θ, the posterior estimates of S_a(t|θ) can be easily obtained using the MCMC samples from the posterior distribution of θ.

3.3 Posterior Computation

Due to the complexity of the likelihood structure for the proposed frailty model, an analytical evaluation of the posterior distribution is not possible. In order to carry out posterior inference, we develop an efficient Gibbs sampling algorithm to sample θ from the posterior distribution in (3.1). We first consider the transformation ${\mathit{\lambda }}_k^{*}=\tau {\mathit{\lambda }}_k$. The Jacobian of this transformation is $\left|\frac{\partial {\mathit{\lambda }}_k}{\partial {\mathit{\lambda }}_k^{*}}\right|={\tau }^{-J_k}$ for k = 1, 2. Write ${\mathit{\theta }}^{*}=(\mathit{\alpha },{\beta }_0,{\gamma }_0,{\mathit{\lambda }}_0,{\beta }_1,{\gamma }_1,{\mathit{\lambda }}_1^{*},{\beta }_2,{\gamma }_2,{\mathit{\lambda }}_2^{*},\tau )$. After the transformation, the posterior distribution of θ^* is given by

$$\pi ({\mathit{\theta }}^{*}|D_{obs})\propto L(\mathit{\alpha },{\beta }_0,{\gamma }_0,{\mathit{\lambda }}_0,{\beta }_1,{\gamma }_1,{\mathit{\lambda }}_1^{*}/\tau ,{\beta }_2,{\gamma }_2,{\mathit{\lambda }}_2^{*}/\tau ,\tau |D_{obs}){\pi }_a(\mathit{\alpha }){\pi }_0({\beta }_0,{\gamma }_0){\pi }_1({\beta }_1,{\gamma }_1)\times {\pi }_2({\beta }_2,{\gamma }_2^{\prime })\pi (\tau |a_{\tau },b_{\tau }){\pi }_{0\mathit{\lambda }}({\mathit{\lambda }}_0){\pi }_{1\mathit{\lambda }}({\mathit{\lambda }}_1^{*}/\tau ){\pi }_{2\mathit{\lambda }}({\mathit{\lambda }}_2^{*}/\tau ){\tau }^{-(J_1+J_2)},$$ (3.4)

where L(α, β₀, γ₀, λ₀, β₁, γ₁, λ₁, β₂, γ₂, λ₂, τ|D_obs) is defined in (2.9).

To facilitate the posterior computation, we introduce two sets of latent variables ${\mathit{E}}^{*}=(E_i^{*},i\in {𝒩}_4)$ and w = (w₁, w₂, …, w_n) so that the augmented posterior distribution of (θ*,E*,w) is given by

$$\pi ({\mathit{\theta }}^{*},\mathit{w},{\mathit{E}}^{*}|D_{obs})\propto \prod _{i=1}^n\{{[L_{1i}(\mathit{\alpha },{\beta }_0,{\gamma }_0,{\mathit{\lambda }}_0|D_i)]}^{1\{{\nu }_i=1,d_i=0\}}{[L_{2i}^{*}(\mathit{\alpha },{\beta }_1,{\gamma }_1,{\mathit{\lambda }}_1,{\beta }_2,{\gamma }_2,{\mathit{\lambda }}_2,w_i|D_i)]}^{1\{{\nu }_i=1,d_i=1\}}\times {[L_{3i}^{*}(\mathit{\alpha },{\beta }_1,{\gamma }_1,{\mathit{\lambda }}_1,{\beta }_2,{\gamma }_2,{\mathit{\lambda }}_2,w_i|D_i)]}^{1\{{\nu }_i=0,d_i=1\}}\times {[L_{4i}^{*}(\mathit{\alpha },{\beta }_0,{\gamma }_0,{\mathit{\lambda }}_0,{\beta }_1,{\gamma }_1,{\mathit{\lambda }}_1^{*},w_i,E_i^{*}|D_i)]}^{1\{{\nu }_i=0,d_i=0\}}\}\times {\pi }_a(\mathit{\alpha }){\pi }_0({\beta }_0,{\gamma }_0)\times {\pi }_1({\beta }_1,{\gamma }_1){\pi }_2({\beta }_2,{\gamma }_2^{\prime })\pi (\tau |a_{\tau },b_{\tau }){\pi }_{0\mathit{\lambda }}({\mathit{\lambda }}_0)[\prod _{k=1}^2{\pi }_{k\mathit{\lambda }}({\mathit{\lambda }}_k^{*}/\tau )]{\tau }^{-(J_1+J_2)},$$ (3.5)

Where L_1i(α, β₀, γ₀, λ₀|d_i) is defined by (2.5), $L_{2i}^{*}(\mathit{\alpha },{\beta }_1,{\gamma }_1,{\mathit{\lambda }}_1^{*},{\beta }_2,{\gamma }_2,{\mathit{\lambda }}_2^{*},w_i|D_i)=P(E_i=1|A_i,{\mathit{x}}_i,\mathit{\alpha })\times [(1+\tau )/{\tau }^2]h_1(y_{Ei}|{\mathit{\lambda }}_1^{*})\text{exp}(A_i{\beta }_1+{\mathit{x}}_i^{\prime }{\gamma }_1)h_2(y_{Gi}|{\mathit{\lambda }}_2^{*})\text{exp}\{A_i{\beta }_{21}+V_i(1-A_i){\beta }_{22}+{\mathit{z}}_i^{\prime }{\gamma }_2\}[\frac{w_i^{1+\frac{1}{\tau }}}{\Gamma (2+\frac{1}{\tau })}]\text{exp}(-w_i[1+H_1(y_{Ei}|{\mathit{\lambda }}_1^{*})\text{exp}(A_i{\beta }_1+{\mathit{x}}_i^{\prime }{\gamma }_1)+H_2(y_{Gi}|{\mathit{\lambda }}_2^{*})\text{exp}\{A_i{\beta }_{21}+V_i(1-A_i){\beta }_{22}+{\mathit{z}}_i^{\prime }{\gamma }_2\}]),L_{3i}^{*}(\mathit{\alpha },{\beta }_1,{\gamma }_1,{\mathit{\lambda }}_1,{\beta }_2,{\gamma }_2,{\mathit{\lambda }}_2,w_i|D_i)=P(E_i=1|A_i,{\mathit{x}}_i,\mathit{\alpha })(1/\tau )h_1(y_{Ei}|{\mathit{\lambda }}_1^{*})\text{exp}(A_i{\beta }_1+{\mathit{x}}_i^{\prime }{\gamma }_1)[\frac{w_i^{\frac{1}{\tau }}}{\Gamma (1+\frac{1}{\tau })}]\text{exp}(-w_i[1+H_1(y_{Ei}|{\mathit{\lambda }}_1^{*})\times \text{exp}(A_i{\beta }_1+{\mathit{x}}_i^{\prime }{\gamma }_1)+H_2(y_{Gi}|{\mathit{\lambda }}_2^{*})\text{exp}\{A_i{\beta }_{21}+V_i(1-A_i){\beta }_{22}+{\mathit{z}}_i^{\prime }{\gamma }_2\}]),\text{and}{L}_{4i}^{*}(\mathit{\alpha },{\beta }_0,{\gamma }_0,{\mathit{\lambda }}_0,{\beta }_1,{\gamma }_1,{\mathit{\lambda }}_1^{*},w_i,E_i^{*}|D_i)={\{P(E_i=1|A_i,{\mathit{x}}_i,\mathit{\alpha })\}}^{-E_i^{*}}{[\frac{w_i^{\frac{1}{\tau }-1}}{\Gamma (\frac{1}{\tau })}]}^{E_i^{*}}\text{exp}\{-w_i{E}_i^{*}[1+H_1(y_i|{\mathit{\lambda }}_1^{*})\text{exp}(A_i{\beta }_1+{\mathit{x}}_i^{\prime }{\gamma }_1)]\}{\{P(E_i=0|A_i,{\mathit{x}}_i,\mathit{\alpha })S_0(y_i|A_i,{\mathit{x}}_i,{\beta }_0,{\gamma }_0,{\mathit{\lambda }}_0)\}}^{1-E_i^{*}}$. It can be shown that ∑_E* ∫ π(θ*, w, E*|D_obs)dw = π(θ*|D_obs), which is given by (3.4). We note that the latent variables (the w_i’s) in (3.5) are different than those ω_i’s in (2.6) – (2.8).

Let [A|B] denote the conditional distribution of A given B. To run the Gibbs sampling algorithm, we sample from the following conditional distributions in turn: (i) $[{\mathit{\lambda }}_0,{\mathit{\lambda }}_1^{*},{\mathit{\lambda }}_2^{*}|{\beta }_0,{\gamma }_0,{\beta }_1,{\gamma }_1,{\beta }_2,{\gamma }_2,\mathit{w},{\mathit{E}}^{*},D_{obs}]$; (ii) $[{\beta }_0,{\gamma }_0,{\beta }_1,{\gamma }_1,{\beta }_2,{\gamma }_2,\tau ,\mathit{w},{\mathit{E}}^{*}|\mathit{\alpha },{\mathit{\lambda }}_0,{\mathit{\lambda }}_1^{*},{\mathit{\lambda }}_2^{*},D_{obs}]$; and (iii) [α|E*,D_obs]. For (ii), we use the modified collapsed Gibbs technique (Liu, 1994; Chen et al., 2000). It is easy to show that

$$[{\beta }_0,{\gamma }_0,{\beta }_1,{\gamma }_1,{\beta }_2,{\gamma }_2,\tau ,\mathit{w},{\mathit{E}}^{*}|\mathit{\alpha },{\mathit{\lambda }}_0,{\mathit{\lambda }}_1^{*},{\mathit{\lambda }}_2^{*},D_{obs}]=[{\beta }_0,{\gamma }_0,{\beta }_1,{\gamma }_1,{\beta }_2,{\gamma }_2,\tau ,{\mathit{E}}^{*}|\mathit{\alpha },{\mathit{\lambda }}_0,{\mathit{\lambda }}_1^{*},{\mathit{\lambda }}_2^{*},D_{obs}][\mathit{w}|{\beta }_1,{\gamma }_1,{\mathit{\lambda }}_1^{*},{\beta }_2,{\gamma }_2,{\mathit{\lambda }}_2^{*},\tau ,{\mathit{E}}^{*},D_{obs}].$$ (3.6)

For (ii), following Chen et al. (2000) and using (3.6), we run a sub-Gibbs sampling algorithm to draw from the following conditional distributions: (iia) $[{\beta }_0,{\gamma }_0,{\beta }_1,{\gamma }_1,{\beta }_2,{\gamma }_2,|\mathit{\alpha },{\mathit{\lambda }}_0,{\mathit{\lambda }}_1^{*},{\mathit{\lambda }}_2^{*},\tau ,{\mathit{E}}^{*},D_{obs}]$; (iib) $[{\mathit{E}}^{*}|\mathit{\alpha },{\beta }_0,{\gamma }_0,{\mathit{\lambda }}_0,{\beta }_1,{\gamma }_1,{\mathit{\lambda }}_1^{*},\tau ,D_{obs}]$; (iic) $[\tau |{\beta }_1,{\gamma }_1,{\mathit{\lambda }}_1^{*},{\beta }_2,{\gamma }_2,{\mathit{\lambda }}_2^{*},{\mathit{E}}^{*},D_{obs}]$; and (iid) $[\mathit{w}|{\beta }_1,{\gamma }_1,{\mathit{\lambda }}_1^{*},{\beta }_2,{\gamma }_2,{\mathit{\lambda }}_2^{*},{\mathit{E}}^{*},D_{obs}]$. Next, we will only discuss the properties of the conditional distribution $[\tau |{\beta }_1,{\gamma }_1,{\mathit{\lambda }}_1^{*},{\beta }_2,{\gamma }_2,{\mathit{\lambda }}_2^{*},{\mathit{E}}^{*},D_{obs}]$ and how to sample τ from this conditional distribution. All other conditional distributions are discussed in detail in Appendix B. We first consider the transformation τ* = 1/τ . Then, the conditional posterior density of τ* is given by

$$\pi ({\tau }^{*}|{\beta }_1,{\gamma }_1,{\mathit{\lambda }}_1^{*},{\beta }_2,{\gamma }_2,{\mathit{\lambda }}_2^{*},{\mathit{E}}^{*},D_{obs})\propto {\prod _{i=1}^n\{(\frac{1}{{\tau }^{*}}+1){({\tau }^{*})}^2\times {[1+H_1(y_{Ei}|{\mathit{\lambda }}_1^{*})\text{exp}(A_i{\beta }_1+{\mathit{x}}_i^{\prime }{\gamma }_1)+H_2(y_{Gi}|{\mathit{\lambda }}_2^{*})\text{exp}\{A_i{\beta }_{21}+V_i(1-A_i){\beta }_{22}+{\mathit{z}}_i^{\prime }{\gamma }_2\}]}^{-{\tau }^{*}-2}\}}^{1\{d_i=1,{\nu }_i=1\}}\times {\{{\tau }^{*}\times [1+H_1(y_{Ei}|{\mathit{\lambda }}_1^{*})\text{exp}(A_i{\beta }_1+{\mathit{x}}_i^{\prime }{\gamma }_1)+H_2(y_{Gi}|{\mathit{\lambda }}_2^{*})\text{exp}{\{A_i{\beta }_{21}+V_i(1-A_i){\beta }_{22}+{\mathit{z}}_i^{\prime }{\gamma }_2\}]}^{-T^{*}-1}\}}^{1\{{\nu }_i=0,d_i=1\}}\times {\left\{{[1+H_1(y_i|{\mathit{\lambda }}_1^{*})\text{exp}(A_i{\beta }_1+{\mathit{x}}_i^{\prime }{\gamma }_1)]}^{-{\tau }^{*}}\right\}}^{E_i^{*}1\{d_i=0,{\nu }_i=0\}}\times {({\tau }^{*})}^{a_{\tau }+{\sum }_{k=1}^2{\sum }_{j=1}^{J_k}{a}_{kj}-3}\text{exp}\{-[b_{\tau }+\sum _{k=1}^2\sum _{j=1}^{J_k}(b_{kj}{\lambda }_{kj}^{*})]{\tau }^{*}\}.$$ (3.7)

We are led to the following theorem.

Theorem 2

Assume that ${\sum }_{i=1}^n[1\{d_i=1,{\nu }_i=1,\}+1\{d_i=1,{\nu }_i=0\}]+a_{\tau }+{\sum }_{k=1}^2{\sum }_{j=1}^{J_K}{a}_{kj}-3>0.$ Then we have (i) the conditional density of τ* given by (3.7) is log-concave; and (ii) the mode of (3.7) is analytically available and given by

$${\widehat{\tau }}^{*}=\frac{-(B_1+B_2+B_3)-\sqrt{{(B_1+B_2+B_3)}^2-4B_1{B}_2}}{2B_1}$$ (3.8)

where $B_1={\sum }_{i=1}^n\{-[1\{d_i=1,{\nu }_i=1\}+1\{d_i=1,{\nu }_i=0\}]\text{log}[1+H_1(y_{Ei}|{\mathit{\lambda }}_1^{*})\text{exp}(A_i{\beta }_1+{\mathit{x}}_i^{\prime }{\gamma }_1)+H_2(y_{Gi}|{\mathit{\lambda }}_2^{*})\text{exp}\{A_i{\beta }_{21}+V_i(1-A_i){\beta }_{22}+{\mathit{z}}_i^{\prime }{\gamma }_2\}]-E_i^{*}1\{d_i=0,{\nu }_i=0\}\text{log}[1+H_1(y_i|{\mathit{\lambda }}_1^{*})\text{exp}(A_i{\beta }_1+{\mathit{x}}_i^{\prime }{\gamma }_1)]\}-[b_{\tau }+{\sum }_{k=1}^2{\sum }_{j=1}^{J_k}(b_{kj}{\lambda }_{kj}^{*})],{\beta }_2={\sum }_{i=1}^n[1\{d_i=1,{\nu }_i=1\}+1\{{\nu }_i=0,d_i=1\}]+a_{\tau }+{\sum }_{k=1}^2{\sum }_{j=1}^{J_k}{a}_{kj}-3,and{B}_3={\sum }_{i=1}^n[1\{d_i=1,{\nu }_i=1\}].$

The proof of Theorem 2 is given in Appendix A. The assumption ${\sum }_{i=1}^n[1\{d_i=1,{\nu }_i=1\}+1\{d_i=1,{\nu }_i=0\}]+{\alpha }_{\tau }+{\sum }_{k=1}^2{\sum }_{j=1}^{J_K}{a}_{kj}-3>0$ ensures the log-concavity and the existence of the mode. This assumption is quite mild. As long as there are more than three patients with disease progression, this assumption still holds even when the improper priors with a_τ = 0 and a_kj = 0 for all k and j are specified for τ and the λ_jk’s. With the log-concavity property, τ* can be exactly drawn from the conditional distribution in (3.7) using the adaptive rejection algorithm of Gilks and Wild (1992). After τ* is generated, we let τ = 1/τ* and then the value of τ is a sample from the conditional distribution $[\tau |{\beta }_1,{\gamma }_1,{\mathit{\lambda }}_1^{*},{\beta }_2,{\gamma }_2,{\mathit{\lambda }}_2^{*},{\mathit{E}}^{*},D_{obs}]$ in (iic). With the analytical form of the mode, the performance of the rejection algorithm can be improved substantially as the algorithm does not need to search for the mode.

3.4 Model Comparison

To carry out Bayesian model comparison, we consider the deviance information criterion (DIC) and the Logarithm of the PseudoMarginal Likelihood (LPML).We define the deviance Dev(θ) = −2 log L(θ|D_obs), where L(θ|D_obs) is the observed-data likelihood defined in (2.9). Let θ̄ and $\overline{\text{Dev}}=E[\text{Dev}(\mathit{\theta })|D_{obs}]$ denote the posterior mean of θ and Dev(θ), respectively. According to Spiegelhalter et al. (2002), the DIC measure is defined as DIC = Dev(θ̄) + 2p_D, where $p_D=\overline{\text{Dev}}-D(\overline{\mathit{\theta }})$ is the effective number of model parameters. The smaller the DIC value, the better the model fits the data. LPML is another useful Bayesian measure of goodness-of-fit statistic, which is defined based on the Conditional Predictive Ordinate (CPO). For the i^th observation, we define CPO as CPO_i = ∫ L(θ|D_i)π(θ|D⁽⁻ⁱ⁾)dθ, where D_i is the observed data defined in Section 2.2, L(θ|D_i) is the observed likelihood for the i^th subject, which is the term inside the product in (2.9), D⁽⁻ⁱ⁾ is the data with D_i deleted, and π(θ|D⁽⁻ⁱ⁾) is the posterior density of θ based on the data D⁽⁻ⁱ⁾. According to Ibrahim et al. (2001), $\text{LPML}={\Sigma }_{i=1}^n$ log (CPO_i). The larger the LPML value, the better the model fits the data.

4 A Simulation Study

To examine the empirical performance of the posterior estimates and DIC and LPML, we carry out a simulation study. Five hundred simulated data sets with n = 500 as well as n = 1, 000 were generated. In the simulation study, the baseline treatment A was generated from a Bernoulli(0.5), corresponding to a randomized trial with a 1:1 sample size allocation; two baseline covariates X₁ and X₂ were independently generated from a U(−1, 1) and a Bernoulli(0.6), respectively. Given A and (X₁, X₂), E was generated from model (2.1) with the coefficients (including an intercept) being 1.6, −1.8, 1, and 0.1, respectively. When E = 0, we simulated T_D from model (2.2) with H₀(t) = t, β₀ = −1 and (γ₀₁, γ₀₂) = (1, 0.2). For E = 1, we first generated ω from a Gamma(1/τ, 1/τ ) with τ = 1. Then, T_E was generated from model (2.3) with H₁(t) = 5t, β₁ = −0.5 and (γ₁₁, γ₁₂) = (1, 0) and an additional prognostic factor Z at disease progression was generated from a U(0, 10) while the selection into treatment switching (V ) for a subject in the control arm (A = 0) was from a Bernoulli(p), where p = exp(−0.5 + 0.3T_E + 0.2X₁ + 0.5Z)/[1+exp(−0.5+0.3T_E +0.2X₁ +0.5Z)]. Moreover, T_G was generated from the model in (2.3) with H₂(t) = t, β₂₁ = −0.3, β₂₂ = −0.5, and γ₂₁ = −0.5, γ₂₂ = 0.5, γ₂₃ = −0.4. Finally, the censoring time was generated from a U(1, 7) and the study duration was τ* = 3. The latter yielded the average proportions of Cases 1 to 4 as 23%, 39%, 19%, and 18%.

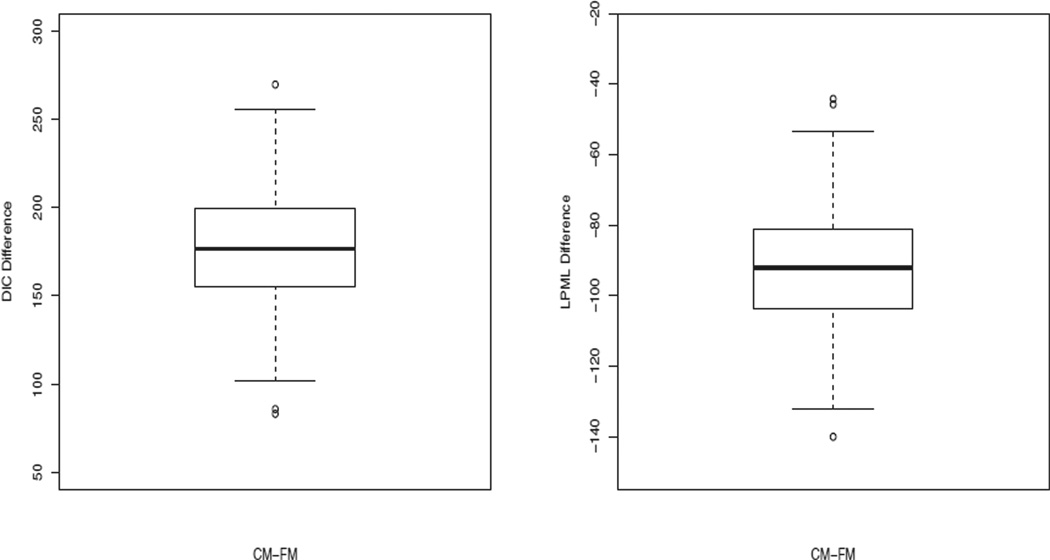
For each simulated dataset, we fit the proposed FM with various values of (J₀, J₁, J₂) and computed DIC and LPML. The mean values of the DICs and LPMLs over the 500 simulated datasets were 2986.22 and −1493.24 for (J₀, J₁, J₂) = (1, 1, 1); 2998.05 and −1499.39 for (J₀, J₁, J₂) = (5, 5, 5); and 3013.21 and −1507.22 for (J₀, J₁, J₂) = (10, 10, 10). We note that the true value of (J₀, J₁, J₂) is (1, 1, 1). Thus, both DIC and LPML correctly identified the true model. Under the best combination of (J₀, J₁, J₂), namely, (1, 1, 1), the average of the posterior means (EST), and the average of the posterior standard deviations (SD), the simulation standard error (SE), the root of the mean squared error (RMSE), and the coverage probability (CP) of the 95% highest posterior density (HPD) intervals for each parameter as well as S_a(t|θ) were computed. The results are given in Table 1. Table 1 shows excellent empirical performance of the posterior estimates for all the parameters as well as the survival probabilities for both n = 500 and n = 1000. In particular, the ESTs are nearly identical to the true values, the SDs are very close to the SEs, and the CPs are very close to 95%. For each simulated dataset, we also fit CM as discussed in Section 2.1 and computed the corresponding DIC and LPML for (J₀, J₁, J₂) = (1, 1, 1). The box plots of the DIC and LPML differences between CM and FM are shown in Fig. 2. From this figure, we see that all of the DIC differences are above 0 and all LPML differences are below 0, indicating that the frailty model fits the data better than the conditional model for all 500 simulated data sets, which is expected since the data were generated from the frailty model. These results further empirically confirm that FM is indeed quite different from CM, and DIC and LPML are two effective Bayesian model comparison measures for identifying the true models.

Table 1.

Posterior estimates under FM in the simulation study

			n = 500					n = 1,000
Parameter	True	EST	SD	SE	RMSE	CP%	EST	SD	SE	RMSE	CP%
						TD model
β0	−1.0	−1.00	0.25	0.24	0.24	0.95	−1.01	0.18	0.18	0.18	0.95
γ01	1.0	0.99	0.20	0.19	0.19	0.95	1.00	0.14	0.14	0.14	0.96
γ02	0.2	0.21	0.23	0.22	0.22	0.96	0.21	0.16	0.15	0.15	0.96
						TE model
β1	−0.5	−0.53	0.22	0.22	0.22	0.94	−0.53	0.16	0.15	0.15	0.95
γ11	1.0	1.02	0.19	0.20	0.20	0.93	1.01	0.13	0.14	0.14	0.95
γ12	0.0	0.01	0.21	0.20	0.20	0.95	0.00	0.15	0.15	0.15	0.95
						TG model
β21	−0.3	−0.31	0.24	0.23	0.23	0.96	−0.31	0.17	0.17	0.17	0.95
β22	−0.5	−0.49	0.23	0.23	0.23	0.95	−0.50	0.16	0.16	0.16	0.93
τ	1.0	1.05	0.15	0.14	0.14	0.95	1.03	0.10	0.10	0.10	0.95
γ22	−0.5	−0.49	0.18	0.19	0.19	0.95	−0.49	0.13	0.13	0.13	0.94
γ23	0.5	0.51	0.21	0.21	0.21	0.95	0.50	0.15	0.16	0.16	0.92
γ24	−0.4	−0.40	0.32	0.32	0.32	0.94	−0.40	0.22	0.23	0.23	0.95
						E model
α0	1.6	1.63	0.24	0.24	0.24	0.95	1.61	0.17	0.16	0.16	0.97
α1	−1.8	−1.81	0.25	0.26	0.26	0.94	−1.80	0.18	0.18	0.18	0.95
α21	1.0	1.01	0.22	0.24	0.24	0.92	1.01	0.15	0.16	0.16	0.95
α22	0.1	0.11	0.24	0.25	0.25	0.94	0.12	0.17	0.17	0.17	0.94
				Estimated Survival function of control arm
S0(τ*/2)	0.44	0.44	0.03	0.03	0.03	0.95	0.44	0.02	0.02	0.02	0.96
S0(τ*)	0.26	0.28	0.03	0.03	0.03	0.93	0.27	0.02	0.02	0.02	0.95
				Estimated Survival function of treatment arm
S1(τ*/2)	0.57	0.57	0.03	0.03	0.03	0.95	0.57	0.02	0.02	0.02	0.93
S1(τ*)	0.36	0.37	0.03	0.03	0.03	0.93	0.37	0.02	0.02	0.02	0.91

Fig. 2.

Box Plots of the DIC and LPML Differences between CM and FM.

5 Analysis of the Panitumumab Study

We carry out here a detailed analysis of a subset of the data from the panitumumab study (PMAB408) conducted by Amgen Inc. (van Cutsem et al., 2007 and Amado et al., 2008). PMAB408 was an open label, randomized, phase III multicenter study designed to compare the efficacy and safety of panitumumab plus best supportive care (P+BSC) versus BSC alone in subjects with EGFr-expressing metastatic colorectal cancer who had documented disease progression during or after prior standard treatment with fluoropyrimidine, irinotecan, and oxaliplatin chemotherapy. Subjects were randomly assigned to receive P+BSC (treatment) or BSC (control). The baseline covariates include initial treatment (P+BSC versus BSC), age in years at screening, baseline Eastern Cooperative Oncology Group (ECOG) score (score 0 or 1 versus ≥ 2 (bECOG01)), primary tumor diagnosis type (rectal versus colon (Rectal)), gender, and region (western Europe (WesternEU), eastern and central Europe (CenEstEU), and rest of the world). In the subset of the data, there were 223 and 231 patients in the control and treatment arms, respectively. There were 424 subjects who died (208 and 207 in the control and treatment arms, respectively), 387 subjects (201 and 186 in the control and treatment arms, respectively) who developed disease progression, and 59 subjects (18 and 41 in the control and treatment arms, respectively) who died without disease progression. The median age was 62.5 years with interquartile range (55, 69) years. There were 388 patients with ECOG score 0 or 1, 287 were males, 151 had rectal cancer, 352 were from Western Europe, 39 were from Eastern and Central Europe, and 63 were from the rest of the world. The median follow-up time was 189.5 days and the interquartile range of the follow-up time was (93, 334) days. Among those 387 patients who developed disease progression, the median disease progression time is 53 days and the interquartile range is (45, 84) days. Of these 201 patients who developed disease progression in the control arm, 167 patients were switched to the treatment arm at the time of disease progression.

The model for the time in months to disease progression includes all the baseline covariates. Among the 387 patients who developed disease progression, the median age at the time of disease progression was 62.1 years with interquartile range (55.0, 69.1), the numbers of patients who had partial response, stable disease, and progressive disease were 19, 86, and 282, respectively. There were 348 patients with baseline ECOG score 0 or 1, 286 patients had a last ECOG score on or prior to disease progression 0 or 1, and 180 patients had grade 2 or above adverse events. The covariates for the time in months from disease progression to death include treatment, bECOG01, age at disease progression, best tumor response with partial response (BTR PR) or stable disease (BTR SD) versus progressive disease according to investigator assessment, last ECOG score on or prior to disease progression (score 0 or 1 versus ≥ 2 (LECOG01)), and adverse events (AE).

We fit both FM and CM with different values of J₀, J₁ and J₂ to the panitumumab data. The DIC and LPML values are given in Table 2. We see from Table 2 that (J₀, J₁, J₂) = (1, 30, 5) achieves the smallest DIC value and the largest LPML value among the 7 combinations of (J₀, J₁, J₂) considered here under both FM and CM and the best DIC and LPML values were 3475.27 and −1741.32 under FM and 3482.62 and −1746.76 under CM, respectively. We also observe that for each of these seven combinations of (J₀, J₁, J₂), FM consistently has a smaller DIC value and a larger LPML value than CM, implying that FM fits the panitumumab data better than CM.

Table 2.

DIC and LPML Values for the Panitumumab Data

Parameter			FM			CM
J0	J1	J2	DIC	pD	LPML	DIC	pD	LPML
1	30	5	3475.27	67.13	−1741.32	3482.64	67.32	−1746.76
3	30	5	3479.02	69.20	−1742.90	3486.14	69.48	−1748.76
5	30	5	3480.09	71.24	−1743.92	3486.92	71.44	−1748.94
1	25	5	3493.38	61.83	−1749.55	3500.00	62.20	−1755.11
1	35	5	3477.89	72.31	−1743.16	3484.61	72.54	−1748.62
1	30	3	3484.99	65.15	−1746.02	3488.20	65.37	−1749.05
1	30	10	3481.34	72.23	−1744.74	3490.95	72.46	−1751.73

Table 3 shows the posterior estimates of the model parameters under FM with (J₀, J₁, J₂) = (1, 30, 5). The 95% HPD intervals for treatment were (−1.753, −0.484) under the E model, (−1.145, 0.175) under the T_D model, (−1.733, −1.148) under the T_E model, and (−1.479, −0.441) under the T_G model.

Table 3.

Posterior Estimates for the Panitumumab Data under FM with (J₀, J₁, J₂) = (1, 30, 5)

Parameter	EST	SD	95% HPD	Parameter	EST	SD	95% HPD
		E Model				TD Model
Intercept	1.512	0.989	(−0.438, 3.463)
Treatment	−1.115	0.324	(−1.753, −0.484)	Treatment	−0.481	0.337	(−1.145, 0.175)
Age	−0.010	0.014	(−0.039, 0.017)	Age	0.023	0.015	(−0.008, 0.052)
bECOG01	1.987	0.346	(1.336, 2.699)	bECOG01	−0.617	0.296	(−1.202, −0.034)
Rectal	0.303	0.337	(−0.342, 0.967)	Rectal	−0.060	0.319	(−0.696, 0.546)
Male	−0.317	0.330	(−0.944, 0.342)	Male	−0.326	0.306	(−0.923, 0.279)
CenEastEU	0.001	0.628	(−1.171, 1.301)	CenEastEU	−0.308	0.638	(−1.545, 0.951)
WesternEU	0.334	0.422	(−0.498, 1.149)	WesternEU	0.231	0.395	(−0.546, 0.991)
		TE Model				TG Model
Treatment	−1.443	0.150	(−1.733, −1.148)	Treatment	−0.975	0.265	(−1.479, −0.441)
Age	−0.019	0.006	(−0.031, −0.007)	V*(1-Treatment)	−1.475	0.256	(−1.968, −0.962)
bECOG01	−0.869	0.220	(−1.297, −0.431)	PR Age	−0.007	0.007	(−0.020, 0.006)
Rectal	−0.112	0.133	(−0.379, 0.138)	BTR PR	−0.254	0.347	(−0.942, 0.413)
Male	−0.129	0.132	(−0.386, 0.131)	BTR SD	−0.088	0.192	(−0.460, 0.296)
CenEastEU	0.190	0.274	(−0.351, 0.727)	bECOG01	−0.445	0.242	(−0.908, 0.034)
WesternEU	−0.074	0.188	(−0.446, 0.286)	LECOG01	−1.186	0.177	(−1.522, −0.829)
				AE	0.348	0.141	(0.082, 0.631)
				τ	0.322	0.083	(0.163, 0.490)

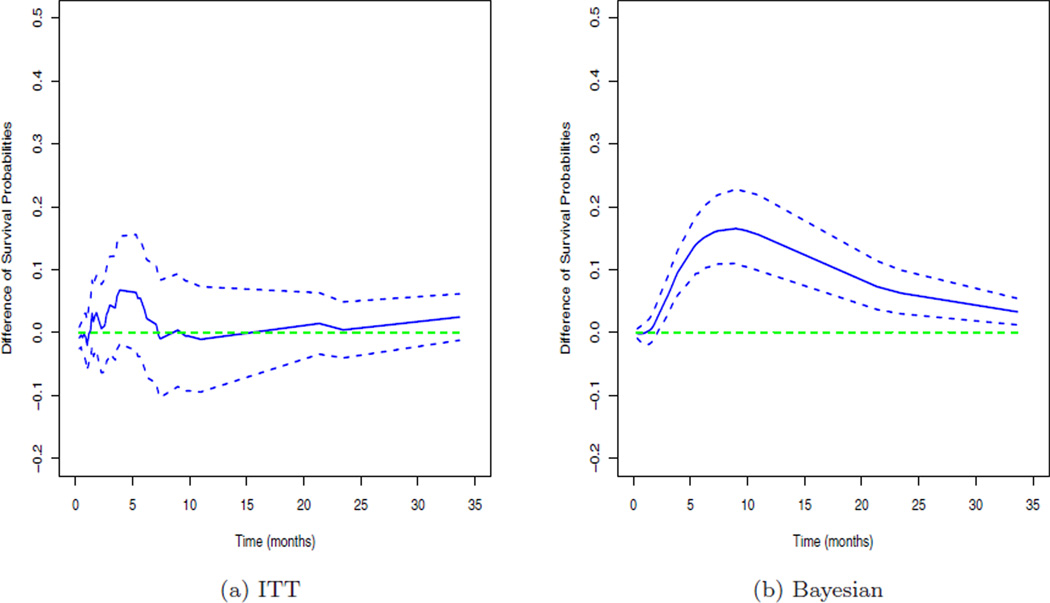
These results imply that treatment is associated with E, T_E, T_G but not with T_D. The other important prognostic factors include bCOG01 under the E, T_D, and T_E model, LECOG01 under the T_G model, age under the T_E model, and AE under the T_G model as their corresponding 95% HPD intervals do not contain 0. The treatment switching variable, V, is also associated with T_G. The posterior mean and 95% HPD interval for τ were 0.322 and (0.163, 0.490), which implies that there is a moderate dependence between T_E and T_G. We also fit the best CM with (J₀, J₁, J₂) = (1, 30, 5) to the panitumumab data and the posterior mean and 95% HPD interval for γ₂₁ in (2.4) were −0.083 and (−0.161, −0.008), which implies that there is a positive association between T_E and T_G. Panel (a) in Figure 3 shows the estimated differences of the survival probabilities and their pointwise 95% confidence intervals (CIs) between the two treatment groups of P+BSC and BSC using the intent-to-treat (ITT) Kaplan-Meier approach and Panel (b) plots the posterior estimates, E[S₁(t|θ)−S₀(t|θ)|D_obs], where S₀(t|θ) and S₁(t|θ) are given in (3.2), and the corresponding pointwise 95% HPD intervals of S₁(t|θ) − S₀(t|θ) between these two treatment groups. From Panel (a) of Figure 3, we see that the ITT approach yields no difference between two treatment groups as all 95% CIs contain 0. In contrast, as shown in Panel (b) of Figure 3, all the posterior estimates of S₁(t|θ) − S₀(t|θ) are above 0 and the corresponding 95% HPD intervals are above 0 after 2.25 months. We note that the maximum estimated difference E[S₁(t|θ) − S₀(t|θ)|D_obs] was attained at approximately 9 months and the corresponding posterior mean and 95% HPD interval were 0.165 and (0.110, 0.227). These posterior estimates indicate that P+BSC does yield a higher survival probability than BSC.

Fig. 3.

The estimated differences with 95% intervals of the survival curves between the treatment and control arms.

In all of the Bayesian computations, we used 20,000 Gibbs samples after a burn-in of 1000 for each model to compute all the posterior estimates, including posterior means, posterior standard deviations, and 95% HPD intervals. Codes were written for the FORTRAN 95 compiler using IMSL subroutines with double precision accuracy. The convergence of the Gibbs sampler was checked using several diagnostic procedures discussed in Chen et al. (2000). The autocorrelations for all model parameters disappeared before lag 10.

6 Discussion

In this paper, we have proposed a novel semi-competing risks Bayesian frailty model that accommodates treatment switching and dependence between the progression time and survival time. This type of scenario arises often in clinical trials in which, once a patient experiences an event, such as progression, they immediately switch to the experimental treatment. As a result of the switch, the model attempts to capture the treatment effect when no subjects would have switched treatment. The innovation in the model lies in the fact that the observed data likelihood is modeled and is based on four possible scenarios, and the model itself has three components. This type of model is quite different from what has been proposed in the literature. Another innovation here lies in the Bayesian approach to fit the model. Efficient MCMC methods based on the collapsed Gibbs sampler facilitate a flexible Bayesian model that is computationally feasible and identifiable. Such a model does not appear computationally feasible from a frequentist perspective. As shown in the simulation studies and real data analysis, our proposed model has several advantages over the conditional model (CM) proposed by others in the literature. It appears to have better performance under certain scenarios and produces a better model fit according to DIC and LPML. The proposed model is useful for practitioners encountering treatment switching studies in the presence of semi-competing risks where one is interested in assessing the treatment effect on overall survival.

Appendix A: Proofs of Theorems

Proof of Theorem 1

Using (3.1) with the prior distributions assumed in the theorem, we have

$$\pi (\theta |D_{obs})\propto L(\mathit{\theta }|D_{obs})\left[\prod _{k=0}^2\prod _{j=1}^{J_K}\frac{1}{{\lambda }_{kj}}\right]\left[\frac{1}{{\tau }^{a_{\tau }}+1}\text{exp}\right(-\frac{b_{\tau }}{\tau }\left)\right].$$

Using (2.9), it is easy to show that

$$L(\mathit{\theta }|D_{obs})\le L_a(\mathit{\alpha }|D_{obs})L_1({\beta }_0,{\gamma }_0,{\mathit{\lambda }}_0|D_{obs})L_2({\beta }_1,{\gamma }_1,{\mathit{\lambda }}_1,{\beta }_{21},{\beta }_{22},{\gamma }_2,{\mathit{\lambda }}_2,\tau |D_{obs})L_3({\beta }_1,{\gamma }_1,{\mathit{\lambda }}_1,\tau |D_{obs}).$$

where $L_a(\mathit{\alpha }|D_{obs})={\prod }_{i\in {\cup }_{\ell =1}^3{𝒩}_{\ell }}\frac{\text{exp}\{E_i({\alpha }_0+A_i{\alpha }_1+{\mathit{x}}_i^{\prime }{\mathit{\alpha }}_2)\}}{1+\text{exp}({\alpha }_0+A_i{\alpha }_1+{\mathit{x}}_i^{\prime }{\mathit{\alpha }}_2)}$,

$$L_1({\beta }_0,{\gamma }_0,{\mathit{\lambda }}_0|D_{obs})=\prod _{i\in {𝒩}_1}{h}_0(y_i|{\mathit{\lambda }}_0)\text{exp}(A_i{\beta }_0+{\mathit{x}}_i^{\prime }{\gamma }_0)\text{exp}\{-H_0(y_i|{\mathit{\lambda }}_0)\text{exp}(A_i{\beta }_0+{\mathit{x}}_i^{\prime }{\gamma }_0)\},$$ (A.1)

$$L_2({\beta }_1,{\gamma }_1,{\mathit{\lambda }}_1,{\beta }_{21},{\beta }_{22},{\gamma }_2,{\mathit{\lambda }}_2,\tau |D_{obs})=\prod _{i\in {𝒩}_2}[(1+\tau )h_1(y_{Ei}|{\mathit{\lambda }}_1)\text{exp}(A_i{\beta }_1+{\mathit{x}}_i^{\prime }{\gamma }_1)\times h_2(y_{Gi}|{\mathit{\lambda }}_2)\text{exp}\{A_i{\beta }_{21}+V_i(1-A_i){\beta }_{22}+{\mathit{z}}_i^{\prime }{\gamma }_2\}\times {\{1+\tau (H_1(y_{Ei}|{\mathit{\lambda }}_1)\text{exp}(A_i{\beta }_1+{\mathit{x}}_i^{\prime }{\gamma }_1)+H_2(y_{Gi}|{\mathit{\lambda }}_2)\text{exp}\{A_i{\beta }_{21}+V_i(1-A_i){\beta }_{22}+{\mathit{z}}_i^{\prime }{\gamma }_2\}\left)\right\}}^{-(2+\frac{1}{\tau })}],$$ (A.2)

and

$$L_3({\beta }_1,{\gamma }_1,{\mathit{\lambda }}_1,\tau |D_{obs})=\prod _{i\in {𝒩}_3}{h}_1(y_{Ei}|{\mathit{\lambda }}_1)\text{exp}(A_i{\beta }_1+{\mathit{x}}_i^{\prime }{\gamma }_1){\{1+\tau H_1(y_{Ei}|{\mathit{\lambda }}_1)\text{exp}(A_i{\beta }_1+{\mathit{x}}_i^{\prime }{\gamma }_1)\}}^{-(1+\frac{1}{\tau })}.$$ (A.3)

To prove propriety of the posterior, it is sufficient to show (a) ∫ L_a(α|D_obs)dα < ∞; (b) $\int L_1({\beta }_0,{\gamma }_0,{\mathit{\lambda }}_0|D_{obs})({\prod }_{j=1}^{J_0}\frac{1}{{\lambda }_{0j}})d{\beta }_{0}d{\gamma }_{0}d{\mathit{\lambda }}_0<\infty$ and (c) $\int L_2({\beta }_1,{\gamma }_1,{\mathit{\lambda }}_1,{\beta }_{21},{\beta }_{22},{\gamma }_2,{\mathit{\lambda }}_2,\tau |D_{obs})L_3({\beta }_1,{\gamma }_1,{\mathit{\lambda }}_1,\tau |D_{obs})\left[{\prod }_{k=1}^2{\prod }_{j=1}^{J_K}\frac{1}{{\lambda }_{kj}}\right][\frac{1}{{\tau }^{a_{\tau }+1}}\text{exp}(-\frac{b_{\tau }}{\tau })]$. dβ₁dγ₁dλ₁dβ₂₁dβ₂₂dγ₂dλ₂dτ < ∞.

Under Conditions (i) and (ii), Theorem 2.1 of Chen and Shao (2001) directly leads to (a). Let j_i be an index such that s_0,ji−1 < y_i ≤ s_0ji. Then we have δ_i0j = 1 for j = j_i and δ_i0j = 0 for j ≠ j_i and

$$h_0(y_i|{\mathit{\lambda }}_0)\text{exp}(A_i{\beta }_0+{\mathit{x}}_i^{\prime }{\gamma }_0)\text{exp}\{-H_0(y_i|{\mathit{x}}_i)\text{exp}(A_i{\beta }_0+{\mathit{x}}_i^{\prime }{\gamma }_0)\}\le {\lambda }_{0j_i}\text{exp}(A_i{\beta }_0+{\mathit{x}}_i^{\prime }{\gamma }_0)\text{exp}\{-{\lambda }_{0j_i}(y_i-s_{0,j_i-1})\text{exp}(A_i{\beta }_0+{\mathit{x}}_i^{\prime }{\gamma }_0)\}\le M_{11},$$ (A.4)

where M₁ > 0 is a constant. Consider the transformation ξ_0j = log(λ_0j), where $d{\xi }_{0j}=\frac{d{\lambda }_{0j}}{{\lambda }_{0j}}$ for j = 1, …, J₀. Under condition (iii), there exist J₀ + p₀ distinct i₁, …, i_J0+p0 ∈ 𝒩₁ such that the (J₀ + p₀) × (J₀+p₀) matrix $X_0^{*}$, which has rows $({\delta }_{i_{\ell }01},\dots ,{\delta }_{i_{\ell }0J_0},A_{i_{\ell }},{\mathit{x}}_{i_{\ell }}^{\prime })$) for ℓ = 1, …, J₀+p₀, is of full rank. Using (A.4), we have

$$\int L_1({\beta }_0,{\gamma }_0,{\mathit{\lambda }}_0|D_{obs})(\prod _{j=1}^{J_0}\frac{1}{{\lambda }_{0j}})d{\beta }_{0}d{\gamma }_{0}d{\mathit{\lambda }}_0\le M_{12}\int [\prod _{\ell =1}^{J_0+p_0}\text{exp}({\xi }_{0j_{i_{\ell }}}+A_{i_{\ell }}{\beta }_0+{\mathit{x}}_{i_{\ell }}^{\prime }{\gamma }_0)\times \text{exp}\{-y_{i_{\ell }}-s_{0,j_{i_{\ell }}-1})\text{exp}({\xi }_{0j_{i_{\ell }}}+A_{i_{\ell }}{\beta }_0+{\mathit{x}}_{i_{\ell }}^{\prime }{\gamma }_0)\}]d{\beta }_{0}d{\gamma }_{0}d{\mathit{\xi }}_0,$$ (A.5)

where M₁₂ > 0 is a constant and ξ₀ = (ξ₀₁, …, ξ_0J0 )′. Now, we take a one-to-one transformation ${\mathit{\varphi }}_0=({\varphi }_{01},\dots ,{\varphi }_{0,J_0+p_0})\prime =X_0^{*}({\mathit{\xi }}_0^{\prime },{\beta }_0,{\gamma }_0^{\prime })\prime$. Using (A.5), we have

$$\int L_1({\beta }_0,{\gamma }_0,{\mathit{\lambda }}_0|D_{obs})(\prod _{j=1}^{J_0}\frac{1}{{\lambda }_{0j}})d{\beta }_{0}d{\gamma }_{0}d{\mathit{\lambda }}_0\le M_{13}\prod _{\ell =1}^{J_0+p_0}{\int }_{-\infty }^{\infty }\text{exp}({\varphi }_{0\ell })\text{exp}\{-(y_{i_{\ell }}-s_{0,j_{i_{\ell }}-1})\text{exp}({\varphi }_{0\ell })d{\varphi }_{0\ell }=M_{13}\prod _{\ell =1}^{J_0+p_0}{(y_{i\ell }-s_{0,j_{i_{\ell }}-1})}^{-1}>\infty ,$$ (A.6)

where M₁₃ > 0 is a constant, which completes the proof of (b).

For (c), we first rewrite (A.2) as follows:

$$L_2({\beta }_1,{\gamma }_1,{\mathit{\lambda }}_1,{\beta }_{21},{\beta }_{22},{\gamma }_2,{\mathit{\lambda }}_2,\tau |D_{obs})=L_{2a}({\beta }_1,{\gamma }_1,{\mathit{\lambda }}_1,\tau |D_{obs})L_{2b}({\beta }_{21},{\beta }_{22},{\gamma }_2,{\mathit{\lambda }}_2|D_{obs},{\beta }_1,{\gamma }_1,{\mathit{\lambda }}_1,\tau ),$$

where

$$L_{2a}({\beta }_1,{\gamma }_1,{\mathit{\lambda }}_1,\tau |D_{obs})=\prod _{i\in {𝒩}_2}{h}_1(y_{Ei}|{\mathit{\lambda }}_1)\text{exp}(A_i{\beta }_1+{\mathit{x}}_i^{\prime }{\gamma }_1){\{1+\tau H_1(y_{Ei}|{\mathit{\lambda }}_1)\text{exp}(A_i{\beta }_1+{\mathit{x}}_i^{\prime }{\gamma }_1)\}}^{-(2+\frac{1}{\tau })},$$ (A.7)

$$L_{2b}({\beta }_{21},{\beta }_{22},{\gamma }_2,{\mathit{\lambda }}_2|D_{obs},{\beta }_1,{\gamma }_1,{\mathit{\lambda }}_1,\tau )=\prod _{i\in {𝒩}_2}[(1+\tau )h_2(y_{Gi}|{\mathit{\lambda }}_2)\text{exp}(A_i{\beta }_{21}+V_i(1-A_i){\beta }_{22}-{\mathit{z}}_i^{\prime }{\gamma }_2\}\times \{1+\tau b_i{H}_2(y_{Gi}|{\mathit{\lambda }}_2)\text{exp}{\{A_i{\beta }_{21}+V_i(1-A_i){\beta }_{22}+{\mathit{z}}_i^{\prime }{\gamma }_2\}\}}^{-(2+\frac{1}{\tau })}],$$ (A.8)

and $b_i={\{1+\tau H_1(y_{Ei}|{\mathit{\lambda }}_1)\text{exp}(A_i{\beta }_1+{\mathit{x}}_i^{\prime }{\gamma }_1)\}}^{-1}$. Let j_i denote the index such that s_2,ji−1 < y_Gi ≤ s_2,ji. Then, we have

$$L_{2b}({\beta }_{21},{\beta }_{22},{\gamma }_2,{\mathit{\lambda }}_2|D_{obs},{\beta }_1,{\gamma }_1,{\mathit{\lambda }}_1,\tau )\le \prod _{i\in {𝒩}_2}[(1+\tau ){\lambda }_{2j_i}\text{exp}(A_i{\beta }_{21}+V_i(1-A_i){\beta }_{22}+{\mathit{z}}_i^{\prime }{\gamma }_2\times \{1+\tau b_i{\lambda }_{2j_i}(y_{Gi}-s_{2j_i-1})\text{exp}{\{A_i{\beta }_{21}+V_i(1-A_i){\beta }_{22}+{\mathit{z}}_i^{\prime }{\gamma }_2\}\}}^{-(2+\frac{1}{\tau })}].$$ (A.9)

Observing that ${(1+rv)}^{1+\frac{1}{r}}\ge 1+v$ for all r > 0 and v > 0, we obtain

$$(1+\tau ){\lambda }_{2j_i}\text{exp}\{A_i{\beta }_{21}+V_i(1-A_i){\beta }_{22}+{\mathit{z}}_i^{\prime }{\gamma }_2\}\times {\{1+\tau b_i{\lambda }_{2j_i}(y_{Gi}-s_{2,j_i-1})\text{exp}\{A_i{\beta }_{21}+V_i(1-A_i){\beta }_{22}+{\mathit{z}}_i^{\prime }{\gamma }_2\}\}}^{-(2+\frac{1}{\tau })}\le \frac{(1+\tau ){\lambda }_{2j_i}\text{exp}\{A_i{\beta }_{21}+V_i(1-A_i){\beta }_{22}+{\mathit{z}}_i^{\prime }{\gamma }_2\}}{1+(1+\tau )b_i{\lambda }_{2j_i}(y_{Gi}-s_{2,j_i-1})\text{exp}\{A_i{\beta }_{21}+V_i(1-A_i){\beta }_{22}+{\mathit{z}}_i^{\prime }{\gamma }_2\}}\le \frac{1}{b_i(y_{Gi}-s_{2,j_i-1})}.$$ (A.10)

Under condition (iii), X₂ is of full rank. Therefore, there exist J₂ + p₂ distinct i₁, …, i_J2+p2 ∈ 𝒩₂ such that the (J₂ +p₂)×(J₂ +p₂) matrix $X_2^{*}$, which has rows (${\delta }_{i_{\ell }21},\dots ,{\delta }_{i_{\ell }2J_2},A_{i_{\ell }},{\mathit{z}}_{i_{\ell }}^{\prime }$) for ℓ = 1, …, J₂ + p₂, is of full rank. Let 𝒩₂₁ = {i₁, …, i_J2+p2} and 𝒩₂₂ = 𝒩₂ − 𝒩₂₁. Using (A.10), we have

$$L_{2b}({\beta }_{21},{\beta }_{22},{\gamma }_2,{\mathit{\lambda }}_2|D_{obs},{\beta }_1,{\gamma }_1,{\mathit{\lambda }}_1,\tau )\le M_{21}[\prod _{i\in {𝒩}_{22}}\frac{1}{b_i}]\times (\prod _{i\in {𝒩}_{21}}[(1+\tau ){\lambda }_{2j_i}\text{exp}\{A_i{\beta }_{21}+V_i(1-A_i){\beta }_{22}-{\mathit{z}}_i^{\text{'}}{\gamma }_2\}\times {\{1+\tau b_i{\lambda }_{2j_i}(y_{Gi}-s_{2,j_i-1})\text{exp}\{A_i{\beta }_{21}+V_i(1-A_i){\beta }_{22}+{\mathit{z}}_i^{\text{'}}{\gamma }_2\}\}}^{-(2+\frac{1}{\tau })}]),$$ (A.11)

where M₂₁ > 0 is a constant. Similar to (A.5) and (A.6), using (A.11), we can show that

$$\int L_{2b}({\beta }_{21},{\beta }_{22},{\gamma }_2,{\mathit{\lambda }}_2|D_{obs},{\beta }_1,{\gamma }_1,{\mathit{\lambda }}_1,\tau )[\prod _{j=1}^{J_2}\frac{1}{{\lambda }_{2j}}]d{\beta }_{21}d{\beta }_{22}d{\gamma }_{2}d{\mathit{\lambda }}_2\le M_{22}[\prod _{i\in {𝒩}_{22}}\frac{1}{b_i}]\times (\prod _{i\in {𝒩}_{22}}[(1+\tau ){\int }_{-\infty }^{\infty }\text{exp}({\varphi }_{2i})\{1+\tau b_i(y_{Gi}-s_{2,j_i-1})\text{exp}{({\varphi }_{2i})\}}^{-(2+\frac{1}{\tau })}d{\varphi }_{2i}])=M_{22}[\prod _{i\in {𝒩}_{22}}\frac{1}{b_i}]\times [\prod _{i\in {𝒩}_{21}}\frac{(1+\tau )}{(1+\frac{1}{\tau })\tau b_i(y_{Gi}-s_{2,j_i-1})}]=M_{23}\prod _{i\in {𝒩}_{22}}(1+\tau H_1(y_{Ei}|{\mathit{\lambda }}_1)\text{exp}(A_i{\beta }_1+{\mathit{x}}_i^{\prime }{\gamma }_1)\},$$ (A.12)

where M₂₂ and M₂₃ are two positive constants. Now, using (A.2), (A.3), (A.7), and (A.12), we obtain

$$\int \left\{L_2\right({\beta }_1,{\gamma }_1,{\mathit{\lambda }}_1,{\beta }_{21},{\beta }_{22},{\gamma }_2,{\mathit{\lambda }}_2,\tau \left|D_{obs}\right)L_3({\beta }_1,{\gamma }_1,{\mathit{\lambda }}_1,\tau |D_{obs})\times [\prod _{k=1}^2\prod _{j=1}^{J_K}\frac{1}{{\lambda }_{kj}}]\times [\frac{\text{exp}(-\frac{b_{\tau }}{\tau })}{{\tau }^{a_{\tau }+1}}\left]\right\}d{\beta }_{21}d{\beta }_{22}d{\gamma }_{2}d{\mathit{\lambda }}_2\le M_{23}\left[{\prod _{i\in {𝒩}_2\cup {𝒩}_3}{h}_1(y_{Ei}|{\mathit{\lambda }}_1)\text{exp}(A_i{\beta }_1+{\mathit{x}}_i^{\prime }{\gamma }_1)\{1+\tau H_1(y_{Ei}|{\mathit{\lambda }}_1)\text{exp}(A_i{\beta }_1+{\mathit{x}}_i^{\prime }{\gamma }_1)\}}^{-(1+\frac{1}{\tau })}\right]\times \left[\prod _{j=1}^{J_1}\frac{1}{{\lambda }_{1j}}\right]\left[\frac{\text{exp}(-\frac{b_{\tau }}{\tau })}{{\tau }^{a_{\tau }+1}}\right].$$ (A.13)

The right hand side of (A.13) is precisely the kernel of the posterior distribution of (β₁, γ₁, λ₁, τ ) under the GORH model of Banerjee et al. (2007). Thus, under conditions (iii) and (iv), following the proof of Theorem 3.1 of Banerjee et al. (2007), we can show that the integration of the right hand side of (A.13) over (β₁, γ₁,λ₁, τ) is finite, which completes the proof of Theorem 1.

Proof of Theorem 2

For the posterior conditional distribution, the first derivative of the log-likelihood function is given by $\frac{\partial \text{log}\pi ({\tau }^{*}|{\beta }_1,{\gamma }_1,{\mathit{\lambda }}_1^{*},{\beta }_2,{\gamma }_2,{\mathit{\lambda }}_2^{*},{\mathit{E}}^{*},D_{obs})}{\partial {\tau }^{*}}\propto {\sum }_{i=1}^n\{{(\frac{1}{{\tau }^{*}}+\frac{1}{{\tau }^{*}+1}-\text{log}[1-H_1(y_{Ei}|{\mathit{\lambda }}_1^{*})\text{exp}(A_i{\beta }_1+{\mathit{x}}_i^{\prime }{\gamma }_1)+H_2(y_{Gi}|{\mathit{\lambda }}_2^{*})\text{exp}\{A_i{\beta }_{21}+V_i(1-A_i){\beta }_{22}+{\mathit{z}}_i^{\prime }{\gamma }_2\}])}^{1\{d_i=1,{\nu }_i=1\}}+(\frac{1}{{\tau }^{*}}-\text{log}[1-H_1(y_{Ei}|{\mathit{\lambda }}_1^{*})\text{exp}(A_i{\beta }_1+{\mathit{x}}_i^{\prime }{\gamma }_1)+H_2(y_{Gi}|{\mathit{\lambda }}_2^{*})\text{exp}{\{A_i{\beta }_{21}+V_i(1-A_i){\beta }_{22}+{\mathit{z}}_i^{\prime }{\gamma }_2\}])}^{1\{d_i=1,{\nu }_i=0\}}-(\text{log}[1-H_1(y_i|{\mathit{\lambda }}_1^{*})\text{exp}{(A_i{\beta }_1+{\mathit{x}}_i^{\prime }{\gamma }_1)}^{E_i^{*}1\{d_i=0,{\nu }_i=0\}}\}+\frac{(a_{\tau }+{\sum }_{k=1}^2{\sum }_{j=1}^{J_K}{a}_{kj}-3)}{{\tau }^{*}}-[b_{\tau }+{\sum }_{k=1}^2{\sum }_{j=1}^{J_K}(b_{kj}{\mathit{\lambda }}_{kj}^{*})]$. The second derivative is given by $\frac{{\partial }^2\text{log}\pi ({\tau }^{*}|{\beta }_1,{\gamma }_1,{\mathit{\lambda }}_1^{*},{\beta }_2,{\gamma }_2,{\mathit{\lambda }}_2^{*},{\mathit{E}}^{*},D_{obs})}{\partial {({\tau }^{*})}^2}\propto {{\sum }_{i=1}^n\{[-\frac{1}{{({\tau }^{*})}^2}-\frac{1}{{({\tau }^{*}+1)}^2}]}^{1\{d_i=1,{\nu }_i=1\}}+{[-\frac{1}{{({\tau }^{*})}^2}]}^{1\{d_i=1,{\nu }_i=0\}}\}-\frac{(a_{\tau }+{\sum }_{k=1}^2{\sum }_{j=1}^{J_K}{a}_{kj}-3)}{{({\tau }^{*})}^2}$.

Assuming that ${\sum }_{i=1}^n[1\{{\nu }_i=1,d_i=1\}+1\{{\nu }_i=0,d_i=1\}]+a_{\tau }+{\sum }_{k=1}^2{\sum }_{j=1}^{J_K}{a}_{Kj}-3>0$, we will always have $\frac{{\partial }^2\text{log}\pi ({\tau }^{*}|{\beta }_1,{\gamma }_1,{\mathit{\lambda }}_1^{*},{\beta }_2,{\gamma }_2,{\mathit{\lambda }}_2^{*},{\mathit{E}}^{*},D_{obs})}{\partial {({\tau }^{*})}^2}<0$. Therefore, the conditional density of τ* given by (3.7) is log-concave. Letting $\frac{\partial \text{log}\pi ({\tau }^{*}|{\beta }_1,{\gamma }_1,{\mathit{\lambda }}_1^{*},{\beta }_2,{\gamma }_2,{\mathit{\lambda }}_2^{*},{\mathit{E}}^{*},D_{obs})}{\partial {\tau }^{*}}=0$, then we have $B_1+\frac{B_2}{{\tau }^{*}}+\frac{B_3}{1+{\tau }^{*}}=0$, where B₁, B₂ and B₃ are defined in Theorem 2. After some algebra, the solution is given by ${\widehat{\tau }}^{*}=\frac{-(B_1+B_2+B_3)-\sqrt{{(B_1+B_2+B_3)}^2-4B_1{B}_2}}{2B_1}$. The reasons are as follows: with b_τ > 0, b_kj > 0 and ${\lambda }_{kj}^{*}>0$, it is obvious that B₁ < 0; and with the previous assumption that ${\sum }_{i=1}^n[1\{{\nu }_i=1,d_i=1\}+1\{{\nu }_i=0,d_i=1\}]+a_{\tau }+{\sum }_{k=1}^2{\sum }_{j=1}^{J_K}{a}_{Kj}-3>0$, then B₂ > 0, so we have (B₁ + B₂ +B₃)² −4B₁B₂ > 0. Therefore, the equation has two roots. Since τ* > 0, then we only keep the positive solution τ̂* since the other root is negative. Since we just showed that the conditional density of τ* given by (3.7) is log-concave, it follows that the mode of (3.7) is analytically available and given by τ̂*.

Appendix B: Computational Development

B.1. Derivation of the Potential Survival Function

After some algebra, we obtain

$$S_a(t|\mathit{\theta })={\int }_{\mathit{x}}P(T_D>t|A=a,\mathit{x},E=0,{\beta }_0,{\gamma }_0,{\mathit{\lambda }}_0)P(E=0|A=a,\mathit{x},\mathit{\alpha })f_X(\mathit{x}|A=a)d\mathit{x}+{\int }_{\mathit{x},\mathit{z},\omega }\{P(T_E>t|A=a,\mathit{x},E=1,{\beta }_1,{\gamma }_1,{\mathit{\lambda }}_1,\omega )+{\int }_0^{t}P(T_G>t-u|A=a,\mathit{z},V=0,E=1,{\beta }_2,{\gamma }_2,{\mathit{\lambda }}_2,\omega )\times f_1(u|A=a,\mathit{x},\omega ,{\beta }_1,{\gamma }_1,{\mathit{\lambda }}_1)du\}f(\omega |\tau )d\omega \times f_Z(\mathit{z}|A=a,\mathit{x},E=1)P(E=1|A=a,\mathit{x},\mathit{\alpha })f_X(\mathit{x}|A=a)d\mathit{z}d\mathit{x}.$$

When J₀ = J₁ = J₂ = 1, we obtain P(T_D > t|A = a, x, E = 0, β₀, γ₀, λ₀) = exp{−tλ₀ exp(Aβ₀ + x′γ₀)}, ∫_ω P(T_E>t | A = a, x, E = 1, β₁, γ₁, λ₁, ω) f (ω | τ)dω = ∫_ω exp[−ωt λ₁ exp(Aβ₁ + x′γ₁)]f(ω|τ) $d\omega ={[\frac{1}{1+{\mathit{\lambda }}_1\text{exp}(A{\beta }_1+{\mathit{x}}^{\prime }{\gamma }_1)t\tau }]}^{\frac{1}{\tau }}$, and ${\int }_w\{{\int }_0^{t}P(T_G>t-u|A=a,\mathit{z},V=0,E=1,{\beta }_2,{\gamma }_2,{\mathit{\lambda }}_2,\omega )f_1(u|A=a,\mathit{x},\omega ,{\beta }_1,{\gamma }_1,{\mathit{\lambda }}_1)du\}f(\omega |\tau )d\omega =\frac{{\mathit{\lambda }}_1\text{exp}(A{\beta }_1+{\mathit{x}}^{\prime }{\gamma }_1)}{{\mathit{\lambda }}_2\text{exp}\{A{\beta }_{21}+V(1-A){\beta }_{22}+{\mathit{z}}^{\prime }{\gamma }_2\}-{\mathit{\lambda }}_1\text{exp}\{A{\beta }_1+{\mathit{x}}^{\prime }{\gamma }_1\}}\{{[\frac{1}{1+{\mathit{\lambda }}_1\text{exp}\{A{\beta }_1+{\mathit{x}}^{\prime }{\gamma }_1\}t\tau }]}^{\frac{1}{\tau }}-{[\frac{1}{1+{\mathit{\lambda }}_2\text{exp}\{A{\beta }_{21}+V(1-A){\beta }_{22}+{\mathit{z}}^{\prime }{\gamma }_2\}t\tau }]}^{\frac{1}{\tau }}\}$.

For the more general case, where the values of J₀, J₁ and J₂ are not specified, we have

$$P(T_D>t|A=a,\mathit{x},E=0,{\beta }_0,{\gamma }_0,{\mathit{\lambda }}_0)=\text{exp}\{-\sum _{j=1}^{J_0}[1\{s_{0,j-1}<t\le s_{0j}\}\{{\lambda }_{0j}(t-s_{0,j-1})+\sum _{g=1}^{j-1}{\lambda }_{0g}(s_{0g}-s_{0,g-1})\}]\text{exp}(A{\beta }_0+\mathit{x}\prime {\gamma }_0)\},{\int }_{\omega }P(T_E>t|A=a,\mathit{x},E=1,{\beta }_1,{\gamma }_1,{\mathit{\lambda }}_1,\omega )f(\omega |\tau )d\omega ={\int }_{\omega }\text{exp}\{-\omega \sum _{j=1}^{J_1}[1\{s_{1,j-1}<t\le s_{1j}\}\{{\lambda }_{1j}(t-s_{1,j-1})+\sum _{g=1}^{j-1}{\lambda }_{1g}(s_{1g}-s_{1,g-1})\}]\text{exp}(A{\beta }_1+\mathit{x}\prime {\gamma }_1)\}f(\omega |\tau )d\omega ={\left[\frac{1}{1+{\sum }_{j=1}^{J_1}[1_{\{s_{1,j-1}<t\le s_{1j}\}}\{{\lambda }_{1j}(t-s_{1,j-1})+{\sum }_{g=1}^{j-1}{\lambda }_{1g}(s_{1g}-s_{1,g-1})\}]\text{exp}[A{\beta }_1+\mathit{x}\prime {\gamma }_1)\tau }\right]}^{\frac{1}{\tau }}.$$

Before the next derivation, we need to align the partitions of the time axis for h₁ and h₂. Let 0 < s_3,1 < s_3,2 < … s_{3, J3} be the ordered distinct values of s_{k, Jk}, where k = 1, 2. For a given time point t, there exists j_t such that t ∈ (s_{3, jt−1}, s_3,jt). In order to facilitate the computation, let s_{3, J3+1} = s_{3, J3}, s_{3, J3} = s_{3, J3−1}, …, s_{3, jt} = t. Then the corresponding constant hazards for each interval are as follows: λ_3kj = λ_kl if s_k,l−1 ≤ s_{3, j−1} < s_{3, j} ≤ s_kl for j ∈ (1, J₃ + 1) and l ∈ (1, J_k), where k = 1, 2. Next let

$$Q={\int }_0^{t}P(T_G>t-u|A=a,\mathit{z},V=0,E=1,{\beta }_2,{\gamma }_2,{\mathit{\lambda }}_2,\omega )f_1(u|A=a,\mathit{x},\omega ,{\beta }_1,{\gamma }_1,{\mathit{\lambda }}_1)du=\sum _{j=1}^{j_t}\{\omega \text{exp}(A{\beta }_1+\mathit{x}\prime {\gamma }_1){\int }_{s_{3,j-1}}^{s_{3,j}}[P(T_G>t-u|A=a,\mathit{z},V=0,E=1,{\beta }_2,{\gamma }_2,{\mathit{\lambda }}_2,\omega )\times {\lambda }_{31j}\text{exp}\{-[\sum _{l=1}^{j-1}{\lambda }_{31l}(s_{3,l}-s_{3,l-1})+{\lambda }_{31j}(u-s_{3,j-1})]\omega \text{exp}(A{\beta }_1+\mathit{x}\prime {\gamma }_1)\}]du\},$$

and

$$Q_j=\omega \text{exp}(A{\beta }_1+\mathit{x}\prime {\gamma }_1){\int }_{s_{3,j-1}}^{s_{3,j}}[P(T_G>t-u|A=a,\mathit{z},V=0,E=1,{\beta }_2,{\gamma }_2,{\mathit{\lambda }}_2,\omega )\times {\lambda }_{31j}\text{exp}\{-[\sum _{l=1}^{j-1}{\lambda }_{31l}(s_{3,l}-s_{3,l-1})+{\lambda }_{31j}(u-s_{3,j-1})]\omega \text{exp}(A{\beta }_1+\mathit{x}\prime {\gamma }_1)\}]du.$$

While u ∈ (s_3,j−1, s_3,j], we have (t − u) ∈ (t − s_3,j, t − s_3,j−1], then there exist j_l and j_u such that (t − s_3,j) ∈ (s_3,jl−1, s_3,jl] and (t − s_3,j−1) ∈ (s_3,ju−1, s_3,ju]. Let r = j_u − j_l. Then the range of r is from 0 to J₃. Therefore, when r = 0, we have

$$Q_j=\frac{{\lambda }_{31j}\text{exp}(A{\beta }_1+\mathit{x}\prime {\gamma }_1)}{{\lambda }_{32j_u}\text{exp}\{A{\beta }_{21}+V(1-A){\beta }_{22}+\mathit{z}\prime {\gamma }_2\}-{\lambda }_{31j}\text{exp}(A{\beta }_1+\mathit{x}\prime {\gamma }_1)}\times \left\{\text{exp}\right[-\{\sum _{l=1}^{j_u-1}{\lambda }_{32l}(s_{3,l}-s_{3,l-1})+{\lambda }_{32j_u}(t+s_{3,j}-s_{3,j_u-1})\}\omega \times \text{exp}\{A{\beta }_{21}+V(1-A){\beta }_{22}+\mathit{z}\prime {\gamma }_2\}-\{\sum _{l=1}^j{\lambda }_{31l}(s_{3,l}-s_{3,l-1})\}\omega \text{exp}(A{\beta }_1+\mathit{x}\prime {\gamma }_1)]-\text{exp}[-\{\sum _{l=1}^{j_u-1}{\lambda }_{32l}(s_{3,l}-s_{3,l-1})+{\lambda }_{32j_u}(t+s_{3,j-1}-s_{3,j_u-1})\}\omega \times \text{exp}\{A{\beta }_{21}+V(1-A){\beta }_{22}+\mathit{z}\prime {\gamma }_2\}-\sum _{l=1}^{j-1}{\lambda }_{31l}(s_{3,l}-s_{3,l-1})\omega \text{exp}(A{\beta }_1+\mathit{x}\prime {\gamma }_1)\left]\right\}.$$

Then

$${\int }_{\omega }{Q}_{j}f(\omega |\tau )d\omega =\frac{{\lambda }_{31j}\text{exp}(A{\beta }_1+\mathit{x}\prime {\gamma }_1)}{{\lambda }_{32j_u}\text{exp}\{A{\beta }_{21}+V(1-A){\beta }_{22}+\mathit{z}\prime {\gamma }_2\}-{\lambda }_{31j}\text{exp}(A{\beta }_1+\mathit{x}\prime {\gamma }_1)}\times \{{[1+\tau (\{\sum _{l=1}^{j_u-1}{\lambda }_{32l}(s_{3,l}-s_{3,l-1})+{\lambda }_{32j_u}(t+s_{3,j}-s_{3,j_u-1})\}\times \text{exp}\{A{\beta }_{21}+V(1-A){\beta }_{22}+\mathit{z}\prime {\gamma }_2\}+\{\sum _{l=1}^j{\lambda }_{31l}(s_{3,l}-s_{3,l-1})\}\text{exp}(A{\beta }_1+\mathit{x}\prime {\gamma }_1))]}^{-\frac{1}{\tau }}-{[1+\tau (\{\sum _{l=1}^{j_u-1}{\lambda }_{32l}(s_{3,l}-s_{3,l-1})+{\lambda }_{32j_u}(t+s_{3,j-1}-s_{3,j_u-1})\}\times \text{exp}\{A{\beta }_{21}+V(1-A){\beta }_{22}+\mathit{z}\prime {\gamma }_2\}+\sum _{l=1}^{j-1}{\lambda }_{31l}(s_{3,l}-s_{3,l-1})\text{exp}(A{\beta }_1+\mathit{x}\prime {\gamma }_1))]}^{-\frac{1}{\tau }}\}.$$

When r ≥ 1, we have

$$Q_j=\frac{{\lambda }_{31j}\text{exp}(A{\beta }_1+\mathit{x}\prime {\gamma }_1)}{{\lambda }_{32j_u}\text{exp}\{A{\beta }_{21}+V(1-A){\beta }_{22}+\mathit{z}\prime {\gamma }_2\}-{\lambda }_{31j}\text{exp}(A{\beta }_1+\mathit{x}\prime {\gamma }_1)}\times \{\text{exp}[-\{\sum _{l=1}^{j_u-1}{\lambda }_{32l}(s_{3,l}-s_{3,l-1})\}\omega \text{exp}\{A{\beta }_{21}+V(1-A){\beta }_{22}+\mathit{z}\prime {\gamma }_2\}-\{\sum _{l=1}^{j-1}{\lambda }_{31l}(s_{3,l}-s_{3,l-1})+{\lambda }_{31j}(t-s_{3,j-1}-s_{3,j_u-1})\}\omega \text{exp}(A{\beta }_1+\mathit{x}\prime {\gamma }_1)]-\text{exp}[-\{\sum _{l=1}^{j_u-1}{\lambda }_{32l}(s_{3,l}-s_{3,l-1})+{\lambda }_{32j_u}(t-s_{3,j_u-1}-s_{3,j-1})\}\omega \text{exp}\{A{\beta }_{21}+V(1-A){\beta }_{22}+\mathit{z}\prime {\gamma }_2\}-\sum _{l=1}^{j-1}{\lambda }_{31l}(s_{3,l}-s_{3,l-1})\omega \text{exp}(A{\beta }_1+\mathit{x}\prime {\gamma }_1)]\}$$

$$+\sum _{j^{*}=1}^{r-1}\frac{{\lambda }_{31j}\text{exp}(A{\beta }_1+\mathit{x}\prime {\gamma }_1)}{{\lambda }_{32(j_u-j^{*})}\text{exp}\{A{\beta }_{21}+V(1-A){\beta }_{22}+\mathit{z}\prime {\gamma }_2\}-{\lambda }_{31j}\text{exp}(A{\beta }_1+\mathit{x}\prime {\gamma }_1)}\times \{\text{exp}[-\sum _{l=1}^{j_u-j^{*}-1}{\lambda }_{32l}(s_{3,l}-s_{3,l-1})\omega \text{exp}\{A{\beta }_{21}+V(1-A){\beta }_{22}+\mathit{z}\prime {\gamma }_2\},-\sum _{l=1}^{j-1}\{{\lambda }_{31l}(s_{3,l}-s_{3,l-1})+{\lambda }_{31j}(t-s_{3,j_u-(j^{*}+1)}-s_{3,j-1})\}\omega \text{exp}(A{\beta }_1+\mathit{x}\prime {\gamma }_1)]-\text{exp}[-\{\sum _{l=1}^{j_u-j^{*}}{\lambda }_{32l}(s_{3,l}-s_{3,l-1})\}\omega \text{exp}\{A{\beta }_{21}+V(1-A){\beta }_{22}+\mathit{z}\prime {\gamma }_2\}-\sum _{l=1}^{j-1}\{{\lambda }_{31l}(s_{3,l}-s_{3,l-1})+{\lambda }_{31j}(t-s_{3,j_u-j^{*}}-s_{3,j-1})\}\omega \text{exp}(A{\beta }_1+\mathit{x}\prime {\gamma }_1)]\}$$

$$+\frac{{\lambda }_{31j}\text{exp}(A{\beta }_1+\mathit{x}\prime {\gamma }_1)}{{\lambda }_{32(j_u-r)}\text{exp}\{A{\beta }_{21}+V(1-A){\beta }_{22}+\mathit{z}\prime {\gamma }_2\}-{\lambda }_{31j}\text{exp}(A{\beta }_1+\mathit{x}\prime {\gamma }_1)}\times \{\text{exp}[-\{\sum _{l=1}^{j_u-r-1}{\lambda }_{32l}(s_{3,l}-s_{3,l-1})+{\lambda }_{32(j_u-r)}(t-s_{3,j_u-r-1}-s_{3,j})\}\omega \times \text{exp}\{A{\beta }_{21}+V(1-A){\beta }_{22}+\mathit{z}\prime {\gamma }_2\}-\sum _{l=1}^j\{{\lambda }_{31l}(s_{3,l}-s_{3,l-1})\}\omega \text{exp}(A{\beta }_1+\mathit{x}\prime {\gamma }_1)]-\text{exp}[-\{\sum _{l=1}^{j_u-r}{\lambda }_{32l}(s_{3,l}-s_{3,l-1})\}\omega \text{exp}\{A{\beta }_{21}+V(1-A){\beta }_{22}+\mathit{z}\prime {\gamma }_2\}-\{\sum _{l=1}^{j-1}{\lambda }_{31l}(s_{3,l}-s_{3,l-1})+{\lambda }_{31j}(t-s_{3,j_u-r}-s_{3,j-1})\}\omega \text{exp}(A{\beta }_1+\mathit{x}\prime {\gamma }_1)]\},$$

for which

$${\int }_{\omega }{Q}_{j}f(\omega |\tau )d\omega =\frac{{\lambda }_{31j}\text{exp}(A{\beta }_1+\mathit{x}\prime {\gamma }_1)}{{\lambda }_{32j_u}\text{exp}\{A{\beta }_{21}+V(1-A){\beta }_{22}+\mathit{z}\prime {\gamma }_2\}-{\lambda }_{31j}\text{exp}(A{\beta }_1+\mathit{x}\prime {\gamma }_1)}\times \{{\{1+\tau [\{\sum _{l=1}^{j_u-1}{\lambda }_{32l}(s_{3,l}-s_{3,l-1})\}\text{exp}\{A{\beta }_{21}+V(1-A){\beta }_{22}+\mathit{z}\prime {\gamma }_2\}+\{\sum _{l=1}^{j-1}{\lambda }_{31l}(s_{3,l}-s_{3,l-1})+{\lambda }_{31j}(t-s_{3,j-1}-s_{3,j_u-1})\}\text{exp}(A{\beta }_1+\mathit{x}\prime {\gamma }_1)]\}}^{-\frac{1}{\tau }}-{\{1+\tau [\{\sum _{l=1}^{j_u-1}{\lambda }_{32l}(s_{3,l}-s_{3,l-1})+{\lambda }_{32j_u}(t-s_{3,j_u-1}-s_{3,j-1})\}\times \text{exp}\{A{\beta }_{21}+V(1-A){\beta }_{22}+\mathit{z}\prime {\gamma }_2\}+\sum _{l=1}^{j-1}{\lambda }_{31l}(s_{3,l}-s_{3,l-1})\text{exp}(A{\beta }_1+\mathit{x}\prime {\gamma }_1)]\}}^{-\frac{1}{\tau }}\}+\sum _{j^{*}=1}^{r-1}\frac{{\lambda }_{31j}\text{exp}(A{\beta }_1+\mathit{x}\prime {\gamma }_1)}{{\lambda }_{32(j_u-j^{*})}\text{exp}\{A{\beta }_{21}+V(1-A){\beta }_{22}+\mathit{z}\prime {\gamma }_2\}-{\lambda }_{31j}\text{exp}(A{\beta }_1+\mathit{x}\prime {\gamma }_1)}\times \{{\{1+\tau [\sum _{l=1}^{j_u-j^{*}-1}{\lambda }_{32l}(s_{3,l}-s_{3,l-1})\text{exp}\{A{\beta }_{21}+V(1-A){\beta }_{22}+\mathit{z}\prime {\gamma }_2\}+\sum _{l=1}^{j-1}\{{\lambda }_{31l}(s_{3,l}-s_{3,l-1})+{\lambda }_{31j}(t-s_{3,j_u-(j^{*}+1)}-s_{3,j-1})\}\text{exp}(A{\beta }_1+\mathit{x}\prime {\gamma }_1)]\}}^{-\frac{1}{\tau }}-{\{1+\tau [\{\sum _{l=1}^{j_u-j^{*}}{\lambda }_{32l}(s_{3,l}-s_{3,l-1})\}\text{exp}\{A{\beta }_{21}+V(1-A){\beta }_{22}+\mathit{z}\prime {\gamma }_2\}+\sum _{l=1}^{j-1}\{{\lambda }_{31l}(s_{3,l}-s_{3,l-1})+{\lambda }_{31j}(t-s_{3,j_u-j^{*}}-s_{3,j-1})\}\text{exp}(A{\beta }_1+\mathit{x}\prime {\gamma }_1)]\}}^{-\frac{1}{\tau }}\}+\frac{{\lambda }_{31j}\text{exp}(A{\beta }_1+\mathit{x}\prime {\gamma }_1)}{{\lambda }_{32(j_u-r)}\text{exp}\{A{\beta }_{21}+V(1-A){\beta }_{22}+\mathit{z}\prime {\gamma }_2\}-{\lambda }_{31j}\text{exp}(A{\beta }_1+\mathit{x}\prime {\gamma }_1)}\times \{{\{1+\tau [\{\sum _{l=1}^{j_u-r-1}{\lambda }_{32l}(s_{3,l}-s_{3,l-1})+{\lambda }_{32(j_u-r)}(t-s_{3,j_u-r-1}-s_{3,j})\}\times \text{exp}\{A{\beta }_{21}+V(1-A){\beta }_{22}+\mathit{z}\prime {\gamma }_2\}+\sum _{l=1}^j\{{\lambda }_{31l}(s_{3,l}-s_{3,l-1})\}\text{exp}(A{\beta }_1+\mathit{x}\prime {\gamma }_1)]\}}^{-\frac{1}{\tau }}-{\{1+\tau [\{\sum _{l=1}^{j_u-r}{\lambda }_{32l}(s_{3,l}-s_{3,l-1})\}\text{exp}\{A{\beta }_{21}+V(1-A){\beta }_{22}+\mathit{z}\prime {\gamma }_2\}+\{\sum _{l=1}^{j-1}{\lambda }_{31l}(s_{3,l}-s_{3,l-1})+{\lambda }_{31j}(t-s_{3,j_u-r}-s_{3,j-1})\}\text{exp}(A{\beta }_1+\mathit{x}\prime {\gamma }_1)]\}}^{-\frac{1}{\tau }}\}.$$

B.2. Sampling from the Conditional Posterior Distributions

In the posterior computation section, a series of conditional posterior distributions are listed. Now we will show how to sample from these distributions.

• (i)$[{\mathit{\lambda }}_0,{\mathit{\lambda }}_1^{*},{\mathit{\lambda }}_2^{*}|{\beta }_0,{\gamma }_0,{\beta }_1,{\gamma }_1,{\beta }_2,{\gamma }_2,\mathit{w},{\mathit{E}}^{*},D_{obs}]$. It is easy to see that conditional on (β₀, γ₀, β₁, γ₁, β₂, γ₂,w, E*, D_obs), (${\mathit{\lambda }}_0,{\mathit{\lambda }}_1^{*},{\mathit{\lambda }}_2^{*}$) are independent. Therefore, the conditional distributions can be sampled separately. Let δ_ikj = 1 if the i^th subject failed or was censored in the j^th interval for j = 1, 2, …J_k and 0 otherwise. It can be shown that (ia) [λ_0j |β₀, γ₀, E*, D_obs] ~ Gamma($a_{0j}^{\pi },b_{0j}^{\pi }$), where $a_{0j}^{\pi }={\sum }_{i=1}^n[{\delta }_{i0j}1\{d_i=0,{\nu }_i=1\}]+a_{0j}$, and $b_{0j}^{\pi }={\sum }_{s_{0,j-1<y_i\le s_{0j}}}(y_i-S_{0,j-1})$ exp $(A_i{\beta }_0+{\mathit{x}}_i^{\prime }{\gamma }_0)[1\{d_i=0,{\nu }_i=1\}+(1-E_i^{*})1\{d_i=0,{\nu }_i=0\}]+{\sum }_{y_i>s_{0j}}(s_{0,j}-s_{0,j-1})$ exp $(A_i{\beta }_0+{\mathit{x}}_i^{\prime }{\gamma }_0)[1\{d_i=0,{\nu }_i=1\}+(1-E_i^{*})1\{d_i=0,{\nu }_i=0\}]+b_{0j})$; (ib) $[{\lambda }_{1j}^{*}|{\beta }_1,{\gamma }_1,\mathit{w},{\mathit{E}}^{*},D_{obs}]~\text{Gamma}(a_{1j}^{\pi },b_{ij}^{\pi }),\text{where}{a}_{1j}^{\pi }={\sum }_{i=1}^n{\delta }_{i1j}[1\{d_i=1,{\upsilon }_i=1\}+1\{d_i=1,{\upsilon }_i=0\}]+a_{1j},\text{and}{b}_{1j}^{\pi }={\sum }_{s_1,j-1<y_i\le s_{1j}}{\mathit{w}}_i(y_{-i}-s_{1j-1})\text{exp}(A_i{\beta }_1+{\mathit{x}}_i^{\prime }{\gamma }_1)[1\{d_i=1,{\upsilon }_i=1\}+1\{d_i=1,{\upsilon }_i=0\}+E_i^{*}1\{{\upsilon }_i=0,d_i=0\}]+{\sum }_{y_i>s_{1j}}{\mathit{w}}_i(s_{1,j}-s_{1,j-1})\text{exp}(A_i{\beta }_1+{\mathit{x}}_i^{\prime }{\gamma }_1)[1\{d_i=1,{\upsilon }_i=1\}+1\{d_i=1,{\upsilon }_i=0\}+E_i^{*}1\{d_i=0,{\upsilon }_i=0\}+b_{1j})$; and (ic)$[{\lambda }_{2j}^{*}|{\beta }_2,{\gamma }_2,\mathit{w},{\mathit{E}}^{*},D_{obs}]$ ~ Gamma ($a_{2j}^{\pi },b_{2j}^{\pi }$), where $a_{2j}^{\pi }={\sum }_{i=1}^n[{\delta }_{i2j}1\{d_i=1,{\nu }_i=1\}]+a_{2j}$ and $b_{2j}^{\pi }={\sum }_{s_{2,j-1<y_i<s_{2j}}}{\mathit{w}}_i(y_i-S_{2,j-1})$ exp $\{A_i{\beta }_{21}+V_i(1-A_i){\beta }_{22}+{\mathit{z}}_i^{\prime }{\gamma }_2\}[1\{d_i=1,{\nu }_i=1\}+1\{d_i=1,{\nu }_i=0\}]+{\sum }_{y_i>s_{2j}}{\mathit{w}}_i(s_{2,j}-s_{2,j-1})\text{exp}\{A_i{\beta }_{21}+V_i(1-A_i){\beta }_{22}+{\mathit{z}}_i^{\prime }{\gamma }_2\}[1\{d_i=1,{\nu }_i=1\}+1\{d_i=1,{\nu }_i=0\}]+b_{2j})$.
• (ii)[$[{\beta }_0,{\gamma }_0,{\beta }_1,{\gamma }_1,{\beta }_2,{\gamma }_2,\tau ,\mathit{w},{\mathit{E}}^{*}|\mathit{\alpha },{\mathit{\lambda }}_0,{\mathit{\lambda }}_1^{*},{\mathit{\lambda }}_2^{*},D_{obs}]$].
• (iia)[$[{\beta }_0,{\gamma }_0,{\beta }_1,{\gamma }_1,{\beta }_2,{\gamma }_2|,\mathit{\alpha },{\mathit{\lambda }}_0,{\mathit{\lambda }}_1^{*},{\mathit{\lambda }}_2^{*},\tau ,{\mathit{E}}^{*},D_{obs}]$]. From the joint posterior distribution, it is obvious that conditional on [$[\mathit{\alpha },{\mathit{\lambda }}_0,{\mathit{\lambda }}_1^{*},{\mathit{\lambda }}_2^{*},\tau ,{\mathit{E}}^{*},D_{obs}]$], the parameters [β₀, γ₀], [β₁, γ₁], [β₂, γ₂] are independent. Therefore, we can sample the following conditional posterior distributions separately.
  • (iiaa)
    [β₀, γ₀|λ₀, E*, D_obs]. This density is proportional to

    $$\prod _{i=1}^n\{{[\text{exp}(A_i{\beta }_0+{\mathit{x}}_i^{\prime }{\gamma }_0)\text{exp}\{-H_0(y_i|{\mathit{\lambda }}_0)\text{exp}(A_i{\beta }_0+{\mathit{x}}_i^{\prime }{\gamma }_0)\}]}^{1\{d_i=0,{\nu }_i=1\}}\times {[\text{exp}\{-H_0(y_i|{\mathit{\lambda }}_0)\text{exp}(A_i{\beta }_0+{\mathit{x}}_i^{\prime }{\gamma }_0)\}]}^{(1-E_i^{*})1\{d_i=0,{\nu }_i=0\}}\}\text{exp}\{-({\beta }_0,{\gamma }_0^{\prime })\prime {\Sigma }_0^{-1}({\beta }_0,{\gamma }_0^{\prime })\}.$$

    It is easy to show that this conditional distribution is log-concave in each component of β₀ and γ₀.

  • (iiab)
    [$[{\beta }_1,{\gamma }_1|\mathit{\alpha },{\mathit{\lambda }}_0,{\mathit{\lambda }}_1^{*},{\mathit{\lambda }}_2^{*},\tau ,{\mathit{E}}^{*},D_{obs}]$]. This density is proportional to

    $$\prod _{i=1}^n\{{({[1+H_1(y_{Ei}|{\mathit{\lambda }}_1^{*})\text{exp}(A_i{\beta }_1+{\mathit{x}}_i^{\prime }{\gamma }_1)+H_2(y_{Gi}|{\mathit{\lambda }}_2^{*})\times \text{exp}\{A_i{\beta }_{21}+V_i(1-A_i){\beta }_{22}+{\mathit{z}}_i^{\prime }{\gamma }_2\}]}^{-\frac{1}{\tau }-2}\text{exp}(A_i{\beta }_1+{\mathit{x}}_i^{\prime }{\gamma }_1))}^{1\{d_i=1,{\nu }_i=1\}}\times {(\text{exp}(A_i{\beta }_1+{\mathit{x}}_i^{\prime }{\gamma }_1){[1+H_1(y_{Ei}|{\mathit{\lambda }}_1^{*})\text{exp}(A_i{\beta }_1+{\mathit{x}}_i^{\prime }{\gamma }_1)+H_2(y_{Gi}|{\mathit{\lambda }}_2^{*})\times \text{exp}\{A_i{\beta }_{21}+V_i(1-A_i){\beta }_{22}+{\mathit{z}}_i^{\prime }{\gamma }_2\}]}^{-\frac{1}{\tau }-1})}^{1\{d_i=1,{\nu }_i=0\}}\times {\{{[1+H_1(y_{Ei}|{\mathit{\lambda }}_1^{*})\text{exp}(A_i{\beta }_1+{\mathit{x}}_i^{\prime }{\gamma }_1)]}^{-\frac{1}{\tau }}\}}^{E_i^{*}1\{d_i=0,{\nu }_i=0\}}\}\text{exp}\{-({\beta }_1,{\gamma }_1^{\prime })\prime {\Sigma }_1^{-1}({\beta }_1,{\gamma }_1^{\prime })\}.$$

    It can also be shown that this conditional distribution is log-concave in each component of β₁ and γ₁.

  • (iiac)
    [$[{\beta }_2,{\gamma }_2|\mathit{\alpha },{\mathit{\lambda }}_0,{\mathit{\lambda }}_1^{*},{\mathit{\lambda }}_2^{*},\tau ,{\mathit{E}}^{*},D_{obs}]$]. This density is proportional to

    $$\prod _{i=1}^n\{{({[1+H_1(y_{Ei}|{\mathit{\lambda }}_1^{*})\text{exp}(A_i{\beta }_1+{\mathit{x}}_i^{\prime }{\gamma }_1)+H_2(y_{Gi}|{\mathit{\lambda }}_2^{*})\times \text{exp}\{A_i{\beta }_{21}+V_i(1-A_i){\beta }_{22}+{\mathit{z}}_i^{\prime }{\gamma }_2\}]}^{-\frac{1}{\tau }-2}\text{exp}\{A_i{\beta }_{21}+V_i(1-A_i){\beta }_{22}+{\mathit{z}}_i^{\prime }{\gamma }_2\})}^{1\{d_i=1,{\nu }_i=1\}}\times {({[1+H_1(y_{Ei}|{\mathit{\lambda }}_1^{*})\text{exp}(A_i{\beta }_1+{\mathit{x}}_i^{\prime }{\gamma }_1)+H_2(y_{Gi}|{\mathit{\lambda }}_2^{*})\times \text{exp}\{A_i{\beta }_{21}+V_i(1-A_i){\beta }_{22}+{\mathit{z}}_i^{\prime }{\gamma }_2\}]}^{-\frac{1}{\tau }-1})}^{1\{d_i=1,{\nu }_i=0\}}\}\text{exp}\{-({\beta }_2,{\gamma }_2^{\prime })\prime {\Sigma }_2^{-1}({\beta }_2,{\gamma }_2^{\prime })\}.$$

    Similarly, this conditional distribution can be shown to be log-concave in each component of β₂ and γ₂.

• (iib)
  [$[{\mathit{E}}^{*}|\mathit{\alpha },{\beta }_0,{\gamma }_0,{\beta }_1,{\gamma }_1,{\mathit{\lambda }}_0,{\mathit{\lambda }}_1^{*},\tau ,D_{obs}]$]. This conditional posterior distribution is given by

  $$[{\mathit{E}}^{*}|\mathit{\alpha },{\beta }_0,{\gamma }_0,{\beta }_1,{\gamma }_1,{\mathit{\lambda }}_0,{\mathit{\lambda }}_1^{*},\tau ,D_{\mathit{\text{obs}}}]\propto \prod _{i=1}^n{\{{({[H_1(y_1|{\mathit{\lambda }}_1^{*})\text{exp}(A_i{\beta }_1+{\mathit{x}}_i^{\prime }{\gamma }_1)+1]}^{-\frac{1}{\tau }}{[1+\text{exp}\{-({\alpha }_0+A_i{\alpha }_1+{\mathit{x}}_i^{\prime }{\mathit{\alpha }}_2)\}]}^{-1})}^{E_i^{*}}\times {(\text{exp}[-H_0(y_i|{\mathit{\lambda }}_0)\text{exp}(A_i{\beta }_0+{\mathit{x}}_i^{\prime }{\gamma }_0)]{[1+\text{exp}({\alpha }_0+A_i{\alpha }_1+{\mathit{x}}_i^{\prime }{\mathit{\alpha }}_2)]}^{-1})}^{(1-E_i^{*})}\}}^{1\{d_i=0,{\nu }_i=0\}}.$$
• (iic)[$[\tau |{\beta }_1,{\gamma }_1,{\mathit{\lambda }}_1^{*},{\beta }_2,{\gamma }_2,{\mathit{\lambda }}_2^{*},{\mathit{E}}^{*},D_{obs}]$]. This one is shown in Theorem 2.
• (iid)$[\omega |{\beta }_1,{\gamma }_1,{\mathit{\lambda }}_1^{*},{\beta }_2,{\gamma }_2,{\mathit{\lambda }}_2^{*},\tau ,{\mathit{E}}^{*},D_{obs}]$. To sample from this conditional distribution, we can sample $[\omega |{\beta }_1,{\gamma }_1,{\mathit{\lambda }}_1^{*},{\beta }_2,{\gamma }_2\text{and}{\mathit{\lambda }}_2^{*},{1/\tau }^{*},{\mathit{E}}^{*},D_{obs}]$ instead. It can be shown that [$\omega |{\beta }_1,{\gamma }_1,{\mathit{\lambda }}_1^{*},{\beta }_2,{\gamma }_2,{\mathit{\lambda }}_2^{*},{1/\tau }^{*},{\mathit{E}}^{*},D_{obs}$] ~ Gamma(a_w, b_w), where $a_w=({\tau }^{*}+2)1\{d_i=1,{\nu }_i=1\}+({\tau }^{*}+1)1\{d_i=1,{\nu }_i=0\}+{\tau }^{*}{E}_i^{*}1\{d_i=0,{\nu }_i=0\}\text{and}{b}_w=[H_1(y_{Ei}|{\mathit{\lambda }}_1^{*})\text{exp}(A_i{\beta }_1+{\mathit{x}}_i^{\prime }{\gamma }_1)+H_2(y_{Gi}|{\mathit{\lambda }}_2^{*})\text{exp}(A_i{\beta }_{21}+V_i(1-A_i){\beta }_{22}+{\mathit{z}}_i^{\prime }{\gamma }_2\}+1][1\{d_i=1,{\nu }_i=1\}+1\{d_i=1,{\nu }_i=0\}]+[H_1(y_i|{\mathit{\lambda }}_1^{*})\text{exp}(A_i{\beta }_1+{\mathit{x}}_i^{\prime }{\gamma }_1)+1]E_i^{*}1\{d_i=0,{\nu }_i=0\}$
• (iii)
  [α|E*, D_obs]. This conditional posterior distribution is given by

  $$[\mathit{\alpha }|{\mathit{E}}^{*},D_{\mathit{\text{obs}}}]\propto \prod _{i=1}^n\{{({[1+\text{exp}({\alpha }_0+A_i{\alpha }_1+{\mathit{x}}_i^{\prime }{\mathit{\alpha }}_2)]}^{-1})}^{1\{d_i=0,{\nu }_i=1\}+(1-E_i^{*})1\{d_i=0,{\nu }_i=0\}}\times {({[1+\text{exp}\{-({\alpha }_0+A_i{\alpha }_1+{\mathit{x}}_i^{\prime }{\mathit{\alpha }}_2)\}]}^{-1})}^{1\{d_i=1,{\nu }_i=1\}+1\{d_i=1,{\nu }_i=0\}+E_i^{*}1\{d_i=0,{\nu }_i=0\}}\}\times \text{exp}\{-({\alpha }_0,{\alpha }_1,{\alpha }_2^{\prime })\prime {\Sigma }_a^{-1}({\alpha }_0,{\alpha }_1,{\alpha }_2^{\prime })\}.$$

  It is easy to show that this density is log-concave in each component of α. Therefore, we apply the adaptive rejection algorithm of Gilks and Wild (1992) to draw α.