The relaxation dynamics of the excited electronic states of retinal in bacteriorhodopsin by two-pump-probe femtosecond studies

Abstract

We present the results of two-pump and probe femtosecond experiments designed to follow the relaxation dynamics of the lowest excited state (S₁) populated by different modes. In the first mode, a direct (S₀ → S₁) radiative excitation of the ground state is used. In the second mode, an indirect excitation is used where the S₁ state is populated by the use of two femtosecond laser pulses with different colors and delay times between them. The first pulse excites the S₀ → S₁ transition whereas the second pulse excites the S₁ → S_n transition. The nonradiative relaxation from the S_n state populates the lowest excited state. Our results suggest that the S₁ state relaxes faster when populated nonradiatively from the S_n state than when pumped directly by the S₀ → S₁ excitation. Additionally, the S_n → S₁ nonradiative relaxation time is found to change by varying the delay time between the two pump pulses. The observed dependence of the lowest excited state population as well as its dependence on the delay between the two pump pulses are found to fit a kinetic model in which the S_n state populates a different surface (called S′₁) than the one being directly excited (S₁). The possible involvement of the A_g type states, the J intermediate, and the conical intersection leading to the S₀ or to the isomerization product (K intermediate) are discussed in the framework of the proposed model.

Halobacterium salinarum (Halobium salinarium) is a member of Halobacteria, which is part of the domain Archaea. In an anaerobic condition under light illumination, H. salinarum demonstrates a pH decrease in cell suspension and ATP synthesis (1, 2), the main features of photosynthesis. The photosynthetic activity in H. salinarum was attributed to bacteriorhodopsin (bR), a 26-kDa protein that is hexagonally packed within the purple membrane (1–4). Since the discovery of the purple membrane, its enigmatically efficient photosynthesis is in the center of the most active research. To our surprise, the archaic organism effectively utilizes more than 50% of the absorbed light energy (5, 6).

Retinal, a light-absorbing polyene, is the bR chromophore and is linked to its Lys-216 by a protonated Schiff base. The chromophore undergoes light-induced isomerization and masters proton transfer across the membrane (7–11). The photoisomerization of retinal initiates a series of retinal protein structural reconformations of the bacteriorhodopsin that lead to the formation of different intermediates and finally return it to its initial state with all-trans-retinal. Overall, this photocycle consists of at least seven intermediates of bR with different visible absorption spectra and lifetimes bR₅₆₈ → S₁ → J → K₆₃₀ → L₅₅₀ → M₄₁₂ → N₅₂₀ → O₆₄₀ → bR₅₆₈ (4).

Retinal in solution shows relatively slow and nonselective photoisomerization around several double bonds (12–14) with low yield. The specific ultrafast, all-trans, 13-cis photoisomerization of the retinal in bR is the purple membrane photosynthesis key event which has a quantum yield of 55%. The photoisomerization in bR has been studied extensively by using methods of ultrafast optical spectroscopy (15–22). The results of time-resolved Raman studies show that retinal isomerization takes place on a picosecond timescale (23). A consistent interpretation of the primary event was developed as a result of an ultrafast transient absorption experiment by Mathies et al. in 1988 (18). Their model (the two-state model) implies that the excited state wave packet moves away from the Franck–Condon region within 100–200 fs because of the extensive torsional motion. Further, within 500 fs this twisted state can evolve into the 13-cis configuration or relax to the all-trans ground state.

The two-state model suggests a repulsive character for the excited state surface. However, a number of experimental observations (24–26; see references cited in ref. 23 for earlier dynamics) unambiguously demonstrated the flat character of the excited state surface and the presence of a small barrier. Therefore, the “three-state” model (24, 27, 28), proposed that both the S₁(B_u) and S₂(A_g) states are involved in the dynamics of the excited state photoisomerization. In this model, a flat part of the potential surface along the torsional coordinate and the barrier were numerically evaluated as a result of the S₁ and S₂ states coupling and their avoided crossing. An alternative explanation for the excited state properties was developed by Olivucci and coworkers (29, 30) using the results of ab initio calculations for a protonated Schiff base. They calculated that the energy plateau may arise as a result of the initial stretch motion that leads the retinal away from the excited state Franck–Condon region in the multidimensional vibronic diagram. The dominant contribution of the initial stretching motion of the retinal in the excited state is in good agreement with the experimental observations of the time-resolved resonance Raman studies of the retinal excited state by Song and El-Sayed (31). However, the ab initio studies (30) did not find a barrier in the excited state surface. The authors suggested that the characteristic flat transition state was not numerically found because the retinal–counterion and the retinal–solvent interactions were neglected. The retinal–environment interactions must play a dominant role in determining the optical and dynamic properties of the chromophore.

Recent reports on time-resolved spectroscopy of the sterically locked retinal in bR (32) and the coherent Raman scattering on purple membrane (33) raised questions about excited state isomerization. It was proposed that the retinal in the J intermediate (formed from the decay of the S₁ state in 0.5 ps) is not in the 13-cis configuration but resembles more the all-trans form. This proposal is also in agreement with the results of previous resonance Raman studies on the S₁ state in which the absence of out-of-plane vibrations was determined (31).

In this work we investigate the dependence of the dynamic of the lowest excited state relaxation of retinal on its excitation mode. We compare the excited state lifetime when it is excited by direct radiative S₀ → S₁ excitation to that when it is excited by an indirect 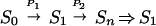process (→ and ⇒ refer to radiative and nonradiative processes, respectively, and P₁ and P₂ are two pump laser pulses delayed from each other by different delay times). It is found that the lowest singlet state relaxes more rapidly when reached by the indirect two-pump excitation mode than by the direct absorption method. Furthermore, the apparent S_n ⇒ S₁ relaxation is found to be sensitive to the delay between the two pump pulses. To explain our results, we suggest a model in the framework of which we discuss the nature and symmetry of the states involved in the dynamics of the retinal relaxation.

Materials and Methods

Halobacteria were grown from the master slant of H. salinarum (ET1–001 strain) kindly provided by R. Bogomolni of the University of California, Santa Cruz. The purple membrane was isolated and purified by a technique described previously (3). Potassium phosphate buffer solutions were used to adjust the pH. All measurements were made at room temperature. Prepared samples were light adapted for at least 30 min before our studies.

A transient absorption spectroscopy setup with femtosecond time resolution was constructed as follows. The 80-fs, 1 mJ per pulse, 1-kHz pulses were generated by a Ti:sapphire laser pumped with a 4-W Innova argon ion laser (Coherent Radiation, Palo Alto, CA) amplified by a regenerative amplifier (Clark MXR, Dexter, MI). The output of the laser was split into two equal parts and was used to pump two identical optical parametric oscillators (TOPAS travelling-wave optical parametric amplifier of superfluorescence generators from Light Conversion, Vilnius, Lithuania). As a result, a tunable excitation beam in a wide spectral window with energies of up to a few 100 μJ was generated in each optical parametric oscillator. Also, one of the harmonics from the Ti:sapphire laser was used as the excitation source. Both excitation beams go through two computer-controlled optical delay lines with a resolution of 3 μm (22 fs), and a small portion of the fundamental frequency (about 40 μJ) was used to generate a femtosecond continuum in a 1-mm sapphire plate. The range of the femtosecond continuum is between 400 and 1000 nm. In some cases, when the probe wavelength was outside this window the output of another optical parametric oscillator was used as probe beam. The probe beam was split into two parts: signal and reference beam. The two pump beams and the signal beam were overlapped on the sample in a way so that the foci of both pump beams were slightly behind the sample. The signal and reference beams were focused into fiber optics coupled to a monochromator. Both excitation beams were modulated by an optical chopper at a frequency of 500 Hz with the same phase. Two photodiodes were used for the kinetic measurements at the exit slit of the monochromator. The photocurrent from the signal and reference photodiodes was amplified and passed through a sample-and-hold circuitry and coupled to a lock-in amplifier locked at 500 Hz. Each point in the kinetic measurements at the single wavelength required 200 shots at fixed delay, and there were about 100–300 points in one delay line scan. The delay line was repeatedly scanned until a reasonable signal-to-noise ratio was achieved. The typical absorbance changes measured were in the range 0.005–0.050. The sample cuvette was rotated to exclude thermal effects and photodegradation.

To study the effect of the excited state dynamics we used the following method. The first excitation pulse at 570–580 nm starts the bR photocycle by exciting the retinal molecule into its excited state S₁. The excited state lifetime is in the 300- to 500-fs range (15–22). S₁ has an absorption maximum at 490 nm (22). Thus, the second excitation pulse with a maximum at 490 nm excites molecules from the S₁ state of the retinal molecule to its higher excited state S_n. As a result, the S₁ state population signal changes in intensity with time because of both the S₁ → S_n absorption and the S_n ⇒ S₁ nonradiative relaxation processes. It is difficult to monitor the lowest excited state population relaxation dynamics by using transient absorption because of the proximity of the probe wavelength to the wavelength of the second excitation pulse. Therefore, to perform this experiment we chose to monitor the time dependence of the population of the retinal lowest excited state by following the intensity of the stimulated emission at 870 nm (21).

In our experiment, the first pump pulse excites about 90% of the bR molecules. This is achieved by decreasing the sample concentration at a given excitation laser pulse energy (≈2 μJ). The second pump pulse affects the population in the S₁ state only. The second pulse excites about 90% of the molecules in the S₁ state formed by the absorption of the first pulse. Finally, the contribution of the lowest excited state that was formed from the excitation of the ground state of bR because of the second pulse was small (<10%).

Simulations of the excited state dynamics were performed by solving numerically the system of differential equations built according to a proposed model. We used several numerical methods: Euler–Cauchy (h²), improved Euler–Cauchy (h³), Heun (h⁴) and a Runge–Cutta (h⁵) algorithm (with the order of the local error term given in parentheses and simulation steps of h = 2.2 fs). For the determination of the transition rates between the energetic levels, the model parameters were fitted by using a Levenberg–Marquardt algorithm (34).

Results

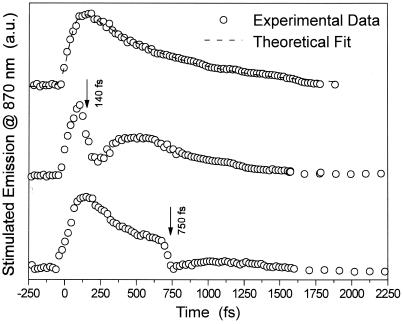
Fig. 1 shows the time-dependent intensity of the time-resolved stimulated emission monitored at 870 nm (reflecting the time-dependent excited state population). The experimental data (shown by open circles) can be fitted to a monoexponential decay with an excited state lifetime of 0.50 ps (shown by the dashed curve). The modification of that decay after application of the second laser pulse at the S₁ → S_n absorption wavelength (490 nm) at different delay times during the decay of the S₁ state population is shown in the other two curves of the figure. The top curve in Fig. 1 shows both the increase of the signal because of excitation at 570 nm and the decay of the S₁ state population in the absence of the second excitation pulse. The other curves show the results of the stimulated emission signal from the lowest excited state as the retinal is excited by the two pulses at different delay times. When the second pulse is turned on after some delay, a drop in the stimulated emission signal is observed because of the transfer of a fraction of the S₁ population to the S_n state. The decrease in the stimulated emission signal is followed by a subsequent recovery because of the nonradiative S_n ⇒ S₁ relaxation process. The effect of this perturbation on the decay of the S₁ population is then determined from the change in the observed dynamics of the stimulated emission signal. The following important results can be concluded from Fig. 1:

Figure 1.

The dependence of the relaxation of the stimulated emission from the lowest excited state (S) on the mode of their excitation. Open circles represent the time-resolved stimulated emission decay of the lowest excited state in bR measured at 870 nm. a.u., arbitrary units. Top curve represents the time-dependent intensity of the stimulated emission excited by one-pump excitation of the S₀→S₁ transition, whereas the rest of curves show the stimulated emission with the second excitation pulse after delay time of 140 or 750 fs as shown. The dashed line in the top curve represents the theoretical fit to simple one-pulse excitation and decay.

(i) As the population of S₁ is transferred radiatively to the S_n state and relaxes to the lowest excited state, the decay time of the stimulated emission decreases.

(ii) The recovery time of the S₁ population after its perturbation with the second pulse occurs in ≈200 fs.

Previous studies (15) have determined a relaxation time from an upper state reached by 780-nm excitation above S₁ to be 320 fs. This suggests that increasing the excitation energy by 1.6 times increases the relaxation rate by the same magnitude.

In addition to the observations made above from Fig. 1, we also found that there is no effect of the second pulse excitation on the absorption intensity of the K intermediate (observed at 630 nm) in which the retinal is in the 13-cis isomeric form. This observation suggests that the quantum yield of the isomerization is not changed noticeably by perturbing the population of the lowest excited state of the retinal during its decay. This gives strong evidence that the isomerization pathway, including its rates, is not influenced by the excitation pathway of the S₁ state.

Discussion

It has been reported in the literature that the decay of the S₁ state (upper curve in Fig. 1) is not exponential and can be fitted to two lifetime components of ≈500 fs (80–95%) and 3 ps (20–5%) (16–23). With a better signal-to-noise ratio, the early lifetime itself is found to be biexponential with 0.24 and 0.75 ps components in the ratio of 2:1 (24). Neglecting the minor contribution of the long component for the moment, we approximate the experimentally detected decay of the stimulated emission with one lifetime of 500–600 fs (dashed line, top curve, Fig. 1).

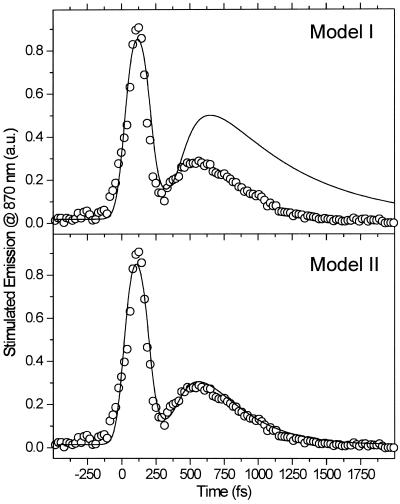
We have tried to fit the results of the two-pump-probe experiments to model I, in which the excited population in S_n relaxes to the originally excited S₁ state. The upper part of Fig. 2 compares the simulation of model I to the experimental results when the delay time between the two pump pulses was 240 fs. As can be seen in Fig. 2, the fit gives unsatisfactory results. This finding suggests that the population relaxation from the S_n state does not lead to the S₁, but rather to a different nearby state, say S′₁. This conclusion could be explained as follows. First, the retinal molecules excited by the second pulse return to the S′₁ state, which is an excited vibrational level of the S₁ electronic state. The dynamics of this vibronic state(s) may be different from those of the S₁ level. It was shown previously (24, 26) that the dynamics of the stimulated emission for the retinal in bR is independent of the excitation wavelength from the ground state. This suggests that the excess of energy in the excited vibrational level of totally symmetric vibrations should not perturb its decay dynamics. It is possible, however, that the relaxation from the S_n state populates surfaces that involve vibronic levels different from the totally symmetric vibrational levels reached by allowed optical absorption. On the other hand, because we know that there is another electronic state (the A_g type state) very near to the S₁ surfaces, one should consider its participation, as is discussed below.

Figure 2.

Model fit (solid lines) to the experimental results (given by circles) of the two-pulse excitation experiments with a delay time of 240 ps. The fit in the upper curve is to model I, which assumes that the population resulting from both the direct (one-pulse) and indirect (two-pulse) excitation reach the same lowest excited state. The lower and better fit is for model II, which assumes that different excitations reach nearby states whose nonradiative relaxation rates are different (see Fig. 3 for details).

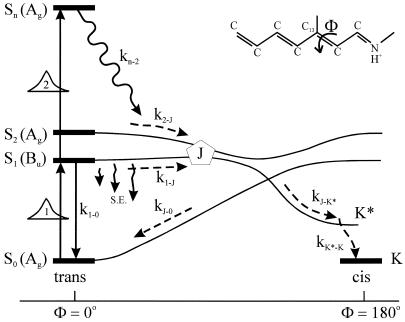
The next attempt to fit our experimental results was done according to model II, which is shown schematically in Fig. 3. In this scheme, the first pulse excites S₀ to S₁ with a rate constant of k₀₁ whereas the second pulse promotes the excited retinal molecule from S₁ to S_n with a rate constant of k_1n. We assume that the molecule in the S_n state relaxes nonradiatively and eventually reaches a lowest excited state called S₁′ with a rate constant of k_n1′. A number of intervening states will undoubtedly be involved in this relaxation. Thus, k_n1′ is the rate constant of the slowest process in the sequence of the processes involving the other states between S_n and S′₁. The states S₁ and S′₁ are assumed to form J with different rate constants, say k_1J and k_1J′, respectively. The J intermediate is proposed to decay to the ground state S₀ or to enter the conical intersection from which isomerization to the vibrationally excited level of the 13-cis form takes place (K*), as was theoretically discussed and experimentally concluded from the time-resolved, coherent Raman studies (33). The latter concluded that the retinal in J is in the all-trans form (35). This then relaxes to the ground state of the 13-cis isomer (K) with a constant k_K*K. In this model, the time dependence of the retinal concentration in each of the different states (x₀, x₁, x_1′ and x_n) and of the intermediates x_J, x_K* and x_K is given by the solution of the following differential equations:

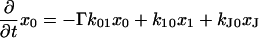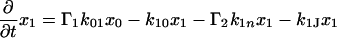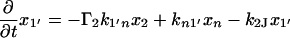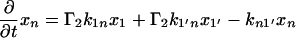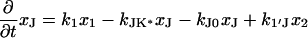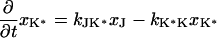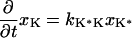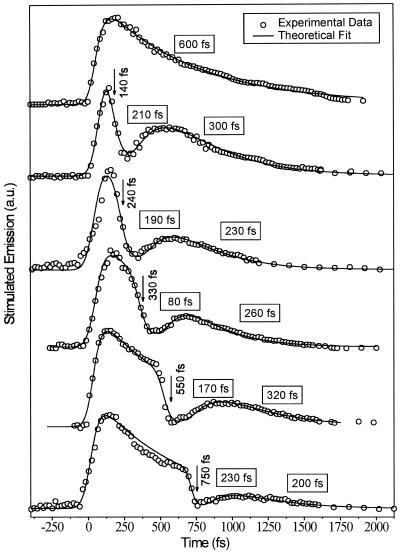
Γ₁ and Γ₂ are the Gaussian functions of the first and second excitation pulses. A number of the rate constants in this model (k₁₀, k_1J, and k_J0) are reported in the literature (10, 32). The best fit for all delay times used allows us to determine the remaining rate constants, which are summarized in Table 1. By using the literature values and the rate constants in Table 1, a good fit to the experimental results was obtained and shown at the bottom of Fig. 2 for the 240-ps delay time and in Fig. 4 for the different delay times studied.

Figure 3.

The schematic presentation of the details developed for model II for excitation with two-pump lasers. The different processes and intermediates involved in this model are given in the text.

Table 1.

Theoretical model parameters on the delay between two excitation pulses

Parameter	Delay
	140 fs	240 fs	330 fs	550 fs	750 fs
1/kn1′ (1/kn2), fs	210	190	80	170	230
1/k1′J (1/k2J), fs	300	230	260	320	200
1/k10, ps (ref. 32)	20	20	20	20	20
1/k1J, fs	600	600	600	600	600
1/kJ0 and 1/kJK*, fs	300	300	300	300	300
1/kKK*, ps (ref. 9)	3.2	3.2	3.2	3.2	3.2

 The nominations in parentheses and k_J0, k_JK*, and k_KK* are valid in a context of the three-state model (see Discussion). 

Figure 4.

The fit of model II (solid lines) to the results (circles) obtained for the two-pulse experiments with different delay times.

Two important conclusions can be drawn from the results of the good fit of the proposed kinetic model II. First, the relaxation of the S_n state ends up in a different state (S_1′); second, the rate constants for the relaxation of the S_n state to the S_1′ state (k_n1′) is found to change with the delay time between the two pulses. This suggests that the nature of either the S_n or S_1′ surface changes with time. From the proposed three-state model, one might assume that it is the S_1′ surface that is changing with time. As a result, the rate constants of its kinetics would change with time.

In Fig. 5 we plot the reciprocal rates 1/k_1′J and 1/k_n1′ as a function of the delay time between the first and the second excitation pulse. As may be seen from Fig. 5, the rate k_1′J is fairly independent of the delay time. In contrast, the rate k_n1′, which is responsible for the nonradiative relaxation of the S_n state, has a maximum at a delay time of 330 fs. The pathway of the S_n ⇒ S_1′ relaxation certainly depends on the initial Franck–Condon preparation of the S_n state. This is a time-dependent process; as S₁ moves away from its Franck–Condon region the Franck–Condon absorption at 490-nm excitation (the second pulse) is expected to excite different regions of the S_n surface. This leads to different relaxation pathways down to the S_1′ surface, which relaxes to the J state (intermediate).

Figure 5.

The reciprocal rates 1/k_1′J and 1/k_n1′ as a function of the delay between the first and the second excitation pulses as determined from fitting the results to model II.

To understand the dynamics of excited retinal in bR, we have to take into account the nature of the states and intermediates involved in the relaxation process. Direct radiative excitation from an A_g type ground state produces dominantly a ¹B_u type excited state. The second pulse can then radiatively excite molecules in the ¹B_u type state to a state (the S_n state) that is predominantly of the ⁿA_g type. The nonradiative relaxation from this state to lower excited states can be faster if it involves a ladder of other A_g type states. Calculations for the retinal in solution by Birge and coworkers (36), by Olivucci and his group (M. Olivucci, personal communication), and the results of near-UV hole-burning studies (37) have all suggested the presence of a number of A_g type states in this energy range. The lowest A_g state is found experimentally (38) to be within 3500 ± 500 cm⁻¹ above the lowest ¹B_u type S₁ state. Thus, the state S_1′ in our model could be a state with a strong intermixed character of that lowest ¹A_g state. This state is a precursor of the J state or could give rise to a different path involving another isomer. One should mention that to observe stimulated emission from S_1′ after excitation with the second pulse, both the S₁ and S_1′ states have to be radiatively mixed with one another. This is possible on account of the fact that the retinal in bR does not possess a center of inversion. The mixing of the B_u type state with the A_g type state (S_1′) leads to its increased radiative probability. The observed lifetimes of the S₁ and S_1′ states, however, are mostly nonradiative and reflect their nonradiative relaxation dynamics.

Conclusion

We investigated the dependence of the dynamics of the population of the lowest excited state of retinal in bR on the mode of its excitation with femtosecond time resolution. One excitation involves the direct one-photon excitation of the molecules in the ground state. In the indirect method, two photon pulses are used, delayed from one another by different times. The first pulse excites S₀ to S₁, whereas the second pulse excites 90% of the population in S₁ to a high excited state, S_n. The latter relaxes to reach the lowest excited state, which is found to have shorter lifetime than the state populated by direct excitation. This finding suggested that this state must be different from the S₁ state because it seems to have different relaxation dynamics (the dependence of the decay of the S₁ and S_1′ states formed at different delay times between the two laser pulses are found to fit a model with these two different states). The nature of these two states is proposed to involve the mixed B_u and A_g type states whose dynamics (are proposed to) involve different relaxation. The different states or intermediates known to be involved in the relaxation of the lowest excited state(s) are included in the presented model.

Abbreviation

bR

bacteriorhodopsin