Coronary artery calcium distributions in older persons in the AGES-Reykjavik study

Abstract

Coronary Artery Calcium (CAC) is a sign of advanced atherosclerosis and an independent risk factor for cardiac events. Here, we describe CAC-distributions in an unselected aged population and compare modelling methods to characterize CAC-distribution. CAC is difficult to model because it has a skewed and zero inflated distribution with over-dispersion. Data are from the AGES-Reykjavik sample, a large population based study [2002-2006] in Iceland of 5,764 persons aged 66-96 years.

Linear regressions using logarithmic- and Box-Cox transformations on CAC+1, quantile regression and a Zero-Inflated Negative Binomial model (ZINB) were applied. Methods were compared visually and with the PRESS-statistic, R² and number of detected associations with concurrently measured variables.

There were pronounced differences in CAC according to sex, age, history of coronary events and presence of plaque in the carotid artery. Associations with conventional coronary artery disease (CAD) risk factors varied between the sexes.

The ZINB model provided the best results with respect to the PRESS-statistic, R², and predicted proportion of zero scores. The ZINB model detected similar numbers of associations as the linear regression on ln(CAC+1) and usually with the same risk factors.

Introduction

The distribution of coronary artery calcium (CAC) has not been widely described for older populations. The large AGES-Reykjavik study sample is population-based and here distributions are presented for an age span exceeding that of previous large epidemiological studies [1-3].

For such descriptions a suitable modelling approach should be identified, as such an estimation model needs to account for the distributional properties of CAC, particularly the skewed distribution, zero inflation and over-dispersion.

Objective

The primary objective of this paper is to describe the distribution of CAC, estimated from Computed Tomography (CT), in older persons and to model cross-sectional associations between CAC and other variables recorded in the AGES-Reykjavik-study. In the course of this analysis we apply a zero inflated negative binomial model (ZINB) and compare it with common analytic regression methods for CAC-modelling, to provide information if there is room for improvement in describing these skewed and zero-inflated distributions in a general population of older persons.

Coronary artery calcium

CAC-burden is associated with risk of Coronary Artery Disease (CAD) and an independent predictor of cardiac events [1, 4-7]. Distributions differ according to sex, age, ethnicity, history of cardiovascular disease and other conventional risk factors for heart disease [3-5, 8-11]. An understanding of such associations can clarify what a CAC score means in terms of coronary heart disease risk. CAC distributions are often non-normal and greatly right skewed, making the use of conventional parametric methods problematic, as some assumptions made for those methods may be violated [9]. Other issues in modelling CAC are excess zero scores or “zero inflation” [12] and possible over-dispersion when the theoretical relationship between the variance and mean of the response implied by the model is different from what is observed in the data. Over-dispersion not accounted for may result in type I errors [13, 14]. Any effective analytical approach should account for these issues.

Regression methods for CAC-scores

Previous studies have applied various methods to study modelling of CAC. A common approach involves logarithmic transformations of CAC-scores to account for non-normality [3, 8, 9, 15-18]. Linear regression using logarithmic transformations of CAC scores greater than zero, while excluding zero scores, have been shown to result in type II errors, that is to miss associations with known risk factors. Logarithmic transformations of CAC+1 retains all data, however distributions remain non-normal due to right skewness [8].

CAC-scores have also been divided into categorical variables or rank values based on percentiles. Categorization into absent, mild moderate or severe have been represented by the ranges of 0, 1-100, 101-400, >400, respectively [11]. These categories discriminate levels of CAD-risk [10]. Some evidence suggests that age- and sex specific CAC-percentiles are better suited to identify people at risk of CAD compared to absolute values [2]. However, results from the Multi-Ethnic Study of Atherosclerosis (MESA) indicate that absolute CAC-scores are a better predictor of coronary heart disease [10].

Logistic regression has been applied using both binary and ordinal analysis of categorized CAC-scores. Associations between known risk factors and CAC are more likely to be missed in binary analyses compared to ordinal regression of the categories [8].

Two-part models have been described to account for properties of CAC-distributions. The first step in such models is usually a binary logistic regression to model the probability of a positive CAC-score. The second step is linear regression on ln(CAC) which has provided good results compared with observed CAC-data [9, 19, 20]. These models seem fairly labour intensive as model stages are usually done separately and not supplied in standard statistical packages.

Zero inflated negative binomial count regression models have not been applied in this context before. These models are appealing in that they are readily available in several statistical packages [21-23] and fit both model stages at once. Since CAC-scores are in part derived from counted pixels corresponding to calcium in CT-images [24], it is reasonable to assume that count regression models can be applied to model the scores. These models may account for the characteristics of CAC-scores, such as excess zeros and over- dispersion [25].

The two parts of Zero inflated models are constructed in three steps. First the probability of a certain zero outcome is estimated using logistic regression, which comprises the first part of the model and provides an odds ratio (OR) for the odds of zero CAC. The second step is a count model for the positive counts. The third and final step is to compute probabilities for any outcome as a mixture of the two processes [14].

Materials and methods

Study design

Cross-sectional analyses were performed on data from the prospective AGES-Reykjavik study, conducted by the Icelandic Heart Association. AGES–Reykjavik was approved by the National Bioethics Committee in Iceland (approval number VSN-00-063, in accordance with the Helsinki Declaration) and by the National Institute on Aging Intramural Institutional Review Board. Informed consent was obtained for all participants.

In summary, the AGES-Reykjavik study is an on-going study of the effects of gene-environment interactions and other risk factors for disease in old age. Many physiological measurements and lifestyles factors are recorded in this study. AGES-Reykjavik is a subset of a larger population based cohort study called the Reykjavik-study. The aim of the original study was to prospectively investigate risk factors for cardiovascular disease in the Icelandic population [26, 27].

The original Reykjavik cohort was established in 1967 with a population based sample of 30,795 individuals borne in the years 1907-1935, and residing in Reykjavik, the capital of Iceland. A random sample of 27,281 persons was invited to participate and 19,381 individuals entered the study and attended examinations. The AGES-Reykjavik sample was constructed in 2002 by randomly selecting 8,030 individuals who were still alive from the original Reykjavik-cohort (n = 11,459). A total of 5,764 individuals (58% women) entered the AGES-Reykjavik study as participants.

Physical, physiological and questionnaire examinations were conducted in three visits for each subject. An extensive data collection was done on various biological aspects, medical history, as well as recording of lifestyle factors. Variables and results from the AGES-Reykjavik Study and the previous Reykjavik-study analyses are described in more detail in Harris et al.[26].

Sample and definitions

Of the 5,764 individuals who agreed to participate in the AGES-Reykjavik study, 5,427 individuals attended the research centre for examinations while 337 received a home visit. A total of 204 individuals did not contribute CT-data at the research centre. Ten individuals who had a CT-scan were excluded due to missing data for smoking status and height or weight. The final sample used in these analyses therefore consisted of 5,213 individuals (58% females).

The definition for previous coronary events included: myocardial infarction diagnosed with electrocardiogram (ECG) at entry into the study, history of either myocardial infarctions (MI), coronary artery bypass graft (CABG) or percutaneous coronary intervention (PCI) confirmed by hospital records.

History of diabetes was recorded at entry into the study and subjects were defined as having newly diagnosed diabetes if fasting glucose levels were greater than 7 mmol/L.

Image acquisition

Images for calcium scoring were acquired using a Siemens Somatom Sensation 4 multi-detector CT scanner (Siemens Medical Solutions, Erlangen, Germany) with prospective ECG triggering. The ECG triggering was set at 50% of the cardiac R-R interval. The entire heart was scanned sequentially in the cranio-caudal direction during suspended inspiration (standard scan setting: slice thickness; 2.5 mm, tube voltage; 140 kilo-voltage, tube-current-time-product; 50 milli-ampere-seconds and scan time 0.361 sec). Study participants weighing more than 110 kg (kilograms) underwent CT with a tube current setting that was 25% higher than the standard scan setting. The images were reconstructed into a display field of view of 350 mm to include a calibration phantom (Image Analysis, Columbia, KY, USA) which was positioned under the thorax of each subject. The phantom contained calibration cells of 0, 50, 100, 200 mg/cm³, equivalent concentration of calcium hydroxyapatite.

Calcium in the coronary arteries was quantified using the Agatston scoring method [24] by 4 image analysts who were certified after appropriate training. Phantom-adjusted CAC was expressed as a sum score for all four coronary arteries. Inter- and intra-observer variability assessment showed high reliability of the calcium scoring. Inter-observer variability based on the re-analysis of randomly selected 365 scans from the core study population by an expert observer showed an average correlation coefficient of 0.99. Intra-observer variability based on re-analysis of 45 scans by each of the four observers resulted in an average correlation coefficient of 0.99. The CAC analysis technique used in this study together with information of its reliability is described in more detail elsewhere [28].

Standard B-mode images of the Carotid Intima Medial Thickness (CIMT) were acquired at four predefined interrogation angles at each side of the common carotid artery (CCA). The average CIMT of the near and far walls at all angles on both sides of the CCA comprised the CIMT outcome parameter. The presence of atherosclerotic lesions of the left and right carotid bifurcation and internal carotid artery (CPs) was quantified on line during the ultrasound examination. The most severe lesions per segment were assessed in a semi-quantitative manner as none, minimal, moderate and severe. The ultrasound protocol of the CIMT and atherosclerotic lesions in described in more detail elsewhere [29].

Statistical Analyses

Descriptive analyses were stratified by sex and age groups, as sex and age differences are extensive for CAC [1, 3, 4, 11, 30]. Preliminary analyses indicated strong associations between CAC and history of coronary events and therefore the data were also stratified by previous coronary events.

Median CAC-scores in the AGES-Reykjavik study were visually compared by sex and age groups to published values from other population based studies examining CAC-distributions; namely Framingham, MESA and the Heinz Nixdorf Recall (HNR) studies [1, 2, 31]. These studies published values for persons in five year groups without history of cardio-vascular disease (CVD) (MESA and Framingham) and by medication use for cardio-vascular conditions (HNR).

Visual comparisons of the methods by year of age as a continuous variable (using linear and quadratic terms for age as opposed to age groups) were made for both sexes by history of coronary event since CAC-burden and incidence of coronary events are known to increase with age [4, 11].

Four different regression models were applied to CAC on established variables having associations with CAC [2, 5, 11]. The following regression methods were applied separately by sex in the full sample and compared with respect to number of detected associations, R² and the PRESS-statistic:

1. Linear regression on log-transformed (ln(CAC+1)) data as this method has been frequently described in the literature and here was used as the basis for comparison.

2. Linear regression on Box-Cox transformed CAC-scores (Box-Cox(CAC+1)). This method can make distributions more normal and stabilize variance by applying an optimal power transformation [32]. When successful, the Box-Cox approach can justify the use of parametric methods to model an otherwise skewed distribution [32, 33]. The Box-Cox power transformation was determined for both sexes at once in order to simplify interpretation.

3. Quantile regression was fitted to model median values.

4. Finally a ZINB model was fit [13, 14]. The Vuong-statistic [14, 34] was considered for the zero inflated model to determine whether it is an improvement over the standard negative binomial model.

Predicted values from a covariate profile differ by type of regression model: the linear regression models provide geometric means after back-transformation; the ZINB models provide arithmetic means and proportions of zero values, and the quantile regression models provide medians. Predicted values were presented and compared to observed values.

The detection of associations between CAC with a set of CAD-risk factors were compared among the methods. This was done by sex, with adjustment for age while excluding individuals with previous coronary events. This was first done in a univariable model for each variable and then a multivariable model.

The following variables (CAD risk factors) were considered: BMI, systolic blood pressure, pulse pressure, total serum cholesterol, HDL cholesterol, triglycerides, C-reactive protein, type II diabetes, smoking, family history of myocardial infarction, chest pain from heart disease, mini stroke or TIA, carotid intima thickness, plaque (moderate or more in carotid artery), analgesics, anticoagulants, aspirin, statins, medication for hypertension.

The ZINB model is the only model which provides a prediction of proportion of zero CAC along with estimation of CAC-extent, for a covariate profile. Zero predictions were obtained from the ZINB model in the full sample (n = 5,213) and calculated according to sex, age group and history of coronary events. The estimates were compared to the observed zero prevalence in the full sample in order to evaluate predictive value.

Finally the multivariable regression models were compared in terms of R² and the PRESS-statistic. Predicted values from the linear regression approaches were back-transformed to original scales for all inter-method comparisons. The R² was calculated as the squared correlation between observed and predicted CAC and the PRESS-statistic was defined as:

$$\mathit{PRESS}=\sum _{i=1}^n{(y_i-{\widehat{y}}_{i,-i})}^2$$ (1)

where $(y_i-{\widehat{y}}_{i,-i})$ are the PRESS-residuals. Here y_i is the observed value for individual i and ${\widehat{y}}_{i,-i}$ is the predicted value when leaving out individual i in the estimation [35]. The PRESS-statistic is based on the “leave one out” approach and measures prediction error in absolute terms, as a corresponding observed value is not included when the model is fit for that instance [35].

A 95% significance level was used for determining associations and interactions and 95% confidence intervals were presented for all estimates. All statistical analyses were conducted using Stata version 12 (StataCorp LP, College Station, Texas).

Results

Descriptive characteristics

Participant males and females were of similar age. Higher proportions of males were current or formers smokers, or had experienced a coronary event. Males had higher CAC-scores and the variance increased with mean values (Table 1).

Table 1.

Baseline characteristics of AGES-Reykjavik participants 2002-2006

Characteristics	Males n = 2,229	Females n = 2,984
Physical and physiological
Age (years) mean (SD)	76.6 (5.4)	76.4 (5.6)
Body Mass Index, mean (SD)	26.8 (3.8)	27.2 (4.8)
Systolic blood pressure (mmHg) mean (SD)	142.8 (20)	142.2 (20.6)
Diastolic blood pressure (mmHg) mean (SD)	76.0 (9.5)	72.3 (9.5)
Pulse pressure (mmHg) mean (SD)	66.8 (17.1)	69.9 (18.9)
Total serum cholesterol (mmol/Liter) mean (SD)	5.2 (1.1)	6.0 (1.1)
Serum HDL cholesterol (mmol/L) mean (SD)	1.41 (0.38)	1.72 (0.44)
Serum LDL cholesterol (mmol/L) mean (SD)	3.2 (0.9)	3.67 (1.0)
Serum triglycerides (mmol/L) mean (SD)	1.16 (0.66)	1.22 (0.64)
Fasting glucose (mmol/L) mean(SD)	5.9 (1.2)	5.6 (1.1)
C-reactive protein (mg/Liter,serum) median (range)	1.8 (0-70.3)	1.9 (0-117)
Diabetes mellitus. type II. No. (%)	337 (15.1)	283 (9.5)
Smoking status, No. (%)
Never	634 (28.4)	1,572 (52.7)
Former	1,338 (60)	1,030 (34.5)
Current	257 (11.5)	382 (12.8)
Cardiovascular profile
Previous coronary event, No. (%)	636 (28.5)	311 (10.4)
Family history of Myocardial Infarction, No. (%)	690 (31)	1,185 (39.8)
Chest pain due to heart disease. No. (%)	391 (17.8)	341 (11.6)
TIA or mini stroke. No. (%)	116 (5.3)	94 (3.2)
Carotid Intima Medial Thickness (mm) mean (SD)	1.2 (0.2)	1.1 (0.2)
Moderate or more plaque in carotid artery No. (%)	1,661 (72.7)	2,141 (68.9)
Medications
Analgesics, No. (%)	694 (31.1)	933 (31.3)
Aniticoagulants. No. (%)	1,108 (49.7)	956 (32.0)
Aspirin No. (%)	968 (43.4)	876 (29.4)
Statins, No. (%)	637 (28.6)	556 (18.6)
Medication for hypertension, No. (%)	1,394 (62.4)	1,930 (64.7)
CAC
Mean (SD)	1,084 (1,300)	449 (733.9)
Variance	1,688,280	538,685
25th percentile	173	15
50th percentile - median (Range)	625 (0-10,265)	151 (0-8,608)
75th percentile	1,517	570
90th percentile	2,744	1,277
Interquartile range	1,344	555
Categories
CAC 0, No. (%)	79 (3.5)	503 (16.9)
CAC 1-10, No. (%)	65 (2.8)	196 (6.3)
CAC 11-100, No. (%)	279 (12.0)	600 (19.3)
CAC 101-400, No. (%)	456 (19.7)	745 (23.9)
CAC >400, No. (%)	1,439 (62.1)	1,065 (34.3)

Abbreviations: CAC, Coronary artery calcium; HDL, High density lipoprotein; LDL, Low density lipoprotein; SD, Standard deviation; TIA, Transient ischemic attack

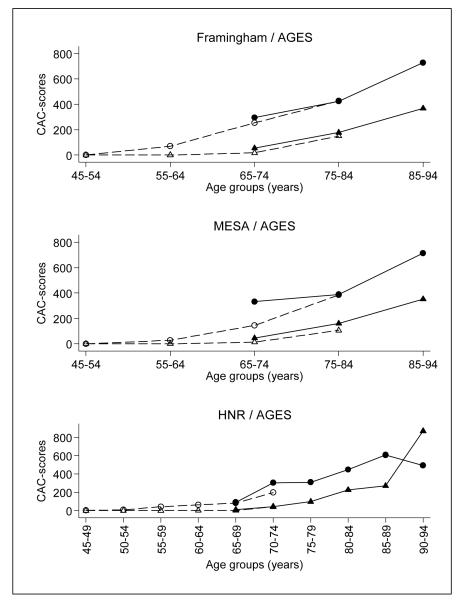
AGES-Reykjavik-medians plotted with median CAC from other populations can be seen in Fig. 1. Other percentile rankings for AGES-Reykjavik, by age, sex and history of coronary events can be seen in Online Resource 1.

Fig 1.

Median CAC from the AGES-Reykjavik study 2002-2006, compared to published datay from the Framingham- (n = 3,240), MESA- (n = 2,503) and HNR-studies (n = 2,434). In Framingham and MESA values represent individuals without history of coronary events and other cardiovascular disorders and in HNR they represent individuals not taking medication for cardiovascular disorders. Corresponding AGES-Reykjavik values were calculated using the same criteria as described in the other studies. AGES-data points are filled symbols with unbroken lines. Males are ○ • and females ▵▴

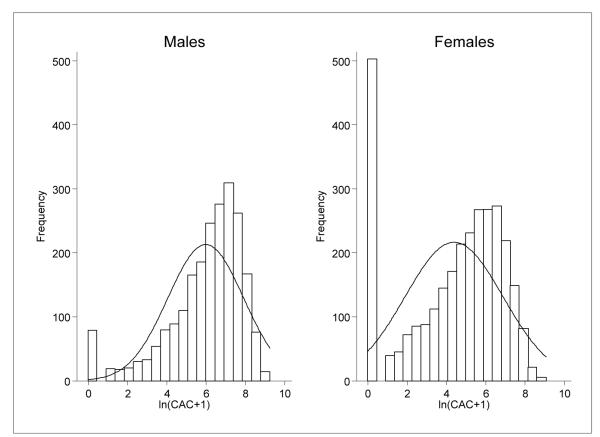
Prevalence of zero CAC was considerably higher in females (16.9% vs. 3.5%) but prevalence of zero scores decreased with age. Persons with previous coronary events had noticeably higher CAC (Table 1,Table 2). There was an excess proportion of zero CAC, particularly in female CAC-distributions (Fig. 2), which warranted the application of a zero inflated regression model.

Table 2.

Prevalence of zero, median and mean CAC in AGES-Reykjavik 2002-2006. Presented stratified for sex, age group, history of coronary events and CAC>0

Sex	Previous coronary event		Age groups (years)
			<70	70-74	75-79	80-84	85+
Males
	No
		n	131	498	475	345	144
		Prev. zero No.(%)	10(7.6)	31(6.2)	20(4.2)	14(4.1)	4(2.8)
		Median	181	342	377	577	736
		Median,CAC>0	201	391	407	654	768
		Mean	511	641	792	1,023	1,194
		Mean,CAC>0	553	683	827	1,066	1,228
	Yes
		n	56	180	204	153	43
		Prev. zero No.(%)	0 (0)	0 (0)	0 (0)	0 (0)	0 (0)
		Median	1,486	1,268	1,384	1,493	1,424
		Median,CAC>0	1,486	1,268	1,384	1,493	1,424
		Mean	1,664	1,625	1,756	1,943	1,949
		Mean,CAC>0	1,664	1,625	1,756	1,943	1,949
Females
	No
		n	316	813	736	595	213
		Prev. zero No.(%)	98(31.0)	198(24.4)	130(17.7)	58(9.7)	12(5.6)
		Median	22	69	129	235	384
		Median,CAC>0	81	141	212	297	460
		Mean	155	238	348	557	741
		Mean,CAC>0	225	314	422	617	785
	Yes
		n	15	69	99	100	28
		Prev. zero No.(%)	1(6.7)	3(4.3)	2(2.0)	1(1.0)	0(0)
		Median	266	835	831	932	1,198
		Median,CAC>0	283	854	861	937	1,198
		Mean	914	993	998	1,281	1,489
		Mean,CAC>0	979	1,038	1,018	1,294	1,489

Abbreviations: CAC, Coronary artery calcium

Fig. 2.

Log-transformed (ln(CAC+1)) CAC-score distributions in AGES-Reykjavik 2002-2006, according to sex with corresponding normal distributions overlaid

Overview of the regression results

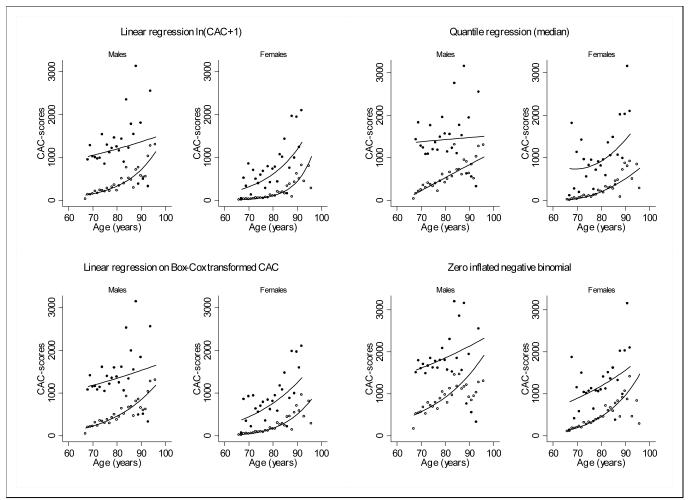
Fitted and summary values from four different modelling methods by sex, age and history of coronary events are shown in Fig. 3. There were significant interactions between age and history of coronary events in both sexes and all models. A quadratic term for age was included in the quantile regression for females.

Fig. 3.

Visual comparison of the fitted methods (full sample n = 5,213) in AGES-Reykjavik 2002-2006. Observed values are back transformed mean CAC values for the ln(CAC+1) and Box-Cox(CAC+1) (power transformation 0.20 (95% CI 0.19, 0.21)), and median values for the quantile regression. The observed values in the ZINB-model are arithmetic means. Males and females are compared according to year of age and history of coronary events. The quantile regression includes a quadratic term for age in females. Coronary event: no = ○, yes = • Overlaid lines represent predicted values

The regression methods modelled different measures of location. The linear regressions modelled geometric means using ln(CAC+1) and Box-Cox(CAC+1) transformed CAC (obtained power transformation 0.20 (95% CI 0.19, 0.21)).

The quantile regression modelled the median values while the ZINB modelled the arithmetic mean [25].

The predicted geometric means obtained from linear regression on ln(CAC+1) were a close approximation of median CAC.

Association comparison

The total number of detected associations for each method provides information on how the methods compare to the more conventional linear regression on ln(CAC+1). Sex and age group adjusted models (Table 3) show similar numbers of detected associations with CAC across methods and usually with the same risk factors. However, only the ZINB model detected an association with cholesterol (males only). The quantile regression for males did not detect an association with smoking whereas all the other methods did. The methods were not consistent in detection of association with diabetes.

Table 3.

Comparison of P-values for each variable, obtained from the applied regression methods on CAC in AGES-Reykjavik 2002-2006 (n = 5,213). Models fitted for each variable separately by sex, adjusting for age and excluding people with history of coronary events

		Males					Females
	Modelled as:	ZINB- logistic part	ZINB- count part	Linear regression ln(CAC+1)	Linear regression Box-Coxc	Quantile regression	ZINB- logistic part	ZINB- count part	Linear regression ln(CAC+1)	Linear regression Box-Coxc	Quantile regression
Physical and physiological
BMI	Continuous	*	***	***	***	***
Systolic blood pressure (10 mmHg)	Continuous					*	**	**	***	***	***
Pulse pressure (10 mmHg)	Continuous					*	***	**	***	***	***
Total serum cholesterol (mmol/L)	Continuous	*	**
HDL cholesterol (mmol/L)	Continuous						**	***	***	***	***
Triglycerides (mmol/L)	Continuous						**	**	***	***	***
C-reactive protein (mg/L)	Continuous		*	**	**			**	***	***	***
Diabetes mellitus, type II (No is reference)	Categorical					** a		* a	** a	** a	*** a
Newly diagnosed											*
Previously known diabetes			**		*	**		*	**	**	***
Smoking Never (reference)	Categorical	** a		*** a	*** a		*** a	*** a	*** a	*** a	*** a
Former		**	*	***	***		***	**	***	***	***
Current				**	**		***	***	***	***	***
Cardiovascular profile
Family history of myocardial infarction	Categorical		**	**	***	***	***	***	***	***	***
Chest pain from heart disease	Categorical								*	**	**
Mini stroke or TIA	Categorical					*	*		*
Carotid intima thickness (mm)	Continuous	***		***	***	***	***	***	***	***	***
Plaque, moderate or more in carotid artery	Categorical	***	***	***	***	***	***	***	***	***	***
Medications
Analgesics	Categorical	*	**	***	***	***	*	***	***	***	***
Anticoagulants	Categorical		***	***	***	***	*	**	***	***	***
Aspirin	Categorical		***	***	***	***	*	**	***	***	***
Statins	Categorical		***	***	***	***	***	**	***	***	***
Medication for hypertension	Categorical	**	***	***	***	***	**	***	***	***	***
Total number of associations b		7	12 (13)	12	13	13	16	15 (17)	18	17	18

^*P-value <0.05

^**P-value <0.01

^***P-value <0.001

Abbreviations: BMI, Body mass index; CAC, Coronary artery calcium; HDL, High density lipoprotein; TIA , Transient ischemic attack; ZINB, Zero inflated negative binomial

^aP-value from Wald-test, Ho: all coefficients=0

^bTotal number of associations from the ZINB-model shown in parenthesis.

^cPower transformation 0.20 (95% CI 0.19, 0.21)

In the multi variable ZINB model there were differences between the sexes in risk factor associations with CAC, both in the logistic and negative binomial part (Table 4). In the logistic part for males there was no association between CAC and age groups. Risk factors associated with decreased odds of a zero CAC-score were: serum cholesterol, smoking, carotid intima medial thickness, plaque burden analgesics, statins and medication for hypertension. Increased odds of a zero CAC were observed for pulse pressure and triglycerides.

Table 4.

Multi variable ZINB model, fitted separately for males and females without history of coronary events in AGES-Reykjavik 2002-2006 (Males n = 1,593; females n = 2,763; total n = 4,266)

	Males								Females
	Logistic part				Negative binomial part				Logistic part				Negative binomial part
	OR a	95% CI b		P-value	Estimatec	95% CI b		P-value	OR a	95% CI b		P-value	Estimate c	95% CI b		P-value
Physical and physiological
Age groups (years)				0.76 d				*** d				*** d				*** d
<70 (reference)
70-74	0.81	0.28,	2.34	0.70	1.38	1.08,	1.77	**	0.65	0.46,	0.92	*	1.48	1.20,	1.82	***
75-79	0.61	0.20,	1.89	0.39	1.43	1.11,	1.83	**	0.51	0.35,	0.75	**	1.79	1.45,	2.20	***
80-84	0.51	0.14,	1.87	0.31	1.93	1.48,	2.51	***	0.27	0.17,	0.43	***	2.58	2.08,	3.22	***
85+	0.46	0.09,	2.33	0.35	2.14	1.56,	2.94	***	0.11	0.04,	0.27	***	3.61	2.74,	4.75	***
BMI	0.92	0.82,	1.02	0.12	1.05	1.03,	1.07	***	0.99	0.96,	1.02	0.43	0.99	0.98,	1.00	0.20
Systolic blood pressure (10 mmHg)	0.76	0.51,	1.14	0.18	1.00	0.93,	1.07	0.95	0.83	0.72,	0.95	**	1.02	0.96,	1.08	0.56
Pulse pressure (10 mmHg)	1.66	1.02,	2.71	*	0.98	0.90,	1.07	0.70	1.16	0.99,	1.35	0.06	1.00	0.94,	1.07	0.92
Total serum cholesterol (mmol/L)	0.43	0.27,	0.69	***	0.95	0.88,	1.02	0.18	0.83	0.72,	0.95	**	0.99	0.93,	1.06	0.76
HDL cholesterol (mmol/L)	1.66	0.69,	4.01	0.26	1.26	1.04,	1.52	*	1.23	0.88,	1.72	0.23	0.82	0.70,	0.96	*
Triglycerides (mmol/L)	2.25	1.23,	4.12	**	0.93	0.81,	1.07	0.31	0.98	0.75,	1.27	0.86	1.06	0.95,	1.18	0.29
C-reactive protein (mg/L)	0.96	0.89,	1.03	0.22	1.01	1.00,	1.02	0.08	0.97	0.94,	1.00	*	1.00	1.00,	1.01	0.27
Diabetes mellitus, type II (No is reference)				0.66 d					0.52 d					0.51 d		0.71 d
Newly diagnosed	0.00	0.00,	e	0.99	0.86	0.63,	1.19	0.37	0.54	0.19,	1.54	0.25	0.92	0.66,	1.30	0.66
Previously known diabetes	1.68	0.55,	5.17	0.37	1.07	0.86,	1.34	0.53	0.94	0.54,	1.63	0.82	1.08	0.86,	1.36	0.50
Smoking Never (reference)				* d					0.26 d					*** d		** d
Former	0.39	0.19,	0.81	*	1.10	0.95,	1.27	0.21	0.58	0.44,	0.76	***	1.07	0.94,	1.22	0.30
Current	0.53	0.19,	1.49	0.23	1.19	0.95,	1.50	0.13	0.41	0.26,	0.65	***	1.30	1.08,	1.56	**
Cardiovascular profile
Family history of myocardial infarction	0.97	0.47,	2.02	0.95	1.20	1.04,	1.39	*	0.67	0.52,	0.87	**	1.27	1.13,	1.43	***
Chest pain from heart disease	1.54	0.70,	3.38	0.29	0.98	0.84,	1.15	0.83	0.91	0.68,	1.20	0.50	1.06	0.93,	1.20	0.40
Mini stroke or TIA	1.12	0.17,	7.51	0.91	1.10	0.81,	1.49	0.55	0.36	0.12,	1.06	0.07	0.81	0.58,	1.13	0.22
Carotid intima thickness (mm)	0.04	0.00,	0.68	*	0.91	0.59,	1.39	0.67	0.14	0.05,	0.39	***	1.38	0.90,	2.11	0.14
Plaque, moderate or more in carotid artery	0.26	0.12,	0.55	***	1.91	1.66,	2.20	***	0.44	0.34,	0.57	***	1.89	1.66,	2.15	***
Medications
Analgesics	0.16	0.03,	0.77	*	1.06	0.87,	1.29	0.58	0.92	0.66,	1.28	0.62	1.15	1.00,	1.34	0.05
Anticoagulants	1.71	0.41,	7.14	0.47	1.19	0.90,	1.56	0.23	1.25	0.52,	2.98	0.62	0.82	0.54,	1.22	0.33
Aspirin	0.92	0.19,	4.49	0.92	0.94	0.69,	1.27	0.67	0.78	0.32,	1.92	0.60	1.25	0.83,	1.89	0.28
Statins	0.09	0.02,	0.53	**	1.30	1.03,	1.62	*	0.43	0.27,	0.70	**	1.11	0.91,	1.34	0.31
Medication for hypertension	0.42	0.18,	0.98	*	1.20	1.04,	1.38	*	1.03	0.79,	1.34	0.82	1.10	0.96,	1.25	0.17

^*P-value <0.05

^**P-value <0.01

^***P-value <0.001

Abbreviations: BMI, Body mass index; CI, Confidence intervals; HDL, High density lipoprotein; OR, Odds ratio; TIA, Transient ischemic attack

^aOdds Ratio comparing odds of a certain zero CAC-score, OR below 1 represents reduced odds of a zero CAC-score

^bConfidence Intervals

^cRelative mean change in CAC-scores

^dP-value from Wald-test, Ho: all coefficients=0

^eVery large number

In the logistic part for females age was associated with decreased odds of zero CAC, as was systolic blood pressure, serum cholesterol, C-reactive protein (untransformed), ,smoking, carotid intima thickness, plaque burden in the carotid artery, family history of myocardial infarction and statin use.

CAC-associated risk factors common to both sexes in the logistic part were serum cholesterol, carotid intima thickness, plaque burden in the carotid artery, smoking and statin use.

The negative binomial part of the model determines the association with positive CAC. In males the following risk factors were associated with increased CAC-burden: age, BMI, HDL, family history of myocardial infarction, plaque burden in carotid artery, statin use and medication for hypertension,

In females the following risk factors were associated with increased CAC-burden: age, HDL, plaque burden in carotid artery, smoking and family history of myocardial infarction.

CAC-associated risk factors common to both sexes in the negative binomial part of the model were age, HDL, family history of myocardial infarction, plaque burden in the carotid artery.

Results from multi variable models using the other regression methods are presented in Online Resource 2.

The Vuong statistic for the multi variable male ZINB model was 1.21 (P-value = 0.11) and 2.35 for the multi variable female ZINB model (P-value = 0.01). The dispersion parameter for the male model was 1.41 (95% CI 1.30, 1.51), P-value <0.001 and for females 1.62 (95% CI 1.52, 1.73), P-value <0.001.

Predicted proportion of zero CAC, obtained from the ZINB model was similar to observed values for sex, age groups and history of previous coronary events (Table 5).

Table 5.

Observed and ZINB-predicted prevalence (%) of zero CAC in the AGES-Reykjavik study 2002-2006 (n = 5,213). presented according to sex, age groups and history of coronary events

		Previous coronary event
		No				Yes
Sex	Age groups	Observed	Predicted	95% CI a		Observed a	Predicted	95% CI a
Males
	<70	7.6	7	2.5,	11.6	0	0	0,	0
	70-74	6.2	5.7	3.6,	7.9	0	0	0,	0
	75-79	4.2	3.8	1.9,	5.6	0	0	0,	0
	80-84	4.1	3.7	1.6,	5.8	0	0	0,	0
	85+	2.8	2.4	0.0,	5.1	0	0	0,	0
Females
	<70	31.0	29	23.8,	34.3	6.7	3.1	0,	6.9
	70-74	24.4	22.6	19.5,	25.6	4.3	2.2	0,	4.9
	75-79	17.7	15.9	13.1,	18.8	2.0	1.5	0,	3.2
	80-84	9.7	8.2	5.8,	10.7	1.0	0.7	0,	1.6
	85+	5.6	4.3	1.1,	7.4	0	0.3	0,	0.8

Abbreviations: CI, Confidence intervals

^a95% confidence intervals

Results for the PRESS-statistic according to regression method were parallel for the sexes (Table 6) and the ZINB model had the lowest sum of squared residuals. The ZINB model had the highest R² of the multi variable models (Table 6).

Table 6.

PRESS-statistic and R² for multi variable models (n_= 5,213). Presented stratified for sex, history of coronary events and each of the applied regression methods in AGES-Reykjavik 2002-2006

Method	Males				Females
	Previous coronary event				Previous coronary event
	No		Yes		No		Yes
	PRESS a	R2	PRESS a	R2	PRESS a	R2	PRESS a	R2
Linear regression ln(CAC+1)	18.4	0.14	15.2	0.09	10.8	0.11	3.9	0.21
Linear regression Box-Cox(CAC+1) b	17.2	0.16	14.4	0.10	10.1	0.13	3.4	0.26
Quantile regression (median)	16.5	0.14	13.1	0.10	10.0	0.13	2.7	0.25
ZINB	14.9	0.16	13.0	0.12	8.8	0.14	3.1	0.29

Abbreviations: CAC, Coronary artery calcium; ZINB, Zero inflated negative binomial

^aValues are multiples by 10⁸

^bPower transformation 0.20 (95% CI 0.19, 0.21), from Stata.

Discussion

CAC-distributions

Prevalence of CAC was high in AGES-Reykjavik, as was occurrence of CAD. This is in keeping with knowledge of CAC in relation to age and as a risk factor for coronary events [5]. Females lag about ten years behind males for corresponding CAC-scores, which is consistent with other populations [11]. Prevalence of CAC-scores greater than 400 in AGES-Reykjavik was similar to published values for corresponding age groups in a smaller U.S study, which included black people as well as white people [36].

Few studies report on population-based CAC-distributions in older individuals [3, 36] Overall, AGES-Reykjavik median values compared well with Framingham-, MESA- and HNR-values in overlapping age groups. AGES-Reykjavik CAC-scores seemed to be a continuation of the trend seen with age, particularly compared to Framingham.

Regression methods and associations

Overall, the methods agreed well with the corresponding observed summary statistics. The ZINB model had not been previously applied in CAC-modelling and performed better than the conventional method of linear regression on ln(CAC+1). The ZINB model gave the best results with respect to the PRESS-statistic and R², which is in keeping with the expected benefit of applying such models to account for zero inflation and over-dispersion. Dispersion parameters from the multi variable adjusted ZINB model confirmed that the CAC-scores were indeed over-dispersed. It has been proposed that models with large numbers and dispersion parameters greater than 1.05 are over-dispersed [14]. This supports that analytical approaches to CAC-modelling should take this into account and the Vuong statistic for the ZINB model also supported application of zero inflated models over the standard negative binomial in females. These results indicate that the ZINB model is a suitable modelling approach for CAC. The ZINB model has the added benefits of estimating proportions of zero scores while inherently acknowledging that there may be two different processes that dictate the presence and extent of CAC.

There were clear differences in prevalence of zero CAC according to sex, age (Online Resource 3) and history of coronary events. Point estimates for zero predictions were accurate from the ZINB model. The other methods only allowed predictions of mean values and not proportions of zero scores.

However, the ZINB model detected similar number of associations compared to the linear regressions, indicating that the conventional ln(CAC+1) method is an applicable estimation approach for associations.

There were differences between the sexes in co-variable associations with CAC in the multi variable ZINB model. Most of the conventional CAD risk factors were associated with CAC which is consistent with other studies of CAC-modelling [8, 9].

Age was a strong predictor of CAC-extent, which is consistent with the literature [2, 3, 8, 9]. The absence of an association in the logistic part of the ZINB model for males is likely due to the relatively low prevalence of zero CAC among males in this age group. An association is likelier to be observed in males younger than participants in this study [11].

The strong association between plaque in the carotid artery and CAC observed in this study supports that plaque burden is a marker for both the presence and extent of CAC. Ultra sonograms of the carotid artery have been proposed as a screening method for asymptomatic CAD and we find an association as well (Online Resource 4) [37].

Association with diabetes status at entry was found to be statistically significant in an age adjusted model but disappeared after adjustment for other risk factors (Online Resource 5).

Family history of myocardial infarction was associated with CAC in both parts of the multi variable ZINB model and also in the ln(CAC+1) model, which is consistent with the MESA study [19].

The quantile regression surpassed the linear regressions according to the PRESS-statistic in both sexes but had slightly lower R² values. The quantile regression detected similar numbers of associations with CAC compared to the other age adjusted models in subjects without history of coronary events. However, in the multi variable adjusted models it detected the fewest associations with CAC (Online Resource 6). The absence of an association between smoking and CAC in the quantile regression, both in age adjusted and full models for males, highlights an interesting drawback of applying the quantile regression in this data set. There could be an explanation in different age associations with CAC in aged, current male smokers (Online Resource 7).

Initial analysis confirmed that simple logarithmic transformations on CAC+1 did not result in normally distributed residuals. It was interesting to see that the linear regression on Box-Cox transformed CAC+1 performed better than ln(CAC+1) in terms of the PRESS-statistic and R². This suggests that although the natural logarithm can be a useful transformation in many analyses, a more flexible approach can be taken in order to make CAC-data more compatible with parametric methods, which assume constant variance and normally distributed errors.

There was considerable unexplained variance after applying all the multi variable adjusted models. According to the literature, this study included all usual risk factors for investigating CAC in relation to CAD [5, 6]. One study reported similar R² values for log-transformed CAC using linear regression on conventional risk factors [9]. It remains to be seen whether the R² could be improved with novel risk factors not applied here. The variable with the highest R² value was the indicator of a previous coronary event (Online Resource 8).

Strengths and limitations

This research was conducted on a genetically homogenous population [38], in which for the age groups of interest, ethnicity was not a confounder as in similar studies [39]. The large study sample was based on a well-established population based cohort study with concurrently measured cardio-vascular risk factors in the Icelandic population. The sample size was a high proportion of people of the corresponding age groups [40] and reaching higher in age than comparison studies. A limitation is not having data for age below 66 years for comparison with age groups presented for other populations.

Conclusions

The strongest associations with CAC were observed for age, sex and history of previous coronary events. In people without history of previous coronary events, most of the conventional risk factors for coronary disease were associated with CAC in simple age adjusted models. However, in multi variable models the strength of associations were attenuated and the R² values were low, leaving most of the variability in CAC unexplained.

After comparing several regression methods in CAC-modelling, including linear regression with logarithmic- and Box-Cox transformations, quantile regression and a ZINB model, we conclude that the ZINB model provided the best results in terms of summary measures. The ZINB model offered an appealing alternative to the conventional linear regression on ln(CAC+1) as it effectively accounted for important distributional characteristics of CAC while estimating presence and extent of CAC in one model. However, in terms of detection of risk factor associations with CAC, the results from linear regression on ln(CAC+1) and the ZINB model were similar.

Abbreviations

CAC

Coronary artery calcium

CAD

Coronary artery disease

CVD

Cardiovascular disease

CI

Confidence interval

CIMT

Carotid Intima Medial Thickness

HDL

High density lipoprotein

OR

Odds Ratio

SD

Standard deviation

TIA

Transient ischemic attack

ZINB

Zero inflated negative binomial