Abstract
Recent experiments have measured the rate of replication of DNA catalyzed by a single enzyme moving along a stretched template strand. The dependence on tension was interpreted as evidence that T7 and related DNA polymerases convert two (n = 2) or more single-stranded template bases to double helix geometry in the polymerization site during each catalytic cycle. However, we find structural data on the T7 enzyme–template complex indicate n = 1. We also present a model for the “tuning” of replication rate by mechanical tension. This model considers only local interactions in the neighborhood of the enzyme, unlike previous models that use stretching curves for the entire polymer chain. Our results, with n = 1, reconcile force-dependent replication rate studies with structural data on DNA polymerase complexes.
The advent of techniques to micromanipulate single molecules (1, 2) has enabled studies of DNA elasticity (3–6) and the kinetics of motor enzymes (7–11). Applying force either to a tethered enzyme or to the substrate polymer is often found to markedly alter enzyme-catalyzed rates and thereby offers insight into conformational changes involved in operation of the molecular motor. We consider such results pertaining to the rate at which DNA polymerases, operating on a stretched single-strand (ss) DNA template, catalyze synthesis of a complementary strand (10, 11). The original interpretation of the data concluded that in the polymerization site of the motor enzyme n = 2 or even n = 4 (depending on the enzyme) ss template bases are converted to double-stranded (ds) geometry during each catalytic cycle, only to have n − 1 of these bases revert to ss geometry before the onset of the next cycle. If correct, this conclusion would have important implications for the mechanisms of DNA replication, proofreading, and editing (15, 16).
Crystal structures of enzyme-DNA complexes indicate, however, that only one template base is converted from ss to ds geometry in the complex (12, 13, 17–19). We attribute this apparent conflict to misleading aspects of the previous models (10, 11) used to interpret the force dependence of the replication rate. We also suggest conceptual amendments that indicate the rate data are compatible with n = 1, in accord with the structural results.
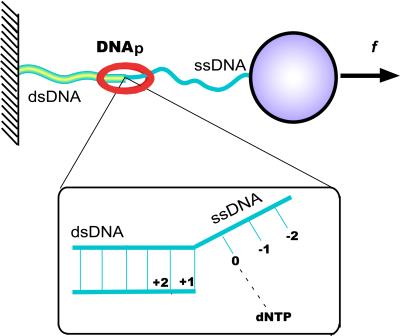
Fig. 1 depicts schematically the elementary rate-limiting step thought to govern DNA replication (12, 14–16). This process involves a change in the conformation of the DNA bound to the enzyme, in which the leading base of the ssDNA template strand (labeled 0) pairs with a complementary dNTP that is incorporated into the growing double helix. A key aspect affecting the response to tension applied to the template is the change in length that occurs during conversion of ss- to dsDNA. This change is specified in terms of a decrease from Lss to Lds, the corresponding contour lengths per residue. Operating as a molecular motor to generate mechanical force from chemical energy, DNA polymerase (DNAp) induces this shrinkage in successive steps as it moves along the template strand.
Figure 1.
Schematic view of DNA polymerase converting ssDNA to dsDNA while an external force f stretches the template (10, 11). A single DNA molecule is strung between a stationary surface and a plastic bead so that it can be micromanipulated with optical or magnetic tweezers. Inset indicates labeling of residues: 0 denotes the template base that pairs, in the active site of the enzyme, with a complementary free nucleotide (dNTP) captured from the ambient solution; +1, +2, … denote successive neighbors upstream, previously paired to form dsDNA; −1, −2, … denote template bases on ssDNA downstream of the active site.
Structural Features of DNAp Complexes
T7 DNAp (14) and several related enzymes (13, 16–19) undergo a conformational change from an open to a closed form during each cycle of nucleotide incorporation. The closed conformation of the enzyme-DNA complex is regarded as a good surrogate for the transition state for replication. Indeed, the previous models for the force dependence (10, 11) postulated that n adjacent template nucleotides are converted from ss to ds geometry in the closed complex. One of these residues pairs with the added base, whereas the other n − 1 were assumed to revert to ss geometry as the complex returns to the open form before the next cycle. The conclusion (10) that n = 2 thus pertains to the residues located at 0 and −1 (Fig. 1) and implies that in the transition state, the contour lengths from +1 to 0 and from 0 to −1 both shrink from Lss to Lds.
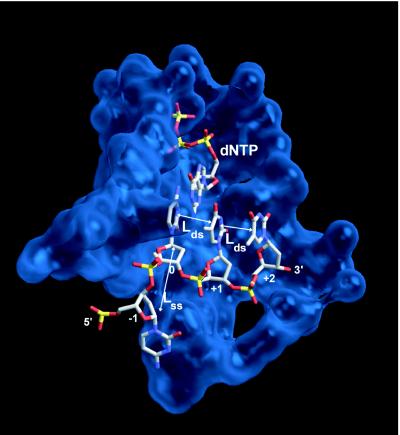
However, this is not seen in crystal structures of the closed complex (12, 14, 18), as shown for T7 DNAp in Fig. 2. In the closed as well as the open forms of the complex, the −1 residue appears to retain ss geometry. For instance, in Fig. 2, the distance between the C1′ atoms of the sugar moieties in the 0 and −1 template residues is 0.81 nm, whereas between the 0 and +1 residues, this distance is only 0.56 nm. These values are typical for ssDNA and dsDNA, respectively (20). The interphosphate distance between the 0 and −1 residues (0.65 nm) is close to that in dsDNA, and this was cited in support of the n = 2 interpretation (10). We consider the interphosphate distance to be less diagnostic than the C1′ spacing, because the phosphorous atoms can rotate about bonds of the DNA backbone with only slight effect on the internucleotide spacing. This is evident in Fig. 2, as the pronounced kink in the DNA template bends the phosphate of residue −1 back towards that of residue 0, artificially shortening the interphosphate distance. The structural data thus indicate that in the closed form of the complex and likely also in the transition state, only residue 0 is converted to ds geometry, which implies n = 1.
Figure 2.
Structure of T7 DNA polymerase complexed with DNA and dNTP, in the region of the active site, for the “closed” configuration of the enzyme [from data of ref. 12 (Protein Data Bank ID code 1t7p)]. Only template nucleotides are shown, labeled as in Fig. 1, plus one incoming dNTP molecule. In this complex as well as related DNA polymerases (13, 16) the dsDNA extending to the 3′ side (nucleotides labeled +1, +2, …) is slightly underwound and has A-form geometry. The template nucleotide on the 5′ side, denoted −1, is stacked on the surface of the polymerase and “flipped out” at nearly a right angle (i.e., γ̂) to its neighbor at the active site, thereby precluding more than one residue from occupying the active site. Residues further to the 5′ side (−2, −3, …) are not strongly bound by the polymerase and are disordered in the crystal structure.
Force Dependence of DNA Replication Rate
Previous Interpretations.
The evidence adduced for n = 2 or more comes from comparing the rate data (10, 11) with a phenomenological model. The dependence of the rate coefficient on the applied force, f, is represented in the form
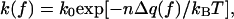 |
1 |
where k0 is the coefficient at zero force, kB the Boltzmann constant, and T the absolute temperature. The force enters solely via a thermodynamic potential difference, Δq(f) = qds(f) − qss(f), taken either as the Gibbs free energy (10) or the enthalpy (11) difference. In either case, Δq(f) is evaluated from experimentally measured curves for the end-to-end extension of ssDNA and dsDNA as functions of the applied force.‖,** Aside from n, the model depends not at all on the enzyme, as the force-extension curves pertain to bare DNA.
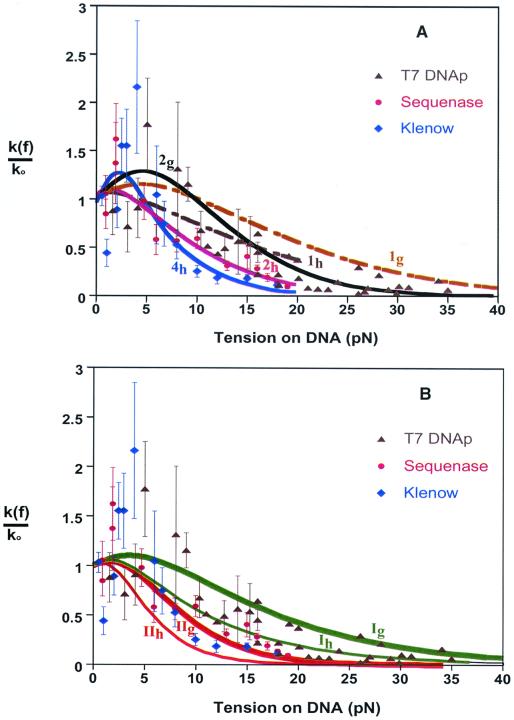
Fig. 3A shows k(f)/k0 curves obtained in this way together with the rate data for catalysis by T7 DNAp and two kindred enzymes, Sequenase (an exonuclease-deficient mutant of T7) and Klenow fragment. Like the structurally related DNA from Thermus aquaticus (18), the polymerizing complexes of Sequenase and Klenow fragment are expected to be very similar to that of T7 DNAp near the active site (12). The model predicts that as the tension is increased, the replication rate first climbs to a maximum and then decreases steadily until polymerization stalls. The maximum is much more pronounced if Δq is taken as the free energy (Δg) rather than the enthalpy (Δh) difference, especially if n > 1. As the experimental scatter is very large for f < 7 pN, however, the size or even presence of an initial maximum is quite uncertain. The value inferred for n thus depends chiefly on the data at higher forces. It also depends on whether Δg or Δh is used in the model. The reported fit (10) to the data for T7 DNAp used Δg and found n = 2; the reported fits (11) for Sequenase and Klenow fragment used Δh and found n = 2.1 ± 0.5 and n = 4 ± 0.7, respectively. Using Δq = Δh in the model of Eq. 1, we find that for f > 7 pN, the T7 DNAp rate vs. force data is consistent with n = 1. In contrast, using Δq = Δg would require n > 7 for Eq. 1 to agree with the Klenow data of ref. 11. Similarly, the k(f)/k0 curve calculated by using Δq = Δg in Eq. 1 does not drop off fast enough to agree with the sequenase data of ref. 11 even for very large n.
Figure 3.
Model calculations and experimental data for force-dependent replication rates catalyzed by three enzymes. Ordinate is normalized to rate at zero force, k0. Data for T7 DNA polymerase (k0 = 130 bases/sec) (▴) from ref. 10, for Sequenase (k0 = 200 bases/sec) (●) and Klenow fragment (k0 = 13.5 bases/sec) (⧫) from ref. 11. (A) Dashed curves from Eq. 1 with n = 1 and Δq either the Gibbs free energy (1g, ref. 10) or the enthalpy (1h, ref. 11), as derived from experimental force-extension curves for ss- and dsDNA.** Full curves show fits to data obtained with n = 2 for T7 DNAp (2g, ref. 10) and Sequenase (2h, ref. 11), and with n = 4 for Klenow fragment (4h, ref. 11). (B) Model curves from Eq. 3 for free-energy and enthalpy variants (subscripts g and h) of limiting Cases I and II; all pertain to n = 1 and the same local contour length and stiffness parameters¶¶ for the three enzymes.
Within the large experimental scatter, the k(f)/k0 data for the three enzymes are fairly similar. In the region of overlap (up to 20 pN), most points for T7 DNAp are near those for Sequenase, and only two data points for Klenow fragment (near 10 and 13 pN) differ significantly from Sequenase. The variations in the nominal values obtained for n may arise in part from differences in the experimental force-extension curves, which can vary significantly with both the nucleotide sequence and the ambient ionic strength (21). In the experiments with Klenow fragment (11), both the GC content of the template DNA and the ionic strength were changed from those with Sequenase. In our view, the implausible variations from n = 1 result because Eq. 1 is not appropriate for modeling kinetic properties. The chief reason is that the end-to-end extensions that define Δq(f) pertain to the entire DNA polymer, whereas the replication process is governed chiefly by local interactions. It occurs in the relatively small portion of DNA, less than 1%, that is complexed with the enzyme near the active site.
In general, the local character of the reaction process may also imply that equilibrium among the polymer modes cannot be presumed for large molecules, whose relaxation processes may be slow in comparison to motion over the reaction barrier (22–25). This has been shown to be important in kindred phenomena such as the response of DNA to a sudden elongational flow (26). For the rate studies considered here (10, 11), however, the timescale probably does not impose a significant limitation.‡‡
Local Model.
These considerations led us to examine a model based solely on conformational changes in the immediate vicinity of the active site of the enzyme complex, with features indicated by the structural data of Fig. 2, including n = 1. As in typical mechanochemical models (8), we retain the form of Eq. 1 but replace nΔq(f) by the force-dependent mechanical work, w(f), done by the enzyme in converting the leading nucleotide (residue 0) of the ssDNA template into a fresh element of the dsDNA helix. As depicted in Fig. 4, we consider movements of just the two polymer segments neighboring the leading residue. The work is then given by
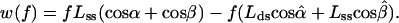 |
2 |
Here the angles α and β specify the orientation, with respect to the direction of the applied force, of the DNA segments between the C1′ atoms of the +1 to 0 and 0 to −1 residues, respectively, for the open conformation of the enzyme; α̂ and β̂ denote the same for the closed conformation. The barrier height, w(f), inhibiting the reaction thus varies with the fluctuating orientations of these polymer segments. As the timescale for these fluctuations is of the order of nanoseconds,‡‡ much shorter than the barrier crossing time (1/k0 ∼ 10–100 msec), we can replace the fluctuating barrier with 〈w(f)〉, its time average (27). This gives the dependence of the rate coefficient on tension as
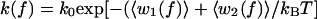 |
3 |
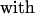 |
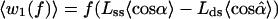 |
 |
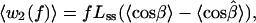 |
the contributions from the two segments. The contrast with Eq. 1 is evident. In effect, Eq. 1 postulates n terms like w1(f); each of those n segments shrinks in length (Lss → Lds) between the open and closed complex. Instead, the model of Eq. 3 postulates that only the leading segment shrinks, but the neighboring segment on the ssDNA template nonetheless can contribute if in w2(f) the averaged angular motion with respect to f differs appreciably between the open and closed complex. This indeed appears likely, because, as seen in Fig. 2, in the closed complex the second segment (0 to −1) is kinked at nearly a right angle to the dsDNA axis.
Figure 4.
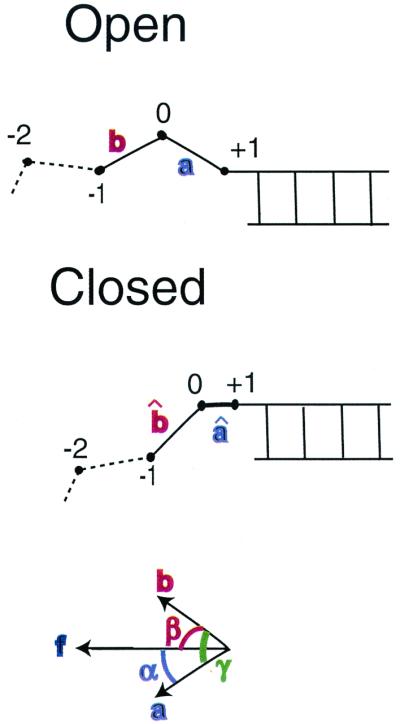
Schematic of the model for Eq. 3. Unit vectors a and b specify orientation of the DNA segments between the C1′ atoms of the +1 to 0 and 0 to −1 residues, respectively, for the open conformation of the enzyme; vectors âand b̂denote the same for the closed conformation. Angles α and β or α̂ and β̂ specify the orientation of the corresponding vectors with respect to the direction of the local applied force vector. Angles between the segments are denoted by γ or γ̂.
Fig. 3B displays k(f)/k0 curves obtained by evaluating the angular averages for two limiting cases. In Case I, we assume that the enzyme interacts only weakly with the DNA segments, in both the open and closed conformations, and thus angular fluctuations would be no more inhibited than the segments of a freely jointed polymer chain (FJC) in the presence of an external force. This is a drastic oversimplification but serves to illustrate how stiffness parameters can be expected to enter. The FJC angular averages are given by the Langevin formula, 〈cosθ〉 = [coth(f/f̃) − (f̃/f)], for θ → α or β, where f̃ = kBT/b and b → bss or bds denotes the Kuhn length of the polymer (twice the persistence length) (28). By contrast, in Case II, we assume that the kink in the template firmly constrains the angle γ̂ between the two segments throughout the force range considered. With γ̂ constant, averaging over the random azimuthal orientations of the segments†† with respect to the force direction gives 〈cosβ̂〉 = cosγ̂/〈cosα̂〉; because γ̂ ≈ 90°, we neglect this term. The contribution from w1(f) thus is the same for both cases, whereas w2(f) does not contribute to I but is likely maximal for II. For f > 8 pN, the parameter dependence of Eq. 3 can be displayed explicitly, as:
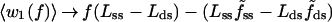 |
4 |
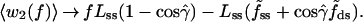 |
5 |
Accordingly, the contribution from 〈w1(f)〉 is chiefly governed by ΔL = Lss − Lds, that from 〈w2(f)〉 by Lss. For simplicity, we have set up Eq. 3 in terms of w(f), which is an enthalpy of activation. Corresponding FJC results in terms of a free energy of activation are readily derived.§§ In Eq. 3, the f 〈cosθ〉 terms are then replaced by terms of the form −f̃xxln[(f/f̃xx)/sinh(f/f̃xx)], with xx = ss or ds; formulas analogous to Eqs. 4 and 5 are the same except for the replacement f̃xx → f̃xxln(2f/f̃xx).
The model k(f)/k0 curves shown in Fig. 3B pertain to a particular set of local parameters,¶¶ taken the same for all three enzyme complexes. The leeway associated with the parameter choice is considerably less than that between Cases I and II and between use of a free energy rather than an enthalpy barrier.§§ We have refrained from adjusting parameters, as the limitations of the rate data and our simple model do not warrant more than prototypic comparisons. Aside from the very noisy region with f < 7 pN, the general trend of the data for the three enzymes lies between our Case I and II curves for the free energy barrier (and thus scatter about the Case I curve for the enthalpy barrier). These results, by contrast with Fig. 3A, serve to demonstrate that the data do not require n > 1.
Discussion
In summary, we contend that, in modeling the force dependence of DNA replication rates, local properties governed by the enzyme complex must be used rather than the global force-extension curves for the template polymer alone. More incisive experimental tests of the relative importance of local vs. global interactions appear feasible. A local model predicts the k(f)/k0 data should be insensitive to changes that do not affect the local environment of the enzyme-template complex but could substantially alter the global stretching curves. For instance, this might be examined by using templates that, in large regions distant from the enzyme complex, differ markedly in base composition.
The access to structural data for polymerase complexes, such as Fig. 2, invites more comprehensive theoretical treatments of motor enzyme dynamics. A realistic model must consider several further aspects. Here we used the usual assumption (8–11) that the force on the enzyme complex can be approximated by the mean force f exerted on the entire template, neglecting fluctuations in the instantaneous force felt by the leading segments at the reaction site. From the Rouse model (25), we estimate that force fluctuations may appreciably modulate the reaction barrier below f ∼ 5–10 pN but become less significant as f increases. Another important issue is whether the rate-limiting transition state actually occurs for the closed form of the enzyme or for some partially closed conformation. Likewise, structural constraints may prove significant even for the open configuration and for more than two segments. It may now be feasible to examine these questions by computer simulations (24, 29).
Our analysis reconciles the observed dependence of replication rate on tension (10, 11) with structural data (12–19) that indicate the rate-limiting conformational change converts only one template base (n = 1) from ss to ds geometry. In our view, the use of end-to-end extension curves to interpret the modulation of rate by tension, which indicated n = 2 or more (10, 11), is not valid. Those curves pertain to the entire template polymer and make no reference to the enzyme, whereas the reaction is governed chiefly by local properties in the neighborhood of the enzyme active site. The local model of Eqs. 3–5, although simplistic, serves to illustrate prospects for incorporating structural information on enzyme-DNA complexes in interpreting single-molecule kinetic experiments.
Acknowledgments
We have benefited from discussions of fluctuating barriers with Eugene Shakhnovich, fluctuating forces with Alexander Grosberg, and other instructive aspects with Martin Karplus and Sunney Xie. We appreciate useful correspondence with Carlos Bustamante and David Bensimon in response to a preliminary version of this paper. A.G. is grateful for support received from a Martinos Fellowship. T.E. acknowledges funding from the National Institute of General Medical Sciences (National Institutes of Health).
Abbreviations
- ss
single-stranded
- ds
double-stranded
- DNAp
DNA polymerase
- FJC
freely jointed polymer chain
Footnotes
The rate data, shown in Fig. 3, were obtained either by observing the change in extension of the DNA template as replication proceeded at constant tension (data of refs. 10 and 11 up to about 16–19 pN) or by measuring change in tension with the extension held constant (data of ref. 10 above 16 pN). The appropriate thermodynamic potential for a process at constant tension and temperature is the Gibbs free energy, and that for a process at constant extension and temperature is the Helmholtz free energy (21). Here we consider just the Gibbs free energy, as in ref. 10, in view of the large scatter of the data taken with fixed extension. The enthalpy, used in ref. 11, is the appropriate potential for constant tension and entropy; in principle, it is not applicable unless the process proceeded so rapidly as to be effectively isentropic (22, 23). Related literature (8) is likewise inconsistent in the usage of enthalpy and free energy.
If the end-to-end extensions (per residue) of ssDNA and dsDNA as functions of the applied force are denoted by xss(f) and xds(f), the change in Gibbs free energy in converting one ss residue to a ds residue is given by Δg(f) = gds(f) − gss(f) = −∫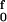 [xds(F) − xss(F)]dF (with −f analogous to pressure and x to volume). Integration by parts gives terms equivalent to those used for Δq = Δg = Δh − TΔs in ref. 10. The corresponding change in enthalpy is Δh(f) = f[xss(f) − xds(f)], equivalent to the expression used for Δq in ref. 11.
[xds(F) − xss(F)]dF (with −f analogous to pressure and x to volume). Integration by parts gives terms equivalent to those used for Δq = Δg = Δh − TΔs in ref. 10. The corresponding change in enthalpy is Δh(f) = f[xss(f) − xds(f)], equivalent to the expression used for Δq in ref. 11.
According to the Zimm Model (25), the longest and shortest relaxation times for a polymer chain can be estimated from τlongest = N3/2τshortest, where N is the number of Kuhn segments and τshortest = (3/π)1/2b3η/kBT, with b the Kuhn length (bss = 1.4 nm, bds = 100 nm) (5, 10, 21) and η the solvent viscosity (water, η = 0.01 g cm−1 sec−1). At room temperature, kBT = 4.1 pN nm. For the 10-kb template used for T7 DNAp in ref. 10 and the 11-kb template used for Klenow in ref. 11, τlongest ∼ 50 msec for dsDNA and ∼250 μsec for ssDNA. Similarly, for the 17-kb template used for Sequenase in ref. 11, τlongest ∼ 100 msec for dsDNA and 500 μsec for ssDNA. For a partially replicated template (say 50% dsDNA), this would mean that the longest relaxation times would be comparable to but not greatly exceed the reaction times (1/k0 ∼ 10–100 msec). The shortest relaxation time, τshortest, can be estimated as the relaxation time of one Kuhn segment. The timescale for fluctuations in the orientations of an individual segment of ssDNA, τshortest ∼ 0.7 nsec, much less than the reaction time (1/k0).
From the geometry depicted in Fig. 4, the pertinent angles are related by cos γ = cosα cosβ + sinα sinβ sinφ, where φ is the dihedral angle between the (a,f) and (b,f) planes. As the azimuthal orientation of the â and/or b̂ segments about the force direction are random, φ is uniformly distributed. Thus, 〈cosγ̂〉 = 〈cosα̂〉〈cosβ̂〉.
Results for both the free energy and enthalpy barriers are displayed in Fig. 3B to facilitate comparison with Fig. 3A. From the perspective of transition-state theory, the appropriate quantity is the Gibbs free energy of activation, Δg‡(f). Although in the Arrhenius equation the activation energy is given by the enthalpy of activation, Δh‡(f), the pre-exponential factor contains the entropy of activation, Δs‡(f). As illustrated in Fig. 3, whether evaluated from the force-extension curves or from our local model, both Δh‡(f) and Δs‡(f) vary strongly with tension. The FJC free energy variant of Eq. 3 has 〈wi(f)〉 → 〈Δgi‡(f)〉, Thus, 〈Δg1‡(f)〉 = ∫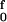 [Lss〈cosα〉 − Lds〈cosα̂〉]dF and 〈Δg2‡(f)〉 = ∫
[Lss〈cosα〉 − Lds〈cosα̂〉]dF and 〈Δg2‡(f)〉 = ∫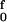 Lss[〈cosβ〉 − 〈cosβ̂〉]dF.
Lss[〈cosβ〉 − 〈cosβ̂〉]dF.
For the local contour lengths, we used Lss = 0.7 nm [consistent with structural data (12, 20) as well as stretching curves at high forces (10)] and Lds = 0.26 nm [pertaining to the A-form DNA (20) present within the enzyme complexes (12, 18) rather than 0.34 nm for the usual B-form assumed previously (10, 11)]. The uncertainty is about ±20% for Lss, ±10% for Lds. The appropriate Kuhn lengths (stiffness parameters) are more uncertain but less significant in Eq. 3. We used bss = 1.4 nm and bds = 100 nm, conventional values (21); varying these by ±50% produces only minor changes in the curves of Fig. 3b (as seen from Eqs. 4 and 5). Because bds extends over many residues, the value for the B form (5, 21) is suitable because the dsDNA is predominantly in that form, except for the short region (3 or 4 base pairs) in A form within the enzyme complex. The corresponding force scale factors are f̃ss = 2.9 pN and f̃ds = 0.04 pN. The contrast between our results with n = 1 and the previous work (10, 11) that inferred n > 1 does not stem from differences in parameters (e.g., our Ig curve is quite similar to the 1g curve in Fig. 3A). Rather, it shows that the local model of Eq. 3, with one base shrinking from ss to ds geometry and a second remaining ss but constrained by the enzyme, can give k(f)/k0 curves resembling Eq. 1 with n > 1. Carlos Bustamante (personal communication) has informed us that, despite the statement in ref. 10 that “closing the fingers organizes n adjacent sugar-phosphate units from single- to double-stranded geometry, n − 1 of which are released when the fingers reopen,” the definition was intended to mean that “the polymerase converts n bases from the ss end-to-end distance to the ds end-to-end distance,” without implying that the n bases are converted to double helix geometry. He disagrees with our contention that the use of global force-extension curves is not valid. David Bensimon (personal communication) still considers that his data imply that the enzyme “undergoes a conformational change against the stretch that is equivalent to a shortening of two to four bases going from ssDNA to dsDNA.” He also feels the use of Eq. 1 with global stretching curves is appropriate, but with Δq as the enthalpy difference rather than the free energy difference.
References
- 1.Ashkin A. Science. 1980;210:1081–1088. doi: 10.1126/science.210.4474.1081. [DOI] [PubMed] [Google Scholar]
- 2.Chu S. Science. 1991;253:861–866. doi: 10.1126/science.253.5022.861. [DOI] [PubMed] [Google Scholar]
- 3.Smith S B, Finzi L, Bustamante C. Science. 1992;258:1122–1126. doi: 10.1126/science.1439819. [DOI] [PubMed] [Google Scholar]
- 4.Perkins T, Smith D, Larson R, Chu S. Science. 1995;268:83–87. doi: 10.1126/science.7701345. [DOI] [PubMed] [Google Scholar]
- 5.Smith S B, Cui Y, Bustamante C. Science. 1996;271:795–799. doi: 10.1126/science.271.5250.795. [DOI] [PubMed] [Google Scholar]
- 6.Bustamante C, Marko J F, Siggia E D, Smith S B. Science. 1994;265:1599–1600. doi: 10.1126/science.8079175. [DOI] [PubMed] [Google Scholar]
- 7.Mehta A D, Rief M, Spudich J A, Smith D A, Simmons R M. Science. 1999;283:1689–1695. doi: 10.1126/science.283.5408.1689. [DOI] [PubMed] [Google Scholar]
- 8.Wang M D, Schnitzer M J, Yin H, Landick R, Gelles J, Block S M. Science. 1998;282:902–907. doi: 10.1126/science.282.5390.902. [DOI] [PubMed] [Google Scholar]
- 9.Davenport R J, White G J, Landick R, Bustamante C. Science. 2000;287:2497–2500. doi: 10.1126/science.287.5462.2497. [DOI] [PubMed] [Google Scholar]
- 10.Wuite G J L, Smith S B, Young M, Keller D, Bustamante C. Nature (London) 2000;404:103–106. doi: 10.1038/35003614. [DOI] [PubMed] [Google Scholar]
- 11.Maier B, Bensimon D, Croquette V. Proc Natl Acad Sci USA. 2000;97:12002–12007. doi: 10.1073/pnas.97.22.12002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Doublie S, Tabor S, Long A M, Richardson C C, Ellenberger T. Nature (London) 1998;391:251–258. doi: 10.1038/34593. [DOI] [PubMed] [Google Scholar]
- 13.Doublie S, Sawaya M R, Ellenberger T. Structure Folding Des. 1999;7:R31–R35. doi: 10.1016/S0969-2126(99)80017-3. [DOI] [PubMed] [Google Scholar]
- 14.Doublie S, Ellenberger T. Curr Opin Struct Biol. 1998;8:704–712. doi: 10.1016/s0959-440x(98)80089-4. [DOI] [PubMed] [Google Scholar]
- 15.Johnson K A. Annu Rev Biochem. 1993;62:685–713. doi: 10.1146/annurev.bi.62.070193.003345. [DOI] [PubMed] [Google Scholar]
- 16.Steitz T A. J Biol Chem. 1999;274:17395–17398. doi: 10.1074/jbc.274.25.17395. [DOI] [PubMed] [Google Scholar]
- 17.Kiefer J R, Mao C, Braman J C, Beese L S. Nature (London) 1998;391:304–307. doi: 10.1038/34693. [DOI] [PubMed] [Google Scholar]
- 18.Li Y, Korolev S, Waksman G. EMBO J. 1998;17:7514–7525. doi: 10.1093/emboj/17.24.7514. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Huang H, Chopra R, Verdine G L, Harrison S C. Science. 1998;282:1669–1675. doi: 10.1126/science.282.5394.1669. [DOI] [PubMed] [Google Scholar]
- 20.Saenger W. In: Principles of Nucleic Acid Structure. Cantor C R, editor. New York: Springer; 1984. [Google Scholar]
- 21.Rouzina I, Bloomfield V A. Biophys J. 2001;80:882–893. doi: 10.1016/S0006-3495(01)76067-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.McClare C W F. J Theor Biol. 1972;35:233–246. doi: 10.1016/0022-5193(72)90036-7. [DOI] [PubMed] [Google Scholar]
- 23.Blumenfeld L A, Tikhonov A N. Biophysical Thermodynamics of Intracellular Processes: Molecular Machines of the Living Cell. New York: Springer; 1994. [Google Scholar]
- 24.Karplus M. J Phys Chem B. 2000;104:11–27. [Google Scholar]
- 25.Grosberg A Y, Khokhlov A R. Statistical Physics of Macromolecules. College Park, MD: American Institute of Physics Press; 1994. [Google Scholar]
- 26.Smith D E, Chu S. Science. 1998;281:1335–1340. doi: 10.1126/science.281.5381.1335. [DOI] [PubMed] [Google Scholar]
- 27.Doering C R, Gadoua J C. Phys Rev Lett. 1992;69:2318–2321. doi: 10.1103/PhysRevLett.69.2318. [DOI] [PubMed] [Google Scholar]
- 28.Bueche F. Physical Properties of Polymers. New York: Interscience; 1962. [Google Scholar]
- 29.Cheatham T E, III, Kollman P A. Annu Rev Phys Chem. 2000;51:435–471. doi: 10.1146/annurev.physchem.51.1.435. [DOI] [PubMed] [Google Scholar]