Decoding myocardial Ca²⁺ signals across multiple spatial scales: a role for sensitivity analysis

Abstract

Numerous studies have employed mathematical modeling to quantitatively understand release of Ca²⁺ from the sarcoplasmic reticulum (SR) in heart. Models have been used to investigate physiologically important phenomena such as triggering of SR Ca²⁺ release by Ca²⁺ entry across the cell membrane and spontaneous leak of Ca²⁺ from the SR in quiescent heart cells. In this review we summarize studies that have modeled myocardial Ca²⁺ at different spatial scales: the sub-cellular level, the cellular level, and the multicellular level. We discuss each category of models from the standpoint of parameter sensitivity analysis, a common simulation procedure that can generate quantitative, comprehensive predictions about how changes in conditions influence model output. We propose that this is a useful perspective for conceptualizing models, in part because a sensitivity analysis requires the investigator to define the relevant parameters and model outputs. This procedure therefore helps to illustrate the capabilities and limitations of each model. We further suggest that in future studies, sensitivity analyses will aid in simplifying complex models and in suggesting experiments to differentiate between competing models built with different assumptions. We conclude with a discussion of unresolved questions that are likely to be addressed over the next several years.

1. Introduction

1.1 The multiscale nature of Ca²⁺ release in heart

In ventricular tissue, release of Ca²⁺ from the sarcoplasmic reticulum (SR) is important both physiologically and pathologically, as described in several contributions to this special issue. With each heart beat, entry of Ca²⁺ through L-type Ca²⁺ channels triggers the release of a larger amount of Ca²⁺ through ryanodine receptors (RyRs) in the SR membrane, a process known as Ca²⁺-induced Ca²⁺ release (CICR). The resulting increase in intracellular [Ca²⁺], called a Ca²⁺ transient, enables contraction. Under pathological conditions, however, spontaneous SR Ca²⁺ release can occur in the form of propagating intracellular Ca²⁺ waves. These events depolarize the cell membrane and can potentially initiate arrhythmias.

Mathematical models of cardiac Ca²⁺ release have generated important predictions that have subsequently been verified experimentally (see [1, 2] for recent reviews). Modeling cardiac Ca²⁺ release is challenging, however, because of the multiscale nature of this process. At the cellular level, for instance, movements of Ca²⁺ into and out of the cell, and between the cytosol and SR, can alter the quantity of released Ca²⁺ and modulate the strength of cellular contraction [3]. At a smaller spatial scale, however, each Ca²⁺ transient reflects the probabilistic triggering of thousands of individual events, Ca²⁺ sparks [4]. Sparks represent the stochastic gating of small clusters of RyRs, and these events are triggered by local [Ca²⁺] in the immediate vicinity of the RyRs rather than by average cellular [Ca²⁺]. To describe cellular Ca²⁺ transients in quantitative terms, then, one must understand the triggering of Ca²⁺ release at the sub-cellular level. At a spatial scale larger than the individual myocyte, electrical connections between cells must be considered to understand how changes in cellular CICR manifest themselves at the tissue and organ levels. The interactions between processes at these different spatial scales must be simulated to predict the physiological consequences of changes in Ca²⁺ release [5].

1.2 Challenges in integrating Ca²⁺ models across scales

In this review, we discuss mathematical models of cardiac Ca²⁺ signaling that have been developed at three spatial scales (Figure 1): (1) the sub-cellular level, at which RyR clusters produce Ca²⁺ sparks; (2) the cellular level, at which Ca²⁺ fluxes across the sarcolemmal and SR membranes produce cellular Ca²⁺ transients; and (3) the multicellular level, at which the sub-cellular and cellular level changes may alter muscle contraction and tissue electrical activity. The development of models at these three levels has largely proceeded independently. In recent years, however, effort has been made to integrate mathematical representations across the different spatial scales to produce more mechanistic models. Although this is a welcome development that will undoubtedly lead to more powerful and accurate models, it comes with drawbacks. First, models at larger spatial scales frequently simplify the representations of smaller-scale events. Sometimes, it is not clear how to relate the predictions of the larger scale, simplified model with those of the smaller scale, detailed model. Second, two models built by different groups may represent the same process, but with different underlying assumptions, and these may be equally successful at reproducing important physiological behaviors. In these cases it is generally not clear how to differentiate between the two representations. Finally, as models become increasingly multiscale and increasingly integrative, they also usually become larger, with additional parameters and state variables, and it is sometimes easy to lose track of which quantities should be considered important. We argue in this review that sensitivity analysis can play an important role in helping to address these concerns.

Figure 1. The multiscale nature of Ca²⁺ regulation in heart.

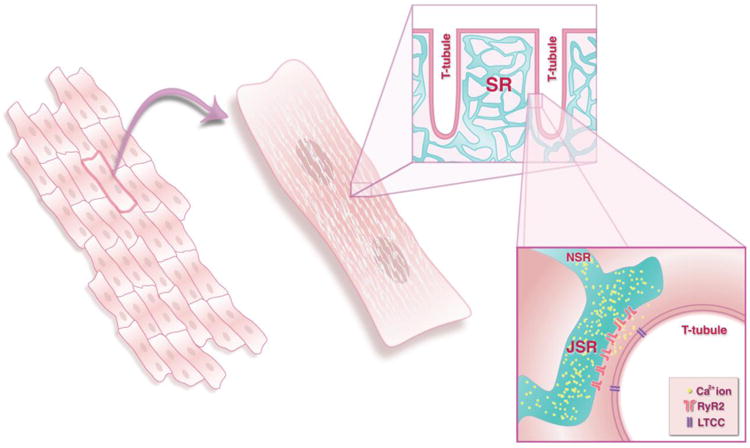
The figure illustrates schematically the different spatial scales at which the effects of cardiac SR Ca²⁺ release must be considered. Considerable research has been performed to investigate electrophysiology and Ca²⁺ release at the level of the individual cardiac myocyte (middle). The physiological effects of changes to cellular Ca²⁺ release, however, occur at the tissue level, when cells are connected to one another through gap junctions (left). At a smaller spatial scale, thousand of individual units of SR Ca²⁺ release, Ca²⁺ sparks, are triggered so-called Ca²⁺ release units (right). These are locations where junctional SR, containing clusters of RyRs, sits in close proximity to T-tubular membranes.

1.3 A role for parameter sensitivity analysis

Parameter sensitivity analysis is a valuable technique for probing and investigating mathematical models of physiological processes. Traditionally, sensitivity analyses are performed by systematically varying each parameter, running simulations, and recording in quantitative terms the effect on model output of each parameter alteration [6-8]. More recently, methods have been developed to compute parameter sensitivities by generating a population of models with variable properties, then using statistical methods to analyze the results generated by the population [9-13]. Regardless of the specific method that is employed, the value of this approach is that it generates a comprehensive set of predictions, potentially experimentally testable, indicating how changes in model parameters influence model outputs.

Here, we review modeling studies of cardiac Ca²⁺ signaling at different spatial scales, considering each category of models from the standpoint of sensitivity analyses that either have been performed or could be performed with the models. We argue that this is a useful perspective for conceptualizing and understanding models, for several reasons. First, sensitivity analyses provide a direct, quantitative comparison between parameters, and these comparisons allow investigators to assess the relative importance of various model parameters in determining physiologically-important outputs. Second, because these analyses generate comprehensive predictions, the approach can suggest straightforward experimental tests to differentiate between competing models that have different mechanistic assumptions. We believe that this strategy can help to address unresolved questions. Third, we highlight cases in which the same physiological process may be described by both a simple, phenomenological model with few parameters and a complex, mechanistic model with many parameters. Sensitivity analyses can help to relate one type of model with the other, thereby providing guidance in how to simplify models when this is required.

Fourth, the most important benefit of sensitivity analysis is obvious but easily overlooked: namely, the process of performing the analysis requires the investigator to define what he or she considers the relevant parameters and the pertinent model outputs. Even with relatively simple models, these choices may not always be apparent. For instance, if a model calculates intracellular [Ca²⁺] as a function of time, this does not indicate which aspects of the Ca²⁺ signal are considered most important: amplitude, frequency, time to peak, decay time, changes with different experimental conditions? As models become increasingly complex and integrative, these questions become more challenging, and therefore more important to define. Once the important parameters and outputs have been identified, however, sensitivity analysis allows for a more sophisticated, higher-level means of conceptualizing a mathematical model (Fig. 2). By itself, a mathematical model may be viewed as simply a machine that converts a set of equations into simulated results (Fig. 2A). Although the output may be experimentally measurable and/or biologically meaningful, the insight that can be gained by a single simulation is rather limited. After a sensitivity analysis is performed, however, the model can be conceptualized as a tool that maps changes in model parameters to changes in model outputs (Fig. 2B). In other words, the model can now predict phenotypes from molecular level changes.

Figure 2. The novel viewpoint provided by sensitivity analysis.

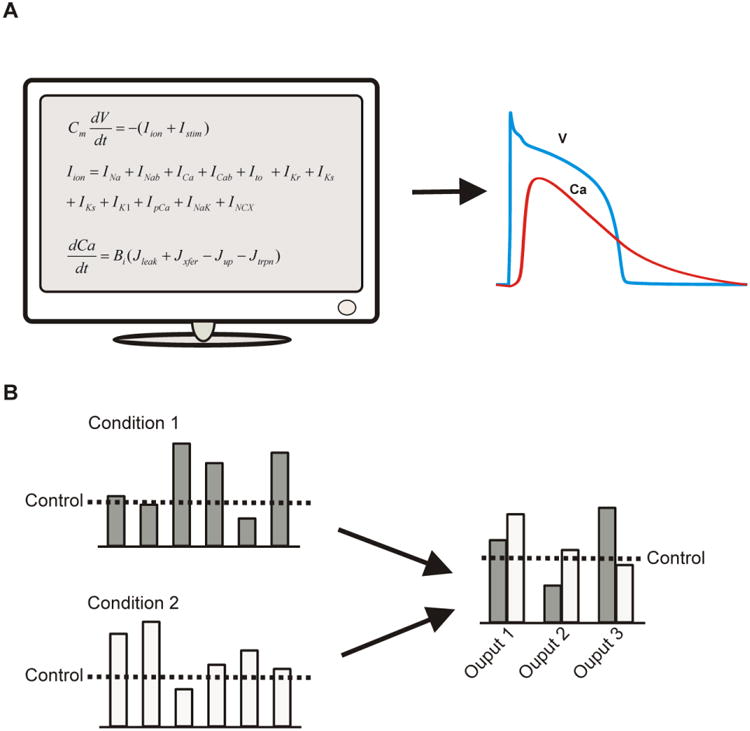
(A) A simulation may be conceived as simply a transformation from a set of equations into meaningful output, such as cellular transmembrane potential (V) and cytosolic Ca²⁺ concentration. The questions of greater interest, however, often concern the predicted changes in physiological outputs due to alterations caused by drugs or disease states. These questions generally cannot be addressed by the model equations themselves, but they can be addressed by systematically perturbing the model, i.e. performing a sensitivity analysis. (B) Once this has been performed, the investigator has a higher-level viewpoint of the model. It can now be seen as transforming changes in model parameters into altered physiological phenotypes.

2. A review of recent and historically-important studies

We discuss how sensitivity analysis can be helpful for understanding mathematical models of cardiac Ca²⁺ signaling at different spatial scales, and we propose that these methods can help to resolve controversies and to assist in integrating models across scales. We focus on models of Ca²⁺ movements and Ca²⁺ release at three levels: (1) sub-cellular models of Ca²⁺ sparks and Ca²⁺ movements within microdomains; (2) cellular models of beat-to-beat regulation and Ca²⁺ cycling within the cardiac myocyte; and (3) multicellular models that explore how cellular Ca²⁺ regulation affects tissue-level physiology.

2.1 Studies at the sub-cellular level

Studies at the microscopic, or sub-cellular, level can be grouped into two general categories. In the first, a number of studies have examined how sub-cellular geometric details influence movements and concentrations of [Ca²⁺] in cellular microdomains [14-21]. These investigations use ordinary differential equations (ODEs) and partial differential equations (PDEs), respectively, to simulate binding of Ca²⁺ to intracellular buffers and diffusion of Ca²⁺ within cellular compartments. Many of these studies have also examined how processes such as binding of Ca²⁺ to fluorescent indicators, indicator diffusion, and blurring by imaging instrumentation influence the properties of measurable Ca²⁺ signals such as Ca²⁺ sparks [22-25]. These models may incorporate subtle geometric details, but Ca²⁺ fluxes through membrane channels or RyRs are generally simulated in a simplified manner. In many models, for instance, RyRs are assumed to open for a fixed period of time [16, 19, 22, 23].

A recent study by Hake et al illustrates the state of the art in this category [25]. These investigators used electron tomography images to build a three-dimensional model of a cardiac release unit, or couplon. The model included spatially realistic representations of transverse tubules, junctional SR, and network SR, as these structures in the model were obtained directly from the electron tomography images. Because these investigators simulated movements of Ca²⁺ in both the myoplasm and the SR, the model could provide inferences about both Ca²⁺ sparks and local SR depletion signals, so-called Ca²⁺ blinks [26]. Two important predictions of this study were: (1) the apparent local SR depletion implied by the Ca²⁺ blink signal can be considerably less than the true depletion, and (2) the distribution of calsequestrin within the SR can significantly affect the time-to-nadir of the Ca²⁺ blink.

The second category consists of models that simulate stochastic gating of RyRs to predict the probabilistic triggering and termination of Ca²⁺ sparks [27-34]. This category originated with the seminal work of Stern [27], who used Monte-Carlo simulations demonstrate the feasibility of his hypothesis that Ca²⁺ release in heart cells was triggered by local increases in [Ca²⁺] rather than by average cytosolic [Ca²⁺]. Subsequent studies have used these models to examine phenomena such as termination of Ca²⁺ sparks [30], the importance of allosteric interactions between RyRs [28, 32, 33], the functional consequences of local depletion of JSR [Ca²⁺] [30, 31], and the mechanisms controlling refractoriness of RyR clusters after Ca²⁺ sparks [34]. These models include schemes representing the details of RyR gating, but they generally use simplified representations of the sub-cellular geometry. For instance, the sub-space between sarcolemmal and SR membranes is frequently assumed to be a single, well-mixed compartment.

We can understand the differences between the two categories of models by considering the type of parameter sensitivity analysis one might perform in either. In the first category, the relevant input parameters would be physical and geometrical variables such as subspace dimensions, diffusion constants for both Ca²⁺ and indicator, plus the abundances, locations, and affinities of intracellular Ca²⁺ buffers. In models that explicitly simulate Ca²⁺ spark formation, the relevant outputs would be quantities such as Ca²⁺ spark amplitude, duration, and width. In the second category, the parameters considered in an analysis would include additional variables such as the number of RyRs per cluster, the permeability of each RyR, and rate constants that describe RyR gating. Because these models are stochastic, the outputs could include probabilistic variables such as the frequency of spontaneous sparks or the probability that a particular trigger (e.g. L-type channel or RyR opening) will induce a spark. In general, one is also interested in quantities that reflect the characteristics of local SR Ca²⁺ release, such as release duration, the amount of Ca²⁺ released per event, and the extent of local JSR depletion. However, since most of these models do not explicitly simulate the processes of spark formation and detection, these outputs do not necessarily correspond to experimentally-measurable variables.

In a recent study, we attempted to both bridge the divide between the two categories of models and to analyze a Ca²⁺ spark model comprehensively [35]. We performed Monte-Carlo simulations with a stochastic model that simulates the random opening and closing of RyRs as Ca²⁺ sparks are triggered and terminate [30, 34], then coupled the results of these simulations to a model of buffering and diffusion that converts a local SR Ca²⁺ release flux into a measurable Ca²⁺ spark [22]. The geometry was idealized, however, as spherically-symmetric diffusion was assumed. We analyzed parameter sensitivities in this model using recently-developed techniques [9, 13]. This process involved generating a population of models with random parameters, running a single simulation with each parameter set, and using statistical regression methods to relate the random parameters to the model outputs. Ca²⁺ spark amplitude and duration were analyzed with multivariable linear regression whereas logistic regression was used to analyze the probability that a single RyR opening triggered a spark. Interestingly, spark amplitude and duration depended on physical and structural parameters such as the JSR volume and the quantity of calsequestrin in the JSR whereas triggering probability depended also on RyR gating parameters. Importantly, in this study [35] predictions of the sensitivity analysis were tested experimentally by measuring Ca²⁺ sparks in cells from genetically-modified mice [36], and the data were found to be consistent with the model predictions.

The results of these recent studies suggest unresolved questions that can be addressed through modeling studies at the Ca²⁺ spark level over the next few years. First, it will be important to continue to integrate spatially-detailed deterministic models with spatially-simplified stochastic models. In this way the models can provide insight into both the factors that control probabilistic triggering of Ca²⁺ sparks and the variables that affect the measurable signals. Thorough parameter sensitivity analyses will allow investigators to directly compare the quantitative effects of changes in RyR gating versus changes in structural quantities. Second, it is important to note that many of the models cited above were built using different assumptions about the underlying mechanisms. For instance, some models postulate an important role for Ca²⁺-dependent inactivation of RyRs in terminating local Ca²⁺ release [28, 33, 37], whereas others do not [30, 34]. At present, most experimental data support the view that termination occurs because of local depletion of JSR [Ca²⁺] rather than Ca²⁺-dependent inactivation [34, 38-40] (reviewed in [41, 42]). Studies that use parameter sensitivity analysis to compare competing models, however, may suggest new experiments that can differentiate between models and potentially uncover a role for inactivation. Third, it will be important to correlate behaviors observed at the Ca²⁺ spark level with cellular-level phenomena such as Ca²⁺ transients and SR Ca²⁺ leak. The next section discusses several recent studies that have initiated these efforts.

2.2 Studies at the cellular level

Mathematical modeling of cardiac cellular physiology has a long history, beginning with the groundbreaking work of Noble [43]. The development of this field has been documented recently in excellent reviews [44-46], and we will not attempt to repeat that effort here. Instead we will discuss selected studies that have focused more specifically on regulation of Ca²⁺ release from the SR. We focus on simulations of triggered cellular Ca²⁺ transients and spontaneous SR Ca²⁺ leak rather than simulations of spontaneous Ca²⁺ waves. Waves have been modeled in many studies [47-50], but these are discussed more fully in another contribution to this special issue [51]. In our discussion of cellular Ca²⁺ transients and SR Ca²⁺ leak, we aim to illustrate the challenges involved in integrating sub-cellular and cellular level models and to highlight the potentially important role of sensitivity analysis for understanding the similarities and differences between alternative mathematical representations.

Given that the importance of Ca²⁺ sparks has been appreciated for several years, one might expect that stochastic spark triggering would be included in all cellular models. In fact, however, for historical and practical reasons, most cellular models have lumped CICR into a few ODEs. Historically, since the development of cellular models predated the discovery of Ca²⁺ sparks, it originally made sense to model CICR with the lumped rate constants that had already proved valuable for simulating membrane ionic currents. Moreover, as a practical matter, the stochastic nature of Ca²⁺ spark triggering makes it difficult and computationally expensive to embed stochastic simulations within cellular models, which usually consist of between 10 and 50 ODEs. As a result, mathematical models of Ca²⁺ release at the cellular level can be grouped into two categories: (1) models that attempt to represent CICR with a few ODEs, and (2) more recently, models that explicitly incorporate the stochastic triggering of Ca²⁺ sparks. It is useful to contrast the two types of models from the standpoint of parameter sensitivity analysis. This illustrates the challenges involved in relating predictions of the two types of models and in developing simplified representations of CICR that are appropriate for incorporation into tissue-level and organ-level models.

Cellular models that lump CICR into a few ODEs have a difficult time reproducing the phenomenon of “graded release,” the well-established experimental result that CICR does not exhibit a threshold. Instead, small changes in the L-type Ca²⁺ current trigger produce small changes in the quantity of released Ca²⁺ [52, 53]. Cellular models in this category either produce all-or-none release [54], introduce non-physiological corrections, such as CICR that depends explicitly on L-type current rather than on local [Ca²⁺] [55, 56], or they must tune parameters carefully to reproduce graded release [57]. Despite this limitation, these lumped cellular models have been valuable for understanding phenomena such as changes in Ca²⁺ transient amplitude with pacing rate [54], altered Ca²⁺ transients and action potentials resulting from heart failure [58, 59], and the development at rapid pacing rates of alternans, or Ca²⁺ transients that alternate in magnitude from one beat to the next [60, 61]. From the standpoint of sensitivity analysis, the inputs that can be tested with these cellular models include parameters controlling the magnitude of cellular L-type Ca²⁺ current, maximal activities of Na⁺-Ca²⁺ exchangers and SERCA pumps, and the lumped parameters that control RyR permeability and gating. Relevant simulation outputs include not only Ca²⁺ transient amplitude at a particular rate, but also the change in amplitude with pacing rate, plus measurable quantities such as diastolic [Ca²⁺] and SR Ca²⁺ content.

In the second category are mathematical models of cells that explicitly simulate the stochastic triggering of Ca²⁺ sparks. The randomness inherent in spark triggering and termination, however, makes this a daunting computational challenge. The first study to simulate both stochastic spark triggering and cellular action potentials (APs) was published by Greenstein and Winslow in 2002 [62]. Several studies published more recently have used either elegant algorithms [63-68], or improvements in computational power [69-74], to develop new models. The biological questions that can be asked with these models, however, are somewhat different from those that can be addressed with the lumped models. For instance, in lumped models leak of Ca²⁺ from the SR is merely a passive flux that is included to balance SERCA pump activity at rest. In these newer models, however, SR Ca²⁺ leak via stochastic gating of RyRs is simulated explicitly. Several studies published in the past few years have computed leak in a resting myocyte as a function of SR [Ca²⁺] and have used the simulations to quantify the relative importance of visible leak in the form of Ca²⁺ sparks, versus “invisible” leak that would be difficult to detect with standard recording techniques [68, 70, 73, 74]. Sensitivity analyses with these newer models can therefore consider additional model outputs, such as the resting spark rate or the number of Ca²⁺ sparks triggered by specific voltage-clamp depolarizations. Parameters analyzed can include the explicit RyR gating rate constants, the number of RyRs per cluster, and geometrical parameters such as the volume of each sub-space or the average distances between RyRs and L-type channels.

Unresolved questions that can be addressed with cellular models include the following. First and most fundamentally, how can we relate the lumped RyR gating rate constants in the simplified models to the parameters of the Ca²⁺ spark triggering models? Despite recent advances in computing power, particularly the advent of graphical processing units (GPUs), there remains a need for simplified representations of CICR for use in tissue level models. We propose that if explicit Ca²⁺ spark triggering models and lumped models are subjected to sensitivity analyses with identical protocols, this comparison will help to illustrate the strengths and weaknesses of the various lumped representation.

Second, sensitivity analyses can help to potentially identify a role for Ca²⁺-dependent inactivation of the RyR. Although evidence strongly suggests that Ca²⁺ dependent inactivation does not terminate Ca²⁺ release on a millisecond time scale (see [41, 42] for a reviews of relevant studies), these results do not rule out a role for inactivation over a time scale of seconds to minutes. A comparison of models built with different assumptions may suggest experiments to demonstrate such a role. Third, sensitivity analyses will be required to determine the quantitative contributions of different changes during disease states such as heart failure. For instance, how important are structural changes such as T-tubule derangement [75-77] compared with changes in SERCA and Na⁺-Ca²⁺ exchange function? Sensitivity analyses performed on cellular models will help to address such questions.

2.3 Studies at the multicellular level

Although studies at the sub-cellular and cellular levels provide critical quantitative data, the physiological effects of myocyte Ca²⁺ signaling occur when cells are embedded within an intact organ. Modeling studies must therefore consider how sub-cellular and cellular phenomena are translated into tissue-level behaviors. Cardiac tissue-level and organ-level modeling has a long history that has been discussed in recent reviews [78, 79], but most studies have focused on how changes in membrane ionic currents influence electrical and mechanical activity at a larger scale. Comparatively less research has been performed to understand the tissue-level consequences of cellular Ca²⁺ release. An example of sub-cellular Ca²⁺ release influencing electrical behavior at the tissue level is the phenomenon known as “alternans,” beat-to-beat alternation in Ca²⁺ transient or AP characteristics [80-82]. However, since this topic is covered in another contribution to this special issue [83], we do not discuss these important studies in detail. Instead we review recent work that has examined a relevant question: what factors determine whether spontaneous Ca²⁺ release in a group of cells initiates a propagating AP in tissue? By examining the studies that have looked at these questions we can appreciate the model simplifications that have been employed to allow for multicellular simulations, and thereby understand the challenges that must be overcome to make multiscale modeling truly mechanistic.

At the cellular level it is well-established that spontaneous Ca²⁺ release from the SR, in the form of a propagating Ca²⁺ wave, can trigger membrane depolarization. A fraction of released Ca²⁺ is extruded from the cell by the Na⁺-Ca²⁺ exchanger, which depolarizes the membrane as it removes Ca²⁺. In tissue, however, cells are electrically connected to one another through gap junctions. Any depolarizing current in a cell will spread to its neighbors, thereby blunting the current's depolarizing effect. Thus, whether or not a Ca²⁺ wave induces an AP depends on tissue characteristics in addition to the Ca²⁺ release event itself.

In an important recent modeling study [84], Xie et al asked the question: how many myocytes must spontaneously release Ca²⁺ simultaneously for a propagating AP to be induced? In one, two, and three-dimensional ventricular models, these investigators simulated spontaneous release in a group of cells by imposing a release flux (J_spon), then quantifying how many cells needed to receive J_spon simultaneously for the event to induce a propagating AP. The results showed that the critical number of cells (N_critical) was considerably greater in multidimensional tissue than in unidimensional tissue because depolarizing current in multidimensional tissue can spread in several directions. Moreover, N_critical depended not only on the magnitude and timing of J_spon, but also on factors such as the strength of electrical coupling between adjacent myocytes, the presence of fibroblasts between myocytes, and the electrical remodeling that occurs during heart failure. More recently, Chen et al examined the same question in a simplified model that did not include explicit ionic currents and treated AP initiation as a threshold phenomenon [85]. The advantage of this simplified representation, however, is that it allowed the authors the authors to derive analytical expressions for the expected waiting time until the occurrence of a spontaneous, potentially arrhythmogenic AP in tissue. These expressions allow for a straightforward understanding of which factors promote, and which suppress, the development of spontaneous propagating APs.

It is useful to consider the parameter sensitivity analyses that could be performed with model presented by Xie et al [84], as this illustrates the hurdles that must be surmounted to mechanistically integrate such a tissue level model with cellular and subcellular models. The primary output in such an analysis would be N_critical, the required number of cells with spontaneous Ca²⁺ release to induce a propagating AP. The potentially important parameters would include the magnitude and kinetics of J_spon, expression of Na⁺-Ca²⁺ exchangers, the inward rectifier conductance (G_K1), the strength of electrical coupling between myocytes, the degree of electrical anisotropy, and coupling between myocytes and fibroblasts. This analysis could therefore provide a quantitative comparison of the relative importance of Ca²⁺ release itself, ionic currents, and structural features of the tissue. It is important to note, however, that in these simulations J_spon was imposed on a group of myocytes, whereas in real cells Ca²⁺ waves originate stochastically when spontaneous Ca²⁺ sparks trigger additional sparks (see review in this special issue [51]). At present, then, the tissue-level simulations cannot directly provide insight into the importance of factors such as changes in RyR gating, the number of RyRs per cluster, spacing between RyR clusters, and the SR Ca²⁺ load. The tissue-level models must be integrated with cellular and sub-cellular models in order for the simulations to provide a comparison of the relative importance of the different parameters. Once these integrative models are developed, sensitivity analyses with these models can address important unresolved questions concerning potential anti-arrhythmic targets. For instance, if the goal is to prevent spontaneous propagating APs, is it better to target sub-cellular characteristics of RyR clusters, cellular ionic currents such as L-type channels, or tissue level structural parameters? Equally important, can sensitivity analyses identify targets that inhibit spontaneous APs without causing undesirable effects that may be pro-arrhythmic, such as a decrease in propagation velocity?

3. Current and future challenges

To conclude, we briefly describe some challenges in cardiac Ca²⁺ modeling that will be encountered by researchers over the next several years. In these areas we believe sensitivity analysis will play an important role in helping to address unresolved questions.

3.1 Integrative models of CICR and additional cellular processes

At the cellular and subcellular scales, a recent trend has been the development of integrative models that simulate both SR Ca²⁺ release and additional Ca²⁺-dependent cellular processes. This development provides exciting new opportunities, since the integrated models allow for quantitative predictions regarding mechanisms and phenomena that could not previously be simulated. As these models become increasingly complex, however, we believe that sensitivity analyses will be required to define the scope and capabilities of each model.

Mitochondrial respiration is a vital cellular process that is Ca²⁺ dependent and closely linked to SR Ca²⁺ release. The rate of ATP production has long been known to depend on mitochondrial [Ca²⁺], and experimental studies have established that these organelles take up and extrude Ca²⁺, although the magnitude and kinetics of changes in mitochondrial [Ca²⁺] remain controversial [86]. In addition, structural studies demonstrate that mitochondria tend to be located in close proximity to Ca²⁺ release units [87], which implies that interactions between SR release and mitochondria take place within local microdomains rather than in the bulk cytoplasm. Several published models simulate the Ca²⁺-dependence of mitochondrial bioenergetics [88, 89]. In these models, important outputs are measures of mitochondrial function such as ATP production, oxygen consumption, or mitochondrial membrane potential. The relevant inputs include both enzyme activities and variables describing Ca²⁺ transport pathways across the mitochondrial membranes, such as the Ca²⁺ uniporter and the mitochondrial Na⁺-Ca²⁺ exchanger. In these models, however, changes in cytosolic Ca²⁺ were simulated separately and imposed on the mitochondrial models as an input [88, 89]. More recently, integrative models have been developed that simulate SR Ca²⁺ release and mitochondrial function together within the same computational framework [90]. From a sensitivity analysis standpoint, then, one can examine how changes in L-type Ca²⁺ current or SR Ca²⁺ uptake can influence outputs such as oxygen consumption or ATP production. Conversely, one can also investigate how changes in mitochondrial respiration might affect cellular Ca²⁺ transients. These models, however, have to date used lumped representations of cellular Ca²⁺ release [54]. To understand more fully how released Ca²⁺ interacts with mitochondria in microdomains, the mitochondrial models must be integrated with stochastic models of SR Ca²⁺ release at the level of the Ca²⁺ spark. Once these models are built, sensitivity analyses can investigate the relative importance for mitochondrial function of cellular Ca²⁺ fluxes versus sub-cellular changes in RyR function or release unit structure. In addition, as pathways for mitochondrial Ca²⁺ entry and efflux become more clearly defined [91], sensitivity analyses of models can be used to predict the quantitative prominence of the different pathways.

A second opportunity for integration is the development of models that simulate both SR Ca²⁺ release, occurring on a millisecond time scale, and activation of biochemical signaling pathways, which occurs on a time scale of seconds to minutes. Important early work by Saucerman et al investigated how stimulation of β-adrenergic receptors affected the characteristics of Ca²⁺ release [92]. These models, however, were largely unidirectional, since β-adrenergic stimulation influenced myocyte Ca²⁺ transport, but Ca²⁺ had only minimal effects on the biochemical signaling. More recent models have examined pathways that are more explicitly Ca²⁺-dependent, such as CaMKII (Ca²⁺/calmodulin-dependent protein kinase) and calcineurin [70, 93, 94]. These models can be bidirectional, since Ca²⁺ influences the biochemical reactions, and the signaling proteins phosphorylate or dephosphorylate targets that affect Ca²⁺ cycling. Sensitivity analyses on such integrative models can therefore consider as inputs both variables controlling Ca²⁺ transport pathways and variables describing enzyme abundances and activities. Outputs can include not only cellular Ca²⁺ transients, but also measurable biochemical signals such as phosphorylated CaMKII. These analyses can help to address questions that have to date remained unresolved. For instance, activated CaMKII phosphorylates multiple targets that can influence Ca²⁺ cycling. What is the quantitative importance of each of these targets in determining myocyte Ca²⁺ regulation and electrophysiology? Similarly, analyzes with these models can address whether enzyme abundances, enzyme affinities, or quantities of Ca²⁺ transport proteins are most important in determining readouts of myocyte physiology such as Ca²⁺ transients. Finally, as signaling models become more closely integrated with sub-cellular models of Ca²⁺ sparks, the importance of enzyme localization, which has been addressed in a few studies [94, 95], can be explored more systematically.

3.2 Scaling from the tissue level to the organ level

Above we have highlighted the challenges in integrating models of CICR from the Ca²⁺ spark level to the multicellular level. These challenges become even more acute when cellular models are embedded in models of the whole organ. Although it is now possible, with advances in computing power, to simulate stochastic SR Ca²⁺ release in a model comprising several cells, simplified representations of CICR will continue to be required for organ-level simulations. Sensitivity analyses that compare mechanistic with simplified representations at the cellular level will play an important role by helping to define which simplified representations generate the most realistic output, not only under baseline conditions, but also under conditions simulating pathology. Moreover, as organ-level models become further developed sensitivity analyses of these models can be used to predict the relative importance of cellular CICR characteristics versus structural features such as muscle mechanics and fiber directions in determining physiological outputs such as ejection fraction.

3.3 Conclusions

In this review we have discussed mathematical models of Ca²⁺ regulation in heart, and we have highlighted the challenges presented by the multiscale nature of this process. The majority of modeling studies published to date have focused on Ca²⁺ signaling at a particular spatial scale, but lately efforts have been made to both integrate across spatial scales and to combine CICR models with representations of other cellular processes. Besides the mathematical and computational challenges posed by this process of integration, this increase in complexity makes it more difficult to understand the relevant inputs and outputs of each model. As the field moves forward, parameter sensitivity analysis is likely to play an important role in helping to: (1) define the capabilities and limitations of each model; (2) predict the relative importance of different factors in determining physiological responses; (3) generate predictions that can be tested experimentally to discriminate between alternative models.