Accuracy of computerized automatic identification of cephalometric landmarks by a designed software

Abstract

Objectives

The purpose of this study was to design software for localization of cephalometric landmarks and to evaluate its accuracy in finding landmarks.

Methods

40 digital cephalometric radiographs were randomly selected. 16 landmarks which were important in most cephalometric analyses were chosen to be identified. Three expert orthodontists manually identified landmarks twice. The mean of two measurements of each landmark was defined as the baseline landmark. The computer was then able to compare the automatic system's estimate of a landmark with the baseline landmark. The software was designed using Delphi and Matlab programming languages. The techniques were template matching, edge enhancement and some accessory techniques.

Results

The total mean error between manually identified and automatically identified landmarks was 2.59 mm. 12.5% of landmarks had mean errors less than 1 mm. 43.75% of landmarks had mean errors less than 2 mm. The mean errors of all landmarks except the anterior nasal spine were less than 4 mm.

Conclusions

This software had significant accuracy for localization of cephalometric landmarks and could be used in future applications. It seems that the accuracy obtained with the software which was developed in this study is better than previous automated systems that have used model-based and knowledge-based approaches.

Introduction

Cephalometric analysis, the measurement of the dimensions and relations of the jaw and teeth, is a vital tool used for describing morphology, diagnosing anomalies, forecasting future relationships, planning treatments, and evaluating growth and treatment results.¹

Three approaches may be used to perform a cephalometric analysis: a full manual approach, a computer-aided approach and an automatic approach. The manual approach is the oldest and most widely used. The computer-aided or digital method uses manual identification of landmarks for computer-aided analysis. In the automatic approach the computer also helps to find the landmarks.²

Errors in cephalometric analysis are usually systematic or random errors.² Systematic errors can arise when obtaining cephalograms if the geometry of the system varies and no compensation is made.³ Random errors involve tracing, landmark identification and measurement errors.²

The greatest source of random errors is difficulty in identifying a particular landmark or imprecision in its definition.³ Savage et al⁴ determined that variability in landmark identification was five times greater than measurement variability. This source of random error exists in both manual and computer-aided approaches. These two methods are also time consuming, although to a different extent.²

Therefore, there have been efforts to automate cephalometric analysis with the aim of reducing the time required to obtain an analysis, improving the accuracy of landmark identification and reducing the errors due to clinicians' subjectivity. Most of these efforts were initially meant for research only, but automatic methods may become increasingly available for clinical purposes.²

Different approaches to design software for locating cephalometric landmarks can be classified into four categories: (1) knowledge-based approaches; (2) model-based approaches; (3) soft-computing approaches; (4) hybrid approaches.²

Early works usually located landmarks based on knowledge-based approaches, using edge detection and image-processing techniques.^5-8 In edge detection techniques, the edges of the image are extracted, then the edge that contains the selected point is traced to locate the landmark. This method is the fastest for finding landmarks which are on the extractable edges of the image according to definition.

The most recent study using a knowledge-based approach was that of Forsyth and Davis,⁸ in which 19 landmarks were selected to be identified on 10 cephalograms. 73% of landmarks were located within approximately 1 mm. The mean error of 7 landmarks was more than 1 mm (but how much more than 1 mm was not mentioned), with 12 landmarks less than 1 mm.

The shortcoming of knowledge-based methods is that their performance is greatly correlated with the quality of input images. In addition, not all landmarks are situated on significant contour edges.⁹ To solve the problems mentioned above, much attention has been paid to model-based approaches.^10-14 The aim of these approaches is to find a locality in image A (testing image) which is most similar to image B (reference image). This method is mostly useful for a group of cephalometric landmarks which have definite and describable structures surrounding them.

In the study by Hutton et al,¹² 16 landmarks were chosen to be identified. 63 pre-treatment cephalograms were landmarked once on a computer by one expert orthodontist to provide a gold standard for evaluating the performance of the software. The porion was the least accurately located landmark (7.3 mm error), and point B was the most precisely located landmark (2.6 mm error).

Kafieh et al¹⁴ implemented 63 cephalograms which were collected by Hutton et al¹² to locate the same 16 landmarks. On average 24% of the 16 landmarks were within 1 mm of the correct co-ordinates, 61% within 2 mm, and 93% within 5 mm.

Soft computing is a new multidisciplinary field that has been proposed by Lotfi Zadeh.¹⁵ The main goal of soft computing is to develop intelligent machines and to solve non-linear and mathematically unmodelled system problems. The applications of soft computing proved two main advantages. First, solving non-linear problems is possible. Second, human knowledges such as cognition, recognition, understanding, learning and others, as introduced into the field of computing. This resulted in the possibility of constructing intelligent systems such as automated design systems.

Neural networks and support vector machines are components of soft computing.^16-19

In the study of Leonardi et al,¹⁹ ten landmarks were the target for identification. Differences in the mean errors of automatic and manual landmarking differences were very small (mean error = 0.21 mm), and they were found at most within a 0.59 mm error.

In some research a combination of previously described approaches has been used (hybrid approach).^9,20,21

In the study of Giordano et al,²¹ 8 landmarks on a set of 26 cephalograms were identified on the basis of cellular neural networks and knowledge-based extraction. The cephalograms were landmarked by an expert orthodontist as a reference. 85% of landmarks were located within a 2 mm error and 73% within a 1 mm error and the mean error was reported to be 1.07 mm.

In the study of Yue et al⁹ a hybrid approach was proposed to locate 12 selected landmarks. The proposed method was tested on 86 radiographic images.

According to the clinical requirement, Yue et al⁹ stated, “If the difference between the location of a feature point obtained by an automatic approach and the standard is less than 2 mm, the result is considered to be correct; if less than 4 mm, it is acceptable. If the rate of unacceptable feature points on an image is more than 20%, the failure of the approach on this image is declared.”

In their study the average rates of the correct and acceptable localization were evaluated to be 71% and 88% respectively.

According to what was stated above, in most previous studies either the software was not accurate enough for identification of landmarks or there were not enough landmarks identified for performing a cephalometric analysis. In this study we tried to design an applicable software for clinical utilization.

Materials and methods

40 digital cephalometric radiographs which had been taken at a private oral and craniofacial radiology centre were used in this study. The radiographs were randomly selected from an archive of more than 200 cephalograms. The randomization technique was accomplished by a table of random numbers. The number which was selected from the table showed the cephalogram's code which should be selected from the archive. This process of selection was continued until 40 cephalograms were selected.

The inclusion criteria were cephalograms of patients pre-treatment, post-treatment and during orthodontic treatment. Also cephalograms of patients with surgical rigid fixations, orthodontic appliances, cervical collar and obvious malposition of the head in the cephalostat were included. Some of the patients had mixed dentition with posterior teeth not in maximum intercuspation. Patients' sex, age, racial group, type of occlusion and skeletal pattern were not considered. We did not assign any exclusion criteria.

A Planmeca (Prolin XC) X-ray unit (Planmeca OY, Helsinki, Finland) with a maximum 80 kVp was used to produce digital images (computed radiography) of the cephalometric radiographs. The size of cephalograms was 2016×2696 pixels. The images were greyscaled with 8 bits per pixel. The pixel size in the cephalograms was approximately 0.26 mm and the resolution was 96 dpi.

16 landmarks were identified: A point (A), anterior nasal spine (ANS), B point (B), gnathion (Gn), gonion (Go), the apex of the lower first incisor (L1A), the tip of the lower first incisor (L1T), menton (Me), nasion (N), orbitale (Or), porion (Po), pogonion (Pog), posterior nasal spine (PNS), sella (S), the apex of the upper first incisor (U1A) and the tip of the upper first incisor (U1T) (Table 1). These landmarks were the ones most used in common analyses.²²

Table 1. Definition of landmarks.

Name	Abbreviation	Definitiona
A point	A	The most posterior midline point in the concavity between ANS and the most inferior point on the alveolar bone overlying the maxillary incisors
Anterior nasal spine	ANS	The anterior tip of the sharp bony process of the maxilla at the lower margin of the anterior nasal opening
B point	B	The most posterior midline point in the concavity of the mandible between the most superior point on the alveolar bone overlying the mandibular incisors and Pog
Gnathion	Gn	A point located by taking the midpoint between the anterior (pogonion) and inferior (menton) points of the bony chin
Gonion	Go	A point on the curvature of the angle of the mandible located by bisecting the angle formed by lines tangent to the posterior ramus and the inferior border of the mandible
Apex of lower first incisor	L1A	The apex of the lower first incisor
Tip of lower first incisor	L1T	The tip of the lower first incisor
Menton	Me	The lowest point on the symphyseal shadow of the mandible seen on a lateral cephalogram
Nasion	N	The most anterior point in the frontonasal suture in the mid-sagittal plane
Orbitale	Or	The lowest point on the inferior rim of the orbit
Porion	Po	The most superiorly positioned point of the external auditory meatus
Pogonion	Pog	The most anterior point on the chin
Posterior nasal spine	PNS	The posterior spine of the palatine bone constituting the hard palate
Sella	S	The geometric centre of the pituitary fossa
Apex of upper first incisor	U1A	The apex of the upper first incisor
Tip of upper first incisor	U1T	The tip of the upper first incisor

^aAccording to Caufield.²²

Three expert orthodontists with at least 6 years of clinical experience manually identified landmarks twice. The interval between the first manual localization and the second one was 4–5 weeks. Landmarking was accomplished by means of digital software in which image enhancement features such as zoom in/out, change of brightness and contrast were available for better finding of the landmarks. Landmarks were identified using a mouse-driven graphics cursor on the displayed digital image. Identified landmarks could be edited and their position changed until the orthodontist was satisfied. The mean position of six manual identifications of each landmark was defined as the baseline landmark. The computer was then able to compare the automatic system's estimate of a landmark with the baseline landmark.

Two computer engineers co-operated to design the software using Matlab programming language. The template-matching technique, which is a subgroup of model-based approaches, was used to find the sella point and posterior nasal spine. In order to find the gnathion, pogonion, A point, anterior nasal spine, B point, nasion, and the tip of the upper first incisor, a knowledge-based approach was used. Since the orbitale neither has a distinct structure surrounding it nor is on the edge, this point was identified according to the fact that it is almost on the middle of the line connecting the nasion and the posterior nasal spine with a usual bias to the right and down; this relation helped the software to find the orbitale more accurately than template matching and edge detection.

Although the location of the orbitale could be identified, the porion is really hard to locate. This is because many similar radiolucencies that resemble the radiolucency of the internal auditory meatus exist in the search region of the template-matching system. Also, no distinguishable edge could be extracted from this search region. To solve the problem the software was designed to measure the inclination of the line connecting the orbitale and porion, which was identified using the template-matching mechanism. Then since the line connecting the nasion and sella normally has an angle of 6–7° to the Frankfort plane,²³ the software added 7° to the inclination of the sella–nasion line. Then these two inclinations (S–N + 7° and the connecting line automatically found Or and Po) were compared with the true horizontal line, and the line which had the least different angle to the true horizontal line was identified as the line of the Frankfort horizontal plane. The computer was then able to compare the angle of this line with the line connecting the baseline orbitale and the baseline porion, identified manually, and report the mean error in degrees.

The inclination of the lines connecting the apex of the upper first incisor (U1A) to the tip of the upper first incisor (U1T), the apex of the lower first incisor (L1A) to the tip of the lower first incisor (L1T) and the gonion to the menton were also identified instead of the landmarks.

An inclination-finding mechanism, based on the edge enhancement approach, was used for locating some landmarks that could not be identified either by the template-matching method or by the edge detection technique. The accurate location of these landmarks was not needed in analyses, but the inclination and the angle of the lines measured by the software was required for the analyses.

To report the results, the mean error of each landmark from the baseline landmark was estimated on each image and the total mean error was calculated by averaging the mean errors. The number of images with mean errors less than 4 mm, 2 mm and 1 mm was counted for each landmark. Also, every landmark was expressed as x (horizontal plane) and y (vertical plane) co-ordinates with an origin fixed to a given pixel.

This method was only applicable for landmarks but not for inclinations and lines, the reason being that the mean errors of the inclinations were reported in degrees. In order to make it easy for our results to be compared with other studies and also the unity of the reports, we calculated the number of degrees that were equivalent to the thresholds of the points at the ends of lines (1 mm, 2 mm and 4 mm) (Figure 1).

Figure 1.

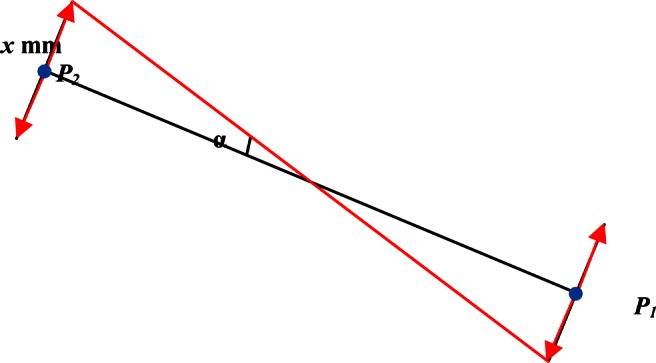
The method of calculating the threshold degrees equivalent to the x mm threshold

According to Figure 1, if the length of a line (P1–P2) and the threshold amount in millimetres (0.5×x mm) are known, the threshold amount in degrees (α) can be calculated by means of the following formula:

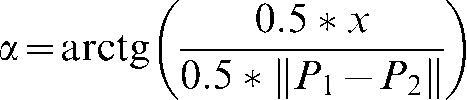(1)

What is needed in this formula is the length of the lines. The length of the lines was measured in this study by averaging the lengths from the 240 images (40 cephalograms that were landmarked 6 times). Table 2 shows the degree thresholds that are approximately equivalent to millimetre thresholds.

Table 2. Degree thresholds approximately equivalent to millimetre thresholds.

Line	1 mm	2 mm	4 mm
Or–Po	0.78°	1.56°	3.12°
Go–Me	0.87°	1.75°	3.49°
U1T–U1A	2.45°	4.89°	9.71°
L1T–L1A	2.60°	5.18°	10.28°

Go, gonion; L1A, apex of lower first incisor; L1T, tip of lower first incisor; Me, menton; Or, orbitale; Po, porion; U1A, apex of upper first incisor; U1T, tip of upper first incisor.

It is obvious that for short lines, such as the length between the apex and the tip of the first incisors, small errors in millimetres would cause large errors in degrees.

Results

Table 3 shows the mean errors and standard deviation for each line and the amounts in millimetres.

Table 3. The mean errors and standard deviations for the automatically identified lines from the baseline lines and the equivalent values in millimetres.

Lines	Mean error (degrees)	Equivalent mean errors (mm)	Standard deviation (degrees)	Standard deviation (mm)	Statistical significance
Or–Po	1.42	1.81	1.76	2.26	0.00
Go–Me	1.32	1.51	3.78	4.34	0.03
U1T–U1A	4.12	1.69	21.41	9.17	0.23
L1T–L1A	0.15	0.06	3.56	1.37	0.79
Average	1.75	1.27	7.63	4.28

Go, gonion; L1A, apex of lower first incisor; L1T, tip of lower first incisor; Me, menton; Or, orbitale; Po, porion; U1A, apex of upper first incisor; U1T, tip of upper first incisor.

Table 4 shows the mean error and the standard deviation in millimetres from the baselines for each landmark on the x- and y-axes.

Table 4. The mean errors and standard deviations for the automatically identified landmarks from the baselines.

Landmark	Mean error (mm)	Standard deviation (mm)	Statistical significance
S (x-axis)	0.71	3.03	0.15
S (y-axis)	0.45	0.67	0.00
N (x-axis)	0.31	3.12	0.54
N (y-axis)	0.74	2.30	0.05
Or (x-axis)	0.14	3.21	0.78
Or (y-axis)	0.80	1.70	0.01
A (x-axis)	0.60	2.85	0.19
A (y-axis)	0.26	2.58	0.53
B (x-axis)	0.94	3.30	0.08
B (y-axis)	1.35	3.46	0.02
ANS (x-axis)	3.65	2.51	0.00
ANS (y-axis)	0.02	1.92	0.95
PNS (x-axis)	0.50	1.97	0.12
PNS (y-axis)	0.72	1.85	0.02
Pog (x-axis)	0.79	2.58	0.06
Pog (y-axis)	1.13	3.80	0.07
Me (x-axis)	0.71	2.68	0.10
Me (y-axis)	0.32	3.30	0.55
Gn (x-axis)	1.64	2.98	0.00
Gn (y-axis)	1.79	3.56	0.00
U1T (x-axis)	0.45	2.37	0.24
U1T (y-axis)	0.89	2.31	0.02

A, A point; ANS, anterior nasal spine; B, B point; Gn, gnathion; Go, gonion; L1A, apex of lower first incisor; L1T, tip of lower first incisor; Me, menton; N, nasion; Or, orbitale; PNS, posterior nasal spine; Po, porion; Pog, pogonion; S, sella; U1A, apex of upper first incisor; U1T, tip of upper first incisor.

Statistical analysis was performed for each line and also each landmark on x- and y-axes according to the paired samples t-test (Tables 3 and 4). According to our analysis (p < 0.05), the slope of two lines was significantly different from the baseline, and in 12 out of 22 measurements the errors were statistically significant.

The mean difference between an automatically identified landmark and the baseline point was measured for each landmark on each image, and the average of the 40 measurements was calculated for the 11 landmarks. Table 5 shows the mean error and standard deviation for each landmark and the total mean error.

Table 5. The mean errors and standard deviations for the automatically identified landmarks from the baselines.

Landmark	Mean error (mm)	Standard deviation (mm)
S	1.71	2.96
N	2.34	3.49
Or	2.74	2.84
A	2.49	3.29
B	3.33	4.21
ANS	4.44	2.58
PNS	1.99	2.26
Pog	2.48	4.46
Me	1.72	4.26
Gn	3.02	4.68
U1T	2.25	2.89
Total	2.59	3.45

A, A point; ANS, anterior nasal spine; B, B point; Gn, gnathion; L1A, apex of lower first incisor; Me, menton; N, nasion; Or, orbitale; PNS, posterior nasal spine; Po, porion; Pog, pogonion; S, sella; U1A, apex of upper first incisor; U1T, tip of upper first incisor.

The total mean error in millimetres according to the 2.59 mm mean error for landmark detection and the 1.27 mm mean error for line detection was 2.18 mm [(2.59×11 + 1.27×5)/16].

According to Table 5, the most precisely identified landmarks were the sella and menton with 1.71 mm and 1.72 mm mean errors. The least precisely identified landmark was the anterior nasal spine which had a mean error of 4.44 mm.

The mean errors of two landmarks (L1A and L1T) were less than 1 mm (12.5% of landmarks < 1 mm), and the mean errors of seven landmarks (S, Go, L1T, L1A, Me, Po and U1T) were less than 2 mm (43.75% of landmarks < 2 mm); other landmarks had more than 2 mm mean errors. The mean errors of all landmarks except the anterior nasal spine were less than 4 mm (93.75% of landmarks < 4 mm).

Discussion

In this study we used 40 digital cephalometric radiographs from an archive of more than 200 cephalograms. The randomization technique was accomplished using a table of random numbers; we did not assign any exclusion criteria because we wanted the quality of cephalograms to resemble the quality of routine cephalograms. Although it is important to have a randomly selected data set without any judgment of the quality, sex, age and so on,¹⁴ some of the early studies deliberately used only radiographs that were judged to be of high quality.¹²

In the study by Yue et al,⁹ the method of selection of the cephalograms was not mentioned. Also they did not even mention whether the cephalograms were selected randomly or not. Some researchers have just stated that the images were selected randomly but did not mention the method of random selection.^8,11-13,20 Hutton et al¹² claimed that the images used in their work had been adopted randomly; however, the cephalograms they used were pre-treatment images and they also rejected five cephalograms that were impossible to landmark, either by orthodontists or by the software. Kafieh et al¹⁴ used the same cephalograms used by Hutton et al,¹² with the same selection method. In the study by Forsyth and Davis⁸ the exclusion criteria were obvious malposition of the head in the cephalostat, incisors unerupted or missing, and unerupted teeth overlying the apices of the incisors. And in Leonardi et al's¹⁹ study the exclusion criteria were the same as in the study by Forsyth and Davis.⁸ They also had two more exclusion criteria: patients with severe craniofacial deviations, and posterior teeth not in maximum intercuspation. In our study we did not identify any exclusion criteria. It is obvious that random selection of the images plays an important role in the precision of landmarking and the applicability of the software. According to what was stated above, direct comparison with previous automated systems is not possible as the accuracy of automated systems is dependent on the quality of the radiographs being applied. It is obvious that for future researchers one standard set of radiographs with definite size, quality and number will be required, so that the studies can be judged fairly on the same images.

The landmarks identified in this study were the ones used in three important analyses (Downs, McNamara and Steiner) so that the software was able to analyse the cephalograms using these landmarks. When a study did not identify some important landmarks, it could be because the system did not have the ability to find those landmarks. Also it must be stated that with limited landmarks, it is not possible to use the software in most of the analyses. In the study of Giordano et al²¹ only eight landmarks could be found. Yue et al's⁹ research did not include A, B, L1A, L1T and U1A, and Leonardi et al¹⁹ did not include ANS, PNS, Or, U1A and L1A. On the other hand, it seems that some studies have identified some easily located landmarks that are used less frequently in common analyses. The inclusion of these landmarks might give better results and show higher efficacy of their software. Examples of such landmarks are the nose and the soft tissue pogonion, which were identified in the studies of El-Feghi et al¹⁸ and Yue et al.⁹

In our study, three expert orthodontists manually identified landmarks twice. The mean of six measurements of each landmark was defined as the baseline landmark. Then it was possible to compare the automatic system's landmarking with the baseline landmarks. Some of the studies have not mentioned the reference to which the automatically identified landmarks were compared.^13,14,16,17 In the studies of Hutton et al,¹² El-Feghi et al¹⁸ and Giordano et al,²¹ the cephalograms were landmarked once by an orthodontist as a reference. This might have caused differences in their results. McWilliam and Welander²⁴ described had interobserver differences may often be greater than the effects of physical image quality. Although Baumrind and Frantz²⁵ reported that reliability is not sufficient if one landmark in a cephalometric image is identified twice, Midtgard et al²⁶ found that an interval of 1 month between two registrations did not significantly affect the reproducibility of the landmark examined.

In this study some cephalometric points showed better results on the horizontal (x) axis (N, Or, B, PNS, Pog, Gn, U1T); others showed less error on the vertical (y) axis (S, A, ANS, Me). This is in agreement with the statement that the distribution of errors for many landmarks is systematic and follows a typical pattern (non-circular envelope).²⁷ In fact, it has been reported that some cephalometric landmarks are more reliable in the horizontal dimension whereas others are more reliable in the vertical dimension.²⁷ The reasons for these differences in distribution of landmark identification error are often related to the anatomical variability of the landmark location.

According to statistical analysis (p < 0.05) the slope of two lines was significantly different from the baseline and 12 out of 22 measurement errors were statistically significant. However, the magnitude of mean errors between automatic identification of each landmark and the best estimate of cephalometric points may not be clinically significant.

In this study the total mean error was 2.59 mm. 12.5% of landmarks had a mean error less than 1 mm, the mean error of 43.75% of landmarks was less than 2 mm and the mean error of 93.75% of landmarks was less than 4 mm.

In Giordano et al's²¹ study, the total mean error was 1.07 mm, which is less than in our study. The method used for landmark location in their study was cellular neural networks. Their study did not include locating the ANS, S, Or and the landmarks that we could find using inclination-finding mechanisms (Po, Go, U1T, L1T and L1A). Table 6 compares the mean errors of the same landmarks in our study and the study of Giordano et al.²¹

Table 6. Comparative results of our study and Giordano et al's²¹ study.

Landmarks	Mean error (mm) in our study	Mean error (mm) in Giordano et al's study
A	2.49	1.34
B	3.33	2
Me	1.72	0.62
N	2.34	1.12
Pog	2.48	0.87
U1T	2.25	0.48

A, A point; ANS, anterior nasal spine; B, B point; Me, menton; N, nasion; Pog, pogonion; U1T, tip of upper first incisor.

It seems that the knowledge-based and model-based algorithms which were used in our study could identify accurately landmarks that are located on structures with definite characteristics, like edges (for example the Me point), or landmarks with a definite structure surrounding them (for example the sella). But lots of programming is needed for software to identify landmarks which have different shapes, structures and positions on different cephalograms. For these landmarks, soft-computing approaches, which were used in the study of Giordano et al,²¹ result in greater accuracy. However considering the fact that their software could find only 8 landmarks whereas our software could identify 16 landmarks, it can be judged that our software did better than that of Giordano et al.²¹

In the study of Leonardi et al,¹⁹ the mean errors were not calculated for each landmark. They only reported the mean differences on the x- and y-axes for each landmark. However, the differences in their study were less than 0.59 mm [the least precisely identified landmark was A (x-axis) with a 0.59 mm mean error]. They used the same technique (cellular neural networks) as Giordano et al,²¹ with a noticeable improvement compared with Giordano et al.²¹ There could be two reasons for this improvement: (1) the use of direct digital X-rays by Leonardi et al¹⁹ (therefore, no need of analogue to digital conversion and an increased resolution of the X-ray files); and (2) the use of improved algorithms in their study; only cephalograms with high resolution were used and this might not resemble a routine clinical condition. Also, their software might have limited clinical application because there did not seem to be enough cephalometric points detected to perform cephalometric analysis: ANS, PNS, Me, Gn, Go, Or, S, U1A and L1A, which are important landmarks for cephalometric analysis, were not located.

In our study two landmarks had a mean error less than 1 mm, the mean error of seven landmarks was less than 2 mm, and the mean error of one landmark (ANS) was more than 4 mm.

In the study of Forsyth et al,⁸ the mean error of 7 landmarks (ANS, Ba, Bo, L1A, Or, PNS, U1A) was more than 1 mm, that of 12 landmarks (A, B, Gl, Gn, Go, L1T, Me, N, Po, Pog, S, U1T) less than 1 mm, and 6 landmarks (A, Gl, L1T, Me, Po, Pog) were identified with a mean error of less than 0.5 mm. They did not report the total mean error and the exact amount of mean error for each landmark. Therefore, for landmarks with a mean error of more than 1 mm, it is not clear how much more than 1 mm the mean error was. Although direct comparison is not possible, their results for some of the landmarks (A, U1T, N, Po, Pog and S) were better than ours. The difference might be due to the exclusion criteria in their study (obvious malposition of the head in the cephalostat, incisors unerupted or missing, and unerupted teeth overlying the apices of the incisors) whereas we did not identify any exclusion criteria.

Table 7 shows the percentage of landmarks identified in the range of different thresholds of errors for different studies. These studies used knowledge-based and/or model-based approaches.

Table 7. The percentage of the landmarks identified in the range of different thresholds of errors in different studies.

Study	Percentage <1 mm	Percentage <2 mm	Percentage <4 mm	Percentage <5 mm
Hutton et al12	13	35	Not Reported	74
Yue et al9	Not reported	71	88	Not reported
Kafieh et al14	24	61	93	Not reported
This study	12.5	43.75	93.75	100

The mean of 13% of the landmarks with less than 1 mm error in the study by Hutton et al¹² is similar to our results. In the study by Yue et al. the percentage of landmarks with less than 2 mm error was less than ours. However, they stated that some images were not included in the study because the algorithm of their software showed failure on these images. These images had a mean error more than 4 mm in locating more than 20% of the landmarks, and if these had been included the average result would be worse. Only 88% of their landmarks were within the 4 mm mean error, whereas in our study all of the landmarks had a mean error of less than 4 mm.

Our results are not in agreement with Kafieh et al's study.¹⁴ In their study the cephalograms and the method (active shape models) were the same as used by Hutton et al.¹² In our study we used randomization for image selection without any exclusion criteria. They used only pre-treatment images and they also excluded five images for being hard to landmark both manually and automatically. For mean errors of high value, this might be because scanned images were used or because of the method used.

In one study, the mean estimating error of landmark identification has been reported to be 1.26 mm. Rakosi²⁸ suggested when locating landmarks that an error of ±2 mm is acceptable. Yue et al⁹ stated that a 2 mm mean error is correct, and a mean error less than 4 mm is acceptable. Chakrabartty et al¹⁷ stated that for a typical orthodontic application a reasonable tolerance distance for identification is around l mm. Another study²⁷ recommended that an acceptable error value should be 0.81 mm. It therefore seems that the 2.59 mm mean error obtained in this study is in the acceptable range.