Interior tomography in x-ray differential phase contrast CT imaging

Abstract

Differential phase contrast computed tomography (DPC-CT) is an x-ray imaging method that uses the wave properties of imaging photons as the contrast mechanism. It has been demonstrated that DPC images can be obtained using a conventional x-ray tube and a Talbot–Lau-type interferometer. Due to the limited size of the gratings, current data acquisition systems only offer a limited field of view, and thus are prone to data truncation. As a result, the reconstructed DPC-CT image may suffer from image artifacts and increased inaccuracy in the reconstructed image values. In this paper, we demonstrate that a small region of interest (ROI) within a large object can be accurately and stably reconstructed using fully truncated projection datasets provided that a priori information on electron density is known for a small region inside the ROI. The method reconstructs an image iteratively to satisfy a group of physical conditions by using a projection onto convex set (POCS) approach. In this work, this POCS algorithm is validated using both numerical simulations and physical phantom experimental data. In both cases, the root mean square error is reduced by an order of magnitude with respect to the truncated analytic reconstructions. Truncation artifacts observed in the latter reconstructions are eliminated using the POCS algorithm.

1. Introduction

It has been known for over a century that the behavior of photons can be understood in terms of both their particle and wave nature. In most medical imaging applications, the wave properties of x-rays are neglected and only attenuation is used as the contrast mechanism. Recently, however, work has been directed toward exploiting wave properties of x-rays in the context of diagnostic medical imaging. To this end, several phase contrast (PC) methods have been proposed and tested experimentally. X-ray PC imaging could potentially yield diagnostically valuable information by providing contrast between tissues that could not be obtained using attenuation-based imaging (Chen et al 2010a, 2010b, 2011, Momose et al 1996, 2000, Takeda et al 2000, Momose 2003, Pfeiffer et al 2006, 2007, Bech et al 2009, Zambelli et al 2010a,2010b, Zambelli 2011, Bevins et al 2012). Quantitative imaging is another application where PC shows interesting results (Herzen et al 2009, Qi et al 2010a, 2010b).

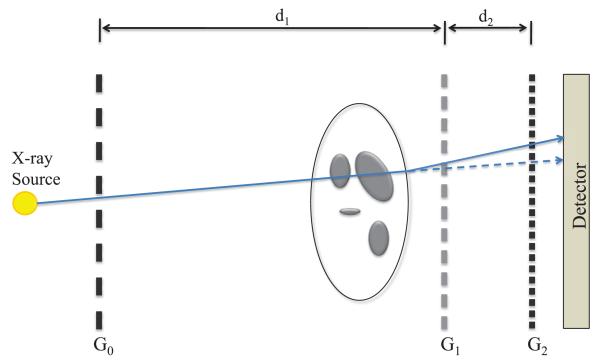
Among the proposed x-ray PC imaging methods, the grating-based differential PC (DPC) imaging method is a promising approach. This method uses a grating-based interferometer—also known as Talbot–Lau interferometer—to measure the refraction angle of x-ray beams (Weitkamp et al 1999, Pfeiffer et al 2006, 2007b). An illustration of the experimental setup is shown in figure 1. The first grating, G₁, is a π-phase shift grating, which generates an interference pattern. The pattern is constituted of strips of alternating intensities and has a maximal visibility at the fractional Talbot distance downstream of the grating. A second grating, G₂, can be used to analyze the interference pattern and determine the angle by which the beam has been refracted. This procedure is applied simultaneously for all the elements of a detector positioned downstream of G₂. This apparatus needs a coherent incident x-ray beam in order to generate an interference pattern. This condition can be met by positioning a third grating, G₀, directly after a conventional rotating anode x-ray source. This apparatus produces images of the angle of refraction of the beam in a plane determined by the grating direction.

Figure 1.

Talbot–Lau interferometer used for DPC x-ray imaging. G₁ is a π-phase shift grating and G₂ is the analyzer grating. G₀ allows us to meet the x-ray beam coherence requirement.

When an x-ray wave propagates through a medium, the response of the medium to the wave is described by the refractive index (n):

$$n=1-\delta +\mathbf{i}\beta ,$$ (1)

where δ is the decrement and β is related to the attenuation coefficient of the medium. The decrement of the refractive index is directly proportional to the electron density of the material (Herzen et al 2009, Qi et al 2010a, 2010b). Using ray dynamics (Born et al 1964) and a para-axial approximation, it can be shown that the refraction angle (Θ) is related to the decrement of the index of refraction (δ) by the following relation (Pfeiffer et al 2007a, 2007b, Qi and Chen 2007, Chen and Qi 2008):

$$ϴ=\frac{\mathrm{d}}{\mathrm{d}\rho }\int \mathrm{d}l\delta \left(\mathbf{x}\right).$$ (2)

This relation is the fundamental imaging equation of DPC computed tomography (DPC-CT). After acquiring the refraction angle data around the image object, it is possible to perform a tomographic reconstruction of the decrement using a filtered backprojection (FBP) algorithm with a Hilbert filter (Pfeiffer et al 2007a, 2007b, Qi and Chen 2007, Chen and Qi 2008). The algorithm can be summarized by the following equation in the parallel-beam case:

$$\delta \left(\mathbf{x}\right)=\frac{1}{4{\pi }^2}{\int }_0^{2\pi }\mathrm{d}\theta {\int }_{-\infty }^{+\infty }\mathrm{d}\rho \frac{1}{x\cos \theta +y\sin \theta -\rho }ϴ(\rho ,\theta ).$$ (3)

A practical problem when using FBP reconstruction methods is that of data truncation. This phenomenon is well known in absorption CT. If the detector does not fully cover the width of the object, images reconstructed using FBP will be plagued by truncation artifacts. In this paper, it is demonstrated that such artifacts affect DPC-CT. In current imaging systems, gratings are made out of 100 mm silicon wafers. As a result, the scanning field of view (SFOV) is approximately 6 cm in diameter in a standard fan-beam configuration, or up to 12 cm in diameter for a half-detector offset configuration (Chen and Qi 2008). Objects larger than the FOV suffer from data truncation when scanned by such a system. It would be desirable to develop a reconstruction algorithm which can produce accurate and artifact-free tomographic reconstructions from truncated datasets. The problem of data truncation in DPC-CT has been discussed in the literature (Pfeiffer et al 2008, Köhler and Noo 2009). The purpose of the research presented here is to adapt the algorithm (Defrise et al 2006, Ye et al 2007, Kudo et al 2008, Courdurier et al 2008) developed to compensate for data truncation in attenuation CT to the case of DPC-CT. The method is validated using both numerical and physical phantom data.

2. POCS algorithm for interior problem: absorption CT POCS algorithm and generalization to DPC-CT

2.1. Data truncation in CT

Data truncation occurs in CT when portions of the projection data are missing from some or all view angles. In realistic applications, this occurs when the scanning beam does not cover the full extent of the object. In such cases, the scanning FOV (SFOV) does not completely enclose the object. The situation in which the object completely contains the SFOV is called the interior problem (Natterer 2001). Until recently, it was believed that the interior problem had no unique solution (Ye et al 2007, Kudo et al 2008, Courdurier et al 2008). Data truncation is particularly problematic, since classical FBP algorithms fail to reconstruct accurate and artifact-free images when parts of the projection dataset are missing. This is due to the fact that the filtration operation in FBP is based on a non-local kernel. During the filtration, the missing sections corrupt the rest of the projection dataset. These aberrations ultimately result in artifacts in the image.

In absorption CT, several approaches have been proposed to mitigate or eliminate truncation artifacts, most of which rely on some a priori knowledge about the object being imaged. Many methods developed to address data truncation essentially rely on the concept of differentiated backprojection (DBP), which is presented next.

2.2. DBP in absorption CT

In order to obtain a DBP image in absorption CT, one differentiates the projection data with respect to the view angle and then backprojects the result. In the case of a fan-beam geometry and a circular scanning trajectory with curved detector configuration, these operations can be summarized as (Zhuang et al 2004)

$$b\left(\mathbf{x}\right)={\int }_{t_a}^{t_b}\mathrm{d}t\frac{w(\mathbf{x},t)}{\mid \mathbf{x}-\mathbf{s}\left(t\right)\mid }\left(\frac{\partial }{\partial t}-\frac{\partial }{\partial \gamma }\right)g_m(\gamma ,t),$$ (4)

where b(x) is the DBP, x is the position in the DBP image, s(t) is the source position at angle t, g_m(γ, t) is the measured projection datum at the angle γ from the iso-ray and source angular position t. The weight w(x, t) is used to select the filtration direction. If the x-axis is selected, the multiplying weight takes the form

$$w(\mathbf{x},t)=\mathrm{sgn}\left(\right(\mathbf{s}\left(t\right)-\mathbf{x})\cdot \widehat{\mathbf{j}}),$$ (5)

where ĵ is the unit vector in the y-direction. The sgn(x) function is defined as

$$\mathrm{sgn}\left(x\right)=\{\begin{array}{cc}-1,\hfill & \text{if}x<0\hfill \\ 0,\hfill & \text{if}x=0\hfill \\ 1,\hfill & \text{if}x>0.\hfill \end{array}\phantom{\}}$$

The equivalent weight for filtration along the y-axis is the following:

$$w(\mathbf{x},t)=\mathrm{sgn}\left(\right(\mathbf{s}\left(t\right)-\mathbf{x})\cdot \widehat{\mathbf{i}}),$$ (6)

where î is the unit vector in the x-direction. Note that in the fan-beam case, an additional weight may also be included to account for data redundancy (Parker 1982).

One may reconstruct the image from the DBP image using a one-dimensional convolution with a Hilbert kernel for all the lines in the image (Zou and Pan 2004, Noo et al 2004, Zhuang et al 2004, Clackdoyle and Noo 2004, Leng et al 2005). If the filtration is selected to be along the x-direction using equation (5), the following formula describes this process explicitly (Zhuang et al 2004):

$$f\left(\mathbf{x}\right)=-\frac{1}{2{\pi }^2}{\int }_{-\infty }^{+\infty }\mathrm{d}{x}^{\prime }{\int }_{-\infty }^{+\infty }\mathrm{d}{y}^{\prime }\frac{1}{x-x^{\prime }}{\delta }_{\mathrm{Dirac}}(y-y^{\prime })b\left({\mathbf{x}}^{\prime }\right),$$ (7)

where f(x) is the reconstruction and δ_Dirac is the Dirac δ-distribution. x is the distance along the x-axis and y is the distance along the y-axis; the prime notation is used for the integration variables. In order to avoid integrating over an infinite range, it is possible to use the finite Hilbert transform (Tricomi 1985, Mikhlin 1957)

$$f\left(\mathbf{x}\right)=-\frac{1}{2{\pi }^2}\frac{1}{\sqrt{{\mathit{L}}^2-x^2}}\left[{\int }_{-L}^L\mathrm{d}{x}^{\prime }\left(\frac{\sqrt{{\mathit{L}}^2-x^{\prime 2}}}{x^{\prime }-x}{\int }_{-\infty }^{+\infty }\mathrm{d}{y}^{\prime }{\delta }_{\mathrm{Dirac}}(y-y^{\prime })b\left({\mathbf{x}}^{\prime }\right)\right)+C\right],$$ (8)

where the compact support of the object is contained in the interval [−L, L]. Also,

$$C=-2\pi g_m({\gamma }_0,t_0),$$ (9)

where g_m(γ₀, t₀) is the projection datum corresponding to the line integral along the filtration line. This approach only requires the DBP to be known over the compact support of the object.

In the context of truncation, the DBP image is particularly interesting since it can be obtained using local operations only—differentiation and backprojection. Thus, the DBP image does not suffer from truncation artifacts. One can reconstruct any line in the image as long as the DBP is known along its length and extends outside of the compact support of the object. However, this approach fails to accurately reconstruct the full SFOV and is incompatible with the interior problem. Iterative algorithms have been shown to solve the interior problem in some cases. For instance, if the object under study is known to be piecewise constant, a total variation minimization algorithm can be used to reconstruct the object (Yu and Wang 2009, Yu et al 2009). Another algorithm based on the DBP has been proposed and is presented in the following section.

2.3. DBP-based projection onto convex sets algorithm

Recently, the principle of DBP and its link to the Hilbert transform of the image were used to demonstrate that the interior problem in attenuation CT is solvable. In the initial formulation of this proof (Defrise et al 2006), it was shown through analytic continuation that the whole SFOV can be reconstructed in a unique and stable manner, given that it extends outside of the object’s compact support. This proof was generalized to the case where the object’s attenuation coefficient is known a priori within a subregion of the scanner FOV (Ye et al 2007, Kudo et al 2008, Courdurier et al 2008). The idea is to have each filtration line of the image satisfy a series of properties that enforce the correctness of the reconstruction. These properties or conditions are the following:

• C_DBP: Hf = DBP within the SFOV;

• C_CS: f(x₀) = 0 for x₀ outside the compact support;

• C_AP: f(x₁) = f_ap(x₁) for x₁ inside region of a priori knowledge, where f_ap is the known object value;

• C_LI: ∫ dxf(x) = R, where R is known from the projection data;

• C_NN: f(x) ≥ 0.

The condition C_DBP enforces that the object’s Hilbert transform be equal to the DBP within the FOV. C_CS constrains the object to be compactly supported within some assumed domain. C_AP stipulates that the image value must be equal to the value known a priori within a small region. C_LI ensures that the integral along the filtration line be equal to the corresponding projection datum. Finally, C_NN is a non-negativity constraint, which is appropriate for attenuation CT.

The image that is compatible with all the conditions is the proper reconstruction. The search procedure can be implemented iteratively using a POCS algorithm (Youla and Webb 1982, Combettes 1993, Stark et al 1998). We may formulate an operator that ‘projects’ an image onto the set of images compatible with a given condition. Each condition C has an associated projector P. The POCS iteration can be written as (Defrise et al 2006, Ye et al 2007, Kudo et al 2008, Courdurier et al 2008)

$$f_{i+1}=P_{\mathrm{NN}}{P}_{\mathrm{LI}}{P}_{\mathrm{AP}}{P}_{\mathrm{CS}}{P}_{\mathrm{DBP}}{f}_i,$$ (10)

with an arbitrary initial guess f₀.

2.4. POCS algorithms for DPC-CT: DPC-POCS algorithm

In the context of DPC-CT, the computation of the DBP image can be substantially simplified (Anastasio and Pan 2007, Qi and Chen 2007, Chen and Qi 2008) as the refraction angle already corresponds to the differentiated projection data. For a fan-beam geometry, the following identity has been demonstrated (Qi and Chen 2007, Chen and Qi 2008):

$$\left(\frac{\partial }{\partial t}-\frac{\partial }{\partial \gamma }\right)g_{\delta }(\gamma ,t)=R\cos \gamma ϴ(t,\gamma ),$$ (11)

where R is distance from the source to the isocenter. Using this identity, the DBP in absorption CT becomes a direct backprojection operation in DPC-CT.

In order to adapt the POCS algorithm described above to the interior problem of DPC-CT, the condition C_LI needs some extra attention. The condition C_LI corresponds to enforcing that each filtration line satisfies the attenuation CT imaging equation. However, the imaging equation of DPC-CT (equation (2)) differs by a derivative. If no truncation were present, it would be possible to integrate the projection dataset using the data from outside the object as a boundary condition. The resulting dataset could be used directly with the projector P_LI used in the attenuation CT POCS. However, in the case of the interior problem, projections do not extend outside the compact support and thus, no boundary conditions are available to perform this integration. An alternative is to forgo the C_LI condition and apply the POCS algorithm using the other conditions only. This is a reasonable approach since the proof of the reconstruction uniqueness does not rely on set C_LI explicitly (Ye et al 2007, Kudo et al 2008, Courdurier et al 2008). The DPC-POCS sets are thus listed as follows:

• C_DBP: Hf = DBP within the SFOV;

• C_CS: f(x₀) = 0 for x₀ outside the compact support;

• C_AP: f(x₁) = f_ap(x₁) for x₁ inside region of a priori knowledge where f_ap is the known object value

• C_NN: f(x) ≥ 0.

2.5. Implementation of the DPC-POCS algorithm

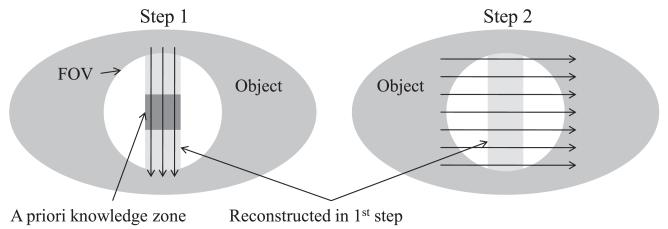
The implementation of the DPC-POCS algorithm is schematically described in the appendix. For convenience, the filtration direction was always chosen to be either vertical or horizontal so that filtration lines coincide with the image matrix. One important caveat is that every filtration line in the image must cross the region of a priori knowledge in order to converge appropriately. In general, the zone of a priori knowledge may be small and span only a small subset of lines. In such a case, a multi-step procedure can be applied. A strip of the image is first reconstructed using an initial filtration direction. The algorithm is then applied again in the perpendicular direction using the strip reconstructed in the first step as a priori information. This technique is explained in the literature (Ye et al 2007, Kudo et al 2008). An illustration of this procedure is shown in figure 2.

Figure 2.

Illustration of the two-step procedure used to maximize the reconstructed region.

The algorithm was implemented using C++ and POSIX Threads computing library (IEEE, NY, USA). This library is used to take advantage of the inherent parallelism of the DPC-POCS algorithm. In effect, filtration lines are independent of one another and can be reconstructed in parallel.

2.6. Validation study of the DPC-POCS algorithm

In this paper, both numerical simulations and experimental phantom studies have been performed to validate the DPC-POCS algorithm. In both cases, data were acquired without truncation and then truncated artificially by discarding them. The image reconstructed without truncation was used as the reference image in accuracy evaluation.

2.6.1. Numerical simulations

Data were generated numerically from a phantom made of an ellipse containing four circles. A ray-tracing algorithm was used to model the refraction of the x-ray beam at interfaces between the different regions using the Snell–Descartes law. No x-ray attenuation was simulated. The beam was assumed to be monochromatic. No noise was added to the data. A decrement value of 0.5 × 10⁻⁶ was used for the ellipse. The superposed circles had a decrement value of either 0 or 1 × 10⁻⁶. 720 view angles were simulated, each with 600 detector elements. A full scan with equi-angular curved detector geometry was modeled. The reconstructed matrix size was 512 × 512.

The artificial truncation was applied such that the FOV was fully contained within the object. In this case, it was assumed that the surrounding larger ellipse had a known index of refraction. A thin strip just within the FOV was used as a priori information. Since every line in either direction did cross the a priori knowledge zone, the algorithm could reconstruct the whole FOV in a single step.

2.6.2. Experimental phantom study

An experimental grating-based DPC system was built at the University of Wisconsin-Madison. It consists of three x-ray gratings, a rotating-anode x-ray tube with a 0.3 mm nominal focal spot size (G1592, Varian Medical Systems, CA, USA) connected to a high-voltage generator (Indico 100, CPI, ON, Canada), a CMOS flat-panel x-ray detector (Rad-icon, Shad-o-Box 2048 EV, CA, USA) with a 48 μm detector pitch across a 1024 × 2048 array coupled to a Kodak Min-R scintillator. A rotating motion stage was employed to enable tomographic data acquisitions. The x-ray gratings were fabricated at the University of Wisconsin-Madison using techniques similar to those published in the literature (David et al 2007).

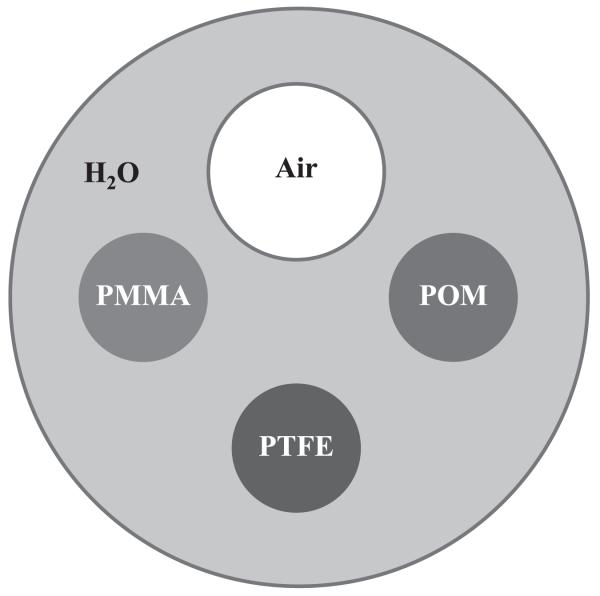
A physical phantom was constructed starting from a water-filled cylinder. Three plastic rods—POM, PTFE and PMMA—as well as an air-filled tube were introduced into the water-filled cavity (figure 3). The phantom was scanned using a tube potential of 40 kVp and a tube current of 20 mA. The exposure time was set to 40 s divided over eight phase steps. A tomographic dataset was acquired from 360 view angles at 1° increments.

Figure 3.

Illustration of the components contained in the physical phantom.

2.6.3. Reconstruction accuracy metric

In order to evaluate the accuracy of the DPC-POCS algorithm proposed above, both datasets were reconstructed using both FBP and DPC-POCS. The reconstructions were compared quantitatively using the normalized root-mean-squared deviation (NRMSD) as define by

$$\mathrm{NRMSD}\left(x\right)=\frac{1}{x_{\max }-x_{\min }}\sqrt{\frac{1}{N}\sum _{i=0}^N{(x_i-{}_{\mathrm{std}}x_i)}^2,}$$ (12)

where x is the image and ${}_{\mathrm{std}}x$ is the non-truncated FBP reconstruction.

3. Results and discussion

3.1. Numerical simulations

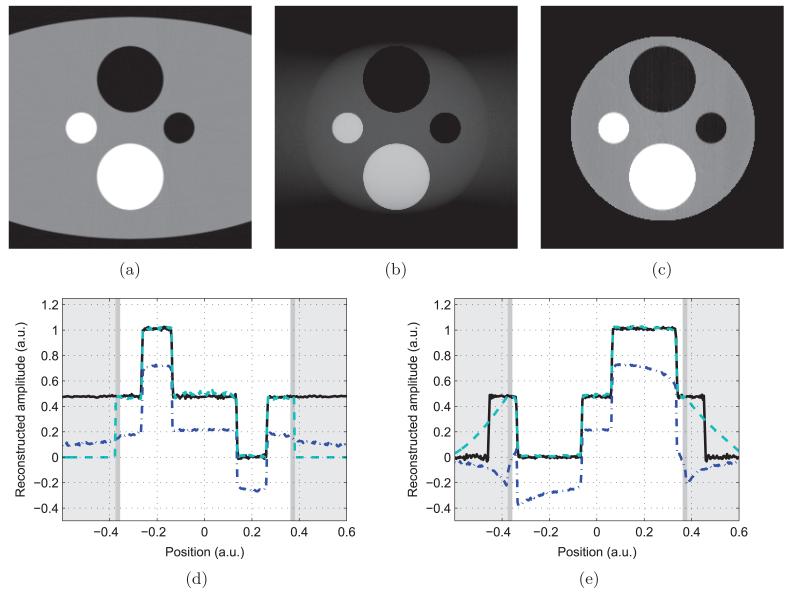
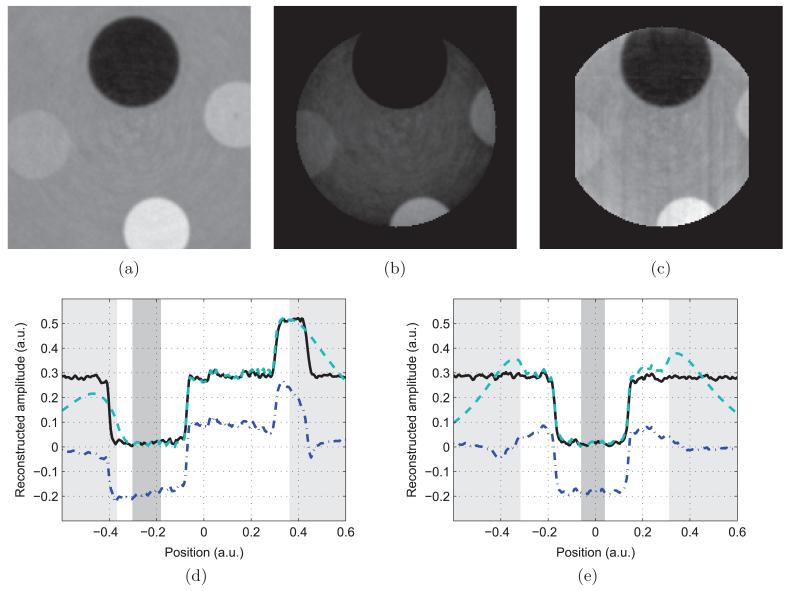
The reconstructions from non-truncated data using FBP and from the truncated data using both FBP and DPC-POCS are shown in figures 4(a)–(c). Profile plots through the horizontal and vertical axes are presented in figures 4(d) and (e).

Figure 4.

Reconstructions of the numerical phantom. (a) is the non-truncated FBP reconstruction, (b) is the truncated FBP reconstruction and (c) is the truncated POCS reconstruction. (d) is a vertical profile, while (e) is horizontal. The non-truncated FBP reconstruction is in solid black, the POCS reconstruction is in dashed teal and the truncated FBP reconstruction is in dot–dashed blue. The white background indicates the scanner FOV, the dark gray corresponds to the zone of a priori knowledge—a thin strip at the border of the SFOV—and the light gray area is truncated.

The DPC-POCS iteration was applied 1000 times for an image matrix of 512 × 512. Excluding the time spent computing the DBP, the algorithm had a running time of approximately 70 s on a Core 2 Quad CPU (Intel, CA, USA) running at 2.66 GHz.

The filtration direction was chosen to be vertical, since the object had a lesser amount of truncation in that direction. The truncated FBP reconstruction had an NRMSD of 30.6%, while the DPC-POCS algorithm yielded a value of 2.0%.

3.2. Experimental phantom study

The non-truncated reconstruction is presented in figure 5(a). In this case, it was assumed that the value of the decrement of the index of refraction was known to be 0 within the air cylinder. A zone of a priori knowledge was manually selected within the air cavity. The two-step DPC-POCS algorithm described in section 2.4 was applied to the artificially truncated dataset and the reconstruction is shown in figure 5(c). The FBP reconstruction from the same truncated dataset is shown in figure 5(b). Horizontal and vertical profiles plots are shown in figures 5(d) and (e).

Figure 5.

Reconstructions of the experimental dataset. (a) is the non-truncated FBP reconstruction, (b) is the truncated FBP reconstruction and (c) is the truncated POCS reconstruction. (d) is a horizontal profile, while (e) is vertical. The non-truncated FBP reconstruction is in solid black, the POCS reconstruction is in dashed teal and the truncated FBP reconstruction is in dot–dashed blue. The white background indicates the scanner FOV, the dark gray corresponds to the zone of a priori knowledge and the light gray area is truncated.

The DPC-POCS iteration was applied 1000 times for an image matrix of 400 × 400. Excluding the time spent computing the DBP, the algorithm had a running time of approximately 50 s on a Core 2 Quad (Intel, CA, USA) running at 2.66 GHz. The filtration direction was chosen to be first vertical to reconstruct a strip of the image, and then horizontal to enlarge the reconstructed area.

The NRMSD was calculated for both truncated reconstructions. The truncated FBP reconstruction had an associated value of 41.3%, while the DPC-POCS had a NRMSD of 4.2%.

Qualitatively, the DPC-POCS reconstructions presented above do not present substantial truncation artifacts as observed in the FBP reconstructions from the same truncated datasets. The quantitative accuracy of the reconstructions is further confirmed by a reduction by an order of magnitude of the NRMSD when using DPC-POCS. This is demonstrated here for both numerical and experimental DPC-CT acquisitions.

One may note in passing that the presence of significant truncation artifacts in the FBP reconstructions contradicts the conclusions from Pfeiffer et al (2008) and confirms the claims from Köhler and Noo (2009).

Furthermore, it was demonstrated that the DPC-POCS algorithm converges accurately—within less than 5% RMS error—even without the line integral condition (C_LI from POCS algorithm). However, the price to pay for forgoing C_LI is an increased number of iterations necessary for convergence. One thousand iterations were used here. It might be interesting to further investigate this finding in the case of attenuation CT.

X-ray DPC systems can also be used to generate small-angle scatter—also known as dark field (Pfeiffer et al 2008, Strobl et al 2008, Bevins et al 2010)—images of the object under study. From the reconstruction standpoint, the imaging equation governing this contrast mechanism is equivalent to that of attenuation CT. Thus, the POCS algorithm (Defrise et al 2006, Ye et al. 2007, Kudo et al 2008, Courdurier et al 2008) can be used without modification for interior small-angle scatter tomography.

Finally, we would like to note that the problem of reconstructing peripheral regions of interest using truncated projection data in so-called exterior tomography can also be solved in DPC-CT. In this case, analytical image reconstruction algorithms developed in absorption CT have been adapted to DPC-CT by the authors’ group (Qi and Chen 2007, Chen and Qi 2008).

4. Conclusion

The projection onto convex sets (POCS) algorithm used to solve the interior problem in attenuation computed tomography (CT) was adapted to differential phase contrast CT (DPC-CT). This was done by forgoing one of the conditions from the POCS algorithm. The DPC-POCS algorithm was shown to eliminate truncation artifacts and to significantly improve the quantitative reconstruction accuracy for both numerical and physical phantom results.

Appendix. Algorithm flowcharts for POCS-DPC

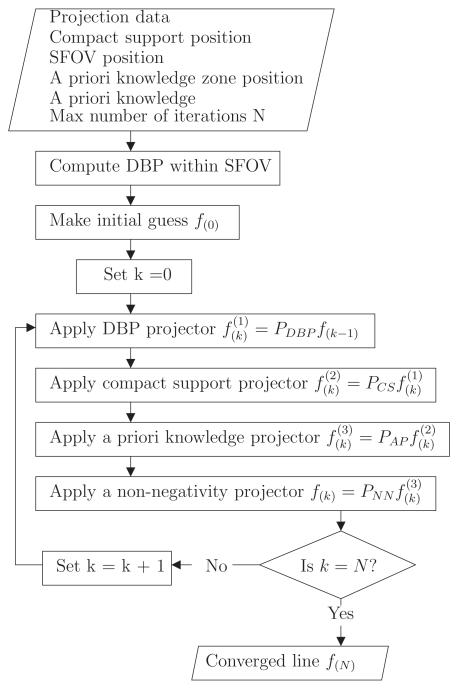
Figure A1.

POCS-DPC algorithm flowchart. Refer to figure A2 for the specific implementation of the projectors.

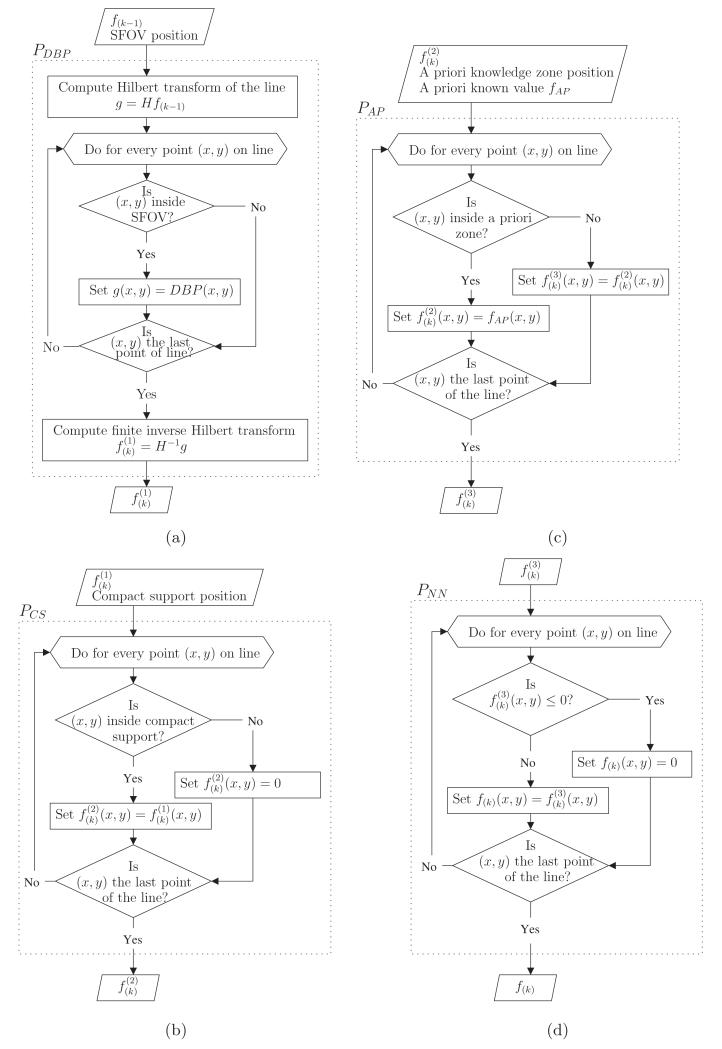
Figure A2.

Projectors algorithm flowcharts. (a) enforces that the Hilbert transform of the image be equal to the DBP within the SFOV. (b) sets any value outside of the compact support to zero. (c) sets the values within the zone known a priori. (d) sets any negative value to zero.