Geometric order in proliferating epithelia: Impact of rearrangements and cleavage plane orientation

Abstract

Regulation of proliferation is required for normal development of tissues and prevention of cancer formation. Continuous control of proliferation leads to regular shaped cells forming characteristic tissue patterns. Epithelial tissues serve as a model system for studying tissue morphogenesis. Several groups have studied epithelial morphogenesis using topological or geometric models, with various assumptions. In this study, we have developed a method to simulate the dynamic process of proliferating epithelia using an off-lattice cellular model. Our method realistically models the shape, size, geometry, lineage, cleavage plane orientation as well as topological properties of individual cells. We find that cellular rearrangements and cleavage plane orientation are critical in the formation of the observed cellular pattern of epithelia, including a high percentage of hexagons in proliferating epithelial cells. It is likely that the rearrangements and orientation of the cleavage plane reduces the overall stress on the cell. We show that a high percentage of hexagons in proliferating epithelia can be obtained using uniform growth rates, which was considered unlikely in previous studies. Our off-lattice cellular model provides an improvement over existing topological for studying the dynamics of proliferating epithelium.

I. INTRODUCTION

Regulation of cell shape and proliferation is essential during the development of tissues. Epithelial tissues serve as a model system to study tissue morphogenesis. Epithelial monolayers are particularly useful as they reduce the problem space to two dimensions. These tissues are well packed and have been known to undergo rearrangements during development. These rearrangements are functionally important, e.g. in a vertebrate lens, the rearrangements result in a hexagonally packed grid which minimizes light scattering [5].

Epithelia have been studied since the beginning of 20th century. F. T. Lewis observed a reproducible distribution of cells with proportionate number of neighbors in cucumber epidermal cells. He also observed that the average number of neighbors was approximately six [7]. Gibson et al. and Patel et al. [1][2] have proposed a simple topological model with regulation of cleavage plane orientation to explain the statistics of this neighbor number. Farhadifar et al. [3] developed a mechanical model to study the neighbor number and Aegerter-Wilmsen et al. [4] extended it by incorporating non-uniform growth rate linked to the area of the cells. This model, however, does not consider cleavage plane or lineage information. McCabe et al. have shown that the area of the cells is tightly regulated and remains homogeneous in the wing disc of Drosophila [8].

In this paper, we study the imaginal wing disc of Drosophila that grows from about 30 to approximately 50,000 epithelial cells [6]. The number of neighbor cells for each cell is dynamic during the growth phase and has been shown to converge to an equilibrium distribution in metazoas [1].

We hypothesize that shape, size, geometry, lineage, cleavage patterns as well as topological properties are necessary and sufficient to reproduce the experimental observations.

II. Methods

A. Modeling

In our study, a cellular system is represented by a vertex model as in previous studies [3][4]. Briefly, cells are represented as polygons. Each vertex represents the junction point where 3 cells meet. Although we use the same vertex model as in previous studies, the physical forces in our model are inspired by the well-studied topic of bubble formation. The compressional forces acting on the vertices are modeled as tension, these include cytoskeletal microfilaments, intermediate filaments, and cell membrane. Forces resisting compression include microtubules and extracellular matrix, these are modeled as pressure.

For an edge between cells a and b, the tension force is always tangential to the edge ab. Pressure force is directly proportional to the difference in pressure in cells a and b and the length of the edge ab. The pressure force is normal to the edge ab.

The net force on a vertex is obtained by summing the forces over all edges incident to the vertex. This net force represents the amount of stress on the vertex at a specific time point. The net force over all vertices sums to zero. During the growth process, the forces acting on a vertex change due to the increase in area of the cell, resulting in a change in stress at the vertex. Local rearrangements of the vertices result in reduction of the stress, which brings the system to the lowest stress state.

B. Topological Changes

There are two types of topological changes when cells grow or shrink. A topological change is required when the same space is occupied by more than one cell. We use two primitives to model these topological changes:

1. Edge Swap: When two originally disconnected cells expand and come into contact, they may push away two previously contacting cells. In this case, we remove the edge between two cells originally in contact, and add a new edge between the two cells that are now in contact.

2. Void Removal: When three cells grow together, new edges are introduced between two contacting cells. When three cells meet at a common vertex, we need to replace the triangular empty space (void) with a new vertex where the three edges meet.

C. Cleavage Plane Orientation

We selected two biologically observed strategies for regulation of cleavage plane orientation, namely, orthogonal and largest-side. Orthogonal orientation as regulation of cleavage plane has been observed in plants [9][10], where the cleavage plane is rotated by 90 degrees in the daughter cells. Thery et al. observed that the orientation of the mitotic spindle in human cells is such that the largest side of the cell is split during cell division, presumably to reduce stress on the largest cell edge [11]. In both these cases the cell splits its area equally into the daughter cells.

D. Simulation Algorithm

We simulate the process of tissue morphogenesis based on our model using the following algorithm. We randomly select a cell from the population and double its area in small steps (random number between five and ten percent of the preferred area). When the area of the cell is doubled in size the cleavage plane is selected based on the specified preference (orthogonal to the mother cell or splitting the largest side). Two new vertices are formed that are joined by an edge passing through the center of the cell. Algorithm 1 is used to update the cell pattern at each step. In order to mimic uniform growth rate, all the cells from one generation divide before the next round of divisions start. The system is allowed to relax and reach a stable state after each set of divisions. We generate 12 generations using this algorithm. For each cleavage plane orientation we run the simulation ten times and draw our conclusions from this ensemble.

Algorithm 1.

UpdateCellPattern (x_t, ΔV(t), σ)

//ε: threshold

while F(x) ≥ ε for all vertices and ΔV (t) not reached

yet do

Obtain updated forces F

Obtain new vertices positions x′ from x′ = x + σF(x)

Update topological changes if required

end while

xt+1 = x′

return xt+1

III. RESULTS AND DISCUSSION

A. Results

We find that both cleavage plane orientations achieve distinct equilibrium distribution as observed in previous studies [1][2]. However, the percentage of different polygon shapes does not agree with those reported in previous studies. This is expected, as the previous studies were based on a topological model, in which a cell is recursively divided. Such a topological model contains no geometric information, and cells become exponentially small after many generations of division. Conclusions in these studies can only be drawn on the topological properties of the cells. Our model is geometric in nature and can capture the effects of rearrangement of cells that occurs during the growth phase. Consequently, our results are more realistic.

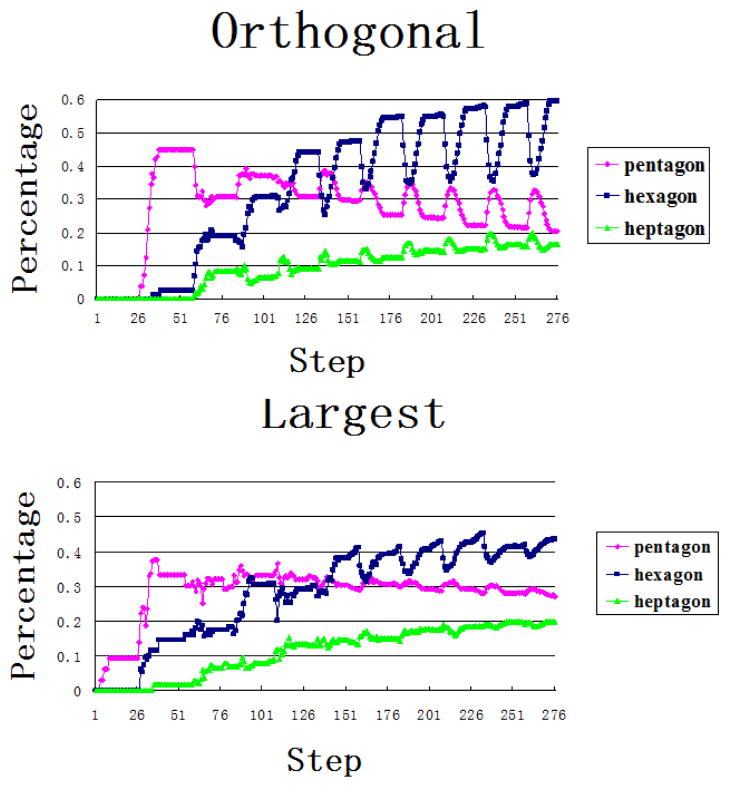
Inspection of the cell shapes obtained by the simulation results (Fig. 3(a) and (b)) show that both simulation schemes yield regular shapes. The largest-side split scheme has small local regions where the cells are slightly elongated, but overall regular shapes dominate. We obtain a very high percentage of hexagons (60 percent Fig. 4 (top)) using the orthogonal cleavage plane orientation model. Such a high percentage has not been observed in previous studies [2]. In fact, it was suggested that global signaling might be needed to obtain more than 60 percent hexagons[2]. Our results clearly demonstrate that this can be achieved by considering the effects of rearrangement of cells and the orientation of cleavage plane during cell growth. We also observed that the variance for different polygon classes in both cleavage patterns was very small, which indicates that initial conditions do not affect the stable configuration of the cellular pattern.

Fig. 3.

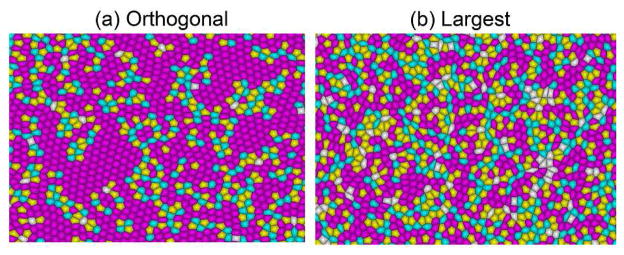
Cell shapes generated by the two schemes (a) Orthogonal cleavage plane orientation (b) Largest side split. Both simulations schemes yield regular shapes. The pentagons are colored yellow, hexagons pink and heptagons cyan.

Fig. 4.

Percentage of pentagons, hexagons and heptagons during the growth using Orthogonal cleavage plane orientation (top) and Largest side split (bottom). The pentagons are colored pink, hexagons blue and heptagons green. The percentage of hexagons is 60 and 44 percent for orthogonal and largest-side split schemes respectively.

1) Comparison to Experimental Data

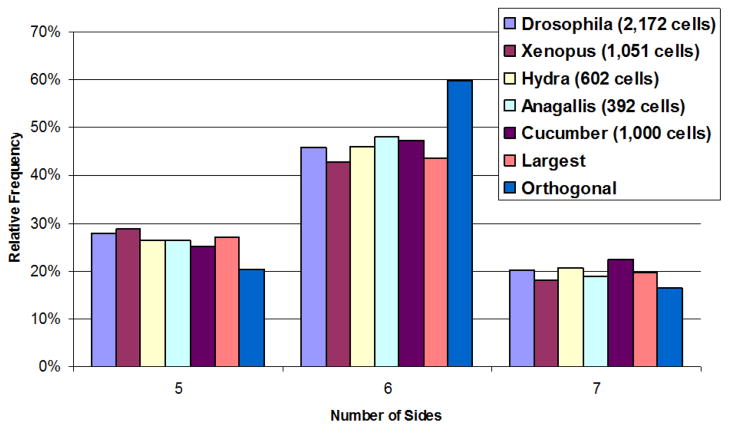
We compare our simulation results with natural proliferating epithelia from Drosophila melanogaster, Xenopus laevis, Hydra vulgaris, Anagallis arvensis and cucumber epidermis. The data was gathered by Patel et al. [2] from different experimental studies, each with replications [1][12][13]. Our data are averages of the results of 10 simulations. We find that the largest-side split scheme strongly agrees with the observed distribution in natural epithelia, while the orthogonal scheme results in very large percentages of hexagonal cells (Fig. 5). These results do not agree with the results of Patel et al., they obtained distribution comparable to the natural epithelia only when using the orthogonal scheme. Our results strongly suggests that topological models as described in [1][2] cannot represent accurately the shape dependent growth of epithelial morphogenesis.

Fig. 5.

Comparison of distribution of pentagons, hexagons and heptagons from the simulation results obtained by cleavage plane orientation schemes(largest-side split and orthogonal) with natural epithelia of five organisms: Drosophila melanogaster, Xenopus laevis, Hydra vulgaris, Anagallis arvensis and cucumber epidermis [12][13][1].

B. Discussion

Our results provide support to the hypothesis that growth of cells is regulated by mechanical stress. It is likely that cells reduce this stress in two ways. First, the orientation of the cleavage plane can be selected such that the largest side is split during division. Second, local rearrangements occur during the growth to achieve more stable tissue conformations. It is possible that a cell uses a combination of two or more cleavage plane orientations, depending on the extracellular signals it receives from the surrounding cells and extracellular matrix. This hypothesis is also supported by the rearrangements in the wing disc of Drosophila melanogaster, where irregular shaped cells rearrange to form a hexagonally packed grid shortly before hair formation [14]. In addition, we show that topological models are not as informative in dynamic systems.

How does the cell know when to stop dividing remains an open question. Recently, it has been proposed that morphogen gradient plays an important role in regulating cell proliferation [16]. Regulation of cell proliferation results in regular cell shapes, which are essential for the function of the cells. As an example, cells in a vertebrate lens are arranged in a hexagonally packed grid, which is important to minimize light scattering.

IV. CONCLUSION

Here we present a method to realistically model the shape, size, geometry, lineage, cleavage plane orientation, as well as topological properties of individual cells. Our method is based on approximately uniform growth rates and produces similar polygon distribution to that observed in natural epithelial cells, without optimizing any free parameters. Specifically, the largest-side split scheme matches the polygon distribution observed in natural epithelia. The orthogonal split scheme results in a very high percentage of hexagons, which was previously thought impossible with uniform growth rates.

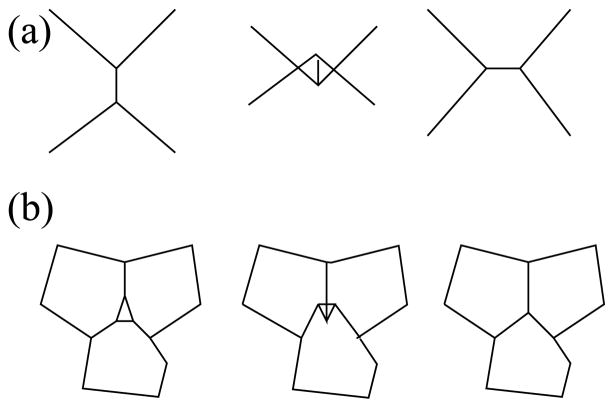
Fig. 1.

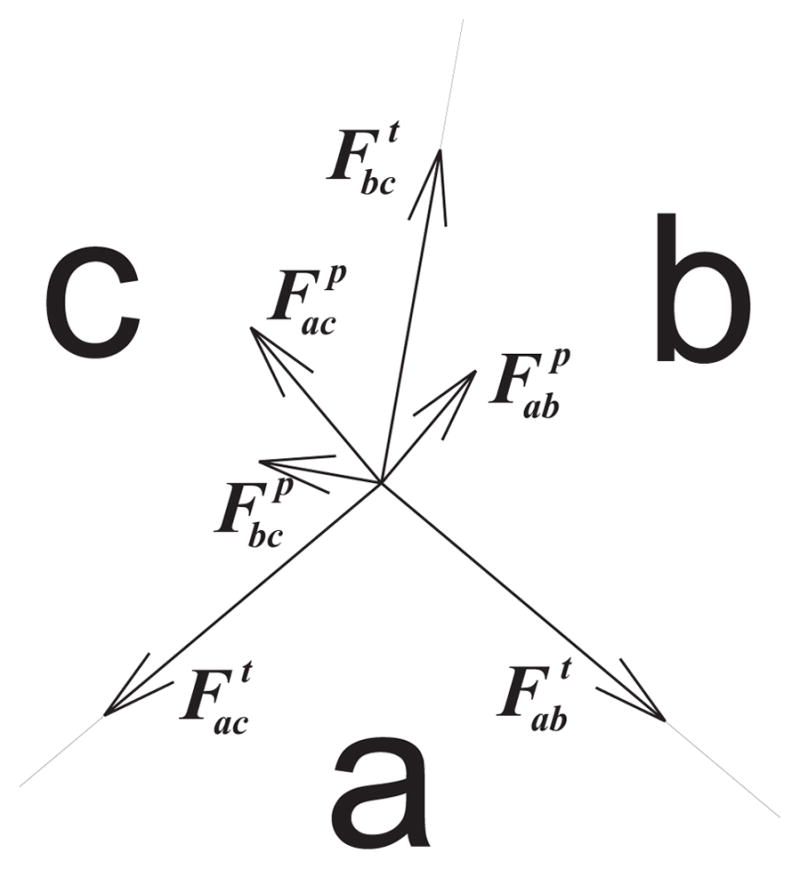
The forces applied to the junction vertex of three cells a, b, and c.

Fig. 2.

Topological changes when cells grow or their boundaries move. (a) Edge swap. When two previously disconnected cells expand to meet while pushing away two previously connected cells, we replace one edge with a new edge.(b) Void removal. When three cells come into contact, the triangular empty space is replaced by a vertex where the edges meet.