Decision Analysis and Cost-effectiveness Analysis

Abstract

Healthcare decision-making can be complex, often requiring decision makers to weigh serious trade-offs, consider patients’ values, and incorporate evidence in the face of uncertainty. Medical decisions are made implicitly by clinicians and other decision-makers on a daily basis. Decisions based largely on personal experience are subject to many biases. Decision analysis and cost-effectiveness analysis are systematic approaches used to support decision-making under conditions of uncertainty that involve important trade-offs. These mathematical tools can provide patients, physicians and policy makers with a useful approach to complex medical decision making.

Introduction

Many decisions that physicians make in the course of their daily practice are part of routine medical care and involve little thought, uncertainty, or risk. However, decisions must also be made in diagnostic or treatment dilemmas for which there are no easy answers. Incorporating evidence, weighing difficult trade-offs between potential benefits and harms, and including patients’ values for these outcomes can be a very complex challenge. Decision analysis and cost-effectiveness analysis are quantitative techniques that provide a systematic approach to integrating evidence within the context of a specific decision problem. The goal of decision analysis is to facilitate sound decisions in complex and uncertain situations by identifying the course of action that will, on average, maximize the desired outcome. We will use the decision about management of lumbar disc herniation to illustrate the principles of medical decision analysis and cost-effectiveness analysis.

Expected value decision making

In most medical decisions, the outcomes are inherently uncertain. For example, it is often not known at the outset what the underlying cause is for a patient presenting with severe back and leg pain. Expected value decision making uses explicit values placed on different outcomes combined with the probability of those outcomes as a guide to choosing between options. Expected value is what would occur “on average” if the decision were repeatedly played out multiple times(1). Most patients will improve after disc surgery but a small percentage of the time a severe complication will occur. The expected value of a treatment choice (e.g. disc surgery) is the weighted average of all the possible outcomes, where the weight is the chance of each outcome occurring. If the decision objective was to maximize quality-adjusted life expectancy, a person following expected value decision making would pick whichever treatment option yielded the highest quality-adjusted life expectancy. In contrast, if the decision objective was to minimize costs, the treatment option that resulted in lowest average costs would be chosen.

Decision Analysis

Decision analysis involves using specific tools and mathematical methods to identify, assess, and represent key features of a decision and can be quite helpful when facing decisions with uncertain outcomes or when treatment options have significant trade-offs between risks and benefits.

The basic steps in decision analysis are as follows: 1) define the decision problem (including specifying the decision-maker and the ultimate goal or objective of the decision); 2) identify all the decision alternatives; 3) list all the possible outcomes of each decision alternative; 4) define the relevant time horizon; 5) map out the sequence of events leading from the initial decision to the relevant outcomes including chance events and secondary decisions; 6) quantify uncertainty: determine the probability of each chance outcome; 7) quantify values: assign a value to each outcome; 8) calculate the expected value of each decision alternative(1). The process of explicitly quantifying the uncertainty and values involved in a decision problem provides valuable insight into the key issues and controversies inherent in the decision.

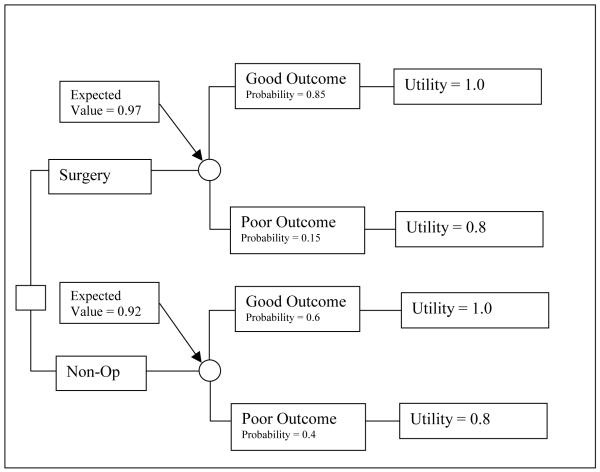
Decision trees are diagrammatic representations of this process. A decision node, typically represented by a square, is a point where several alternatives are possible. A chance node, typically represented by a circle, is a point in a decision tree where chance determines which event will occur. The sum of probabilities for all branches emanating from a chance node must equal 1.0, because one of the events must occur.

A very basic decision tree for two treatment options is shown in Figure 1. The value of each decision alternative is obtained by multiplying the value of each outcome by its respective probability. These results can be added at the previous chance node on a decision tree, also known as “folding back the tree.” In this case the surgery has a higher probability of a “good outcome” and yields higher expected value on average than non-operative care and would be the preferred choice.

Figure 1.

A basic decision tree.

Valuing Clinical Outcomes

Depending upon the decision perspective and objective, multiple possible outcomes can be used in decision analysis. Common outcomes include survival (the probability of death/survival), 5-year survival, costs, quality-adjusted life expectancy (QALE), and quality-adjusted life years (QALYs). QALYs require assigning a value or utility to represent the level of desirability of each outcome, anchored at zero for dead, and one for perfect health. The three major techniques for capturing preference-based quality-of-life values include the standard (reference) gamble, the time trade-off, and the rating scale(2).

The standard gamble incorporates uncertainty into the preference measurement and yields a utility as defined by von Neumann and Morgenstern(3). Participants are offered a choice between the health state of interest and a gamble between perfect health, with probability p, and immediate death, with probability 1-p. The probability of the best outcome within the gamble is changed until the respondents are indifferent between the health state of interest and the gamble. At the point where participants are indifferent, the utility for the health state of interest is p, the expected value of the gamble. For example, if an individual is indifferent between continuing with his health state and a gamble with a 20% chance of death (utility of 0) and an 80% chance of perfect health (utility 1), then the utility for his current health state is 0.8.

The time tradeoff technique offers a choice between life in the health state of interest (e.g. life expectancy of 30 years) and life in perfect health for a shortened duration. The amount of time in perfect health, x, is varied until participants reach their point of indifference. The ratio of time in perfect health to life expectancy in the health state of interest, x/30, yields the elicited preference. Strengths include its choice-based elicitation method, and the similarity of the elicitation choice to many health decisions people make on a regular basis.

A rating scale is often presented as a visual analog scale on which participants mark the value for health states, anchored at 0 dead and 100 for perfect health. Although one advantage is the simplicity of administration, evidence suggests there may be some degree of cognitive challenge for participants(4). The lack of explicit choice or uncertainty is perceived by some as a weakness of the rating scale for public health policy applications (5).

Having emerged from different disciplines and conceptual frameworks, each preference elicitation method has unique strengths and limitations. Many studies report differences between preferences obtained by these methods, often finding health state values are highest for the standard gamble, intermediate for time tradeoff, and lowest for the rating scale (6-8).

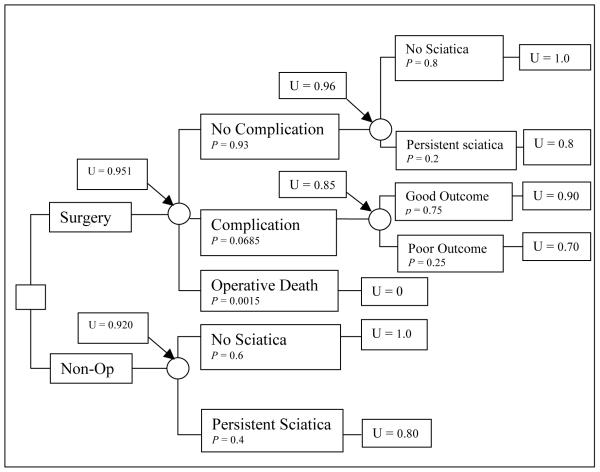
A simple decision tree (Figure 2) illustrates possible decisions and potential outcomes for a patient with six weeks of low back pain, L5 radicular symptoms with severe sciatica, a positive contralateral straight leg raising test, and an extruded disc at L5-S1 on MRI. Surgery offers a more rapid improvement in symptoms but carries with it a risk of complications. Conservative medical therapy offers good outcomes in the long term with no major risks, but with greater symptoms in the short term(9-11). The decision has been diagrammed and the probabilities of the outcomes are available, but the optimal choice is not yet obvious. The best choice will depend on how the patient values the outcome states. In the hypothetical example shown, the probabilities and utilities yield a higher expected value for surgery, and this would be the preferred choice in this case.

Figure 2.

A simple decision tree for lumbar discectomy for a hypothetical patient with severe sciatica. p represents the probability of each outcome at the chance node and U represents the utility of each outcome.

Quality-Adjusted Life Years (QALYs)

Obviously, the decision tree in Figure 2 and in particular the final outcomes states such as “continued symptoms” or “major improvement” are vastly oversimplified; in particular there is no consideration of how quickly improvement occurred or how long patients would remain in any particular health state. The quality-adjusted life year (QALY) was developed in an effort to combine the attributes of length and quality of life into a single numeric measure. The U.S. Panel on Cost-Effectiveness in Health and Medicine recommended QALYs as the most desirable effectiveness measure for economic analyses of health interventions (12). Health outcomes or “states” are assigned a value on a scale anchored at zero, representing worst imaginable health or death, and one, representing best imaginable health or perfect health. The length of time in each health state is weighted according to its “health state value.” By definition, one year of perfect health is worth one QALY and one year of less than perfect health is worth less than 1 QALY(13). If, for example we found, using the standard reference gamble, that living with severe sciatica had a utility of 0.8, then 2 years spent with persistent sciatica would result in 1.6 QALYs.

Decision analysis can incorporate an individual patient’s health state values when the focus is decision-making for an individual. However, it is frequently used to inform decisions on a broader policy level where overall societal values for different outcomes and health states are a more appropriate metric. Direct measurement of societal health state values is a resource intensive endeavor, requiring development of relevant health state descriptions, access to a representative population sample, and in-person interviews. Therefore, researchers may prefer to measure health states and health effects directly on the population of interest and convert these to societal health state values. Preference-weighted health state classification systems were developed for this purpose.

Preference-weighted health state classification systems define each respondent’s health state using a health status questionnaire and assign a societal health state value with a scoring algorithm that incorporates preferences from a general population sample. This approach allows researchers to use societal health state values with minimal resource requirements compared to direct preference measurement. The most widely used systems(14) include the EuroQol 5D (EQ-5D),(15, 16) the Health Utilities Index (HUI)(17), the Quality of Well-Being Scale (QWB)(18), and the SF-36-derived SF-6D(19).

Sensitivity analysis

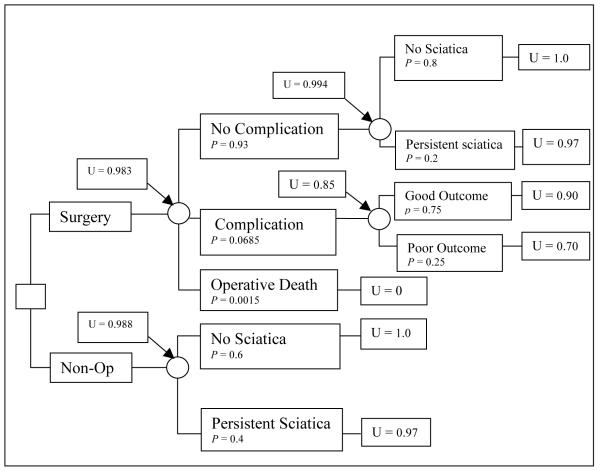
One of the advantages of a formal decision analysis is the ability to vary model input probabilities and values (i.e., parameters) within the tree in a systematic fashion in order to assess how sensitive the decision alternative identified as having the best expected value is to uncertainties in the model. This is known as a sensitivity analysis. A sensitivity analysis is performed by varying model parameters to determine which assumptions in the model are fundamental and how changing utilities or probabilities will affect the decision. Using our previous example, we might find that patients with mild sciatica have a utility for their health state of 0.97 (compared to 0.8 for the previous example of severe sciatica). In this case, non-operative therapy becomes the preferred choice (Figure 3).

Figure 3.

A simple decision tree for lumbar discectomy for a hypothetical patient with mild sciatica. p represents the probability of each outcome at the chance node and U represents the utility of each outcome.

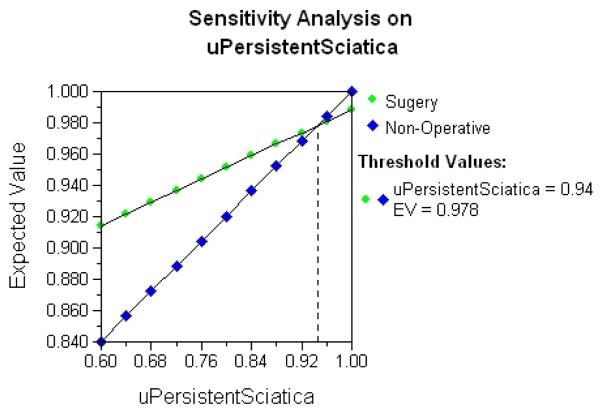
Results from a one-way sensitivity analysis where the utility for persistent sciatica is systematically varied from 0.6 to 1.0 are shown in Figure 4. The expected value for each treatment alternative (vertical axis) is plotted as the utility for persistent sciatica changes on the horizontal axis. The crossing lines for surgery and non-operative treatment indicate that a threshold health state utility for persistent sciatica exists. Above a utility of 0.94, non-operative care is the preferred decision alternative, while below 0.94 surgery is preferred.

Figure 4.

Results from a one-way sensitivity analysis where the utility for persistent sciatica is systematically varied from 0.6 to 1.0. Crossing lines indicate that a threshold health state utility for persistent sciatica exists. (Color version of figure is available online.)

Limitations of decision analysis

While decision analysis is a powerful tool, there are significant limitations which limit its widespread use in medicine. Formal decision analysis, involving creating decision trees and utility scales and performing sensitivity analyses, is time consuming and can be impractical in clinical practice with individual patients. However, as computer technology advances, performing decision analysis will likely become easier and more user-friendly. Another limitation is the over-simplification of complex medical problems and values of patients inherent in decision analysis, which can be extremely helpful in some settings but quite limiting in others (20). Finally, decision models require the availability of accurate and valid data on the likelihood of specific patient outcomes, which often may not be available.

Cost-effectiveness analysis

Decision analysis can be used to assess the expected costs of decision alternatives. In this era when health-care dollars are increasingly limited and resources may be scarce, there is frequently a trade-off between health outcomes and costs. The underlying goal of public health care allocation decisions is to attain maximal health benefit for a given budget, and this requires information about program effects on health and associated costs(21). Cost-effectiveness analysis refers to methods within the realm of economic evaluation used to analyze the costs and health consequences of alternatives(2, 12, 22). In practice, cost-effectiveness analysis most often involves the comparison of two or more alternatives where one offers improved health but at increased cost; the goal is to determine whether the expected results of an intervention are “worth” the added costs.

The perspective used to conduct economic evaluation is critical in framing every aspect of the analysis. A range of perspectives can be used, including that of an employer, a health care insurer, health care provider, governmental agency or society at large. An evaluation from an insurer’s perspective would include costs and effects important to the insurer and would differ from those of interest to a health care provider group. For public policy applications, the recommended perspective is societal(12), meaning that study design should reflect society’s interest in the effects of interventions on all stakeholder groups. Therefore, the societal perspective requires the broadest approach to characterizing costs and health outcomes of treatment, regardless of who experiences them. For health effects, it should include the full range of results, desired and undesired. Costs should include all resource use, including those for which money is not actually exchanged. Examples of outcomes that can be used in a cost-effectiveness analysis are estimates of years of life saved, number of injuries averted, number of correct diagnoses made, degree of blood pressure reduction, etc. However, as noted earlier, for economic evaluation to inform public policy the recommended measure of health effect is the QALY, which requires preference based health state values from the societal perspective using representative population samples(23).

Incremental cost-effectiveness ratio

The incremental cost-effectiveness ratio(ICER) is the primary outcome measure in cost-effective analysis (24); it is the ratio of the incremental costs of an intervention to the change in health outcomes due to the intervention, compared to a defined alternative. The numerator of the ICER is the costs, in monetary units (e.g dollars). The denominator is the health improvement related to an intervention, typically measured in QALYs. If a new treatment is both more effective and less expensive, then that treatment is “dominant” and the choice is clear. Similarly if it is less effective and more expensive, the treatment is obviously inferior and again the choice is clear. However if a treatment is more effective but also more expensive, or conversely somewhat less effective but cheaper, the ICER quantifies that trade-off between the added cost and the QALYs gained. While interventions with incremental ratios of less than $50,000 to $100,000 per QALY gained are often regarded as reasonably “cost effective” (25), the value of each intervention must be compared with the value of commonly accepted treatment alternatives.

Determining costs

An important characteristic of a good CEA is that all aspects of a decision should be identified and that all the relevant costs are measured accurately. In determining both costs and health benefits, the analyst should consider all those affected by the intervention and include direct, indirect, and future costs in the analysis. Direct costs are the traditional health care related costs such as physician fees and hospital costs. Indirect costs are costs related to the condition or the treatment that are not directly related to the provision of the health care service such as patient time lost from work, travel expenses, child care expenses and costs associated with caregiving by family members or others(23). Costs after the intervention, or future costs, such as rehabilitation costs or lost wages post-operatively, should also be considered in the analysis.

Future costs are typically discounted to reflect the idea that future dollars (and thus future expenses) are worth less than present dollars and expenses. For example, people pay interest to have money sooner rather than later because it is of more value to them in the present than the future. Future health should also be discounted at the same rate (typically 3%).

The method of determining costs has a decisive impact on the determination of cost-effectiveness. For instance, using average prices charged to third-party payers (rather than actual costs) may cause an intervention to seem more costly than it is. Guidelines for calculating and reporting cost-effectiveness analyses are available (23, 24, 26). In order to be relevant to health policy decision making, CEAs should typically be calculated from the societal perspective rather than the perspective of the health care provider, patient, or payor(24).

Interpreting cost-effectiveness analyses

Understanding how to evaluate the cost-effectiveness of an intervention requires critical reading skills and a familiarity with the information that should be presented in a thorough analysis. A good-quality published CEA should allow the reader to determine the perspective and boundaries of the analysis, understand the methodology behind it, and provide the quantitative results as well as an assessment of the degree of uncertainty in the estimates. To understand these concepts, we will review several analyses that have been published on the cost effectiveness of lumbar discectomy for symptomatic lumbar disc herniation (27-31).

Framework

After stating the problem to be studied, a good-quality article should report the study framework, including study design and data sources. For example, Malter et al.(29) used a model which combined previously published efficacy data with newly gathered cost data to try to determine their cost-effectiveness ratio. Van den Hoot et al.(31) performed cost effectiveness analysis as part of a clinical trial, prospectively measuring costs and effectiveness in the two treatment groups of a randomized-controlled trial and comparing the outcomes in both groups using a cost-effectiveness ratio. When cost-effectiveness is measured in a trial, methodologic characteristics of the trial related to study quality and validity such as subject selection, allocation concealment, blinding, and drop-out rates are important features that should be reported in the cost-effectiveness analysis.

The scope or boundaries of the analysis, for instance the time frame and extent of benefits and harms that are included, are critical for determining the applicability of the results. Interventions with a higher up-front cost but improved long-term outcomes, like surgery, will look less cost-effective in a short time-frame and more cost-effective over a longer time-frame. In addition, understanding the perspective of the analysis is vital; both costs and benefits can be viewed from the patient, payor, provider, or societal perspectives with potentially very different results.

Data and methods

The article should clearly describe the outcome of interest and how it was measured; it is important to determine in detail how both costs and benefits have been determined(32). For cost data, the sources of direct costs, and methods for measuring and valuing indirect costs should be available. Hansson and Hansson(27) calculate costs and benefits from a societal perspective with direct costs consisting of medical costs and travel expenses and indirect costs consisting of lost productivity and disability benefits estimated from patients’ journals of lost work and their reported salary or disability benefits (representing the societal perspective). The methods for determining QALYs should be described and supported and should typically use a standard, validated preference-weighted health state classification system or describe in detail the population and methods used for eliciting preference weights. The discount rate used for future costs and health effects as well as the specifics of sensitivity analyses should be described(33).

Results

The base or reference case gives the results of the CEA using the authors’ best estimates for each of the parameters in their model(34). The reference case results should include total costs and effectiveness of the proposed treatment and incremental cost-effectiveness ratios to allow the reader to understand the magnitude of cost and health benefits. Review of the incremental costs and effects allows the reader to verify the methods used and assess their validity. For example, Tosteson et al. found that surgical patients improved by a total mean difference of 0.21 QALYs compared to nonsurgical patients(28). The study found that total mean costs for surgically treated patients were $14,233 more than for non-operative patients. Increased costs within the surgically treated group were attributed not only to direct medical costs but also increased missed work. Given the incremental costs of $14,233 and incremental effectiveness of 0.21 QALYs with surgery, the study found that the cost per QALY gained for surgery compared to non-operative care for the general population was $69,403 ($14,233/0.21 QALYs).

Uncertainty of the results should be directly addressed in any CEA. Confidence intervals around the ICER should be estimated based on either statistical methods or simulations(23). Sensitivity analyses, testing alternative cost and utility data or alternative discounting strategies, and demonstrating the robustness of the analysis, are critical; one way sensitivity analyses (varying only one factor in the model) may underestimate the degree of uncertainty in a CEA and multiway sensitivity analysis, in which several estimates or assumptions are varied simultaneously, are recommended(33). In the aforementioned CEA, Tosteson et al. performed a sensitivity analysis analyzing patients 65 and older using Medicare costs, giving a cost/effectiveness ratio of $34,355/QALY (markedly less than the $69,403/QALY based on private payor costs), showing that the analysis was relatively sensitive to the cost of surgery. In additional sensitivity analyses, the model results were similar when costs were limited to direct medical costs or medical costs with lost work days, indicating that their model was fairly robust to the types of costs included(28).

Discussion

A review of the summary of the reference case results, as well as the robustness of the sensitivity analysis should be available in the discussion section of the cost-effectiveness analysis. As with any good-quality study, a discussion of the study limitations should be available to assist the reader in determining the generalizability of the results and sources of error or bias. Malter et al.(29) state that their findings are not completely generalizable in that their model was based on a relatively young population with unequivocal radiographic and symptomatic indications for surgery. They remark that limitations of the study include estimating cost and effectiveness from data collected on different subjects 10 to 20 years prior to the analysis. Because cost-effectiveness is relative, absolute statements as to the cost-effectiveness of an intervention should be viewed with skepticism. Typically results are compared to other established interventions as being relatively more or less cost-effective.

The complexity of cost-effectiveness studies may cause readers to become lost in the details available. A checklist (Table 1) may be of assistance to a reader attempting to assess the quality and validity of a CEA.

Table 1.

Checklist for reviewing cost-effectiveness analysis

Framework

Outline of the problem

Research objectives

Study design, including time horizon and type of analysis

Data and methods

Outcomes of interest

Perspective of the analysis

Description of model used and its assumptions

Descriptions of tools used to estimate effectiveness, health states and resource use

Methods of obtaining estimates of effectiveness, costs, and preferences

Methods used for weighing information and discounting future costs and benefits

Results

Results of model validation

Reference case results: total costs and effectiveness, incremental costs and  effectiveness and incremental cost-effectiveness ratios

Results of sensitivity analyses

Discussion

Summary of reference case results

Summary of robustness or sensitivity of results

Limitations of the study

Comparisons to related cost-effectiveness analyses

Adapted from Siegel et al. (1996).³²

Limitations of cost-effectiveness analysis

As stated previously, cost-effectiveness analysis is a method for determining the most cost-effective management strategy to achieve a specific health outcome as well as the best way to maximize overall health with a given budget(35). While it is a powerful tool, it has limitations. Since costs are measured in dollars and benefits are measured clinically, there is no way to determine whether benefits exceed costs; there is no absolute criterion, other than convention, to decide how much one “ought” to be willing to pay for a QALY. In addition, extreme care must be employed in evaluating the methods and assumptions employed in the model as subtle biases in the specification of the model can dramatically alter the results.

Overall, the number of published cost-effectiveness analyses has steadily grown over the past 20 years(36), and use by policy-makers appears to be increasing(37). In some jurisdictions, including the UK, Australia, and the Canadian provinces of Ontario and British Columbia, a formal role for cost-effectiveness analysis in pharmaceutical coverage decisions is mandated(37, 38). In others, such as the US, explicit use of cost-effectiveness analysis is more limited(39-42).

Conclusion

Decisions are often made using implicit knowledge or values. Decision analysis deconstructs decisions, identifying all important aspects of a decision, representing each potential choice schematically, and assigns a value to each potential outcome in order to evaluate the overall situation. Common outcomes include survival, quality-adjusted life years (QALYs), and cost. After a decision model has been created, a sensitivity analysis can determine the robustness of the results to the value and probability estimates used in the model.

Cost-effectiveness analysis takes an additional step of directly addressing the potential trade-offs of added costs and improved health outcomes and allows decision makers to evaluate the allocation of resources by characterizing the cost of health interventions per added unit of benefit. More and more, cost-effectiveness analysis is being incorporated directly into the design of prospective clinical trials. Physicians familiar with cost-effectiveness analysis reading a published CEA study should be able to determine the perspective, understand the methodology used to calculate the costs and QALYs, determine the ICER, understand the degree of uncertainty in the estimates, and understand how robust the results are to variations in the model parameters from a sensitivity analysis. While cost-effectiveness analysis has limitations, if performed correctly, it can provide useful information to patients, physicians, and policy-makers.