Abstract
Objective
There is growing interest in using closed-loop anesthetic delivery (CLAD) systems to automate control of brain states (sedation, unconsciousness and antinociception) in patients receiving anesthesia care. The accuracy and reliability of these systems can be improved by using as control signals electroencephalogram (EEG) markers for which the neurophysiological links to the anesthetic-induced brain states are well established. Burst suppression, in which bursts of electrical activity alternate with periods of quiescence or suppression, is a well-known, readily discernible EEG marker of profound brain inactivation and unconsciousness. This pattern is commonly maintained when anesthetics are administered to produce a medically-induced coma for cerebral protection in patients suffering from brain injuries or to arrest brain activity in patients having uncontrollable seizures. Although the coma may be required for several hours or days, drug infusion rates are managed inefficiently by manual adjustment. Our objective is to design a CLAD system for burst suppression control to automate management of medically-induced coma.
Approach
We establish a CLAD system to control burst suppression consisting of: a two-dimensional linear system model relating the anesthetic brain level to the EEG dynamics; a new control signal, the burst suppression probability (BSP) defining the instantaneous probability of suppression; the BSP filter, a state-space algorithm to estimate the BSP from EEG recordings; a proportional-integral controller; and a system identification procedure to estimate the model and controller parameters.
Main Results
We demonstrate reliable performance of our system in simulation studies of burst suppression control using both propofol and etomidate in rodent experiments based on Vijn and Sneyd, and in human experiments based on the Schnider pharmacokinetic model for propofol. Using propofol, we further demonstrate that our control system reliably tracks changing target levels of burst suppression in simulated human subjects across different epidemiological profiles.
Significance
Our results give new insights into CLAD system design and suggest a control-theory framework to automate second-to-second control of burst suppression for management of medically-induced coma.
1. Introduction
Development of a closed-loop anesthetic delivery (CLAD) system is a standard feedback control problem. An anesthetic drug is delivered to a patient using a computer-controlled infusion pump, based on a model of how the drug affects the anesthetic states of the brain. A control signal that relates the brain’s response to the anesthetic is defined in terms of an electroencephalogram (EEG) signature. The control signal is computed in real-time and used to generate an error signal, the difference between the measured value of the EEG signature and the level targeted to maintain the desired anesthetic state. Given a specific control strategy, the error signal is processed and fed back in real-time to adjust the rate of drug administration by the infusion pump. CLAD systems offer the possibility of continuous, close control of a patient’s anesthetic state while using less drug than an anesthesiologist would by manual control [1–9].
Bickford proposed the first CLAD system more that 60 years ago [10]. However, system development did not begin in earnest until the 1980s [11]. Since then, there have been many clinical studies on the use of CLAD systems in anesthesiology practice, and systems are now commercially available [12]. Although most CLAD systems have focused on delivering anesthetics to achieve sedation or unconsciousness [1–6,8–11,13–26], a recent report studied control of unconsciousness and antinociception [7]. The control signals have included the median frequency of the spectrogram [22, 23], entropy measures [7], a wavelet-based depth of anesthesia index [24], an auditory evoked potential index [17], and most frequently, the Bispectral Index (BIS) [1–6, 8, 9, 13–16, 20, 21]. These systems have used a range of standard and non-standard control strategies [2,7,11,14,17].
Despite the significant progress in CLAD system design, further improvements should be possible. First, for each control signal a monotonic relationship between the signal and the anesthetic state is assumed or established, yet the neurophysiological mechanism of how each signal relates to the specific state is not known. Second, although BIS has been the most widely used control signal in CLAD studies, BIS computations require up to a 20-second delay to output a new value, making true real-time feedback not possible with this index [27]. Third, the control target has often been specified as a range—say, a BIS between 40 and 60. Maintenance of the BIS within this range is considered successful control. Maintenance of the anesthetic state at a specific value of the control signal, as has been demonstrated in some studies [11], is more challenging but would represent a tighter level of control [5]. Therefore, a plausible approach to improving CLAD system design is to identify neurophysiologically-based EEG signatures that relate directly to well-defined anesthetic states and that can be processed in real-time to achieve reliable individual control.
We hypothesize that developing a CLAD system to control burst suppression would be a good starting point for studying the feasibility of these possible improvements. Burst suppression, an EEG pattern in which periods of bursts of electrical activity alternate with periods of isoelectricity, i.e. flatlines, (Fig. 1A), is a state of profound brain inactivation and unconsciousness seen in deep general anesthesia, hypothermia, significantly compromised brain development and coma [28, 29]. Burst suppression is a much studied anesthetic state. A long-standing interpretation is that burst-suppression represents an active thalamic stimulus being transmitted to a largely inactivated cortex [30]. A recent modeling study has shown that burst-suppression likely arises when the brain rates of ATP production are insufficient to maintain the integrity of ATP-dependent potassium channels [31]. Maintenance of burst suppression for extended periods is a practice used in intensive care units to treat patients with brain injuries [32]. Anesthetic drugs such as propofol, barbiturates, midazolam and fentanyl are administered to brain injury patients during their acute recovery periods to render them unconscious and to reduce brain swelling by decreasing cerebral metabolism and blood flow [32]. Similarly, large doses of propofol, barbiturates or inhaled anesthetics are the last-line treatment for patients with refractory status epilepticus, i.e., uncontrollable seizures [33,34]. When anesthetics are administered in this way the drug-induced state is termed a medically-induced coma [35].
Figure 1. Illustrative example of burst suppression.
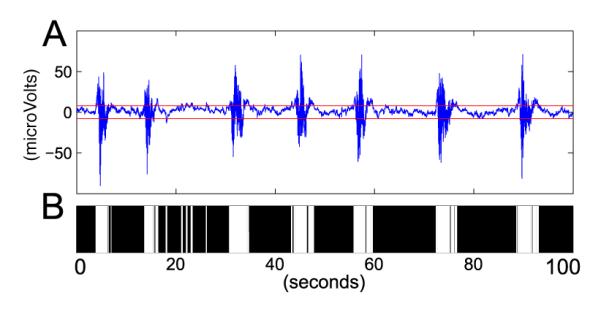
(A) A 100-second epoch of burst suppression recorded from the EEG of a human in response to bolus administration of the anesthetic propofol. Red lines are the 5 microVolt amplitude thresholds. (B) Binary representation of EEG computed from the amplitude threshold. White (black) indicates burst (suppression) events or 0s (1s) when the absolute value of the EEG amplitude is greater (less) than the 5 microVolt threshold. The data were recorded at 1KHz and filtered between 0.1 and 70 Hz.
The current approach for controlling a medically-induced coma—choosing a target level of burst suppression, monitoring continually the EEG, and adjusting manually the anesthetic infusion rate—is inefficient. Because the state of coma is often maintained for several days, it is unrealistic to expect human management to maintain close control on a minute-to-minute basis. Close control is advantageous for balancing important trade-offs: providing adequate brain protection; allowing intermittent arousals to assess neurological status; and avoiding the undesirable consequences of anesthetic overdose syndrome [36]. This suggests that the control of medically-induced coma could be automated by designing a CLAD system to control the level of burst suppression [31,32].
The level of burst suppression can be quantified by computing the burst suppression ratio (BSR) defined as the proportion of time the EEG is suppressed in a given time interval [37]. The BSR ranges from 0, meaning no suppression, to 1, meaning an isoelectric EEG. Vijn and Sneyd designed CLAD systems for rat models of propofol and etomidate using BSR as the control signal [38]. The objective of their investigation was to develop a model-free approach to CLAD design to determine if performance in a CLAD system could provide useful information for drug development. Their error signal, the difference between a specified BSR level and the BSR computed from the EEG, was the input to a deterministic controller constructed as the product of a proportional term and an integral term. Although the authors claim that their CLAD system maintained BSR at specific targets for both propofol and etomidate, they reported BSR time courses only for the average of 3 rats and for no individual animal. The Vijn and Sneyd system was recently implemented to test the efficacy of new etomidate-based anesthetics in controlling BSR in rats [39]. These authors also reported only average BSR time courses. To our knowledge there are no studies using CLAD systems to control burst suppression in human experiments or to control it in the intensive care unit to maintain medically-induced coma.
We conduct a theoretical study of CLAD system design for maintenance of burst suppression using a new concept, the burst suppression probability (BSP), as the control signal. We reanalyze the Vijn and Sneyd data and derive a two-compartment burst-suppression-specific model for both propofol and etomidate in rats. We also establish a 2-dimensional model for propofol in humans by deriving approximations to the standard 4-compartment model [40]. We use these models to design drug-specific proportional-integral (PI) controllers to maintain the BSP at target levels. Our simulation studies show that this model, with a PI controller and BSP signal estimated from the EEG using a binary filter algorithm, can control burst suppression maintained by propofol and etomidate over a broad range of target values.
2. Theory
To construct our CLAD system we define the state model, the control signal, the state estimation algorithm, the system identification procedure, and the controller.
2.1. A State Model of Burst Suppression
We assume that two is the minimal dimension of a state model required to define the brain’s state of burst suppression in response to administration of an anesthetic. We construct our state model by adapting a two-compartment linear pharmacokinetics system for intravenous drug infusion (Fig. 2). We let x(t) = (x1(t),x2(t))’ be the state of the system at time t where x1(t) is the amount of anesthetic in the peripheral compartment, x2(t) is the amount of the anesthetic in the brain or the effect-site compartment, and ’ denotes the transpose of the vector. We let I(t) denote the infusion rate of the anesthetic at time t. We assume that: drug enters into the peripheral compartment; drug flows back and forth between the peripheral and the brain compartments; drug is eliminated from the body only through the peripheral compartment; and the amount of drug in the brain compartment determines the EEG level of burst suppression. The differential equation defining our state model (Fig. 2) is
| (1) |
where
| (2) |
where A is the matrix of rate coefficients controlling the flow of anesthetic between the compartments and the elimination from the body and u(t) is the external input to the system comprised of I(t) the drug infusion rate modulated by a gain coefficient b.
Figure 2. Two-compartment pharmacokinetics-binary observation model.
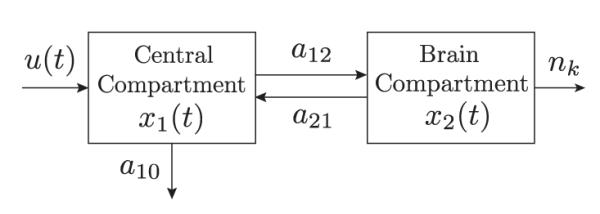
The pump infusion rate u(t) governs the flow of anesthetic into the central compartment. The kinetic rate parameters a12 and a21 govern the anesthetic flow between the central compartment and the brain compartment. The variable x1(t) is the amount of anesthetic in the central compartment and the variable x2(t) is the amount of anesthetic in the brain compartment. The rate parameter a10 governs the rate of anesthetic clearance from the central compartment. The observation nk is the binary form of the EEG at time t = kΔ. By Eqs. (3) to (5) the probability of observing nk is a function of x2(t).
One justification for this model comes from considering how burst suppression is produced and how the pharmacokinetics of anesthetics are modeled. In general, 3- and 4-compartment models are commonly used to describe the pharmacokinetics of anesthetics. Burst suppression is a profound state of general anesthesia so that once the brain is in this state, its activity falls into a limited dynamic range. That is, if sufficient drug has been administered to induce burst suppression, then administering more will only deepen the state of burst suppression, i.e., lengthen the suppression periods, until the EEG is isoelectric. Similarly, if the infusion rate is decreased or turned off, burst suppression will gradually disappear. As a consequence, once the brain is in burst suppression, the model need only describe transitions to higher or lower levels of burst suppression. A second-order system using a peripheral and a brain compartment is a flexible, elementary model for describing these dynamics. This effectively means using the peripheral compartment to represent all of the compartments other than the brain compartment that are typically in the 3- and 4-compartment models. An alternative justification of the 2-dimensional model can be derived by showing that it approximates a recently reported neural-metabolic model of burst suppression [31].
2.2. Notation, Observation Model and the Definition of Burst Suppression Probability
We assume that the control experiment is conducted on the interval [0, T]. We discretize by choosing a large integer K and defining Δ = K−1T to divide the interval (0, T] into K subintervals of width Δ. Subinterval k is defined as ((k − 1)Δ, kΔ] for k = 1, 2, …, K and the value of the system in Eq. (1) for t ∈ ((k − 1)Δ, kΔ] is given by its value at t = kΔ. We let k denote the time t = kΔ and we use the notation (·)k to express the model components evaluated in discretized time. For example, we have at time t = kΔ, xk = (x1,k, x2,k)’.
The response of the brain to the anesthetic is monitored by the EEG. We assume that a sufficient dose of an anesthetic is administered to a subject to induce burst suppression and that the effects of the anesthetic can be observed continuously in time by recording the EEG. To link the EEG state of burst suppression to our model in Eq. (1) we assume K is chosen sufficiently large to ensure that Δ is sufficiently small so that each subinterval ((k − 1)Δ, kΔ] contains at most one binary event nk. We define nk = 1 if there is a suppression in the subinterval k and nk = 0 if there is a burst in the subinterval (Fig. 1B).
Using this discretization, we define the burst suppression probability (BSP) as
| (3) |
where
| (4) |
is a standard sigmoidal function. Because pk defines the probability of a suppression event in subinterval k given x2,k, it follows that nk obeys the Bernoulli process
| (5) |
Equation (3) maps x2,k, the amount of anesthetic in the brain, defined on [0, ∞), into pk, a well-defined probability on [0, 1). In this way, pk provides an instantaneous output of the probability of the brain being suppressed.
2.3. State Estimation: The Burst Suppression Probability Filter Algorithm
To implement the CLAD system we require a way to estimate pk, or equivalently, the brain state, x2,k, from the binary time-series nk. We develop a version of a binary filter algorithm [41, 42] to compute estimates of pk and x2,k in real time. We assume a simplified, stochastic version of the state model in Eq. (1) by using a natural logarithmic transformation
| (6) |
where zk obeys the Gaussian random walk model such that
| (7) |
where the vk are independent, zero-mean Gaussian random variables with variance . The transformation in Eq. (6) ensures that x2,k remains non-negative. Given estimates of z0 and , the following binary filter algorithm can be applied to the nk to compute pk∣k and x2,k∣k. It is
| (8a) |
| (8b) |
| (8c) |
| (8d) |
where
| (8e) |
for k = 1, … , K, and the notation zk∣s denotes the estimate of zk given the data up through subinterval s. It follows from Eqs. (3), (8a), and (8c) that at time k (meaning kΔ) the estimates for x2,k and pk are, respectively
| (9) |
| (10) |
We term Eqs. (8a) through (10) the BSP filter algorithm. It is constructed using the well-known Bayes’ Rule Chapman-Kolmogorov equations [41]. The algorithm computes recursively Gaussian approximations to the Chapman-Kolmogorov equation or one-step prediction density defined as p(zk ∣ n1, n2, … , nk−1) and to the posterior density defined as p(zk ∣ n1, n2, … , nk). Equations (8a) and (8b) are respectively the mode and variance of the Gaussian approximation to p(zk ∣ n1, n2, … , nk−1), which is the probability density of the state zk given the data up through time k−1. Equations (8c) and (8d) are the mode and variance respectively of the Gaussian approximation to p(zk ∣ n1, n2, … , nk), which is the probability density of the state zk given the data up through time k.
The derivation of this filter algorithm follows that given in [41] for the state space model defined by Eqs. (5) and (7). Computing a Gaussian approximation to p(zk ∣ n1, n2, … , nk) is equivalent to computing a quadratic approximation to the log posterior density, log(p(zk ∣ n1, n2, … , nk)). Equations (8c) and (8d) follow by computing respectively the first and second derivatives of log(p(zk ∣ n1, n2, … , nk)) with respect to zk. These equations are implicit functions of zk∣k, because, by Eqs. (9) and (10), pk∣k depends on zk∣k. At each update time k of the BSP algorithm we apply a Newton-Rhaphson procedure to the first derivative of log(p(zk ∣ n1, n2, … , nk)) computed with respect to zk to find zk∣k which maximizes log(p(zk ∣ n1, n2, … , nk)). The posterior variance, , is computed by evaluating Eq. (8c) at the solution zk∣k. Because Δ is small, we use zk∣k−1 as the initial guess for the 1 Newton-Rhaphson procedure at time k. To simplify computations and ensure stability of the algorithm, we replace the second derivative of the log posterior density in the Newton-Rhaphson procedure with its expected value. Therefore, we maximize the log posterior density at each time step of the BSP filter algorithm using a Fisher scoring algorithm [43]. As a consequence, is estimated as the expected value of the negative inverse of the second derivative of the log posterior density instead of as the negative inverse of the second derivative.
2.4. System Identification for the BSP Algorithm and the State Model
System identification for our CLAD system entails estimating the parameters A and b. We use the subscript j to index time in order to make clear that the time interval for system identification is different from the time interval on which the control experiment is conducted. For the rodent simulation studies we derive from the experimental data for propofol and etomidate reported by Vijn and Sneyd [38] approximate time course of x2,j for each drug in response to a bolus dose. For the human simulation studies we derive an approximate time course of x2,j from simulations of the Schnider pharmacokinetics model for propofol in response to a bolus dose [40]. We describe the specific approach to deriving the approximate time course of x2,j below in the discussion of each experiment. We treat this approximate time course as observed data and estimate A and b by non-linear least squares using the criterion function
| (11) |
where J is the number of observations in the time course of x2,j with Δ = 5 msec and x2,j(A, b) is computed from Eq. (1) by a Runge-Kutta procedure for any values of A and b.
2.5. Design of a Proportional-Integral Controller
To complete the design of the CLAD system, we define the controller for the state model in Eq. (1). For this purpose, we choose a proportional integral (PI) controller because it is simple, proven effective [44], and as we show below robust to noise. We construct the controller in continuous time to match the system in Eq. (1) then give its formulation in discrete time. For the PI controller, u(t), the system input, i.e. the infusion rate, is calculated as
| (12) |
where the coefficients ap and ai are to be determined using the standard control design prescription given below. The signal e(t) is the error defined by
| (13) |
where, for the purposes of controller design, we assume that the state variable x2(t) is available. The target value is the effect-site concentration that corresponds to a specific target BSP and is defined as , where f(x) is defined in Eq. (4). It follows that the transfer function from e(t) to x2(t) is given by
| (14) |
Here, X2(s) and E(s) are the Laplace transforms of x2(t) and e(t), respectively, and the poles of the closed-loop system are the solutions of the characteristic equation
| (15) |
From Eqs. (14) and (15) we can select ai and ap to affect the location of the closed-loop poles within the s-plane, and, specifically, to achieve a balance between rise time and overshoot, the latter being undesirable in anesthetic induction. From this specification, we design the system to be critically damped—i.e., Eq. (15) has real and repeated roots.
Using standard controller design methods [44,45], we first set the ratio
| (16) |
thereby inducing a pole-zero cancellation in Eq. (14), yielding
| (17) |
Substituting this simplified open-loop transfer function into Eq. (15), the poles of our closed-loop system are given by the solutions of
| (18) |
It follows from the discriminant of Eq. (18) that the PI controller gains that achieve critical damping are
| (19) |
and
| (20) |
While numerous other design algorithms exist for selecting PI controller gains, Eqs. (19) and (20) provide explicit design equations in terms of the underlying system parameters.
Finally, to implement the controller as shown in Figure 3, x2,k∣k from Eq. (9) provides the estimate of x2(t) in Eq. (13). We compute the input uk∣k by discretizing Eq. (12) as
| (21) |
where ej∣j is the discretized time form of the error in Eq. (13) defined as
| (22) |
for j = 1, 2, …, k, and , are obtained from ap, ai through a standard PI control discretization [45].
Figure 3. Block diagram of the CLAD system.

The target level of burst suppression is set by ptarget and is converted into the target brain anesthetic by inverting Eq. (3). The control signal, the current state estimate x2,k∣k computed from the BSP filter in Eq. (9), is subtracted from to compute . The controller uses Eq. (21) to compute the pump’s infusion rate uk∣k. By Eq. (1) the infusion rate changes the anesthetic level in the central compartment and in the brain compartment. Changing the brain compartment level changes the level of burst suppression on the EEG, and hence, the value of the binary time series, nk+1 at time k + 1. The BSP filter uses nk+1 to compute pk+1,k+1, and the update of the control signal x2,k+1∣k+1, which is fed back to compute the next control output uk+1∣k+1.
2.6. Controller stability and robustness
The controller described above is robust to parametric uncertainty. We characterize this robustness in terms of stability margins [44]. In particular, assume that the ‘true’ parameters a10, a21 deviate from the model by multiplicative factors σ10 and σ21, respectively. It follows from Eqs. (14), (19) and (20) that the open loop transfer function is given by
| (23) |
Using a standard root-locus argument, it can be verified that the poles of the corresponding closed-loop system are stable for all ap > 0 if the following condition holds:
| (24) |
A conservative sufficient condition for Eq. (24) is
| (25) |
which constitutes a generous tradeo relationship in parametric uncertainty, that is, the parameters a10 and a21 would have to be severely misidentified in order to potentially affect the closed-loop stability. Furthermore, if Eq. (24) holds, arbitrary uncertainty in a12 or b will not destabilize the system (since such uncertainty enters multiplicatively in ap).
3. Results
3.1. A Rodent CLAD Model for Control of Burst Suppression
System Identification
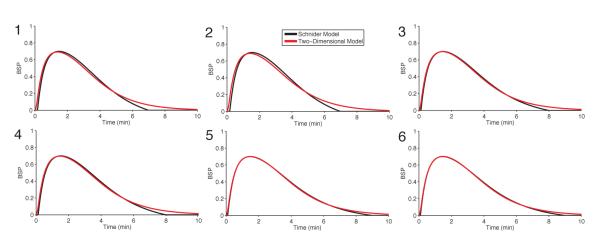
To develop CLAD models for propofol and etomidate, we reanalyzed the experimental data reported by Vijn and Sneyd (V&S) [38] for these anesthetics and conducted system identification for our two-dimensional model in Eq. (1) and its control parameters in Eqs. (19) and (20). These authors administered bolus injections of propofol and etomidate to rats and measured the time course of burst suppression by computing the BSR in 15-second non-overlapping intervals. For each drug they computed the average BSR trace as a function of time and scaled it to compute the weighting function for their closed-loop controller (V&S, Fig. 3). We rescaled the weighting functions so that the maximum was 0.95, the typical maximum BSR achieved by each drug (V&S, Fig. 2). We assumed that this average curve represented the average burst suppression response of the rats to the particular anesthetic. We fit our two-dimensional model in Eq. (1) to the average BSR time course for propofol and etomidate by non-linear least squares (Eq. (11)) to estimate the parameters A and b for each drug. The estimated model parameters (Table 1) gave very good fits to the average BSR time courses of both propofol and etomidate (Fig. 4), suggesting that the two-dimensional model offers a plausible approximation to the essential dynamic features of this system.
Table 1.
Rat Model Drug-Specific Parameter Estimates The estimated rate parameters , scale factor , and control parameters and for the two-dimensional rat control model for propofol and etomidate.
| Propofol | Etomidate | |
|---|---|---|
| 0.01557 | 0.01547 | |
| 0.9599 | 0.6703 | |
| 4.552 | 1.993 | |
| 0.5885 | 0.8394 | |
| 565.4 | 76.51 | |
| 9.045 | 0.8548 |
Figure 4. Analysis of the Vijn and Sneyd rat burst suppression experiments.
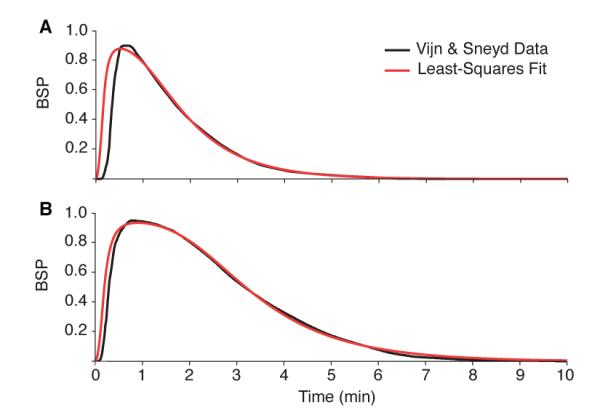
BSP time courses from the V&S rat experiments for propofol (A) and etomidate (B), and the first of the two-compartment model in Eq. (1). The black curves are the BSP time courses computed from the impulse response functions in V&S and the blue curves are non-linear least-squares fits of the two-compartment model. The parameter estimates are given in Table 1.
Testing the BSP Filter Algorithm
To demonstrate that each model with the estimated parameters could produce binary time-series that would resemble those computed from the EEG in burst suppression in response to a bolus dose of propofol and a bolus dose of etomidate, we simulated binary observations using the two-dimensional model in Eq. (1) and the Bernoulli model in Eqs. (3) to (5) for both drugs evaluated at the estimated parameter values (Table 1). We simulated the model using a single 8 mg kg−1 bolus dose of propofol and a single 3.5 mg kg−1 bolus dose of etomidate each administered to a 0.26 kg rat over 10 seconds. For both propofol (Fig. 5A) and etomidate (Fig. 5B), we simulated 10 realizations of binary observations over ten minutes with a sampling interval of Δ = 5 msec to give 120,000 observations per realization. We estimated the BSP time course from the simulated binary data by applying the BSP filter in Eqs. (8) to (10) using and , where is the fraction of suppression events in the first 2 seconds with Δ = 5 msec. We found that these choices of and z0 gave good approximations to the maximum likelihood estimates of these parameters for this problem [42]. The BSP filter recovered BSP time courses for propofol (Fig. 5C, red curves) and for etomidate (Fig. 5D, red curves) that closely resembled the average BSR time courses (Fig. 5C, 5D, black curves) we extracted by rescaling the V&S weighting functions for these drugs (Fig. 4).
Figure 5. Testing the BSP filter algorithm.
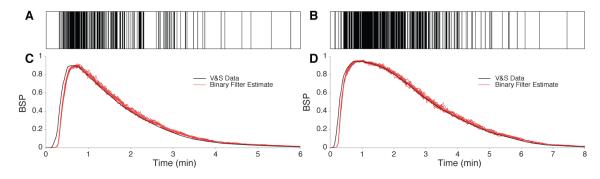
Realizations of binary series simulated from Eqs. (1) to (5) using the estimated propofol parameters (A) and the estimated etomidate parameters (B) in Table 1 based on bolus administration of each anesthetic. BSP time courses (black curves) computed by evaluating Eqs. (1) and (3) at the estimated propofol and etomidate (D) parameters. BSP filter estimates (red curves) of the BSP time course computed from the 10 different simulated binary series for propofol (C) and etomidate (D).
Simulation Studies of the CLAD Model
Applying Eqs. (19) and (20) to the estimated model parameters we solved for the proportional ap and integral ai controller gains in our models for propofol and etomidate (Table 1). We tested our controller performance with two different observation models, at each of six different target burst suppression levels. The burst suppression targets were equally spaced on the interval [0.15, 0.9]. In the first observation model, x2(t) was directly observable; in the second, x2,k∣k was observable though a binary process. The latter case simulated the actual scenario of burst suppression being observed in the EEG and converted to a binary time series through thresholding and segmentation.
To begin each experiment we converted the target BSP, ptarget (Fig. 6, horizontal dashed lines), into the brain state target, as and we set (x1(0), x2(0)) = [e−5, e−5], to approximate empty compartments. In the first case, in which x2(t), the brain site anesthetic level, is directly observable, our PI controller worked well for both propofol (Fig. 6A) and etomidate (Fig. 6B), as the system attained each target level in a short period. The average rise time (t90% – t10%) was 1.32 minutes for propofol and 3.03 minutes for etomidate. As specified by the controller design, there was no overshoot in either simulation study.
Figure 6. BSP control in simulated rat experiments.
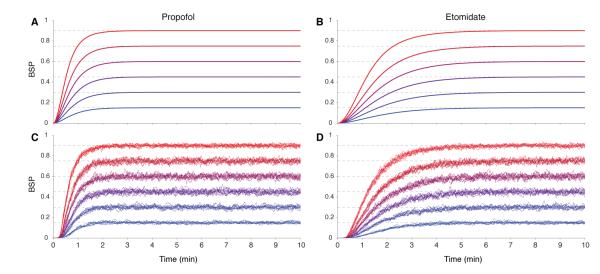
Each experiment uses 6 different burst suppression target levels for propofol (A, C) and etomidate (B, D). In the first experiment (A, B) control is achieved assuming that the observable is the brain level of the anesthetic, x2(t). In the second experiments (C, D) control is achieved by using the estimated brain anesthetic level, x2,k∣k, from the BSP filter in Eqs. (8) to (10). Control with the binary filter is demonstrated with 10 binary series realizations at each of the 6 levels for both anesthetics.
In the second case, we simulated the two-dimensional model, but as in Fig. 5, we simulated binary observations based on Eqs. (3) to (5). Because the observable in this case is the time-series of binary observations, we estimate x2,k and pk from the BSP filter as xk∣k and pk∣k respectively in Eqs. (9) and (10). We applied the remainder of the control algorithm as in the deterministic noise-free case by treating xk∣k as the observed value of the control variable. We simulated 10 control experiments to illustrate between-run variation for each BSP target level. To emulate the function of an actual anesthetic infusion pump we updated the BSP estimate pk∣k every 5 msec and uk∣k, the control signal, every second. After incorporating the BSP filter into the closed loop, the PI controller continued to perform well throughout a range of burst suppression targets with rise times that were comparable to the noise-free case with no overshoot for propofol (Fig. 6C) or for etomidate (Fig 6D). This finding suggests that the BSP filter estimates, xk∣k and pk∣k, accurately captured the time courses of x2,k and pk respectively for both drugs.
Although Vijn and Sneyd developed what they termed a non-model-based controller, our results demonstrate that a highly structured model underlies the data reported in their experiments and that this model may be used to construct a PI controller to control burst suppression.
3.2. A Human CLAD Model for Control of Burst Suppression
Model Formulation and System Identification
We next used our paradigm to develop a CLAD system for burst suppression control in humans for propofol. As we stated in the Theory section, we assume that burst suppression is a sufficiently profound state of brain inactivation and that once the brain is in this state, its activity falls into a limited dynamic range. Under the further assumption that the level of burst suppression depends directly on the amount of anesthetic in the brain (effect-site) compartment we postulate that these dynamics can be described by our two-dimensional model (Fig. 2). The Schnider four-compartment model is an established pharmacokinetics model that describes the effects of propofol on the brain and body [40]. We did not study etomidate in humans because it is no longer administered in the intensive care unit by long-term infusion because of the high risk of adrenal suppression [46].
To test our approximation hypothesis, we used the Schnider model to simulate bolus administration of a sufficient dose of propofol to induce burst suppression in six human subjects: a 30 year-old, 180 cm 70 kg man; a 30 year-old 150 cm, 50 kg woman; a 40 year-old 170 cm 90 kg man; a 40 year old, 165 cm, 60 kg woman and a 50 year old 196 cm 100 kg man; and a 50 year-old 175 cm 80 kg woman. We chose these six different profiles to test whether our approximation would apply across the broad range of patients commonly encountered in the intensive care unit. The propofol induction dose was 3.5mg/kg administered over 10 seconds. We simulated the Schnider model for 9 minutes, treated the time course of the brain compartment for each anesthetic as the observed data, and fit our 2-dimensional model to each time course using nonlinear least-squares. We transformed the simulated time courses and the time course estimates computed from our two-dimensional model into their associated BSP time courses using 3. In all 6 subjects, the two-dimensional model estimates (red curves) gave good fits to the propofol data (black curves), capturing well the rapid rise and the slow decline of the effect-site concentration (Fig. 7). For subjects 1 and 5, and to a lesser extent for subjects 2 and 4, the two-dimensional model performed less well in describing the time course of the four-compartment model during declining periods at low BSP levels. The lack of agreement between the two models occurred below a BSP of 0.2, suggesting that the additional compartments of the Schnider model are likely needed to account for this rapid decline. These findings support our hypothesis that a two-dimensional approximation can be constructed to the standard four-compartment Schnider model for a broad range of patients when the dose of propofol being administered is sufficient to produce burst suppression.
Figure 7. System identification of the parameters for the 2-dimensional model of propofol.
The experiments simulate the Schnider model for propofol in response to bolus administration of 3.5 mg kg−1 for each patient. Patient 1, a 30 year-old, 180 cm 70 kg man; Patient 2, a 30 year-old 150 cm, 50 kg woman; Patient 3, a 40 year-old 170 cm 90 kg man; Patient 4, a 40 year-old, 165 cm, 60 kg woman; Patient 5, a 50 year-old 196 cm 100 kg man; and Patient 6, a 50 year-old 175 cm 80 kg woman. The black curves are the BSP time courses simulated from the four-dimensional Schnider model and the red curves are non-linear least-squares fits of the two-compartment model approximations in 1. The parameter estimates are given in Table 2.
Simulation Studies of a Human CLAD Model
By evaluating the estimated model parameters (Table 2) in Eqs. (19) and (20), we computed the control parameters ap and ai. As in the rodent example, we again tested our controller performance with two different observation models, at each of six different target burst suppression levels equally spaced on the interval [0.15, 0.9]. In the first observation model, the effect-site concentration, x2(t) was directly observable; and in the second x2(t) was observable through the binary process defined in Eq. (5). We show the results for Subjects 1 and 6 as the results for the other four subjects were similar. With x2(t) directly observable, our controller easily achieved and maintained each target level of burst suppression without overshoot for both subjects (Fig. 8). The average rise time was 7.35 minutes. We simulated 10 control experiments in which x2(t), observed through the binary time-series, was estimated as x2,k∣k using the BSP filter algorithm (Fig. 8). In each individual simulation of binary data, at each BSP target level, our controller achieved and maintained the target levels without overshoot and with rise times comparable to those achieved when x2(t) was directly observable.
Table 2.
Drug-Specific Human Model Parameters The estimated rate parameters , scale factor , and control parameters and for the two-dimensional control model for propofol for six simulated human patients.
| Patient | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| 1.010e-4 | 1.358e-4 | 1.417e-4 | 2.260e-4 | 1.687e-4 | 1.478e-4 | |
| 0.760 | 0.717 | 0.707 | 0.731 | 0.741 | 0.710 | |
| 0.761 | 0.716 | 0.708 | 0.732 | 0.741 | 0.710 | |
| 0.1310 | 0.1156 | 0.04828 | 0.1177 | 0.06741 | 0.08111 | |
| 10040 | 7044 | 12260 | 8028 | 13120 | 10510 | |
| 127.3 | 87.00 | 149.0 | 95.90 | 155.0 | 124.0 |
Figure 8. BSP control in the simulated human patients using propofol.
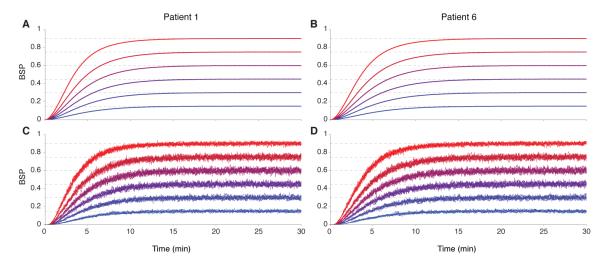
For propofol, the control experiment sets 6 different burst suppression target levels, evenly spaced from 0.15 to 0.9, and tracks them using the model and control parameters (Table 2) for Patients 1 and 6 (Fig. 7). In the first experiments (A, B) control is achieved assuming that the observable is x2,k, the brain level of propofol. In the second experiments (C,D) control is achieved by estimating x2,k∣k the brain level of propofol from the BSP filter in Eq. (8a). Control with the BSP filter is demonstrated with 10 binary series realizations at each of the 6 levels.
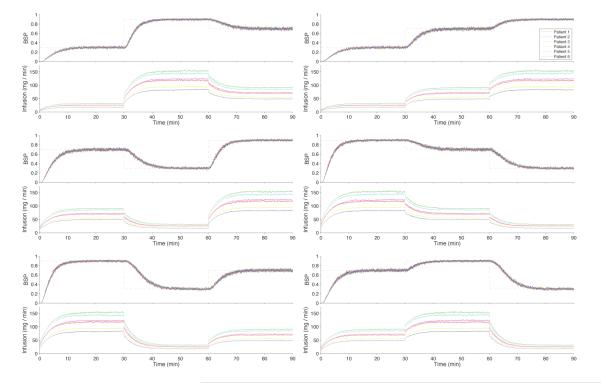
To gain further insight into how the controller might perform in more realistic circumstances and to provide a sensitivity analysis for our framework, we simulated 6 different propofol control experiments in each of six subjects. Each subject was required to track each of 6 different trajectories derived by considering the 3! = 6 permutations of the three BSP target levels of 0.3, 0.7, and 0.9. Every 30 minutes we changed the BSP target level that the controller was required to achieve and maintain. We used the model parameters estimated by fitting the two-dimensional approximation to simulated bolus response data from the four-compartment Schnider model for propofol (Table 2, rows 1-4) to compute the control parameters for each individual subject (Table 2, rows 5 and 6). We chose and z0 as in the rodent experiments and we updated the BSP estimate pk∣k every 5 msec and uk∣k, the control signal, every second. For each of the six subjects, for each of the six trajectories, the controller achieved and maintained the target level of burst suppression (Fig. 9). During the ascents to a higher from a lower BSP target level, the controller achieved the new level with a rise time of approximately 7.35 minutes (Fig. 9) with no overshoot, as it did when x2(t) was directly observable (Fig. 8). When the target BSP level was decreased, the controller required approximately 10 minutes to achieve the new level in all six subjects. Although the control trajectories agreed for all six subjects, their instantaneous infusion rates differed (Fig. 9).
Figure 9. BSP control performance in simulated human patients using propofol.
The control targets are 3! = 6 different sequences of the BSP levels 0.3, 0.7 and 0.9 (dashed lines BSP subpanels) with each level maintained for 30 minutes. Each of the 6 patients (Table 2) must achieve control of each of the 6 target trajectories. In each panel, the upper subpanel shows the time course of the BSP control output, x2,k∣k and the lower subpanel shows the infusion rates, uk∣k required to achieve the control output. The BSP time courses and the infusion rates are: red for Patient 1; dark blue for Patient 2; light blue for Patient 3; yellow for Patient 4; green for Patient 5; and purple for Patient 6.
Our findings suggest that a two-dimensional model combined with the BSP filer algorithm and a PI controller can be used to control burst suppression in humans at levels that could be chosen to maintain medically-induced coma.
4. Discussion
There is a growing interest in anesthesiology to use CLAD systems to automate control of brain states for patients requiring anesthesia care. The accuracy and reliability of CLAD systems can be enhanced by using EEG markers for which the neurophysiological link to the anesthetic-induced brain state is well established. Burst suppression is a readily discernible EEG signature that is known to be associated with a state of profound brain inactivation characterized by decreased neuronal and metabolic activity. Therefore, we have established a CLAD system to control burst suppression that consists of: a two-dimensional linear system model to describe the effect of the drugs on the EEG; the new concept of the burst suppression probability, defining the instantaneous probability of the EEG being suppressed; the BSP filter to compute the state of burst suppression from EEG recordings converted to binary observations; a system identification procedure to determine the parameters of the pharmacokinetics model; and a PI controller.
We demonstrated that the parameters of our two-dimensional control model could be estimated from the rat experimental data reported by Vijn and Sneyd [38] for propofol and etomidate (Fig. 4, Table 1). We simulated the performance of our PI controller using a directly observable control signal and a control signal observable through a binary time series derived from the EEG (Figs. 1 and 5). In each condition, for both of the drugs, the controller achieved the specified level of burst suppression without overshoot (Fig. 6). We also showed that our two-dimensional model could be used to control burst suppression in simulated human subjects using propofol and etomidate by deriving an approximation to the standard four-dimensional human pharmacokinetics models for these anesthetics (Figs. 7 and 8). Finally, we demonstrated using propofol that our control system could reliably achieve and maintain changing levels of burst suppression across a broad dynamic range of control conditions by testing it in simulated patients with different epidemiologic profiles (Fig. 9).
To conduct either the rodent or human experiments, the prescription for implementing our paradigm is to: 1) administer a bolus dose of the anesthetics sufficient to achieve burst suppression; 2) use the BSP filter algorithm in Eq. (8a) with an EEG segmentation algorithm to convert the EEG into the BSP; 3) perform the system identification using the estimated BSP data to obtain the parameters for the two-dimensional linear model in Eq. (1); 4) compute the PI control parameters from the pharmacokinetics parameters using Eqs. (19) and (20) and the discretization correction in [44]; 5) Set a target level of burst suppression and implement control. For the human studies the system identification can also be carried out by simulating bolus administration of propofol using the Schnider model and fitting the linear two-dimensional model to the simulated data as in Figure 7.
4.1. Strategies for Controller Design
Our reanalysis of the Vijn and Sneyd data allowed us to place their analyses in a formal control theory framework. These authors implemented what is effectively a PI control strategy by devising a scheme to weight their sequence of control errors and use that weighted sequence to adjust anesthetic infusion rates. The weights for their error sequences were determined by the impulse response profiles they generated for each drug. Our analyses showed that their impulse response profiles could be efficiently described by our two-dimensional linear system 1, and that therefore, these response profiles could be used to estimate the parameters of this model by conducting formal system identification (Fig. 4). The weights for the error sequence in our approach were then determined not directly from the impulse response profile, but rather by standard results for PI controller design, as detailed in Eqs. (12)-(20).
By simulating human EEG data based on the Schnider model for propofol [40] and the Arden model for etomidate [47], we demonstrated that our two-dimensional model could successfully approximate the standard four-compartment models typically used to describe the pharmacokinetics of these anesthetics. This strategy predicts that when controlling burst suppression is the objective a low-order representation can be used to approximate the behavior of the more complex models. Having fewer parameters to identify in the two-dimensional models makes control design much more feasible.
The two-dimensional model is the lowest order representation that allows us to capture two essential properties of induction and maintenance of burst suppression. First, there have to be at least two compartments in the model, since the drug cannot be administered directly into the primary effect site, the brain, it must therefore first enter a central or outer compartment. Second, burst suppression being a profound state of brain inactivation means that sufficient anesthetic has been administered to bypass the other less profound states. Hence, once it has been achieved, increasing (decreasing) the anesthetic infusion rate will only increase (decrease) the level of burst suppression. If required, a more detailed state model of burst suppression could be incorporated into our paradigm by considering approximations to the neuronal metabolic model of burst suppression developed by Ching et al [31].
To illustrate our CLAD systems in both the rat and human studies we used the estimated pharmacokinetics parameters and the models in Eqs. (1)-(3) to simulate binary time series. Application of our paradigm in actual experimental studies will require the additional steps of thresholding and segmenting the EEG recordings into binary time series (Fig. 1). These steps can be accomplished in real time [48]. Another important component of our control paradigm is the use of the BSP filter algorithm Eqs. (8)–(10) to estimate the BSP from the EEG. This algorithm is approximately optimal having been designed from the established Bayes’ Theorem-Chapman-Kolmogorov framework used to construct state-space filter algorithms such as the Kalman filter [41]. Unlike the BSR which requires 4 [37], 15 [38], or 60 [49] seconds to compute an update, our BSP filter algorithm can compute BSP updates in real-time at 1-second intervals or shorter, making real-time control with our paradigm straightforward to realize.
We developed our controller using a deterministic control paradigm. It was constructed implicitly assuming that the state of burst suppression could be readily estimated, or effectively observed, from the EEG recordings. Among the advantages of our PI design is a high tolerance to noise. As shown in our analysis (see Eqs. (23)-(25)), our PI controller is robust to large uncertainty in model parameters. Moreover, a feature of the PI controller is robustness to input disturbances [44] such as noise affecting the pump or flow of anesthetic. Nevertheless, our use of a basic controller design method means there is much room in the study of this problem for application of advanced techniques, such as stochastic [50] and model predictive control [51] strategies. Any further elaborations of the control design must go hand-in-hand with testing of our paradigm in actual burst suppression experiments.
4.2. Application of the PI Controller to Control Medical Coma
Along with being a clearly defined EEG signature for CLAD system testing, burst suppression is a marker rhythm for medically-induced coma. Hence, the development of plausible strategies to control burst suppression can have immediate therapeutic implications for aiding the recovery of patients following traumatic and hypoxic brain injuries, and for treating patients with uncontrollable seizures.
Our simulation results provide strong evidence that maintenance of the brain in a medically-induced coma at a precise level of burst suppression is highly feasible. Testing of our paradigm for control of burst suppression in rat and human experiments will be topics of future reports. Finally, our current paradigm applies only to burst suppression. Other models need to be formulated to control other brain states for which the EEG response dynamics are different [29, 52]. Our paradigm suggests how these systems could be designed.
Acknowledgments
This work was supported by: NIH Awards DP1-OD003646 (ENB), and the Burroughs-Wellcome Fund Award 1010625 (SC).
References
- [1].Struys MM, De Smet T, Versichelen LF, Van De Velde S, Van den Broecke R, Mortier EP. Comparison of closed-loop controlled administration of propofol using bispectral index as the controlled variable versus “standard practice” controlled administration. Anesthesiology. 2001;95:6–17. doi: 10.1097/00000542-200107000-00007. [DOI] [PubMed] [Google Scholar]
- [2].Puri GD, Kumar B, Aveek J. Closed-loop anaesthesia delivery system (CLADS) using bispectral index: a performance assessment study. Anaesth Intensive Care. 2007;35:357–62. doi: 10.1177/0310057X0703500306. [DOI] [PubMed] [Google Scholar]
- [3].Agarwal J, Puri GD, Mathew PJ. Comparison of closed loop vs. manual administration of propofol using the bispectral index in cardiac surgery. Acta anaesthesiologica Scandinavia. 2009;53:390–7. doi: 10.1111/j.1399-6576.2008.01884.x. [DOI] [PubMed] [Google Scholar]
- [4].De Smet T, Struys MM, Neckebroek MM, Van den Hauwe K, Bonte S, Mortier EP. The accuracy and clinical feasibility of a new bayesian-based closed-loop control system for propofol administration using the bispectral index as a controlled variable. Anesth Analg. 2008;107:1200–10. doi: 10.1213/ane.0b013e31817bd1a6. [DOI] [PubMed] [Google Scholar]
- [5].Hemmerling TM, Charabati S, Zaouter C, Minardi C, Mathieu PA. A randomized controlled trial demonstrates that a novel closed-loop propofol system performs better hypnosis control than manual administration. J. Can. Anesth. 2010;57:725–735. doi: 10.1007/s12630-010-9335-z. [DOI] [PubMed] [Google Scholar]
- [6].Liu N, Chazot T, Trillat B, Michel-Cherqui M, Marandon JY, Law-Koune JD, Rives B, Fischler M. Closed-loop control of consciousness during lung transplantation: an observational study. J Cardiothorac Vasc Anesth. 2008;22:611–5. doi: 10.1053/j.jvca.2008.04.022. [DOI] [PubMed] [Google Scholar]
- [7].Liu N, Le Guen M, Benabbes-Lambert F, Chazot T, Trillat B, et al. Feasibility of closed-loop titration of propofol and remifentanil guided by the spectral M-Entropy monitor. Anesthesiology. 2012;116:286–295. doi: 10.1097/ALN.0b013e318242ad4f. [DOI] [PubMed] [Google Scholar]
- [8].Liu N, Chazot T, Genty A, Landais A, Restoux A, McGee K, Laloe PA, Trillat B, Barvais L, Fischler M. Titration of propofol for anesthetic induction and maintenance guided by the bispectral index: closed-loop versus manual control: a prospective, randomized, multicenter study. Anesthesiology. 2006;104:686–95. doi: 10.1097/00000542-200604000-00012. [DOI] [PubMed] [Google Scholar]
- [9].Absalom AR, Kenny GN. Closed-loop control of propofol anaesthesia using bispectral index: performance assessment in patients receiving computer-controlled propofol and manually controlled remifentanil infusions for minor surgery. Br J Anaesth. 2003;90:737–741. doi: 10.1093/bja/aeg137. [DOI] [PubMed] [Google Scholar]
- [10].Bickford RG. Automatic electroencephalographic control of general anesthesia. EEG Clin. Neurophysiol. 1950;2:93–96. doi: 10.1016/0013-4694(51)90058-2. [DOI] [PubMed] [Google Scholar]
- [11].Schwilden H, Schüttler J, Stoeckel H. Closed-loop feedback control of methohexital anesthesia by quantitative EEG analysis in humans. Anesthesiology. 1987;67:341–347. doi: 10.1097/00000542-198709000-00011. [DOI] [PubMed] [Google Scholar]
- [12].Glass PSA. Automated control of anesthesia ten years later: futuristic novelty or present day reality. Can J Anesth. 2010;57:715–719. doi: 10.1007/s12630-010-9336-y. [DOI] [PubMed] [Google Scholar]
- [13].Absalom AR, Sutcliffe N, Kenny GN. Closed-loop control of anesthesia using bispectral index: performance assessment in patients undergoing major orthopedic surgery under combined general and regional anesthesia. Anesthesiology. 2002;96:67–73. doi: 10.1097/00000542-200201000-00017. [DOI] [PubMed] [Google Scholar]
- [14].De Smet T, Struys MM, Greenwald S, Mortier EP, Shafer SL. Estimation of optimal modeling weights for a bayesian-based closed-loop system for propofol administration using the bispectral index as a controlled variable: a simulation study. Anesth Analg. 2007;105:1629–38. doi: 10.1213/01.ane.0000287269.06170.0f. [DOI] [PubMed] [Google Scholar]
- [15].Haddad WM, Bailey JM, Hayakawa T, Hovakimyan N. Neural network adaptive output feedback control for intensive care unit sedation and intraoperative anesthesia. IEEE Transactions on Neural Networks. 2007;18:1049–66. doi: 10.1109/TNN.2007.899164. [DOI] [PubMed] [Google Scholar]
- [16].Hegde HV, Puri GD, Kumar B, Behera A. Bi-spectral index guided closed-loop anaesthesia delivery system (CLADS) in pheochromocytoma. J Clin Monit Comput. 2009;23:189–96. doi: 10.1007/s10877-009-9181-0. [DOI] [PubMed] [Google Scholar]
- [17].Kenny GN, Mantzaridis H. Closed-loop control of propofol anaesthesia. Br J Anaesth. 1999;83:223–8. doi: 10.1093/bja/83.2.223. [DOI] [PubMed] [Google Scholar]
- [18].Liu HY, Zeng HY, Cheng H, Wang MR, Qiao H, Han RG. Comparison of the effects of etomidate and propofol combined with remifentanil and guided by comparable BIS on transcranial electrical motor-evoked potentials during spinal surgery. J Neurosurg Anesthesiol. 2012;24:133–8. doi: 10.1097/ANA.0b013e31823dfb2e. [DOI] [PubMed] [Google Scholar]
- [19].Mendez JA, Torres S, Reboso JA, Reboso H. Adaptive computer control of anesthesia in humans. Comput Methods Biomech Biomed Engin. 2009;12:727–34. doi: 10.1080/10255840902911528. [DOI] [PubMed] [Google Scholar]
- [20].Morley A, Derrick J, Mainland P, Lee BB, Short TG. Closed loop control of anaesthesia: an assessment of the bispectral index as the target of control. Anaesthesia. 2000;55:953–9. doi: 10.1046/j.1365-2044.2000.01527.x. [DOI] [PubMed] [Google Scholar]
- [21].Mortier E, Struys M, De Smet T, Versichelen L, Rolly G. Closed-loop controlled administration of propofol using bispectral analysis. Anaesthesia. 1998;53:749–54. doi: 10.1046/j.1365-2044.1998.00467.x. [DOI] [PubMed] [Google Scholar]
- [22].Schwilden H, Stoeckel H. Closed-loop feedback controlled administration of alfentanil during alfentanil-nitrous oxide anaesthesia. Br J Anaesth. 1993;70:389–93. doi: 10.1093/bja/70.4.389. [DOI] [PubMed] [Google Scholar]
- [23].Schwilden H, Stoeckel H, Schuttler J. Closed-loop feedback control of propofol anaesthesia by quantitative EEG analysis in humans. Br J Anaesth. 1989;62:290–6. doi: 10.1093/bja/62.3.290. [DOI] [PubMed] [Google Scholar]
- [24].Hahn J-O, Dumont GA, Ansermino JM. Closed-loop anesthetic drug concentration estimation using clinical-effect feedback. 2011;58(1) doi: 10.1109/TBME.2010.2076811. [DOI] [PubMed] [Google Scholar]
- [25].Bickford RG. Use of frequency discrimination in the automatic electroencephalographic control of anesthesia (servo-anesthesia) EEG Clin. Neurophysiol. 1951;3:83–86. doi: 10.1016/0013-4694(51)90058-2. [DOI] [PubMed] [Google Scholar]
- [26].Mayo CW, Bickford RG, Faulconer A., Jr. Electroencephalographically controlled anesthesia in abdominal surgery. J Am Med Assoc. 1950;144:1081–1083. doi: 10.1001/jama.1950.02920130033008. [DOI] [PubMed] [Google Scholar]
- [27].Pilge S, Zanner R, Schneider G, Blum J, Kreuzer M, et al. Time delay of index calculation: analysis of cerebral state, bispectral, and narcotrend indices. Anesthesiology. 2006;104:488–494. doi: 10.1097/00000542-200603000-00016. [DOI] [PubMed] [Google Scholar]
- [28].Amzica F. Basic physiology of burst-suppression. Epilepsia. 2009;50(12):38–39. doi: 10.1111/j.1528-1167.2009.02345.x. [DOI] [PubMed] [Google Scholar]
- [29].Brown EN, Lydic R, Schiff ND. General anesthesia, sleep, and coma. N Engl J Med. 2010 Dec;363(27):2638–2650. doi: 10.1056/NEJMra0808281. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [30].Steriade M, Amzica F, Contreras D. Cortical and thalamic cellular correlates of electroencephalographic burst-suppression. Electroencephalogr Clin Neurophysiol. 1994;90:1–16. doi: 10.1016/0013-4694(94)90108-2. [DOI] [PubMed] [Google Scholar]
- [31].Ching S, Purdon PL, Vijayan S, Kopell NJ, Brown EN. A neurophysiological-metabolic model for burst suppression. Proc Natl Acad Sci USA. 2012;109(8):3095–3100. doi: 10.1073/pnas.1121461109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [32].Doyle PW, Matta BF. Burst suppression or isoelectric encephalogram for cerebral protection: evidence from metabolic suppression studies. Can J Anaesth. 1999;57:725–735. doi: 10.1093/bja/83.4.580. [DOI] [PubMed] [Google Scholar]
- [33].Rossetti AO, Reichhart MD, Schaller MD, Despland PA, Bogousslavsky J. Propofol treatment of refractory status epilepticus: a study of 31 episodes. Epilepsia. 2004;45:757–763. doi: 10.1111/j.0013-9580.2004.01904.x. [DOI] [PubMed] [Google Scholar]
- [34].Mirsattari SM, Sharpe MD, Young B. Treatment of refractory status epilepticus with inhalational anesthetic agents isoflurane and desflurane. Arch Neurol. 2004;61:1254–1259. doi: 10.1001/archneur.61.8.1254. [DOI] [PubMed] [Google Scholar]
- [35].Wijdicks EF, Wijdicks MF. Coverage of coma in headlines of US newspapers from 2001 through 2005. Mayo Clin Proc. 2006;81:1332–1336. doi: 10.4065/81.10.1332. [DOI] [PubMed] [Google Scholar]
- [36].Kam PC, Cardone D. Propofol infusion syndrome. Anaesthesia. 2007;62(7):690–701. doi: 10.1111/j.1365-2044.2007.05055.x. [DOI] [PubMed] [Google Scholar]
- [37].Rampil IJ, Weiskopf RB, Brown JG, Eger EI, II, Johnson BH. I653 and isoflurane produce similar dose-related changes in the electroencephalogram of pigs. Anesthesiology. 1988;69:298–302. doi: 10.1097/00000542-198809000-00002. [DOI] [PubMed] [Google Scholar]
- [38].Vijn PCM, Sneyd JR. I.v. anaesthesia and EEG burst suppression in rats: bolus injections and closed-loop infusions. Br J Anaesth. 1998;81:415–421. doi: 10.1093/bja/81.3.415. [DOI] [PubMed] [Google Scholar]
- [39].Cotten JF, Ge RL, Banacos N, Pejo E, Husain SS, Williams JH, Raines DE. Closed-loop continuous infusions of etomidate and etomidate analogs in rats: A comparative stufy of dosing and the impact on adrenocortical function. Anesthesiology. 2011;115(4):764–773. doi: 10.1097/ALN.0b013e31821950de. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [40].Schnider TW, Minto CF, Gambus PL, Andresen C, Goodale DB, Shafer SL, Youngs EJ. The influence of method of administration and covariates on the pharmacokinetics of propofol in adult volunteers. Anesthesiology. 1998;88(5):1170–82. doi: 10.1097/00000542-199805000-00006. [DOI] [PubMed] [Google Scholar]
- [41].Smith AC, Brown EN. Estimating a state-space model from point process observations. Neural Comput. 2003;15:965–991. doi: 10.1162/089976603765202622. [DOI] [PubMed] [Google Scholar]
- [42].Chemali JJ, Kevin Wong KF, Solt K, Brown EN. A state-space model of the burst suppression ratio. IEEE EMBC 2011; Boston, MA. August 30–September 3, 2011; [DOI] [PMC free article] [PubMed] [Google Scholar]
- [43].Fahrmeir L, Tutz G. Multivariate statistical modeling based on generalized linear models. Springer; New York: 2001. [Google Scholar]
- [44].Franklin GF, Powell JD, Emami-Naeini A. Feedback control of dynamic systems. Pearson; 2010. Number v. 10 in Alternative Etext Formats. [Google Scholar]
- [45].Golnaraghi F, Kuo BC. Automatic Control Systems. Wiley; 2009. [Google Scholar]
- [46].Forman SA. Clinical and molecular pharmacology of etomidate. Anesthesiology. 2011 Mar;114(3):695–707. doi: 10.1097/ALN.0b013e3181ff72b5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [47].Arden JR, Holley FO, Stanski DR. Increased sensitivity to etomidate in the elderly: initial distribution versus altered brain response. Anesthesiology. 1986;65(1):19–27. doi: 10.1097/00000542-198607000-00004. [DOI] [PubMed] [Google Scholar]
- [48].Bruhn J, Bouillon TW, Shafer SL. Bispectral Index (BIS) and burst suppression: revealing a part of the BIS algorithm. J Clin Monit Comput. 2000;16(8):593–6. doi: 10.1023/A:1012216600170. [DOI] [PubMed] [Google Scholar]
- [49].Luo T, Leung LS. Basal forebrain histaminergic transmission modulates electroencephalo-graphic activity and emergence from isoflurance anesthesia. Anesthesiology. 2009;111:725–733. doi: 10.1097/ALN.0b013e3181b061a0. [DOI] [PubMed] [Google Scholar]
- [50].Bertsekas D. Dynamic Programming and Optimal Control. Athena Scientific; 2005. [Google Scholar]
- [51].Camacho E, Bordons C. Model Predictive Control. 2nd edition Springer-Verlag; London: 2004. [Google Scholar]
- [52].Kuizenga K, Kalkman CJ, Hennis PJ. Quantitative electroencephalographic analysis of the biphasic concentration-effect relationship of propofol in surgical patients during extradural analgesia. Br J Anaesth. 1998 Jun;80(6):725–732. doi: 10.1093/bja/80.6.725. [DOI] [PubMed] [Google Scholar]