Abstract
Rotation is thought to drive cyclic magnetic activity in the Sun and Sun-like stars. Stellar dynamos, however, are poorly understood owing to the scarcity of observations of rotation and magnetic fields in stars. Here, inferences are drawn on the internal rotation of a distant Sun-like star by studying its global modes of oscillation. We report asteroseismic constraints imposed on the rotation rate and the inclination of the spin axis of the Sun-like star HD 52265, a principal target observed by the CoRoT satellite that is known to host a planetary companion. These seismic inferences are remarkably consistent with an independent spectroscopic observation (rotational line broadening) and with the observed rotation period of star spots. Furthermore, asteroseismology constrains the mass of exoplanet HD 52265b. Under the standard assumption that the stellar spin axis and the axis of the planetary orbit coincide, the minimum spectroscopic mass of the planet can be converted into a true mass of 
, which implies that it is a planet, not a brown dwarf.
Keywords: extrasolar planets, stellar oscillations, stellar rotation
Space photometry has made possible high-precision seismology of Sun-like stars (1–5). Precise measurements of the frequencies of the global modes of acoustic oscillations place tight constraints on the internal structure of these stars (6). For example, improved stellar parameters are used to refine the physics of stellar interiors and find many applications in astrophysics. Accurate determinations of the radii, masses, and ages of planet-host stars are essential for the characterization of exoplanets detected in transits (7–9).
In this paper, we present an unambiguous measurement of mean internal rotation (rotation averaged over the entire stellar interior) and inclination angle of a Sun-like star by means of asteroseismology. Internal rotation is a fundamental physical property of stars: it affects stellar evolution through increased mixing of chemicals and mass loss, and is responsible for magnetic activity (10). Our study extends earlier studies of the seismic signature of rotation in α Centauri A (11, 12) and in red giant stars (13, 14).
The star HD 52265 was observed continuously for 117 d between November 2008 and March 2009 in the asteroseismic field of the space telescope “convection, rotation, and planetary transits” (CoRoT) (15). This relatively bright star (visual magnitude, 6.3) was selected as a primary target because it hosts a planetary companion, which was detected through the wobbling of the star via the radial velocity method (16–18). With an effective temperature (4) of 
and an absolute luminosity (4) of 
, HD 52265 is a main-sequence G0V star. Combining these two values, the stellar radius is deduced to be 
. Isochrone fits (19, 20) give a stellar mass near 1.2 
with a typical error of 0.05 
and a stellar age between 2.1 and 2.7 Gy. The planetary companion, HD 52265b, orbits the star with a period of 119 d, a semimajor axis of 0.5 astronomical unit (AU), and a minimum mass 
, where 
is the true mass of the planet and 
is the inclination of the orbital axis to the line of sight (18). HD 52265 is overmetallic with respect to the Sun 
, a property that has been associated with the formation of hot Jupiters (21). See Table 1 for a summary of basic properties.
Table 1.
Parameters of star HD 52265
| Parameter | Value | Method |
| Distance | 28.95 ± 0.34 pc | Astrometry (43) |
| Luminosity | 2.09 ± 0.24 LSun | Astrometry (4) |
| Effective temperature | 6,100 ± 60 K | Spectroscopy (4) |
| Metallicity, [M/H] | 0.19 ± 0.05 | Spectroscopy (4) |
| Main-sequence lifetime | ∼ 6 × 109 y | Mass–luminosity relation |
; 
.
The power spectrum of the HD 52265 CoRoT data exhibits a series of peaks near 2 mHz caused by global acoustic oscillations (Fig. 1). As in the Sun and other stars with outer convection zones, these oscillations are continuously excited by near-surface convection (2). The star oscillates in high-overtone modes whose horizontal spatial patterns are given by spherical harmonics 
, where l is the harmonic degree and m the azimuthal order with 
. The comb-like structure of the power spectrum is due to a repeating sequence of pulsations observable in quadrupole 
, radial 
, and dipole 
modes. The 
and 
modes are remarkably well resolved in frequency space and enable unambiguous identification of modes.
Fig. 1.
Power spectrum of global acoustic oscillations of HD 52265. The p modes have measurable power in the range 1.6–2.6 mHz. At low frequencies, the power is due to stellar convection and magnetic activity; at high frequencies it is dominated by photon noise. Inset shows the power spectrum in the interval 1.97–2.17 mHz, where acoustic modes are labeled with their spherical harmonic degrees, 
. Indicated are the large-frequency separation between consecutive radial modes, 
(sensitive to mean density), and the small-frequency separation between adjacent radial and quadrupole modes, 
(sensitive to age). Mode identification is unambiguous by virtue of the analogy with the solar spectrum.
To first order (22), the spectrum of the mode frequencies is specified by two characteristic frequencies (Fig. 1, Inset): the “large-frequency separation,” 
, and the “small-frequency separation,” 
. The large-frequency separation between consecutive 
modes is the inverse of the sound travel time across a stellar diameter. The small-frequency separation between adjacent 
and 
modes is sensitive to the radial gradient of sound speed in the nuclear-burning core, and thus to helium content and the age of the star (23).
Fig. 2A shows the power spectrum in échelle format (24) of HD 52265 using a folding frequency of 98.5 μHz. Modes have measurable power over 10 consecutive oscillation overtones (radial orders), 
. For comparison, Fig. 2B shows the échelle spectrum of the Sun computed using a folding frequency of 135.3 μHz and 117 d of observations from the VIRGO (25) instrument onboard the Solar and Heliospheric Observatory (SoHO). Although photon noise is higher for HD 52265, the similarity between the two power spectra is striking. HD 52265 is an object that pulsates like the Sun, although there are measurable differences.
Fig. 2.
Échelle spectrum and comparison with the Sun. (A) Échelle spectrum of HD 52265 using a folding frequency of 98.5 μHz. The power spectrum is cut into frequency segments, which are stacked in the vertical direction. Integers along the right axis indicate the number of frequency segments, starting from zero frequency, i.e., the radial order of the 
modes. The nearly vertical ridges of power (labeled according to spherical harmonic degree l) indicate that the folding frequency is close to the large separation 
. (B) For comparison and mode identification, we show the échelle spectrum of the Sun using 117 d of SoHO/VIRGO photometry (25) (green channel) and a folding frequency of 135.3 μHz.
Results
Global Fit of the Power Spectrum.
We estimate the parameters of the individual modes of oscillation by fitting a global parametric model to the power spectrum using a maximum-likelihood technique (26), by considering that the probability density function of the power at any given frequency is an exponential distribution. All modes with 
are fitted together in the range of 
. The expectation value of the power spectrum of each individual mode is modeled by a Lorentzian, whose height and width are allowed to vary with frequency. To improve the robustness of the fit, the large- and small-frequency separations are taken to be smooth (polynomial) functions of the radial order. The noise background is modeled as the sum of a convective component and a white-noise component. As for the Sun, the convective component is well approximated by the sum of two Lorentzians, representing the two dominant timescales of convection, granulation and supergranulation (2).
We include the effects of stellar rotation in the model. First, rotation removes the frequency degeneracy of the 
azimuthal components. Assuming a slowly rotating star, the frequency of mode 
may be approximated by the following:
 |
where Ω is a suitable radial average of the angular velocity over the star (27). Second, mode visibility depends on the angle i between the rotation axis and the line of sight. Assuming (as for the Sun) energy equipartition in a multiplet 
between azimuthal components, mode power is proportional to the following:
 |
where the 
are associated Legendre functions (28). For example, for dipole modes, 
and 
. Thus, the ratios in mode power between azimuthal components tell us about i, whereas the splitting between mode frequencies tells us about Ω.
The fitted multiplets are shown in Fig. 3. The values of Ω and 
are inferred at the same time as the mode frequencies and other mode parameters. The random errors associated with the estimated mode parameters are deduced from Monte Carlo simulations.
Fig. 3.
Power spectra of the radial (
, Left), dipole (
, Middle), and quadrupole modes (
, Right) of HD 52265 (gray curves). Nine consecutive radial orders 
are shown, with n decreasing from Top to Bottom. In each panel, the frequency axis is shifted by the central frequency of the multiplet, 
, obtained from the global fit. The global fit (red curves) is an estimate of the expectation value of the power spectrum and includes the effects of rotation on oscillations. Each azimuthal component 
in a multiplet is modeled by a Lorentzian line profile, describing damped harmonic oscillation.
Seismic Stellar Model.
In the frequency range of 1.85–2.30 mHz where the mode power is the largest, we measure an average large-frequency separation of 
and an average small-frequency separation of 
. The large-frequency separation is proportional to the square root of the mean stellar density, implying that HD 52265 is less dense than the Sun by a factor of 
. This seismic constraint on the mean stellar density is 60 times more precise than the spectroscopic constraint.
We have estimated the fundamental stellar properties of HD 52265 by finding the best-fit stellar model among an extended grid of stellar models computed with the Aarhus Stellar Evolution Code. Using the average large- and small-frequency separations given above together with the observed effective temperature of the star and its metallicity (Table 1), the SEEK optimization procedure (29) returns a best-fit stellar model with a seismic radius 
and a seismic mass 
, where formal error bars are severalfold smaller than the classical ones (Table 2). The seismic age is 
Gy, where we quote the formal error. By comparison, stellar ages deduced from isochrone fits lead to typical errors (30) of 30–50%, which are significantly worse. Detailed asteroseismic modeling of HD 52265 not only places tight constraints on the mass, radius, and age of the star but also on its initial chemical composition (31).
Table 2.
Asteroseismic vs. classical constraints on properties and rotation of HD 52265
| Stellar property | Asteroseismology | Classical methods |
| Radius | 1.34 ± 0.02 RSun | 1.30 ± 0.08 RSun [spectroscopy (4)] |
| Mass | 1.27 ± 0.03 MSun | 1.21 ± 0.05 MSun [isochrone fits (20)] |
| Age | 2.37 ± 0.39 × 109 y |
 × 109 y [isochrone fits (20)] |
Bulk rotation, 
|
 |
|
Star spot rotation, 
|
2.15 and 2.52 [photometry (4)] | |
| Inclination of stellar rotation axis, sin i |  |
 [star spot modeling (4, 33)] |
| Sky-projected rotational velocity |
 km·s−1*
|
 km·s−1 [spectroscopy (4)]†
|
Solar reference values: 
; 
; 
.
, where R and 
are seismic estimates.
from spectroscopic rotational broadening. The value 4.7 ± 0.5 km⋅s−1 quoted in ref. 20 is probably an overestimate due to the macroturbulence model used.
Internal Stellar Rotation.
The global fit of the power spectrum returns a rotational splitting frequency 
and the inclination 
. The inferred rotational splitting of HD 52265 is about 2.3 times larger than that of the Sun (Table 2).
To further test our methodology, we average the power spectrum over multiplets with the same l value to smooth out random variations of power with frequency due to the realization noise (Fig. 3). This average is computed over nine consecutive radial orders 
, after shifting multiplets by their central frequencies 
using Fourier interpolation. A similar averaging procedure was used in the early days of helioseismology (32) to measure the small frequency separation 
.
The average spectra of HD 52265 for 
, 
, and 
are shown in Fig. 4. The widths at half-maximum of the profiles for 
and 
modes are larger than that of the 
singlet by 20% and 90%, respectively. Thus, the nonradial multiplets are broadened by rotation, confirming that stellar rotation (Table 2) has a measurable effect, as inferred rigorously from the maximum-likelihood model fit. However, the individual m components are not resolved due to the intrinsic line width of the modes, which (near the maximum power) is about twice as large as the rotational splitting—a situation comparable to that of the Sun.
Fig. 4.
Influence of stellar rotation on oscillations. Power spectra are shown for the radial (Top), dipole (Middle), and quadrupole modes (Bottom), after averaging over the nine consecutive radial orders from Fig. 3. The gray curve is the average power spectral density and the red is the average of the fits. For clarity, the frequency resolution is reduced by a factor of 3. Although the rotational splitting is too small to separate the azimuthal components, a rotational broadening of the average line profiles of 
and 
is clearly visible. The dashed, dotted, and solid blue lines show the azimuthal components 
, 
, and 
, which contribute to the average power. The 
frequencies of the azimuthal components, split by rotation 
, are marked by arrows at the bottom of each panel and labeled by the azimuthal order m. The visibility amplitudes of the azimuthal components are computed for the best-fit inclination angle of 
.
Our seismic estimates of Ω and i are remarkably consistent with independent measurements from spectroscopy and star spot rotation, as shown in Fig. 5. The observed (4) spectroscopic rotational velocity 
km⋅s−1 is fully consistent with the seismic value 
km⋅s−1 (surface and bulk rotation rates of solar-type stars are expected to be similar, as in the Sun). In addition, the photometric time series of HD 52265 is modulated by the rotation of star spots at two prominent periods of 10.8 and 12.7 d, corresponding to the cyclic frequencies 
and 1.07 μHz, values that are consistent with seismology. The two periods may be associated with star spots at different latitudes, thus providing some indication of latitudinal differential rotation. Star spot modeling of the CoRoT time series including differential rotation (4, 33) returns a rotational frequency at the equator 
and 
(which again is consistent) (Table 2). The general agreement between all these independent measurements strongly supports our seismic determination of mean internal rotation and inclination angle of HD 52265.
Fig. 5.
Constraints on stellar rotation and planet mass. The dark-red and light-red regions are the 1-σ and 2-σ seismic constraints on stellar rotation in the plane 
, where Ω is the bulk angular velocity, 
μHz is the solar (Carrington) rotational frequency, and i is the inclination of the stellar rotation axis to the line of sight. The black diamond with error bars gives the best-fit seismic values, 
and 
. For comparison, the two horizontal green lines mark the angular velocity of stellar activity (star spots) deduced from two prominent peaks in the low-frequency part of the power spectrum. The filled green ellipse represents the 1-σ bound of the equatorial rotation and inclination angle obtained from star spot modeling of the photometric time series (4, 33). The spectroscopic constraints are given by the dashed (observations) and the solid (1-σ errors) blue curves, as expressed through the sky-projected angular velocity 
, where 
km⋅s−1 is the observed spectroscopic rotational broadening and 
is the seismic stellar radius. The minimum mass of the planet from radial velocity measurements (18) is 
, where 
is the inclination of the normal of the planetary orbit to the line of sight. Assuming 
, the seismic constraint on 
can be converted into a constraint (top axis and gray region “HD 52265b”) on the true mass of the planet,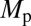 
, which is well below the brown dwarf limit of 
.
Discussion
The seismic radius and mass of HD 52265 have been inferred with a formal error of 2% and the stellar age with a formal error of 5% of the main-sequence lifetime. This level of precision on fundamental stellar properties, required to characterize planets in transit around Sun-like stars (6, 7, 34), is a significant improvement over classical estimates (Table 2). Although the planetary companion orbiting HD 52265 does not transit its host, the seismic determination of the direction of the spin axis of the star provides useful information to further characterize the mass of the exoplanet.
Mass of Exoplanet HD 52265b.
Under the assumption that the rotation axis of the star and the normal to the planetary orbit coincide, i.e., 
, the knowledge of the minimum mass of HD 52265b from Doppler spectroscopy 
can be used together with the inclination of the stellar spin axis from seismology to constrain the true mass, 
. The 1-σ seismic bound 
(irrespective of the value of Ω) implies that 
. Such a mass is well under the lower limit of brown dwarfs, 
. Deuterium burning cannot be sustained below this mass threshold. Thus, HD 52265b is likely to be a planet and not a brown dwarf. [Note that the values 
and 
, obtained from Hipparcos intermediate astrometry (35), have low significance due to insufficient angular resolution of the Hipparcos data (36).] The best seismic fit (Fig. 5, black cross) implies 
. Together, the seismic, spectroscopic, and star spot constraints on i give 
. Some relevant characteristics of the exoplanet are listed in Table 3.
Table 3.
Characteristics of exoplanet HD 52265b
| Characteristic | Value | Method |
Minimum planet mass, 
|
 |
Radial velocity (18) |
| Semimajor axis of planetary orbit |  |
Radial velocity (18) |
| Planet mass, Mp |  |
Asteroseismology |
; 
.
Formation of Planetary Systems.
The formation of Jupiter-mass planets in close orbits (hot Jupiters), like HD 52265b, remains a mystery. In one theory, hot Jupiters are formed in the outer regions of protoplanetary disks and migrate toward the inner regions via friction (37). This scenario favors systems with 
. However, a study based on the Rossiter–McLaughlin effect (38) revealed that 80% of a sample of transiting planets show a sky-projected spin-orbit misalignment, λ, greater than 20°. Alternative formation scenarios like Kozai cycles (39) and planet scattering (40, 41) are required to explain large spin-orbit misalignments. The misalignment of the HD 52265 system is not excluded, as the alignment timescale through tidal interaction (42) is much greater than the age of the star. For other planets discovered with the transit method, 
is known and the knowledge of i (through asteroseismology and/or spot modeling) and λ would give the true angle between the stellar rotation axis and the planet orbital axis. Asteroseismology has much to contribute to the study of the evolutionary history of exoplanetary systems.
Acknowledgments
The CoRoT space mission has been developed and is operated by the Centre National d'Études Spatiales, with the contribution of Austria, Belgium, Brazil, the European Space Agency (Research and Scientific Support Department and Science Programme), Germany, and Spain. L.G. and T.S. acknowledge support from Deutsche Forschungsgemeinschaft Sonderforschungsbereich 963 “Astrophysical Flow Instabilities and Turbulence” (Project A18). J.B. acknowledges support from Agence Nationale de la Recherche through project SiROCO. I.R. acknowledges support from the Leverhulme foundation under Grant 2012-035/4. The National Center for Atmospheric Research is supported by the National Science Foundation. SoHO is a mission of international cooperation between the European Space Agency and the National Aeronautics and Space Administration.
Footnotes
The authors declare no conflict of interest.
References
- 1.Bruntt H. Asteroseismology with the WIRE satellite. Commun Asteros. 2007;150:326–332. [Google Scholar]
- 2.Michel E, et al. CoRoT measures solar-like oscillations and granulation in stars hotter than the Sun. Science. 2008;322(5901):558–560. doi: 10.1126/science.1163004. [DOI] [PubMed] [Google Scholar]
- 3.Chaplin WJ, et al. Ensemble asteroseismology of solar-type stars with the NASA Kepler mission. Science. 2011;332(6026):213–216. doi: 10.1126/science.1201827. [DOI] [PubMed] [Google Scholar]
- 4.Ballot J, et al. Accurate p-mode measurements of the G0V metal-rich CoRoT target HD 52265. Astron Astrophys. 2011;530:A97. [Google Scholar]
- 5.Appourchaux T, et al. Oscillation mode frequencies of 61 main-sequence and subgiant stars observed by Kepler. Astron Astrophys. 2012;543:A54. [Google Scholar]
- 6.Christensen-Dalsgaard J, et al. Asteroseismic investigation of known planet hosts in the Kepler field. Astrophys J. 2010;713:L164–L168. [Google Scholar]
- 7.Batalha NM, et al. Kepler’s first rocky planet: Kepler-10b. Astrophys J. 2011;729:27. [Google Scholar]
- 8.Howell SB, et al. Kepler-21b: A 1.6 REarth planet transiting the bright oscillating F subgiant star HD 179070. Astrophys J. 2012;746:123. [Google Scholar]
- 9.Borucki WJ, et al. Kepler-22b: A 2.4 Earth-radius planet in the habitable zone of a Sun-like star. Astrophys J. 2012;745:120. [Google Scholar]
- 10.Noyes RW, Hartmann LW, Baliunas SL, Duncan DK, Vaughan AH. Rotation, convection, and magnetic activity in lower main-sequence stars. Astrophys J. 1984;279:763–777. [Google Scholar]
- 11.Fletcher ST, Chaplin WJ, Elsworth Y, Schou J, Buzasi D. Frequency, splitting, linewidth and amplitude estimates of low-l p modes of α Cen A: Analysis of Wide-Field Infrared Explorer photometry. Mon Not R Astron Soc. 2006;371:935–944. [Google Scholar]
- 12.Bazot M, et al. Asteroseismology of α Centauri A. Evidence of rotational splitting. Astron Astrophys. 2007;470:295–302. [Google Scholar]
- 13.Beck PG, et al. Fast core rotation in red-giant stars as revealed by gravity-dominated mixed modes. Nature. 2012;481(7379):55–57. doi: 10.1038/nature10612. [DOI] [PubMed] [Google Scholar]
- 14.Deheuvels S, et al. Seismic evidence for a rapidly rotating core in a lower-giant-branch star observed with Kepler. Astrophys J. 2012;756:19. [Google Scholar]
- 15.Fridlund M, Baglin A, Lochard J, Conroy L, editors. The CoRoT Mission, Pre-launch Status, Stellar Seismology and Planet Finding. Noordwijk, The Netherlands: ESA Publication Division; 2006. p. ESA SP-1306. [Google Scholar]
- 16.Butler RP, et al. Planetary companions to the metal-rich stars BD −10°3166 and HD 52265. Astrophys J. 2000;545:504–511. [Google Scholar]
- 17.Naef D, et al. The CORALIE survey for southern extrasolar planets. V. 3 new extrasolar planets. Astron Astrophys. 2001;375:205–218. [Google Scholar]
- 18.Butler RP, et al. Catalog of nearby exoplanets. Astrophys J. 2006;646:505–522. [Google Scholar]
- 19.Gonzalez G, Laws C, Tyagi S, Reddy BE. Parent stars of extrasolar planets. VI. Abundance analyses of 20 new systems. Astron J. 2001;121:432–452. [Google Scholar]
- 20.Valenti JA, Fischer DA. Spectroscopic properties of cool stars (SPOCS). I. 1040 F, G, and K dwarfs from Keck, Lick, and AAT planet search programs. Astrophys J Suppl Ser. 2005;159:141–166. [Google Scholar]
- 21.Fischer DA, Valenti J. The planet-metallicity correlation. Astrophys J. 2005;622:1102–1117. [Google Scholar]
- 22.Tassoul M. Asymptotic approximations for stellar nonradial pulsations. Astrophys J Suppl Ser. 1980;43:469–490. [Google Scholar]
- 23.Gough D. Seismological measurement of stellar ages. Nature. 1987;326:257–259. [Google Scholar]
- 24.Grec G, Fossat E, Pomerantz MA. Full-disk observations of solar oscillations from the geographic South Pole—latest results. Sol Phys. 1983;82:55–66. [Google Scholar]
- 25.Fröhlich C, et al. VIRGO: Experiment for helioseismology and solar irradiance monitoring. Sol Phys. 1995;162:101–128. [Google Scholar]
- 26.Anderson ER, Duvall TL, Jr, Jefferies SM. Modeling of solar oscillation power spectra. Astrophys J. 1990;364:699–705. [Google Scholar]
- 27.Hansen CJ, Cox JP, van Horn HM. The effects of differential rotation on the splitting of nonradial modes of stellar oscillation. Astrophys J. 1977;217:151–159. [Google Scholar]
- 28.Gizon L, Solanki SK. Determining the inclination of the rotation axis of a Sun-like star. Astrophys J. 2003;589:1009–1019. [Google Scholar]
- 29.Quirion P-O, Christensen-Dalsgaard J, Arentoft T. Automatic determination of stellar parameters via asteroseismology of stochastically oscillating stars: Comparison with direct measurements. Astrophys J. 2010;725:2176–2189. [Google Scholar]
- 30.Saffe C, Gómez M, Chavero C. On the ages of exoplanet host stars. Astron Astrophys. 2005;443:609–626. [Google Scholar]
- 31.Escobar ME, et al. Precise modeling of the exoplanet host star and CoRoT main target HD 52265. Astron Astrophys. 2012;543:A96. [Google Scholar]
- 32.Grec G, Fossat E, Pomerantz M. Solar oscillations—full disk observations from the geographic South Pole. Nature. 1980;288:541–544. [Google Scholar]
- 33.Mosser B, et al. Short-lived spots in solar-like stars as observed by CoRoT. Astron Astrophys. 2009;506:245–254. [Google Scholar]
- 34.Stello D, et al. Radius determination of solar-type stars using asteroseismology: What to expect from the Kepler mission. Astrophys J. 2009;700:1589–1602. [Google Scholar]
- 35.Han I, Black DC, Gatewood G. Preliminary astrometric masses for proposed extrasolar planetary companions. Astrophys J. 2001;548:L57–L60. [Google Scholar]
- 36.Pourbaix D. The Hipparcos observations and the mass of sub-stellar objects. Astron Astrophys. 2001;369:L22–L25. [Google Scholar]
- 37.Lin DNC, Bodenheimer P, Richardson DC. Orbital migration of the planetary companion of 51 Pegasi to its present location. Nature. 1996;380:606–607. [Google Scholar]
- 38.Triaud AHMJ, et al. Spin-orbit angle measurements for six southern transiting planets. New insights into the dynamical origins of hot Jupiters. Astron Astrophys. 2010;524:A25. [Google Scholar]
- 39.Kozai Y. Secular perturbations of asteroids with high inclination and eccentricity. Astron J. 1962;67:591–598. [Google Scholar]
- 40.Rasio FA, Ford EB. Dynamical instabilities and the formation of extrasolar planetary systems. Science. 1996;274(5289):954–956. doi: 10.1126/science.274.5289.954. [DOI] [PubMed] [Google Scholar]
- 41.Naoz S, Farr WM, Lithwick Y, Rasio FA, Teyssandier J. Hot Jupiters from secular planet-planet interactions. Nature. 2011;473(7346):187–189. doi: 10.1038/nature10076. [DOI] [PubMed] [Google Scholar]
- 42.Hut P. Tidal evolution in close binary systems. Astron Astrophys. 1981;99:126–140. [Google Scholar]
- 43.van Leeuwen F, editor. 2007. Hipparcos, the New Reduction of the Raw Data, Astrophysics and Space Science Library (Springer, Berlin), Vol 350.