Increased transmissibility explains the third wave of infection by the 2009 H1N1 pandemic virus in England

Abstract

In the 2009 H1N1 pandemic, the United Kingdom experienced two waves of infection, the first in the late spring and the second in the autumn. Given the low level of susceptibility to the pandemic virus expected to be remaining in the population after the second wave, it was a surprise that a substantial third epidemic occurred in the UK population between November 2010 and February 2011, despite no evidence for any significant antigenic evolution of the pandemic virus. Here, we use a mathematical model of influenza transmission embedded within a Bayesian synthesis inferential framework to jointly analyze syndromic, virological, and serological surveillance data collected in England in 2009–2011 and thereby assess epidemiological mechanisms which might have generated the third wave. We find that substantially increased transmissibility of the H1N1pdm09 virus is required to reproduce the third wave, suggesting that the virus evolved and increased fitness in the human host by the end of 2010, or that the very cold weather experienced in the United Kingdom at that time enhanced transmission rates. We also find some evidence that the preexisting heterologous immunity which reduced attack rates in adults during 2009 had substantially decayed by the winter of 2010, thus increasing the susceptibility of the adult population to infection. Finally, our analysis suggests that a pandemic vaccination campaign targeting adults and school-age children could have mitigated or prevented the third wave even at moderate levels of coverage.

In April 2009 a new strain of swine-origin influenza A, denoted H1N1pdm09, was identified in Mexico, triggering the first influenza pandemic of the 21st century. The newly emerged H1N1pdm09 virus caused two successive waves of infection in the United Kingdom during 2009–2010. The first wave emerged in May 2009, peaked in late July 2009, and rapidly extinguished after the start of the summer school holidays. When schools reopened in September 2009, the United Kingdom experienced a second clear wave of transmission, which died out at the end of January 2010. A serological study conducted in England during the 2009 pandemic concluded that the low levels of susceptibility to H1N1pdm09 virus left in the population at the end of the second wave (particularly in school-age children, 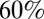of whom were infected) suggested that a third wave of infection in the 2010–2011 influenza season was unlikely without significant antigenic evolution of the H1N1pdm09 virus (1). However, in winter 2010–2011, the H1N1pdm09 virus caused a third wave of infection in the United Kingdom with a greater burden of severe illness compared with the previous year (2).

There is no evidence that the 2010 virus had drifted antigenically from its 2009 progenitor (3), which raises the question of what mechanism allowed the third UK wave to occur. One possibility is that the transmissibility of the virus increased, either due to changes in the virus, or due to the climate being more conducive to transmission in winter 2010 than in the summer/autumn of 2009 (times of year where transmission of seasonal influenza viruses is typically low). A number of nonsynonymous substitutions had occurred in both hemagglutinin (HA) and other viral segments by late 2010 (4, 5), and it is possible that these may have increased the epidemiological fitness of the third wave virus, whereas the winter of 2010 was unusually cold by UK standards. An alternative explanation for the third wave is that the preexisting cross-reactive immunity that protected much of the adult population from infection in 2009 had waned substantially by the winter of 2010, given nearly 2 y would have passed since the last seasonal influenza epidemic of 2008/2009.

Here, we test whether increases in transmissibility (whether caused by viral or environmental factors) or waning of prior immunity or a combination of both can successfully reproduce the observed patterns of infection and disease across all three waves of infection. We couple a compartmental mathematical model of influenza transmission with a statistical model which captures the observation processes underpinning the available surveillance data and estimate epidemiologically relevant parameters, such as the effective reproduction number, 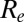, and the incidence of infection in the general population. Notably, to test hypotheses about the waning of prior immunity, we mechanistically link the age-specific prevalence of preexisting cross-reactive antibodies to H1N1pdm09 measured before the pandemic to a quantitative measure of protection against infection. Our study (which builds on refs. 6, 7) melds syndromic, virological, and serological surveillance data in a single inferential framework, thus providing a coherent picture of both the dynamics of disease incidence and of how population immunity develops during an epidemic.

Results

We fit six different model variants to the Influenza-Like Illness (ILI) consultations and virological data collected in England during 2009–2011 and to the serological data collected in England in the 2009 pandemic (1). Each model variant is defined in Table 1 and is obtained from the combination of three different assumptions on virus transmissibility (constant across the waves, varying in wave 3, varying in each wave) and two different assumptions on prior immunity (waning, not waning). By “transmissibility,” we mean the probability of transmission per contact 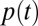(Materials and Methods, Transmission Model). “Prior” immunity is defined as the partial cross-protection acquired from cross-reactive immunity before the emergence of the H1N1pdm09 virus due to exposure to heterologous viruses. “Homologous” immunity is defined as the complete protection acquired after infection by the H1N1pdm09 virus. The transmission model describing the dynamics of disease spread is represented in SI Appendix, Fig. S2. The parameter estimates are relatively consistent across all model variants and can be found in SI Appendix, Table S2, if not stated otherwise.

Table 1.

Description of model variants analyzed and relative assumptions on transmissibility and rate of decay of prior immunity

Model	Transmissibility	Decay of prior immunity
1	Same for all waves	No decay
2	Same for all waves	Estimated
3	Different for wave 3	No decay
4	Different for each wave	No decay
5	Different for wave 3	Estimated
6	Different for each wave	Estimated

Homologous immunity is assumed not to wane.

Model Comparison.

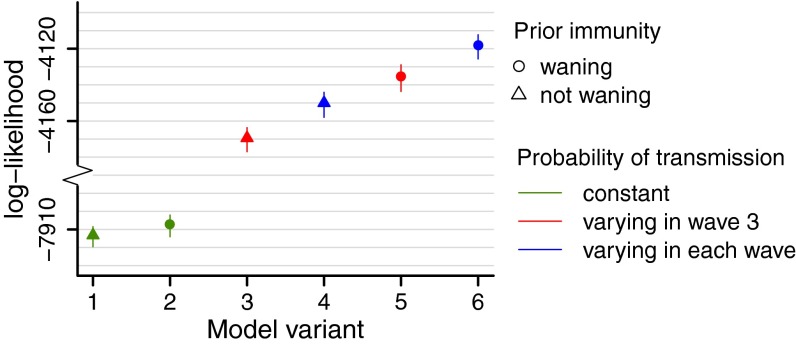
Fig. 1 shows the posterior mean and 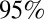credible interval (CrI) of the log-likelihood obtained for models 1–6. Models which allow viral transmissibility to differ between waves (variants 3–6) show a considerably higher log-likelihood than models with no change in transmissibility (models 1 and 2) (Fig. 1). In terms of the qualitative fit of the model to the data, variants assuming constant transmissibility (variants 1 and 2) fail to reproduce the third wave (SI Appendix, Figs. S4 and S5). Within the variants which allow transmissibility to change (variants 3–6), those including decay of prior immunity (variants 5 and 6) show a higher log-likelihood compared with those without decay of prior protection (Fig. 1), although all can qualitatively reproduce the third wave (SI Appendix, Figs. S6–S9). The Deviance Information Criterion scores of model variants 1–6 are shown in Fig. S3 and suggest the same ranking observed in Fig. 1.

Fig. 1.

Estimates of the posterior mean and 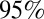CrI of the log-likelihood for models 1–6.

Transmissibility.

All model variants allowing transmissibility to vary between waves estimate that transmissibility increased over time. Transmissibility is estimated to have increased by between 8% and 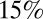from wave 1 to wave 2, with transmissibility in wave 3 being between 67% and 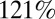higher than that in wave 1, depending on the model variant. Model variants assuming that transmissibility was the same in waves 1 and 2 but potentially different in wave 3 estimate smaller increases in transmissibility than models allowing transmissibility to be different for each wave. Moreover, the estimated increase in transmissibility is consistently smaller when we further allow prior immunity to wane in time than when assuming no waning of prior immunity. According to the best-fitting model variant (variant 6), transmissibility was 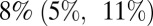higher in the second wave compared with the first wave, and 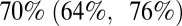higher in the third wave compared with the first wave.

Prior Immunity.

The half-life of the decay of prior immunity is estimated to be ∼1 y for model variant 6, implying that at the start of the first wave (mid-2009) the proportion of individuals with protective cross-reactive immunity against H1N1pdm09 was about half the estimated proportion at the median time the baseline serological data were collected (mid-2008). For the same model variant, we estimate that in mid-2008, over 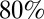of people over 15 y of age had some degree of prior immunity to infection, but that less than 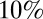of children under 15 y of age had such prior immunity. An individual with such prior immunity had an estimated degree of protection (reduction of susceptibility) of 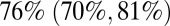. Notably, we estimated that only 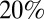of people with prior immunity would test seropositive to H1N1pdm09 [i.e., exhibit haemagglutination inhibition (HI) titers >1:32], suggesting HI seroprevalence gives a very partial picture of immune protection acquired via past exposure to heterologous (or even heterosubtypic) viruses.

Effect of School Holidays.

During holiday periods we estimate a larger reduction in the frequency of contacts between school-age children (5–14 y) than for other age classes. During the summer holidays the number of contacts is significantly reduced in and between all age classes, with school-age children having 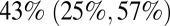of the contacts with each other they have during term and the rest of the population having 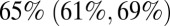of their usual contacts (for model variant 6). Interestingly, the impact of other school holidays on contact rates of the non–school-age population was estimated to be negligible, whereas the impact on contact rates between school age children was larger, although the latter estimates varied more between model variants (SI Appendix, Table S2).

Reporting Rates.

We estimate that the probability of reporting ILI symptoms due to H1N1 infection decreased after the introduction of the National Pandemic Flu Service (NPFS) and remained stable thereafter. NPFS was a web and telephone service activated by the Department of Health during the pandemic to relieve the pressure on general practitioners (GPs); NPFS was launched on week 30 of 2009 and withdrawn on week 7 of 2010 (see SI Appendix for further details). For model variant 6, we estimate that about 8 out of 1,000 people infected by the H1N1pdm09 virus in the 25–44 age group reported ILI symptoms to their GPs in the first wave, and that this reporting rate reduced to about 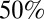of the initial rate after the introduction of NPFS. The reporting rates of the other age classes are assumed to scale proportionally with that of the 25–44 age group according to the observed propensities to consult the GP (Materials and Methods, Model Parameterization), so overall we estimate that 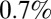of all people infected in the first two waves visited their GP. By comparison, the empirical estimate of reporting probability (dividing total ILI incidence reported at sentinel GPs weighted by the proportion testing positive for H1N1pdm09 by the measured population serological attack rate in waves 1 and 2) is .

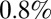Model Fit.

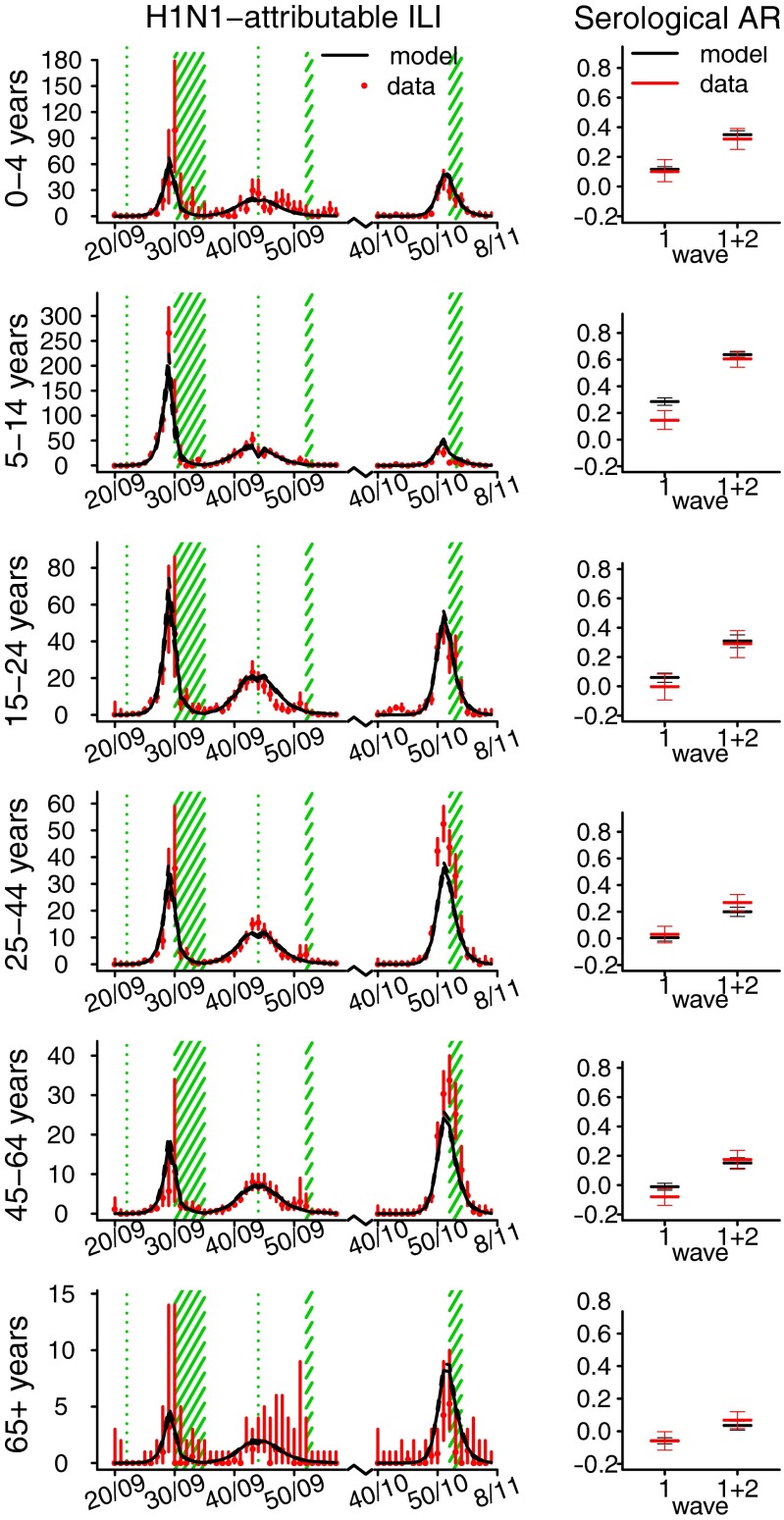
Fig. 2 shows the fit of model variant 6 to the observed H1N1-attributable ILI incidence data (Left) and to the observed serological attack rates (ARs) in the first and second waves (Right). The H1N1-attributable ILI incidence curves have been obtained by multiplying the weekly ILI incidence reported to GPs in each age group by the fraction of virological samples taken that week in the same age group that tested positive for H1N1pdm09 (SI Appendix, Fig. S1). Serological ARs are computed by taking the difference of seroprevalence at successive times (seroprevalence was assessed at a prepandemic baseline, after the first wave and after the second wave, ref.1). The fit to seroprevalence (as compared with serological attack rates) obtained with model variant 6 is shown in SI Appendix, Fig. S9. Fig. 2 shows that we successfully fit the observed H1N1-attributable ILI incidence curves by age class, with some minor deviations. For instance, the model cannot capture the slower exponential growth rate observed in the 45–64 age group during the first wave and in the 65+ age group in the third wave, nor reach quite the peak incidences observed in the 25–44 and 45–64 age groups in the third wave. The model fit to cumulative seroconversion rates across the first two waves is good, but we generally tend to overestimate the first wave serological AR, especially in the 5–14 and 45–64 age groups. However, the geographically biased nature of the sera samples used for assessing seroprevalence and the regional heterogeneity seen in seroprevalence after the first wave means that precise assessment of national seroconversion rates for the first wave is difficult.

Fig. 2.

Age-specific illness and infection rates estimated using model variant 6. (Left) Observed (red) and simulated (black) H1N1-attributable ILI incidence (x100,000) by week. Solid black lines represent the mean; dashed black lines represent the 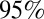credible interval of the simulations. Red bars show the exact 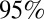confidence interval around the data. Green shaded areas represent holiday weeks. (Right) Observed mean and exact 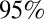confidence interval (red) and simulated mean and 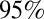credible interval (black) of the serological AR from baseline to postwave 1 serology (wave 1) and from baseline to postwave 2 serology (wave 1 + 2).

Reproduction Number and Estimated Incidence of Infection.

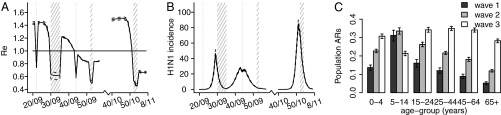
For all model variants, we estimate that the effective reproduction number 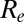was ∼1.4 at the start of the pandemic, consistent with past estimates (8). Fig. 3A shows estimates from model variant 6 of the effective reproduction number 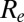over time. Despite the increase in transmissibility, 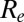is smaller (about 1.2) in the second wave than in the first wave, in agreement with the observed exponential growth rate in ILI incidence. The second wave peaked out after the midterm autumn school break, when 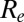crossed the threshold value of 1. A combination of increased transmissibility and waning of prior immunity increased 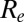to ∼1.5 by the start of the third wave (Fig. 3A), larger than its value at the start of the first wave. Fig. 3B shows the estimated weekly incidence of H1N1pdm09 infection per 1,000 in the English population across the three waves. Although the overall peak incidence was higher in the first (mean 46, 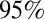CrI (42, 51) per 1,000) than in the second wave (mean 27, 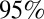CrI (25, 29) per 1,000) (Fig. 3B), the estimated population attack rates (i.e., cumulative incidence of infection in the population) were higher in the second than in the first wave in all age classes (Fig. 3C). At a population level, the overall attack rate was highest in the third wave [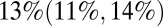; ; 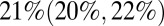and 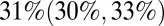in waves 1, 2, and 3, respectively].

Fig. 3.

Estimates of (A) effective reproduction number over time (solid line represents the mean, the dashed lines represent the 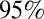credible interval, the horizontal line is drawn at the threshold value of 1, and the shaded areas represent holiday weeks); (B) incidence of H1N1 cases in the population (×1,000) in time (solid line represents the mean, dashed lines represent the 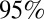credible interval, and shaded areas represent holiday weeks); and (C) attack rates by age class and wave (mean and 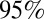credible interval) obtained with model variant 6.

Model Predictions.

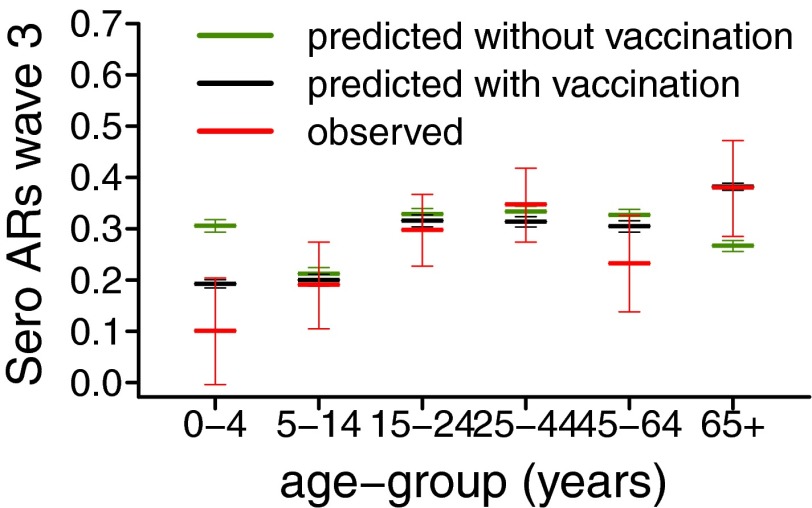
In many fields, model adequacy is evaluated by partitioning the data into a training dataset, which is used for parameter inference, and a validation dataset, which is used for assessing the goodness of model predictions. Such approach is rarely feasible when analyzing epidemic data, as the temporal dependency found in these data means it is often impossible to partition them. However, the recent publication of serological data on the third wave (9) allowed us to validate model predictions of the third wave serological attack rates. Fig. 4 shows the observed and predicted serological ARs in the third wave across the age classes, obtained using model 6 calibrated on the 2009–2010 serology. The predicted serological ARs (in green in Fig. 4) fall into the 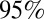confidence interval of the observed serological ARs (in red in Fig. 4) for all age groups except 0–4 and 65+, the two age classes which were targeted by an extensive vaccination program during 2010–2011. In the United Kingdom, immunization of under 5s with the pandemic vaccine started in January 2010, whereas seasonal vaccination of 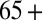age group started in October 2010 (9–11). Once we included vaccination in those age groups in the model, model predictions of third-wave attack rates were consistent with serological data for all age groups (Fig. 4), with attack rates of 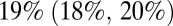and 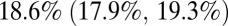in the 0–4 and 65+ age groups, respectively. Accounting for vaccination causes our estimate of the overall population attack rate in the third wave to fall to 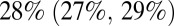. Finally, we fitted model 6 in its variant with and without vaccination to the complete 2009–2011 surveillance data (i.e., including the third-wave serological data, ref. 9) and found parameter estimates (SI Appendix, Table S5) consistent with those obtained without fitting third-wave serology. Further out-of-fit predictions (SI Appendix, section 3.5) show the importance of serological data in setting the actual size of the waves and as a consequence in producing reliable estimates of the reporting rates. However, serological data alone do not provide information on the exponential growth rate of the ILI, thus highlighting the importance of integrating the different sources of data in a single, unifying modeling framework.

Fig. 4.

Observed mean and exact 95% confidence interval (red) and predicted mean and 95% CrI of the serological attack rates in the third wave across the age classes. Predictions have been obtained using model variant 6 without modeling of vaccination (green) and with modeling of vaccination (black).

Sensitivity Analysis.

We tested whether the data were consistent with any waning of homologous immunity (i.e., immunity acquired after infection with the H1N1pdm09 virus), which would permit people infected in wave 1 or 2 to be reinfected in wave 3. We found that there is no significant difference in terms of parameter estimates and log-likelihood between models allowing homologous immunity to wane and models assuming no decay of homologous immunity (SI Appendix, Tables S2 and S4). To further check the robustness of our results, we performed sensitivity analysis on a number of other assumptions. We found that it was possible to improve the fit of the shift toward the adult age classes observed in the H1N1-attributable ILI in the third wave using a less constrained parameterization of reporting rates (SI Appendix, Fig. S24). A more parsimonious representation of holidays could still reproduce the observed incidence patterns across the age groups but penalizes the log-likelihood (SI Appendix, Fig. S25 and Table S7). When we relaxed the assumption that H1N1pdm09 infections always lead to seroconversion, we estimated that 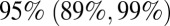of infections seroconverted, and found that this model variant produced very similar results in terms of log-likelihood and parameter estimates to the ones obtained assuming certain seroconversion after infection. We also verified that model results are not sensitive to different age distributions of seeded infections. Last, we verified that our results were unlikely to be substantially affected by the inclusion of demographic stochasticity within our modeling framework (SI Appendix, section 3.6).

Simulated Vaccination Strategies.

Finally, we explored the effect of alternative vaccination scenarios on the third wave. In addition to the vaccination campaign targeting children under 5 y, we simulated vaccination programs covering from 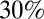to of the population over 5 y of age. We found that blanket 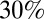coverage would have delayed and mitigated the third wave (SI Appendix, Figs. S36 and S40) and coverage over 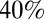would have prevented the third wave completely, at least until the beginning of 2012 (SI Appendix, Figs. S37–S39 and S41).

Discussion

No substantial antigenic drift was observed in H1N1pdm09 viruses from their emergence in 2009 until 2012 (3–5), as illustrated by the A/California/7/2009 virus strain being recommended for both the southern and northern hemisphere seasonal influenza vaccines in 2010–2011 (12). Through an integrated analysis of available syndromic, virological and serological surveillance data, we have shown that whereas the second wave was mainly caused by the school holidays, in the absence of antigenic evolution of the virus, a substantial increase in viral transmissibility is the epidemiological mechanism able to explain the third wave of the UK 2009–10 H1N1 pandemic. Our analysis has also shown that waning of preexisting (before the pandemic) cross-protective immunity may have also had a secondary role in explaining the restarting of H1N1pdm09 transmission in the winter of 2010, but is insufficient on its own to explain the third wave. Moreover, our results do not support decay of homologous immunity (which would permit reinfection with H1N1pdm09) as a mechanism explaining the third wave and the associated shift in the age distribution of cases between the second and third waves. To a lesser extent, models with transmissibility varying between each wave are preferred to models with transmissibility changing only between the second and the third waves, and we consistently estimate that transmissibility increases between each successive wave.

An increase in transmissibility may have been caused by climatic factors or further genetic adaptation of the virus to the human host. There is evidence that temperature and absolute humidity modulate viral survival and transmissibility (13, 14) and can also affect human immunity (15). The third wave of H1N1pdm transmission in England (November 2010–January 2011) coincided with a period of atypically cold and relatively dry weather (SI Appendix, Fig. S42), which may have substantially affected the ability of the virus to transmit compared with the first (May–August 2009) or the second wave (September–December 2009), both of which occurred largely outside the usual period for influenza transmission in northern hemisphere temperate countries. Secondly, signs of adaptation of H1N1pdm09 virus to the human host and the rise of distinct clusters were observed in the United Kingdom (4, 5) and in Taiwan (16) during 2009. In winter 2010 genetically distinct variants which were antigenically indistinguishable from the 2009 H1N1pdm09 virus were observed in Australia, New Zealand, and Singapore (17).

Analyses suggest that the basic reproduction number (and hence the underlying virus transmissibility) increased between successive waves of the 1968–1969 pandemic (18), although in that case, there is evidence that antigenic evolution occurred (19, 20). We found that although the effective reproduction number 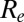declined from wave 1 to wave 2 of the 2009 pandemic in England, underlying virus transmissibility may nevertheless have increased over that time. This highlights that effective reproduction number estimates provide an imperfect measure of underlying transmissibility, as 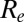is fundamentally affected by the degree of population immunity.

We estimate that the reporting rates dropped after the introduction of NPFS and that people were less likely to consult the GP when symptomatic during 2010–2011 than during the pandemic year, consistent with previous studies (2, 6). Also in agreement with past work (6), we find that the cumulative attack rate in the second wave was higher than in the first wave, despite peak reported ILI incidence being higher in the first than in the second wave, a conclusion not apparent from the syndromic surveillance data alone.

Our model successfully reproduces the shift in the age distribution of cases between the second and third waves, although it somewhat underestimates peak ILI incidence in older adults in the third wave. Unsurprisingly, using a less constrained parameterization of the reporting rates allowed the model to better reproduce adult peak ILI incidence. Rather than fixing children’s propensity to consult their GP due to ILI in the third wave (as for the first and second waves), we estimated this additional parameter. We found that in the third wave children’s propensity to consult the GP due to ILI was lower than in adults, opposite to what is estimated for the first and second waves. Behavioral data on changes over time in age-specific healthcare-seeking behavior is lacking, however, so we are unable to validate this conclusion.

Recent work (21) has highlighted the importance of including changing mixing patterns in epidemic models. Here, we modeled contact reduction during school-holiday times by introducing a specific multiplicative factor for the contacts of school-age children with school-age children (5–14 y) and another factor for all other contacts. The chosen representation of holidays is clearly a simplification of how contacts change in reality, but it allowed us to capture the reduction observed in all age classes and especially between school-age children in a parsimonious manner (21). Parsimony also motivates other simplifying model assumptions. The chosen piecewise constant parameterization of 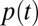is certainly a simplification, but it allows exploration of the impact of changes in transmissibility over time while limiting the numbers of estimated parameters. For the same reason, we adopted a piecewise constant parameterization for reporting rates, and fixed age-specific differences in the propensity of people with H1N1pdm09 to consult the GP using the ratio of observed age-specific ILI and serological attack rates (SI Appendix, section 1.5.1).

Our analysis gives interesting insights into the nature and magnitude of preexisting cross-protective immunity acquired before the pandemic. To be able to explain the age-specific attack rates seen in the first two waves of the pandemic, a much larger proportion of older adults must have had such prior immunity than is revealed by HI titer levels in prepandemic samples. Our model estimates that only 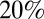with prior protection had HI titers over 1:32, implying nearly everyone over 65 had some level of cross-reactive protection at the start of the pandemic. However, note that we estimate such protection was not complete, but rather reduced the risk of infection per exposure by between about 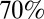and 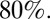Hence, although we conclude that cross-reactive HA antibody levels revealed through the HI assay are a correlate of protection, the precise relationship between titer level and protection is more complex than that established for homologous antibodies (22, 23). Furthermore, a role for (potentially heterosubtypic) antibody or T-cell responses targeting non-HA antigens cannot be ruled out (24).

The publication of serological data on the third wave (9) during the preparation of this paper provided an opportunity to test model predictions regarding the third wave. We find that once we account for immunization in 2010 of under 5s with the pandemic vaccine and over 65s with the seasonal vaccine, the model predicts infection attack rates in the third wave well (Fig. 4). However, the model only partially reproduces the approximately 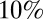decline in seroprevalence between the end of the second wave and the start of the third seen in all but the under 5s in the latest data (SI Appendix, Fig. S10), even when we fitted the model to the third-wave serological data (SI Appendix, Figs. S21 and S23). Part of the explanation may be differences in the sample populations between the postsecond-wave and prethird-wave serum samples (1, 9), since additional residual serum samples from chemical pathology laboratories were used for the wave 1 and 2 serology, and these may have been biased toward hospitalized subjects with a higher rate of underlying conditions and exposure to both the virus and vaccine (25).

Although the large third wave seen in the United Kingdom was unexpected, it is interesting in hindsight to examine how the large stockpile of vaccine acquired by the UK government during the pandemic could have been used to mitigate or prevent the epidemic seen in 2010. We find that a vaccination campaign in early 2010 which achieved 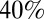coverage in the population over 5 would have generated enough population immunity to prevent the third wave. Although delivery of such a large-scale universal campaign would have been costly, its significant potential benefits in reducing morbidity and mortality in any third wave suggests that future pandemic vaccination planning needs to more explicitly take account of the risks posed by multiple waves of transmission over more than just the first year of a pandemic.

In conclusion, we have developed a model of influenza pandemic transmission dynamics that can reproduce the three waves of infection seen in England in 2009–2010, both in terms of observed H1N1-attributable ILI and seroprevalence. We show that the third wave can be best explained by a combination of an increase in transmissibility and decay of prior immunity, where the increase in transmissibility plays the major role. Climatic factors and viral adaptation are two plausible causes of increased transmissibility, but further research will be required to assess the relative contribution of these two mechanisms.

Materials and Methods

Syndromic, Virological, and Serological Data.

We analyzed weekly GP ILI consultation data collected by QSurveillance and weekly virological data collected by the Royal College of General Practitioners and the Health Protection Agency (HPA) Regional Microbiology Network from week 20/09 (early May 2009) to week 5/10 (late January 2010) and from week 40/10 (end September 2010) to week 7/11 (beginning February 2011), together with serology data collected by the HPA (1). We generated a synthetic serology dataset representative of all England by computing a population-weighted average of the “London” and “Outside London” serological data published in ref. 1 (SI Appendix, section 1.1.3). Syndromic, virological, and serological data used in this work were specific to England and stratified into six age groups (0–4, 5–14, 15–24, 25–44, 45–64, and 65+ y). In our notation, week 01/09 (the first week of 2009) was the week starting on 29/12/2008.

Demographic and Social Contact Data.

Using raw data from the UK arm of a diary-based survey of social contact patterns (26), we computed the daily frequency of all (physical and nonphysical) contacts between and within the six age groups listed above. The population sizes by age were obtained from the Office for National Statistics midyear population estimates of 2009 for England (27).

Transmission Model.

We define an age-structured, deterministic, transmission model with the six age groups listed above. We assume that at the beginning of the pandemic a fraction of the population (the PS compartment) has preexisting cross-protective immunity to H1N1pdm09, whereas the rest of the population is completely naive (S compartment). Once infected, individuals are infectious (I) for 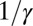days on average and then recover and are fully immune. We assume that recovered individuals test seronegative 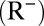for the first 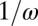days on average and then seroconvert 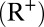. The force of infection is given by 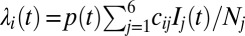(with 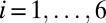), where 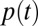is the probability of getting infected upon a contact with an infectious individual, 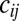indicates the mean frequency of contacts between an individual of age class i with individuals of age class j, and 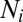represents the size of age class i. We did not model births or deaths. We assume that 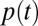is piecewise constant in each wave with 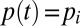in wave 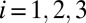. Full model details are given in SI Appendix. By definition, individuals in 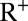show HI titers >1:32 with certainty. We assume that individuals in the PS compartment have probability ξ of showing HI titers >1:32 and that individuals in the other states (S, I, or 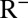) are seronegative. We represented the impact of the school vacations on contact patterns by multiplying the contact rates 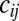in school-age children and the rest of the population by factors to be estimated from the data (SI Appendix, section 1.5.2). We fitted these factors separately for the summer holidays and for all other types of holidays.

Vaccination.

We represented vaccination of <5 y old and 65+ y old in 2010–2011 by moving a fraction 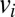of the population in age class i to state 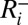at the time of vaccination (we assume that vaccinated individuals seroconvert after an average of 14 d). Fraction 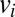represents the fraction of effectively vaccinated individuals in age class i. We model pandemic vaccination of children <5 as occurring in early April 2010 at a coverage of 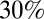(10). Based on data on the coverage and timing of seasonal vaccination in 2010 (11), we model vaccination of ≥65-y-olds as occurring in mid-November 2010 with a coverage of 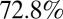. 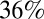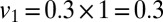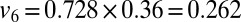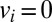We further assume that all children <5 seroconverted after receiving the pandemic vaccine (28, 29), but that only of those receiving the seasonal vaccination in the 65+ age group seroconverted (30), thus setting and ( for ).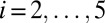

Model Parameterization.

We assigned the generation time of infection 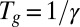as 2.9 d (8, 31, 32). The average time from infection or vaccination for an individual to seroconvert was taken to be 14 d (33). We assumed that the reporting rate 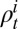depended on the age class i and time t. To reduce the number of estimated parameters, we fitted the reporting rate of 25–44-y-olds, 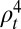, and fixed the ratios of reporting rates in other age groups to the reporting rate of the 25–44 age group according to the observed propensity of H1N1pdm09-infected individuals in each age class to consult a GP due to ILI (see SI Appendix, section 1.5.1 for details):

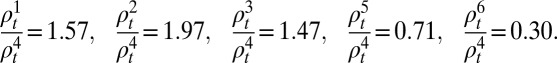We further assumed that the reporting rate was piecewise constant in the time windows from the beginning of the epidemic to the week of introduction of NPFS (week 30/2009), from the introduction of NPFS to the end of the second wave and in the third wave.

Model Variants.

We explore six different model variants obtained from the combination of three different assumptions on transmission with two different assumptions on decay of prior immunity. We test the following assumptions on transmissibility: constant transmissibility across the waves (i.e., 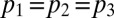); transmissibility varies in wave 3 only (i.e., 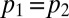); transmissibility varies in each wave. We test the following assumptions on decay of prior immunity: prior immunity wanes (i.e., 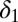is estimated); prior immunity does not wane (i.e., ).

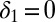Statistical Model.

We extend the framework developed in ref. 7 and formulate a statistical model for the joint analysis of observing the ILI, virological, and serological data. 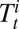and 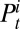denote the number of virological samples tested and found positive, respectively, in age class i at week t. 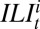and 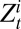, respectively, denote the total number of ILI cases and the expected number of H1N1pdm09-infected cases in the monitored population in age class i and week t, whereas 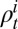is the probability that an individual in age class i infected with H1N1pdm09 reports ILI symptoms in week t. Following ref. 7, we then formulate the likelihood of the syndromic and virological data given the model, 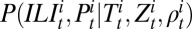. 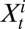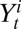To incorporate serological data, we let and represent the total number of serological samples tested in age class i at week t and the number testing seropositive among those, respectively. 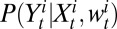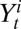We assume that the distribution of given 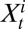and 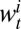is binomial, where 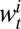denotes the probability of testing seropositive for an individual in age class i at time t. Using θ to denote the vector of all fitted model parameters, the posterior likelihood is defined by

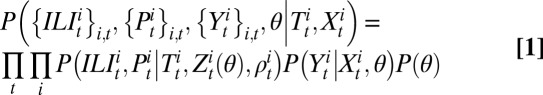where 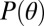denotes the prior distribution. A full derivation of the log-likelihood is given in SI Appendix, Statistical Model.

Model Fitting.

In a Bayesian setting, we explore the joint posterior distribution of parameters by Markov chain Monte Carlo (MCMC) sampling. We implemented the Metropolis–Hastings algorithm (34) with uniform priors for all parameters. Parameters were updated in blocks of 4–5 parameters each. MCMC chains were run until convergence was achieved (by visual inspection) and additional 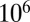iterations were performed to explore the posterior distribution; parameter estimates and equal-tailed 95% credible intervals were obtained from 10,000 values thinned from the last 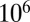samples.