Open-atmosphere sustenance of highly volatile attoliter-size droplets on surfaces

Abstract

The controlled formation and handling of minute liquid volumes on surfaces is essential to the success of microfluidics in biology, chemistry, and materials applications. Even though current methods have demonstrated their potential in a variety of experimental assays, there remain significant difficulties concerning breadth of applicability, standardization, throughput, and economics. Here we introduce a unique microfluidic paradigm in which microscopic volatile droplets are formed, sustained, and manipulated in size and content at any desired spot on unpatterned substrates. Their sustainability is warranted by continuous replacement of the rapidly vaporizing sessile fluid through controlled equivalent volume deposition of smaller discrete liquid entities by an electrohydrodynamic nanodripping process. Using nanoparticle inks we show that the concentration of solutes in so-stabilized droplets can be linearly increased at isochoric conditions and user-defined rates. An intriguing insensitivity of the droplet shape toward surface heterogeneities ensures robustness and experimental reproducibility, even when handling attoliter quantities. The unique capabilities and technical simplicity of the presented method introduce a high degree of flexibility and make it pertinent to a diverse range of applications.

The use of small liquid quantities for chemical and biological assays has significantly beneficial consequences on material consumption and waste production as well as process duration and parallelization (1, 2). In this context the use of (sub)micrometer-sized droplets is of special interest because their surface acts as a natural wall, giving rise to well-defined reaction volumes, which can exist in parallel in very large numbers (3, 4). However, formation and stabilization of droplets of micro- or even nanoscopic size is strongly hindered by their inherently unstable nature in an open atmosphere, owing to high volatility even at saturation conditions (5). To prevent (sub)micrometer droplets from vaporizing rapidly during an experiment, they must be contained in a small, closed environment where stable equilibrium conditions can be imposed and maintained (5). In liquid surroundings, an elegant approach of maintaining and manipulating small droplets is by encapsulating them in an immiscible liquid shell (3, 4, 6). In this configuration, the contained droplets can be dragged along a prepatterned network of microfluidic channels, where operations such as droplet fission (7), fusion (8), sorting (7, 9), or content mixing (10) can be performed in a highly parallel manner. Practical assays, however, are restricted by the initial design and configuration of the system, as well as the potential vulnerability to cross-contamination in the case of poorly stabilized interfaces (11, 12). Accordingly, such systems are not well standardized and difficult to integrate into industrial environments (2). Furthermore, their use is only economically attractive in large assays owing to extensive flow initiation requirements (2). By comparison, the approach of digital microfluidics allows extraction of droplets from a variety of reservoirs and their movement along individualized paths (13). Different ways of moving drops in a controlled manner have been used so far, most notably those based on electrowetting (14, 15). Drawbacks of such systems are the risk of cross-contamination and the difficulty of process adjustment for various liquids as well as the inherent limitation in operational frequency (2, 4, 13). Additionally, owing to cross-contamination issues inherent in moving drops in the same area such platforms may rapidly degrade.

A novel form of repeatedly generating and accurately depositing discrete, ultra-small liquid quantities down to the zeptoliter range has recently been demonstrated (16). This technique, which is conceptually related to electrospraying (17) and electrospinning (18), produces electrically charged droplets by nanodripping from a small nozzle. Here we show that nanodripping-based liquid accumulation can be used for locally creating well-defined, temporally stable attoliter liquid droplets that can be manipulated in size and solute content at will under normal atmospheric conditions, despite their size-related high volatility.

Results and Discussion

Process of Active Equilibration and Maintenance of Volatile, Sessile Micro- and Nanodroplets.

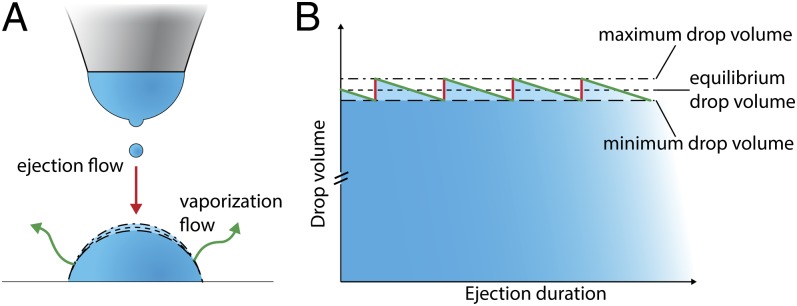
In the nanodripping mode individual droplets are ejected from the apex of a larger meniscus at highly homogeneous size and frequency (Fig. 1A), giving rise to a constant volumetric ejection flow rate 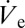(16). Whereas the frequency of droplet ejection was shown to reach values of up to 100 kHz, droplet diameters can be as small as 50 nm (16). After deposition on a surface, the volumetric rate at which a sessile droplet vaporizes can be expressed by the following equation (19):

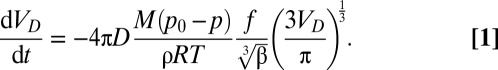Here V_D is the deposited volume, D is the diffusion coefficient of fluid vapor in air, M its molar mass, R is the universal gas constant, T the temperature, p₀ the apparent saturation vapor pressure, and p the background vapor pressure. In Eq. 1, β is a function of the contact angle θ and f is an empirical fitting function, solely depending on θ. A solution for f has been reported by Picknet and Bexon (19) and was shown to be in reasonable agreement with several alkanes (20). For 0° < θ ≤ 180° a change in θ will cause the term fβ^−1/3 to change in the opposite direction, that is, an increase of θ leads to a decrease in the vaporization flow rate. If 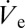> dV_D/dt, more liquid is deposited than vaporized and the deposited volume will start to grow. Because Eq. 1 also implies a proportionality of vaporization rate and deposited liquid volume, the latter only grows until the average volumetric ejection flow rate 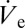is compensated exactly by dV_D/dt. Such deposited liquid volumes attain a quasi-steady state with their volume undergoing small ratchet-like fluctuations as shown in Fig. 1B and disappear in a matter of milli- or even microseconds depending on size, if the nanodripping liquid supply is terminated. The formation and sustenance of an actively equilibrated volatile liquid volume of such small size is therefore inseparably connected to the ultra-fast nanodripping feedback mechanism, which continuously replenishes the vaporized fluid in a highly controllable manner. By rearranging Eq. 1 and setting dV_D/dt = 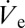an expression for the equivalent radius r_D of the deposited volume can be found:

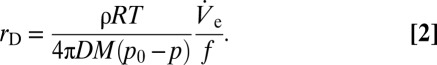Fig. 1.

Process of active equilibration of volatile sessile microdroplets. (A) Small droplets are ejected from a nozzle by nanodripping, resulting in the accumulation of a sessile droplet. Once this droplet reaches a certain size, volumetric vaporization at its surface (green arrows) and incoming volume of airborne droplets (red arrow) will be balanced, resulting in active volume stabilization. (B) Graph representing the ratchet-like fluctuation of the volume of a stabilized sessile droplet. After the impact of an airborne droplet (red line), subsequent vaporization (green line) will decrease the droplet volume in an approximately linear fashion (30) until the droplet attains its minimal extent (minimum drop volume), before the impact of a new airborne droplet. The process can be adjusted such that the fluctuations are essentially negligible in comparison with the overall droplet volume.

Precise Formation and Manipulation of Attoliter Sessile Droplets.

To prove that actively equilibrated, volatile liquid volumes can indeed be sustained according to the concept introduced above, droplets were ejected by nanodripping onto a glass substrate vapor-phase coated with a self-assembled monolayer (SAM) of 1H,1H,2H,2H-perflurooctyltrichlorosilane and observed in situ by a home-built laser scanning microscope. Droplet ejection is initiated by applying a voltage in the range of ∼100 V between the liquid situated in a gold-coated capillary glass pipette and an indium tin oxide (ITO)-coated glass slip situated below the substrate. In the nanodripping mode electrically charged droplets will be continuously ejected at a natural frequency as long as the voltage is maintained (16). Even though impact velocities in the nanodripping mode are as high as O(100) ms⁻¹, the droplet impact was previously shown to be very soft, primarily owing to strong viscous damping (16). This implies an important shape insensitivity of the sustained volume toward inertial impact forces.

Owing to difficulties inherent with accumulating electrically charged droplets onto a nonconductive substrate, controlled ejection at dc voltages was generally unstable. The charged cumulative sessile droplet was often found to repel incoming airborne droplets, leading to undesirable spraying effects well known from electrospraying (17). Therefore, dc ejection was replaced by an ac voltage signal, consisting of short adjacent pulses of alternating polarity (Fig. S1). Each pulse leads to the ejection of a few droplets, followed by an equal amount of oppositely charged droplets after polarity switching (illustrated in more detail in Fig. S1). The deposited droplet therefore sustains charge neutrality, which in addition prevents its possible disintegration by Rayleigh fission (21).

Owing to its low vapor pressure but sufficiently high electrical conductivity, pure dipropylenglycol-n-butyl ether (DPnB) was used in the first set of experiments. Depositing DPnB onto SAM-coated glass slips resulted in the immediate accumulation of a sessile droplet, which could be reduced in size by manipulating the air pressure at the back opening of the capillary pipette (discussed in more detail below). It should be noted that we do not attempt to reproduce the size of printed DPnB droplets analytically by Eq. 2. The values of 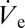were found to be too low to be directly measurable. However, an indirect method for estimating 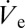will be presented in the section treating isochoric thickening of nanoparticle inks.

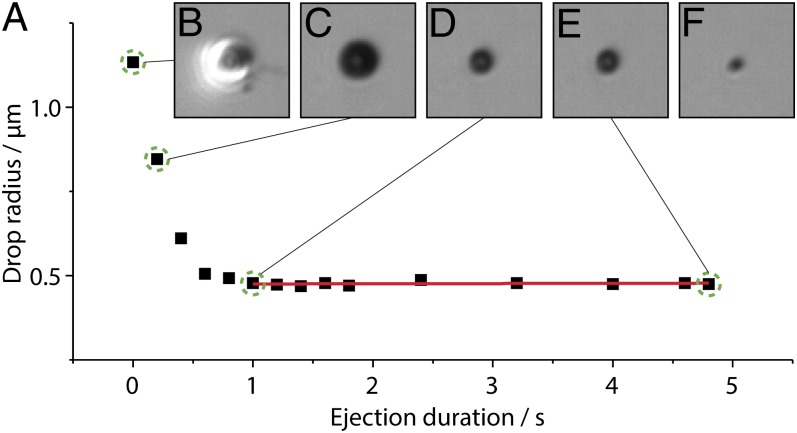
Fig. 2A shows a graph of the diameter of an accumulated sessile droplet measured during its formation by nanodripping at a nozzle–substrate separation of ∼10 µm and a voltage of 250 V. Fig. 2 B–E display optical micrographs of the same droplet at different times indicated in Fig. 2A by dashed circles. It is found that the process is initiated with the ejection of a large fluid quantity owing to start-up conditions (Fig. 2B) but very quickly stabilizes and produces smaller droplet sizes with remarkable consistency. Investigated sessile droplets were formed with a placement precision of a few hundred nanometers. Fig. 2 C and D conveys the process of volume shrinking and eventual stabilization after about 1 s at an equivalent droplet radius of ∼500 nm. Due to the interferometric capabilities of our microscope we can additionally calculate the droplet contact angle, which is 57° ± 3° (Materials and Methods). The calculated sessile volume is only ∼100 aL. We note that the contact angle is considerably higher than the ∼47.3° receding contact angle measured on a freshly prepared substrate with macroscopic droplets. Once the sessile droplet reaches its actively equilibrated state it is found to be extremely stable with no measurable size change until ∼4.9 s of ejection duration (Fig. 2E), that is, until the voltage is voluntarily turned off. The last stage is illustrated by Fig. 2F showing not the sessile drop but its dried leftover, only a few tens of milliseconds after ejection termination. The overall process of sessile droplet formation and stabilization is shown in Movie S1.

Fig. 2.

Experimental observation of active sessile drop stabilization. (A) Radius of an actively stabilized sessile DPnB droplet. Different phases of drop formation are indicated with green dashed circles in A and illustrated by optical micrographs, showing the drop after (B) 0, (C) 0.2, (D) 1, and (E) 4.8 s. (F) The last micrograph shows the dried solid content, 80 ms after ejection termination. The applied voltage was 250 V.

Based on Eq. 2, it is feasible to dynamically manipulate the diameter of a deposited sessile droplet by a variation of 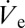. Large-scale variations can be achieved by applying a predefined air pressure at the back opening of the capillary pipette. To controllably form small droplets, experiments with DPnB were performed by applying slight negative pressure of approximately −100 mbar. This was sufficient to reduce the droplet diameter from O(10) µm to O(1) µm and below. The influence of the back pressure on 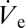is further illustrated in Fig. S2. Due to the inherently low flow rates in the nanodripping mode, small changes in the applied pressure already lead to large variations in the size of deposited droplets. A single nozzle can therefore be used for generating a very broad range of liquid volumes. Whereas external pressure adjustment may be used to set an offset droplet size (SI Text), precise small-scale adjustments are achieved by simply changing the ejection voltage used. 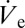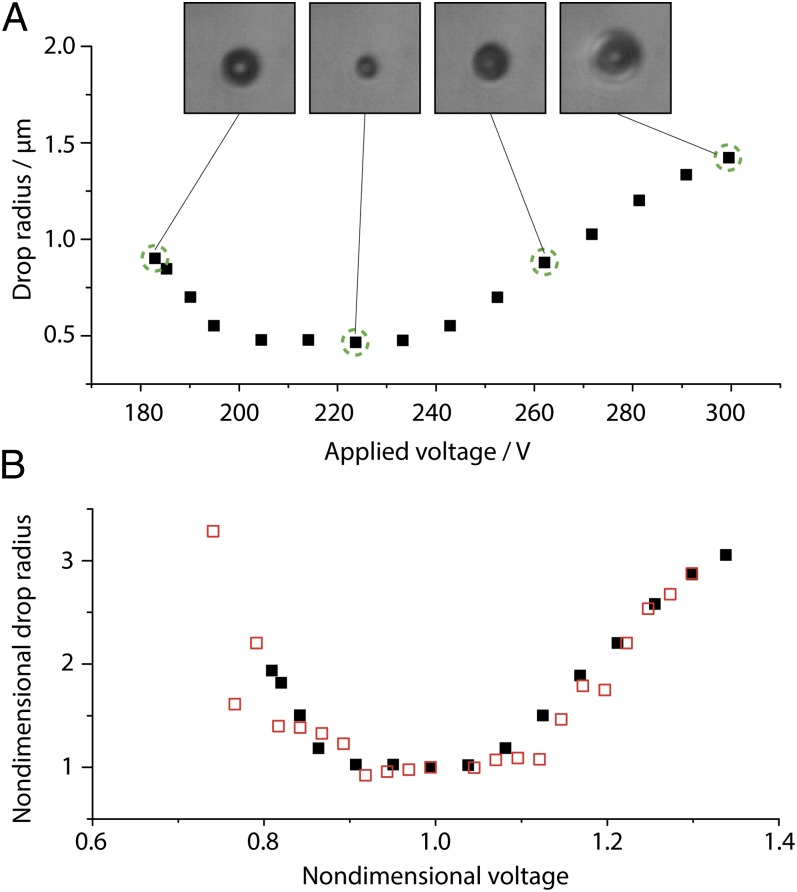In the nanodripping mode, is known to change when varying the applied voltage (16), which can be exploited for facile control of deposited volumes. This form of volume control is not prone to adjustment-related delays, nor does it necessitate additional equipment. In the following experiment the ac signal used (Fig. S1) was modulated with a ramping function, which linearly decreases the voltage amplitude from 300 V to 0 V at a ramp rate of 12 V⋅s⁻¹. In the course of an experiment, the deposited volume is therefore expected to change its size according to the respective variation of 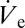. Values of r_D measured by optical means in the course of a single ramping experiment are plotted in Fig. 3A together with corresponding micrographs showing droplets at the different stages as indicated in the graph. It is found that r_D varies from ∼465 nm to ∼1.4 µm in a continuous but nonmonotonic manner (ref. 16 and SI Text give details on the dependence of 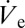on applied voltage in the nanodripping mode). The entire process is shown in Movie S2.

Fig. 3.

Drop volume manipulation with attoliter precision. (A) DPnB droplet radii measured in the course of a linear voltage ramping. Optical micrographs of the drop are taken at the stages indicated with dashed green circles. (B) Nondimensional values of r_D (black filled squares) and 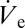(red open squares) as a function of the nondimensional ejection voltage. As suggested by Eq. 2, r_D is found to be directly proportional to .

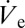To prove that r_D is proportional to 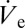we plot in Fig. 3B nondimensional values (Materials and Methods) of r_D and 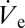as a function of the applied voltage. 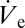has been obtained with an equivalent pipette by the footprint method introduced in ref. 16 (SI Text). Judging from the values of flow rate and sessile droplet diameter presented in Fig. 3B, the proportionality suggested by Eq. 2 is evident. The possibility of increasing the size of deposited droplets by an adjustment of 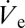enables the calculation of an advancing contact angle (Materials and Methods), which is found to be 61.1° ± 2.8°, in good agreement with the measured 63.7° advancing contact angle of a macroscopic sessile droplet. The advancing contact angle is only slightly higher than the receding one, in contrast to the strong hysteresis observed for macroscopic droplets. A potential explanation for this behavior will be discussed later.

Evaporative Isochoric Thickening.

In addition to pure fluids, solute-laden solvents also can be deposited. For demonstrational purposes, gold nanoparticles will be used here as solute. These nanoparticles were stably dispersed in n-tetradecane. The continuous nanofluid addition through the nanodripping process combined with the simultaneous sessile droplet vaporization yields a linear increase of the solute concentration while maintaining the deposited volume constant. This leads to isochoric thickening of the sustained sessile droplet.

Ejection was performed at different durations onto SAM-coated silicon chips, in the absence of back pressure. SAM-coated silicon was sufficiently conductive to prohibit charging even at dc voltages. Owing to inherent limitations of the optical setup used (∼450 nm lateral resolution) droplets were not analyzed in situ but indirectly on the basis of the dried nanoparticle structures. According to the thickening principle described above, the obtained dried structures must grow larger for increased ejection duration. Importantly, the rate of isochoric thickening (defined as the absolute increase of the nanoparticle concentration per second), for a given ink, can be adjusted in a controllable manner through modulation of the radius of the stabilized sessile droplet (e.g., by varying 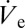as described above). Because dV_D/dt ∼ r_D and V_D ∼ r_D³, the rate of isochoric thickening is proportional to r_D⁻².

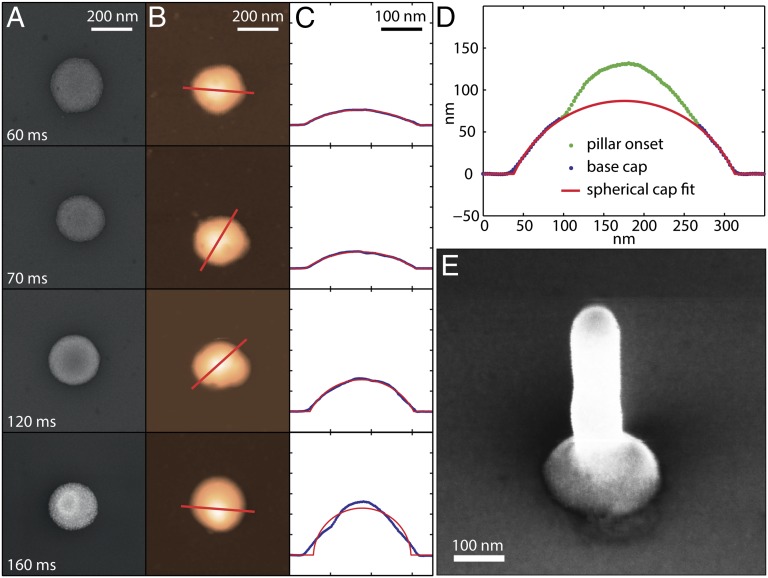
Fig. 4 summarizes SEM micrographs (Fig. 4A), atomic force microscope (AFM) height micrographs (Fig. 4B), and AFM height profiles (Fig. 4C) of nanoparticle clusters obtained after ejecting for 60, 70, 120, and 160 ms. Printing has been performed at a voltage of 200 V, a nozzle–substrate separation of 4 µm, and with an ink having a nanoparticle concentration of ∼0.7 vol%. Evidently, all structures have approximately the same diameter of 232.2 ± 6.5 nm, but different heights. Additionally, all but the last structure are well represented by spherical caps (red line) having contact angles of 34.3, 38.7, and 68.9°, respectively. The equality of contact radii is the result of an actively equilibrated droplet diameter which, after ejection discontinuation, remained pinned throughout its vaporization. The complete pinning of the receding contact line has been confirmed by measurements of a macroscopic droplet (Table S1 lists measured dynamic and static contact angles of differently concentrated inks).

Fig. 4.

Evaporative isochoric thickening. (A) SEM and (B) AFM micrographs of nanoparticle-based structures formed after the ejection of droplets for 60, 70, 120, and 160 ms. (C) AFM height profiles (blue line) taken along the indicated lines in B demonstrate that all structures but the last (i.e., at 160 ms) have the shape of an equally wide spherical cap (red lines) with a contact angle, increasing with ejection duration. In (D) fitting of the last structure is only performed at its basis. This lower part represents the shape of the original sessile droplet, which in the course of isochoric thickening has been subject to sudden crystallization of its nanoparticle content. Owing to a change in wettability, a nanopillar starts to grow on top of this crystallized pedestal. Whereas at 160 ms in D the nanopillar is merely a nipple, it substantially grows when ejecting for an extended period of 500 ms (E). The applied voltage in all experiments was 200 V.

Spherical-cap-shaped colloidal crystals (i.e., nanoparticle clusters) have also been obtained after vaporization-induced volume shrinkage of much larger nanoparticle-laden sessile droplets (22). It is noteworthy, however, that in the present study the concentration increase takes place at an essentially constant volume (i.e., at isochoric conditions). The isochoric thickening condition may be prolonged at will, up to the limit of spontaneous formation of a solid colloidal superlattice (often termed colloidal crystal). In the case of crystal formation by droplet shrinkage it has been shown that the quality of nanoparticle packing can be negatively affected by the velocity of the droplet–air interface during its contraction, especially for microscopic droplets (23). Using isochoric thickening, such limitations are avoided, owing to the essentially static nature of the droplet–air interface. In addition, the same colloidal crystals may be formed independently of the initial ink concentration and the presence of contact-line pinning, which is in strong contrast to conventional volume-shrinking techniques (22).

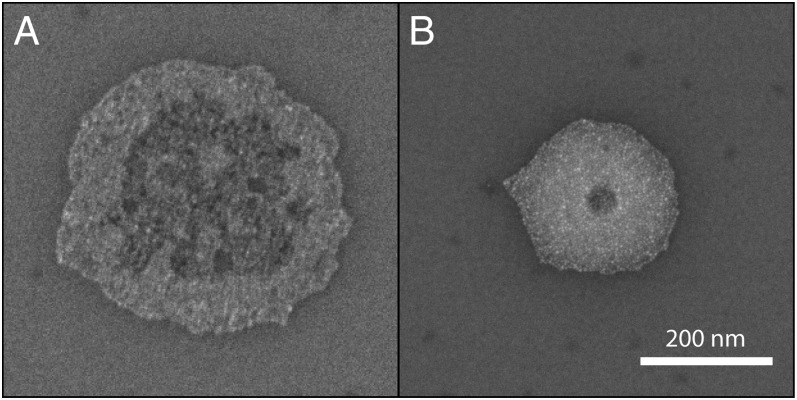
According to the principle of spontaneous crystal formation, it will now be shown that for the structure printed at 160 ms isochoric thickening has led to crystallization of a spherical cap already during the course of printing. From a partial fitting of this structure (Fig. 4D) it is evident that its lower part represents a spherical cap. Going a step further, we show in Fig. 4E an SEM micrograph of a structure that has been printed at extended ejection duration of 500 ms. The figure depicts a “nanonail” structure consisting of a straight nanopillar on a spherical cap pedestal, the formation of which is possible owing to sudden droplet crystallization. The straight nanopillar portion appears identical to pillars grown by nanodrip printing directly (without a pedestal) on a highly wettable substrate (16) at otherwise equal conditions. Accordingly, the emergence of a nanonail structure can be linked to a change in wettability resulting from the sudden solidification of the sessile droplet. Owing to excellent wettability of this colloidal crystal, any recurring accumulation of fluid will be prevented. The long-term dispersion of nanoparticles in a fluid body is therefore no longer sustained, leading to their sedimentation after each individual droplet deposition cycle. This radical process change introduces the eventual emergence of a nanopillar on top of the crystalized pedestal. Considering that the crystallized pedestal is approximately equal in shape to the original sessile droplet, one can calculate the corresponding contact angle, which results in 77.5° (SI Text gives more details on this estimate). This value is almost 10° larger than the macroscopic advancing contact angle (Table S1) and thereby contrasts with the findings of other authors, who reported the contact angles of submicroscopic droplets to be smaller than those of macroscopic ones (24, 25). A possible explanation for this behavior was based on the influence of local surface heterogeneities (24). With respect to the frequent occurrence of such defects also in the present study (shown by the dark spots on the SEM micrographs in Fig. 4A), both the high contact angles and the almost perfectly circular structure morphology are intriguing. A possible explanation for this unexpected behavior will be given later in the section addressing droplet depinning.

By plotting the volume of spherical caps and the nanonail structures as a function of the respective process duration, the ejection flow rate 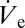is calculated to be ∼6.4 µm³⋅s⁻¹. According to Eq. 2 this value may be used to estimate the size of a stabilized sessile droplet theoretically. Accounting for a necessary adjustment for concentration effects based on meniscus vaporization (SI Text gives details), the calculated value of V_D indeed matches our experimental results. In both cases we obtain a droplet volume of a few attoliters. This confirms the framework of sessile droplet sustenance according to Eq. 2. Finally, by dividing the obtained 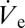by the sessile droplet volume, the exact rate of thickening can be calculated, which results in ∼350 vaporized sessile droplet volumes per second.

Water Drop Formation.

For the handling of biological materials such as ribonucleic acids or proteins (an important area of possible applications of the method presented here) compatibility with aqueous solutions needs to be demonstrated. As recently shown, proteins can be deposited by electrohydrodynamic means without losing their biological activity (26). However, because water vaporizes at a rate of more than 100 times faster than n-tetradecane and DPnB in an open atmosphere, its active equilibration at small volumes on surfaces is a serious challenge.

To circumvent difficulties originating from charge accumulation while still providing excellent optical access, we have used electrically conducting ITO-coated glass slips as substrates. These substrates are also much more hydrophilic than SAM-coated glass slips. The pipette we used had a diameter of ∼2.5 µm and was positioned at a distance of 14 µm from the substrate. To effect nanodripping, the back pressure of the capillary pipette was reduced by about 500 mbar, leading to a distinct stabilization of the ejection process. Fig. 5A presents an optical micrograph of a water drop stabilized on an ITO-coated glass slip at a voltage of 367 V (Movie S3). By optical interferometry measurements (Materials and Methods) the drop contact angle can be accurately calculated as 4.6°. Based on this contact angle, the drop shown in Fig. 5A has a radius of ∼3.35 µm (indicated by the dashed circle) and a volume of only ∼2.4 fL.

Fig. 5.

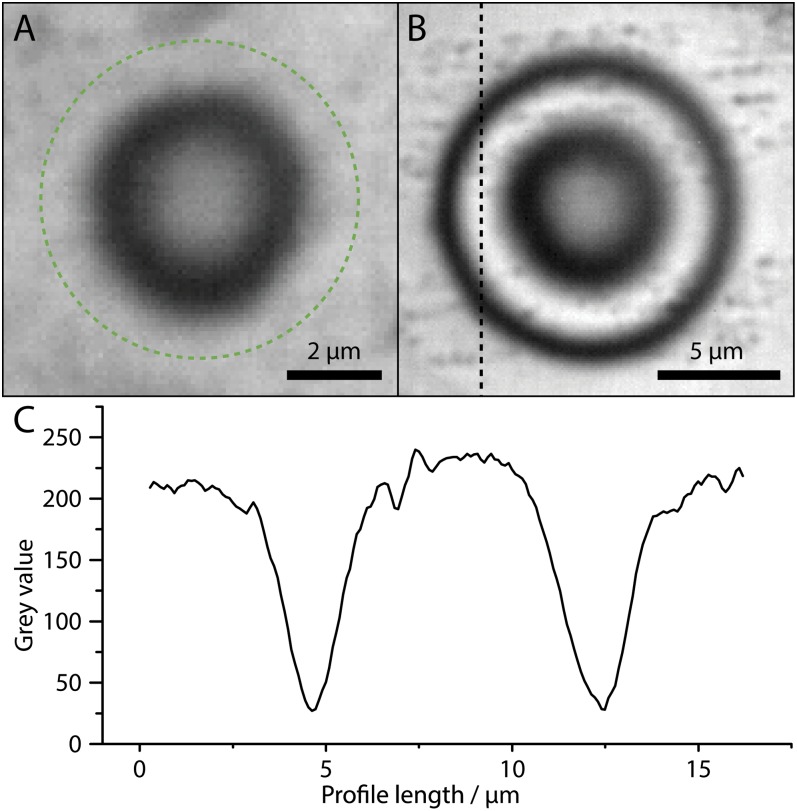
Active equilibration of sessile water droplets. (A) Optical micrograph of a ∼2.4-fL water drop, which has been formed and stabilized on an ITO substrate at 367 V. Owing to the small contact angle of 4.6° the thin wedge of the drop is not fully visible. Based on optical interferometry (Materials and Methods) the droplet radius is estimated at ∼3.35 µm. The full droplet extent is indicated by a dashed green circle. (B) Sessile water droplet with r_D ∼7.5 µm, sustained at 345 V. (C) The equality of measured optical intensity at the background and the positive interference ring, along the profile indicated in B, demonstrates that the droplet is stable. If the droplet fluctuated at a rate invisible to the camera (25 Hz), the interference rings would be smeared. It is also noteworthy that independent of the substantial substrate roughness in B the drop attains an almost perfectly circular shape.

The high vapor pressure gives rise to a very rapid fluid exchange (water addition and vaporization) compared with the available imaging frame rate. Owing to the dynamics involved in active stabilization, a drop may change its radius considerably during a frame period, rendering the optically detected signal to be interpreted as an average. In Fig. 5B we therefore present an optical micrograph of a slightly larger sessile droplet (∼7.5 µm), which has been generated at a printing voltage of 345 V (Movie S4). Clearly visible are highly contrasted rings of alternating intensity, which are a result of light interference (Materials and Methods gives details). The equality of the intensity of background and constructive interference rings (Fig. 5C) confirms the overall droplet stability. For a dynamically fluctuating droplet, these rings would be smeared. Remarkably, Fig. 5B demonstrates that droplets can be formed even on rough substrates without being influenced by comparably large surface heterogeneities.

Impact-Driven Droplet Depinning.

Throughout our experiments we have observed that the shape of equilibrated sessile droplets showed an intriguing insensitivity to surface heterogeneities. This is unexpected, especially for droplets that are not much larger than even the smallest surface defects (24, 27). We hypothesize that the insensitivity of droplets to surface defects is related to a shape-correcting “external” energetic action of the continuous droplet impact. This action triggers the release of pinning and renders the contact line mobile, even under conditions in which the deposit alone would have remained pinned.

In Fig. 6 A and B two nanoparticle structures are shown that have been printed with 40- and 50-ms ejection duration, respectively, by the same nozzle and at the same experimental conditions as the structures shown in Fig. 4A. Especially the radius of the structure shown in Fig. 6A is substantially larger than the one of those printed at durations of 60 ms and beyond (Fig. 4A). That the contact radius of the colloidal structures becomes smaller with increasing ejection duration is easily explained by our experimental findings with DPnB. Because owing to start-up effects 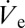has to stabilize from an initially higher value, a sessile droplet will first want to shrink in volume to reach its quasi-equilibrium diameter (exemplified by Fig. 2). If the sessile droplets are laden with nanoparticles, this contact line retraction is in principle not possible owing to perfect pinning of the contact line (Table S1). We note, however, that this pinning restriction is only present when a droplet is left to dry. When droplet ejection sustaining the deposit is ongoing, the contact line is shown to be mobile and can adjust to changes in volume while maintaining the contact angle at its equilibrium value. Upon ejection termination, the contact line is immobilized, resulting in an immediate transition from constant contact angle to constant contact line dynamics. Accordingly, the nanoparticle clusters shown in Fig. 6 represent time frames of the shrinking process, which reveal how far the contact area diameter has already advanced toward its quasi-equilibrium value. Along this line, structures obtained at printing durations of 60 ms and beyond (Fig. 4) have evidently concluded this convergence.

Fig. 6.

Contact line depinning. (A) SEM micrograph of a gold nanoparticle structure printed at 40-ms ejection duration. (B) Another structure, obtained after 50 ms of ejection, is much smaller and more circular than that shown in A. The structures essentially represent time frames during the volume reduction of a sustained sessile droplet. The continuous impact of airborne droplets allows the sessile deposit to shrink while maintaining its equilibrium contact angle. Once ejection is discontinued, the contact line immediately immobilizes, and the droplet dries at constant contact line conditions. Applied voltage was 200 V. (Scale bar, 200 nm.)

On the substrates we used depinning is likely initiated by an impact-driven weakening of the nanoparticle–substrate interaction. This will allow a capillarity-driven inward movement of the contact line, dragging the nanoparticles along. Correspondingly, it is anticipated that the ring-like profile obtained by the structure shown in Fig. 6A is not caused by the coffee-stain effect (28) but rather by the inward dragging of nanoparticles situated at the contact line. The evolution of the structural profiles in Figs. 4 and 6 additionally underpin the shape-correcting effect of impact-driven depinning. Whereas the profile of nanoparticle clusters in Fig. 6 suggests considerable droplet pinning at surface heterogeneities, once the droplets approach their quasi-equilibrium diameter (Fig. 4) they are essentially relieved from such shape-deforming activity. Impact-induced depinning, as is evident in Fig. 6, also explains the reduced hysteresis of sessile DPnB drops, as well as the insensitivity of water drops to surface heterogeneities. The observed behavior is of fundamental importance in proving the inherent robustness of the proposed method with respect to surface imperfections.

Conclusion

In the present study we have demonstrated and quantitatively explained a unique microfluidic paradigm for the controlled placement and active sustenance at open-atmosphere conditions of ultra-small sessile droplets reaching the attoliter range. From the viewpoint of making a critical step toward potential novel microfluidic platforms, the liquid volume does not have to be moved on a substrate, but instead it is formed, maintained, and manipulated at a fixed position. To this end a normal, simple glass slip may therefore be envisioned with the proposed method as a host surface for millions of individual, spatially well-separated experiments. The demonstrated inherent insensitivity of the contactless drop formation process to surface heterogeneities through impact-driven depinning facilitates maximal reproducibility and substrate utilization. Detection of conceivable assays may be performed in situ (e.g., by optical means or by subsequent external analysis of the spatially separated dried spots). The effect of isochoric thickening is another unique capability of the present method. Handling solutes at low concentration followed by local enrichment in ultra-small, confined volumes implies material savings or improved detection capabilities. Potential applications are also possible in the context of protein purification and crystallization. Ultimately, the capability of rapid, gradual concentration increase may even pave the way to entirely new experimental procedures, for example by measuring concentration-dependent enzymatic catalysis in a single shot. The same effect, however, may be equally used in the formation of well-defined colloidal crystals for material sciences. Such crystals have been shown to be of great interest for future applications (29) and could be formed with superior control by isochoric thickening. To what degree assays will be limited by simultaneous pollution or salt thickening will be a matter of future research. Based on the combination of several unique capabilities it contains, the presented microfluidic method has the potential to advance or extend significantly the current state of biologically, chemically, and technically relevant micro- and nanoscale fluid handling.

Materials and Methods

Printing Setup.

The basic printing setup consists of a sharp, liquid-laden glass nozzle, an underlying piezostage, and an electrical actuation system. These basic components have been described in detail elsewhere (16). For the work with glass samples, optical detection was performed from below the sample by a home-built laser (532 nm) scanning microscope. For experiments using silicon substrates, optical detection was performed with a sideways objective, mounted at a sufficient angle with respect to the nozzle–substrate axis. A standard goose-neck white-light source was used for illumination and voltage signals were directly applied between nozzle and sample. Voltage signals in all experiments were verified by oscilloscope measurements.

Nozzle–substrate separations were adjusted according to the diameter of sustained droplets to prevent mutual contact. For comparison purposes, when using nanoparticle inks, the nozzle–substrate separation was chosen to be equal to the value used in one of our previous studies (16).

Inks and Solvents.

Gold nanoparticle (∼5 nm in diameter) inks were acquired from ULVAC and diluted in n-tetradecane. Pure n-tetradecane was found to be unsuitable for controlled nanodripping ejection owing to its negligible electrical conductivity of ∼10⁻¹⁴ S⋅m⁻¹. In contrast, the conductivity of the n-tetradecane–based ink was measured at 6.8 × 10⁻⁸ S⋅m⁻¹, whereas the conductivities of DPnB and water were 1.0 × 10⁻⁶ S⋅m⁻¹ and 6.1 × 10⁻⁶ S⋅m⁻¹ (measured by the dispensing unit), respectively. DPnB was acquired from Sigma-Aldrich and water was sourced at ultrapure quality from a Millipore DirectQ filter unit.

Interferometry Measurements.

The use of a coherent light source for illumination of sessile droplets allows obtaining information about its shape by analyzing the interference pattern of light reflected from the glass–liquid and the liquid–air interfaces. Details on this approach are provided in SI Materials and Methods.

Nondimensionalization Approach.

In Fig. 3B, nondimensionalization has been performed by dividing 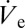(measured by the footprint method) and r_D by the respective value at which these values become minimum. The applied voltage was nondimensionalized through division by the voltage value at which the nondimensional 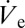and r_D become equal to unity. This approach is justified owing to the fact that the nozzle size was approximately equal for the two experiments. The two liquids (DPnB and n-tetradecane) we used can be nondimensionally compared owing to their practically equal surface tension.