Decoding continuous limb movements from high-density epidural electrode arrays using custom spatial filters

Abstract

Objective

Our goal was to identify spatial filtering methods that would improve decoding of continuous arm movements from epidural field potentials as well as demonstrate the use of the epidural signals in a closed-loop brain-machine interface (BMI) system in monkeys.

Approach

Eleven spatial filtering options were compared offline using field potentials collected from 64-channel high-density epidural arrays in monkeys. Arrays were placed over arm/hand motor cortex in which intracortical microelectrodes had previously been implanted and removed leaving focal cortical damage but no lasting motor deficits. Spatial filters tested included: no filtering, common average referencing (CAR), principle component analysis (PCA), and eight novel modifications of the common spatial pattern (CSP) algorithm. The spatial filtering method and decoder combination that performed the best offline was then used online where monkeys controlled cursor velocity using continuous wrist position decoded from epidural field potentials in real time.

Main results

Optimized CSP methods improved continuous wrist position decoding accuracy by 69% over CAR and by 80% compared to no filtering. Kalman decoders performed better than linear regression decoders and benefitted from including more spatially-filtered signals but not from pre-smoothing the calculated power spectra. Conversely, linear regression decoders required fewer spatially-filtered signals and were improved by pre-smoothing the power values. The ‘position-to-velocity’ transformation used during online control enabled the animals to generate smooth closed-loop movement trajectories using the somewhat limited position information available in the epidural signals. The monkeys’ online performance significantly improved across days of closed-loop training.

Significance

Most published BMI studies that use electrocortographic signals to decode continuous limb movements either use no spatial filtering or CAR. This study suggests a substantial improvement in decoding accuracy could be attained by using our new version of the CSP algorithm that extends the traditional CSP method for use with continuous limb movement data.

1. Introduction

Motor-based brain-machine interface (BMI) systems decode one’s intended movement from cortical signals and use that motor command to drive the motion of a device in real time. Individuals paralyzed due to high-level spinal cord injury, brainstem stroke, and amyotrophic lateral sclerosis have used implanted BMI systems to control various assistive devices using the neural activity associated with their natural thoughts of movement [1-11]. Many research studies are also now investigating the use of BMIs in stroke and traumatic brain injury as a therapeutic tool to encourage beneficial plasticity and enhance motor recovery [12-38]. Given that the estimated number of stroke survivors in the United States has now grown to 7,000,000 [39], BMIs may help fill the significant need for more effective therapies for this growing population.

Both human and animal studies have now demonstrated the usefulness of epidural and subdural field potentials for reliably extracting continuous arm and hand movement information [40-57]. Electrode technologies that record from within the skull but outside the brain may provide a good balance between recording resolution and safety. Epidural recordings, in particular may have a good risk-benefit ratio as the electrodes don’t breech the dura and therefore should have a lower risk of brain infections compared to subdural options. Developing new signal processing methods that improve movement decoding accuracy from these extracortical field potentials could help move the BMI field forward.

Spatial filtering is the process of generating new signals from linear combinations of the raw field potentials. Spatial filtering is performed to accentuate the useful information in the field potentials while suppressing common noise. BMI studies performed with non-invasive electroencephalographic (EEG) signals almost always use some form of spatial filtering [58]. However, most of the subdural or epidural studies that extract continuous hand or arm movement data either don’t use any spatial filtering [40-47] or use simple common average referencing (CAR) [47-57]. In this study, we set out to determine if more sophisticated spatial filtering methods could improve decoding of continuous arm movement information from extracortical field potentials.

Common spatial pattern analysis (CSP) is a ‘supervised’ spatial filtering method. It generates spatial filter coefficients using knowledge about the movements associated with the recorded signals. In theory, this knowledge should enable the algorithm to generate spatial filters customized specifically for extracting the information of interest. The CSP algorithm was originally designed to improve classification of data collected under two discrete states [59]. In these situations, CSP has been shown to significantly improve classification accuracy in both electroencephalographic (EEG) [59-66] and electrocorticographic (ECoG) studies [66, 67]. However, the CSP algorithm has not yet been applied to continuous movement data.

In this study, we developed and tested eight new ways of applying the CSP algorithm to continuous arm movement data. We then compared offline decoding accuracy using epidural signals spatially-filtered using the eight different CSP options as well as CAR, PCA, and no spatial filtering. In addition, we also compared decoding accuracy when using different numbers of the spatially-filtered signals, different amounts of temporal smoothing, and two different decoding functions. Our new CSP methods resulted in substantial improvements in continuous position decoding accuracy over the commonly used CAR and unfiltered methods (69% improvement over CAR and 80% improvement over unfiltered). These results suggest that much more movement information may be available in extracortical field potentials than is currently being utilized in most research studies.

We then demonstrated online use of the new CSP spatial filtering method by having monkeys use their CSP-filtered signals to control a cursor in a two dimensional center-out task in real time. Our initial offline analysis indicated that continuous wrist position was much more accurately decoded from our animals than velocity regardless of the decoder or spatial filter type used. Our previous work suggested that closed-loop cursor control would be smoother and more stable in this situation if we used the decoded wrist position to control cursor velocity instead of using either the decoded position or velocity values directly (see [68] for more information). Here we put theory into practice and demonstrated effective use of this position-to-velocity mapping in a closed-loop BMI. The animals easily learned this position-to-velocity transformation, which resulted in smoother movements than one would expect if using either the decoded position or velocity command directly. Both animals improved closed-loop performance with practice.

In total, this study accomplished three things: (1) It demonstrated that our modified CSP spatial filtering algorithms could substantially improve continuous movement decoding from high-density epidural field potentials. (2) It demonstrated the real-time use of those improved decoded continuous movements for closed-loop cursor control, and (3) it demonstrated the effective implementation of a position-to-velocity mapping during closed-loop control. All of the above testing was performed in animals that had some cortical damage due to prior removal of intracortical microelectrode arrays. Therefore, results from the spatial filter comparison should be evaluated for their relative performance levels as the absolute performance values may differ from what one could achieve with unaltered cortex. However, given that cortical maps are often altered after stroke and even after spinal cord injury [69-71], the supervised CSP spatial filtering algorithm demonstrated in this study may be especially valuable for optimizing decoding as it does not rely on assumptions about how the movement information is distributed in the cortex [15].

2. Methods

2.1 Experimental Design Overview

Two rhesus macaques were implanted with high-density, epidural-field-potential recording arrays over the upper-limb motor cortex and trained to perform center-out reaching movements in a virtual environment. In the first part of the study, field potentials were collected along with arm movements for offline analysis. These data were used to compare different spatial filtering options, smoothing windows, and decoding functions for decoding continuous two-dimensional (2D) wrist position and velocity. In the second part of the study, the spatial filtering, smoothing, and decoding options optimized in part one of the study were then applied during a closed-loop, center-out, target acquisition task. All study procedures and tests were approved by the Cleveland Clinic Institutional Animal Care and Use Committee.

2.2 Part 1: Offline Analysis and Optimization

2.2.1. Electrode Implantation

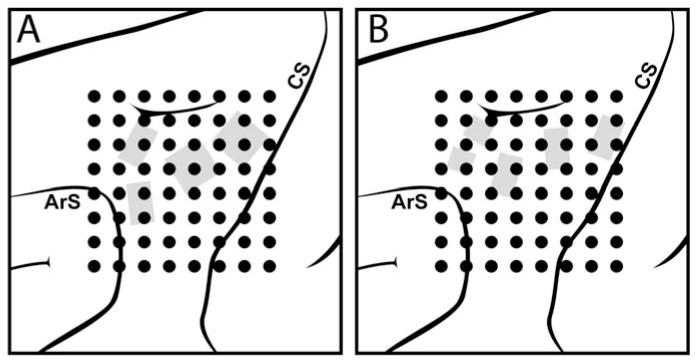
Each animal was chronically implanted with a custom-made 64-channel epidural recording array consisting of an 8×8 grid of wire contacts that spanned a 1.7 cm × 1.7 cm area in monkey I and 1.5 cm × 1.5 cm area in monkey II who was smaller than monkey I. Figure 1 shows the approximate size and location of the electrode grid relative to the cortical structures. After several months, Monkey II’s first epidural array was replaced with a second array of a similar size. Details of each array’s construction are included in the supplement along with example recordings (figure S1) and power spectra (figure S2).

Figure 1.

Epidural electrode array placement. The 8×8 grid of dots indicates the approximate placement of the 64-channel epidural wire-and-acrylic electrode arays. The implant location was chosen to target upper-limb areas of the motor and premotor cortices (ArS=Arcuate sulcus; CS=Central sulcus). Grey areas indicate locations in which intracortical microelectrode arrays had previously been implanted and removed in monkey I (A) and monkey II (B).

Each monkey previously had multiple intracortical microelectrode arrays implanted in motor and premotor cortical areas. The previously-implanted intracortical arrays were removed prior to this study due to loss of signals and/or connector damage, and the dura was sutured back in place. Previous recording arrays consisted of a variety of 16-, 32-, and 64-channel arrays for a total of 192 or 128 channels in monkeys I and II respectively. Some of the cortex in which the electrodes were embedded adhered to the electrodes during removal. This damage resulted in temporary motor deficits in the contralateral arm. However, both animals appeared to make a full motor recovery within a few weeks after electrode removal and prior to the start of this new study. Some dural thickening was noted in both animals upon intracortical electrode removal and during implantation of the epidural arrays.

In spite of the animals’ functional recovery, these dural changes and cortical damage should be kept in mind when interpreting the results of this study. Specifically, one should focus on the relative differences in performance between spatial filtering methods compared in this study. The absolute decoder performance values may under-represent what one could achieve with fresh dura and undamaged cortex. Therefore, our results may be more representative of a lower bound for normal cortex. Now that clinical trials have begun for testing chronic intracortical electrodes in humans, our results also demonstrate that epidural electrode arrays are an important alternative available to these individuals if their intracortical electrodes fail and need to be removed down the road. Results from this study also point to the potential usefulness of this methodology for stroke and traumatic brain injury applications as well as research studies requiring focal lesions. However, further studies with more controlled levels of damage are needed to fully evaluate these methods for use in stroke or traumatic brain injury.

2.2.2. Data collection for offline spatial filter comparison

In each day’s recording session, the animals performed a standard two-dimensional, four-target, center-out reaching task in the vertical plane. The animals could move their right arm freely in space. An Optotrak motion capture system (Northern Digital) was used to track their wrist position, and that wrist position was used to control the position of a spherical cursor in a virtual world in real time. Each trial began with a target appearing in the center of the workspace. The animal had to bring the wrist-controlled cursor to the center target on the screen by bringing its wrist to a central position in its workspace. Once the animal maintained the cursor within the center target for 200 to 500ms, one of four radial targets was presented, and the animal was given up to three seconds to move the cursor to the peripheral target by moving its wrist to the analogous position in space. Radial targets were situated at the corners of a square in the vertical plane and required the animal make 10 cm radial movements from the center hold location. The trial ended when the animal either held the cursor in the peripheral target for the required 200 to 500 ms, or the maximum allotted movement time of three seconds expired. This process continued in a block-random fashion such that each peripheral target was presented once before any target was repeated.

During arm movements, epidural field potentials were sampled at 6.1 kHz, band pass filtered between 1 and 500 Hz, with a notch filter at 60 Hz, and down sampled to 762.95 Hz (Tucker Davis Technologies, RZ2 with low impedance head stages). Wrist position, target position, and other task-specific information were synchronized with recorded field potential data and saved every 100 ms. Neural and position data were recorded continuously while the animals performed 40-60 blocks of movements during each day’s session. Data from breaks, trials where the Optotrak sensor went out of tracking range, and trials where the target was not successfully acquired were excluded from offline analysis. Seventeen sessions were recorded from monkey I. Data was collected in monkey II for 17 sessions with one epidural array. That array was then replaced and an additional 30 sessions of data were collected from this second array. Therefore, a total of 64 testing sessions were collected for offline analysis. Note a full comparison of the performance differences between these three electrode designs is currently underway and will be reported in a separate paper. The focus of this paper is on comparing spatial filtering options, and the differences in spatial filtering options were consistent across all three electrode types.

2.2.3. Signal Processing Overview

All 64 data sets were analyzed offline by applying a variety of signal processing and decoding options to the each data set to predict arm movements. The relative accuracies of the predicted movements using each combination of methods were then compared. All combinations of spatial filtering, smoothing, and decoding options evaluated in this study are listed in table 1 in the order in which they were performed on the data. A ten-fold cross-validation process was used where each combination of steps used in building the decoding function were generated using 90% of the data (training set) and then prediction accuracy of each decoding function was tested on the remaining 10% of the data (testing set). This process was repeated ten times with each 10% of the data acting as the independent testing set.

Table 1.

Processing steps (left column) and options tested (right column). The complete sequence of all combinations listed below was performed for decoding continuous 2D wrist position and again for decoding continuous 2D wrist velocity.

Build spatial filters on 90% of the data from a given recording session.	11 different spatial filtering methods tested (CAR, PCA, 8 versions of CSP, and unfiltered) as described in section 2.2.4.
Select a subset of the calculated spatially- filtered signals to use for decoding.	For each filtering method tested, use the best 4, 8, 12, 16, or 32 of the calculated spatial filters as described in section 2.2.5.
Calculate power in different bands as a function of time from each spatially-filtered signal in the specific subset of filtered signals being tested.	Regardless of the spatial filtering method used, the following set of power bands were calculated from each spatially filtered signal: 8–12, 12–18, 18–24, 24–35, 35–42, 42–70, and 70–200 Hz. Power was then log transformed (see section 2.2.6).
Smooth resulting power data over time.	Smooth each power signal by taking a moving average of the calculated power over 1 (unsmoothed), 3, or 5 100 ms time steps as described in section 2.2.6.
Using the same 90% training data, calculate position or velocity decoding functions from the smoothed power data and the simultaneously- recorded kinematic data.	Calculate 2D decoding functions using Kalman filtering or linear regression as described in section 2.2.6.
Apply spatial filters, power calculations, power smoothing, and decoding functions to the remaining 10% of the data to generate predicted position or velocity data.	Assess accuracy of the different signal processing options by calculating the coefficient of determination (R2) between the actual and predicted continuous wrist movement values as described in section 2.2.7 (X and Y components calculated separately and averaged together)
Repeat the above process using the next 10% of the data for testing and the remaining 90% of the data for training.	All options are repeated ten times to get 10 different performance measures for each combination of options.

2.2.4. Spatial Filter Generation

Spatial filters were calculated using the 90% training data from each recording session as follows: CAR was simply calculated by subtracting the average of the remaining signals from each individual signal at each timestep [58]. PCA was calculated using Matlab’s princomp function. CSP analysis used the 1D method outlined in [72] but applied to continuous data broken into two classes as described below. In addition, each data set was also processed with no spatial filtering as a control.

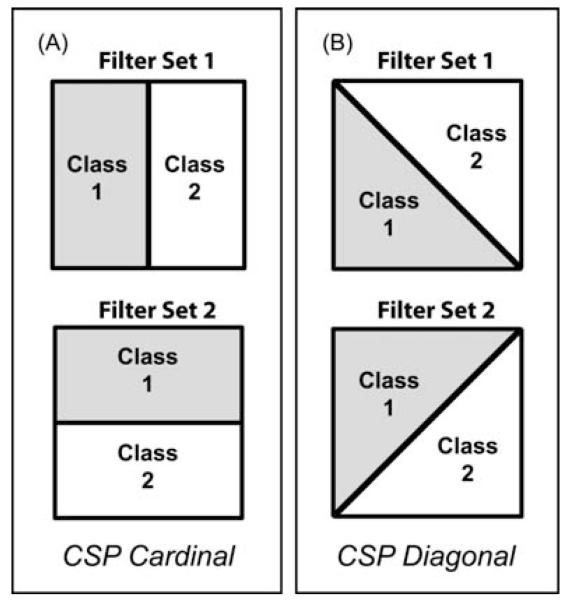
The CSP algorithm requires that the data used to build the filter coefficients be assigned into two classes. For example, dividing the continuous movement data into general categories of leftward movements versus rightward movements should result in spatial filters designed to emphasize aspects of the field potentials most modulated with the horizontal component of the continuous movement vectors. Because we are trying to decode 2D movement kinematics from the data, we need to apply the CSP algorithm twice in order to generate spatial filters for each orthogonal movement component. Panels A and B in figure 2 illustrates the two different options tested for orthogonally subdividing the continuous data in order to extract information about the two orthogonal component of movement. The continuous wrist position data was always assigned to class one (grey) or class two (white) based on which side of a dividing line the position data fell at each time step. Figure 2A illustrates the option where two sets of complementary spatial filers were generated using horizontal and vertical dividing lines (referred to as ‘CSP Cardinal’). Figure 2B illustrates the option where two sets of complementary spatial filters were generated using two different diagonal dividing lines (referred to as ‘CSP Diagonal’).

Figure 2.

Pairs of dividing lines used to build orthogonal sets of spatial filters for extracting orthogonal movement components of 2D kinematic data. A) ‘CSP Cardinal’ set of orthogonal dividing lines. Continuous data was assigned to one of two classes across the dividing line based on the horizontal (filter set 1) or vertical (filter set 2) component of movement for generating spatial filters designed to extract the horizontal or vertical components of movement (respectively). B) ‘CSP Diagonal’ set of orthogonal dividing lines. Just as in panel A, continuous data was assigned to one of two classes based on which side of the dividing line it fell. The CSP Diagonal pair of dividing lines also generated two sets of spatial filters customized for detecting two orthogonal components of movement but along different set of orthogonal axes than the CSP Cardinal option.

Divisions similar to those shown in figure 2 were also done when assigning time points into two classes based on velocity. In this case, rather than dividing points based on the position in the workspace, data was divided based on the X and Y components of the instantaneous velocity vectors calculated at each time point.

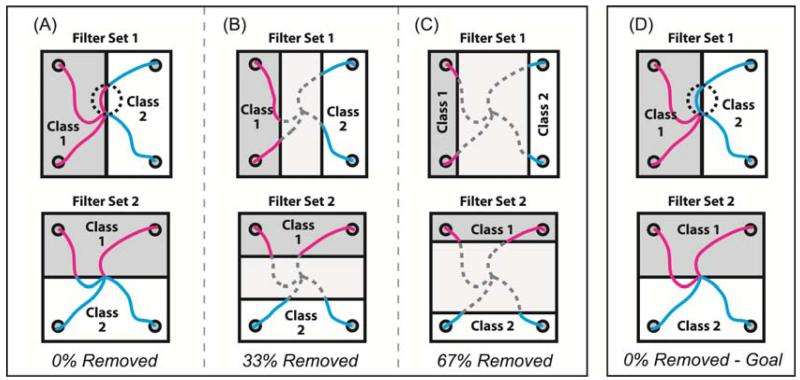
The above two pairs of orthogonal filter sets were further refined by testing if continuous arm movement decoding was improved when data points in the midrange of the position or velocity distribution were eliminated from CSP analysis. Eliminating data points close to the dividing line would make the two groups of remaining data points more distinct. Since the CSP algorithm was originally designed for use with data from two distinctly different categories or classes, removing data points from the middle of the movement distribution could potentially result in better CSP filter generation. Therefore, three variants of each spatial filter type were generated by removing 0%, 33%, or 67% of the midrange data before applying the CSP algorithm to the remaining data. A position classification example is shown in figure 3. In the 0%-removed variant (figure 3A), all data points were assigned into one class or the other for applying the CSP algorithm. However, in the 33% (figure 3B) or 67% (figure 3C) removed variants, only data from the outer 67% or 33% of the distribution were used to build CSP filters respectively. It is important to note that these midrange data were removed only to build the spatial filters. These data were included when training or using the decoders as described below.

Figure 3.

Options for assigning continuous data into two classes for use with the CSP algorithm. Each square shows four example trajectories and how those data points were assigned to one of two classes based on position. Data points shown in magenta were assigned to class 1. Data points in cyan were assigned to class 2. Trajectory points shown in dashed gray lines were discarded and not used to build filters. Upper row illustrates class assignments used to build filters for extracting the horizontal component of movement, and the bottom row illustrates class assignments used to build filters for extracting the vertical component. A) All time points in a movement trajectory got assigned to one of two classes based on which half of the dividing line they were on (0% removed). B) 33% of the midrange trajectory points were discarded and only the outer 67% were assigned to each class. C) 67% of the midrange trajectory points were discarded and only the outer 33% were assigned to each class. D) All time points in a movement trajectory got assigned to their class based on which half of the workspace the intended reach goal resided.

One additional variant of the 0%-removed filter building scheme was also tested for position-based classifications. Rather than classifying each point based on its location within the workspace, each point was classified based on the location of the intended goal of the movement. Figure 3D shows the same set of trajectories as Figure 3A but assigned to classes based on intended goal instead current position. Note the dotted circle in figure 3A and figure 3D point out the difference between the goal- and position-based class assignment schemes. In the upper panel, a part of the trajectory heading for a right target passes through the left side of the work space. In the goal-based class assignment scheme, the whole trajectory is assigned to the ‘right’ category whereas in the position-based classification scheme, parts of that same trajectory are assigned to different classes depending on the location at each time point throughout the movement.

2.2.5. Spatial filter subset selection

This study also compared decoding performance when the number of spatially-filtered signals used for decoding was varied. Optimizing the number of filtered signals used for decoding is important, especially if you have limited data on which to build your decoding functions or some of the signals are only conveying noise unrelated to the movement. Here we compared decoder accuracy when using the best 4, 8, 12, 16, or 32 available spatially-filtered signals. Note that the CSP process used here generated twice as many spatially-filtered signals to choose from as the CAR, PCA, and unfiltered options. This was because the CSP algorithm was applied twice—once for each orthogonal component of movement as shown in figure 2. Therefore, when decoding with 4, 8, 12, 16, or 32 channels using CSP filters, half (i.e. the best 2, 4, 6, 8, or 16 respectively) were selected from each of the two orthogonal CSP filter sets to keep the total number of filtered signals consistent across options for comparison.

The CSP and PCA algorithms generated filters sets that were already ordered based on likely relevance or rank. Therefore, the top 4, 8, 12, etc. filtered signals were easily chosen for use in decoding simply based on the order of the filters generated by the CSP and PCA algorithms. However, in order to pick the top 4, 8, 12, 16, or 32 subsets of signals from the unfiltered or CAR-filtered signals for comparison, a separate ranking process needed to be performed. Decoding performance was calculated for each unfiltered and CAR-filtered signal individually and used to rank order the signals. Specifically, least squares regression was used to generate decoding functions from individual signals for predicting the X and Y components of continuous wrist position or velocity (decoding methods the same as described in 2.2.6 and 2.2.7, but applied here to one signal at a time). To quantify decoding performance of each individual signal, the correlation coefficient, R, between the actual and predicted continuous wrist position or velocity values was calculated and then squared to get the coefficient of determination, R². R² values were calculated for X and Y movement components separately and averaged together to get an overall R² value for each CAR and unfiltered signal. These R² values were then used to rank order the signals when picking the top 4, 8, 12, 16 or 32 for decoding.

2.2.6. Power calculation and smoothing

Each spatial filtering option described above was built with 90% of the data (training set) and then decoding functions were generated using the spatially-filtered signals from the same training set. For each spatially-filtered signal used, power was calculated using a fast Fourier transform applied to a 300 ms sliding window of data at 100 ms intervals. Power in seven specific frequency bands (8–12 Hz, 12-18 Hz, 18–24 Hz, 24-35 Hz, 35–42 Hz, 42–70 Hz, and 70–200 Hz) was extracted from each spatially-filtered signal, log transformed and then z-score normalized. This process resulted in a time series of power values in 100 ms increments, which were then further smoothed over time using one of three options. The calculated power values were either left alone (no smoothing), or a moving average mean was taken using the power values from the latest three or five 100ms time bins. Supplemental figure S3 diagrams this power calculation and smoothing process.

2.2.7 Decoder building

Two different decoding functions were generated for each combination of spatial filter type, spatial filter number, and each level of power smoothing. Linear regression was applied as follows. For each 90% training data, a set of least squares regression coefficients, B, were identified for the following linear equation using Matlab’s pinv() function

$$\mathbf{XY}=\mathbf{P}\ast \mathbf{B}$$ eq 1

were XY was an Nx2 array of the continuous x(t) and y(t) wrist position values over the N time steps in that training set, P was an N×F array where F was the number of features (equal to the number of spatial filters used multiplied by the seven power bands calculated from each filtered signal). B was an F×2 array of least squares regression coefficients calculated via Matlab’s pinv() function. The entire process was used for decoding wrist position and also repeated for wrist velocity.

Kalman filter decoders were also applied as described in detail in [73] using the same sets of power data, P, to predict the same time series of wrist position and velocity values as was used for linear regression decoding.

The entire above process was repeated for each set of training data and the resulting decoding functions were then applied to each associated testing set thus resulting in a complete set of predicted x(t), y(t) positions and velocities values for each testing session for each combinations of decoder type, spatial filter type, spatial filter number, and smoothing window used.

Decoding accuracy was assessed for each combination of methods by first calculating the correlation coefficient, R, between the predicted and actual continuous wrist movement values in each cross-validation testing set. Separate R calculations were made for the X and Y components of wrist position and of wrist velocity. Each correlation coefficient, R, was then squared to get the coefficient of determination, R², which reflected the proportion of variability in each data set that was accounted for by the decoder. The R² values for the X and Y movement components from each cross-validation testing set were then averaged together to get one mean R² value per recording session for each combination of signal processing and decoding options evaluated.

2.3 Part 2: Closed-Loop Control

2.3.1 Why use a position-to-velocity mapping?

Results from our offline analysis showed that wrist velocity was consistently decoded much less accurately than wrist position in our particular animals. Under these circumstances, one might think that closed-loop control would be most successful if we used the more-accurately-decoded wrist position to control the cursor position instead of using the poorly-decoded wrist velocity to control cursor velocity. However, in our previous human closed-loop BMI simulator study [68], we demonstrated the functional benefits of using velocity commands over position commands to drive a brain-controlled device. Our previous study showed that, even small errors in a decoded position command could make the brain-controlled device jump around the desired location. However, the same relative magnitude of decoding errors in a velocity command caused significantly fewer control problems because the velocity decoding errors integrated out over time thus causing relatively minor deviation in the overall trajectories. That same study also indicated that, if position was more accurately decoded than velocity (as was the case with our monkeys), remapping the decoded position command to control the cursor velocity would be a more effective control option than using either the position or velocity command directly (see [68] for further discussion).

In this study, we put theory into practice and used the position-to-velocity mapping that was recommended in [68] for this situation. Specifically, during the closed-loop brain-control task, the monkey’s decoded wrist position was used to control the cursor velocity in real time much like one would use the position of a joystick to control the velocity of an object in a video game. The human subjects in our previous study found this wrist-position-to-cursor-velocity mapping very intuitive, and easily learned to control the cursor in this manner with just a few minutes of practice. To ensure our monkeys could also make this transformation before starting any closed-loop testing, the animals practiced a non-brain-control version of the center-out task using the position-to-velocity mapping (i.e. the wrist position of the animal’s free arm was tracked via an Optotrak motion capture system, and that position data was used to control the cursor velocity in real time). Both animals easily learned to control cursor movements using this wrist-position-to-cursor-velocity mapping within one training session. However, each monkey continued to practice the non-brain-controlled version of the task for over 10 sessions before any closed-loop brain-control testing was started.

2.3.2 Closed-loop brain-control sessions

Once we were certain the animals understood how to use their arm like a joystick and acquire targets using the wrist-position-to-cursor-velocity mapping, daily closed-loop brain-control sessions were started. Each day’s testing session started with the animals performing five to ten minutes of the normal center-out task where their wrist position (tracked via the Optotrak motion capture system) was used to control the position of the cursor directly just as it had been during data collection for offline analysis on previous days (described above in section 2.2.2.). Spatial filters were generated from this normal center-out baseline data using the CSP cardinal method with 67% of the data removed. Power was calculated from the top-ranked 32 CSP filters in the bands listed in table 1. The log-transformed power bands of the spatially-filtered signals along with the associated wrist position data were then used to generate Kalman filter decoding functions for use in subsequent closed-loop brain-control testing.

Once the decoding function was generated from the normal center-out arm movement data, the task was changed to the brain-controlled cursor task using the position-to-velocity mapping (i.e. the monkeys used their decoded wrist position to control the cursor velocity in real time). Monkey I performed the brain-controlled version of the four-target center-out task for 23 testing sessions. Monkey II performed the brain-controlled version of the four-target center-out task for eight testing sessions. The number of radial targets was then increased from four to eight for an additional seven closed-loop testing sessions.

To ensure the closed-loop brain-control task was neither too easy nor too hard for each animal, target sizes were automatically adjusted after each block of movements in an attempt to maintain approximately a 70% target hit rate (i.e. cursor and target radii were reduced or increased if the animal hit more or less than 70% of the targets in the previous block respectively). This kept the animals challenged while also preventing them from getting frustrated and giving up. The targets were located 10 cm from the center starting position, and no target radius was allowed to exceed 3 cm or allowed to shrink below 1.3 cm (note, target radius during the baseline hand-control task was 1.4 cm). Targets were presented in block-random fashion such that each radial target was presented once before any target was repeated.

3. Results

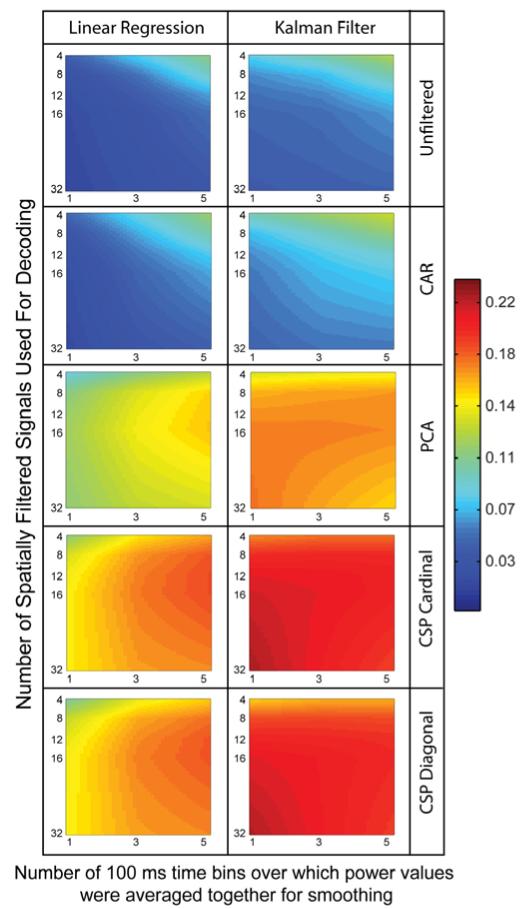
Offline wrist position decoding accuracy is shown in figure 4 as a function of decoder type, spatial filter type, amount of smoothing of the power data, and number of spatially-filtered signals used for decoding. The plotted color values represent the mean coefficient of determination, R², calculated between the actual and predicted continuous wrist position coordinates. R² values plotted are averaged across the X and Y movement components, all ten cross-validation testing sets per session, and all 64 recording sessions. Linear interpolation was used to create continuous color values between data points. Only CSP with 67% removed is included in figure 4. Other CSP filter variants had similar profiles to the 67%-removed versions shown. A complete set of plots are available in the supplement (see figures S4 and S5).

Figure 4.

Average position decoding performance as measured by the coefficient of determination, R², calculated between the actual and predicted continuous wrist position. Continuous position decoding accuracy (R²) is shown when using a linear regression decoder (left column) or a Kalman filter decoder (right column) with five of the spatial filtering options. Only the 67%-removed variant is shown for the CSP filters. Additional CSP options look similar and can be found in the supplement. Mean R² values are plotted as a function of the amount of smoothing applied to the power values and the number of spatially filtered signals used for decoding. Data shown are averaged across all 64 recording sessions, all ten crossvalidation testing sets per session, and the X and Y components of continuous wrist position.

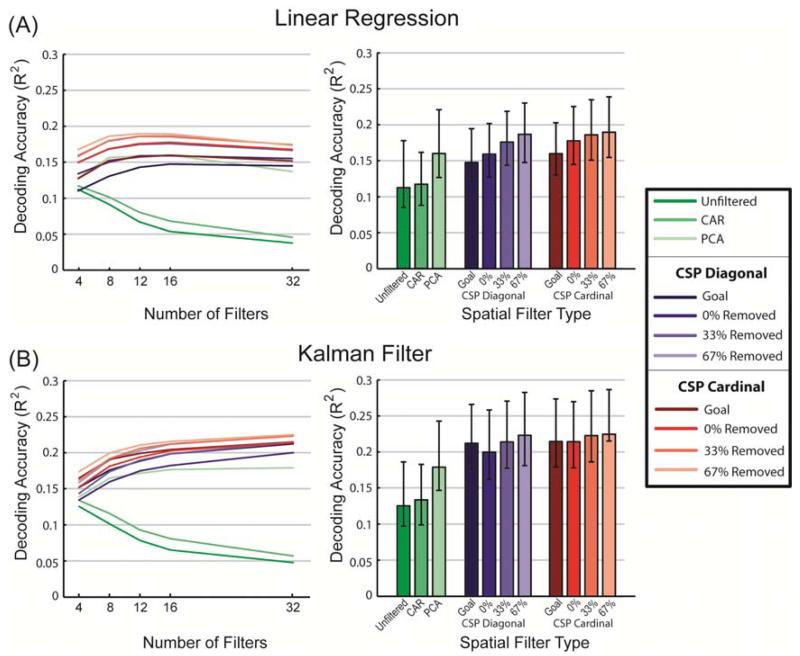
Several results stand out from figures 4, S4 and S5. First, all versions of the CSP filters performed better than unfiltered and CAR-filtered data regardless of which decoder was used, how many filters were used, or how much smoothing was applied to the power signal before decoding. PCA also performed better than unfiltered and CAR but did not out perform most CSP filter options. Kalman filtering in general was better than linear regression. Linear regression benefited from prior smoothing of the power data whereas Kalman filtering did not except in the low-performing unfiltered and CAR-filtered cases.

Figure 5 compares spatial filter options at each filter set’s optimal smoothing. Figure 5A shows results for linear regression decoding, and figure 5B shows results when Kalman filters were used. The left two panels show the average results across all 64 data sets when the highest-ranked 4, 8, 12, 16, or 32 filtered signals were used for decoding. The bar graphs on the right show the decoding performance for each filter type when both smoothing and number of filters were optimized independently for each spatial filter type.

Figure 5.

Average position decoding accuracy (R²) of different spatial filtering methods at the optimal smoothing. A) Linear regression decoding. B) Kalman filter decoding. Line graphs on the left show how each filter type preformed when different numbers of filters were used for decoding under optimal smoothing conditions. Bar graphs on the right represent the decoding accuracy when both smoothing and number of filters were optimized independently for each filter type. As in figure 4, the R² values represent the coefficient of determination between the actual and predicted continuous wrist position data (values are averaged across the X and Y movement components and cross-validation testing sets; error bars in the right bar graphs indicate the standard deviation of these values across the 64 recording sessions).

Table 2 lists the mean R² position decoding performance measure for each filter type and decoder combination using its optimal amount of smoothing and number of spatial filters. The asterisk indicates the top performing option and the grey shaded rows indicate other options that were not statistically different from the top value (Wilcoxon Sign Rank test, p>0.05). A more complete statistical comparison between all optimized pairs can be found in the supplemental data (figure S6).

Table 2.

Mean position decoding R² when the smoothing window and the number of spatially-filtered singals were optimized individually for each spatial filter and decoder combination. The asterisk (*) indicates the best filter/decoder combination. Grey shaded rows mark other top performing filters that were not statistically different from the best filter marked by the asterisk.

Spatial Filter and Decoder type	R2 (mean±std)	Optimal number of filtered signals	Optimal smoothing window (ms)
Linear Regression
Unfiltered	0.112±0.078	4	500
CAR	0.117±0.068	4	500
PCA	0.160±0.096	16	500
CSP Diagonal
Goal	0.147±0.063	16	500
0 % removed	0.159±0.066	16	500
33% removed	0.176±0.067	16	500
67% removed	0.187±0.072	16	500
CSP Cardinal
Goal	0.160±0.066	16	500
0 % removed	0.177±0.071	16	500
33% removed	0.186±0.074	12	500
67% removed	0.189±0.072	12	500
Kalman Filter
Unfiltered	0.125±0.086	4	500
CAR	0.134±0.078	4	500
PCA	0.179±0.105	32	100
CSP Diagonal
Goal	0.212±0.090	32	100
0 % removed	0.200±0.087	32	100
33% removed	0.214±0.095	32	100
67% removed	0.223±0.088	32	100
CSP Cardinal
Goal	0.215±0.092	32	100
0 % removed	0.214±0.097	32	100
33% removed	0.223±0.091	32	100
* 67% removed	0.225±0.084	32	100

Surprisingly, R² decoding accuracy measures for wrist velocity were an order of magnitude lower than for wrist position regardless of spatial filter type used (data not shown). These results were inconsistent with what others have found when using similar high-density epidural arrays [40] and inconsistent with evidence that both position and velocity information are strongly encoded in the motor cortical spiking activity [74-77]. Likely reasons for this are discussed later on. However, these offline velocity result inspired us to use the position-to-velocity transformation recommended in [68] for closed-loop control in this situation. Specifically the monkey’s continuous wrist position value was decoded from the neural activity in real time and used to control the cursor velocity at each timestep. This real-time remapping enabled us to use the best decoded command signal (i.e. position) to control a device in the manner that was most resistant to noise (i.e. controlling device velocity) (see [68] for additional information).

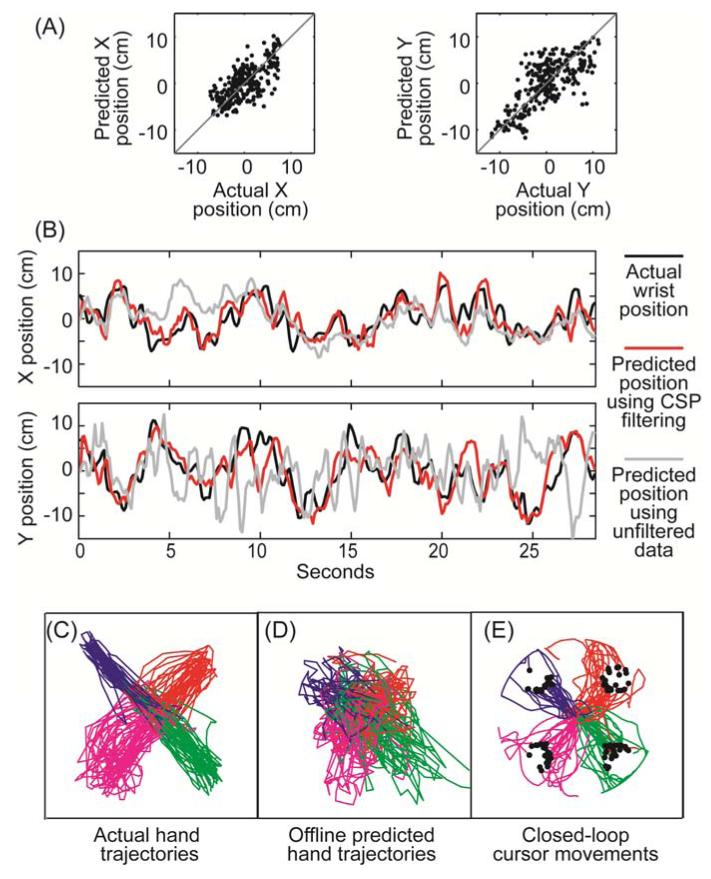
Figure 6 shows example data from the closed-loop task. In 6A, individual X and Y wrist position values from one testing set are plotted against their offline predicted values; offline predictions were generated using CSP spatial filters (32 filters, Cardinal, 67% removed) and a Kalman filter decoder without additional smoothing. Figure 6B shows examples of actual and predicted wrist position data plotted as a function of time (from the same testing set as in 6A). Predictions were made using either CSP spatial filters as in 6A (red line) or using unfiltered data (grey line). Again, a Kalman filter decoding function with no power smoothing was used in both cases.

Figure 6.

Examples of actual and predicted movements using Kalman filter decoding. A) Actual vs. offline-predicted wrist position values from one cross-validation testing set. Predictions were made using 32 spatially-filtered signals (CSP Cardinal 67% removed). B) Actual (black line) and offline-predicted wrist position as a function of time. Red line indicates predictions made with the same CSP filters as used in part A. Grey lines show offline predictions when no spatial filtering was used. C) 2D wrist trajectories when the animal’s actual hand position controlled the cursor position in real time. D) Predicted wrist positions using the neural data collected during the movements plotted in C. E) Cursor trajectories during closed-loop control using the same spatial filters and Kalman filter decoding function that was used offline in part D. Note that during closed-loop control, decoded wrist position was used to control cursor velocity in real time. Trajectories are color coded by intended target and black dots indicate when the cursor hit the target.

Figure 6C shows full 2D trajectories of the actual wrist position during initial baseline data collection (i.e. when the monkey’s actual wrist position was used to control the cursor position in standard center-out task). Figure 6D shows trajectories predicted offline from the field potentials recorded in tandem with the wrist movements shown in figure 6C. Cross-validated offline R² was 0.38 in this example. Figure 6E shows what happened when the same spatial filters and decoding function used to predict wrist position offline in figure 6D were used during closed-loop control where the predicted wrist position was used to control cursor velocity in real time. Note how jittery the offline decoded position is in figure 6D and how much better the closed-loop trajectories look in figure 6E. Several factors likely contributed to this difference. First, figure 6D shows offline predictions whereas figure 6E shows trajectories generated during closed-loop control. During closed-loop control, the animals had visual feedback of the decoded trajectory and could, therefore, make corrective movements as needed. More importantly, as we have previously shown in [68], the position-to-velocity mapping inherently smoothes out jitter due to decoding errors. Large position decoding errors have less of an impact over time in this case because remapping ensures the decoded position command as well as its associated errors only make small incremental changes in the cursor position at each timestep (i.e. Δposition/Δtime). If these position decoding errors have a zero mean, these errors will integrate out over time causing relatively little disruption to the overall movement trajectory during closed-loop control.

For comparison, we tried closed-loop control using decoded wrist velocity to control cursor velocity directly. However, due to the poor quality of the velocity decoder, control was so poor that the animal quickly stopped trying. Trajectories from this initial attempt are included in the supplement (see figure S7). Also included in the supplement are plots showing what the monkey’s actual hand was doing during the brain-control task (figure S8). Each animal still generally moved its arm out in the direction of the desired target (figure S8A). However, if the brain-controlled trajectory started to deviate from the desired path, the animal would adjust its arm position as needed to modify the cursor velocity in real time and steer the cursor back toward the target (see figures S8B&C for an example showing steering).

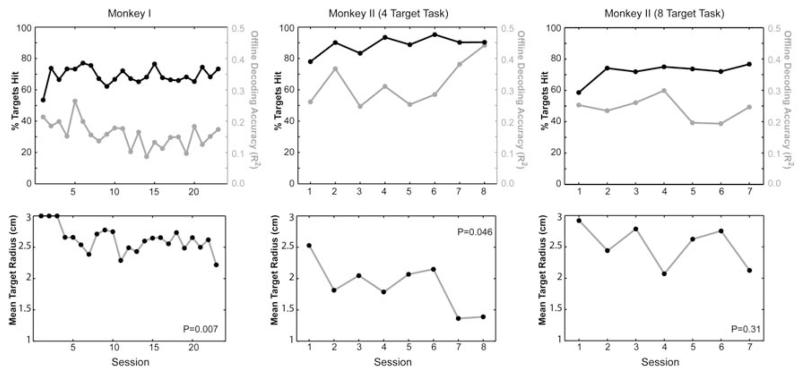
Summary results for the closed-loop testing across days are plotted in figure 7. The black lines in the top row of plots indicate the mean percentage of targets hit during each day’s testing session. The grey lines in those same plots indicate the offline cross-validated decoding R² values calculated from the initial set of neural and wrist movement data collected at the beginning of each day’s session (cross-validated R² values calculated just as they had been in the previous offline analysis shown in figures 4 and 5). These values are included here to provide a reference frame for how the offline R² values relate to online control performance.

Figure 7.

Closed-loop performance measures across testing sessions. In all closed-loop sessions, the target radius was automatically increased or decreased after each block to maintain approximately a 70% hit rate thus making the mean target radius a more useful measure of performance. P-values in the lower plots refer to the probability the slope of a least squares regression line through the data was zero. Note, monkey II’s percentage of targets hit in the four-target task consistently exceeded 70% due to the limit set on how small the target could become and due to the number of early blocks where performance exceeded 70% before the target got small enough to challenge the animal.

Recall the target and cursor sizes were automatically adjusted as needed after each block of movements to try to maintain a consistent difficulty level to keep the animal challenged but motivated. Specifically, the radii were incrementally increased or decreased by 2 mm after each block of movements until the animals could hit the targets approximately 70% of the time. Therefore, the mean target radius can be thought of as a measure of closed-loop performance accuracy. As intended, monkey I’s percentage of targets hit was maintained at about 70% across the 23 days of closed-loop testing. However, during that time, her mean target radius significantly decreased indicating she improved her movement accuracy across days (probability of the slope being zero was p=0.007 when fitting target radius as a function of session number via Matlab’s regress function)

In spite of the automatic adjustments intended to keep the target hit rate at about 70%, monkey II’s target hit rate was consistently well above 70%. This higher-than-intended hit rate was due to the fact that the lower limit set for the target radius did not make the task difficult enough and also because the targets first started out larger at the beginning of each day’s session and took about 10 to 15 blocks of incremental adjustments before the automatic algorithm reduced the target radius enough to start challenging the animal. Nevertheless, monkey II’s mean target radius also significantly declined during the eight days she performed the four target closed-loop task suggesting that her accuracy also improved across days (p=0.046).

Monkey II was given over a two-month break before restarting testing in the eight-target closed-loop task. Except for her first day back in training, she still exceeded the 70% anticipated hit rate because performance in the initial blocks in each session consistently exceeded 70% before the target radius got small enough to produce a 30% error rate. Note however, her movement accuracy never returned to the level it had been in the four target task. This may have been due to her being out of practice after a long break and/or due to her unfamiliarity with the eight-target task. The range of offline decoding R² values was also slightly lower in general during the eight-target sessions compared to the four-target sessions. This shift in offline R² may be due to changes in the signal as well as inherent day-to-day variability in the animal’s level of attention and movement consistency during each day’s initial data collection.

For both the four- and eight-target closed loop sessions, the baseline data used to build each day’s decoding function still consisted only of movements to four targets (see hand movement examples in figure 6C). This raised the question—did the animal have a more difficult time getting to the new targets over the more-practiced targets during the eight-target closed-loop control task? We compared the closed-loop hit rate for the four targets used during spatial filter and decoder building versus the new targets only presented during the closed-loop task (new targets were the same size and radial distance as the original targets but interspersed between the old targets). The mean closed-loop performance was 74±7% for the targets presented during training and 70±7% for the new targets. This small difference was not significant (p=0.21, paired t-test).

4. Discussion

Attempts to decode continuous natural limb movements or control continuous device motion using epidural or subdural field potentials have traditionally used either no spatial filtering [40-47, 78-84] or simple common average referencing [47-57]. In this study we compared 11 spatial filtering options applied to epidural field potentials with the intent to improve decoding of continuous arm movement information. Options tested included several novel spatial filtering methods that expanded upon the classic CSP algorithm to make the algorithm applicable to continuous movement data. All variants of our new CSP method significantly improved arm movement decoding accuracy over using CAR or no spatial filtering. This study suggests that significantly more useful information may be available from extracortical field potentials than is currently being acquired in most labs and research studies.

Kalman filter decoders typically resulted in higher decoding accuracies than their linear regression decoding counterparts. However, the results from this study highlighted several other important differences between Kalman filter decoding and linear regression decoding. First, Kalman filtering performed best when the power values were not pre-smoothed whereas linear regression significantly benefitted from first smoothing the power signals. The Kalman filter decoding process used current neural signals plus past predicted movements to predict current movement. This process itself ensured some continuity between sequential movement predictions, and this continuity tended to smooth out high-frequency decoding errors. This inherent smoothing in the Kalman filtering process itself could have made pre-smoothing the power unnecessary and even harmful if pre-smoothing averaged out useful temporal information used by the Kalman decoder.

On the other hand, pre-smoothing of the power data was consistently beneficial when using linear regression decoders. In this study, our linear regression decoders only used the latest power calculation to predict current movement state. However, linear decoders that use up to a second or more of past power data to predict current movement are common in the BMI field. This inclusion of past neural data can also serve to smooth out high frequency decoding errors. Therefore, pre-smoothing may be less beneficial if multiple past time bins of data are used to predict current movement. However, increasing the number of time bins of past data will also increase the number of free parameters in the decoder. More free parameters in the decoding function will require more initial data to generate the decoding function in order to avoid overfitting. The benefits of pre-smoothing demonstrated in this study may be a useful alternative to expanding the number of past neural time bins used by the decoder, especially if the amount of data available to build the decoding functions is limited. The specific balance of how much to pre-smooth versus how many past power calculations to use in any linear decoding function will likely require joint optimization of these factors and will depend on the amount of data available for building the decoding function in any given application.

The second prominent difference between the Kalman filter decoders and linear regression decoders was the number of spatially-filtered signals that resulted in the highest prediction accuracy. With both PCA and all CSP filters, Kalman filter decoders performed significantly better when using the most filtered signals tested (32). However, linear regression decoders had their peak performance when fewer spatially-filtered signals were included in the decoder (12-16). Since Kalman filter algorithm requires fitting more free parameters than the simple linear decoding function used here [85], the drop in performance with more filters in the linear regression case cannot be due to overfitting¹. If overfitting were a problem, we would have also seen a similar or worse drop in cross-validated performance when using more filters with the Kalman decoders.

Since the spatially-filtered signals were inherently rank ordered by the CSP and PCA algorithms, the additional 16 signals that were added when increasing the spatial filter count from 16 to 32 likely contained less useful movement information and more noise than the first set of 16 signals used on their own. With linear regression, the addition of these noisier signals did more harm than good. However, Kalman filtering may have benefitted from including these additional noisier signals if these noisy signals helped refine the estimate of the prediction error from the neural signals thus enabling the Kalman algorithm to more optimally weight predictions coming from the current neural signals with predictions based on the recent past kinematic data.

Another notable difference between Kalman filter decoding and linear regression was seen regarding CSP filters generated based on the goal of the movement path. Goal-based CSP filters performed worse than their 0%, 33% and 67% removed counter parts when using a linear regression decoder, but goal-based CSP filters were more beneficial when using Kalman filter decoding. Assigning complete continuous trajectories into the same class based on the end goal of the movements may have resulted in CSP-filtered signals that had more continuity of signal characteristics throughout each trajectory. This continuity of signal characteristics may have been particularly advantageous for Kalman filter decoding, which used past movement predictions along with the current neural data to make current movement predictions.

With both Kalman filters and linear decoders, prediction accuracy was improved when midrange data was removed before applying the CSP algorithm (67% removed was better than 33% removed which was better than 0% removed²). This may be because the CSP algorithm is designed to maximize the difference between data labeled as coming from two discrete states. Removing the midrange data made the available data in each class more distinct. However, removing the midrange data also reduced the amount of data available for generating the CSP filter coefficients, which could have led to overfitting. Since the best cross-validated decoding performance was generated when the most midrange data was removed, it is unlikely that overfitting was an issue in this study. Since the CSP algorithm is prone to problems with overfitting if there is not enough training data to fit all the free parameters [61, 62], it is possible that the benefits of removing midrange data may decline if only a small amount of training data is available. The optimal amount of midrange data to remove may need to be re-evaluated for applications where the amount of training data is limited.

In this study, velocity decoding was an order of magnitude worse than position decoding regardless of which decoding function or spatial filter option was used. Low-pass filtering the position data before differentiation did improve decoding accuracy somewhat, but R² values were still only about a third as high as with position decoding. Historically, velocity has been robustly decoded from intracortical unit activity [74-77], and recent data from another monkey study that utilized high-density epicortical arrays has shown roughly equivalent decoding accuracy for position and velocity [40]. One likely reason for poor velocity decoding in our particular study may be that our animals were over trained in the center-out task and moved very fast to and from the different targets. Since kinematic data was sampled every 100ms, and power was calculated using 300ms of the latest neural data, a significant portion of the calculated power values were from 300ms time bins where the hand was moving in one direction at the start of the time bin and moving in the opposite direction by the end of the time bin. This mismatch between the coarsely-sampled, rapid velocity changes and the temporally-smoothed power signals likely impacted the accuracy of the velocity decoding. Pre-smoothing the kinematic data improved the calculated accuracy measure of the velocity decoder. However, it is unclear whether that improvement was due to truly increasing decoder accuracy or simply due to manipulating the actual velocity values to better match the smoothed nature of the predicted velocity. Regardless, our findings suggest it might be preferable to collect baseline data using random target locations and a variety of different target sizes to elicit a more diverse range of limb speeds [86] when building velocity decoders.

Our previous study indicated that velocity commands still may be preferable to use in a BMI over position commands, even when the position signals are more accurately decoded [68]. This is because brain-controlled devices are more robust to noise in a velocity command compared to the same relative amount of noise in a position command. Random decoding errors in a velocity command will tend to average out when integrated over time resulting in relatively smooth device trajectories. However, the same relative level of error in a position command will cause a device to continuously jump around its intended location, thus creating a much more substantial control problem [68].

This study demonstrated the benefits of using this position-to-velocity re-mapping in the case where position was much more accurately decoded than velocity. This re-mapping allowed us to use the more accurate of the two command signals to control the cursor in the most robust manner. Figure S7 shows that the very poor decoding of velocity made it unusable as a command signal. Although position was more accurately decoded than velocity, figure 6D shows that the position command had enough noise or jitter that it still would have made directly controlling the cursor position a challenge. However, by using decoded wrist position to control cursor velocity (figure 6E), the animal was able to generate relatively smooth brain-controlled movements. Even though some trajectories deviated off course, in most cases, the animal was able to successfully steer the cursor back to the target in time to get a reward.

Although this study utilized cortex that had some prior damage due to the removal of intracortical electrodes, the full recovery of the animals suggest the cortex was still fully capable of generating the necessary motor commands for normal function. Although minor dural thickening was noted during the replacement surgery in Monkey II, this likely had only a minimal effect on the overall decoder performance given that the impact of the normal dura itself has been shown to be relatively small. Modeling work by Slutzky et al. [87] showed that much of the difference between epidural and subdural signals is primarily due to distance of the epidural electrodes from the cortical surface. The epidural recording resolution approached that of subdural electrodes when the size of the cerebrospinal fluid layer was reduced to a negligible amount suggesting the impedance of the dura itself has only a small impact on recording resolution. Nevertheless, because of the prior cortical and dural damage in the animal models used here, the spatial filter options tested should be compared based on their relative differences in decoding performance. The absolute level of decoding accuracy shown in this study should not be interpreted to represent what would be expected from normal cortex and dura.

For many growing therapeutic BMI applications, such as retraining the brain after stroke or traumatic brain injury, cortical damage is likely to be the norm [12-36]. Even in healthy spinal-cord-injured individuals, the cortical signals are still likely to have changed with disuse over time [69-71]. Chronic intracortical microelectrode arrays may also fail at some point over the long lifetime of most young adult spinal-cord-injured BMI users thus requiring removal and/or replacement technology as was done in this animal study. Given the variable nature of the condition of the cortex and dura in many potential BMI users, there is high value in developing data-driven spatial filtering methods like the CSP methods demonstrated here. Unlike CAR, Laplacian, and other spatial filtering methods, these CSP methods do not rely on any prior assumptions about the how the movement information or unrelated noise is spatially distributed in the cortex. The algorithm itself is designed to optimally sort out that relationship for us using known information about the movements the user is trying to make.

As different extracortical field potential recording technologies are being developed [6, 88-91], advancing our signal processing methods in parallel, as we have done here, will ensure that we continue to obtain the full range of useful information available from these new electrode configurations. Only then will we be able to make informed decisions on the risk/benefit ratios of different electrode options and wisely choose which electrode technologies to use for different clinical and research applications.