On the Nonnegative Rank of Euclidean Distance Matrices

Abstract

The Euclidean distance matrix for n distinct points in ℝ^r is generically of rank r + 2. It is shown in this paper via a geometric argument that its nonnegative rank for the case r = 1 is generically n.

1. Introduction

Any given nonnegative matrix A ∈ ℝ^m×n can be expressed as the product A = UV for some nonnegative matrices U ∈ ℝ^m×k and V ∈ ℝ^k×n with k ≤ min{m, n}. The smallest k that makes this factorization possible is called the nonnegative rank of A. For convenience, we denote the nonnegative rank of A by rank₊(A). Trivially the nonnegative rank has bounds such as

$$\text{rank}(A)\le {\text{rank}}_{+}(A)\le min\{m,n\}.$$ (1)

Determining the exact nonnegative rank and computing the corresponding factorization, however, are known to be NP-hard [6, 18]. If the nonnegative matrix A is such that rank₊(A) = rank(A), then we say that A has a nonnegative rank factorization (NRF). Even in this case, there is no known effective algorithm to compute the NRF.

It is shown recently that, if k < min{m, n}, then the probability that a matrix A with rank₊(A) = k should also have rank(A) = k is one. In other words, matrices which have an NRF are generic. To put it more plainly, if A = UV where U ∈ ℝ^m×k and V ∈ ℝ^k×n are randomly generated nonnegative matrices, then with probability one we have rank(A) = k. The converse is nevertheless not true. Indeed, the question of computing the probability for a 4 × 4 nonnegative matrix of rank 3 to have nonnegative rank 3 is not trivial at all. It is very much analogous to the Sylvester’s four-point problem which, to this date, does not admit a determinate solution [14, 16]. For this reason, there has been considerable interest in the literature to identify nonnegative matrices with or without NRF.

A necessary and sufficient condition qualifying whether a nonnegative matrix has an NRF can be found in [17], but that result appears too theoretical for numerical verification. A few sufficient conditions for constructing nonnegative matrices without NRF have been given in [13, 15]. The simplest example is the 4 × 4 matrix

$$\mathcal{C}=\left[\begin{array}{cccc}1& 1& 0& 0\\ 1& 0& 1& 0\\ 0& 1& 0& 1\\ 0& 0& 1& 1\end{array}\right],$$

with rank( ) = 3 and rank₊( ) = 4. Other known conditions for the existence of an NRF are for more restrictive subclasses of matrices such as the so called weakly monotone nonnegative matrices [12], λ-monotone [11], or matrices with nonnegative 1-inverse [4]. Still, given a nonnegative matrix, finding its (numerical) rank is computationally possible, but ensuring its nonnegative rank is an extremely hard task. Thus far, we know very little in the literature about nonnegative matrices which do not have NRF. This factorization has also be studied in the literature under the notion of prime matrices [3, 15].

The purpose of this short communication is to add the important class of Euclidean distance matrices to the list of matrices having no NRF. This note represents perhaps only a modest advance in the field, but it should be of interest to confirm the precise rank and nonnegative rank of a distance matrix.

2. Rank condition and standard form

Given n points p₁, …, p_n in the space ℝ^r, the corresponding Euclidean distance matrix (EDM) is the n × n symmetric and nonnegative matrix Q(p₁, …, p_n) = [q_ij] whose entry q_ij is defined by

$$q_{ij}={\Vert {\mathbf{p}}_i-{\mathbf{p}}_j\Vert }^2,i,j=1,\dots ,n,$$ (2)

where ||·|| denotes the Euclidean norm in ℝ^r. As an exhaustive record of relative spacing between any two of the n particles in ℝ^m, the distance matrix Q(p₁, …, p_n) has many important applications in distance geometry. See, for example, the discussions in [7, 8, 9, 10]. Our attention here is solely on the rank condition of Q(p₁, …, p_n).

Theorem 2.1

For any n ≥ r + 2, the rank of Q(p₁, …, p_n) is no greater than r + 2 and is generically r + 2.

Proof

(This is a classical and well known fact. There are many elegant ways to verify this result, but for the sake of comparing the associated factorizations we find the following equality representation is most constructive and straightforward.) Regarding each p_ℓ as a column vector and q_ij = 〈p_i − p_j, p_i − p_j〉 with 〈·, ·〉 denoting the Euclidean inner product, we can write [1]

$$Q({\mathbf{p}}_1,\dots ,{\mathbf{p}}_n)=\underset{U}{\underbrace{\left[\begin{array}{ccc}\langle {\mathbf{p}}_1,{\mathbf{p}}_1\rangle & 1& -2{\mathbf{p}}_1^{\top }\\ ⋮& ⋮& ⋮\\ \langle {\mathbf{p}}_i,{\mathbf{p}}_i\rangle & 1& -2{\mathbf{p}}_i^{\top }\\ ⋮& ⋮& ⋮\\ \langle {\mathbf{p}}_n,{\mathbf{p}}_n\rangle & 1& -2{\mathbf{p}}_n^{\top }\end{array}\right]}}\underset{V}{\underbrace{\left[\begin{array}{ccccc}1& \dots & 1& \dots & 1\\ \langle {\mathbf{p}}_1,{\mathbf{p}}_1\rangle & \dots & \langle {\mathbf{p}}_j,{\mathbf{p}}_j\rangle & \dots & \langle {\mathbf{p}}_n,{\mathbf{p}}_n\rangle \\ {\mathbf{p}}_1& & {\mathbf{p}}_j& & {\mathbf{p}}_n\end{array}\right]}}.$$ (3)

Note that U ∈ ℝ^n×(r+2) and V ∈ ℝ ^(r+2)×n. Unless the points p₁, …, p_n satisfy some specific algebraic equations, such as ||p_ℓ|| = 1 for all ℓ = 1, … n, the matrices U and V are generically of rank r + 2.

The fact that the rank of an EDM depends on r, but is independent of the size n, is very interesting. The rank deficiency indicates that many entries in the matrix provide redundant information. It is curious to know whether rank₊(Q(p₁, …, p_n)) has similar property. Note that the two factors U and V in (3) cannot be both nonnegative, so the (minimum) nonnegative factorization of Q(p₁, …, p_n) is yet to be determined.

In a recent paper [1], it is estimated via an intriguing algebraic argument that for a nonnegative matrix of rank 3 to have nonnegative rank 10, we would need a matrix of order at least 252. The discussion in the sequel clearly indicates that the actual order can be much lower.

Suppose that a nonnegative matrix A has two factorizations, A = BC and A = FG. We say that these two factorizations are equivalent if there exist a permutation matrix P and a diagonal matrix D with positive diagonal elements such that BDP = F and P^⊤D⁻¹C = G [1]. With this notion in mind, it suffices to consider the nonnegative factorization for an EDM in a special form.

Lemma 2.1

Suppose n ≥ r + 2 ≥ 3. Then any nonnegative factorization of Q(p₁, …, p_n) is equivalent to the form

$$Q({\mathbf{p}}_1,\dots ,{\mathbf{p}}_n)=\left[\begin{array}{ccccc}1& 0& \ast & \ast & \dots \\ \ast & 1& 0& \ast & \dots \\ 0& \ast & 1& \ast & \dots \\ \ast & \ast & \ast & \ast & \\ ⋮& & & & \end{array}\right]\left[\begin{array}{ccccc}0& \ast & +& \ast & \dots \\ +& 0& \ast & \ast & \\ \ast & +& 0& \ast & \\ \ast & \ast & \ast & \ast & \\ ⋮& & & & \end{array}\right]$$ (4)

where * stands for some undetermined nonnegative numbers and + stands for three undetermined positive numbers.

Proof

Suppose Q(p₁, …, p_n) = UV is a nonnegative factorization. Then there must exist an index 1 ≤ k₁ ≤ n such that u_1k1v_k13 > 0. Permuting both the first and the k₁th columns of U and the first and the k₁th rows of V simultaneously will not affect the product and will place u_1k1 at the (1, 1) position and v_k13 at the (1, 3) position. After scaling u_1k1 to unit, rename without causing ambiguity the permuted matrices as U and V, respectively. The corresponding v₁₁ in the new V must be zero. Consequently, there must exist an index 2 ≤ k₂ ≤ n such that u_2k2v_k21 > 0. Permuting the second and the k₂th columns of U and the second and the k₂th rows of V simultaneously will not affect the product, will not alter the first column of U or the first row of V, and will place u_2k2 at the (2, 2) position and v_k21 at the (2, 1) position. Again, after scaling u_2k2 to unit and renaming the permuted matrices as U and V, it must be u₃₁ = v₂₂ = 0. It follows that there exist an index 3 ≤ k₃ ≤ n such that u_3k3v_k32 > 0. Permuting the third and the k₃th columns and rows and scaling u_3k3 to unit will give rise to the structure specified in the lemma.

It is important to note that the procedure described in the above proof cannot be continued to the fourth or other rows or columns. For this reason, we refer to (4) as the standard nonnegative factorization of Q(p₁, …, p_n).

When reference to the points p₁, …, p_n is not critical, we abbreviate a generic Q(p₁, …, p_n) as Q_n. The notion of nonnegative rank has an interesting geometric meaning [5] which will be our main toll for verifying the nonnegative rank of Q_n. Let the columns of a general nonnegative matrix $A\in {\mathbb{R}}_{+}^{m\times n}$ be denoted by A = [a₁, …, a_n]. Define the scaling factor σ(A) by

$$\sigma (A):=\text{diag}\{{\Vert {\mathbf{a}}_1\Vert }_1,\dots ,{\Vert {\mathbf{a}}_n\Vert }_1\},$$ (5)

where ||·||₁ stands for the 1-norm in ℝ_m, and the pullback map ϑ(A) by

$$\vartheta (A):=A\sigma {(A)}^{-1}.$$ (6)

Each column of ϑ(A) can be regarded as a point on the (m − 1)-dimensional probability simplex 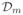defined by

$${\mathcal{D}}_m:=\left\{\mathbf{x}\in {\mathbb{R}}_{+}^m\mid x_i\ge 0,\sum _{i=1}^m{x}_i=1\right\}.$$ (7)

Suppose a given nonnegative matrix A can be factorized as A = UV, where $U\in {\mathbb{R}}_{+}^{m\times p}$ and $V\in {\mathbb{R}}_{+}^{p\times n}$. Because UV = (UD)(D⁻¹V) for any invertible nonnegative matrix D ∈ ℝ^p×p, we may assume without loss of generality that U is already a pullback so that σ(U) = I_n. We can write

$$A=\vartheta (A)\sigma (A)=UV=\vartheta (U)\vartheta (V)\sigma (V).$$ (8)

Note that the product ϑ(U)ϑ(V) itself is on the simplex 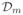. It follows that

$$\vartheta (A)=\vartheta (U)\vartheta (V),$$ (9)

$$\sigma (A)=\sigma (V).$$ (10)

In particular, if p = rank₊(A), then we see that rank₊(ϑ(A)) = p, and vice versa. The expression (9) means that the columns in the pullback ϑ(A) are convex combinations of columns of ϑ(U). The integer rank₊(A) stands for the minimal number of vertices on 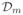so that the resulting convex polytope encloses all columns of the pullback ϑ(A).

3. Nonnegative rank and factorization for linear EDM

Given a permutation σ of the set {1, 2, …, n}, define the permutation matrix P_σ:= [δ_iσ(j)] where δ_st denotes the Kronecker delta function. Then it is easy to see that

$$P_{\sigma }^{\top }Q({\mathbf{p}}_1,\dots ,{\mathbf{p}}_n)P_{\sigma }=Q({\mathbf{p}}_{\sigma (1)},\dots {\mathbf{p}}_{\sigma (n)}).$$ (11)

In other words, the conjugation of an EDM by any permutation matrix remains to be an EDM. In the one dimensional case, i.e., r = 1, we may assume without loss of generality that the point are arranged is ascending order, p₁ < … < p_n. Define s_i:= p_i+1 − p_i, i = 1, …, n − 1. Entries in the linear EDM has a special ordering pattern that radiates away from the diagonal per column and row, i.e.

$$Q({\mathbf{p}}_1,\dots ,{\mathbf{p}}_n)=\left[\begin{array}{ccccc}0& s_1^2& {(s_1+s_2)}^2& {(s_1+s_2+s_3)}^2& \dots \\ s_1^2& 0& s_2^2& {(s_2+s_3)}^2& \dots \\ {(s_1+s_2)}^2& s_2^2& 0& s_3^2& \dots \\ {(s_1+s_2+s_3)}^2& {(s_2+s_3)}^2& s_3^2& 0& \\ ⋮& & & & \end{array}\right]$$ (12)

We shall exploit this particular ordering to help to obtain some initial insight into the nonnegative rank of the EDM. Unless mentioned otherwise, the subsequent discussion is for the case r = 1.

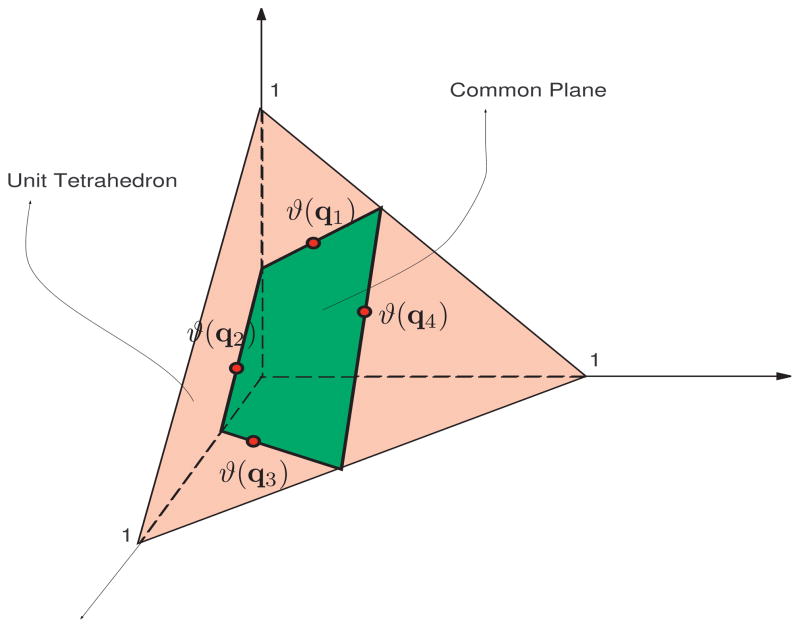
It is illuminating to begin the analysis with the case n = 4. For convenience, we adopt the colon notation as in Matlab to pick out selected rows, columns or elements of vectors. Denote the columns of Q₄ by Q₄ = [q₁, …, q₄]. The probability simplex 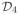can easily be visualized via the unit tetrahedron S₃ in the first octant of ℝ³ if we identify the 4-dimensional vector x by the vector [x₁, x₂, x₃]^⊤ of its first three entries. In this way, columns of ϑ(Q₄) can be interpreted as points ϑ(q₁), ϑ(q₂), ϑ(q₃), ϑ(q₄) depicted in Figure 1. Note that the four points ϑ(q₁), ϑ(q₂), ϑ(q₃), ϑ(q₄) are coplanar because rank(Q₄) = 3. The y-intercept of this common plane is $\frac{s_1{s}_2}{s_1{s}_2-s_3(s_1+s_2+s_3)}$ which is either negative or positive with value greater than 1. In either case, the plane intersects the tetrahedron as a quadrilateral. The first three points sit on three separate “ridges” of the quadrilateral and hence cannot be enclosed by any triangle within the quadrilateral except the one with vertices at these three points. If rank₊(Q₄) < 4, then ϑ(q₄) must be inside this triangle and hence be a convex combination of ϑ(q₁), ϑ(q₂), ϑ(q₃), which translates to that the vector q₄ must be a nonnegative combination of q₁, q₂, q₃, but this impossible because q₄₄ = 0. Thus rank₊(Q₄) = 4.

Figure 1.

A geometric representation of the matrix ϑ(Q₄) when r = 1.

The expression Q₄ = UV in the form (4) represents a polynomial system of 22 equations in 23 unknowns whereas one of the nonzero unknowns can be normalized to unit. This nonlinear system is solvable. Other than the trivial factorization Q₄ = I₄Q₄ where I₄ stands for the identity matrix, we find that there are only three nontrivial nonnegative factorizations which we list in Table 1. While the first set of factorization in the table is equivalent to Q₄I₄, it is important to note that the last two sets of factorizations correspond to the four vertices of the quadrilateral shown in figure 1. This observation also shows that Q₄ is not prime [2, 15].

Table 1.

Standard nonnegative factorizations of Q₄.

U	V
$$\left[\begin{array}{cccc}1& 0& \frac{{s_1}^2}{s_2^2}& {(s_1+s_2+s_3)}^2\\ \frac{{s_2}^2}{{(s_1+s_2)}^2}& 1& 0& {(s_2+s_3)}^2\\ 0& \frac{{(s_1+s_2)}^2}{{s_1}^2}& 1& {s_3}^2\\ \frac{{s_3}^2}{{(s_1+s_2)}^2}& \frac{{(s_1+s_2+s_3)}^2}{{s_1}^2}& \frac{{(s_2+s_3)}^2}{{s_2}^2}& 0\end{array}\right]$$	$$\left[\begin{array}{cccc}0& 0& {(s_1+s_2)}^2& 0\\ {s_1}^2& 0& 0& 0\\ 0& {s_2}^2& 0& 0\\ 0& 0& 0& 1\end{array}\right]$$
$$\left[\begin{array}{cccc}1& 0& 0& \frac{(s_1+s_2)s_2(s_1+s_2+s_3)}{s_2+s_3}\\ 0& 1& 0& {s_2}^2\\ 0& \frac{s_3(s_1+s_2)}{(s_2+s_3)s_1}& 1& 0\\ \frac{s_3(s_2+s_3)}{(s_1+s_2)s_1}& 0& \frac{(s_2+s_3)(s_1+s_2+s_3)}{(s_1+s_2)s_2}& 0\end{array}\right]$$	$$\left[\begin{array}{cccc}0& {s_1}^2& \frac{s_3{s}_1(s_1+s_2)}{s_2+s_3}& 0\\ {s_1}^2& 0& 0& \frac{s_3(s_2+s_3)s_1}{s_1+s_2}\\ \frac{(s_1+s_2)s_2(s_1+s_2+s_3)}{s_2+s_3}& {s_2}^2& 0& 0\\ 0& 0& 1& \frac{(s_2+s_3)(s_1+s_2+s_3)}{(s_1+s_2)s_2}\end{array}\right]$$
$$\left[\begin{array}{cccc}1& 0& 0& {s_1}^2\\ \frac{s_2(s_2+s_3)}{(s_1+s_2)(s_1+s_2+s_3)}& 1& 0& 0\\ 0& \frac{s_3(s_1+s_2)}{(s_2+s_3)s_1}& 1& 0\\ 0& 0& \frac{(s_2+s_3)(s_1+s_2+s_3)}{(s_1+s_2)s_2}& \frac{s_3(s_2+s_3)s_1}{s_1+s_2}\end{array}\right]$$	$$\left[\begin{array}{cccc}0& 0& \frac{s_2(s_1+s_2)(s_1+s_2+s_3)}{s_2+s_3}& {(s_1+s_2+s_3)}^2\\ {s_1}^2& 0& 0& \frac{s_3(s_2+s_3)s_1}{s_1+s_2}\\ \frac{s_2(s_1+s_2)(s_1+s_2+s_3)}{s_2+s_3}& {s_2}^2& 0& 0\\ 0& 1& \frac{s_3(s_1+s_2)}{(s_2+s_3)s_1}& 0\end{array}\right]$$

When n > 4, such a visualization in geometry is not possible, but the idea remains justifiable via an algebraic argument with which we precede as follows.

Theorem 3.1

Suppose that the linear EDM Q_n is of rank 3. Then rank₊(Q_n) = n.

Proof

Because rank(Q_n) = 3, its columns reside on a 3-dimensional subspace of ℝⁿ. The pull-back map ϑ can be considered as the intersection of this subspace and the hyperplane defined by ${\sum }_{i=1}^n{x}_i=1$. Columns of ϑ(Q_n) therefore are “coplanar” whereas by their common plane we refer to a 2-dimensional affine subspace in ℝⁿ. Identifying any n-dimensional vector x ∈ 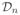by its first n−1 entries [x₁, …, x_n−1]^⊤, we thus are able to “see” columns ϑ(q₁), …, ϑ(q_n) as n points residing within the unit polyhedron 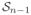in the first orthotant of ℝⁿ⁻¹. These points remain to be coplanar. (Indeed, the 2-dimensional affine subspace can be identified by a fixed point, say, ϑ(q₁), and two coordinate axes, say, v₁:= ϑ(q₂) − ϑ(q₁) and v₂:= ϑ(q₃) − ϑ(q_n), where all points in the 2-dimensional affine subspace can be represented as ϑ(q₁) + α₁v₁ + α₂v₂ with scalars α₁ and α₂. The drawing in Figure 1, therefore, is still relatively instructive.)

For 1 ≤ i ≤ n − 1, it is clear that ϑ(q_i) cannot possibly be a convex combination of any other ϑ(q_j) because of the unique zero at its ith entry. We claim further that ϑ(q_n) cannot possibly be in the convex hull spanned by ϑ(q₁), …, ϑ(q_n−1). Assume otherwise, then we would have

$$\vartheta ({\mathbf{q}}_n)=\sum _{i=1}^{n-1}{c}_i\vartheta ({\mathbf{q}}_i)$$

for some c_i ≥ 0 with ${\sum }_{i=1}^{n-1}{c}_i=1$. Note that ||ϑ(q_n)||₁ = 1. However, ${\Vert {\sum }_{i=1}^{n-1}{c}_i\vartheta ({\mathbf{q}}_i)\Vert }_1<1$ because ||ϑ(q_i)||₁ < 1 after chopping away the last row of ϑ(Q_n). This is a contradiction. The smallest number of vertices for a convex hull to enclose ϑ(q₁), …, ϑ(q_n), therefore, has to be n, implying that rank₊(Q_n) = n.

There is a subtle difference between the standard nonnegative factorization of Q₄ and that of Q_n when n ≥ 5. Except for the trivial factorization, both factors U and V in Table 1 for Q₄ are of rank 3. This is not the case in general.

Lemma 3.1

Suppose n ≥ 5 and Q_n = UV is a standard nonnegative factorization for the matrix Q_n. Then it cannot be such that both U and V are of rank 3 simultaneously.

Proof

Observe first that for n ≥ 3, assuming the generic condition rank(Q_n) = 3, we can partition Q_n as

$$Q_n=\left[\begin{array}{cc}{Q}_3& Q_3\mathrm{\Phi }\\ {\mathrm{\Phi }}^{\top }{Q}_3& {\mathrm{\Phi }}^{\top }{Q}_3\mathrm{\Phi }\end{array}\right]$$ (13)

where Φ ∈ ℝ^3×(n−3) is uniquely determined. Indeed, if we write Φ = [φ₄, … φ_n], then it can be shown that

$${\phi }_j=\left[\begin{array}{c}\frac{\left({\sum }_{\ell =2}^{j-1}{s}_{\ell }\right)\left({\sum }_{\ell =3}^{j-1}{s}_{\ell }\right)}{s_1(s_1+s_2)}\\ -\frac{\left({\sum }_{\ell =1}^{j-1}{s}_{\ell }\right)\left({\sum }_{\ell =3}^{j-1}{s}_{\ell }\right)}{s_1{s}_2}\\ \frac{\left({\sum }_{\ell =1}^{j-1}{s}_{\ell }\right)\left({\sum }_{\ell =2}^{j-1}{s}_{\ell }\right)}{s_2(s_1+s_2)}\end{array}\right],j=4,\dots ,n.$$ (14)

Note that the second entry in φ_j is always negative.

Assume by contradiction that both U and V of Q_n are of rank 3. As U and V appear in the standard form (4), their 3 × 3 leading principal submatrices U₁₁ and V₁₁ are nonsingular. Thus similar to (13), we can partition the nonnegative factors into blocks

$$Q_n=\left[\begin{array}{cc}{U}_{11}& U_{11}\mathrm{\Theta }\\ {\mathrm{\Lambda }}^{\top }{U}_{11}& {\mathrm{\Lambda }}^{\top }{U}_{11}\mathrm{\Theta }\end{array}\right]\left[\begin{array}{cc}{V}_{11}& V_{11}\mathrm{\Gamma }\\ {\mathrm{\Delta }}^{\top }{V}_{11}& {\mathrm{\Delta }}^{\top }{V}_{11}\mathrm{\Gamma }\end{array}\right],$$ (15)

where Θ, Λ, Γ and Δ are real matrices of compatible sizes. Upon comparison with (13), we see that Λ = Φ = Γ. Taking a closer look at the product Λ^⊤U₁₁, we find that the signs of its entries are given by

$${\mathrm{\Lambda }}^{\top }{U}_{11}=\left[\begin{array}{ccc}+& -& +\\ ⋮& ⋮& ⋮\\ +& -& +\end{array}\right]\left[\begin{array}{ccc}1& 0& \ast \\ \ast & 1& 0\\ 0& \ast & 1\end{array}\right]=\left[\begin{array}{ccc}\ast & \begin{array}{|c|}\hline ·\\ \hline\end{array}& +\\ ⋮& ⋮& ⋮\\ \ast & \begin{array}{|c|}\hline ·\\ \hline\end{array}& +\end{array}\right],$$

where, again, * indicates some undetermined nonnegative numbers, + some undetermined positive numbers, and ⊡ some nonnegative numbers which can further be determined. Similarly, the signs for entries of V₁₁Γ are given by

$$V_{11}\mathrm{\Gamma }=\left[\begin{array}{ccc}0& \ast & +\\ +& 0& \ast \\ \ast & +& 0\end{array}\right]\left[\begin{array}{ccc}+& \dots & +\\ -& \dots & -\\ +& \dots & +\end{array}\right]=\left[\begin{array}{ccc}\ast & \dots & \ast \\ +& \dots & +\\ \begin{array}{|c|}\hline ·\\ \hline\end{array}& \dots & \begin{array}{|c|}\hline ·\\ \hline\end{array}\end{array}\right].$$

Being nonnegative, U and V are complementary to each other in the sense that u_ijv_ji = 0 for all indices i and j. It follows that the +’s in the middle row of V₁₁Γ must cause the ⊡’s in the middle column of Λ^⊤U₁₁ to become zeros. This implies that the very same u₃₂ would have to satisfy the equalities

$$-\frac{\left({\sum }_{\ell =1}^{j-1}{s}_{\ell }\right)\left({\sum }_{\ell =3}^{j-1}{s}_{\ell }\right)}{s_1{s}_2}+\frac{\left({\sum }_{\ell =1}^{j-1}{s}_{\ell }\right)\left({\sum }_{\ell =2}^{j-1}{s}_{\ell }\right)}{s_2(s_1+s_2)}{u}_{32}=0,$$

for all j = 4, … n, which is not possible if n ≥ 5.

To compute the nonnegative factorization of Q_n for n ≥ 5 is considerably harder. The case n = 5, for example, involves a polynomial system of 39 nonlinear equations in 41 unknowns two of which can be normalized. A short cut from a geometric point of view might be worth mentioning. Write

$$Q_5=\left[\begin{array}{cc}{Q}_4& {\mathbf{q}}_5\\ {\mathbf{q}}_5^{\top }& 0\end{array}\right],$$ (16)

with q₅ ∈ ℝ^4×1. Consider the submatrix [Q₄, q₅] only. Clearly, its columns are coplanar and, hence, ϑ(q₅) is a point in the interior of the quadrilateral drawn in Figure 1. In particular, if Q₄ = UV is one of the two nontrivial standard nonnegative factorizations of Q₄, i.e., columns of ϑ(U) (or ϑ(V^⊤)) are the four vertices of the quadrilateral, then q₅ is a nonnegative combination of columns of U (or V^⊤). In this way, two of the nontrivial standard nonnegative factorizations of Q₅ are given by

$$Q_5=\left[\begin{array}{cc}U& \mathbf{0}\\ {\mathbf{0}}^{\top }& 1\end{array}\right]\left[\begin{array}{cc}V& {\mathbf{w}}_5\\ {\mathbf{q}}_5^{\top }& 0\end{array}\right]=\left[\begin{array}{cc}U& {\mathbf{q}}_5\\ {\mathbf{z}}^{\top }& 0\end{array}\right]\left[\begin{array}{cc}V& \mathbf{0}\\ {\mathbf{0}}^{\top }& 1\end{array}\right],$$ (17)

respectively, where w₅ and z₅ are some nonnegative vectors satisfying Uw₅ = V^⊤z₅ = q₅. This procedure can be generalized to higher n, but there might be other nonnegative factorizations which are not of this particular form specified in (17).

4. A conjecture for higher dimensional EDM

In higher dimensional vector spaces, points p₁, …, p_n cannot be totally ordered. Thus, for r > 1 and n ≥ r + 2, the EDM will not enjoy the inherent structure indicated in (12). Nevertheless, if we denote p_j = [p_ij], then we can write

$$Q({\mathbf{p}}_1,\dots ,{\mathbf{p}}_n)=\sum _{i=1}^{r}Q(p_{i1},\dots ,p_{in}).$$

We have shown earlier that generically rank₊(Q(p_i1, …, p_in)) = n for each 1 ≤ i ≤ r. Representing the distance matrices for respective components, these r linear EDMs in general are not related to each other. For their summation (of nonnegative entries) to cause a reduction of rank, they must satisfy some delicate algebraic constraints. We thus conjecture that rank₊(Q(p₁, …, p_n)) = n generically for all r.

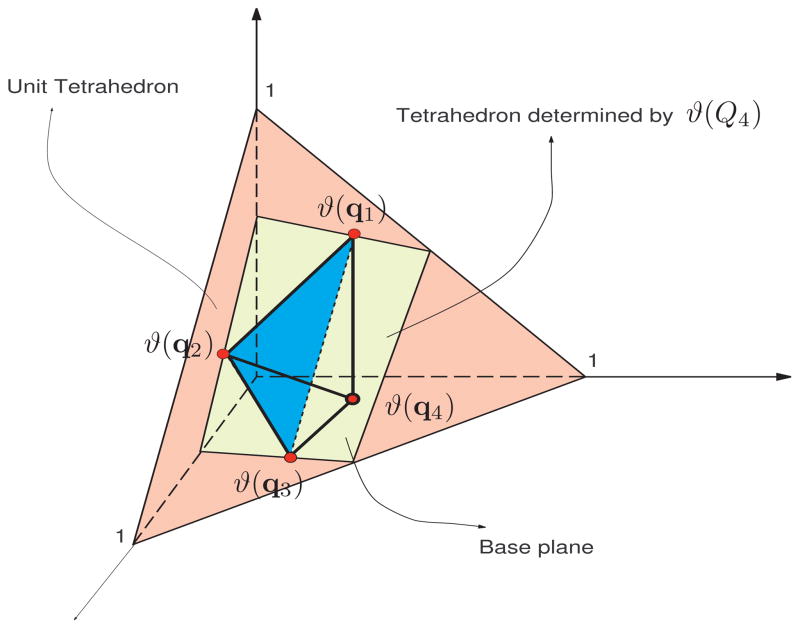
It might be informative to reexamine the geometric representation of the matrix Q₄ when r > 1. In contrast to the setting in Figure 1, columns of Q₄ are not coplanar. Their representation becomes that depicted in Figure 2. The vertex ϑ(q₄) resides on the simplex 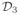. How the base plane determined by vertices ϑ(q₁), ϑ(q₂), and ϑ(q₃) intersects the axes characterizes the zero structure of nonnegative factors. Different from the case r = 1, there are several possibilities and there is simply no general rules here. The one shown in Figure 2 implies that the corresponding Q₄ is prime, which is another interesting contrast to the case when r = 1.

Figure 2.

A geometric representation of the matrix ϑ(Q₄) when r > 1.