Q-Learning: A Data Analysis Method for Constructing Adaptive Interventions

Abstract

Increasing interest in individualizing and adapting intervention services over time has led to the development of adaptive interventions. Adaptive interventions operationalize the individualization of a sequence of intervention options over time via the use of decision rules that input participant information and output intervention recommendations. We introduce Q-learning, which is a generalization of regression analysis to settings in which a sequence of decisions regarding intervention options or services are made. The use of Q is to indicate that this method is used to assess the relative quality of the intervention options. In particular, we use Q-learning with linear regression to estimate the optimal (i.e., most effective) sequence of decision rules. We illustrate how Q-learning can be used with data from sequential multiple assignment randomized trials (SMART; Murphy, 2005) to inform the construction of a more deeply tailored sequence of decision rules than those embedded in the SMART design. We also discuss the advantages of Q-learning compared to other data analysis approaches. Finally, we use the Adaptive Interventions for Children with ADHD SMART study (Center for Children and Families, SUNY at Buffalo, William E. Pelham as PI) for illustration.

Introduction

The advantages of adaptive interventions are widely acknowledged in the behavioral and social sciences. In adaptive interventions the composition and/or the intensity of the intervention are individualized based on individuals’ characteristics or clinical presentation, and then adjusted in response to their ongoing performance (see, e.g., Bierman, Nix, Maples, & Murphy, 2006; Connell, Dishion, Yasui, & Kavanagh, 2007; Marlowe et al., 2008; Schaughency & Ervin, 2006). The conceptual idea of an adaptive intervention can be operationalized by using decision rules (Bierman et al., 2006) that link subjects’ characteristics and ongoing performance with specific subsequent intervention options (i.e., the type and the intensity/dosage of the intervention). The assignment of particular intervention options is based on participants’ values on tailoring variables—baseline and time-varying variables which strongly moderate the effect of certain intervention options, such that the type or intensity of the intervention should be tailored according to these moderators (see the companion paper, Nahum-Shani et al., 2011, for more details and examples of decision rules).

High-quality adaptive interventions are constructed by selecting good decision rules, namely decision rules that are expected to optimize the overall effectiveness of the sequence of tailored intervention options. In recent years intervention scientists have become increasingly interested in experimental designs and data analysis methods that are specifically suited for selecting high-quality decision rules for intervention development (Brown et al., 2009; Collins, Murphy & Strecher, 2007; Rivera, Pew & Collins, 2007). The sequential multiple assignment randomized trials (SMART) was developed to provide data specifically for the purpose of constructing adaptive interventions. In a SMART design, participants proceed through multiple intervention stages (corresponding to critical decision points) and at each stage, each individual is randomized among intervention options (see the companion paper, Nahum-Shani et al., 2011, for an overview of SMART designs). Nahum-Shani et al. (2011) provide methods that can be used to compare intervention options at different stages of the adaptive intervention as well as to compare the relatively simple adaptive interventions embedded in a SMART design. However, investigators are often interested in constructing interventions that are more complex than those embedded in the SAMRT design. For example, investigators often collect information concerning potential moderators (e.g., baseline characteristics of the individual and/or context, adherence to and/or side effects from prior intervention stages) and plan to use this information to investigate whether and how intervention options should be tailored according to these variables. In other words, investigators are interested in using additional information collected as part of the SMART study to explore ways to more deeply tailor the adaptive intervention. Accordingly, data analysis methods are needed in order to construct the best sequence of decision rules that employ additional potential useful tailoring variables at each intervention stage.

Here, we introduce Q-learning (Watkins, 1989)—a novel but straightforward methodology drawn from computer science that can be used for the construction of high-quality adaptive interventions from data. Our implementation of Q-learning will utilize a series of linear regressions to construct the sequence of decision rules (i.e., the sequence of adaptive intervention options) that maximizes a continuous outcome. Q-learning is used to assess the quality of the decision (i.e., the intervention option) at each critical decision stage (i.e., intervention stage), while appropriately controlling for effects of both past and subsequent adaptive decisions (i.e., adaptive intervention options).

We first provide a general framework for Q-learning with linear regression. Then, drawing on hypothetical examples from the area of goal-setting in organizational research (based on ideas from Erez, 1990 and Fried & Slowik, 2004), we illustrate how Q-learning can be employed to analyze data from four common types of SMART studies. We also compare Q-learning with other data analysis approaches that might be used in constructing adaptive interventions. Finally, we illustrate Q-learning using data from a SMART study aiming to develop an adaptive intervention for improving the school-based performance of children with attention deficit hyperactivity disorder (ADHD; Center for Children and Families, SUNY at Buffalo, William E. Pelham as PI).

Motivation for Q-learning

One way to develop a high-quality adaptive intervention is to use data to construct an optimal sequence of decision rules, namely an optimal sequence of adaptive or individualized intervention options. For example, assume an investigator is interested in finding the best way to set goal difficulty on a complex task in order to maximize employee performance. The investigator conducts a SMART study (see the companion paper Nahum-Shani et al., 2011 for more details concerning SMART designs) on N employee participants involving two critical goal-setting stages (i.e., intervention stages); at each stage there are two goal-setting options (i.e., two intervention options). At the first stage of the goal-setting process (e.g., the beginning of the year), employees were randomized with probability .5 to one of two goal-setting options. Let denote the randomized goal-setting options (i.e., the first-stage intervention options) at the first stage, coded -1 for a moderate goal (i.e., a goal with a moderate level of difficulty) and 1 for a difficult goal. At the second stage of the goal-setting process (e.g., the middle of the year), employees were re-randomized with probability .5 to one of two goal-setting options. Let A₂ denote the randomized goal-setting options at the second stage of the goal-setting process, coded -1 for a moderate goal and 1 for a difficult goal. Let Y denote the supervisor’s annual assessment of the employee’s performance at the end of the second stage, coded so that high values are preferred.

Assume the investigator considers the baseline self-efficacy of the employee (i.e., the employee’s judgment of his/her capability to accomplish a certain level of performance; Bandura, 1986) as a candidate tailoring variable for the first-stage goal. Denote the employee’s baseline self-efficacy by O₁. Assume the investigator also considers the attainment of the first-stage goal (i.e., whether or not the employee achieved the first-stage goal) as a candidate tailoring variable for the second-stage goal-setting options. Denote the attainment of the first-stage goal by O₂. Accordingly, the data record for each of the N employees is O₁,A₁,O₂,A₂,Y¹.

In general, O_t contains predictors of the primary outcome. O₁ can be a vector of baseline measures (e.g., baseline performance, personality and demographic characteristics), and O₂ can be a vector of intermediate outcomes measured prior to the second stage of the intervention (e.g., self-efficacy, affect, and goal commitment prior to the second stage of the goal-setting process). O₁ and O₂ might condition (moderate) the effects of the intervention options; additionally O₂ might be affected by A₁ and O₁ (e.g., the attainment of the first-stage goal might depend on whether the first-stage goal was moderate or difficult, as well as on the employee’s baseline level of self-efficacy).

Now consider using the data on the N employees to construct a sequence of decision rules, that is, a sequence of goal-setting options that adapt to the employee’s baseline self-efficacy, as well as to the attainment of the first-stage goal. A decision rule at the first stage is denoted by d₁, where the available information (employee’s baseline self-efficacy, denoted by O₁) is the input, and the goal-setting option at the first-stage (a₁) is the output. A decision rule at the second stage is denoted by d₂. In this decision rule, the input is the available information on the employee’s baseline self-efficacy, the first-stage goal-setting option, and the attainment of the first-stage goal (O₁,a₁,O₂), and the output is the second-stage goal-setting option (a₂).

Suppose we are interested in using the data described above to construct an optimal adaptive intervention. Here, the word optimal means that if these decision rules were used to assign goals to the entire study population, then this would lead to the maximal expected annual assessment of the employee’s performance. Denote the optimal adaptive intervention by the sequence of decision rules $(d_1^{\ast },d_2^{\ast })$. Q-learning is a method for using data to construct the decision rules $(d_1^{\ast },d_2^{\ast })$ that operationalize the optimal adaptive intervention. Q-learning uses backwards induction (Bellman & Dreyfus, 1962) to construct a sequence of decision rules that map or link the observations (here captured by the tailoring variables) to the actions the agent (decision maker) ought to take in order to maximize a primary outcome. In terms of constructing an adaptive intervention, Q-learning can be used to find the sequence of decision rules that link the observed information concerning an individual (e.g., characteristics and responses to past intervention options) to the most efficient intervention type and intensity/dosage. Q-learning allows us to contrast the intervention options at each stage controlling for effects of both past and subsequent adaptive intervention options. This enables investigators to contrast intervention options when used as part of a sequence, as opposed to contrasting intervention options as stand-alone options for each stage (see the companion paper Nahum-Shani et al., 2011 for more details). In the following section we show how Q-learning can be used to construct an optimal sequence of decision rules.

Q-Learning

To illustrate the intuition behind Q-learning, it is useful to first consider the case in which an expert² provides the multivariate distribution of O₁,O₂, and Y, for every sequence of decisions a₁,a₂. In this case, we construct the optimal sequence of decision rules using backwards induction as follows. We begin by finding the optimal decision rule at the second stage, namely $d_2^{\ast }(O_1,a_1,O_2)$.

$$d_2^{\ast }(O_1,a_1,O_2)=\underset{a_2}{\arg \max }{Q}_2(O_1,a_1,O_2,a_2),$$

where Q₂(O₁,a₁,O₂,a₂) = E[Y|O₁,a₁,O₂,a₂]. Accordingly, the optimal second-stage decision rule $d_2^{\ast }(O_1,a_1,O_2)$ is the second-stage intervention option a₂ for which Q₂(O₁,a₁,O₂,a₂) (i.e., the expected primary outcome, conditional on information available up to the second stage) attains its maximal value. The use of Q to denote the conditional expectation is a mnemonic to indicate that this expectation is used to assess the quality of the intervention option. Q₂ is the conditional expectation that provides the quality of choosing second-stage option a₂, given the information available (O₁,a₁,O₂).

Then, we move backwards in time to construct the optimal decision rule at the first stage, namely $d_1^{\ast }\left(O_1\right)$.

$$d_1^{\ast }\left(O_1\right)=\underset{a_1}{\arg \max }{Q}_1(O_1,a_1)$$

where Q₁(O₁,a₁) = E[max_az Q_Z(O₁,a₁,O₂,a₂)|O₁,a₁] is the conditional expectation that provides the quality of choosing first-stage intervention option a₁, controlling for the use of the best second-stage intervention option and given the information available (O₁). Accordingly, the optimal first-stage decision rule $d_1^{\ast }\left(O_1\right)$ equals the first-stage option a₁ for which Q₁(O₁,a₁) attains its maximal value (i.e., the first-stage intervention option that, given the information available up to the first stage, leads to the maximal expected mean outcome obtained by choosing the optimal second-stage intervention option). Q₁ and Q₂ are often called Q-functions (Sutton & Barto, 1998). Note that the optimal sequence of decision rules $(d_1^{\ast },d_2^{\ast })$ output the first-stage and second-stage intervention options that maximize Q₁,Q₂ respectively.

Here, we focus on using SMART study data to construct the optimal sequence of decision rules, because we do not know the true multivariate distribution of O₁,O₂ and Y. We represent the study data by {O_1i,A_1i,O_2i,A2_i,Y_i},i = 1,…,N, where N is the number of study participants. Throughout, for simplicity, we assume that participants are randomly assigned to one of two intervention options at each of the two intervention stages (e.g., A₁ and A₂ are randomized).

We estimate the Q-functions, from which we construct the optimal sequence of decision rules as described above, using Q-learning. In general Q-learning involves any one of a variety of regression techniques (linear regression, non-parametric regression, additive regression) and can be used with a variety of outcomes including longitudinal and/or binary, ordinal and continuous outcomes. For clarity we present Q-learning with linear regression and a continuous outcome Y. In this case, the second-stage Q-function might be modeled as

$$\begin{array}{cc}\hfill Q_2(O_1,A_1,& O_2,A_2;{\gamma }_2,{\alpha }_2)\hfill \\ \hfill & ={\gamma }_{20}+{\gamma }_{21}{O}_1+{\gamma }_{22}{A}_1+{\gamma }_{23}{O}_1{A}_1+{\gamma }_{24}{O}_2+({\alpha }_{21}+{\alpha }_{22}{A}_1+{\alpha }_{23}{O}_2)A_2,\hfill \end{array}$$ (1)

where, γ₂ = (γ₂₀,γ₂₁,γ₂₂,γ₂₃,γ₂₄), and α₂ = (α₂₁,α₂₂,α₂₃). Notice that our main interest lies primarily in the parameters α₂, because they contain information with respect to how the second-stage intervention (A₂) should vary as a function of the candidate tailoring variables (here A₁ and O₂). Based on Equation (1) one can see that the second-stage intervention option (a₂) that maximizes Q₂ is the one that maximizes the term (α₂₁ + α₂₂A₁ + α₂₃O₂)a₂. If (α₂₁ + α₂₂A₁ + α₂₃O₂) > 0, the term (α₂₁ + α₂₂A₁ + α₂₃O₂)a₂ attains its maximal value by a₂ = 1; if (α₂₁ + α₂₂A₁ + α₂₃O₂) < 0, the term (α₂₁ + α₂₂A₁ + α₂₃O₂)a₂ attains its maximal value by a₂ = −1. We estimate the vector parameters γ₂ and α₂ by the following regression:

$$Y\sim {\gamma }_{20}+{\gamma }_{21}{O}_1+{\gamma }_{22}{A}_1+{\gamma }_{23}{O}_1{A}_1+{\gamma }_{24}{O}_2+({\alpha }_{21}+{\alpha }_{22}{A}_1+{\alpha }_{23}{O}_2)A_2.$$

Next, we estimate the quality of the optimal second-stage option. This is

$${\tilde{Y}}_i=\underset{a_2}{\max }{Q}_2(O_{1i},A_{1i},O_{2i},a_2;{\widehat{\gamma }}_2,{\widehat{\alpha }}_2),i=1,\dots ,n.$$

Here, ${\tilde{Y}}_i$ reduces to

$${\tilde{Y}}_i={\widehat{\gamma }}_{20}+{\widehat{\gamma }}_{21}{O}_{1i}+{\widehat{\gamma }}_{22}{A}_{1i}+{\widehat{\gamma }}_{23}{O}_{1i}{A}_{1i}+{\widehat{\gamma }}_{24}{O}_{2i}+\mid {\widehat{\alpha }}_{21}+{\widehat{\alpha }}_{22}{A}_{1i}+{\widehat{\alpha }}_{23}{O}_{2i}\mid .$$ (2)

${\tilde{Y}}_i$ is the expected mean outcome obtained by choosing the optimal second-stage intervention option, given the information available (O₁,a₁,O₂).

We use a linear regression for the first stage Q-function as well:

$$Q_1(O_1,A_1,;{\gamma }_1,{\alpha }_1)={\gamma }_{10}+{\gamma }_{11}{O}_1+({\alpha }_{11}+{\alpha }_{12}{O}_1)A_1,$$ (3)

where, γ₁ = (γ₁₀,γ₁₁), and α = (α₁₁,α₁₂). Based on Equation (3), the first-stage option (a₁) that maximizes Q₁ is the value of a₁ that maximizes the term (α₁₁ + α₁₂O₁)a₁; that is, if (α₁₁ + α₁₂O₁) > 0, a₁ = 1 maximizes the term (α₁₁ + α₁₂O₁)a₁, and if (α¹¹ + α₁₂O₁) < 0, a₁ = −1 maximizes the term (α₁₁ + α₁₂O₁)a₁. We again use regression to estimate γ₁ and α₁ as follows:

$$\tilde{Y}\sim {\gamma }_{10}+{\gamma }_{11}{O}_1+({\alpha }_{11}+{\alpha }_{12}{O}_1)A_1.$$

Notice that this time we regress the estimated quality of the optimal second-stage option (i.e., the maximal expected primary outcome obtained by taking the best second-stage intervention options) on A₁,O₁, and A₁O₁.

In summary, the estimated optimal sequence of decision rules (i.e., the best adaptive first-stage and second-stage intervention options) is

$$\begin{array}{cc}\hfill {\widehat{d}}_2^{\ast }(O_1,A_1,O_2)=& \arg {\max }_{a_2}{Q}_2(O_1,A_1,O_2,a_2,{\widehat{\gamma }}_2,{\widehat{\alpha }}_2)=\text{sign}({\widehat{\alpha }}_{21}+{\widehat{\alpha }}_{22}{A}_1+{\widehat{\alpha }}_{23}{O}_2)\hfill \\ \hfill {\widehat{d}}_1^{\ast }\left(O_1\right)=& \arg {\max }_{a_1}{Q}_1(O_1,a_1;{\widehat{\gamma }}_1,{\widehat{\alpha }}_1)=\text{sign}({\widehat{\alpha }}_{11}+{\widehat{\alpha }}_{12}{O}_1),\hfill \end{array}$$

where ${\widehat{d}}_2^{\ast }(O_1,A_1,O_2)$ is the estimated best second-stage intervention option (a₂); that is, the second-stage intervention option that maximizes the mean of the primary outcome, given (O₁,A₁,O₂); ${\widehat{d}}_1^{\ast }\left(O_1\right)$ is the estimated best first-stage intervention option (a₁) that, given (O₁), maximizes the mean of the maximal expected primary outcome (i.e., the maximal expected primary outcome obtained by taking the best second-stage intervention option).

Under the assumption that the linear models for Q₁ and Q₂ are correct and the observations from one individual to another are independent, the estimators of the regression coefficients are consistent (unbiased in large samples) for the true regression coefficients³³. Also as is the case with all generalized linear models (e.g., logistic regression, ordinal regression, etc.), a crucial assumption is that the sample size is sufficiently large so that the distribution of the estimators for the regression coefficients can be well approximated by the normal distribution. Practically, the sample size must be larger if Y and/or any of the variables in O₂ have highly non-continuous, skewed, or heavy tailed distributions than if all of these variables have continuous symmetric distributions.

Consider the construction of confidence intervals and/or hypothesis testing concerning the regression coefficients in Q₂. Note that the second-stage linear regression for Q₂ is an ordinary linear regression. Hence, in large samples bootstrap can be used to estimate standard errors, form confidence intervals and conduct hypothesis tests.⁴ Inference for the estimators of the regression coefficients in Q₁ is less standard. To see this, consider Equation (2) and note that the formula for $\tilde{Y}$ (i.e., the dependent variable for the first-stage regression) contains an absolute value function. Because the absolute value function is non-differentiable at the point 0, the distribution of the estimators of the regression coefficients in Q₁ cannot be consistently approximated by standard methods such as the bootstrap. That is, in these cases, standard large-sample bootstrap-based tests and confidence intervals might perform poorly (Chakraborty, Murphy, & Strecher, 2010; Robins, 2004). To provide confidence intervals for the first-stage regression coefficients, methods that address the problem of non-differentiability are required. The software (provided at http://methodology.psu.edu/ra/adap-treat-strat) utilizes the Soft-thresholding with percentile bootstrap method in which Q-learning is applied to each bootstrap sample with one small adjustment to the formula for $\tilde{Y}$. More specifically, the term $\mid {\widehat{\alpha }}_{21}+{\widehat{\alpha }}_{22}{A}_1+{\widehat{\alpha }}_{23}{O}_{22}\mid$ is replaced by $\mid {\widehat{\alpha }}_{21}+{\widehat{\alpha }}_{22}{A}_1+{\widehat{\alpha }}_{23}{O}_{22}\mid {\left(1-\frac{\lambda }{\mid {\widehat{\alpha }}_{21}+{\widehat{\alpha }}_{22}{A}_1+{\widehat{\alpha }}_{23}{O}_{22}\mid }\right)}^{+}$, where λ is equal to $3{(1,A_1,O_{22})}^T{\widehat{\Sigma }}_2(1,A_1,O_{22})∕N$ and ${\widehat{\Sigma }}_2∕N$ is the estimated covariance matrix of ${\widehat{\alpha }}_2$. This adjustment tests whether $({\widehat{\alpha }}_{21}+{\widehat{\alpha }}_{22}{A}_1+{\widehat{\alpha }}_{23}{O}_{22})$ is close to zero and, if so, shrinks $\mid {\widehat{\alpha }}_{21}+{\widehat{\alpha }}_{22}{A}_1+{\widehat{\alpha }}_{23}{O}_{22}\mid$ to zero. Chakraborty et al. (2010) found that bootstrap intervals using this small adjustment achieve the desired confidence level across a wide variety of simulated settings.

Using Q-learning to Analyze Data from Four Different Types of SMART Studies

In the companion paper (Nahum-Shani et al., 2011) we describe four common SMART studies: (a) SMART designs that do not use intermediate outcomes as part of the experimental design (i.e., SMARTs with no embedded tailoring variables, as in Figure 2 of Nahum-Shani et al., 2011); (b) SMART designs in which whether or not to re-randomize depends on an intermediate outcome (as in Figure 1 of Nahum-Shani et al., 2011); (c) SMART designs in which participants are re-randomized to different second-stage intervention options depending on an intermediate outcome (as in Figure 3 of Nahum-Shani et al., 2011); and (d) SMART designs in which whether or not to re-randomize depends on an intermediate outcome and prior treatment (as in Figure 4 of Nahum-Shani et al., 2011). In the following, we illustrate the use of Q-learning with respect to data from each of these four types of SMART designs. In general, there are three main differences between the four designs in terms of the use of Q-learning. First, the regression models might differ. Second, the subsample of the SMART data used for estimating Q₂ might differ. Third, there might be differences in the construction of the estimated quality of the optimal second-stage intervention option $\tilde{Y}$. To clarify this, we use hypothetical examples from the area of goal-setting in organizational research.

SMARTs with no embedded tailoring variables

In these SMART designs all participants are re-randomized regardless of any observed information (e.g., intermediate outcomes such as response or adherence, or the intervention options offered in prior stages). Accordingly, assume an investigator obtained data from the goal-setting study described previously, in which at the first-stage (i.e., beginning of the year) and at the second stage (i.e., middle of the year) employees were randomly assigned (with .5 probability) to one of two goal-setting options (A₁/A₂= −1 for a moderate goal, A₁/A₂= 1 for a difficult goal). Recall that in addition the investigator obtained data on two candidate tailoring variables: self-efficacy at baseline (O₁) and goal-attainment (O₂). Assume self-efficacy is a continuous measure that the investigator has standardized (mean=0, STD=1). Also assume goal-attainment was measured in terms of whether (coded as 1) or not (coded as 0) the first-stage goal was achieved. The investigator is interested in using this data to obtain the optimal (i.e., in terms of the employee’s annual performance assessment) sequence of goal-setting options while assessing (a) whether and how to tailor the first-stage goal-setting options to the employee’s self-efficacy at baseline; and (b) whether and how to tailor the second-stage goal-setting options to the first-stage goal-setting option assigned to the employee, and to the employee’s attainment of the first-stage goal.

To apply Q-learning in this context, begin with the second stage of the goal-setting process, considering the first-stage goal-setting option (A₁) as well as goal-attainment (O₂), as candidate-tailoring variables for the second-stage goal-setting options. Here the model in Equation (1) can be used for Q₂; regress the primary outcome Y on the predictors to obtain the parameter estimates ${\widehat{\gamma }}_2,{\widehat{\alpha }}_2$. Based on the estimated regression coefficients, estimate the term $({\widehat{\alpha }}_{21}+{\widehat{\alpha }}_{22}{A}_1+{\widehat{\alpha }}_{23}{O}_2)$ for every given level of A₁ and O₂. If (α₂₁ + α₂₂A₁ + α₂₃O₂) > 0 the decision rule recommends assigning a difficult goal (A₂ = 1) at the second stage; if (α₂₁ + α₂₂A₁ + α₂₃O₂₂) < 0, the decision rule recommends assigning a moderate goal (A₂ = −1) at the second stage of the goal-setting process. For example, if (α₂₁ + α₂₂ + α₂₃) > 0, the decision rule recommends assigning a difficult goal at the second stage (A₂ = 1) to employees who achieved (O₂ = 1) a difficult goal (A₁ = 1) at the first stage of the goal-setting process; if (α₂₁ + α₂₂) < 0 the decision rule recommends assigning a moderate goal at the second stage (A₂ = −1) to employees who failed to achieve (O₂ = 0) a difficult goal (A₁ = 1) at the first stage of the goal-setting process.

Now move backwards in time to find the best first-stage goal-setting option (A₁) controlling for the best second-stage goal-setting option (i.e., assuming all participants were assigned to the best second-stage goal-setting option, given their first-stage goal-setting option and goal-attainment). Use Equation (2) to estimate the quality, $\tilde{Y}$, of the optimal second-stage goal-setting option. Then, model Q₁ by Equation (3) and regress $\tilde{Y}$ on the predictors to obtain ${\widehat{\gamma }}_1$ and ${\widehat{\alpha }}_1$. Based on these estimated regression coefficients, estimate the term $({\widehat{\alpha }}_{11}+{\widehat{\alpha }}_{12}{O}_1)$ for every value of O₁ that is of special interest (e.g., the mean and mean ± 1 STD). If (α₁₁ + α₁₂O₁) > 0, the decision rule recommends assigning a difficult goal (A₁ = 1) at the first stage of the goal-setting process; and if (α₁₁ + α₁₂O₁) < 0, the decision rule recommends assigning a moderate goal (A₁ = −1) at the first stage of the goal-setting process. For example, if (α₁₁ + α₁₂) > 0, the decision rule recommends assigning a difficult first-stage goal (A₁ = 1) to employees who reported relatively high levels of self-efficacy at baseline (i.e., when O₁ = 1, that is the level of self-efficacy is one standard deviation above the sample mean); if (α₁₁ − α₁₂) < 0, the decision rule recommends assigning a moderate first-stage goal (A₁ = −1) to employees who reported relatively low levels of self-efficacy at baseline (i.e., when O₁ = −1; that is, the level of self-efficacy is one standard deviation below the sample mean).

SMARTs in which whether to re-randomized or not depends on an intermediate outcome

In these SMART designs an observed intermediate outcome (usually response or adherence to prior intervention option) is used to determine whether or not a participant should be re-randomized. Accordingly, consider data obtained from a two-stage goal-setting SMART study in which at the first-stage (e.g., the beginning of the year) employees were randomized (with .5 probability) to one of two goal-setting options: to receive a moderate goal (A₁= −1), or to receive a difficult goal (A₁= 1). At the second stage (e.g., the middle of the year) only employees who did not achieve the first-stage goal were re-randomized (with .5 probability) to one of two goal-setting options: to reduce the difficulty of the first-stage goal (A₂= −1), or to maintain the level of difficulty of the first-stage goal (A₂=1). Employees who achieved the first-stage goal were not re-randomized and received another goal, similar in its level of difficulty to the first-stage goal. Notice that in this SMART design, goal-attainment is a tailoring variable that is embedded in the design. It is used to determine whether the employee should be re-randomized at the second stage of the goal-setting process.

Assume that the investigator also obtained data on two candidate tailoring variables (that are not embedded in the design): the employee’s self-efficacy at baseline (O₁); and the employee’s commitment to the first-stage goal, namely the employee’s unwillingness to abandon or change the initial goal (Donovan & Radosevich, 1998; O₂). Assume both measures are continuous. The investigator is interested in using this data to estimate the optimal (i.e., in terms of the employee’s annual performance evaluation) sequence of goal-setting options that adapt to the employee’s goal-attainment, while assessing (a) whether and how the first-stage goal-setting options should be tailored to the employee’s level of self-efficacy at baseline; and (b) for employees who failed to achieve the first-stage goal, whether and how to tailor the second-stage goal-setting options to the first-stage goal-setting option assigned to the employee and to the employee’s commitment to the first-stage goal.

To apply Q-learning in this context, begin with the second stage of the goal-setting process, aiming to find the best second-stage goal-setting option for employees who failed to achieve the first-stage goal. Accordingly, use Equation (1) to model Q₂ for employees who failed to achieve the first-stage goal and use only data from employees who failed to achieve the first-stage goal in the regression analysis for obtaining ${\widehat{\gamma }}_2$ and ${\widehat{\alpha }}_2$. Based on the estimated regression coefficients obtain $({\widehat{\alpha }}_{21}+{\widehat{\alpha }}_{22}{A}_1+{\widehat{\alpha }}_{23}{O}_2)$ for every given level of A₁ and levels of O₂ that are of special interest (e.g., mean, and mean ± 1SD). If (α₂₁ + α₂₂A₁ + α₂₃O₂) > 0, the decision rule recommends maintaining the level of goal difficulty (A₂ = 1) for employees who failed to achieve the first-stage goal; and if (α₂₁ + α₂₂A₁ + α₂₃O₂₂) < 0 the decision rule recommends reducing the level of difficulty (A₂ = −1) for employees who failed to achieve the first-stage goal.

Now, move backwards in time to find the best first-stage goal-setting option (A₁), controlling for the best second-stage goal-setting option for employees who fail to achieve the first-stage goal. Accordingly, use Equation (2) to estimate $\tilde{Y}$ (i.e., the quality of the optimal second-stage goal-setting option) for employees who failed to achieve the first-stage goal, and set $\tilde{Y}=Y$ for employees who achieved the first-stage goal (these employees were not re-randomized). Then, use Equation (3) to model Q₁ and regress $\tilde{Y}$ on the predictors to obtain ${\widehat{\gamma }}_1$ and ${\widehat{\alpha }}_1$. Based on these estimated regression coefficients, estimate the term $({\widehat{\alpha }}_{11}+{\widehat{\alpha }}_{12}{O}_1)$ for every value of O₁ that is of special interest (e.g., the mean and mean ± 1 SD). If (α₁₁ + α₁₂O₁) > 0, the decision rule recommends assigning a difficult goal (A₁ = 1) at the first stage of the goal-setting process; and if (α₁₁ + α₁₂O₁) < 0, the decision rule recommends assigning a moderate goal (A₁ = −1) at the first stage of the goal-setting process.

SMARTs in which re-randomization to different second-stage intervention options depends on an intermediate outcome

In these SMART designs, an observed intermediate outcome is used to determine to which set of intervention options a participant should be re-randomized. Accordingly, consider data obtained from a two-stage goal-setting SMART study in which at the first stage of the goal-setting process employees were randomized (with .5 probability) to one of two goal-setting options: to receive a moderate goal (A₁=−1), or to receive a difficult goal (A₁=1). At the second stage of the goal-setting process employees who achieved the first-stage goal were re-randomized (with .5 probability) to one of two second-stage goal-setting options: to maintain the difficulty of the first-stage goal (A₂= -1); or enhance the difficulty of the first-stage goal (A₂=1). Employees who failed to meet the first-stage goal were re-randomized (with .5 probability) to one of two goal-setting options: to reduce the difficulty of the first-stage goal (A₂= -1), or to maintain the difficulty of the first-stage goal (A₂=1). Notice that the two second-stage goal-setting options (A₂) are different depending on whether or not the first-stage goal was achieved.

Assume that the investigator also obtained data on three candidate tailoring variables: the employee’s self-efficacy at baseline (O₁); the quality of the strategies the employee used (see Chesney & Locke, 1991) to achieve the first-stage goal (O₂₁); and the employee’s commitment to the first-stage goal (O₂₂). The investigator is interested in using this data to estimate the optimal (in terms of the employee’s annual performance evaluation) sequence of goal-setting options that adapt to an employee’s attainment of the first-stage goal, while assessing (a) whether and how to tailor the first-stage goal-setting options to the employee’s level of self-efficacy at baseline; (b) for employees who achieved the first-stage goal, whether and how to tailor the second-stage goal-setting options to the first-stage goal-setting option and to the quality of strategies the employee used to achieve the first-stage goal; and (c) for employees who failed to achieve the first-stage goal, whether and how to tailor the second-stage goal-setting options to the first-stage goal-setting option, and to the employee’s commitment to the first-stage goal. Notice that the candidate tailoring variables considered for employees who achieved the first-stage goal (A₁,O₂₁) are different from the candidate tailoring variables considered for employees who failed to achieve the first-stage goal (A₁,O₂₂).

To apply Q-learning in this context, begin with the second stage of the goal-setting process, aiming to find the best second-stage goal-setting option for employees who failed to achieve the first-stage goal and the best second-stage goal-setting options for employees who achieved the first-stage goal. Accordingly, model Q₂ by

$$\begin{array}{cc}\hfill Q_2& (O_1,A_1,O_{21},O_{22},A_2;{\gamma }_2,{\alpha }_2)={\gamma }_{20}+{\gamma }_{21}{O}_1+{\gamma }_{22}{A}_1+{\gamma }_{23}{A}_1{O}_1+{\gamma }_{24}{O}_{21}+{\gamma }_{25}{O}_{22}+\hfill \\ \hfill & [{\alpha }_{21}R+{\alpha }_{22}(1-R)+{\alpha }_{23}{A}_{1}R+{\alpha }_{24}{A}_1(1-R)+{\alpha }_{25}{O}_{21}R+{\alpha }_{26}{O}_{22}(1-R\left)\right]A_2,\hfill \end{array}$$

where R indicates whether (R=1) or not (R=0) an employee achieved the first-stage goal⁵. That is, for employees who achieved the first-stage goal (R=1), Q₂ is modeled by

$$\begin{array}{cc}\hfill Q_2& (O_1,A_1,O_{21},O_{22},A_2;{\gamma }_2,{\alpha }_2)\hfill \\ \hfill & ={\gamma }_{20}+{\gamma }_{21}{O}_1+{\gamma }_{22}{A}_1+{\gamma }_{23}{A}_1{O}_1+{\gamma }_{24}{O}_{21}+{\gamma }_{25}{O}_{22}+({\alpha }_{21}+{\alpha }_{23}{A}_1+{\alpha }_{25}{O}_{21})A_2.\hfill \end{array}$$

and for employees who failed to achieve the first-stage goal (R=0) Q₂ is modeled by

$$\begin{array}{cc}\hfill Q_2& (O_1,A_1,O_{21},O_{22},A_2;{\gamma }_2,{\alpha }_2)\hfill \\ \hfill & ={\gamma }_{20}+{\gamma }_{21}{O}_1+{\gamma }_{22}{A}_1+{\gamma }_{23}{A}_1{O}_1+{\gamma }_{24}{O}_{21}+{\gamma }_{25}{O}_{22}+({\alpha }_{22}+{\alpha }_{24}{A}_1+{\alpha }_{26}{O}_{22})A_2.\hfill \end{array}$$

Accordingly, regress the primary outcome Y on the predictors to obtain ${\widehat{\gamma }}_2$ and ${\widehat{\alpha }}_2$. Then, use these estimated regression coefficients to obtain $({\widehat{\alpha }}_{21}+{\widehat{\alpha }}_{23}{A}_1+{\widehat{\alpha }}_{25}{O}_{21})$ and (α₂₂ + α₂₄A₁ + α₂₆O₂₂) for every given level of A₁ and every value of O₂₁ and O₂₂ of special interest (e.g., mean, and mean ± 1 SD). For employees who achieved the first-stage goal, the decision rule recommends enhancing the difficulty (A₂ = 1) of the goal if (α₂₁ + α₂₃A₁ + α₂₅O₂₁) > 0 and to maintain the level of goal difficulty (A₂ = −1) if (α₂₁ + α₂₃A₁ + α₂₅O₂₁) < 0. For employees who failed to achieve the first-stage goal, the decision rule recommends maintaining the level of goal difficulty ( (A₂ = 1) if (α₂₂ + α₂₄A₁ + α₂₆O₂₂) > 0 and reducing the level of goal difficulty (A₂= −1) if (α₂₂ + α₂₄A₁ + α₂₆O₂₂) < 0.

Now, move backwards in time to find the best first-stage goal-setting option (A₁), controlling for the best second-stage goal-setting option for employees who achieve the first-stage goal and for employee who fail to achieve the first-stage goal. Accordingly, use $\tilde{Y}={\widehat{\gamma }}_{20}+{\widehat{\gamma }}_{21}{O}_1+{\widehat{\gamma }}_{22}{A}_1+{\widehat{\gamma }}_{23}{A}_1{O}_1+{\widehat{\gamma }}_{24}{O}_{21}+\mid {\widehat{\alpha }}_{21}+{\widehat{\alpha }}_{23}{A}_1+{\widehat{\alpha }}_{25}{O}_{21}\mid$ to estimate the quality of the optimal second-stage goal-setting option for employees who achieved the first-stage goal, and $\tilde{Y}={\widehat{\gamma }}_{20}+{\widehat{\gamma }}_{21}{O}_1+{\widehat{\gamma }}_{22}{A}_1+{\widehat{\gamma }}_{23}{A}_1{O}_1+{\widehat{\gamma }}_{25}{O}_{22}+\mid {\widehat{\alpha }}_{22}+{\widehat{\alpha }}_{24}{A}_1+{\widehat{\alpha }}_{26}{O}_{22}\mid$ to estimate the quality of the optimal second-stage goal-setting option for employees who failed to achieve the first-stage goal. Then, use Equation (3) to model Q₁ and regress $\tilde{Y}$ on the predictors to obtain ${\widehat{\gamma }}_1$ and ${\widehat{\alpha }}_1$. Based on these estimated regression coefficients, estimate the term $({\widehat{\alpha }}_{11}+{\widehat{\alpha }}_{12}{O}_1)$ for every value of O₁ that is of special interest (e.g., the mean and mean ± 1 STD). If (α₁₁ + α₁₂O₁) > 0, the decision rule recommends assigning a difficult goal (A₁ = 1) at the first stage of the goal-setting process; and if (α₁₁ + α₁₂O₁) < 0, the decision rule recommends assigning a moderate goal (A₁ = −1) at the first stage of the goal-setting process.

SMARTs in which whether to re-randomize or not depends on an intermediate outcome and prior treatment

In these SMART designs an intermediate outcome as well as the prior intervention option are used to determine whether or not a participant should be re-randomized. Accordingly, consider data obtained from a two-stage goal-setting SMART study in which at the first stage of the goal-setting process (i.e., beginning of the year) employees were randomized (with .5 probability) to one of two goal-setting options: to receive a moderate goal (A₁=−1), or to receive a difficult goal (A₁=1). At the second stage of the goal-setting process (e.g., middle of the year) only employees who failed to achieve a difficult goal at the first-stage were re-randomized (with .5 probability) to two options: to maintain the difficulty of the first-stage goal (A₂= −1), or to reduce the difficulty of the first-stage goal (A₂=1). Employees who achieved a difficult first-stage goal or employees who received a moderate first-stage goal were not re-randomized. More specifically, employees who achieved a difficult first-stage goal received another difficult goal. Employees who received a moderate first-stage goal received another moderate goal if they failed to achieve the first-stage goal, or a difficult goal if they achieved the first-stage goal.

Assume that in addition the investigator obtained information on two candidate tailoring variables: the employee’s self-efficacy at baseline (O₁); and the employee’s commitment to the first-stage goal (O₂). Assume the investigator is interested in using this data to estimate the optimal (i.e., in terms of the employee’s annual performance evaluation) sequence of goal-setting options that adapt to an employee’s attainment of the first-stage goal, while assessing (a) whether and how to tailor the first-stage goal-setting options to the employee’s level of self-efficacy at baseline; and (b) for employees who failed to achieve a difficult first-stage goal, whether and how to tailor the second-stage goal-setting options to the employee’s goal commitment.

To apply Q-learning in this context, begin with the second stage of the goal-setting process, aiming to find the best second-stage goal-setting option for employees who failed to achieve a difficult first-stage goal. Accordingly, model Q₂ for employees who failed to achieve a difficult first-stage goal by

$$Q_2(O_1,O_2,A_2;{\gamma }_2,{\alpha }_2)={\gamma }_{20}+{\gamma }_{21}{O}_1+{\gamma }_{22}{O}_2+({\alpha }_{21}+{\alpha }_{22}{O}_2)A_2,$$

and use only data from employees who failed to achieve a difficult first-stage goal in the regression analysis for obtaining ${\widehat{\gamma }}_2$ and ${\widehat{\alpha }}_2$. Then, use these estimated regression coefficients to obtain $({\widehat{\alpha }}_{21}+{\widehat{\alpha }}_{22}{O}_2)$ for every value of O₂ that is of special interest (e.g., mean, and mean ± 1 SD). The decision rule recommends maintaining the same goal (A₂ = 1) for employees who failed to achieve a difficult first-stage goal if (α₂₁ + α₂₂O₂) > 0 and to reduce the difficulty of the first-stage goal (A₂= −1) if (α₂₁ + α₂₂O₂) < 0.

Now, move backwards in time to find the best first-stage goal-setting option (A₁), controlling for the best second-stage goal-setting option for employees who fail to achieve a difficult first-stage goal. Accordingly, use $\tilde{Y}={\widehat{\gamma }}_{20}+{\widehat{\gamma }}_{21}{O}_1+{\widehat{\gamma }}_{22}{O}_2+\mid {\widehat{\alpha }}_{21}+{\widehat{\alpha }}_{22}{O}_2\mid$ to estimate the quality of the optimal second-stage goal-setting option for employees who failed to achieve a difficult first-stage goal. Set $\tilde{Y}=Y$ for employees who were not re-randomized (i.e., those who achieved a difficult first-stage goal or received a moderate goal at the first-stage). Then, use Equation (3) to model Q₁ and regress $\tilde{Y}$ on the predictors to obtain ${\widehat{\gamma }}_1$ and ${\widehat{\alpha }}_1$. Based on these estimated regression coefficients, estimate the term $({\widehat{\alpha }}_{11}+{\widehat{\alpha }}_{12}{O}_1)$ for every value of O₁ that is of special interest (e.g., mean, and mean ± 1SD). If $({\widehat{\alpha }}_{11}+{\widehat{\alpha }}_{12}{O}_1)>0$, the decision rule recommends assigning a difficult goal (A₁ = 1) at the first stage of the goal-setting process; and if $({\widehat{\alpha }}_{11}+{\widehat{\alpha }}_{12}{O}_1)<0$, the decision rule recommends assigning a moderate goal (A₁ = −1) at the first stage of the goal-setting process.

Alternatives to Q-learning

A natural alternative to Q-learning is a single regression approach. More specifically, one might want to construct $(d_1^{\ast },d_2^{\ast })$ using a single regression that includes the first-stage options, the second-stage options and the candidate tailoring variables. Consider, for example, the goal-setting SMART study with no embedded tailoring variables described above. The single regression equation might be

$$Y\sim {\theta }_0+{\theta }_1{O}_1+{\theta }_2{A}_1+{\theta }_3{O}_1{A}_1+{\theta }_4{O}_2+{\theta }_5{A}_2+{\theta }_6{A}_1{A}_2+{\theta }_7{A}_2{O}_2.$$ (4)

However, using estimates based on this equation to construct the optimal sequence of decision rules $(d_1^{\ast },d_2^{\ast })$ is problematic in two main aspects. First, because O₂ (e.g., goal-attainment) might be an outcome of A₁ and a potential predictor of Y, O₂ cuts off any portion of the effect of A₁ on Y that occurs via O₂. To clarify this, O₂ can be conceptualized as a mediator in the relationship between A₁ and Y (e.g., the effect of the first-stage goal-setting options on annual performance assessment can be transmitted through the attainment of the first-stage goal). Adding O₂ to a regression in which A₁ is used to predict Y will reduce the effect of A₁. In the presence of O₂, the coefficient for A₁ no longer expresses the total effect of the first-stage goal-setting options on the outcome, but rather what is left of the total effect (the direct effect) after cutting off the part of the effect that is mediated by A₁ (the indirect effect; Baron & Kenny, 1986; MacKinnon, Warsi, & Dwyer, 1995). Note that ascertaining the total effect of the intervention options (e.g., the goal-setting options) at a given stage (say, A₁) is crucial to finding the best decision rule (e.g., $d_1^{\ast }$), because it provides information concerning the overall effect of the these intervention options. Although the direct effect of the intervention options at a given stage might be helpful in identifying mechanisms or processes through which these intervention options might affect the outcome, it is not as helpful in deciding which intervention option is superior. Accordingly, any inference concerning the optimal intervention option at the first stage based on Equation (4) is likely to be misleading.

Second, even if O₂ is not a mediator, the coefficients of the A₁ terms (main effects and interactions) in Equation (4) can be impacted by unknown causes of both O₂ and Y so that A₁ might appear to be falsely less or more correlated with Y. This bias occurs when A₁ affects O₂ while O₂ and Y are affected by the same unknown causes (see Figure 1).

Figure 1.

Illustration of unmeasured confounders affecting O₂ and Y.

In order to demonstrate the way in which Q-learning reduces the bias resulting from unmeasured causes, consider again the goal-setting SMART trial with no embedded tailoring variables described above. For simplicity, assume there are no baseline variables O₁. Also assume U~N(0,1) is an unmeasured cause (say a personality characteristic) that has an effect on the annual performance assessment (Y) and the attainment of the first-stage goal (O₂). More specifically, suppose Y = 1 + 0.5U + ε_Y, and O₂ = 1 + 0.5U + 0.5A₁ + ε₀. For both models the error terms (ε’s) are independent and standard normally distributed. Notice that in this example, O₂ does not mediate the relationship between A₁ and Y; A₁ affects O₂, but neither A₁ nor A₂ affect Y. We generated 1,000 samples (N=500 each) using the above example. On each data set we used the single-regression approach and Q-learning. The single-regression model is

$$Y\sim {\theta }_0+{\theta }_1{A}_1+{\theta }_2{O}_2+{\theta }_3{A}_2+{\theta }_4{A}_1{A}_2.$$ (5)

A natural approach to using Equation (5)⁶ to construct the optimal sequence of decision rules is as follows: we construct the optimal decision rule at the second stage by finding the value of A₂ that maximizes Equation (5) (i.e., that maximizes the term $[{\widehat{\theta }}_3+{\widehat{\theta }}_4{A}_1]A_2)$. That is, ${\widehat{d}}_2^{\ast }\left(A_1\right)=\text{sign}({\widehat{\theta }}_3+{\widehat{\theta }}_4{A}_1)$. Replacing A₂ by $\text{sign}({\widehat{\theta }}_3+{\widehat{\theta }}_4{A}_1)$, the estimated maximal expected outcome is

$${\widehat{\theta }}_0+{\widehat{\theta }}_1{A}_1+{\widehat{\theta }}_2{O}_2+\mid {\widehat{\theta }}_3+{\widehat{\theta }}_4{A}_1\mid .$$ (6)

Now, we rewrite the maximal expected outcome in Equation (6) as

$$\begin{array}{cc}\hfill & {\widehat{\theta }}_0+{\widehat{\theta }}_1{A}_1+{\widehat{\theta }}_2{O}_2+\mid {\widehat{\theta }}_3+{\widehat{\theta }}_4{A}_1\mid ={\widehat{\theta }}_0+{\widehat{\theta }}_1{A}_1+{\widehat{\theta }}_2{O}_2+\frac{A_1+1}{2}\mid {\widehat{\theta }}_3+{\widehat{\theta }}_4\mid +\frac{1-A_1}{2}\mid {\widehat{\theta }}_3-{\widehat{\theta }}_4\mid \hfill \\ \hfill & ={\widehat{\theta }}_0+{\widehat{\theta }}_2{O}_2+\frac{1}{2}(\mid {\widehat{\theta }}_3+{\widehat{\theta }}_4\mid +\mid {\widehat{\theta }}_3-{\widehat{\theta }}_4\mid )+\left[{\widehat{\theta }}_1+\frac{1}{2}(\mid {\widehat{\theta }}_3+{\widehat{\theta }}_4\mid -\mid {\widehat{\theta }}_3-{\widehat{\theta }}_4\mid )\right]A_1.\hfill \end{array}$$

Next, we find the value of A₁=1 that maximizes the above. Accordingly, if $\left[{\widehat{\theta }}_1+\frac{1}{2}(\mid {\widehat{\theta }}_3+{\widehat{\theta }}_4\mid -\mid {\widehat{\theta }}_3-{\widehat{\theta }}_4\mid )\right]>0$, we can conclude that A₁=1 (a difficult goal) is the best first-stage goal-setting option, given that we are going to choose the best second-stage goal-setting option. If $\left[{\widehat{\theta }}_1+\frac{1}{2}(\mid {\widehat{\theta }}_3+{\widehat{\theta }}_4\mid -\mid {\widehat{\theta }}_3-{\widehat{\theta }}_4\mid )\right]<0$ we conclude that A₁= −1 (a moderate goal) is the best first-stage goal-setting option, given that we are going to choose the best second-stage goal-setting option.

On the other hand, consider Q-learning. In analogy to Equation (5) we use the models

$$\begin{array}{cc}\hfill Q_2(A_1,O_2,A_2;{\gamma }_2,& {\alpha }_2)={\gamma }_{20}+{\gamma }_{21}{A}_1+{\gamma }_{22}{O}_2+{\alpha }_{21}{A}_2+{\alpha }_{22}{A}_1{A}_2\hfill \\ \hfill & \text{and}{Q}_1(A_1;{\gamma }_1,{\alpha }_1)={\gamma }_{10}+{\alpha }_{11}{A}_1.\hfill \end{array}$$

Applying the Q-learning algorithm, we obtain estimates of the parameters $({\widehat{\gamma }}_j,{\widehat{\alpha }}_j),j=1,2$. We estimate the best second-stage intervention options by choosing $A_2=\text{sign}({\widehat{\alpha }}_{21}+{\widehat{\alpha }}_{22}{A}_1)$, and the best first-stage intervention option by choosing $A_1=\text{sign}\left({\widehat{\alpha }}_{11}\right)$. Using this approach ${\widehat{\alpha }}_{11}$ is the estimated effect of the first-stage goal-setting options, given that we are going to choose the best second-stage goal-setting option.

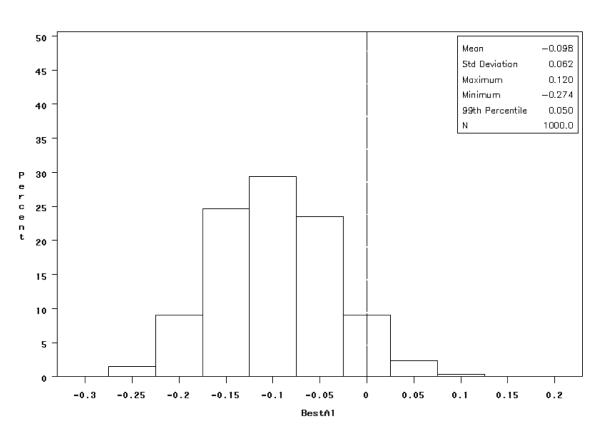
In conclusion, we know that the sign of $\left[{\widehat{\theta }}_1+\frac{1}{2}(\mid {\widehat{\theta }}_3+{\widehat{\theta }}_4\mid -\mid {\widehat{\theta }}_3-{\widehat{\theta }}_4\mid )\right]$ determines which first-stage goal-setting option is selected as best in the single-stage regression approach, whereas the sign of ${\widehat{\alpha }}_{11}$ determines which first-stage goal-setting option is selected as best in Q-Learning. We compare the distribution of these two quantities across the 1000 generated samples. Recall that in our example the first-stage goal-setting options have no effect (i.e., the effect of A₁ equals zero); thus both distributions should be centered at zero. Figure 2 presents the distribution of $\left[{\widehat{\theta }}_1+\frac{1}{2}(\mid {\widehat{\theta }}_3+{\widehat{\theta }}_4\mid -\mid {\widehat{\theta }}_3-{\widehat{\theta }}_4\mid )\right]$ and Figure 3 presents the distribution of ${\widehat{\alpha }}_{11}$. It is easy to see that the distribution of the Q-learning-based estimate is centered around zero (SD = .06), while the distribution of the single-regression-based estimate has a mean of −.10 (SD = .06). Thus, if there are unobserved causes of both O₂ and Y, the single-regression approach in Equation (6) might lead to erroneous conclusions concerning the best sequence of decision rules. In contrast, the Q-learning method provides unbiased estimators of the parameters needed to construct the optimal sequence of decision rules.

Figure 2.

Distribution of estimated coefficient $\left[{\widehat{\theta }}_1+\frac{1}{2}(\mid {\widehat{\theta }}_3+{\widehat{\theta }}_4\mid -\mid {\widehat{\theta }}_3-{\widehat{\theta }}_4\mid )\right].$.

Figure 3.

Distribution of estimated coefficient of $\left({\widehat{\alpha }}_{11}\right)$.

Data Example: Adaptive Interventions for Children with ADHD

Attention-Deficit Hyperactivity Disorder (ADHD) is a chronic disorder affecting 5-10% of school age children. It adversely impacts functioning at home, at school and in social settings (Pliszka 2007). The limited success of pharmacological and behavioral interventions in the treatment of childhood ADHD has led to the now-common clinical practice of combining these two modalities (see Pelham et al., 2000). While the literature clearly supports the efficacy of this combined approach to treatment, little is known about the optimal way to sequence pharmacological and behavioral interventions (Pelham & Fabiano, 2008; Pelham & Gnagy, 1999). Accordingly, a SMART study was conducted (William E. Pelham, PI) with the general aim to find the optimal sequence of intervention options to reduce ADHD symptoms and improve school performance among children.

Design and Research Questions

Recall that the observable SMART study data for one participant is denoted by {O₁,A₁,O₂,A₂,Y}. In the first stage of the ADHD SMART study (at the beginning of a school year) children were randomly assigned (with probability .5) to a low dose of medication (A₁ coded as −1) or a low-intensity behavioral intervention (A₁ coded as 1). Beginning at the eighth week, each child’s response to the first-stage intervention was evaluated monthly until the end of that school year. Monthly ratings from the Impairment Rating Scale (IRS; Fabiano et al., 2006; available from http://wings.buffalo.edu/adhd), and an individualized list of target behaviors (ITB) (e.g., Pelham et al., 2002; Pelham, Evans, Gnagy, & Greenslade, 1992) were used to evaluate response. At each monthly assessment, children whose average performance on the ITB was less than 75% and who were rated by teachers as impaired on IRS in at least one domain were designated as inadequate responders to the first stage of the intervention. If the child was classified as a responder, then he/she remained in the first stage of the intervention and continued the assigned first-stage intervention option. If the child was classified as an inadequate responder, he/she entered the second stage of the intervention. These children were re-randomized (with probability .5) to one of two second-stage intervention options, either to increasing the dose/intensity of the first-stage intervention option (A₂ coded as −1) or to augmenting the first-stage intervention option with the other type of intervention (i.e., adding behavioral intervention for those who started with medication, or adding medication for those who started with behavioral intervention; A₂ coded as 1). Note that there are only two key decisions in this trial: the first-stage intervention decision (A₁), and then the second-stage intervention decision (A₂) for those not responding satisfactorily to the first stage of the intervention. The structure of this study is illustrated in Figure 4.

Figure 4.

Sequential Multiple Assignment Randomized Trial for ADHD study.

By design, the only embedded tailoring variable in the ADHD study is whether or not the child responded to the first stage of the intervention. However, it is interesting to assess whether the data can be used to construct a more deeply tailored adaptive intervention. For example, the investigators might be interested in assessing whether and how (a) the first stage of the intervention should be tailored according to whether or not the child received medication prior to the first stage of the intervention; (b) the second stage of the intervention should be tailored according to the child’s level of adherence to the first stage of the intervention; and (c) the second stage of the intervention should be tailored according to the intervention option offered at the first stage. Q-learning can be used to estimate the best sequence of decision rules while evaluating these three candidate tailoring variables.

Sample

149 children (75% boys) between the ages of 5-12 (mean 8.6 years) participated in the study. Due to drop-out and missing data⁷, the effective sample used in the current analysis was 138. At the first stage of the intervention, 70 children were randomized to low dose of medication, and 68 were randomized to low dose of behavioral intervention. By the end of the school year, 81 children had met the criteria for non-response at one of the monthly evaluations and had been re-randomized to one of the two second-stage intervention options (40 non-responding children were assigned to increasing the dose of the first-stage intervention, and 41 non-responding children were assigned to augmenting the first-stage intervention with the other type of intervention).

Measures

Primary Outcome (Y)

The level of children’s classroom performance based on the Impairment Rating Scale (IRS) after an 8-month period is our primary outcome. This outcome ranges from 1 to 5, with higher values reflecting better classroom performance.

Medication Prior to First-Stage Intervention (O₁₁)

This measure reflects whether the child did (coded as 1) or did not (coded as 0) receive medication at school during the previous school year (i.e., prior to the first stage of the intervention).

Baseline measures

(a) ADHD symptoms at the end of the previous school year, reflecting the mean of teacher’s evaluation on 14 ADHD symptoms (the Disruptive Behavior Disorders Rating Scale; Pelham et al., 1992), ranging from 0 to 3 and inverse coded so that larger values reflect fewer symptoms (i.e., better classroom performance; labeled O₁₂); (b) oppositional defiant disorder (ODD) diagnosis indicator, reflecting whether the child was (coded as 1) or was not (coded as 0) diagnosed with ODD before the first-stage intervention (labeled O₁₃).

Month of non-response (O₂₁)

The month during the school year at which the child showed inadequate response to the first stage of the intervention, and hence entered the second stage of the intervention. This measure is relevant only for those who showed inadequate response during the school year (i.e., classified as non-responders to the first stage of the intervention).

Adherence to first-stage intervention (O₂₂)

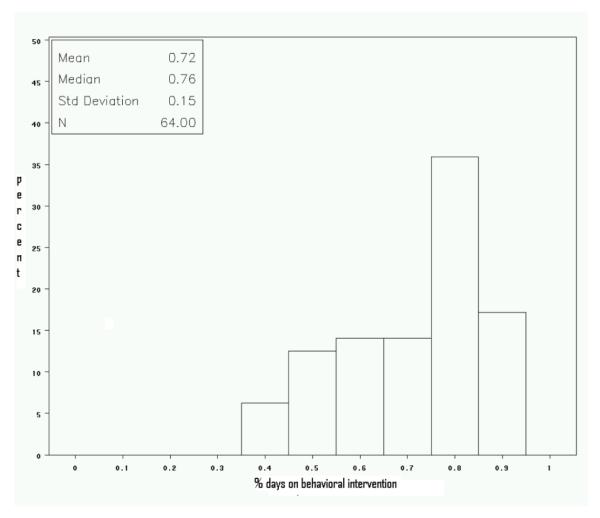
This measure reflects whether adherence to the first-stage intervention was high (coded as 1) or low (coded as 0). We constructed this indicator based on two other measures that express (a) the percentage of days the child received medication during the school year calculated based on pill counts (for those assigned to low-dose medication at the first stage of the intervention), and (b) the percentage of days the child received the behavioral intervention during the school year based on the teacher’s report of behavioral interventions used in the classroom (for those assigned to behavioral intervention at the first stage of the intervention). The distributions of these two measures are presented in Figures 5 and 6. Based on these distributions, we constructed O₂₂, such that for those assigned to behavioral intervention at the first stage of the intervention, low adherence (O₂₂ =0) means receiving less than 75% days of behavioral intervention, and for those assigned to medication at the first stage of the intervention, low adherence (O₂₂=0) reflects receiving less than 100% days of medication⁸.

Figure 5.

Distribution for % days on behavioral intervention for those assigned to low-intensity behavioral intervention at the first stage of the intervention.

Figure 6.

Distribution for % days on medication for those assigned to low dose of medication at the first stage of the intervention.

Data Analysis Procedure

Using the Q-learning approach, the optimal sequence of decision rules can be estimated based on two regressions, one for each intervention stage. We start from the second stage, aiming to find the best second-stage intervention option for non-responding children, given the information we have up to the second stage (O₁₁,O₁₂,O₁₃,A₁,O₂₁,O₂₂). Because children were classified as non-responders at different time points along the school year, we included the month of non-response (O₂₁) in this regression. We also included the two baseline measures (O₁₂,O₁₃) in the regression in order to reduce error variance. We consider the first-stage intervention (A₁) as well as the level of adherence to the first-stage intervention (O₂₂), as candidate tailoring variables for the second stage of the intervention. Q₂ for non-responders is modeled by

$$\begin{array}{cc}\hfill Q_2(O_{11},O_{12},& O_{13},A_1,O_{21},O_{22},A_2;{\gamma }_2,{\alpha }_2)\hfill \\ \hfill ={\gamma }_{20}+{\gamma }_{21}{O}_{11}& +{\gamma }_{22}{O}_{12}+{\gamma }_{23}{O}_{13}+{\gamma }_{24}{A}_1+{\gamma }_{25}{A}_1{O}_{11}+{\gamma }_{26}{O}_{21}+{\gamma }_{27}{O}_{22}\hfill \\ \hfill & +({\alpha }_{21}+{\alpha }_{22}{A}_1+{\alpha }_{23}{O}_{22})A_2.\hfill \end{array}$$ (7)

In general, this regression might include further baseline variables or other potential tailoring variables such as negative/ineffective parenting styles and medication side effects. We obtained ${\widehat{\gamma }}_2,{\widehat{\alpha }}_2$ by using regression on the data from the children who did not respond in the first stage. In this simple case, the decision rule recommends augmenting the first-stage intervention option with the alternative type of intervention (A₂ = 1) for a child who does not respond to the first stage of the intervention if (α₂₁ + α₂₂A₁ + α₂₃O₂₂) > 0 and increasing the dose of the first-stage intervention option (A₂ = −1) if (α₂₁ + α₂₂A₁ + α₂₃O₂₂) < 0. We used the GLM procedure in SAS to obtain estimated coefficients based on Equation (7). To obtain $({\widehat{\alpha }}_{21}+{\widehat{\alpha }}_{22}{A}_1+{\widehat{\alpha }}_{23}{O}_{22})$ for every combination of A₁ and O₂₂, we used the Estimate statement in GLM (this statement enables the researcher to estimate linear combinations of the regression parameters and their standard errors). More specifically, for A₁ = 1 and O₂=0, we obtained $({\widehat{\alpha }}_{21}+{\widehat{\alpha }}_{22})$; for A₁ = −1 and O₂₂=0, we obtained $(-{\widehat{\alpha }}_{21}+{\widehat{\alpha }}_{22})$; for A₁ = 1 and O₂₂=1, we obtained $({\widehat{\alpha }}_{21}+{\widehat{\alpha }}_{22}+{\widehat{\alpha }}_{23})$; and for A₁ = −1 and O₂₂=1, we obtained $(-{\widehat{\alpha }}_{21}+{\widehat{\alpha }}_{22}+{\widehat{\alpha }}_{23})$. The standard test statistic (t-test) provided by the GLM procedure was used to assess whether each of these estimates significantly differ from zero. Additionally, because A₂ can obtain −1/1 values, we estimated the difference between the two second-stage intervention options conditional on A₁ and O₂₂ (e.g., the estimated simple effect of A₂) by $({\widehat{\alpha }}_{21}+{\widehat{\alpha }}_{22}{A}_1+{\widehat{\alpha }}_{23}{O}_{22})-(-{\widehat{\alpha }}_{21}-{\widehat{\alpha }}_{22}{A}_1-{\widehat{\alpha }}_{23}{O}_{22})=2({\widehat{\alpha }}_{21}+{\widehat{\alpha }}_{22}{A}_1+{\widehat{\alpha }}_{23}{O}_{22}).$.

Now we move backwards in time, aiming to find the best first-stage intervention option (A₁) controlling for the best second-stage intervention option. Based on Equation (7) the estimated quality of the optimal second-stage intervention option for non-responders is

$$\tilde{Y}={\widehat{\gamma }}_{20}+{\widehat{\gamma }}_{21}{O}_{11}+{\widehat{\gamma }}_{22}{O}_{12}+{\widehat{\gamma }}_{23}{O}_{13}+{\widehat{\gamma }}_{24}{A}_1+{\widehat{\gamma }}_{25}{A}_1{O}_{11}+{\widehat{\gamma }}_{26}{O}_{21}+{\widehat{\gamma }}_{27}{O}_{22}+\mid {\widehat{\alpha }}_{21}+{\widehat{\alpha }}_{22}{A}_1+{\widehat{\alpha }}_{23}{O}_{22}\mid .$$

Because responders remain on their first-stage intervention option, we set $\tilde{Y}=Y$ for responders. Q₁ is modeled by

$$Q_1(O_{11},O_{12},O_{13},A_1;{\gamma }_1,{\alpha }_1)={\gamma }_{10}+{\gamma }_{11}{O}_{11}+{\gamma }_{12}{O}_{12}+{\gamma }_{13}{O}_{13}+({\alpha }_{11}+{\alpha }_{12}{O}_{11})A_1$$

Again we used the SAS GLM procedure to regress $\tilde{Y}$ on the predictors and obtain ${\widehat{\gamma }}_1$ and ${\widehat{\alpha }}_1$. We used the Estimate statement in GLM to obtain $({\widehat{\alpha }}_{11}+{\widehat{\alpha }}_{12}{O}_{11})$ for every level of O₁₁. If (α₁₁ + α₁₂O₁₁) > 0, the best first-stage intervention option would be low-intensity behavioral intervention (A₁ = 1). If (α₁₁ + α₁₂O₁₁) < 0, the best first-stage intervention option would be low dose of medication (A₁ = −1). Additionally, because A₁ can obtain −1/1 values, the estimated difference between the two first-stage intervention options conditional on O₁₁ (e.g., the estimated simple effect of A₁) is $({\widehat{\alpha }}_{11}+{\widehat{\alpha }}_{12}{O}_{11})-(-{\widehat{\alpha }}_{11}-{\widehat{\alpha }}_{12}{O}_{11})=2({\widehat{\alpha }}_{11}+{\widehat{\alpha }}_{12}{O}_{11}).$. We used the soft-thresholding method (Chakraborty et al., 2009) to provide confidence intervals for the first-stage regression coefficients.

Results

Table 1 presents the results for the second-stage regression. Based on these estimates, we estimated the formula $({\widehat{\alpha }}_{21}+{\widehat{\alpha }}_{22}{A}_1+{\widehat{\alpha }}_{23}{O}_{22})$ for every given combination of A₁ and O₂₂ (see Table 2).

Table 1.

Estimated Coefficients for Q₂ (N=81).

Effect	Estimate	SE	Lower limit 95% CI	Upper limit 95% CI
Intercept	1.36	0.53
O11 (medication prior to first-stage intervention)	−10.27	0.31
O12 (baseline: ADHD symptoms)	0.94	0.26
O13 (baseline: ODD diagnosis)	0.93	0.28
O21 (month of non-response)	0.02	0.10
O22 (adherence to first-stage intervention)	0.18	0.27
A1 (first-stage intervention options)	0.03	0.14
A2 (second-stage intervention options)	−0.72	0.22	−1.15	−0.29
O22*A2 (adherence to first-stage intervention*second-stage intervention options)	0.97	0.28	0.41	1.53
A1*A2 (first-stage intervention options*second-stage intervention options)	0.05	0.13	−0.22	0.32

Table 2.

Estimates of $({\widehat{\alpha }}_{21}+{\widehat{\alpha }}_{22}{A}_1+{\widehat{\alpha }}_{23}{O}_{22})$ for every combination of A₁ and O₂₂ (N=81)

A1	O22	Estimated $({\widehat{\alpha }}_{21}+{\widehat{\alpha }}_{22}{A}_1+{\widehat{\alpha }}_{23}{O}_{22})$	SE	Lower limit 95% CI	Upper limit 95% CI
−1 (medication)	1 (high adherence)	0.20	0.23	−0.26	0.67
−1 (medication)	0 (low adherence)	−0.77	0.27	−1.30	−0.23
1 (behavioral intervention)	1 (high adherence)	0.30	0.22	−0.13	0.74
1 (behavioral intervention)	0 (low adherence)	−0.67	0.24	−1.14	−0.19

The results in Table 1 show that the effect of the second-stage intervention options (A₂) is negative and statistically significant ${\widehat{\alpha }}_{21}{=}_{{-}_{.}}72$, lower limit 95% CI= −1.15, upper limit 95% CI= −.29). Although the interaction between the first-stage intervention options (A₁) and the second-stage intervention options (A₂) is not statistically significant (${\widehat{\alpha }}_{22}=0.05$, lower limit 95% CI= −.22, upper limit 95% CI= .32), the interaction between adherence to the first stage of the intervention (O₂₂) and the second-stage intervention options (A₂) is statistically significant (${\widehat{\alpha }}_{23}=.97$, lower limit 95% CI=.41, upper limit 95% CI= 1.53).

The results in Table 2 indicate that when adherence to the first stage of the intervention is low (O₂₂ = 0), the term $({\widehat{\alpha }}_{21}+{\widehat{\alpha }}_{22}{A}_1)$ is negative and statistically significant, regardless of whether the first-stage intervention option was low dose of medication (${\widehat{\alpha }}_{21}-{\widehat{\alpha }}_{22}=-.77$, lower limit 95% CI= −1.30, upper limit 95% CI= −0.32), or low-intensity behavioral intervention (${\widehat{\alpha }}_{21}+{\widehat{\alpha }}_{22}=.67$, lower limit 95% CI= −1.14, upper limit 95% CI= −.19). Accordingly, when adherence to the first stage of the intervention is low, the term (α₂₁ + α₂₂A₁)A₂ is maximized when A₂ = −1 (augment the first-stage intervention option with the alternative type of intervention). However, when adherence to the first stage of the intervention is high (O₂₂ = 1), the term $({\widehat{\alpha }}_{21}+{\widehat{\alpha }}_{22}{A}_1+{\widehat{\alpha }}_{23})$ was not found to be significantly different from zero, regardless of whether the first-stage intervention option was low dose of medication ($({\widehat{\alpha }}_{21}-{\widehat{\alpha }}_{22}+{\widehat{\alpha }}_{23}=.20$; lower limit 95% CI= −.26, upper limit 95% CI= .67) or low-intensity behavioral intervention (${\widehat{\alpha }}_{21}+{\widehat{\alpha }}_{22}+{\widehat{\alpha }}_{23}=.30$, lower limit 95% CI= −.13, upper limit 95% CI= .74).

Overall, the results of the second-stage regression suggest that if a child does not respond to the first stage of the intervention (regardless of whether the first-stage intervention option was low dose of medication or low-intensity behavioral intervention), and if adherence to the first stage of the intervention is low, augmenting the first-stage intervention option with the alternative type of intervention (A₂ = −1), leads to better classroom performance relative to increasing the dose/intensity of the first-stage intervention option (A₂ = 1). However, if adherence to the first stage of the intervention is high, there is inconclusive evidence with respect to the difference between the two second-stage intervention options. Figure 7 presents the predicted means for each of the second-stage intervention options (A₂), given the first-stage intervention options (A₁) and adherence to the first stage of the intervention (O₂₂).

Figure 7.

Predicted mean of classroom performance for each of the second-stage intervention options (A₂), given the first-stage intervention (A₁) and adherence to first-stage intervention (O₂₂).

Table 3 presents the results for the first-stage regression. Based on these estimates, we estimated the term $({\widehat{\alpha }}_{11}+{\widehat{\alpha }}_{12}{O}_{11})$ for each value of O₁₁ (see Table 4). The results in Table 4 indicate that the effect of the first-stage intervention options (A₁) is positive and marginally significant (${\widehat{\alpha }}_{11}=.17$, lower limit 90% CI= −.01, upper limit 90% CI=.34), and the interaction between the first-stage intervention options (A₁) and medication prior to the first stage of the intervention (O₁₁) is negative and marginally significant (${\widehat{\alpha }}_{12}=-.32$, lower limit 90% CI= −.59, upper limit 90% CI= −.06).

Table 3.

Estimated coefficients and soft-threshold confidence intervals for Q₁ (N=138).

Effect	Estimate	SE	Lower limit 90% CI	Upper limit 90% CI
Intercept	2.61	0.16
O11 (medication prior to first-stage intervention)	−0.37	0.14
O12 (baseline: ADHD symptoms)	0.73	0.11
O13 (baseline: ODD diagnosis)	0.75	0.13
A1 (first-stage intervention options)	0.17	0.07	−0.01	0.34
O11*A1 (medication prior to first-stage intervention*first-stage intervention options)	−0.32	0.14	−0.59	−0.06

Table 4.

Estimates of $({\widehat{\alpha }}_{11}+{\widehat{\alpha }}_{12}{O}_{11})$ for each level of O₁₁.

O11	Estimated $({\widehat{\alpha }}_{11}+{\widehat{\alpha }}_{12}{O}_{11})$	SE	Lower limit 90% CI	Upper limit 90% CI
1 (medication prior to first-stage intervention)	−0.15	0.12	−0.44	0.11
0 (no medication prior to first-stage intervention)	0.17	0.07	−0.01	0.34

Based on the mates in Table 4, we estimated the formula $({\widehat{\alpha }}_{11}+{\widehat{\alpha }}_{12}{O}_{11})$ for every given value of O₁₁ (see Table 5). The results in Table 5 indicate that when O₁₁ = 0, the term $\left({\widehat{\alpha }}_{11}\right)$ is positive and marginally significt (Estimate = .17, anlower limit 90% CI= −.01, upper limit 90% CI= .34). However, when O₁₁ =1 the term $({\widehat{\alpha }}_{11}+{\widehat{\alpha }}_{12})$ is not significantly different from zero (estimate= −.15, lower limit 90% CI= −.44, upper limit 90% CI= .11). This means that controlling for the optimal second-stage intervention option (offered to non-responders), low dose of behavioral intervention (A₁=1) leads to better classroom performance relative to low dose of medication (A₁= −1), for children who did not receive medication prior to the first stage of the intervention (O₁₁ = 0). However, there is inconclusive evidence with respect to the difference between the two first-stage intervention options for children who received medication at school prior to the first stage of the intervention. Figure 8 presents the predicted means for each of the first-stage intervention options (A₁), given whether or not the child received medication at school prior to the first stage of the intervention (O₁₁).

Figure 8.

Predicted estimated quality of the second-stage intervention for each of the first-stage intervention options (A₁), given whether or not the child received medication at school prior to first-stage intervention (O₁₁).

 Overall, the optimal sequence of decision rules based on this data analysis is as follows:
 IF the child received medication prior to the first stage of the intervention
  THEN offer low dose of medication or low-intensity behavioral intervention.
 ELSE IF the child did not receive medication prior to the first stage of the intervention
   THEN offer low-intensity behavioral intervention.
Then,
 IF the child shows inadequate response to the first stage of the intervention
  THEN IF child’s adherence to first stage of the intervention is low,
    THEN augment the first-stage intervention option with the
    other type of intervention.
   ELSE IF child’s adherence to the first stage of the intervention is high
    THEN augment the first-stage intervention option with the
    other type of intervention or intensify the first-stage
    intervention option.
 ELSE IF the child show adequate response to the first stage of the intervention,
  THEN continue first-stage intervention.

Discussion

In the current study, we introduced Q-learning: a novel regression-based data analysis method for constructing high-quality decision rules. We discussed how Q-learning can be used to investigate the possibility of more deeply tailored adaptive interventions than those embedded in the SMART study. We provided a general framework for Q-learning and also demonstrated how this framework can be generalized for the analysis of data from four common types of SMART designs. We then discussed three advantages of the Q-learning approach over a single-regression-based approach. First, Q-learning appropriately controls for the optimal second-stage intervention option when assessing the effect of the first-stage intervention. Second, the effects estimated by Q-learning incorporate both the direct and indirect effects of the first-stage intervention options, the combination of which is necessary for making intervention decision rules. Third, Q-learning reduces potential bias resulting from unmeasured causes of both the tailoring variables and the primary outcome. Finally, we illustrated the application of Q-learning using a simplified version of the Adaptive Interventions for Children with ADHD study, with the general aim to guide researchers who wish to apply this method to construct high-quality adaptive interventions.

Q-learning can be used to estimate the optimal sequence of decision rules in a straightforward and intuitive manner. Although in the current study we focused on only two intervention stages, and used dichotomous tailoring variables with only two values, Q-learning can be used for studies with more than two stages, and can be easily extended to continuous as well as categorical tailoring variables. Additionally, we used effect coding (1, -1) to denote the randomized intervention options at each stage. However, dummy coding (0,1) can also be used. The regression approach presented here can be generalized via a generalized linear model in cases of binary (more generally, categorical) outcomes. An R package for using Q-learning with data from a two-stage SMART design is available at http://methodology.psu.edu/ra/adap-treat-strat/qlearning.

Still, applying this method involves several challenges. First, when the data are from observational studies, direct implementation of this analysis might give biased results due to unmeasured confounding factors that predict the probability of being offered intervention options A₁ or A₂, given past intervention history. This reflects a selection bias caused by non-random treatment. For example, in the context of the ADHD example, assume that children’s family functioning affected whether they would be initially offered medication or behavioral intervention. In such cases, Q-learning should be implemented in combination with methodologies that adjust for confounding (see Robins, 1999).

Second, inferential challenges caused by non-differentiability should be taken into consideration when applying Q-learning. As noted previously, in Q-learning, non-differentiability arises because the formula for $\tilde{Y}$ (i.e., the dependent variable for the first-stage regression) contains an absolute value function. Because the absolute value function is non-differentiable at the point 0, the distribution of the estimators of the regression coefficients in Q₁ cannot be consistently approximated by standard methods such as the bootstrap. In the current analysis, we used the soft-threshold operation recommended by Chakraborty et al. (2010). Although the efficiency of this approach in reducing the bias of the intervention effects was documented (see Chakraborty et al., 2010), improved inferential methods are possible and are currently under development.

Third, in the current analysis we considered only two candidate tailoring variables. However, studies often collect information on a large set of covariates (e.g., multiple surveys of mental health status and functioning) from which a smaller subset of variables must be selected for any practical implementation of adaptive interventions. Accordingly, researchers might be interested in using the data to select a subset of tailoring variables that depicts the estimated optimal sequence of decision rules as closely as possible to the optimal rule which uses all variables. Biernot and Moodie (2010) discuss methods for selecting tailoring variables in randomized settings, comparing two selection methods (reducts-- a variable selection tool from computer sciences, and the S-score criterion proposed by Gunter Zhu, & Murphy, 2011). Still, additional research effort should be directed towards developing and exploring methods for the selection of tailoring variables.

Finally, because our data analysis was illustrative in nature, we handled missing data (resulting from dropout, unavailability during data collection period, or unwillingness/inability of teachers to respond), by using listwise deletion, ignoring subjects with incomplete information. Because this approach can have serious drawbacks (see, e.g.,Qin, Zhang & Leung, 2009; Little & Rubin, 1987; Schafer & Olsen, 1998), we recommend that researchers consider applying modern missing data techniques, such as multiple imputation (MI; Rubin, 1987), which allow more efficient estimation from incomplete data (see Shortreed, Laber, Pineau, & Murphy, 2010 for recent research on using MI to adjust for missing data in SMART studies).

Despite these challenges, our research demonstrates that the construction of the optimal sequence of decision rules from data can be achieved by a relatively simple regression-based procedure. In light of the growing interest in developing evidence-based individualized interventions in the behavioral sciences, the current research is part of an ongoing endeavor to advance methodological research relevant to adaptive interventions, hoping to further increase researchers’ awareness of the conceptual appeal and practical advantages of this approach.