On the effect of prestrain and residual stress in thin biological membranes

Abstract

Understanding the difference between ex vivo and in vivo measurements is critical to interpret the load carrying mechanisms of living biological systems. For the past four decades, the ex vivo stiffness of thin biological membranes has been characterized using uniaxial and biaxial tests with remarkably consistent stiffness parameters, even across different species. Recently, the in vivo stiffness was characterized using combined imaging techniques and inverse finite element analyses. Surprisingly, ex vivo and in vivo stiffness values differed by up to three orders of magnitude. Here, for the first time, we explain this tremendous discrepancy using the concept of prestrain. We illustrate the mathematical modeling of prestrain in nonlinear continuum mechanics through the multiplicative decomposition of the total elastic deformation into prestrain-induced and load-induced parts. Using in vivo measured membrane kinematics and associated pressure recordings, we perform an inverse finite element analysis for different prestrain levels and show that the resulting membrane stiffness may indeed differ by four orders of magnitude depending on the prestrain level. Our study motivates the hypothesis that prestrain is important to position thin biological membranes in vivo into their optimal operating range, right at the transition point of the stiffening regime. Understanding the effect of prestrain has direct clinical implications in regenerative medicine, medical device design, and and tissue engineering of replacement constructs for thin biological membranes.

1. INTRODUCTION

Since Y.C. Fung’s classical opening angle experiment in arteries more than two decades ago [15, 16], we all know, at least theoretically, that biological tissues display residual stresses, stresses that are relieved when biological substructures are isolated from their native environment. In fact, engineers have utilized the concept of residual stresses in prestressed concrete to structurally strengthen high-rise buildings and long-span bridges since the early 1950s [50]. Because of their elegant shape and aesthetic appearance, prestrained thin membrane structures have become an architecturally innovative design element in large outdoor roofs and pavilions [40]. While residual stresses in engineering structures may result from well-defined fabrication processes such as tensile elements, plastic deformation, or heat treatment, residual stresses in biological structures typically originate from development, growth, or remodeling, phenomena which, themselves, are only poorly understood [3, 44]. It is therefore not surprising that we often forget about the existence of residual stresses when analyzing living systems. Since we only know so little about them, why can we not simply ignore the effects of residual stresses in biological systems?

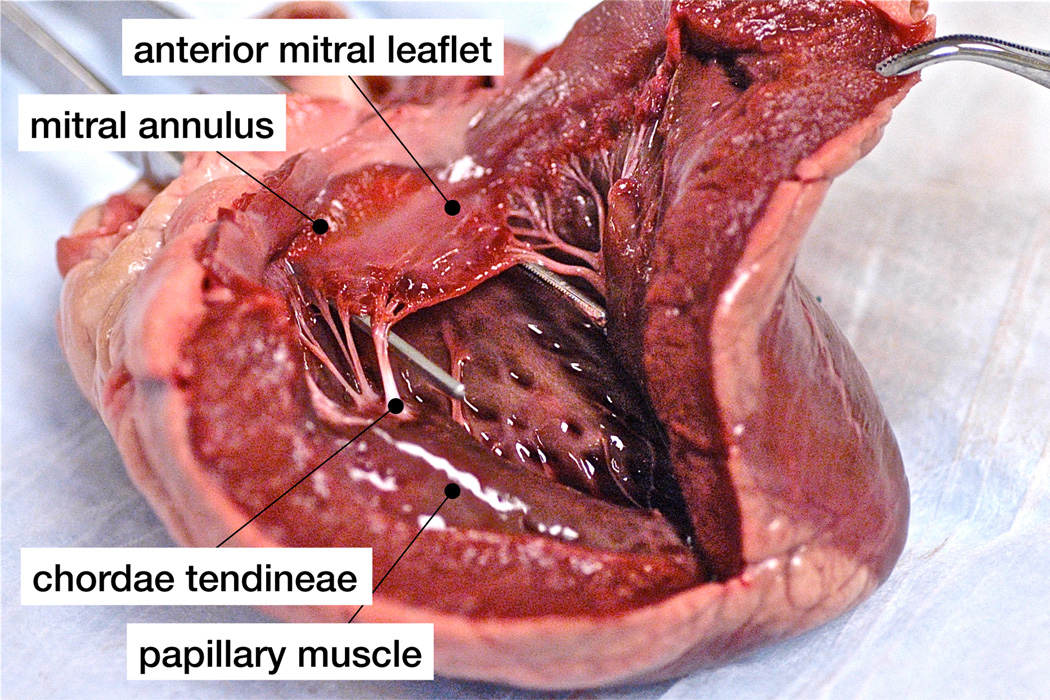
Prestrained thin architectural membranes find their natural equivalent in the mitral valve leaflet, a thin biological membrane supported by a stiff reinforcing ring, the mitral annulus, and by tension cables, the chordae tendineae, see Figure 1. The mitral leaflet has become an object of intense study throughout the past four decades [47], tested first uniaxially [11, 17, 31] then biaxially [19, 33], harvested from animals [31, 33] and from humans [11, 17, 19], characterized initially ex vivo [19, 31, 33] and now in vivo [28, 25]. While it would be overly optimistic to expect ex vivo and in vivo studies to yield identical mechanical characteristics, it is surprising that the reported stiffness values differ by up to three orders of magnitude [28]. When comparing the reported ex vivo and in vivo data more closely, we observe three major inconsistencies, one in kinematics, one in equilibrium, and one in the constitutive response.

Figure 1.

The anterior mitral leaflet is a typical example of a prestrained thin biological membrane, structurally supported by a stiff reinforcing ring, the mitral annulus, and by tension cables, the chordae tendineae. Under physiological conditions, the closed leaflet is subjected to blood pressure from underneath, as the left ventricle contracts.

The kinematic controversy manifests itself in significantly larger strains measured ex vivo than in vivo. Ex vivo, in a left heart simulator designed to reproduce the leaflet’s natural environment, explanted mitral leaflets displayed stretches in the order of 1.2 to 1.3 when subjected to physiological conditions [21, 26]. In vivo, in controlled animal experiments in sheep, both sonomicrometry [46] and video fluoroscopy [7, 41] revealed stretches in the order of 1.05 to 1.1, less than half of the ex vivo values. If membrane stretches were less than 1.1 in vivo, the true load carrying capacity of collagen associated with the uncrimping of collagen fibrils in stretch regimes beyond 1.2 [19] would not be activated at all under physiological conditions.

The equilibrium controversy manifests itself in larger stresses estimated in vivo than measured ex vivo. Ex vivo, measured failure stresses of healthy human mitral leaflets were in the order of 900kPa [19]. In vivo, computationally predicted stresses were as large as 3,000kPa in a forward finite element analysis based on in vivo data [29]. If membrane stresses were in the order of megapascales in vivo, more than three times larger than the failure stress, leaflets would be in serious danger of rupturing under physiological conditions.

The constitutive controversy manifests itself in significantly larger stiffness values identified in vivo than measured ex vivo. Ex vivo, measured pre- and post-transition moduli, the tangent stiffnesses before and after the onset of stress locking in collagenous tissues, were consistently reported in the orders of 10kPa and 1MPa in all previous studies [11, 17, 31, 33, 19]. In vivo, the mitral leaflet stiffness identified from in vivo data using linear inverse finite element analyses was in the order of 10 to 100MPa [28, 30]. Nonlinear constitutive models displayed a similar mismatch with significantly larger material parameter values when fitted to in vivo data [45] than when compared to ex vivo data [38]. In a finite element simulation with the ex vivo fitted parameters, the computational analysis overestimated structural deformations by a factor two [38] indicating that the assumed stiffness was too low. If the membrane stiffness was up to three orders of magnitude larger in vivo than ex vivo, what are the mechanisms responsible for this tremendous stiffness increase in vivo?

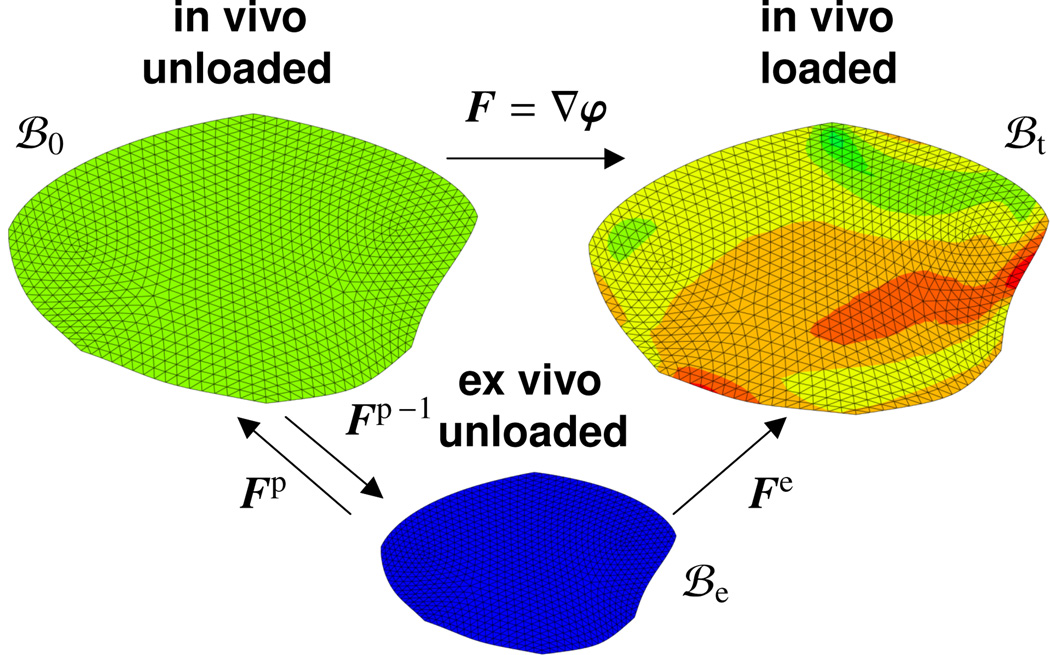
Here we demonstrate that the concept of residual stress, or rather the concept of prestrain, is capable of explaining all three inconsistencies, in strain, in stress, and in stiffness, between ex vivo and in vivo data. A recent study revealed that mitral leaflets in vivo are indeed exposed to significant residual strains which can be released upon leaflet explantation [4]. Leaflets contracted by 17% in area when excising the heart from the body and by a total of 43% when further excising the leaflet from the heart. The ease of measuring kinematic changes suggests to characterize the difference between in vivo and ex vivo phenomena in terms of strains rather than stresses, and use a kinematic approach towards modeling residual stresses [22]. In particular, we propose to adopt the concept of fictitious configurations [23, 27], in which we decompose the total elastic deformation gradient multiplicatively into prestrain-induced and load-induced parts, see Figure 2. In this approach, we parameterize the stored energy as a function of the total elastic strain [2]. The degree of prestrain defines the remaining stored energy upon removal of all in vivo loads and naturally introduces the notion of residual stress [9, 35]. In cylindrical structures, residual stresses have been visualized using the classical opening angle experiment both in arteries [15, 16] and in the heart [37]. First mathematical models for residual stresses in cylindrical structures are now on their way [10, 12, 49], and algorithmic protocols have been developed to efficiently incorporate prestrain in finite element simulations [5, 14]. In thin films, prestrain has been thoroughly characterized analytically, numerically, and experimentally using nano- and micro-indentation [6, 51]. In thin biological membranes, prestrain has been recognized to play a critical role in tissue engineered artificial heart valves [36]. Prestrain has recently been characterized experimentally ex vivo [4] and has been identified as an important mechanism in mitral valve mechanics [45]. However, to date, the effects of prestrain and residual stress in thin biological membranes have never been quantified systematically in vivo. This is the goal of the present manuscript.

Figure 2.

Kinematics of finite deformation with prestrain. The elastic tensor F^e = F · F^p is multiplicatively decomposed into a prestrain-induced part F^p and a load-induced part F = ∇φ, where the latter is the gradient of the in vivo deformation map φ from the in vivo unloaded configuration ℬ₀ to the loaded in vivo configuration ℬ_t. While it is difficult to explicitly quantify the prestrain F^p, we can easily measure the inverse prestrain F^p−1 as the membrane shrinkage upon tissue explantation.

The remainder of this manuscript is organized as follows. In Section 2, we summarize the general kinematics of prestrain and specify this concept to model prestrain in thin membranes. In Section 3, we illustrate the general constitutive equations for prestrained systems and specify the free energy functions for prestrained isotropic circular thin films and prestrained transversely isotropic mitral leaflets. In Section 4, we discuss the computational modeling of prestrain and specify the benchmark problem of circular thin films and the clinical problem of mitral leaflets. In Section 5, we summarize the results of both problems with a particular focus on their sensitivity with respect to the prestrain levels. In Section 6, we discuss our results and compare them to existing studies in the literature, before we conclude by reiterating the role of prestrain and residual stress in thin biological membranes in Section 7.

2. KINEMATICS OF PRESTRAIN

To characterize the kinematics of prestrain, we adopt the formulation of finite strain kinematics based on the deformation map φ, which maps material points from the in vivo unloaded configuration ℬ₀ to the in vivo loaded configuration ℬ_t. Its spatial gradient, the deformation gradient

$$\mathit{F}=\mathbf{\nabla }\mathit{\phi }:T{ℬ}_0\to T{ℬ}_{\mathrm{t}}$$ (1)

maps elements from tangent space of the in vivo unloaded configuration Tℬ₀ to the tangent space of the in vivo loaded configuration Tℬ_t. Throughout this manuscript, we assume that the in vivo unloaded configuration ℬ₀ is neither stress- nor strain-free. We interpret prestrain as the strain required to bring the membrane from the ex vivo unloaded configuration ℬ_e to the in vivo unloaded configuration ℬ₀ and denote the associated tangent map with F^p : Tℬ_e → Tℬ₀. While it is difficult to measure F^p directly, we can experimentally measure the inverse prestrain F^p−1 : Tℬ₀ → Tℬ_e as the kinematic change upon tissue explantation [4]. After characterizing the deformation gradient F and the prestrain F^p, we can determine the second order elastic tensor

$${\mathit{F}}^{\mathrm{e}}=\mathit{F}·{\mathit{F}}^{\mathrm{p}}:T{ℬ}_{\mathrm{e}}\to T{ℬ}_{\mathrm{t}},$$ (2)

which we multiplicatively decompose into volumetric and isochoric parts,

$${\mathit{F}}^{\mathrm{e}}={\mathit{F}}_{\text{vol}}^{\mathrm{e}}·{\mathit{F̄}}^{\mathrm{e}}\text{with}{\mathit{F}}_{\text{vol}}^{\mathrm{e}}={(J^{\mathrm{e}})}^{1/3}\mathit{I}\text{and}{\mathit{F̄}}^{\mathrm{e}}={(J^{\mathrm{e}})}^{-1/3}{\mathit{F}}^{\mathrm{e}}.$$ (3)

This decomposition implies that J̄^e = det(F̄^e) = 1 and thus $J_{\text{vol}}^{\mathrm{e}}=J^{\mathrm{e}}=\text{det}({\mathit{F}}^{\mathrm{e}})\ge 0$. We can then determine the elastic right Cauchy-Green deformation tensor C^e and its relation to the total right Cauchy-Green deformation tensor C and to its isochoric part C̄^e,

$${\mathit{C}}^{\mathrm{e}}={\mathit{F}}^{\mathrm{e}\mathrm{t}}·{\mathit{F}}^{\mathrm{e}}={\mathit{F}}^{\mathrm{p}\mathrm{t}}·\mathit{C}·{\mathit{F}}^{\mathrm{e}}={(J^{\mathrm{e}})}^{2/3}{\mathit{C̄}}^{\mathrm{e}}\text{with}\mathit{C}={\mathit{F}}^{\mathrm{t}}·\mathit{F}\text{and}{\mathit{C̄}}^{\mathrm{e}}={\mathit{F̄}}^{\mathrm{e}\mathrm{t}}·{\mathit{F̄}}^{\mathrm{e}}.$$ (4)

We account for the characteristic tissue microstructure with a single family of collagen fibers modeled through the structural tensor N = n₀ ⊗ n₀, where n₀ with ‖n₀‖ = 1 denotes the unit vector in the ex vivo unloaded configuration ℬ_e. Accordingly, we introduce the following three elastic invariants

$$J^{\mathrm{e}}=\text{det}({\mathit{F}}^{\mathrm{e}})\text{and}{Ī}_1^{\mathrm{e}}={\mathit{C̄}}^{\mathrm{e}}:\mathit{I}\text{and}{Ī}_4^{\mathrm{e}}={\mathit{C̄}}^{\mathrm{e}}:\mathit{N},$$ (5)

where the Jacobian J^e = det(F^e) characterizes the incompressible response, the first isochoric invariant ${Ī}_1^{\mathrm{e}}={\mathit{C̄}}^{\mathrm{e}}:\mathit{I}$ characterizes the isotropic response, and the fourth isochoric invariant ${Ī}_4^{\mathrm{e}}={\mathit{C̄}}^{\mathrm{e}}:\mathit{N}$ characterizes anisotropic response.

Remark 1 (Kinematics of prestrained thin membranes). The simplest approach to model prestrain in thin membranes, which we adopt here, is to assume that the membrane prestrain is transversely isotropic with respect to the membrane normal m₀,

$${\mathit{F}}^{\mathrm{p}}={\lambda }^{\mathrm{p}}[\mathit{I}-{\mathit{m}}_0\otimes {\mathit{m}}_0]+[{\mathit{m}}_0\otimes {\mathit{m}}_0]/{\lambda }^{\mathrm{p}2}.$$

This allows us to parameterize prestrain in terms of a single scalar-valued variable, the in-plane prestretch λ^p. The first term, λ^p [I − m₀ ⊗ m₀], is associated with the in-plane prestretch λ^p and with an area change λ^p2, while the second term, [m₀ ⊗ m₀]/λ^p2, is associated with the thickness contraction 1/λ^p2. This implies that our prestrain is incompressible, i.e., J^p = det (F^p) = 1. Because of its simple rank-one update structure, we can explicitly invert the membrane prestrain,

$${\mathit{F}}^{\mathrm{p}-1}=[\mathit{I}-{\mathit{m}}_0\otimes {\mathit{m}}_0]/{\lambda }^{\mathrm{p}}+{\lambda }^{\mathrm{p}2}{\mathit{m}}_0\otimes {\mathit{m}}_0,$$

using the Sherman Morison formula. We can visualize and measure the inverse prestretch 1/λ^p as the membrane contraction upon tissue explantation, see Figure 2.

3. CONSTITUTIVE EQUATIONS FOR PRESTRAINED SYSTEMS

To model the constitutive response of prestrained systems, we adopt an incompressible, transversely isotropic, hyper-elastic free energy function, characterized through a volumetric part U and an isochoric part ψ̄, both parameterized exclusively in terms of the elastic invariants J^e, ${Ī}_1^{\mathrm{e}}$, and ${Ī}_4^{\mathrm{e}}$,

$$\psi =U(J^{\mathrm{e}})+\mathrm{\psi ̄}({Ī}_1^{\mathrm{e}},{Ī}_4^{\mathrm{e}}).$$ (6)

The additive decomposition of the free energy manifests itself in an additive decomposition of the Piola-Kirchhoff stress,

$$\mathit{S}=2\frac{\partial \psi }{\partial \mathit{C}}{\mathit{F}}^{\mathrm{p}}·{\mathit{S}}^{\mathrm{e}}·{\mathit{F}}^{\mathrm{p}\mathrm{t}}\text{with}{\mathit{S}}^{\mathrm{e}}=2\frac{\partial \psi }{\partial {\mathit{C}}^{\mathrm{e}}}={\mathit{S}}_{\text{vol}}^{\mathrm{e}}+{\mathit{S}}_{\text{iso}}^{\mathrm{e}},$$ (7)

where the volumetric and isochoric parts take the following explicit representations,

$${\mathit{S}}_{\text{vol}}^{\mathrm{e}}=2\frac{\partial U}{\partial {\mathit{C}}^{\mathrm{e}}}=J^{\mathrm{e}}\mathrm{p̂}{({\mathit{C}}^{\mathrm{e}})}^{-1}{\mathit{S}}_{\text{iso}}^{\mathrm{e}}=2\frac{\partial \mathrm{\psi ̄}}{\partial {\mathit{C}}^{\mathrm{e}}}={(J^{\mathrm{e}})}^{-2/3}{\mathbb{P}}^{\mathrm{e}}:{\mathit{S̄}}^{\mathrm{e}}.$$ (8)

The volumetric stress ${\mathit{S}}_{\text{vol}}^{\mathrm{e}}$ depends primarily on the deriviative p̂ ≔ ∂U/∂J^e. The isochoric stress ${\mathit{S}}_{\text{iso}}^{\mathrm{e}}$ depends on the second order tensor S̄^e,

$${\mathit{S̄}}^{\mathrm{e}}=2\frac{\partial \mathrm{\psi ̄}}{\partial {\mathit{C̄}}^{\mathrm{e}}}=2{\mathrm{\psi ̄}}_1^{\mathrm{e}}\mathit{I}+2{\mathrm{\psi ̄}}_4^{\mathrm{e}}\mathit{N},$$ (9)

whose weighting factors ${\mathrm{\psi ̄}}_i^{\mathrm{e}}=\partial {\mathrm{\psi ̄}}^{\mathrm{e}}/\partial {Ī}_i^{\mathrm{e}}$ we will determine later when we specify the particular form of the isochoric free energy function ψ̄. In equation (8.2), ${\mathbb{P}}^{\mathrm{e}}=𝕀-\frac{1}{3}{({\mathit{C}}^{\mathrm{e}})}^{-1}\otimes {\mathit{C}}^{\mathrm{e}}$ denotes the isochoric projection tensor in terms of the fourth order identity tensor $𝕀=\frac{1}{2}[\mathit{I}\otimes ̅\mathit{I}+\mathit{I}\otimes ̲\mathit{I}]$, with the understanding that {●⊗̅○}_ijkl = {●}_ik{○}_jl and {●⊗̲○}_ijkl = {●}_il{○}_jk. To efficiently solve the nonlinear boundary value problem, we linearize the Piola-Kirchhoff stress S with respect to the right Cauchy-Green deformation tensor C to obtain the fourth order tangent moduli

$$ℂ=4\frac{{\partial }^2\psi }{\partial \mathit{C}\otimes \partial \mathit{C}}=[{\mathit{F}}^{\mathrm{p}}\otimes ̅{\mathit{F}}^{\mathrm{p}}]:{ℂ}^{\mathrm{e}}:[{\mathit{F}}^{\mathrm{p}\mathrm{t}}\otimes ̅{\mathit{F}}^{\mathrm{p}\mathrm{t}}]\text{with}{ℂ}^{\mathrm{e}}=2\frac{\partial {\mathit{S}}^{\mathrm{e}}}{\partial {\mathit{C}}^{\mathrm{e}}}={ℂ}_{\text{vol}}^{\mathrm{e}}+{ℂ}_{\text{iso}}^{\mathrm{e}},$$ (10)

which we can again decompose into volumetric and isochoric parts,

$${ℂ}_{\text{vol}}^{\mathrm{e}}=2\frac{\partial {\mathit{S}}_{\text{vol}}^{\mathrm{e}}}{\partial {\mathit{C}}^{\mathrm{e}}}=J^{\mathrm{e}}[\mathrm{p̂}+J^{\mathrm{e}}\mathrm{𝓀̂}]{({\mathit{C}}^{\mathrm{e}})}^{-1}\otimes {({\mathit{C}}^{\mathrm{e}})}^{-1}-2J^{\mathrm{e}}\mathrm{p̂}{𝕀}_{C^{\mathrm{e}-1}}{ℂ}_{\text{iso}}^{\mathrm{e}}=2\frac{\partial {\mathit{S}}_{\text{iso}}^{\mathrm{e}}}{\partial {\mathit{C}}^{\mathrm{e}}}={(J^{\mathrm{e}})}^{-4/3}{\mathbb{P}}^{\mathrm{e}}:{\mathrm{ℂ̄}}^{\mathrm{e}}:{\mathbb{P}}^{\mathrm{e}\mathrm{t}}+\frac{2}{3}[{(J^{\mathrm{e}})}^{-2/3}{\mathit{S̄}}^{\mathrm{e}}:{\mathit{C}}^{\mathrm{e}}{\mathrm{\mathbb{P}̄}}^{\mathrm{e}}-{[{\mathit{S̄}}^{\mathrm{e}}\otimes {({\mathit{C}}^{\mathrm{e}})}^{-1}]}^{\text{sym}}].$$ (11)

The volumetric part depends primarily on the second derivative 𝓀̂ ≔ ∂²U/∂J^e2. The isochoric part depends on the fourth order tensor

$${\mathrm{ℂ̄}}^{\mathrm{e}}=2\frac{\partial {\mathit{S̄}}^{\mathrm{e}}}{\partial {\mathit{C̄}}^{\mathrm{e}}}=4[{\mathrm{\psi ̄}}_{11}^{\mathrm{e}}\mathit{I}\otimes \mathit{I}+2{\mathrm{\psi ̄}}_{14}^{\mathrm{e}}{[\mathit{I}\otimes \mathit{N}]}^{\text{sym}}+{\mathrm{\psi ̄}}_{44}^{\mathrm{e}}\mathit{N}\otimes \mathit{N}],$$ (12)

whose weighting factors ${\mathrm{\psi ̄}}_{ij}^{\mathrm{e}}=\partial {\mathrm{\psi ̄}}^{\mathrm{e}}/\partial {Ī}_i^{\mathrm{e}}\partial {Ī}_j^{\mathrm{e}}$ we will specify later. In equation (11.2), ${\mathrm{\mathbb{P}̄}}^{\mathrm{e}}={𝕀}_{{\mathrm{C}}^{\mathrm{e}-1}}-\frac{1}{3}{({\mathit{C}}^{\mathrm{e}})}^{-1}\otimes {({\mathit{C}}^{\mathrm{e}})}^{-1}$ and ${𝕀}_{{\mathrm{C}}^{\mathrm{e}-1}}=\frac{1}{2}[{({\mathit{C}}^{\mathrm{e}})}^{-1}\otimes ̅{({\mathit{C}}^{\mathrm{e}})}^{-1}+{({\mathit{C}}^{\mathrm{e}})}^{-1}\otimes ̲{({\mathit{C}}^{\mathrm{e}})}^{-1}]$ are two additional fourth order tensors related to the isochoric projection. The proposed approach is generally applicable to incompressible, transversely isotropic materials. In sections 3.1 and 3.2, we specify the isochoric free energy function ψ̄^e for isotropic and transversely isotropic materials and determine its derivatives ${\mathrm{\psi ̄}}_i^{\mathrm{e}}$ and ${\mathrm{\psi ̄}}_{ij}^{\mathrm{e}}$ to specify the isochoric stress S̄^e and the isochoric tangent moduli ℂ̄^e.

3.1. Prestrained circular thin films

To specify the isochoric free energy ψ̄^e of equation (6) for the benchmark problem of thin circular films, we select a simple isotropic Neo-Hookean material model parameterized exclusively in terms of the first invariant ${Ī}_1^{\mathrm{e}}$ weighted by the shear modulus c₀,

$${\mathrm{\psi ̄}}^{\mathrm{e}}=c_0[{Ī}_1^{\mathrm{e}}-3].$$ (13)

From the first derivative of this isochoric free energy function with respect to the first and fourth invariants,

$${\mathrm{\psi ̄}}_1^{\mathrm{e}}=c_0\text{and}{\mathrm{\psi ̄}}_4^{\mathrm{e}}=0,$$ (14)

we conclude that, for this particular model, the isochoric stress S̄^e of equation (9) depends only on the shear modulus c₀. Accordingly, the second derivatives of the isochoric free energy function with respect to the first and fourth invariants are all zero,

$${\mathrm{\psi ̄}}_{11}^{\mathrm{e}}=0\text{and}{\mathrm{\psi ̄}}_{14}^{\mathrm{e}}=0\text{and}{\mathrm{\psi ̄}}_{44}^{\mathrm{e}}=0,$$ (15)

and the isochoric tangent moduli ℂ̄^e of equation (12) vanish identically.

3.2. Prestrained mitral leaflets

To specify the isochoric free energy ψ̄^e of equation (6) for the clinical problem of mitral leaflets, we select a well-calibrated constitutive model for mitral valve tissue [34, 38]. Transversely isotropic in nature, the mitral leaflet is characterized through a single representative fiber family. Its isochoric free energy is based on an exponential function in terms of the first and fourth invariants ${Ī}_1^{\mathrm{e}}$ and ${Ī}_4^{\mathrm{e}}$ weighted by three material parameters c₀, c₁, and c₂,

$${\mathrm{\psi ̄}}^{\mathrm{e}}=c_0[\text{exp}(c_1{[{Ī}_1^{\mathrm{e}}-3]}^2+c_2{[{Ī}_4^{\mathrm{e}}-1]}^2)-1].$$ (16)

The free energy function is polyconvex in the case of incompressibility provided the fibers are only subjected to tension, i.e., ${Ī}_4^{\mathrm{e}}\ge 1$ [38]. To determine the isochoric stress S̄^e in equation (9), we evaluate the first derivatives of the isochoric free energy function with respect to the first and fourth invariants ${\mathrm{\psi ̄}}_i^{\mathrm{e}}=\partial {\mathrm{\psi ̄}}^{\mathrm{e}}/\partial {Ī}_i^{\mathrm{e}}$,

$${\mathrm{\psi ̄}}_1^{\mathrm{e}}=2c_0{c}_1[{Ī}_1^{\mathrm{e}}-3]\text{exp}(c_1{[{Ī}_1^{\mathrm{e}}-3]}^2+c_2{[{Ī}_4^{\mathrm{e}}-1]}^2){\mathrm{\psi ̄}}_4^{\mathrm{e}}=2c_0{c}_2[{Ī}_4^{\mathrm{e}}-1]\text{exp}(c_1{[{Ī}_1^{\mathrm{e}}-3]}^2+c_2{[{Ī}_4^{\mathrm{e}}-1]}^2).$$ (17)

To determine the isochoric tangent moduli ℂ̄^e in equation (12), we evaluate the second derivatives of the isochoric free energy function with respect to the first and fourth invariants ${\mathrm{\psi ̄}}_{ij}^{\mathrm{e}}={\partial }^2{\mathrm{\psi ̄}}^{\mathrm{e}}/\partial {Ī}_i^{\mathrm{e}}\partial {Ī}_j^{\mathrm{e}}$,

$${\mathrm{\psi ̄}}_{11}^{\mathrm{e}}=2c_0{c}_1[1+2c_1{[{Ī}_1^{\mathrm{e}}-3]}^2]\text{exp}(c_1{[{Ī}_1^{\mathrm{e}}-3]}^2+c_2{[{Ī}_4^{\mathrm{e}}-1]}^2){\mathrm{\psi ̄}}_{14}^{\mathrm{e}}=4c_0{c}_1{c}_2[{Ī}_1^{\mathrm{e}}-3][{Ī}_3-1]\text{exp}(c_1{[{Ī}_1^{\mathrm{e}}-3]}^2+c_2{[{Ī}_4^{\mathrm{e}}-1]}^2){\mathrm{\psi ̄}}_{44}^{\mathrm{e}}=2c_0{c}_2[1+2c_2{[{Ī}_3^{\mathrm{e}}-1]}^2]\text{exp}(c_1{[{Ī}_1^{\mathrm{e}}-3]}^2+c_2{[{Ī}_4^{\mathrm{e}}-1]}^2).$$ (18)

Unlike most transversely isotropic models for non-living materials, this particular constitutive model introduces an inherent constitutive coupling between the isotropic and anisotropic response through the first and fourth invariants ${Ī}_1^{\mathrm{e}}$ and ${Ī}_4^{\mathrm{e}}$. This coupling manifests itself in non-vanishing mixed second derivatives, ${\mathrm{\psi ̄}}_{14}^{\mathrm{e}}\ne 0$.

4. COMPUTATIONAL MODELING OF PRESTRAIN

To simulate prestrain using a standard, commercially available finite element solver, we adopt a three-step prestrain protocol as illustrated in Figure 2: First, we virtually create the ex vivo configuration ℬ_e. Starting with a known in vivo unloaded configuration ℬ₀, for a given Green-Lagrange prestrain E^p = [λ^p2 − 1]/2, we shrink the geometry with the inverse membrane prestrain F^{p − 1} = [I − m₀ ⊗ m₀] / λ^p + λ^p2 m₀ ⊗ m₀ with λ^p = [2 E^p + 1]^1/2. Second, we recreate the in vivo unloaded configuration ℬ₀. Starting with the virtually created ex vivo configuration ℬ_e, we apply the membrane prestrain F^p = λ^p[I − m₀ ⊗ m₀] + m₀ ⊗ m₀ / λ^p2 and verify the prescribed prestrain level. Third, we create in vivo loaded configuration ℬ_t. Starting with the in vivo unloaded configuration ℬ₀, now prestrained, we apply the in vivo Dirichlet and Neumann boundary conditions along with the in vivo loading to solve for the deformation φ and the deformation gradient F = ∇φ. We calculate the resulting stresses and tangent moduli using the elastic tensor F^e = F·F^p as the composition of the mappings F^p and F from steps two and three. In what follows, we adopt this three-step protocol to explore the effect of prestrain in the benchmark problem of circular thin films and in the clinical problem of mitral leaflets. For both cases, we study different prestrain levels by systematically varying the in-plane Green-Lagrange prestrain $E^{\mathrm{p}}=\frac{1}{2}[{\lambda }^{\mathrm{p}2}-1]$ in increments of 10%.

4.1. Prestrained circular thin films

To illustrate the effect of prestrain on thin membranes, we simulate two easily reproducible, simple, generic benchmark problems. For the simulation, we use the commercially available, implicit finite element solver ABAQUS/ Standard Version 6.9 [1]. For easy reproducibility, we adopt a simple incompressible Neo-Hookean material model according to Section 3.1 with a shear modulus of c₀ = 1MPa. We model the membrane as a flat circular film with a radius of 1 mm and a thickness-to-radius ratio of 0.01. Using symmetry conditions, we discretize a quarter of the system with 2,350 SR4 bi-linear quadrilateral finite strain shell elements with discrete Kirchhoff thin shell kinematics. To virtually generate prestrain in the film, we adopt the three-step prestrain protocol for prestrain levels of E^p = [0%, 10%, 20%, 30%]: First, starting with a circular disc of radius 1 mm, we virtually create the unloaded configuration ℬ_e by shrinking the disc with the inverse membrane prestrain F^{p −1}. Second, from this configuration ℬ_e, we start the simulation and apply the membrane prestrain F^p to recreate the configuration ℬ₀. Third, we clamp the membrane at its outer edges and apply the in vivo-equivalent loading to solve for the deformation φ and the deformation gradient F = ∇φ, which characterize the configuration ℬ_t. For the first benchmark problem motivated by the mechanics of the mitral valve [45], we simulate the inflation of the thin film with a homogeneous pressure. For the second benchmark problem motivated by prestrain studies in the literature [6, 51], we simulate the indentation of the thin film with a frictionless spherical indenter of an indenter-to-film radius of 0.1. We gradually increase both the inflation pressure and the indentation force until the center deflection of the thin film reaches a deflection-to-radius ratio of 0.4.

4.2. Prestrained mitral leaflets

To explore the effect of prestrain on mitral valve mechanics, we implement the constitutive model described in Section 3.2 as a user subroutine into the commercially available, implicit finite element solver ABAQUS/Standard Version 6.9 [1]. In particular, we utilize the framework UANISOHYPER INV for user-defined anisotropic hyperelastic material models parameterized in an invariant formulation. We create the finite element discretization of the anterior mitral leaflet as a smooth surface [18] approximating the averaged coordinates of 23 radiopaque tantalum markers, which have been implanted onto the the anterior mitral leaflets of 57 male Dorsett sheep [8, 32], see Figure 3, left. We discretize the biological membrane with 1,920 S3R linear triangular finite strain shell elements with discrete Kirchhoff thin shell kinematics [38], see Figure 3, middle. Specifically, we use an incompressible finite element formulation, which is realized in ABAQUS/Standard as a mixed formulation based on the deformation map φ and an independent Lagrange multiplier p̂. For S3R elements, the Lagrange multiplier p̂, which enforces the incompressibility constraint J^e − 1 = 0 in a weak sense, is constant on the element level and C⁻¹- continuous [1]. After a series of sensitivity studies, we select a constant leaflet thickness of 1 mm and a transverse shear stiffness of 100MPa [45]. From the experimentally measured marker coordinates acquired at 60 frames per second, we select eight consecutive time frames starting with the image just before leaflet separation, which we define as the in vivo unloaded reference configuration ℬ₀. We then go backwards in time towards the image at end systole, which we define as the in vivo loaded configuration ℬ_t [28]. In this particular simulation interval, the mitral valve is closed, hemodynamic effects are negligible, and the possible effects of contracting smooth muscle cells are minimized [45]. To account for the characteristic transversely isotropic microstructure of the mitral leaflet, we create discrete collagen fiber orientation maps from tissue histology [45] and confirm the results with collagen orientations reported in the literature [13, 39], see Figure 3, right. We support the leaflet belly through chordae tendinae, which we model as incompressible Neo-Hookean tension-only rods inserting into the leaflet center [39]. We assume a chordae stiffness of 20MPa and a total cross-sectional area of 1 mm² for each branch. Throughout all eight time steps, we apply inhomogeneous Dirichlet boundary conditions to all boundary nodes using the experimentally measured boundary marker coordinates. At the same time, we pressurize the membrane from underneath with the experimentally measured transvalvular pressure, the pressure difference between the left ventricle and the left atrium acquired using catheter micromanometer pressure transducers [28]. To virtually generate prestrain in the mitral leaflet, we adopt the three-step prestrain protocol for prestrain levels of E^p = [0%, 10%, 20%, …, 100%]: First, for each prestrain level, we virtually create the corresponding ex vivo leaflet geometry ℬ_e by shrinking the experimentally acquired in vivo leaflet coordinates with the inverse membrane prestrain F^p−1. Second, from the ex vivo leaflet geometry, we start the simulation and apply the membrane prestrain F^p to recreate the in vivo unloaded leaflet geometry ℬ₀. Third, we apply the in vivo acquired inhomogeneous Dirichlet boundary conditions and the in vivo acquired transmembrane pressure to solve for the deformation φ and the deformation gradient F = ∇φ, which characterize the in vivo loaded leaflet geometry ℬ_t. To identify the material parameters for the different prestrain levels, we perform an inverse finite element analysis. We apply a genetic algorithm using MATLAB to minimize the average nodal displacement error e by systematically varying the material parameters c₀, c₁, and c₂. We start with an initial parameter set and perform a first generation of finite element simulations. After the simulation, for each parameter set, we calculate the error $e={\sum }_{t=0}^{n_{\mathrm{t}}}{\sum }_{m=1}^{n_{\mathrm{m}}}\Vert {\mathbf{\phi }}_{t,m}^{\text{exp}}-{\mathbf{\phi }}_{t,m}^{\text{sim}}\Vert /(n_{\mathrm{t}}{n}_{\mathrm{m}})$ as the distance between all m = 1, …, n_m experimentally measured inner leaflet markers ${\mathbf{\phi }}_{t,m}^{\text{exp}}$ and all computationally simulated inner leaflet markers ${\mathbf{\phi }}_{t,m}^{\text{sim}}$ summed over all t = 0, …, n_t time steps. For our particular case, the number of inner markers is n_m = 9 and the number of time steps is n_t = 8. Whenever the simulation does not converge, we assign an error value that is larger than previously encountered values for converged solutions. Based on the average nodal displacement error e, the genetic algorithm generates a new input parameter set through 20% mutation and 80% cross-over. The genetic algorithm iteratively minimizes the error until it reaches a user-defined convergence criterion. After finding a converged parameter set, we repeat the optimization algorithm for varying population sizes and initial parameter sets to ensure that the converged solution represents a global minimum.

Figure 3.

Computational model of the anterior mitral leaflet created from 23 discrete marker positions, left. The resulting finite element model consists of 1,920 S3R linear triangular finite strain shell elements, middle. Discrete collagen fiber orientation maps were extracted from tissue histology, right.

Remark 2 (Kinematic compatibility of prestrain). Here, for the sake of simplicity, we assume that the prestrain tensor F^p is kinematically compatible, i.e., that it can be constructed as the gradient of a prestrain deformation field. In this sense, we conceptually adapt a well-accepted two-step protocol to model prestrain in arteries [5, 14], in which an open arterial segment is first closed to calculate the prestrain tensor F^p, before the in vivo loads are applied to calculate the in vivo deformation gradient F = ∇φ. This successive application of prestrain and deformation simplifies the algorithmic formulation, in that the finite element algorithm can conveniently work with the elastic tensor F^e = F · F^p as the composition of both mappings. From this elastic tensor, we can easily calculate the stresses S^e = 2 ∂ψ/∂C^e and the elastic tangent moduli ℂ^e = 2 ∂S^e/∂C^e introduced in equations (7) and (10) with reference to an assumed-to-be-known ex vivo unloaded configuration ℬ_e. Alternatively, if the ex vivo configuration ℬ_e is unknown, we can work with the total stresses S = F^p · S^e · F^pt and with the total tangent moduli ℂ = [F^p ⊗̅ F^p] : ℂ^e : [F^pt ⊗̅ F^pt] using pushed forward operations to map the stresses and tangent moduli to the known in vivo unloaded configuration ℬ₀.

5. RESULTS

5.1. Prestrained circular thin films

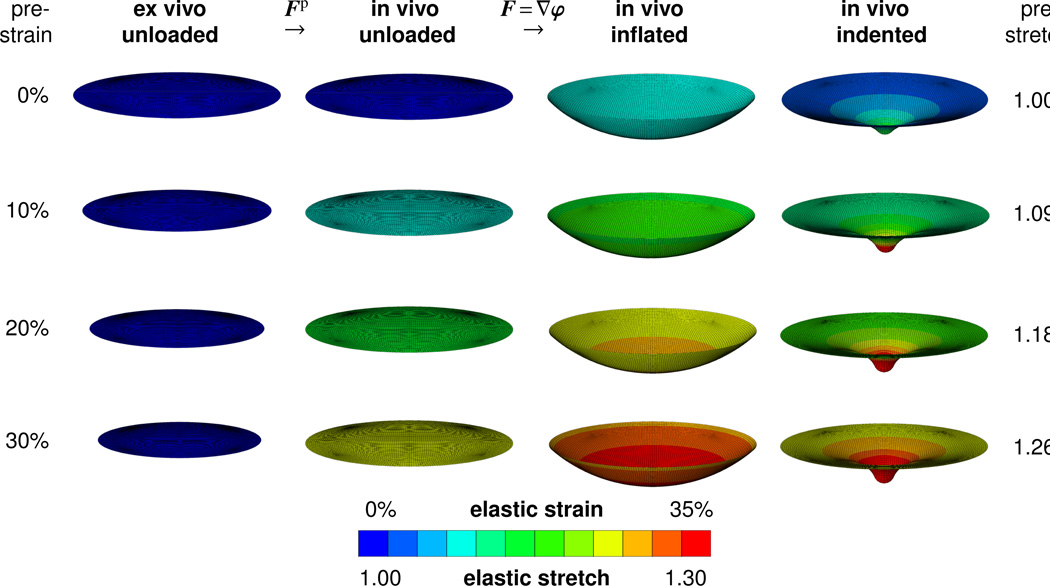
Figure 4 illustrates the maximum principal elastic Green Lagrange strains and the corresponding elastic stretches for the benchmark problem of prestrained circular thin films. The first column displays the ex vivo unloaded configuration, which is mapped onto the in vivo unloaded configuration displayed in the second column through the membrane prestrain F^p. The third and fourth columns display the elastic strains in the prestrained membrane, either subject to inflation or to indentation, characterized through the deformation gradient F = ∇φ. The color-coded elastic strains are a result of the composition of both mappings, F^e = F · F^p, influenced through both the prestrain F^p and the deformation gradient F. Each row corresponds to a different prestrain level, increasing gradually from 0% to 30% in increments of 10%. In agreement with intuition, increasing the membrane prestrain increases the elastic strains to generate the same vertical center deflection of 0.4mm upon membrane inflation and upon membrane indentation. In agreement with the literature, increasing the membrane prestrain induces a sharper indentation profile associated with a more localized deformation pattern [51].

Figure 4.

Maximum principal elastic Green Lagrange strains and corresponding elastic stretches for different prestrain levels. From the ex vivo unloaded configuration in the first column to the in vivo unloaded configuration in the second column, the membrane is prestrained through a prestrain F^p of different levels. From the in vivo unloaded configuration to the in vivo loaded configurations the membrane is either subjected to inflation, third column or to indentation, fourth column, reflected through the deformation gradient F = ∇φ. The color-coded elastic strains are a result of the composition of both mappings, F^e = F · F^p.

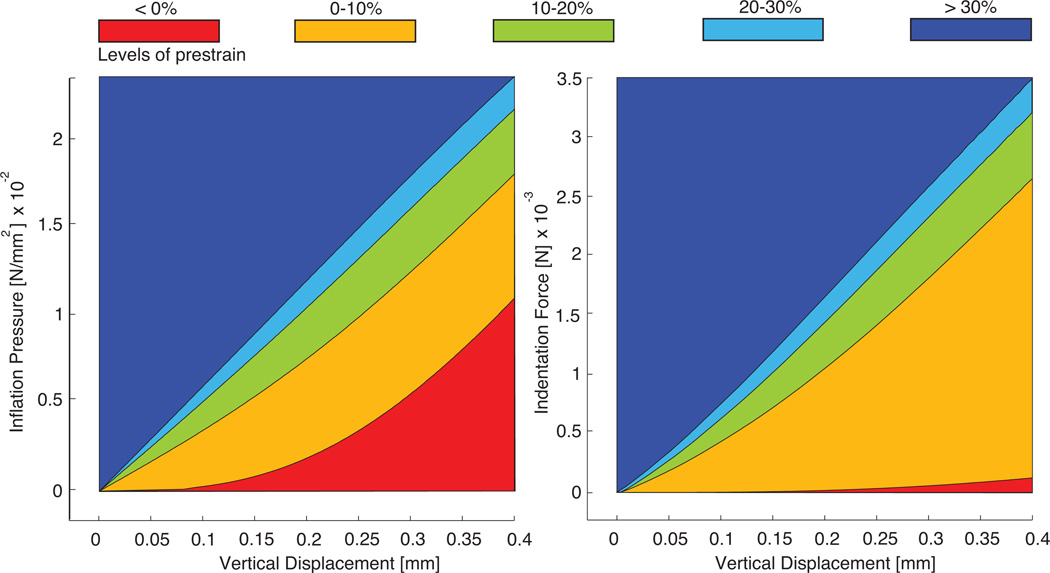
Figure 5 illustrates the effect of prestrain on the constitutive response of circular thin films. It displays the inflation pressure as a function of the central vertical displacement, left, and the indentation force as a function of the central vertical displacement, right. To highlight the continuous dependence of the constitutive behavior on the prestrain level, we color-coded the regions between the curves of the individual prestrain levels ranging from red at no prestrain to blue at the highest simulated prestrain. In agreement with the literature, for both benchmark problems, the inflation test and the indentation test, the membrane stiffness represented through the slope of the curves increases markedly with increasing prestrain [6, 51].

Figure 5.

Inflation pressure vs. vertical displacement, left, and indentation force vs. vertical displacement, right, for circular thin films at different prestrain levels. The membrane stiffness, the slope of the curves, increases markedly with increasing membrane prestrain.

5.2. Prestrained mitral leaflets

The parameter identification for the mitral leaflet has converged successfully for all eleven prestrain levels. For each prestrain level, we have identified an optimal parameter set c₀, c₁ and c₂, minimizing the total error between the experimentally measured and the computationally simulated inner marker coordinates.

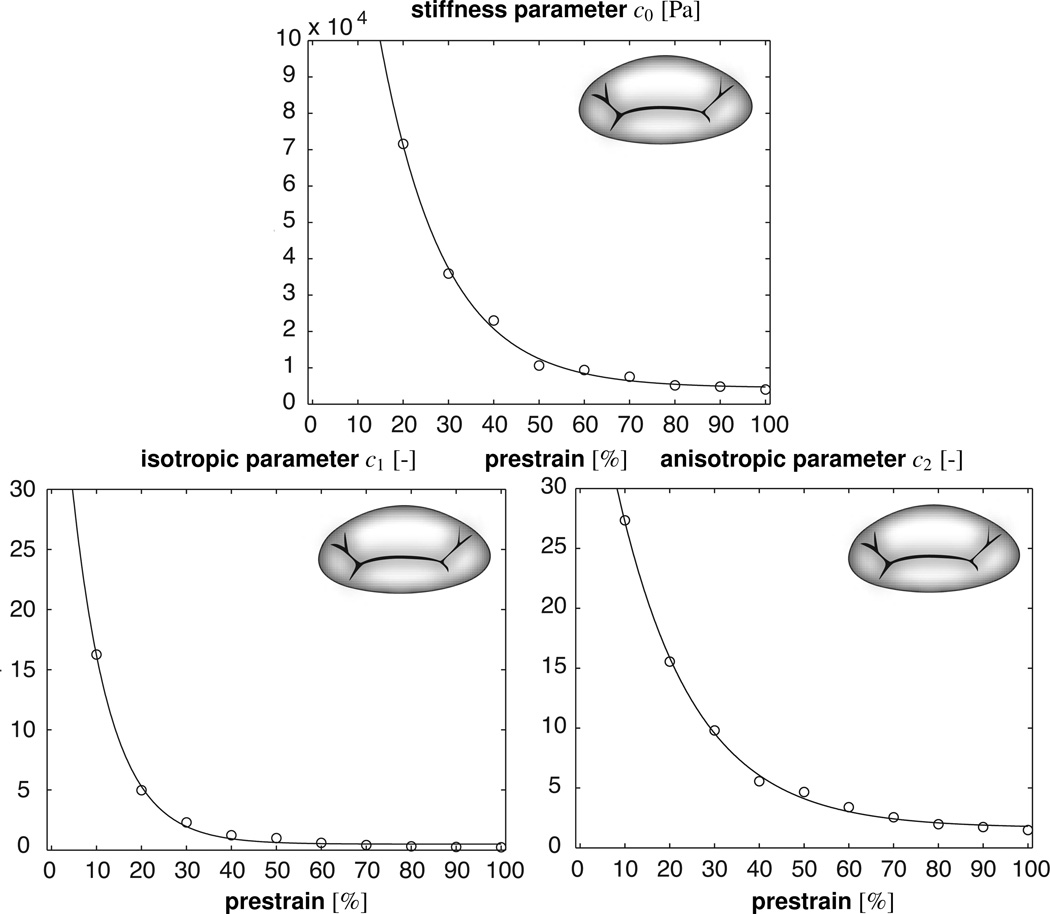
Table 1 summarizes the identified parameter sets for Green Lagrange prestrains E^p = [λ^p2 − 1]/2 varying from 0% to 100% corresponding to a membrane prestretch of λ^p varying from 1.000 to 1.732. All associated error values are smaller than 1 mm, which lies within the range of the expected experimental measuring error. Variation between error values is minimal with approximately 6% difference between the maximal and minimal values. All three material parameters decrease monotonically with increasing levels of prestrain. While the isotropic and anisotropic parameters c₁ and c₂ decrease by approximately two orders of magnitude, the stiffness parameter c₀ decreases by four orders of magnitude. Parameter c₂ associated with the anisotropic invariant I₄ is consistently larger than parameter c₁ associated with the isotropic invariant I₁. The ratio between c₂ and c₁ increases with prestrain from a ratio of approximately 1.2 at 0% prestrain to a ratio of 7.5 at 100% prestrain.

Table 1.

Material parameter values for mitral leaflet tissue identified for different prestrain levels.

prestrain [%]	prestretch [−]	c0 [kPa]	c1 [−]	c2 [−]	error [mm]
0	1.000	119,020.7	152.4	185.5	0.561
10	1.095	817.9	16.2	27.3	0.551
20	1.183	71.6	5.0	15.6	0.567
30	1.265	35.9	2.3	9.8	0.575
40	1.342	23.0	1.2	5.6	0.582
50	1.414	10.6	1.0	4.7	0.587
60	1.483	9.4	0.6	3.4	0.588
70	1.549	7.5	0.4	2.5	0.590
80	1.613	5.2	0.3	2.0	0.592
90	1.673	4.8	0.3	1.7	0.593
100	1.732	4.0	0.2	1.5	0.595

Figure 6 illustrates the prestrain dependence of the three model parameters. For illustration purposes, we have fitted an exponential function to the discrete parameter values. All three parameters, c₀, c₁, and c₂, display a sharp exponential decay. Their initial rapid decrease flattens out at higher prestrain levels. The graphs confirm that the parameter c₂ associated with the anisotropic invariant I₄ is consistently larger than the parameter c₁ associated with the isotropic invariant I₁, which displays a faster exponential decay.

Figure 6.

Material parameter values for mitral leaflet tissue identified for different prestrain levels.

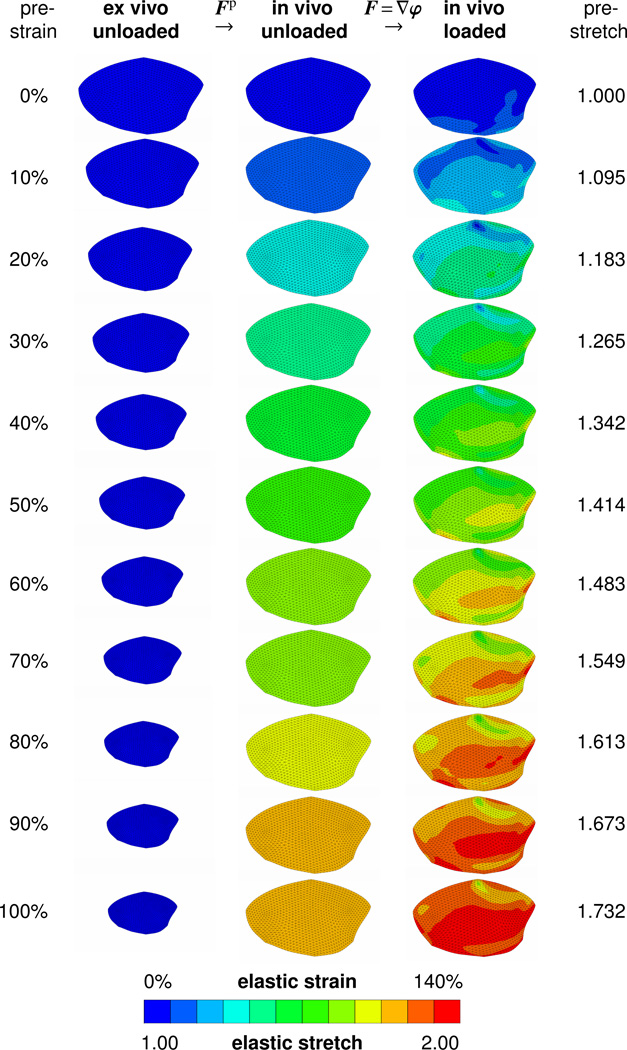
Figure 7 visualizes the three configurations of the thin membrane for prestrain levels varying from 0% to 100%. All leaflets are color-coded for the maximum principal elastic Green Lagrange strain and are drawn to scale. The first column contains the leaflets in the ex vivo unloaded configuration ℬ_e, before we apply prestrain. Elastic Green Lagrange strains are zero across all the leaflets. With increasing levels of prestrain, the leaflet size in the first column decreases as we isotropically scale down the leaflet dimensions. The second column contains the leaflets in the in vivo unloaded configuration ℬ₀, after we applied the corresponding prestrain level. Elastic Green Lagrange strains in the second column are homogeneous and present the individual prestrain levels. By construction, the elastic Green Lagrange strains of the in vivo unloaded configuration ℬ₀ increase with the prestrain level. The third column contains the leaflets in the in vivo loaded configuration ℬ_t, after we applied prestrain and the in vivo loading. Elastic Green Lagrange strains in the third column are inhomogeneous and increase nonlinearly with the prestrain level.

Figure 7.

Maximum principal elastic Green Lagrange strains and corresponding elastic stretches for different prestrain levels. From the ex vivo unloaded configuration ℬ_e to the in vivo unloaded configuration ℬ₀, the membrane is prestrained through a prestrain F^p of different levels. From the in vivo unloaded configuration ℬ₀ to the loaded configuration ℬ_t, the membrane is subjected to the experimentally measured load resulting in the deformation gradient F = ∇φ. The color-coded elastic strains are a result of the composition of both mappings, F^e = F · F^p.

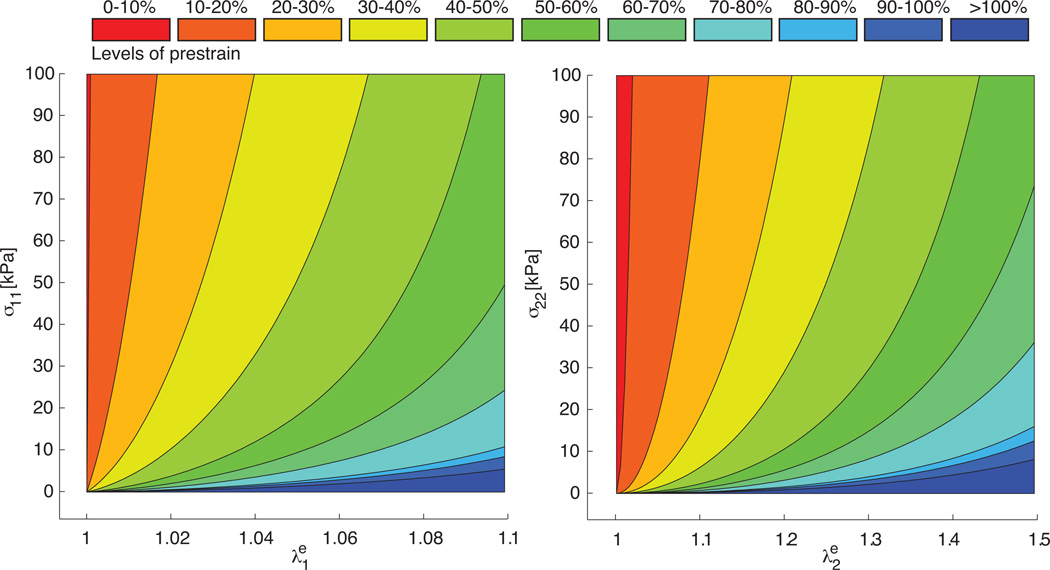
Figure 8 illustrates the effect of the different parameter sets on the constitutive response of a thin biological membrane in a homogeneous biaxial tension test. It displays the Cauchy stresses parallel and perpendicular to the collagen fiber direction σ₁₁, left, and σ₂₂, right, as functions of the corresponding elastic stretches ${\lambda }_1^{\mathrm{e}}$ and ${\lambda }_2^{\mathrm{e}}$. To highlight the continuous dependence of the stress-stretch behavior on the prestrain level, we color-coded the regions between the curves of the individual prestrain levels. The curves demonstrate the typical nonlinear stress-elastic-stretch behavior characteristic for collagenous soft biological tissues. As we increase the prestrain level, the material parameters c₀, c₁, and c₂ decrease, and the overall response seems to soften. Consequently, the stress-stretch curves flatten with increased prestrain levels.

Figure 8.

Homogeneous biaxial tension test for different prestrain levels. Cauchy stresses parallel to fiber direction σ₁₁ vs. elastic stretch ${\lambda }_1^{\mathrm{e}}$, left, and Cauchy stresses perpendicular to fiber direction σ₂₂ vs. elastic stretch ${\lambda }_2^{\mathrm{e}}$, right. To calculate the stress-stretch curves, we used the individual parameter sets for the different prestrain levels summarized in Table 1.

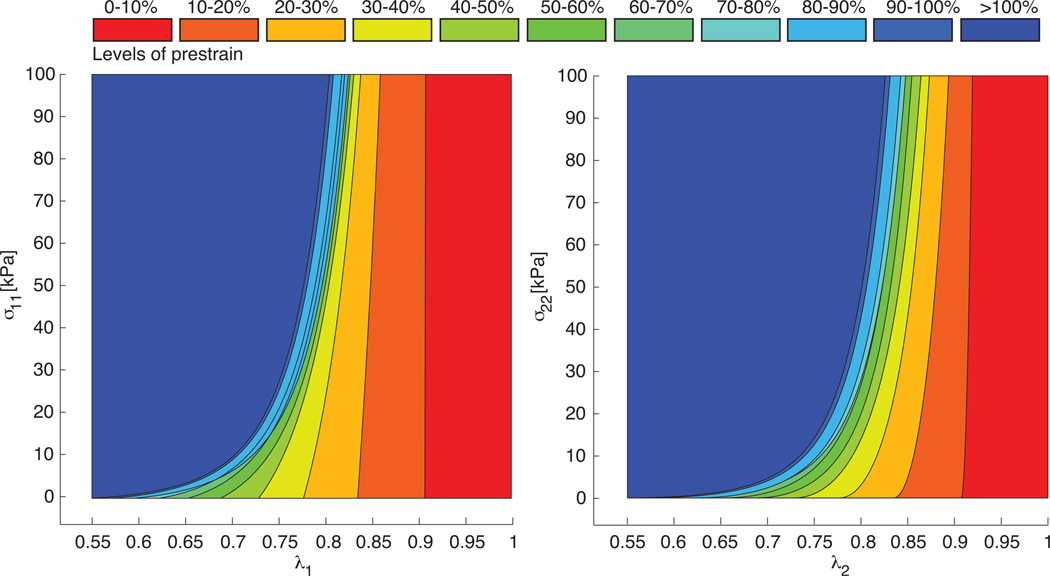
Figure 9 further illustrates the effect of the different parameter sets on the constitutive response of a thin biological membrane in a homogeneous biaxial tension test. In contrast to Figure 8, Figure 9 displays the Cauchy stresses parallel and perpendicular to the collagen fiber direction σ₁₁, left, and σ₂₂, right, as functions of the corresponding total stretches ${\lambda }_1={\lambda }_1^{\mathrm{e}}/{\lambda }^{\mathrm{p}}$ and ${\lambda }_1={\lambda }_2^{\mathrm{e}}/{\lambda }^{\mathrm{p}}$. This implies that we have virtually removed the prestrain λ^p. Accordingly, the curves shift to the left, depending on the prestrain level. The stretch-axis intercepts at σ = 0 indicate the inverse prestrain level 1/λ^p and the stress-axis intercepts at λ = 1 indicate the residual stress induced through prestrain. While the stress-elastic-stretch curves shown in Figure 8 seem to flatten with increased prestrain level parameters, the stress-stretch curves in Figure 9 demonstrate that these curves actually display a significant exponential stiffening at comparable stretch levels λ.

Figure 9.

Homogeneous biaxial tension test for different prestrain levels. Cauchy stresses parallel to fiber direction σ₁₁ vs. in vivo stretch ${\lambda }_1={\lambda }_1^{\mathrm{e}}/{\lambda }^{\mathrm{p}}$, left, and Cauchy stresses perpendicular to fiber direction σ₂₂ vs. elastic stretch vs. in vivo stretch ${\lambda }_2={\lambda }_2^{\mathrm{e}}/{\lambda }^{\mathrm{p}}$, right. To calculate the stress-stretch curves, we used the individual parameter sets for the different prestrain levels summarized in Table 1.

6. Discussion

Residual stresses, stresses that are relieved when a biological sub-system is isolated from its natural environment [15, 16], are inherent to virtually all living systems [10, 49]; yet, we know very little about them. While residual stresses are usually difficult to measure, residual strains are relatively easy to access as the inverse kinematic change upon isolation from the living system [4]. The concept of fictitious configurations [23, 27] provides an elegant theoretical framework to model prestrain and residual stress through the multiplicative decomposition of the total elastic deformation into prestrain-induced and load-induced parts, see Figure 2. In the present study, we extracted the load-induced kinematics and pressure values from in vivo experiments in sheep [41, 45], see Figures 1 and 3. To explore the effect of prestrain, we systematically prescribed different prestrain levels, and studied their impact on the overall mechanical characteristics of the mitral leaflet, see Figure 7, left column. Our central finding is that prestrain has a drastic effect on strain, stress, and stiffness. Because of the multiplicative nature of the kinematic model, a linear increase in prestrain is associated with a nonlinear increase in the overall strain, see Figure 7, right column. Because of the characteristic exponential strain-stiffening behavior of collagenous biological tissues, a linear increase in prestrain is associated with an exponential decrease in the apparent material stiffness, see Table 1 and Figure 6. For similar reasons, a linear increase in prestrain is associated with a nonlinear alterations in stress, see Figures 8 and 9.

6.1. Comparison to previous studies

Our in vivo mitral leaflet kinematics agree nicely with previously reported strains in sheep from sonomicrometry [46] and from video fluoroscopy [7, 41]. Circumferential and radial stretches of approximately 1.05 and 1.08 are in good qualitative agreement with values found for both techniques. However, our in vivo stretches are significantly lower than the ex vivo circumferential and radial stretches of 1.2 and 1.5 measured in porcine leafets in a left heart simulator under physiological loading conditions [20, 21, 26]. This difference between in vivo and ex vivo kinematics has previously been noted [41], but has never been explained to date. In view of the present study, we attribute this difference to the prestrain F^p between the ex vivo unloaded configuration ℬ_e and the in vivo unloaded configuration ℬ₀, see Figure 2. Under similar physiological loading conditions, the ex vivo experiments record the total elastic deformation F^e = F · F^p, i.e., the deformation between the ex vivo configuration ℬ_e and the in vivo loaded configuration ℬ_t, while the in vivo experiments only record the in vivo deformation F = ∇φ, i.e., the deformation between the in vivo unloaded configuration ℬ₀ and the in vivo loaded configuration ℬ_t. This difference is visualized in Figure 8 and 9, where we plot the stresses of a biaxial tension test against the ex vivo recordable total elastic stretches λ^e, Figure 8, and against the in vivo recordable load-induced stretches λ = λ^e/λ^p, Figure 9. First experimental studies on mitral leaflets in the early 1970s were based on ex vivo uniaxial testing of explanted human leaflets in the circumferential direction. To account for the fundamentally different constitutive response before and after collagen stiffening, these early studies introduced two different tangent moduli and reported the pre- and post-translational leaflet stiffnesses to $E_{\mathrm{c}\mathrm{c}}^{\text{pre}}=10\mathrm{k}\mathrm{P}\mathrm{a}$ and $E_{\mathrm{c}\mathrm{c}}^{\text{post}}=\mathrm{4,833}\mathrm{k}\mathrm{P}\mathrm{a}$ averaged over four human leaflets [17], and to $E_{\mathrm{c}\mathrm{c}}^{\text{pre}}=11.3\mathrm{k}\mathrm{P}\mathrm{a}$ and $E_{\mathrm{c}\mathrm{c}}^{\text{post}}=\mathrm{2,970}\mathrm{k}\mathrm{P}\mathrm{a}$ averaged over 25 human leaflets [11]. In the early 1990s, similar ex vivo uniaxial experiments were performed on porcine mitral leaflets, but now in both circumferential and radial directions with $E_{\mathrm{c}\mathrm{c}}^{\text{pre}}=44\mathrm{k}\mathrm{P}\mathrm{a},E_{\mathrm{c}\mathrm{c}}^{\text{post}}=\mathrm{5,976}\mathrm{k}\mathrm{P}\mathrm{a},E_{\mathrm{r}\mathrm{r}}^{\text{pre}}=16\mathrm{k}\mathrm{P}\mathrm{a}$, and $E_{\mathrm{r}\mathrm{r}}^{\text{post}}=\mathrm{1,557}\mathrm{k}\mathrm{P}\mathrm{a}$ [31]. Stiffness ranges were similar to the human leaflet, however, this study revealed the characteristic leaflet anisotropy with a three times larger stiffness circumferentially than radially, i.e., in the direction of the principal collagen fiber orientation. A combined uniaxial and biaxial study of porcine mitral leaflets in the mid 1990s confirmed these observations with $E_{\mathrm{c}\mathrm{c}}^{\text{pre}}=89.3\mathrm{k}\mathrm{P}\mathrm{a},E_{\mathrm{c}\mathrm{c}}^{\text{post}}=\mathrm{8,960}\mathrm{k}\mathrm{P}\mathrm{a},E_{\mathrm{r}\mathrm{r}}^{\text{pre}}=60.5\mathrm{k}\mathrm{P}\mathrm{a}$, and $E_{\mathrm{r}\mathrm{r}}^{\text{post}}=\mathrm{2,400}\mathrm{k}\mathrm{P}\mathrm{a}$ [33]. Last, a systematic study on healthy and diseased human mitral leaflets about a decade ago reported the healthy post-transitional moduli to $E_{\mathrm{c}\mathrm{c}}^{\text{post}}=\mathrm{3,550}\mathrm{k}\mathrm{P}\mathrm{a}$ and $E_{\mathrm{r}\mathrm{r}}^{\text{post}}=\mathrm{2,292}\mathrm{k}\mathrm{P}\mathrm{a}$, and found these values to double in the diseased state [19]. In summary, stiffness values of all studies lie consistently in the same range, even for different species, with a stiffening of approximately two orders of magnitude between the pre- and post-translational regimes.

A few years ago, a study based on marker videofluoroscopy and linear inverse finite element analysis reported the first in vivo mitral leaflet stiffness in the beating ovine heart [28]. Surprisingly, the study identified the circumferential and radial leaflet stiffnesses to E_cc=43,000kPa and E_rr=11,000kPa, stiffness values that were consistently one and three orders of magnitude larger than the previously reported pre- and post-transitional stiffness values [30]. This tremendous stiffness difference between ex vivo and in vivo data stimulated vivid discussions and ongoing debate about the possible mechanisms of in vivo stiffening. A potential explanation is active muscle cell contraction, present in vivo but not ex vivo [25, 48]. To quantify the impact of active contraction throughout the cardiac cycle, stiffness values were identified during isovolumetric contraction and isovolumetric relaxation with circumferential and radial stiffnesses increasing by 41.3% and 54.5% during the contractile phase [29]; yet, not enough to explain a difference of orders of magnitude. To increase active contraction, the mitral valve complex was subjected to vegal nerve stimulation to further increase the circumferential and radial stiffnesses by 63.6% and 80.0% [25]; again, not enough to explain a difference of orders of magnitude. The effect of prestrain, as discussed in this manuscript, could easily explain these controversies, however, only in combination with a nonlinear constitutive equation.

Up until the mid 1990s, it was quite common in the bioengineering community to model the constitutive behavior of biological membranes through a bi-linear model with two distinct stiffness values in the pre- and post-translational regimes. The first study to use an exponential Fung-type free energy function for biological membranes was proposed two decades ago [24]. It was soon adapted for porcine mitral leaflets using the free energy function $\mathrm{\psi ̄}={\mathrm{c̄}}_0[\text{exp}({\mathrm{c̄}}_1{[{Ī}_1^{\mathrm{e}}-3]}^2+{\mathrm{c̄}}_2{[{{Ī}_4^{\mathrm{e}}}^{1/2}-1]}^4)-1]$ with the following three material parameter values c̄₀ = 0.399kPa, c̄₁ = 4.325, c̄₂ = 1446.5 [34] calibrated with earlier ex vivo data [33]. Here, we used a slight modification of this free energy function $\mathrm{\psi ̄}=c_0[\text{exp}(c_1{[{Ī}_1^{\mathrm{e}}-3]}^2+c_2{[{Ī}_4^{\mathrm{e}}-1]}^2)-1]$ as introduced in equation (16). When calibrated with the same ex vivo data [33], its parameters take the following values c₀ = 0.0520kPa, c₁ = 4.63, and c₂ = 22.6 [38]. When calibrated with in vivo data using marker videofluoroscopy and nonlinear inverse finite element analysis, we found its parameters to take the following values c₀ = 119; 020.7kPa, c₁ = 152.4, and c₂ = 185.5, see Table 1. Qualitatively, these in vivo parameters of the nonlinear model lie within the same range as the in vivo parameters of the linear model [28]. However, consistent with the ex vivo and in vivo parameters of the linear constitutive model, the ex vivo and in vivo parameters of the nonlinear constitutive model differ by orders of magnitude. This raises the question which parameters we should use in future simulations? Or, more provokingly, how useful are ex vivo determined material parameters when we try to make predictions of a living system?

In linear finite element simulations with the in vivo fitted parameters, the computational analysis overestimated the stresses by a factor three beyond the failure stress [29]. In nonlinear finite element simulations with the ex vivo fitted parameters, the computational analysis overestimated the structural deformations by a factor two [38]. The nonlinear model we propose here is calibrated to in vivo data [45]; its computational analysis inherently predicts the correct structural deformations for all prestrain levels. So the question is rather, what is the correct prestrain level?

Recent prestrain measurements indicate an area reduction of 43% upon leaflet explantation [4]. Assuming the pre-strain is isotropic in the leaflet plane F^p = λ^p [I − m₀ ⊗ m₀] + [m₀ ⊗ m₀] / λ^p2, this would correspond to a prestretch of λ^p = 1/[1.00 − 0.43]^1/2 = 1.32. For this prestretch level, we interpolate the following parameter values c₀ = 26.7kPa, c₁ = 1.5, and c₂ = 6.8 from the data in Table 1, illustrated also in Figure 6. Although not identical, these in vivo parameter values with λ^p = 1.32 prestretch are much closer to the previously reported ex vivo parameter values of c₀ = 0.052kPa, c₁ = 4.63, c₂ = 22.6 [38].

6.2. Limitations

We view this study as a first prototype analysis of prestrain and residual stress in thin biological membranes. As such, it provides valuable insight into the interplay between prestrain-induced and load-induced deformation. Despite these promising first results, some limitations are inherent to the proposed method. Some have already been addressed in detail in previous publications, e.g., limitations related to the experimental data acquisition [7, 32], limitations related to data averaging over 57 animals [42, 43], limitations related to creating a smooth surface from 23 discrete points [18], limitations related to the inverse finite element analysis itself [28], limitations related to additional parameters such as chordae stiffness and leaflet thickness [45], and limitations related to differences in species such as pig, sheep, and human [42]. Additional potential limitations specific to this particular study are limitations related to this specific constitutive model [34, 38], limitations related to the assumption of a transversely isotropic prestrain [4], and limitations related to the compatibility of prestrain [9, 14].

7. Conclusion

This study has, for the first time, systematically quantified the effects of prestrain and residual stress in thin biological membranes in vivo. Previous studies had revealed three unresolved discrepancies in kinematic, equilibrium, and constitutive properties derived from ex vivo and in vivo measurements: Ex vivo strains were larger by a factor two than in vivo strains; in vivo stresses were larger by a factor three than ex vivo failure stresses; and, most drastically, in vivo stiffnesses were up to three orders of magnitude larger than ex vivo stiffnesses. Here we have shown that all three discrepancies can be explained by the concept of prestrain. Since the degree of prestrain in thin biological membranes has not been fully characterized to date, we systematically explored the effect of different prestrain levels, first in an in vivo parameter identification, then in an ex vivo biaxial test. Our studies reveal that the reported area reduction of 43% upon leaflet explantation associated with a prestretch of 1.32 would indeed reduce the membrane stiffness from 119,020.7kPa for the prestrain-free case to 26.7kPa for the reported prestrain level, an apparent stiffness reduction of four orders of magnitude. While these numbers might be specific to the anterior mitral leaflet, we believe that other thin collagenous membranes such as the fetal membrane, liver capsule, renal capsule, ear drum, pericardium, peritoneum, pia mater, dura mater, and skin display conceptually similar characteristics. Our findings suggests that prestrain plays a critical role in the mechanics of thin biological membranes. Neglecting its effects might fundamentally change the underlying load carrying mechanisms and might result in significantly under- or over-estimated material and structural properties. As such, our findings have direct implications in medical device design, in tissue engineering, and in other fields of material sciences targeted at designing replacement materials which resemble the native characteristics of thin biological structures.