Emergent properties during dorsal closure in Drosophila morphogenesis

Abstract

Dorsal closure is an essential stage of Drosophila development that is a model system for research in morphogenesis and biological physics. Dorsal closure involves an orchestrated interplay between gene expression and cell activities that produce shape changes, exert forces and mediate tissue dynamics. We investigate the dynamics of dorsal closure based on confocal microscopic measurements of cell shortening in living embryos. During the mid-stages of dorsal closure we find that there are fluctuations in the width of the leading edge cells but the time-averaged analysis of measurements indicate that there is essentially no net shortening of cells in the bulk of the leading edge, that contraction predominantly occurs at the canthi as part of the process for zipping together the two leading edges of epidermis and that the rate constant for zipping correlates with the rate of movement of the leading edges. We characterize emergent properties that regulate dorsal closure, i.e., a velocity governor and the coordination and synchronization of tissue dynamics.

1. Introduction

We have been investigating the molecular, cellular and emergent properties that collectively result in dorsal closure, an essential stage of Drosophila development that is a model system for cell sheet morphogenesis and wound healing [1–5]. The Drosophila embryo is comprised of cells that are specialized into distinct cell types, which organize into tissues. These cells grow, divide and die; form mechanical attachments and exert forces on neighboring cells; produce molecular signals to influence other cells both near and far; and respond to both molecular and mechanical signals [6]. The genome encodes the possibilities for molecular and cellular activities and the activities can vary spatially from cell-to-cell and temporally from one stage of development to another. Accounting for the dynamic tissue geometry exhibited during closure requires characterizing emergent properties, i.e., properties in addition to the multiplicity of molecular and cellular activities that arise when considering tissues as a collection of interconnected cells.

Dorsal closure has been the subject of extensive biological investigations [7–11]. Closure commences about ~10–10.5 h after egg laying and completes in ~2.5–3 h. More than 60 genes are known to contribute to dorsal closure [1, 8, 9], which involves three distinct epithelial tissue types that undergo little or no cell division during this stage of development. Dorsal closure can be imaged in living embryos, where the expression of green fluorescent fusion proteins provides contrast, and embryos can be gently flattened against a glass coverslip so that most of closure can be viewed in a single image plane (Movie 1, Supplemental Material, 7) stacks.iop.org/PhysBio/5/015004. Figure 1(a) presents a confocal micrograph of the dorsal surface showing the lateral epidermis, the leading edge of the lateral epidermis that contains a supracellular purse string and the amnioserosa. Throughout closure, the leading edges of two advancing flanks of lateral epidermis demarcate an eye-shaped opening on the dorsal side of the embryo. This opening exhibits approximate symmetries that are preserved throughout much of closure such that the dynamic geometry of the dorsal opening is somewhat reminiscent of the sun setting over a flat horizon (figure 2(a)). Nevertheless, clear and consistent asymmetries characterize real closure [12]. The amnioserosa completely fills the dorsal opening, with the amnioserosa cells extending below the two leading edges a distance corresponding to the length of a lateral epidermal cell or equivalently to the width of an amnioserosa cell. This structural relationship is maintained throughout closure, indicating that leading edge cells do not crawl over an amnioserosa substrate. The two leading edges meet and are adhesively zipped at each canthi, i.e., the two corners of the eye-shaped dorsal opening (figure 1), where the opposing leading edge cells are aligned when zipped together at each canthus [8, 9, 13]. Recently some patterned positional exchange of a small number of cells along each leading edge has been observed prior to entering the zipping process [13]. As we will show, this cellular remodeling of the free leading edge does not seem to significantly alter the net length of the purse string in a systematic way.

Figure 1.

(a) Confocal fluorescent image of wild-type dorsal closure. AS indicates the amnioserosa and LE indicates the lateral epidermis. The two leading edges are determined by the fluorescence from the two purse strings, which defines the eye-shaped dorsal opening. The two canthi, separated by a distance W along the dorsal midline, are located at the corners of the dorsal opening where the two leading edges are ‘zipped’ together. The maximum height h of the dorsal opening defines the symmetry point. The two dashed boxes are expanded in (b) and (c). The asterisks identify four examples of fiducial markers. Expanded views of the columnar cells of the lateral epidermis and the polygonal cells of the amnioserosa (b) near the anterior canthus and (c) along the free leading edge. Each length bar is 20 µm.

Figure 2.

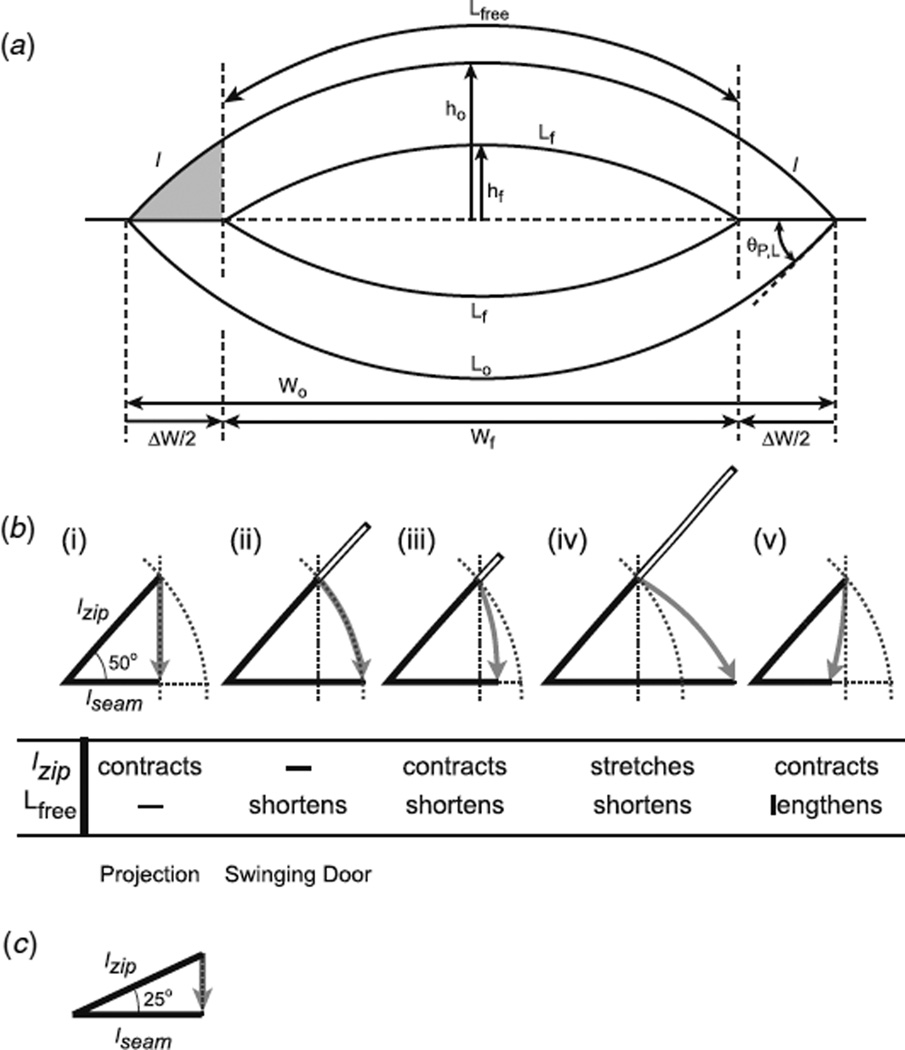
(a) Geometry for an idealized, fully symmetric dorsal opening at two times relative to ten zipping steps occurring approximately midway through closure. The original time t_o at the beginning of the first step and the final time t_f at the end of the tenth step are drawn to scale (compare figure 1(a) to original dorsal opening in figure 2(a)). The lower leading edges L_o and L_f are labeled by original and final times, respectively. Note that L_free, the fraction of L_o within the inner pair of dashed vertical lines, can be translated into L_f. The leading edge cells in the two segments l, each contain ten cells, and constitute those parts of L_o that are incorporated into the anterior and posterior seams, respectively, as represented in L_f. h(t) is the height of the dorsal opening at the symmetry point. The original h_o and final h_f are shown slightly displaced from the symmetry point for clarity. θ(t_o) = θ_P,L(t_o), here shown on a diagram of a fully symmetric dorsal opening. W_o and W_f are the canthus-to-canthus distances, but have been translated below the dorsal opening for clarity. ΔW is the growth in length of the two seams during the ten zipping steps. A key issue is summarized schematically by the gray region at the left canthus: how is the length of l reconciled with the length of Δ W/2? (b) Five alternative scenarios for the zipping step at θ(t_i) = 50° (see the text), where the gray region has been rescaled for a single zipping step. The dotted vertical and curved lines in cases (i)-(v) are for comparison to the projection (case (i)) and swinging door (case (ii)) models, respectively. The open bars in cases (ii)-(iv) represent the excess length taken up by contraction of L_free during a zipping step, where in each case the sum of the lengths of l_zip and the open bar produce the hypotenuse of a right triangle analogous to the gray zone of figure 1 (a). In essence, the length of the open bar keeps track of any excess length that is not processed by the leading edge cell l_zip during a zipping step and instead is processed by L_free. The table summarizes the changes in l_zip and L_free that occur as a consequence of each of the cases. (c) Case (i) for θ(t_i) = 25°.

We have investigated the mechanics of dorsal closure using the tools of genetics, in vivo confocal microscopy, laser microsurgery, digital image processing and biophysical modeling to quantify the processes that are responsible for closure [12, 14]. We developed a UV laser microbeam with subcellular spatial resolution that can be steered across the dorsal surface to selectively perturb specific biological processes [15]. We showed that four biological processes are responsible for dorsal closure: the contractile force of the actomyosin-rich purse string, the contractile force of the cortical actomyosin networks of the amnioserosa cells, the resistive force due to stretching of the lateral epidermis and zipping at each canthus [14]. We assessed the relative magnitudes for the three applied forces and for the force due to visco-elastic drag acting on a point of the leading edge, which were summarized as dimensionless ratios normalized by the smallest stress/force in each ladder (bv_native in the first ladder, σ_LEds_LE in the second ladder):

$$~510:380:130:1\ge {\sigma }_{\text{LE}}:{\sigma }_{\text{AS}}:T\kappa :{\text{bv}}_{\text{native}}\ge ~490:380:110:1$$ (1)

$$~15:3:1\ge T:{\sigma }_{\text{AS}}\mathrm{d}{s}_{\text{AS}}:{\sigma }_{\text{LE}}\mathrm{d}{s}_{\text{LE}}\ge ~6:3:1$$ (2)

where σ_LE and σ_AS are the magnitudes of the stress and ds_LE and ds_AS are the width of the lateral epidermis and the amnioserosa cells, respectively. T is the magnitude of the tension in the purse string, κ is the curvature of the leading edge, Tκ is the component of the forces produced by the purse string perpendicular to the dorsal midline and bv_native is the magnitude of the viscous drag/unit length [12, 14]. The sum of the applied stresses due to the lateral epidermis, the amnioserosa or the supracellular purse string is thus a small fraction (1/100–1/500) of each of the applied stresses in the direction of motion or if the magnitude of applied forces are compared to the net force, the fractions are in the range 1/1000 to 1/10 000. Most interestingly, for native dorsal closure in the absence of laser perturbations the net effect of the applied forces is to move each leading edge toward the dorsal midline with a constant speed v_native = dh/dt = 6.0 ± 0.3 nm s⁻¹ [12], i.e., a velocity governor effect, where h is the distance from the symmetry point of the leading edge to the dorsal midline (figure 1(a)).

We previously described the zipping process by a rate equation, initially a phenomenological insight [14] that was subsequently shown to be a geometric property of intersecting circular arcs [12]. For an idealized, fully symmetric dorsal opening, the rate equation is (equation (B.11) of [12]),

$$\mathrm{d}W/\mathrm{d}t=-k_{\mathrm{z}}/\text{tan}\theta$$ (3)

where W is a measure of the canthus-to-canthus distance along the dorsal midline (figures 1(a) and 2(a)), k_z is the rate constant for zipping and the angle is defined by the intersection of a leading edge with the dorsal midline as described in section 2. Interestingly, another geometric property of the dorsal opening is a correlation between the rate constant for zipping and v_native with k_z = −2v_native in the limit of constant curvature of the leading edges throughout closure. This correlation is relatively insensitive to the small changes in curvature of the leading edges experimentally observed during the mid-stages of dorsal closure due to a geometric property of intersecting circular arcs [12].

Equation (3) can be generalized to a more realistic, asymmetric geometry for the dorsal opening (equation (5) of [12]):

$$\mathrm{d}W/\mathrm{d}t=-k_{\mathrm{z},\mathrm{A}}/[\text{tan}{\theta }_{\mathrm{A},\mathrm{R}}(t)+\text{tan}{\theta }_{\mathrm{A},\mathrm{L}}(t)]-k_{\mathrm{z},\mathrm{P}}/[\text{tan}{\theta }_{\mathrm{P},\mathrm{R}}(t)+\text{tan}{\theta }_{\mathrm{P},\mathrm{L}}(t)]$$ (4)

where k_z,A and k_z,P are the rate constants for zipping at the anterior and posterior canthus, respectively. By convention, views of the dorsal surface are presented with the anterior side to the left and the posterior side to the right. As a consequence, the embryo’s right is presented above the dorsal midline and the embryo’s left is presented below the dorsal midline. Therefore, the four angles defined by the intersections of the two leading edges with the dorsal midline are θ_A,R, θ_A,L, θ_P,R and θ_P,L (figure 2(a)). For the idealized, fully symmetric embryo k_z,A = k_z,P = k_z and θ_A,R = θ_A,L= θ_P,R= θ_P,L = θ and equation (4) is equivalent to equation (3). In Peralta et al [12], we observed k_z,A was ~44% larger than k_z,P during native closure, i.e., an antero-posterior asymmetry, and applied equation (4) to investigations of the resiliency of dorsal closure as summarized in the following paragraph.

Dorsal closure is remarkably resilient to laser perturbation of any one of the four biological processes, which is attributable to the capacity of the remaining processes to compensate [11, 12, 14]. One process for compensation is the asymmetric upregulation of the zipping rate constants, which is correlated with the native asymmetry summarized in the previous paragraph. More specifically, k_z,P almost doubled when zipping at the anterior canthus was laser perturbed, while k_z,A increased by less than 10% when zipping at the posterior canthus was laser perturbed [12]. Another process for compensation is the upregulation in the force produced by the amnioserosa, which was increased by ~37% when zipping at both canthi was laser perturbed [12]. Remarkably, for each of these examples of upregulation there essentially was no overall delay due to laser perturbation and dorsal closure completed on schedule [14].

Dorsal closure slows considerably and eventually fails in embryos homozygous for basket, myospheroid or scab mutations. Basket encodes the Drosophila Jun-N-terminal kinase, a member of an essential signaling pathway that specifies, patterns and regulates dorsal closure through the transcipritional activation of target genes [16]. In addition, myospheroid and scab encode the α_PS3 and β_PS subunits, respectively, of the integrin, transmembrane adhesion and signaling protein [17–19]. A quantitative comparison of dorsal closure in wild-type embryos to closure in these mutant embryos indicated that defects in zipping precede absolute failure of the closure process heralded by rips between the leading edge and amnioserosa cells due to defects in cell–cell adhesion [12, 14]. The scab mutant phenotype is a remarkable example, where at the anterior canthus the rate of seam formation (see figure 2(f), [12]) and thus the zipping rate constant k_z,A were zero.

One geometric feature of dorsal closure is that the two leading edges, which are well approximated as circular arcs, eventually form a linear seam as a consequence of the zipping process at the two canthi (figures 1 and 2). Since the contour length for a curve between two points necessarily exceeds the length of the straight line between those two points, this raises the question as to what biological processes account for the difference between the contour length of the leading edge L and the length of the seam W, i.e., the excess length L — W.

Here we experimentally characterize the geometric properties of the dorsal opening and, in particular, track the widths of the leading edge cells during native dorsal closure in wild-type embryos, i.e., in the absence of genetic or laser perturbations. Based on these observations, we further characterize the zipping process, identify the biological process that accounts for the excess length and provide a rationale for a velocity governor, which ensures constant v_native with respect to time during wild-type dorsal closure.

2. Materials and methods

The fly genetics and optical design have been described in detail previously [7, 11, 15] and will be summarized here. All Drosophila melanogaster fly lines were homozygous for a transgene that encodes GFP fused to the actin binding region of moesin and is expressed under the control of the spaghetti squash promoter rendering F-actin fluorescent in vivo in essentially all cells. Wild-type flies were collected, dechorionated and subsequently mounted in a modified chamber between a gas permeable membrane (Teflon) and a glass coverslip that allowed development to proceed while time-lapsed confocal images were collected.

Fluorescent images were collected with a Zeiss LSM410 (488 nm excitation) laser confocal microscope using a 40 ×, 1.3 NA oil-immersion objective. Scanning time per image was either 1.08 or 1.14 s and either two or eight scans were averaged to produce an image. Three-to-five images were obtained at 0.49–0.58 µm depth intervals to produce a z-stack and were collected every 3–4 min. Sequences of images were stored for subsequent analysis and z-stacks were projected onto each other to facilitate image analysis.

The contours of the fluorescent leading edges from the confocal images were digitized using a customized active contour algorithm [20] implemented in ImageJ [21]. Once digitized, various geometrical parameters of the dorsal opening were obtained using custom programs in Mathematica and analyzed further. Each leading edge was visually inspected to identify fiducial markers, segmenting the leading edge into groups where each group had 5–20 cells, which could be tracked throughout closure. Unless otherwise noted, all results are reported as mean ± SEM (N), where SEM is standard error of mean and N is the number of trials.

Each angle θ_A,R, θ_A,L, θ_P,R or θ_P,L was determined from the dorsal midline and one of four line segments tangential to a leading edge, e.g., θ_P,L and its associated tangent as shown in figure 2(a). The first step was to locate each canthus. This was achieved by monitoring the separation between the two opposing leading edges, measured normal to the dorsal midline, which is indicated by W in figure 1(a). Since the width of a purse string is ~2 µm, we located the canthus point when the distance between the two leading edges was within 3 µm of each other. The second step then determined the tangential line segment. Note that curvature is evident for ten cells near the canthus (figures 1(a), (b) and 2(a)), but not for a single cell (figures 1(b) and 2(b)). Starting from the canthus point, the tangent was formed by stepping sequentially from the canthus point through the points of the digitized leading edge until a point no longer fell in line, i.e., curvature was realized. Using this algorithm, typically five or six points were collinear and defined the tangential line segment used to calculate each θ.

3. Results and discussion

3.1. Overview

The rationale underlying this approach includes testing models for the zipping step by taking advantage of accurate measurements of the geometry of the dorsal opening and circumventing limitations in optical resolution. Our imaging system cannot provide concurrently both cellular resolution and a global view of closure (figure 1). In contrast, in this global view we can make precise measurements as a function of time of the contour lengths of the two leading edges, the canthus-to-canthus length of the dorsal opening and the angles at the two canthi. Based on these measurements, we can quantitatively compare models for the zipping process. Since this analysis depends only on time-dependent measurements of the contour lengths of the leading edge, the canthus-to-canthus length and the angles at the canthi, it is generally applicable.

We investigated the dorsal opening as a whole to account for the difference between the contour lengths of the two leading edges and the canthus-to-canthus length, where this difference is the excess length. Our rationale is based on the geometric property that the contour length for a curve between two points necessarily exceeds the length of the straight line between those two points. Thus by the completion of closure, the excess length needs to be processed, i.e., accounted for by biological processes that take up the excess length. A key step was to compare this global analysis of the excess length to possible alternative cellular processes during a zipping step, i.e., a local analysis of the processing of excess length during a zipping step. We considered the ramification of this analysis for a proposed velocity governor, an emergent property of dorsal closure.

3.2. Excess length

We define the contour lengths of the two leading edges, L_R and L_L, which are well approximated as circular arcs. Here L can refer to either L_R or L_L. The difference between a contour length L and the straight-line canthus-to-canthus distance W is the excess length L – W. In the following discussion θ refers to the θ_A,R, θ_A,L, θ_P,R or θ_P,L that correlates both with L_R or L_L and with the end of the embryo that is being analyzed. At the early stages of closure (θ ≈ 50°), a typical leading edge has ~80 leading edge cells, with an average width of ~2.6 µm each, contributing to the overall length L. Three possibilities for taking up excess length are shortening/contraction of the leading edge cells, incorporation of leading edge cells into the seam due to the zipping process at each canthi and movement of the canthi toward the anterior or posterior pole away from the dorsal opening independent of the zipping process. Recently, it has been observed that five ptc cells from the lateral epidermis reproducibly advance to segments A1–A5 of the leading edge in a patterned positional exchange [13]. This is a relatively small number of cells and the remodeling occurs prior to the involvement of segments A1–A5 in the zipping process. Consequently, we do not consider positional exchange to be relevant to the leading edge cells involved in a zipping step. Below we will consider the possibility that remodeling changes the overall length of either leading edge.

Figure 2(a) superimposes two idealized dorsal openings, drawn to scale for a separation in time corresponding to ten zipping steps during the mid-stages of closure (i.e., at each canthus, ten lateral epidermal cells from the left and right leading edges are zipped together into the anterior and posterior seams), where the outer dorsal opening is earlier and the inner dorsal opening is later. By mathematical convention, we refer to the earlier time as ‘original’ and the later time as ‘final’ in the analysis of these ten zipping steps, with the expectation to iterate the analysis for the next ten zipping steps, etc. We define the contour length of the ‘free’ leading edge L_free as that fraction of the overall leading edge L not involved in zipping. The inner pair of vertical dashed lines highlights a geometric property of L_free that will prove to be advantageous in the following analysis. Note that the contour length L_free at the original time is identical to L_f at the final time. In addition, the gray region at the anterior canthus in figure 2(a) indicates the region of the dorsal opening that is lost as a consequence of ten zipping steps, where geometrically the arc l defines the upper edge and the lower edge is the horizontal line segment ΔW/2. l corresponds to the fraction of the leading edge at the original time and ΔW/2 corresponds to the fraction of the seam at the final time that were involved in this particular iteration of ten zipping steps.

Figure 2(b) summarizes five alternative cases for changes in individual cell widths during a zipping step at the anterior canthus. This consideration assumes that the leading edge cells do not exchange positions along either leading edge when near the canthi nor do they enter or leave their leading edge. We distinguish cell contraction or stretching that occurs as part of the zipping process from cell shortening or lengthening that occurs independent of the zipping process, i.e., along the ‘free’ leading edge L_free. For now, we do not consider any movement of the canthi independent of the zipping process, but will address this possibility in section 3.3. The five alternative scenarios for a zipping step are summarized in figure 2(b), which is drawn to scale for θ(t_o) = 50°. When drawn to scale for a single zipping step, we do not visualize curvature in the upper, angled edges in each case of figure 2(b), which contrasts with what we observed in the ten zipping steps that separate the original L_o and W_o (where curvature is observed) and the final L_f and W_f in figure 2(a). In each case of figure 2(b) and (c), l_zip is the average width of the leading edge cell at the beginning of a zipping step and is compared to the length of l_seam at the end of the zipping step, which lies along the horizontal. For the purpose of this illustration, l_zip is the same length for all cases, while the length of l_seam will be case specific.

The five cases presented in figure 2(b) survey the reasonable geometric possibilities for processing the excess length during a zipping step. The arrow idealizes the movement of one end of the leading edge cell l_zip as it rotates during a zipping step. Case (i) is the projection model, where l_zip contracts to l_zip cos θ(t_i) as the leading edge rotates into the seam. In this case, the change in excess length is completely coincident with and accounted for by zipping. For comparison purposes, the dotted vertical lines are included in the other cases to reference the projection model. Case (ii) is the swinging door model, where the leading edge cell rotates into the seam without contraction (l_zip then equals l_seam) and consequently the change in excess length (open bar in figure 2(b), case (ii)) is taken up by shortening L_free. Again for comparison, the dotted curved lines are included in the other cases to reference the swinging door model. For case (iii), the width of the leading edge cell contracts, is rotated into the seam, and there is shortening in L_free, i.e., case (iii) is an intermediate between the projection and swinging door models. For case (iv), the width of the leading edge cell stretches, rotates into the seam and all shortening occurs in L_free. In case (v), the width of the leading edge cell contracts, rotates into the seam and there is lengthening in L_free.

The extent of rotation and the amount of cell contraction or stretching during a zipping step systematically change as dorsal closure progresses. As a graphic representation of this property of dorsal closure, consider the projection model presented in figure 2(b), case (i), and in figure 2(c). The former corresponds to the geometry of the original dorsal opening in figure 2(a), θ(t_o) = 50°, while the latter corresponds to the geometry of the final dorsal opening, θ(t_f) = 25°, in that figure. As dorsal closure progresses, on average θ(t_i) decreases and consequently the amount of rotation during a zipping step decreases, and for the projection model for zipping the length of l_zip cos θ(t_i) also increases and approaches l_zip, i.e., a decrease in the amount of contraction (as discussed further in section 3.3).

Figure 3 reports an analysis of experimental measurements that tracks the length of the leading edge cells independent of the zipping process. Since our imaging system does not have the resolution we deem sufficient to track the width of a single leading edge cell with the precision we require, each leading edge was segmented into groups, each of which contains 5–20 cells, according to available fiducial markers (e.g., particularly bright cell boundaries depicted by asterisks in figure 1(a)). Each segment l_i, as shown schematically in the inset of figure 3(a), was tracked in time as long as it was independent of the zipping process (i = 2–6 in figure 3(a)). Figure 3(b) plots the percentage change in the length of segment l_i (t₀), [l_i(t) – l_i(t₀)]/l_i(t₀), indicating the order of magnitude for fluctuations is 10% of l_i. Summing the segments l_i yields L_bulk:

$$L_{\text{bulk}}=\mathrm{\Sigma }{l}_i\text{and}{l}_{\text{bulk}}=L_{\text{bulk}}/n$$ (5)

where n is the number of leading edge cells in L_bulk and consequently l_bulk is the average length of a leading edge cell contained in L_bulk. L_bulk(t) is an experimentally determined value. While the contour length L_free(t_i) decreases when iterating from zipping step i to zipping step i + 1, it is constant during the step and consequently referred to as L_free during a zipping step. In the ideal case, the length of L_bulk can be equal to the length of L_free, but in practice appropriate fiducial markers (see above) cannot always be found and consequently L_bulk ≤ L_free and both are less than L(t). Most importantly, L_bulk(t) tracks the change in length of the bulk of the leading edge not associated with the zipping process. Figure 3(c) plots L, W and L_bulk as functions of time. The step in L_bulk is a consequence of the onset of zipping in the cells of the outer segments l₂ and l₆; consequently, l₂ and l₆ were dropped in the determination of L_bulk starting at 1500 s.

Figure 3.

(a) Plots of the lengths l_i (t), for i = 2–6, determined from in vivo confocal images of dorsal closure, where the inset shows the segmentation of the leading edge into l_i (t), for i = 1–7. The experimental uncertainty in determining l_i (t) is ±0.6 µm, less than the widths of the symbols. L_bulk(t) is the sum for i = 2–6. Note that the outer segments l₂ and l₆ terminate once they participate in the zipping process at ~1250 s and ~1500 s, respectively. (b) Plots of the percentage change in length [l_i (t) – l_i (t₀)]/l_i (t₀). The error bars represent the propagation of the uncertainty in the experimental values for l_i (t) through the mathematical steps when performing this calculation. (c) Plots of L, W and L_bulk as a function of time, where the experimental uncertainties are less than the widths of the symbols.

Two key findings that can be drawn from the results summarized in figure 3(c) are that there is essentially no net shortening in L_bulk and L(t) correlates with W(t) but not with L_bulk. Thus applying equation (5) to the data in figure 3(c), we determined that dl_bulk/dt is not significantly different from zero during the mid-stages of dorsal closure, i.e., dl_bulk/dt = − 1.7 (±2.4) × 10⁻² nm s⁻¹ (4 embryos, 39 segments in total), thus we find that l_zip = l_bulk as each cell transitions from L_bulk(t) to participate in a zipping step and this experimental result validates our choice to hold l_zip constant for the purposes of illustration of the alternative cases of figures 2(b) and (c). Our analysis of L_bulk shows no clear evidence of an increase in length due to remodeling of the leading edge [13]. Our measurements track much of the duration of dorsal closure (θ ranges from ~50° to ~10°), but include neither the onset nor the very final stages of closure where circular arcs no longer provide a good fit to experimental data. Early closure may include some systematic shortening [9, 11] and the edge-to-edge character of late closure confounds interpretation [11, 12, 14]. Based on the results of figure 3, for these mid-stages of closure we conclude that on average the excess length L – W is predominantly taken up by the zipping process and consequently the projection model for zipping applies (case (i) of figures 2(b) and (c)).

Another key finding is that there are fluctuations in the length of segments l_i, each of which contains 5–20 cells, with cancellation occurring in the summation of L_bulk (equation (5)). While on average we observe essentially no change in l_bulk, due to cancellation the fluctuations in the width of an individual leading edge cell may be somewhat larger. Furthermore, it is possible that single leading edge cells are subject to additional higher frequency, albeit lower amplitude fluctuations than are resolved in our measurements. Consequently, a detailed model of the zipping process will need to accommodate significant fluctuations in the widths of the leading edge cells. Thus individual zipping steps may well be described by some or all of the other cases listed in figure 2(b) as individual leading edge cells are incorporated in a seam. Nevertheless, it is clear that on average the projection model depicted by case (i) describes the data accurately.

Previous measurements of dorsal closure found that the leading edge cells are shortening [11]. That study included the investigation of relatively early stages of dorsal closure where the supracellular purse string exhibited a dynamic, scalloped morphology, which is not seen in the later stages investigated here. One possibility is that the onset of the tension T in the purse string during these earlier stages leads to more consistent cell shortening as the scalloped geometry of the purse string transitions into an arc [9, 11].

3.3. Constraints on time-averaged zipping

The discussion of excess length reported in section 3.2 is based on the analysis of L and W, i.e. the dorsal opening as a whole. In this section, we demonstrate that this global analysis of a zipping step is consistent with a local analysis of processing the change in excess length via the projection model for zipping. We find that motion of the canthi independent of the zipping process, i.e. Δx_anterior and Δx_posterior, is not required to account for the change in excess length. We also consider the implications of the time-averaged projection model for the biological process of zipping.

The global perspective indicates that on average changes in excess length are processed by zipping, which must be consistent with the local analysis of the capability of zipping to fully process that change in excess length. While the global analysis relies on accurate measurements of L, W and L_bulk, the local analysis requires accurate measurements of θ_A,R, θ_A,L, θ_P,R and θ_P,L, as was summarized in section 2, and the two analyses must be quantitatively consistent. Figure 4(a) plots L, W and L – W. Since we are subtracting two large quantities in L and W, we verified that L – W retains significance. Indeed, L – W does exceed the noise and its slope is discernable as required for the following analysis. Furthermore, L and W can be well approximated as second-order polynomials. This allows facile estimates of dL/dt and dW/dt, which will be required for the analysis described below, as numerical determination of derivatives directly from the data is inherently noisy and typically useless in practice.

Figure 4.

(a) Polynomial fits to plots of L, W and the excess length L – W. L(t) = 229 µm – (1.35 × 10⁻² µm s⁻¹)t – (3.14 × 10⁻⁶ µm s⁻²)t² and W(t) = 208 µm – (7.36 × 10⁻² µm s⁻¹)t – (3.62 × 10⁻⁶ µm s⁻²)t². (b) Comparison of local (×’s) and global (solid curve) determinations of l_seam/l_zip. (c) Comparison of local (open squares) and global (dashed line) determinations of v_native. These are typical results (N = 12).

Before delving into the mathematical details for modeling an asymmetric dorsal opening, we will first frame the modeling approach in terms of a fully symmetric embryo with no motion of the canthi independent of the zipping process, i.e. Δx_anterior = Δx_posterior = 0. Figure 2 implicitly assumed no motion of either canthus independent of the zipping process during a zipping step, while the inset to figure 5(a) provides a graphic depicting canthus motion in addition to a zipping step and is described in detail later in this subsection. To test for consistency between the global and local perspectives, we model a time-averaged zipping step to start at t_i and end at t_ii, where Δt_zip(t_i) = t_ii – t_i. We treat zipping at the anterior and posterior canthi as occurring synchronously, an idealization that does not compromise our conclusions. An attribute of this model is it cites these start and end times for a zipping step, when we are informed by experimental measurements (figures 3 and 4(a)), and is insensitive at intermediate times to shape changes of those leading edge cells that are being incorporated into the seam during a zipping step. l in figure 2(a) is representative of ten zipping steps drawn to scale, but for the purposes of this paragraph can be reinterpreted as a single zipping step not drawn to scale. Then at the beginning of the zipping step l = l_zip, and for this idealized case L_bulk = L_free and L(t_i) = 2l_zip(t_i) + L_free. At the end of the zipping step L(t_ii) = L_free, l_seam(t_ii) = ΔW/2 and W(t_ii) = W(t_i) – 2l_seam(t_ii). Consequently, one net effect of this zipping step is to decrease L(t_i) by 2l_zip, where section 3.2 showed that the time-averaged value for l_zip is constant from one zipping step to the next. A second net effect of a zipping step is to decrease W(t_ii) by 2l_seam(t_ii), where the time dependence enters through the angular dependence as l_seam(t_ii) = l_zip cosθ (t_i) for the projection model for time-averaged zipping and θ(t_i) decreases from one zipping step to the next (figure 2). A third net effect, again invoking the projection model, is the change in the excess length, i.e. Δ (L – W) = − 2[l_zip – l_seam(t_ii)] = −2l_zip [1 – cosθ(t_i)].

Figure 5.

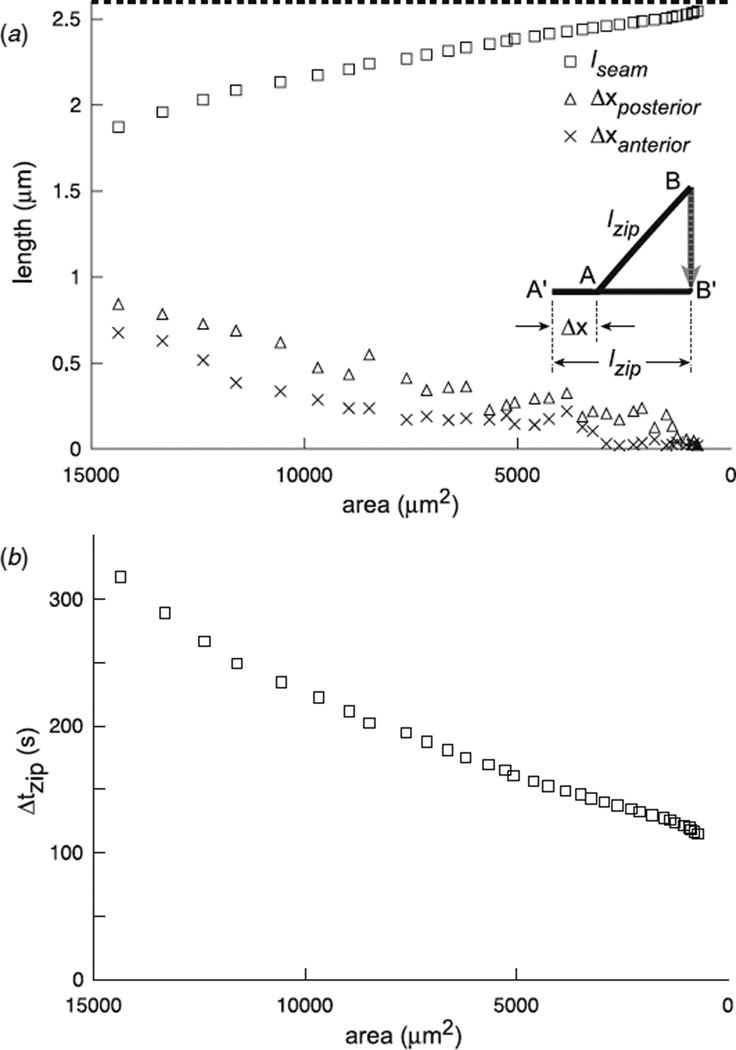
(a) l_seam based on the projection model for zipping where the change in excess length is processed by contraction, i.e., 2l_seam(t_ii) = l_zip cos θ_A(t_i) + l_zip cos θ_P(t_i). In addition, Δx_posterior and Δx_anterior based on an alternative model for zipping summarized in the inset where the proposed movement Δx of the anterior seam toward the anterior pole occurs coincidentally with the rotation of l_zip as part of the zipping step (see the text). The horizontal line at 2.6 µm represents the value for l_zip. (b) The time for a zipping step Δt_zip as determined by equation (6). All plots are as a function of the area of the dorsal opening. These are typical results (N = 12).

Given this framework, we now state the model for comparing the global and local processing of the change in the excess length in mathematical detail for an asymmetric dorsal opening. Δt_zip(t_i) and l_seam(t_ii) can be determined from the data presented in figure 4(a). Since from the local perspective ΔL(t_i)/Δt_zip(t_i) = −2 l_zip/Δt_zip(t_i) and ΔW(t_ii)/Δt_zip(t_i) = −2l_seam(t_ii)/Δt_zip(t_i), and from the global perspective ΔL(t_i)/Δt_zip(t_i) = dL(t_i)/dt and ΔW(t_ii)/Δt_zip(t_i) = dW(t_ii)/dt, we find

$$\mathrm{\Delta }{t}_{\text{zip}}(t_i)=-2l_{\text{zip}}/(\mathrm{d}L(t_i)/\mathrm{d}t)$$ (6)

$$l_{\text{seam}}(t_{\text{ii}})=-\frac{1}{2}(\mathrm{d}W(t_{\text{ii}})/\mathrm{d}t)\mathrm{\Delta }{t}_{\text{zip}}(t_i).$$ (7)

Inserting equation (6) into equation (7),

$$l_{\text{seam}}(t_{\text{ii}})/l_{\text{zip}}=(\mathrm{d}W(t_{\text{ii}})/\mathrm{d}t)/(\mathrm{d}L(t_i)/\mathrm{d}t).$$ (8)

Note that the term on the left-hand side of equation (8) is equivalent to cos θ(t_i), which is experimentally determined from a local analysis of a canthus. To take account of the asymmetric dorsal opening, we need to analyze the angles both at the anterior and posterior canthi, where for evaluations of L_R we define θ_A= θ_A,R and θ_P = θ_P,R and for evaluations of L_L we define θ_A = θ_A,L and θ_P = θ_P,L. This yields $l_{\text{seam}}(t_{\text{ii}})/l_{\text{zip}}=\frac{1}{2}[\text{cos}{\theta }_{\mathrm{A}}(t_{\mathrm{i}})+\text{cos}\theta P(t_{\mathrm{i}})]$. In contrast, the term on the right-hand side of equation (8) is to be determined from a global analysis, where it is straightforward to evaluate each time derivative from the fitted curves of W and L such as those presented in figure 4(a).

Consequently, equation (8) tests the consistency of the local and global perspectives. Figure 4(b) compares data for the left-hand side (×) to the curve generated by the right-hand side (solid curve) of equation (8). The two compare favorably, indicating the change in excess length determined from a global consideration of the dorsal opening can be processed during a zipping step. More specifically, the comparison of the global (solid curve) and local (×) perspectives for one embryo as shown in figure 4(b) is consistent for times longer than ~800 s, with the possible exception of times near 3600 s; however, this pattern is not systematic from embryo to embryo and deviation between the fits and the data are of similar magnitude, but largely random with respect to time during closure.

Deviations between the global and local analyses may be an indication that motion of the canthi independent of the zipping process plays a role, albeit relatively small. To explicitly consider this possibility, make the assumption that on average there is no net contraction during a zipping step, which is a logical alternative to the assumption that there was no motion of the canthi based on the projection model for zipping. In contrast to the swinging door model of case (ii) of figure 2(b), where the change in excess length is processed by L_free, for the model based on this new assumption the excess length essentially is taken up by motion of the canthi, i.e., a zipping step is motion of the canthus by the length Δx_anterior = l_zip[1 – cos θ_A(t_i)] and rotation, but no contraction. This can be visualized in the inset to figure 5(a), where Δx_anterior would move the anterior canthus from A to A′. Since l_zip would rotate about this moving end A, when l_zip has been fully incorporated into the seam, its end B would have moved to B′ as idealized by the arrow. Consequently, the net result would be the location of the anterior canthus due to motion and zipping has moved from A to B′. Figure 5(a) plots Δx_anterior and Δx_posterior. Δx_posterior > Δx_anterior is inconsistent with our previous observation that due to head involution, which occurs during the later stages of closure, the amount of motion at the anterior end of the dorsal opening is greater than that at the posterior end (figure 6 of [12]). However, when we hypothesized that the change in excess length was taken up by motion of the canthi, the implication was Δx_anterior should be greater than Δx_posterior. We conclude that the projection model without motion of the canthus is the dominant effect; however, small motion of the canthi independent of zipping may occur.

Having established that the projection model for a zipping step can consistently account for the loss of excess length as determined by the global analysis of the dorsal opening, we propose quantitative tests for future detailed models of the zipping process. Figure 5(a) presents l_seam(t_ii) as determined by equation (7) and Δx_anterior and Δx_posterior, and figure 5(b) presents Δt_zip(t_i) as determined by equation (6), where each is plotted as a function of the area of the dorsal opening. While l_seam at the end of a zipping step contracts by 30% of its initial length at the early stage of dorsal closure, it contracts a few per cent near the final stages. From the early to final stages, Δt_zip decreases by 60%. Measurements of l_seam(t_ii) are quite difficult given imaging resolution. Recognizing that the width of the leading edge cell is fluctuating as the cell is incorporated into the seam, it seems Δt_zip(t_i) may serve as a better measure for assessing detailed models of the zipping process.

3.4. Velocity governor

During our investigations of dorsal closure in wild-type embryos we repeatedly and uniformly observe that dh/dt = v_native is remarkably constant [12, 14], which is a velocity governor effect. Since the value for v_native does vary from embryo to embryo, we report uncertainties that are therefore primarily due to averaging over multiple embryos, i.e., v_native = −6.0 ± 0.3 nms⁻¹ [12], while the uncertainties in determining v_native for a single embryo are smaller (e.g. SEM(1) ≤ 0.8% of the rate; see table S1 in [14]).

The projection model for zipping offers a rationale for this empirical velocity governor. While the zipping process involves contraction and rotation, the free leading edge more-or-less uniformly translates toward the dorsal midline, as idealized in figure 2(a). The distance of the translation is determined by the angle of rotation, such that

$$\mathrm{\Delta }h/\mathrm{\Delta }{t}_{\text{zip}}(t_i)=-l_{\text{zip}}\text{sin}\theta (t_i)/\mathrm{\Delta }{t}_{\text{zip}}(t_i).$$ (9)

Figure 4(c) presents the local (open squares) and global (dashed line) perspectives for determining v_native. The data are determined by equation (9) and the line is determined from a linear least-squares fit of h(t) at the maximum dorsal opening for this embryo. Similar to the previous section, the comparison is favorable and while there are differences between the data and the dashed line, the pattern of difference is not systematic from embryo to embryo. Furthermore, using equations (2) and (7) and recognizing v_native = Δh/Δt_zip and l_seam = l_zip cos θ(t_i), equation (9) becomes

$${\upsilon }_{\text{native}}=-\frac{1}{2}{k}_{\mathrm{z}}.$$ (10)

For an asymmetric dorsal opening k_z,A and k_z,P contribute linearly and consequently the effective k_z will be the average of the two. The experimental values compare favorably: v_native = −6.0 ± 0.3 nm s⁻¹ and k_z = 13.0 ±1.0 nm s⁻¹, where k_z,A = 15.3 ± 0.7 nm s⁻¹ and k_z,P = 10.6 ± 1.7 nm s⁻¹ [12].

This result is consistent with the previous observation of the geometric correlation between k_z and − 2v_native, and in particular with k_z = − 2v_native in the limit of constant curvature of the leading edge [12]. Note that the correlation is between v_native, which is a measure of the rate of movement of the leading edge toward the dorsal midline and the zipping rate constant k_z. In contrast, the rate of zipping dW/dt along the dorsal midline is given by equation (3), where dW/dt is not constant due to the tan θ dependence. An increase in the rate of zipping is consistent with the systematic decrease both in the extent of rotation and the amount of contraction associated with a zipping step (figures 2(b) and (c)) and is reflected in the systematic decrease in the time required for a zipping step Δt_zip (figure 5(b)).

Consequently, we can characterize a velocity governor as a key emergent property of dorsal closure. This velocity governor is an attribute of the intersecting, circular arc geometry [12]; the time-averaged lack of contraction in L_bulk (figure 3(c)) and the net applied forces that act on each leading edge cell to translate L_free and to produce torques that support rotation in a zipping step. The rate constants for zipping k_z,A and k_z,P are strongly correlated with v_native and apparently function as a rate limiting process, although cause and effect remain an open research question. It is clear, however, that just as σ_LE, σ_AS and Tκ contribute to the net force on a leading edge cell, they also will contribute to the net torque that results in rotation during a zipping step.

4. Conclusion and outlook

We have investigated changes in the length of leading edge cells during the course of wild-type dorsal closure, advancing our understanding of the time-averaged zipping, a velocity governor and fluctuations. On average, the excess length is not taken up by shortening of L_free and instead is predominantly taken up by contraction as part of the zipping steps, which is consistent with severe defects in zipping observed when nonmuscle myosin is absent from a cell in the leading edge [9]. Consequently, on average the net effect of a zipping step can be described by the projection model (figure 2(b), case (i)). We conclude that both contraction and rotation occur as part of a zipping step, in decreasing amounts as closure progresses (case (i) of figure 2(b) and (c)). In addition, the duration of a zipping step also decreases as closure progresses (figure 5(b)).

Our time-averaged analysis of the velocity governor indicates the rate constants for zipping correlate with the rate of translation of the leading edges. Previously this correlation has been noted as a geometric property of the intersecting arcs defined by the two leading edges [12]. Here the tight coupling of the rate constant for zipping to v_native has been rationalized in terms of both contraction and rotation during the zipping process. Rotation during the zipping process quantitatively correlates with the translation of the leading edge. At this time, we do not fully understand how this tight coupling occurs given the compliant tissues involved in dorsal closure. It is clear that the zipping process alone does not account for the translation of L_free and that neither the leading edges, the bulk of the lateral epidermis, nor the amnioserosa are rigid bodies. To more fully account for this correlation we are exploring the role of the transition in curvature of the leading edge near the ends of L_free, where a change in curvature occurs to accommodate rotation in the zipping process.

It is interesting to consider the significant fluctuations observed in measurements in the widths of the leading edge cells in terms of the apparent synchronization and coordination of the dorsal opening during wild-type dorsal closure. While the applied forces acting on the leading edge cells during dorsal closure are the consequence of cellular activities in three tissues, we treat each as fluctuating about mean values. The order of magnitude of these fluctuations is significant, i.e., 10% of the time-averaged value. We interpret both the contraction of the leading edge cell being zipped and the shortening of the width of the free leading edge cell as actomyosin-II-based contraction [9]. Fluctuations in the widths of leading edge cells suggest that the cell-to-cell variability in intracellular active contractile mechanisms is also in the 10% range, a reasonable value given the observed 5% variability from embryo to embryo for k_z and for v_native [12]. Our outlook is that an emergent property underlies the correlation between the constant values for the rate constant for zipping and v_native that is insensitive to and thus accommodates inherent variability in the molecular and cellular processes that are responsible for closure. Thus, this emergent property would contribute to the coordination and synchronization of the dynamics of dorsal closure.

These observations have focused on native dorsal closure in wild-type embryos, in the absence of genetic or laser perturbations. In short, we have been characterizing the typical kinematics and dynamics of wild-type dorsal closure. In the past, we also have investigated laser and genetically perturbed dorsal closure [11, 12, 14], characterizing the range of dynamics that the dorsal opening is capable of producing in response to these perturbations. These include observations that suggest zipping is not always a rate limiting step for closure. In the future, we will investigate further how these emergent properties manifest themselves during perturbed closure.

Notation

b

viscous damping constant for a segment of the leading edge

ds_AS

width of an amnioserosa cell projected along the leading edge

ds_LE

width of a leading edge cell

h

maximum perpendicular separation (height) between a purse string and the dorsal midline. h_o indicates height at the original time and h_f indicates height at the final time with respect to a given zipping step or steps

k_z

rate constant for zipping, which can be specified for the anterior (k_z,A) or posterior (k_z,P) canthus or as an averaged result (k_z)

l

as shown in figure 2(a), the length of the arc of leading edge cells that will be incorporated into a seam in the next ten zipping steps

l_i

a segment of the free leading edge used in calculating L_bulk, containing 5–20 leading edge cells

l_bulk

the average width of a single leading edge cell in the free leading edge as determined experimentally by measuring L_bulk and the number n of leading edge cells

l_seam

the average width of a single leading edge cell upon incorporation into the seam at the end of a zipping step at time t_ii

l_zip

the average width of a single leading edge at the beginning of a zipping step at time t_i

L

contour length of a purse string from canthus to canthus. For an ideal embryo with left/right symmetry, both purse strings have the same value for L. For an embryo with left/right asymmetry, the two possible values are specified by L_R and L_L

L_bulk

measured part of the contour length L not involved with the zipping step(s) under consideration. An experimental approximation of L_free

L_free

idealized length of that part of contour length L not involved with the zipping step(s) under consideration

L–W

excess length. When considering a transition due to a zipping step(s), the change in excess length is A(L – W)

n

number of leading edge cells in L_bulk

t

time. Indices can be used to distinguish original (t_o) and final (t_f) stages when multiple zipping steps are considered or to distinguish between the beginning (t_i) and end (t_ii) of a single zipping step

T

tension in a purse string

v_native

velocity of a leading edge segment at a symmetry point. v_native = dh/dt and is very well approximated as a constant during much of wild-type dorsal closure

W

canthus-to-canthus distance along the dorsal midline

Δt_zip(t_i)

duration of a zipping step

Δx

movement of a canthus, specified to Δx_anterior for the anterior canthus and Δx_posterior for the posterior canthus

ΔW

as shown in figure 2(a), the change in the length of both seams during the next ten zipping steps

κ

curvature of a purse string

θ

angle between the dorsal midline and the tangent of a purse string at a canthus. For an ideal, fully symmetric embryo the four possible angles have the same value. For an embryo with left/right symmetry but anterior/posterior asymmetry, the possible angles are specified by θ_A and θ _P. For a fully asymmetric embryo, the possible angles are specified by θ_A,R, θ_A,L, θ_P,L and θ_P,L

σ_AS

force per unit length of the amnioserosa on a purse string

σ_LE

force per unit length of the leading edge cell on a purse string