Doubly robust and efficient estimators for heteroscedastic partially linear single-index models allowing high dimensional covariates

Summary

We study the heteroscedastic partially linear single-index model with an unspecified error variance function, which allows for high dimensional covariates in both the linear and the single-index components of the mean function. We propose a class of consistent estimators of the parameters by using a proper weighting strategy. An interesting finding is that the linearity condition which is widely assumed in the dimension reduction literature is not necessary for methodological or theoretical development: it contributes only to the simplification of non-optimal consistent estimation. We also find that the performance of the usual weighted least square type of estimators deteriorates when the non-parametric component is badly estimated. However, estimators in our family automatically provide protection against such deterioration, in that the consistency can be achieved even if the baseline non-parametric function is completely misspecified. We further show that the most efficient estimator is a member of this family and can be easily obtained by using non-parametric estimation. Properties of the estimators proposed are presented through theoretical illustration and numerical simulations. An example on gender discrimination is used to demonstrate and to compare the practical performance of the estimators.

1. Introduction

We study the partially linear single-index model

$$\begin{array}{ccc}{Y}_i={\mathbf{x}}_i^T\gamma +g({\mathbf{z}}_i^T\beta )+{\epsilon }_i,& E({\epsilon }_i\text{|}{\mathbf{x}}_i,{\mathbf{z}}_i)=0,& i=1,\dots ,n,\end{array}$$ (1)

where ${\mathbf{x}}_i\in {ℝ}^{d_{\gamma }}$ and ${\mathbf{z}}_i\in {ℝ}^{d_{\beta }}$ are random variables with possibly high dimensions d_γ and d_β respectively. We do not assume any parametric form for the conditional distribution of ε. In particular, we allow ε to be heteroscedastic. For identifiability, we assume that the first component of β is 1, and we use z₋₁ to denote the last d_β − 1 components of z. Let θ = (γ^T, β^T)^T and d = d_β + d_γ − 1. Without loss of generality, we assume that E(z_i) = 0 in what follows. The interest is usually in estimating θ, whereas all the other unknown components of model (1), such as the unspecified function g(·) and the unknown error distribution, are termed nuisance parameters.

Model (1) was proposed by Carroll et al. (1997). It is a natural extension of the partially linear model (Engle et al., 1986) in the situation when multiple covariates need to be included non-parametrically. It can also be viewed as an extension of the single-index model or as a special case of the multi-index model. See Xia et al. (1999) and Xia (2008) and the references therein for a discussion on the links. The parametric component x^Tγ provides a simple summary of covariate effects which are of the main scientific interest, the index z^Tβ enables us to simplify the treatment of the multiple auxiliary variables which may have high dimension and the smooth baseline component g (·) enriches model flexibility.

Estimation of model (1) has been studied in Carroll et al. (1997), Yu and Ruppert (2002) and Xia and Härdle (2006), in which consistently estimating g(·) is mandatory during the estimation process to ensure consistency of the estimator of θ. An intriguing finding here is that the consistency of the parameter estimator for θ can be achieved without estimating g(·). In addition, although Carroll et al. (1997), Yu and Ruppert (2002) and Xia and Härdle (2006) did not explicitly make an equal variance assumption for ɛ, they did not account for the heteroscedasticity of model (1) either. Consequently, none of these estimators are efficient. One might think that an inverse-to-variance weighting scheme can lead to efficiency. However, we discover that it is not always so. In fact, a formal study on the efficient estimator for model (1) has only been conducted in the homoscedastic error case (Wang et al., 2010), where an efficient estimator is constructed when the covariates are assumed elliptical. In this paper we construct an estimator that reaches the optimal semiparametric efficiency bound under heteroscedasticity and without distributional assumptions on the covariates.

When d_β is potentially large, a routinely assumed condition in the dimension reduction literature (Li, 1991) is the linearity condition

$$E(\mathbf{z}|{\mathbf{z}}^T\beta )={\text{P}}_{\beta }\mathbf{z}.$$ (2)

Here ${\text{P}}_{\beta }={\sum }_z\beta {({\beta }^T{\sum }_z\beta )}^{-1}{\beta }^T$ and ${\sum }_z=\mathrm{var}(\mathbf{z})$. Wang et al. (2010) also assumed this condition to facilitate their investigation on the consistency of the estimators in the homoscedastic partially linear single-index model. We find that this condition is unnecessary in our methodological development and it does not contribute to an improved efficiency of estimation. The only utility of condition (2) is in computation, in that it simplifies the construction of a non-optimal consistent estimator. We emphasize here that the linearity condition (2) does not lead to any simplification of the efficient estimator.

In summary, we propose a general class of estimating equations to estimate the parameters β and γ in model (1) with a heteroscedastic error. The estimating equations have several robustness properties, in the sense that they allow us to obtain a consistent estimator for β and γ even when several components, including g(·), are not consistently estimated or are misspecified. Consistent estimation of β and γ without consistently estimating g(·), whether with a homoscedastic or heteroscedastic error, has not been discovered before in the literature. In addition, the consistency holds without any distributional assumption on the covariates. In particular, the linearity condition (2) is not required although it can simplify some of the computations when it is true. Relaxing the linearity condition under this framework has also never been achieved before as far as we are aware. Note that here all the robustness properties hold in the sense that consistency of $\widehat{\beta }$ and $\widehat{\gamma }$ is preserved under misspecification of several components of the model. If practical interest is in estimating some of these model components, then we can still estimate them. If we estimate all the components involved in the estimating equations consistently, then the resulting estimator for β and γ is guaranteed to be efficient. In other words, the optimal member of the general class requires consistent estimation of the various components, including g(·) and g′(·). To the best of our knowledge, this is the first time that efficient estimation in model (1), with possibly high dimensional covariates, has been proposed.

The rest of the paper is organized as follows. In Section 2, we examine a class of weighted estimators and propose a general class of consistent estimators for heteroscedastic model (1) that has a double-robustness property. We identify a member of this class that is easy to compute under condition (2). The efficient estimator is derived in Section 3 where a simple algorithm is provided and g(·) is also estimated as a by-product. The performance of the estimators proposed is illustrated in simulation studies in Section 4 and in real data in Section 5. We discuss some extensions of our method in Section 6.

2. A general class of consistent estimators

Our goal in this section is to present a general class of consistent estimators for θ that has a double-robustness property. Double robustness has also been discovered in other contexts. See, for example, Robins and Rotnitzky (2001) and Tan (2010). We explore this double-robustness property and derive a simplified estimation procedure in the presence of the linearity condition (2). We also reveal a limitation of the standard weighting method in handling the heteroscedastic error variance and hence provide an explanation why heteroscedastic errors are usually not accounted for even if it is acknowledged.

To ease the presentation of consistency considerations among different estimators, we present each estimator as a solution to an estimating equation. The consistency of the estimator is studied through the consistency of the estimating equation. We consider the following class of estimating equations:

$$n^{-1/2}{\displaystyle \sum _{i=1}^n\{Y_i-{\mathbf{x}}_i^T\gamma -f({\mathbf{z}}_i^T\beta )\}[a({\mathbf{x}}_i\text{, }{\mathbf{z}}_i)-\stackrel{\sim }{E}\{a({\mathbf{x}}_i,{\mathbf{z}}_i){\text{|z}}_i^T\beta \}]=0},$$ (3)

where f(z^Tβ) is a given function of z^Tβ that may or may not equal $\begin{array}{cc}g({\mathbf{z}}^T\beta ),& \stackrel{\sim }{E}(\cdot |{\mathbf{z}}^T\beta )\end{array}$ denotes a function of z^Tβ which may or may not be the true $E(\cdot |{\text{z}}^T\beta )$ and a(·, ·) $\in {ℝ}^d$ is an arbitrary function of x and z. It is easily verified that, at the true parameter values of β and γ, equation (3) has mean 0. We can view equation (3) as a sample version of the population mean. We assume that, when n → ∞, equation (3) has a unique solution in the neighbourhood of the true parameter values of β and γ. Because $Y_i-{\mathbf{x}}_i^T\gamma -g({\mathbf{z}}_i^T\beta )$ is the ith error ɛ_i, we can rewrite equation (3) as

$$n^{-1/2}{\displaystyle \sum _{i=1}^n\{{\epsilon }_i+g({\mathbf{z}}_i^T\beta )-f({\mathbf{z}}_i^T\beta )\}[a({\mathbf{x}}_i,{\mathbf{z}}_i)-E\{a({\mathbf{x}}_i,{\mathbf{z}}_i)|{\mathbf{z}}_i^T\beta \}+E\{a({\mathbf{x}}_i,{\mathbf{z}}_i)|{\mathbf{z}}_i^T\beta \}-\stackrel{\sim }{E}\{a({\mathbf{x}}_i,{\mathbf{z}}_i)|{\mathbf{z}}_i^T\beta \}]=0}.$$

It is now easy to recognize that the above estimating equation has a double-robustness property. On the one hand, if f(·) = g(·), then equation (3) is consistent whether or not $\stackrel{\sim }{E}(\cdot |{\mathbf{z}}^T\beta )=E(\cdot |{\mathbf{z}}^T\beta )$. In an extreme case, we can simply set $\stackrel{\sim }{E}(\cdot |{\mathbf{z}}^T\beta )=0$. This choice combined with the choice $a(\mathbf{x},\mathbf{z})={({\mathbf{x}}^T,{\mathbf{z}}_{-1}^T)}^T$ or $a(\mathbf{x},\mathbf{z})={({\mathbf{x}}^T,g^{\prime }({\mathbf{z}}^T\beta ){\mathbf{z}}_{-1}^T)}^T$ yields

$$n^{-1/2}{\displaystyle \sum }_{i=1}^n\{Y_i-{\text{x}}_i^T\gamma -g(z_i^T\beta )\}{({\text{x}}_i^T,{\text{z}}_{-1,i}^T)}^T=0$$

or

$$n^{-1/2}{\displaystyle \sum _{i=1}^n\{Y_i-{\mathbf{x}}_i^T\gamma -g({\mathbf{z}}_i^T\beta )\}{({\mathbf{x}}_i^T,g^{\prime }({\mathbf{z}}_i^T\beta ){\mathbf{z}}_{-1,i}^T)}^T=0},$$

which are the most familiar forms of estimator. On the other hand, if $\stackrel{\sim }{E}(\cdot |{\mathbf{z}}^T\beta )=E(\cdot |{\mathbf{z}}^T\beta )$, then equation (3) is also consistent whether or not f(·) = g(·). In an extreme case, we can set $f({\mathbf{z}}_i^T\beta )=0$. Making the natural choice of $a(\mathbf{x},\mathbf{z})={({\mathbf{x}}^T,{\mathbf{z}}_{-1}^T)}^T$, we obtain a consistent estimator from the estimating equation

$$n^{-1/2}{\displaystyle \sum _{i=1}^n(Y_i-{\mathbf{x}}_i^T\gamma )[{({\mathbf{x}}_i^T,{\mathbf{z}}_{-1,i}^T)}^T-E\{{({\mathbf{x}}_i^T,{\mathbf{z}}_{-1,i}^T)}^T|{\mathbf{z}}_i^T\beta \}]=0}.$$

Of course, the two choices of g(·) or E(·|z^Tβ) can also be combined as we now illustrate. For example, we can directly set g(·) = 0 in one part of the estimating equations and still retain the two different choices of either g(·) or E(·|z^Tβ) in the other part of the estimating equations. Specifically, we can consider estimating equations of the form

$$\begin{array}{c}{n}^{-1/2}{\displaystyle \sum _{i=1}^n\{Y_i-{\mathbf{x}}_i^T\gamma -f({\mathbf{z}}_i^T\beta )\}\{{\mathbf{x}}_i-\stackrel{\sim }{E}({\mathbf{x}}_i|{\mathbf{z}}_i^T\beta )\}=0},\\ n^{-1/2}{\displaystyle \sum _{i=1}^n(Y_i-{\mathbf{x}}_i^T\gamma )\{{\mathbf{z}}_i-E({\mathbf{z}}_i|{\mathbf{z}}_i^T\beta )\}=0}.\end{array}$$ (4)

In this construction, the first d_γ-dimensional equation corresponds to choosing the first dγ components of a(x_i, z_i) in equation (3) to be x_i, and the second d_β-dimensional equation corresponds to choosing f = 0 and the second d_β components of a(x_i, z_i) in equation (3) to be z_i and $\stackrel{\sim }{E}({\mathbf{x}}_i|{\mathbf{z}}_i^T\beta )=E({\mathbf{x}}_i|{\mathbf{z}}_i^T\beta )$. The construction (4) has a fully fixed form in the second d_β equations, while still leaving the flexibility of using either f(·) = g(·) or $\stackrel{\sim }{E}({\mathbf{x}}_i|{\mathbf{z}}_i^T\beta )=E({\mathbf{x}}_i|{\mathbf{z}}_i^T\beta )$ in the first d_γ equations. The above estimating equation (4) still offers consistent estimators for both γ and β.

Next we examine the role that the linearity condition (2) plays in the estimating equation. We use the estimating equation (4) as an illustrative example. When condition (2) is true, expression (4) becomes

$$\begin{array}{c}{n}^{-1/2}{\displaystyle \sum _{i=1}^n\{Y_i-{\mathbf{x}}_i^T\gamma -f({\mathbf{z}}_i^T\beta )\}\{{\mathbf{x}}_i-\stackrel{\sim }{E}({\mathbf{x}}_i|{\mathbf{z}}_i^T\beta )\}=0},\\ n^{-1/2}{\displaystyle \sum _{i=1}^n(Y_i-{\mathbf{x}}_i^T\gamma )(I-P_{\beta }){\mathbf{z}}_i=0}.\end{array}$$ (5)

We shall see that expression (5) leads to the simplest consistent estimator for model (1).

To solve equations (5), we rewrite the second equation as

$${\displaystyle \sum _{i=1}^n{\mathbf{z}}_i(Y_i-{\mathbf{x}}_i^T\gamma )={\sum }_z\beta \left\{{\displaystyle \sum _{i=1}^n{({\beta }^T{\sum }_z\beta )}^{-1}{\beta }^T{\mathbf{z}}_i(Y_i-{\mathbf{x}}_i^T\gamma )}\right\}.}$$

The quantity in the curly brackets of this equation is a scalar. Hence we can ‘profile out’ β by setting

$$\widehat{\beta }(\gamma )=c(\gamma ){\widehat{\sum }}_z^{-1}\{\widehat{E}(\mathbf{z}Y)-\widehat{E}(\mathbf{z}{\mathbf{x}}^T\gamma )\}.$$

Here, Ê(·) and ${\widehat{\sum }}_z$ are the sample mean and covariance estimates, and the constant c(γ) ≠ 0 is a normalizing constant to ensure that the first component of $\widehat{\beta }$ is 1. Specifically, c(γ) is the inverse of the first component of ${\widehat{\sum }}_z^{-1}\{\widehat{E}(\mathbf{z}Y)-\widehat{E}(\mathbf{z}{\mathbf{x}}^T\gamma )\}$. Two possibilities are available in obtaining $\widehat{\gamma }$ corresponding to the two choices of specifying g(·) or E(x|z^Tβ) If we decide to specify E(x|z^Tβ), we can set f(z^Tβ)= 0 and plug in $\widehat{\beta }(\gamma )$ to solve for γ from

$${\displaystyle \sum _{i=1}^n(Y_i-{\mathbf{x}}_i^T\gamma )[{\mathbf{x}}_i-E\{\mathbf{x}|{\mathbf{z}}_i^T\widehat{\beta }(\gamma )\}]=0}.$$

If we decide to specify g(·), we can set Ẽ(x_i|z_i^Tβ)= 0 and solve for γ from

$${\displaystyle \sum _{i=1}^n[Y_i-{\mathbf{x}}_i^T\gamma -g\{{\mathbf{z}}_i^T\widehat{\beta }(\gamma )\}]{\mathbf{x}}_i=0}.$$

If we do not have sufficient information or are reluctant to specify any one of the two functions, we can estimate one of them or both by using, for example, the standard kernel non-parametric regression or local linear approximation, provided that sufficient smoothness or regularity conditions hold.

To take advantage of the linearity condition (2), we have chosen to set $f({\mathbf{z}}_i^T\beta )=0$ in the second of equations (5) because of its simplicity. In general, f(·) can be any function of ${\mathbf{z}}_i^T\beta$. However, f(·) needs to satisfy

$$E[{\mathbf{z}}_i^T\beta \{g({\mathbf{z}}_i^T\beta )-f({\mathbf{z}}_i^T\beta )\}]\ne 0;$$ (6)

otherwise degeneration will occur and the second of equations (5) (corresponding to a special f(·) = 0) will not yield a solution. We give a detailed account of this phenomenon in the on-line supplementary information for this paper.

The estimating equation class (3) does not take into account the error variance form. A natural correction for this is to include inverse variance weights to improve the efficiency of estimation. Denote w_i = w(x_i, z_i) = var (ɛ_i|x_i, z_i)⁻¹. The weighted estimating equation class is then

$$n^{-1/2}{\displaystyle \sum _{i=1}^{n}w({\mathbf{x}}_i,{\mathbf{z}}_i)\{Y_i-{\mathbf{x}}_i^T\gamma -f({\mathbf{z}}_i^T\beta )\}[a({\mathbf{x}}_i,{\mathbf{z}}_i)-\stackrel{\sim }{E}\{a({\mathbf{x}}_i,{\mathbf{z}}_i)|{\mathbf{z}}_i^T\beta \}]=0}.$$ (7)

However, class (7) lacks some of the nice properties of the original family (3). It can be easily verified that, even if w_i can be consistently estimated or is completely known, the consistency of $\widehat{\gamma }$ and $\widehat{\beta }$ now always requires a consistent estimation of g(·). Thus, not only the double-robustness property is lost, but also the simplification that is contributed by the linearity condition (2) becomes limited. Similar controversy is discovered for the partially linear model in Ma et al. (2006), and we suspect that this is why a standard inverse variance weighting scheme is not pursued in the partially linear single-index model in the literature, even when there is heteroscedasticity.

3. Efficient estimator via proper weighting

To improve the estimation variance through incorporating the weights w_i while retaining the nice properties of expression (3), we perform a slight modification of expression (7) and propose

$$\begin{array}{c}{n}^{-1/2}{\displaystyle \sum _{i=1}^n{w}_i\{Y_i-{\mathbf{x}}_i^T\gamma -f({\mathbf{z}}_i^T\beta )\}\left\{{\mathbf{x}}_i-\frac{\stackrel{\sim }{E}(w_i{\mathbf{x}}_i|{\mathbf{z}}_i^T\beta )}{\stackrel{\sim }{E}(w_i|{\mathbf{z}}_i^T\beta )}\right\}=0},\\ n^{-1/2}{\displaystyle \sum _{i=1}^n{w}_i\{Y_i-{\mathbf{x}}_i^T\gamma -f({\mathbf{z}}_i^T\beta )\}b({\mathbf{z}}_i^T\beta )\left\{{\mathbf{z}}_{-1,i}-\frac{\stackrel{\sim }{E}(w_i{\mathbf{z}}_{-1,i}|{\mathbf{z}}_i^T\beta )}{\stackrel{\sim }{E}(w_i|{\mathbf{z}}_i^T\beta )}\right\}=0}.\end{array}$$ (8)

For simplicity in expression (8), we directly set $a(\mathbf{x}\text{, }\mathbf{z})={({\mathbf{x}}^T,b({\mathbf{z}}^T\beta ){\mathbf{z}}_{-1}^T)}^T$, which is the simplest form to use in practice. Here b(·) can be an arbitrary function and is included here for increased flexibility.

Similarly to expression (3), expression (8) provides a consistent estimator under several misspecifications. For example, we can use f(·) that is not a consistent estimate of g(·); as long as Ẽ(·|z^Tβ) = E(·|z^Tβ), expression (8) yields consistent estimators for β and γ. We can also choose not to estimate E(·|z^Tβ) carefully, by using some parametric model or even simply setting it to zero; as long as f(·) = g(·), expression (8) is still valid. Finally, the weights w_i can also be misspecified; as long as one of g(·) and E(·|z^Tβ) is correctly specified or both are consistently estimated, we still have consistency for β and γ. If we adopt a weight w that depends on x and z only through z^Tβ, expression (8) becomes a member of class (7). This indicates that the weighting scheme in expression (7) is valid only in some limited situations.

In addition to the robustness property, expression (8) also provides an efficient estimating equation when we have the correct weights, use a consistent estimator of g as the f-function, use a consistent estimator of g′ as the b-function and at the same time estimate the conditional expectation E(·|z^Tβ) consistently. To see this, we first derive the semiparametric efficient score function for model (1). The semiparametric efficient score is defined as the projection of the score vector onto the orthogonal complement of the nuisance tangent space; for details, see Bickel et al. (1993) and Tsiatis (2006).

Proposition 1

Assume that the conditional probability density function of ɛ given (x, z), p_ɛ. (ɛ|x, z), is differentiable with respect to ɛ and that 0 < E(ɛ²|x,z) < ∞ almost everywhere. Denote w = w(x, z) = E(ɛ²|x, z)⁻¹. The semiparametric efficient score is

$$S_{\text{eff}}=w\epsilon {\left({\mathbf{x}}^T-\frac{E(w{\mathbf{x}}^T{\text{|z}}^T\beta )}{E(w|{\mathbf{z}}^T\beta )},g^{\prime }({\mathbf{z}}^T\beta )\{{\mathbf{z}}_{-1}^T-\frac{E(w{\mathbf{z}}_{-1}^T|{\mathbf{z}}^T\beta )}{E(w|{\mathbf{z}}^T\beta )}\}\right)}^T.$$

The expression for S_eff suggests that, by carefully choosing w,f and b in expression (8), we should obtain a semiparametric efficient $\widehat{\beta }$ as the solution to expression (8). The proof of proposition 1 is given in the on-line supplementary document.

Obtaining w or the error variance var. (ɛ|x, z) through a non-parametric regression of the residuals on the covariates (x, z) is itself a high dimensional problem which suffers from the curse of dimensionality. To focus our presentation on the main concepts, we assume that there is a low dimensional variable ξ = ξ(x, z) such that var. (ɛ|x, z) = var (ɛ|ξ) and ξ has a known form. For example, ξ can be z^Tβ, indicating that the error variance depends on the covariates through z^Tβ only. ξ can also be x^Tγ, indicating that the error variance depends on the covariates through x^Tγ only. It can also be a combination of these two or can have any other form. In practice, a reasonable approximation of ξ can be obtained via standard procedures to model error variance, using the residuals from an initial estimation of the model. We shall concentrate on the case where ξ is univariate. It is worth noting that this assumption is often made to simplify the estimation of weights. The assumption can be weakened to include intermediate multivariate models as components, e.g. with additive structures, so that the univariate convergence rates remain achievable and that the variance structure is still very flexible.

If we use non-parametrically estimated g, g′, w, E(w|z^Tβ), E(wx|z^Tβ) and E(wz₋₁|z^Tβ), the estimator that is obtained from expression (8) can be written as the solution to

$$\begin{array}{c}0=n^{-1/2}{\displaystyle \sum _{i=1}^n\{Y_i-{\mathbf{x}}_i^T\gamma -\widehat{g}({\mathbf{z}}_i^T\beta )\}\widehat{w}({\mathbf{x}}_i,{\mathbf{z}}_i)\left[{\mathbf{x}}_i\frac{\widehat{E}\{\widehat{w}(\mathbf{x},\mathbf{z})\mathbf{x}|{\mathbf{z}}_i^T\beta \}}{\widehat{E}\{\widehat{w}(\mathbf{x},\mathbf{z})|{\mathbf{z}}_i^T\beta \}}\right]},\\ 0=n^{-1/2}{\displaystyle \sum _{i=1}^n\{Y_i-{\mathbf{x}}_i^T\gamma -\widehat{g}({\mathbf{z}}_i^T\beta )\}\widehat{w}({\mathbf{x}}_i,{\mathbf{z}}_i){\widehat{g}}^{\prime }({\mathbf{z}}_i^T\beta )\left[{\mathbf{z}}_{-1,i}-\frac{\widehat{E}\{\widehat{w}(\mathbf{x},\mathbf{z}){\mathbf{z}}_{-1}|{\mathbf{z}}_i^T\beta \}}{\widehat{E}\{\widehat{w}(\mathbf{x},\mathbf{z})|{\mathbf{z}}_i^T\beta \}}\right]}.\end{array}$$ (9)

In expression (9), the quantities with circumflexes can be estimated via kernel estimation. To be precise, let K be a kernel function and K_h(·) = h⁻¹K(·/h). Recall also the notation for w(x_i,z_i) and ξ_i = ξ(x_i, z_i) defined in Section 3. For bandwidths h₁, h₂ and h₃, we set

$$\widehat{g}({\mathbf{z}}_i^T\beta )=\sum _{j\ne i}{K}_{h_1}({\mathbf{z}}_j^T\beta -{\mathbf{z}}_i^T\beta )(Y_i-{\mathbf{x}}_i^T\gamma )/\sum _{j\ne i}{K}_{h_1}({\mathbf{z}}_j^T\beta -{\mathbf{z}}_i^T\beta ),{\widehat{g}}^{\prime }({\mathbf{z}}_i^T\beta )=h_1^{-1}\{\sum _{j\ne i}{K^{\prime }}_{h_1}({\mathbf{z}}_j^T\beta -{\mathbf{z}}_i^T\beta )(Y_i-{\mathbf{x}}_i^T\gamma )\sum _{j\ne i}{K}_{h_1}({\mathbf{z}}_j^T\beta -{\mathbf{z}}_i^T\beta )-\sum _{j\ne i}{K}_{h_1}({\mathbf{z}}_j^T\beta -{\mathbf{z}}_i^T\beta )(Y_i-{\mathbf{x}}_i^T\gamma )\times \sum _{j\ne i}{K^{\prime }}_{h_1}({\mathbf{z}}_j^T\beta -{\mathbf{z}}_i^T\beta )\}/{\{\sum _{j\ne i}{K}_{h_1}({\mathbf{z}}_j^T\beta -{\mathbf{z}}_i^T\beta )\}}^2,\widehat{w}({\mathbf{x}}_i,{\mathbf{z}}_i)=\sum _{j\ne i}{K}_{h_2}({\xi }_j-{\xi }_i)/\sum _{j\ne i}{K}_{h_2}({\xi }_j-{\xi }_i)e_i^2,\widehat{E}\{\widehat{w}(\mathbf{x},\mathbf{z})\mathbf{x}|{\mathbf{z}}_i^T\beta \}=\sum _{j\ne i}{K}_{h_3}({\mathbf{z}}_j^T\beta -{\mathbf{z}}_i^T\beta )\widehat{w}({\mathbf{x}}_i,{\mathbf{z}}_i){\mathbf{x}}_i/\sum _{j\ne i}{K}_{h_3}({\mathbf{z}}_j^T\beta -{\mathbf{z}}_i^T\beta ),\widehat{E}\{\widehat{w}(\mathbf{x},\mathbf{z})|{\mathbf{z}}_i^T\beta \}=\sum _{j\ne i}{K}_{h_3}({\mathbf{z}}_j^T\beta -{\mathbf{z}}_i^T\beta )\widehat{w}({\mathbf{x}}_i,{\mathbf{z}}_i)/\sum _{j\ne i}{K}_{h_3}({\mathbf{z}}_j^T\beta -{\mathbf{z}}_i^T\beta ),\widehat{E}\{\widehat{w}(\mathbf{x},\mathbf{z}){\mathbf{z}}_{-1}|{\mathbf{z}}_i^T\beta \}=\sum _{j\ne i}{K}_{h_3}({\mathbf{z}}_j^T\beta -{\mathbf{z}}_i^T\beta )\widehat{w}({\mathbf{x}}_i,{\mathbf{z}}_i){\mathbf{z}}_{-1,i}/\sum _{j\ne i}{K}_{h_3}({\mathbf{z}}_j^T\beta -{\mathbf{z}}_i^T\beta ).$$

We remark that we use the same bandwidth in the last three quantities, because a same bandwidth already suffices to guarantee the efficiency of the estimate that is obtained from expression (9); see the proof of proposition 2. The algorithm to solve expression (9) is as follows.

• Step 1: we use the estimation procedure that was described in Section 2 to obtain an initial estimator $\stackrel{\sim }{\theta }={({\stackrel{\sim }{\gamma }}^T,{\stackrel{\sim }{\beta }}^T)}^T$.

• Step 2: obtain ĝ and ĝ′ by using non-parametric regression of $Y-x^T\stackrel{\sim }{\gamma }$ on ${\mathbf{z}}^T\stackrel{\sim }{\beta }$ described above. Denote $\stackrel{\sim }{Y}=Y-\widehat{g}({\mathbf{x}}^T\stackrel{\sim }{\beta })$.

• Step 3: obtain the residual $e_i=Y_i-{\text{x}}_i^T\stackrel{\sim }{\gamma }-\widehat{g}(z_i^T\stackrel{\sim }{\beta })$. Estimate σ²(x,z) according to the variance model by using the data {ξ(x_i, z_i), e_i²} and the initial parameter values $\stackrel{\sim }{\theta }$ if necessary. Set ${\widehat{w}}_i={\widehat{\sigma }}^{-2}({\mathbf{x}}_i,{\mathbf{z}}_i)$.

• Step 4: obtain $\widehat{E}(\mathbf{x}\widehat{w}|{\mathbf{z}}^T\stackrel{\sim }{\beta })$ and $\stackrel{\sim }{E}(\stackrel{\sim }{w}|{\mathbf{z}}^T\stackrel{\sim }{\beta })$ via non-parametric regression by using the data $({\mathbf{x}}_i{\widehat{w}}_i,{\mathbf{z}}_i^T\stackrel{\sim }{\beta },{\widehat{w}}_i)$. Set $\stackrel{\sim }{\mathbf{x}}=\mathbf{x}-\widehat{E}(\mathbf{x}\widehat{w}|{\mathbf{z}}^T\stackrel{\sim }{\beta })\text{/}\widehat{E}(\widehat{w}|{\mathbf{z}}^T\stackrel{\sim }{\beta })$.

• Step 5: obtain $\widehat{E}({\mathbf{z}}_{-1}\widehat{w}|{\mathbf{z}}^T\stackrel{\sim }{\beta })$ via non-parametric regression by using the data $({\mathbf{z}}_{-1,i}{\widehat{w}}_i,{\mathbf{z}}_i^T\stackrel{\sim }{\beta })$. Set ${\stackrel{\sim }{\mathbf{z}}}_{-1}={\mathbf{z}}_{-1}-\widehat{E}({\mathbf{z}}_{-1}\widehat{w}|{\mathbf{z}}^T\stackrel{\sim }{\beta })\text{/}\widehat{E}(\widehat{w}|{\mathbf{z}}^T\stackrel{\sim }{\beta })$.

• Step 6: update the estimate for γ from

  $$\widehat{\gamma }=\widehat{E}{(\stackrel{\sim }{w}\stackrel{\sim }{x}{x}^T)}^{-1}\widehat{E}(\stackrel{\sim }{w}\stackrel{\sim }{x}\stackrel{\sim }{Y})$$

  where the Ê are simply the sample averages. Solve for β from

  $${\displaystyle \sum }_{i=1}^n\{Y_i-x_i^T\widehat{\gamma }-\widehat{g}(z_i^T\beta )\}{\widehat{w}}_i{\widehat{g}}^{\prime }(z_i^T\stackrel{\sim }{\beta }){\stackrel{\sim }{z}}_{-1,i}=0.$$

Here ĝ(·) and ĝ′(·) are treated as known functions and hence do not need to be updated, and ${\widehat{w}}_i{\widehat{g}}^{\prime }({\mathbf{z}}_i^T\stackrel{\sim }{\beta }){\stackrel{\sim }{\mathbf{z}}}_{-1,i}$ are the previously obtained values.

In this algorithm, each time that a kernel estimation procedure needs to be performed, if a new bandwidth needs to be selected, we can simply use the traditional cross-validation procedure. In our experience, the performance of the estimation is very insensitive to the choice of bandwidth, which agrees with the common observation in many semiparametric problems and is also explained by the wide range of possible choices of bandwidth in the following regularity condition 6. In particular, we do not need to undersmooth anywhere. This is a by-product of the double-robustness and will be justified in proposition 2. It is a property that is also shared by the profile likelihood method (Lin and Carroll, 2006). We also emphasize that the only estimating equation that needs to be solved is in step 6. Since this step does not involve any non-parametric procedures, it is a simple parametric estimating equation and can be solved via for example the Newton–Raphson procedure. In finite sample situations, it can happen that no roots are available for an estimating equation. In this case, instead of solving for zero, one can aim at minimizing the square of the estimating equation. One may note that, although the linearity condition (2) can simplify the initial estimation $\stackrel{\sim }{\theta }$, it will not contribute to the subsequent operations at all. The way in which the weights w_i enter expression (9) requires a different type of linearity condition to achieve simplification, namely a weighted linearity condition of the form

$$E(w\mathbf{z}|{\mathbf{z}}^T\beta )=P_{\beta }\mathbf{z}E(w|{\mathbf{z}}^T\beta ).$$ (10)

We can easily see that, when w is a function of z^Tβ or when w is uncorrelated with z conditional on z^Tβ, equation (10) is equivalent to condition (2). This indicates that equation (10) is not much stronger than the usual linearity condition (2) and may hold in various situations. If we are willing to make this assumption, then the second equation in expression (9) is simplified and it suffices to solve

$${\displaystyle \sum }_{i=1}^n\{Y_i-x_i^T\widehat{\gamma }-\widehat{g}(z_i^T\beta )\}{\widehat{w}}_i{\widehat{g}}^{\prime }(z_i^T\stackrel{\sim }{\beta })z_{-1,i}=0.$$ (11)

Therefore, the above algorithm can be simplified through skipping step 5, and replacing the last estimating equation in step 6 with equation (11).

We now list a set of regularity conditions that are sufficient for our main proposition to hold. These conditions are not the weakest possible, but they facilitate our technical derivations.

• Condition 1. The second moments of all covariates are finite, i.e. ${\max }_{1\le i\le d_{\gamma }}E({\mathbf{x}}_i^2)<\infty$ and ${\max }_{1\le j\le d_{\beta }}E({\mathbf{z}}_j^2)<\infty$. There is a positive constant δ such that E(ɛ^4+δ|x, z) < ∞.

• Condition 2. There are v(·), ξ = ξ(x, z) and positive constants c₁ and c₂, such that E(ɛ²|x, z) = v(ξ), 0 < c₁ < v(·) < c₂ < ∞, and E(X_i²|ξ) < ∞.

• Condition 3. The functions E(x|z^Tβ), E(z|z^Tβ), E(w|z^Tβ), E(wz|z^Tβ) and E(wx|z^Tβ) are twice continuously differentiable with finite derivatives. As a function of (x, z), ξ(x, z) is three times continuously differentiable with finite derivatives. The functions g(z^Tβ) and v(ξ) are four times continuously differentiable with finite derivatives.

• Condition 4. Assume that the random variables ξ and z^Tβ have densities f_ξ(ξ) and $f_{{\mathbf{z}}^T\beta }({\mathbf{z}}^T\beta )$ such that f_ξ(ξ) and f_zt_β(z^tβ) are twice continuously differentiable with finite derivatives, satisfying 0 < inf f_ξ(ξ) ≤ sup f_ξ(ξ) < ∞ and 0 < inf f_zT_β(z^Tβ) ≤ sup f_zT_β(z^Tβ) < ∞.

• Condition 5. The kernel function K is symmetric, and its derivative K′ is continuous in compact support [−1, 1].

• Condition 6. The bandwidths h_i that are used in the kernel estimators satisfy log²(n)/(nh_i) →0 for i = 1,2,3. In addition, $n{h}_1^4\to \infty$ and $n{h}_1^8\to 0,h_1^4{\log }^2(n)/h_i\to 0$ and log⁴(n)/(nh₁h_i) → 0 for i = 2,3, and h₂ = O(n^−1/5) and h₃ = O(n^−1/5).

Proposition 2

Assume that $\widehat{\gamma }$ and $\widehat{\beta }$ solve expression (9) or expression (9) with the second equation replaced by equation (11). Then, under the above regularity conditions, $\widehat{\gamma }$ and $\widehat{\beta }$ reach the optimal semiparametric efficiency bound. In particular, when n → ∞,

$$\{{({\widehat{\gamma }}^T,{\widehat{\beta }}^T)}^T-{({\gamma }^T,{\beta }^T)}^T\}\surd n\to N(0,{\text{V}}^{-1})$$

in distribution, where

$$\text{V}=(E(S_{\text{eff}}{S}_{\text{eff}}^T))=\left(\begin{array}{cc}{\text{V}}_{11}& {\text{V}}_{12}\\ {\text{V}}_{21}& {\text{V}}_{22}\end{array}\right),$$

and

$$\begin{array}{c}{\text{V}}_{11}=E\left\{w\mathbf{x}{\mathbf{x}}^T-\frac{E(w\mathbf{x}|{\mathbf{z}}^T\beta )E(w{\mathbf{x}}^T|{\mathbf{z}}^T\beta )}{E(w|{\mathbf{z}}^T\beta )}\right\},\\ {\text{V}}_{12}=E\left[g^{\prime }({\mathbf{z}}^T\beta )\left\{w\mathbf{x}{\mathbf{x}}_{-1}^{\text{T}}-\frac{E(w\mathbf{x}|{\mathbf{z}}^T\beta )E(w{\mathbf{x}}_{-1}^T|{\mathbf{z}}^T\beta )}{E(w|{\mathbf{z}}^T\beta )}\right\}\right],\\ {\text{V}}_{21}=E\left[g^{\prime }({\mathbf{z}}^T\beta )\left\{w{\mathbf{z}}_{-1}{\mathbf{x}}^T-\frac{E(w{\mathbf{z}}_{-1}|{\mathbf{z}}^T\beta )E(w{\mathbf{x}}^T|{\mathbf{z}}^T\beta )}{E(w|{\mathbf{z}}^T\beta )}\right\}\right],\\ {\text{V}}_{22}=E\left[g^{\prime }{({\mathbf{z}}^T\beta )}^2\left\{w{\mathbf{z}}_{-1}{\mathbf{x}}_{-1}^T-\frac{E(w{\mathbf{z}}_{-1}|{\mathbf{z}}^T\beta )E(w{\mathbf{x}}_{-1}^T|{\mathbf{z}}^T\beta )}{E(w|{\mathbf{z}}^T\beta )}\right\}\right].\end{array}$$

The proof of proposition 2 is given in the on-line supplementary document. The above results suggest that, as long as regularity conditions 1–6 hold, the non-parametric estimator does not cause any loss of efficiency. In other words, $\widehat{\theta }$ is asymptotically equivalent to the solution to expression (9) with known g, g′, w, E(w|z^Tβ), E(wx|z^Tβ) and E(wz₋₁|z^Tβ); hence the optimal semiparametric efficiency is practically achieved. We can also see that the presence of the linearity condition (2) or the corresponding weighted form (10) does not improve efficiency. Hence the benefit of these conditions is merely computational, in that, if condition (2) or (10) holds, then the corresponding non-parametric regression of z or w or wz on z^Tβ can be avoided. In addition, the classical linearity condition (2) alone cannot contribute to computational simplification of the efficient estimator. Therefore, although the linearity condition is routinely assumed in the dimension reduction literature, it is not necessary in our case. In the special case when the error is homoscedastic and hence w is a constant, our resulting efficient estimation variance is the same as that given in Carroll et al. (1997). However, even in the homoscedastic error case, the result in proposition 2 is stronger than the efficient result in Carroll et al. (1997). This is because their efficient result was established only for the normal error case, whereas our result is not restricted to any special distributional form.

4. Simulations

In this section, we conduct simulation studies to evaluate the performance of various estimation procedures. We generate X₁ from a uniform distribution U(0, 1), X₂ from a binomial distribution with success probability 0.5 and X₃ from a Poisson distribution with parameter 2. We generate other covariates as follows.

1. In case 1, we generate (X₄,…, X_dγ, Z₁,…, Z_dβ)^T from a multivariate normal distribution with mean 0 and variance–covariance matrix (σ_ij)_{(d−2) × (d−2)} where σ_ij = 0.5^|i−j| and d = d_γ + d_β − 1. In this case, the covariates z = (Z₁,…, Z_dβ)^T satisfy the linearity condition (2).

2. In case 2, we replace Z₅ in case 1 by ${\mathbf{z}}_4^2$ so that the linearity condition (2) is violated. All other covariates remain unchanged.

With the covariate vectors x = (X₁,…, X_dγ)^T and z = (Z₁,…, Z_dβ)^T, we generate Y from a normal distribution with mean x^Tγ + exp(z^Tβ) and variance function |z^Tβ| where γ = (2,1,−1, 0:5,0/^T and β = (4,1,1,1,1)^T/√20. When d_γ > 5 or d_β > 5, the additional components of γ or β are 0.

We carry out a group of simulations to examine the finite sample performance of the estimators corresponding to the following estimating equations (a)–(e):

$${\displaystyle \sum _{i=1}^n(Y_i-{\mathbf{x}}_i^T\widehat{\gamma }-{\mathbf{z}}_i^T\widehat{\beta })\left(\begin{array}{c}{\mathbf{x}}_i\\ {\mathbf{z}}_i\end{array}\right)=0,}$$ (a)

$$\begin{array}{c}{\displaystyle \sum _{i=1}^n\{Y_i-{\mathbf{x}}_i^T\widehat{\gamma }-\widehat{g}({\mathbf{z}}_i^T\widehat{\beta })\}\{{\mathbf{x}}_i-\widehat{E}(\mathbf{x}|{\mathbf{z}}_i^T\widehat{\beta })\}=0,}\\ {\displaystyle \sum _{i=1}^n(Y_i-{\mathbf{x}}_i^T\widehat{\gamma }-{\mathbf{z}}_i^{\text{T}}\widehat{\beta }){\mathbf{z}}_i=0,}\end{array}$$ (b)

$$\begin{array}{c}{\displaystyle \sum _{i=1}^n\{Y_i-{\mathbf{x}}_i^T\widehat{\gamma }-\widehat{g}({\mathbf{z}}_i^T\widehat{\beta })\}\{{\mathbf{x}}_i-\widehat{E}(\mathbf{x}|{\mathbf{z}}_i^T\widehat{\beta })\}=0},\\ {\displaystyle \sum _{i=1}^n\{Y_i-{\mathbf{x}}_i^T\widehat{\gamma }-{\mathbf{z}}_i^T\widehat{\beta })\}\{{\mathbf{z}}_i-\widehat{E}(\mathbf{z}|{\mathbf{z}}_i^T\widehat{\beta })\}=0},\end{array}$$ (c)

$${\displaystyle \sum }_{i=1}^n\{Y_i-x_i^T\widehat{\gamma }-\widehat{g}(z_i^T\widehat{\beta })\}\widehat{w}(x_i,z_i)\left(\begin{array}{c}{x}_i-\frac{\widehat{E}\{xw(x,z)|z_i^T\widehat{\beta }\}}{\widehat{w}(x_i,z_i)}\\ {\widehat{g}}^{\prime }(z_i^T\widehat{\beta })z_i\end{array}\right)=0,$$ (d)

$${\displaystyle \sum _{i=1}^n\{Y_i-{\mathbf{x}}_i^T\widehat{\gamma }-\widehat{g}({\mathbf{z}}_i^T\widehat{\beta })\}\widehat{w}({\mathbf{x}}_i,{\mathbf{z}}_i)\left(\begin{array}{c}{\mathbf{x}}_i-\frac{\widehat{E}\{\mathbf{x}w(\mathbf{x},\mathbf{z})|{\mathbf{z}}_i^T\widehat{\beta }\}}{\widehat{w}({\mathbf{x}}_i,{\mathbf{z}}_i)}\\ {\widehat{g}}^{\prime }({\mathbf{z}}_i^T\widehat{\beta })\left[{\mathbf{z}}_i-\frac{\widehat{E}\{\mathbf{z}w({\mathbf{z}}_i^T\widehat{\beta })\}}{\widehat{w}({\mathbf{x}}_i,{\mathbf{z}}_i)}\right]\end{array}\right)=0}.$$ (e)

We choose these estimating equations on the basis of the following considerations. The estimator that is obtained from (a) corresponds to the ordinary least squares estimator in the classical linear model, which is asymptotically biased without any condition; estimators obtained from (b) are consistent only when condition (2) is satisfied. Owing to the double-robustness property, estimator (c) is always consistent. Similarly, estimator (d) offers consistent estimation, and the resulting estimator is efficient if condition (2) is satisfied; estimator (e) offers consistent and efficient estimates even when condition (2) is violated. In addition, for estimators (b)–(e), we also experimented with their corresponding oracle version, where ĝ and ĝ′ are replaced by the true functions g and g′. In all the non-parametric regression procedures, the Epanechnikov kernel function is used, and the bandwidth is always set to be $2.2152\sigma {(\frac{3}{4}n)}^{-1/3}\approx 0.5$, where σ = 1:26 is the standard deviation of the regression covariate when z satisfies the linearity condition (2), and 2.2152 is the adjustment from the normal kernel to the Epanechnikov kernel. We used an undersmoothed bandwidth rate of n^−1/3 to ensure the consistency of the estimating equations (c) and (d). Although we could have implemented an optimal bandwidth for both (b) and (e), we decided not to do so for fair comparison. Similarly to the optimal bandwidth, this undersmoothed bandwidth still suffices to ensure the consistency of (b) and the efficiency of estimator (e).

We now evaluate the accuracy of estimation of β and γ on the basis of 1000 data replications. The bias (‘bias’) and the standard deviation (‘std’) of the estimates of γ and a subset of β are summarized in Table 1 for case 1 where condition (2) is satisfied and (n, d_γ, d_β) = (250, 5, 5). We can clearly see that estimator (a) has very large biases, whereas the biases for all other situations are much smaller. In terms of the estimation variability, (d) and (e) produce estimates with smaller variance than all other estimating equations, which also complies with our expectation since (d) and (e) are efficient. In addition, we can see that the estimating equations (b)–(e) offer competitive or sometimes even better estimators than their corresponding oracle versions which use the true link function g and its first derivative g′. This is in line with our theoretical finding in proposition 2, which indicates that non-parametric smoothing does not affect the first-order asymptotic property of the estimator.

Table 1.

Simulation results of estimating equations (a)–(e) for case 1 where linearity condition (2) is satisfied when n = 250, d_γ = 5 and d_β = 5^†

Estimator	Parameter	γ1 (%)	γ2 (%)	γ3 (%)	γ4 (%)	γ5 (%)	β1(%)	β2(%)	β5(%)
(a)	bias	189.43	65.28	31.49	−0.12	0.23	−2.82	0.33	−0.54
	std	54.11	42.83	12.98	26.31	31.38	5.39	12.13	9.93
	mse	38811.01	6095.64	1160.10	692.10	984.88	37.03	147.34	98.84
(b)	bias	1.48	0.07	−0.15	−0.01	2.64	−2.81	0.39	−0.41
	std	26.03	14.69	5.22	8.47	11.22	5.31	11.81	9.80
	mse	679.84	215.90	27.26	71.68	132.84	36.07	139.51	96.15
Oracle	bias	1.50	0.10	−0.13	−0.00	2.65	−2.81	0.39	−0.41
	std	26.23	14.81	5.23	8.52	11.27	5.31	11.81	9.80
	mse	690.25	219.26	27.32	72.58	133.94	36.06	139.60	96.28
(c)	bias	1.65	0.08	−0.16	−0.15	−0.20	−0.13	−0.60	−0.44
	std	22.20	13.33	4.68	7.75	8.93	1.94	5.07	4.20
	mse	495.49	177.79	21.89	60.09	79.71	3.76	26.05	17.80
Oracle	bias	1.57	0.07	−0.15	−0.16	−0.18	−0.15	−0.54	−0.41
	std	22.11	13.28	4.67	7.76	8.88	2.02	5.05	4.30
	mse	491.48	176.30	21.88	60.24	78.83	4.10	25.75	18.66
(d)	bias	1.74	0.11	−0.17	−0.20	0.38	−0.30	−0.05	−0.05
	std	21.66	12.96	4.55	7.64	8.28	1.29	3.80	3.23
	mse	472.34	167.91	20.72	58.35	68.64	1.74	14.43	10.46
Oracle	bias	1.15	0.09	−0.04	−0.08	3.62	−4.49	0.28	−1.16
	std	22.51	12.90	4.65	7.62	10.00	7.15	15.66	12.91
	mse	508.23	166.41	21.59	58.02	113.19	71.27	245.36	168.01
(e)	bias	1.71	0.11	−0.17	−0.19	0.36	−0.29	−0.10	−0.05
	std	21.61	12.95	4.54	7.65	8.29	1.31	3.86	3.28
	mse	469.85	167.77	20.68	58.54	68.85	1.79	14.87	10.75
Oracle	bias	1.34	0.07	−0.09	−0.22	0.33	−0.28	−0.02	−0.06
	std	19.09	11.33	3.96	6.72	7.38	1.34	3.82	3.33
	mse	366.31	128.47	15.67	45.25	54.62	1.86	14.61	11.12

^†The oracle estimates of (b)–(e) assume that the link function g and its first derivative g′ are known.

The parallel simulation results are reported in Table 2 for case 2 where condition (2) is violated and (n, d_γ, d_β) = (250,5,5). Again, estimator (a) has a non-ignorable bias. Since condition (2) is violated, estimator (b) also shows a large bias, and we can see that estimator (c) outperforms (b), and (e) is superior to (d) in terms of both the bias and the variance. This is especially clear in estimating β. This indicates that the linearity condition (2) needs to be verified. Blindly using a non-verified linearity condition will lead to biased results. The double-robustness form helps to achieve small bias without all the non-parametric regressions. It also yields superior finite sample performance when all the non-parametric regressions are performed.

Table 2.

Simulation results of estimating equations (a)–(e) for case 2 where linearity condition (2) is violated when n = 250, d_γ = 5 and d_β = 5^†

Estimator	Parameter	γ1 (%)	γ2 (%)	γ3 (%)	γ4 (%)	γ5 (%)	β1(%)	β2(%)	β5(%)
(a)	bias	190.81	65.45	31.65	−0.90	1.19	−16.89	−3.37	24.65
	std	75.56	50.20	15.79	34.89	39.33	13.17	11.26	14.94
	mse	42118.11	6804.15	1250.82	1218.09	1548.57	458.83	138.20	831.06
(b)	bias	1.04	0.25	0.12	−0.85	27.03	−19.49	−2.89	26.63
	std	37.22	21.01	7.90	12.96	21.30	14.36	11.34	15.32
	mse	1386.34	441.56	62.46	168.78	1184.42	586.24	136.86	943.95
Oracle	bias	1.76	0.40	0.28	−0.98	27.42	−19.53	−2.90	26.64
	std	39.78	23.71	9.17	14.03	22.32	14.41	11.34	15.33
	mse	1585.19	562.29	84.12	197.75	1249.73	588.90	137.07	944.92
(c)	bias	1.85	0.38	−0.09	0.06	−0.21	−0.24	−0.41	−0.23
	std	21.68	13.14	4.62	7.82	8.96	1.93	5.18	4.07
	mse	473.36	172.93	21.38	61.21	80.37	3.76	27.03	16.61
Oracle	bias	1.91	0.34	−0.09	0.02	−0.14	−0.25	−0.35	−0.27
	std	21.48	13.10	4.59	7.76	8.86	1.96	5.16	4.09
	mse	464.99	171.68	21.09	60.27	78.56	3.92	26.75	16.81
(d)	bias	1.66	0.26	−0.14	−0.11	0.47	−0.31	−0.13	0.28
	std	20.96	12.52	4.48	7.59	8.24	1.27	3.93	2.83
	mse	441.97	156.89	20.08	57.57	68.05	1.70	15.45	8.10
Oracle	bias	2.01	−0.03	0.15	−0.46	13.60	−11.98	−2.10	15.46
	std	23.22	13.80	5.06	8.58	11.25	8.57	14.14	10.28
	mse	542.97	190.36	25.66	73.90	311.56	216.89	204.47	344.57
(e)	bias	1.64	0.25	−0.15	−0.10	0.36	−0.26	−0.18	−0.22
	std	20.97	12.52	4.48	7.61	8.20	1.31	3.97	2.99
	mse	442.47	156.76	20.12	57.90	67.44	1.78	15.76	8.96
Oracle	bias	1.53	0.10	−0.07	−0.25	0.55	−0.35	−0.13	−0.10
	std	18.83	11.22	4.03	7.15	8.42	2.14	4.55	3.23
	mse	356.86	125.96	16.27	51.13	71.19	4.71	20.67	10.47

^†The oracle estimates of (b)–(e) assume that the link function g and its first derivative g′ are known.

To study the performance of the estimators when the covariates are of high dimension, we further increased the dimension of z to 10 and the bias and the standard deviation in estimating γ and β are summarized in Tables 3 and 4 for (n, d_γ, d_β) = (250, 5, 10). These results convey similar messages.

Table 3.

Simulation results of estimating equations (a)–(e) for case 1 where linearity condition (2) is satisfied when n = 250, d_γ = 5 and d_β = 10^†

Estimator	Parameter	γ1 (%)	γ2 (%)	γ3 (%)	γ4 (%)	γ5 (%)	β1(%)	β2(%)	β5(%)
(a)	bias	189.56	63.33	31.82	0.72	0.39	−5.66	−0.59	−1.23
	std	56.03	40.14	13.50	26.16	29.27	5.91	12.23	11.33
	mse	39073.67	5622.59	1194.71	684.93	857.03	66.97	149.94	129.78
(b)	bias	−0.45	0.29	0.15	0.00	4.17	−5.67	−0.62	−1.10
	std	27.34	16.19	5.67	9.17	11.64	5.81	12.04	11.02
	mse	747.82	262.35	32.12	84.06	152.93	65.84	145.44	122.57
Oracle	bias	−0.43	0.39	0.17	−0.03	4.20	−5.67	−0.62	−1.10
	std	27.44	16.46	5.71	9.23	11.82	5.82	12.04	11.03
	mse	753.23	271.04	32.67	85.12	157.34	66.00	145.28	122.84
(c)	bias	0.00	0.23	−0.05	−0.33	−0.74	−0.76	−0.55	−0.40
	std	23.67	13.46	4.78	7.45	9.18	2.10	5.29	4.86
	mse	560.16	181.34	22.88	55.67	84.88	4.98	28.31	23.80
Oracle	bias	−0.13	0.22	−0.06	−0.30	−0.80	−0.76	−0.57	−0.45
	std	23.47	13.38	4.76	7.50	9.23	2.10	5.28	4.87
	mse	550.80	179.12	22.63	56.29	85.85	5.00	28.24	23.94
(d)	bias	0.10	0.36	−0.08	−0.13	−0.35	−0.64	−0.31	−0.08
	std	22.34	12.59	4.52	7.08	8.23	1.45	4.15	3.90
	mse	499.22	158.59	20.44	50.20	67.78	2.52	17.35	15.21
Oracle	bias	0.13	0.31	0.01	0.20	7.38	−9.17	−1.79	−2.52
	std	24.53	14.68	5.16	8.14	10.77	7.73	15.29	14.04
	mse	601.92	215.64	26.61	66.31	170.42	143.85	236.98	203.48
(e)	bias	0.18	0.34	−0.09	−0.13	−0.35	−0.65	−0.34	−0.09
	std	22.35	12.63	4.50	7.06	8.18	1.47	4.24	3.93
	mse	499.37	159.56	20.29	49.87	67.06	2.60	18.10	15.42
Oracle	bias	0.23	0.30	−0.09	−0.10	−0.22	−0.69	−0.13	−0.10
	std	19.45	11.12	3.91	6.28	7.34	1.53	4.25	3.72
	mse	378.44	123.85	15.31	39.40	53.89	2.83	18.06	13.84

^†The oracle estimates of (b)–(e) assume that the link function g and its first derivative g′ are known.

Table 4.

Simulation results of estimating equations (a)–(e) for case 2 where linearity condition (2) is violated when n = 250, d_γ = 5 and d_β = 10^†

Estimator	Parameter	γ1 (%)	γ2 (%)	γ3 (%)	γ4 (%)	γ5 (%)	β1(%)	β2(%)	β5(%)
(a)	bias	187.83	64.28	32.53	0.69	0.34	−18.25	−3.89	23.04
	std	73.24	53.39	17.42	35.13	38.64	12.46	11.53	14.24
	mse	40645.36	6983.39	1361.69	1234.67	1493.53	488.42	148.09	733.60
(b)	bias	−0.83	0.53	0.05	0.21	26.34	−20.78	−3.60	25.01
	std	38.21	22.40	7.73	12.35	19.77	13.44	11.54	14.63
	mse	1460.43	502.20	59.76	152.60	1084.49	612.39	146.11	839.40
Oracle	bias	−0.03	0.50	0.15	0.41	26.56	−20.83	−3.58	25.04
	std	42.51	23.54	8.39	13.14	20.75	13.46	11.56	14.64
	mse	1806.81	554.54	70.48	172.89	1135.78	615.05	146.46	841.32
(c)	bias	0.48	0.17	−0.09	−0.20	−0.80	−0.90	−0.60	−0.14
	std	23.57	13.10	4.83	7.34	9.25	2.15	5.28	4.42
	mse	555.96	171.68	23.34	53.92	86.17	5.44	28.25	19.59
Oracle	bias	0.57	0.22	−0.13	−0.21	−0.75	−0.92	−0.63	−0.04
	std	23.49	13.07	4.85	7.29	9.17	2.19	5.29	4.55
	mse	551.97	170.79	23.53	53.21	84.69	5.66	28.40	20.75
(d)	bias	0.25	0.49	−0.06	−0.08	−0.16	−0.71	−0.27	0.27
	std	21.68	12.44	4.45	6.97	8.13	1.39	4.36	2.92
	mse	470.15	155.02	19.81	48.61	66.06	2.43	19.08	8.61
Oracle	bias	−0.38	0.33	0.11	0.28	16.23	−15.95	−3.47	14.28
	std	25.71	15.44	5.41	8.69	11.96	9.41	14.33	10.15
	mse	661.40	238.64	29.26	75.62	406.37	342.74	217.35	306.85
(e)	bias	0.31	0.44	−0.06	−0.10	−0.22	−0.67	−0.22	−0.34
	std	21.79	12.43	4.43	6.98	8.11	1.41	4.42	3.09
	mse	475.10	154.77	19.61	48.68	65.89	2.43	19.55	9.66
Oracle	bias	0.03	0.19	−0.05	−0.10	−0.11	−0.72	−0.15	−0.24
	std	19.24	11.12	3.87	6.28	7.37	1.47	4.34	3.39
	mse	370.22	123.67	14.99	39.46	54.35	2.69	18.87	11.58

^†The oracle estimates of (b)–(e) assume that the link function g and its first derivative g′ are known.

Since estimator (e) provides an efficient estimator regardless of whether the linearity condition (2) is satisfied or not or whether the error is homoscedastic or heteroscedastic, it is not surprising to note that estimator (e) always offers estimates with the smallest Monte Carlo standard errors among all estimators. Table 5 further reports the average estimated standard deviation and the Monte Carlo standard deviation, as well as the empirical coverage probabilities of the 95% confidence intervals for $\widehat{\gamma }$ from the 1000 simulations. As we can see, the estimated standard deviations match the Monte Carlo counterparts reasonably well, and the coverage probabilities are close to the nominal level.

Table 5.

Average estimated standard deviation $\widehat{\text{sd}}$, Monte Carlo standard deviation sd and 95% confidence interval coverage CI of $\widehat{\gamma }$ from estimating equation (e)

Case	Parameter	γ1	γ2	γ3	γ4	γ5
(n, d, dβ) = (250, 5, 5)
1	$$\widehat{\text{sd}}$$	0.2091	0.1206	0.0426	0.0696	0.0755
	sd	0.2161	0.1295	0.0454	0.0765	0.0829
	CI	94.1%	93.4%	94.5%	92.9%	92.7%
2	$$\widehat{\text{sd}}$$	0.2045	0.1180	0.0417	0.0681	0.0743
	sd	0.2097	0.1252	0.0448	0.0761	0.0820
	CI	95.4%	93.6%	93.8%	92.6%	92.8%
(n, dγ, dβ) = (250, 5, 10)
1	$$\widehat{\text{sd}}$$	0.2045	0.1178	0.0417	0.0682	0.0740
	sd	0.2235	0.1263	0.0450	0.0706	0.0818
	CI	93.2%	94.4%	93.8%	95.1%	92.0%
2	$$\widehat{\text{sd}}$$	0.2000	0.1153	0.0408	0.0667	0.0727
	sd	0.2179	0.1243	0.0443	0.0698	0.0811
	CI	93.4%	94.0%	93.2%	94.4%	92.1%

5. Example

The Fifth National Bank of Springfield facedagender discrimination suit in which it was charged with paying substantially lower salaries to its female employees than to its male employees. The bank’s employee database (based on 1995 data) is listed in Albright et al. (1999), with only the bank’s name being changed. For each of its 208 employees the data set includes each employee’s annual salary Y and gender X₁.

The average salary for the male employees (X₁ = 1) is 45.505 (in thousands of dollars) and the average for the females (X₁ = 0) is 37.262, yielding a p-value of less than 10⁻⁶ from a two-sample t-test. However, a naive comparison of the average salaries of males and females may not be suitable because there are many confounding factors that may affect salary. To make a faithful and complete comparison, we must account for these confounding factors. In this data set, three categorical and three continuous confounders are collected. The categorical confounders include a binary variable X₂ indicating whether the employee’s job is computer related or not, a five-level categorical variable (X_3,1,…, X_3,4) representing the employee’s educational level and a six-level categorical variable denoting the employee’s current job level (X_4,1,…, X_4,5). The three continuous confounders are respectively working experience at the current bank (Z₁, measured by the year when an employee was hired), the employee’s age (Z₂) and experience at another bank before working at the Fifth National Bank (Z₃, measured by the number of years at another bank). There was an obvious outlier in the data set, which was removed from our subsequent analysis. The continuous confounders Z_i were standardized marginally to have mean 0 and variance 1.

To account for the effect of the confounders, two models arise naturally: the linear model

$$Y={\gamma }_{\text{0}}+{\gamma }_{\text{1}}{X}_1+{\gamma }_{\text{2}}{X}_2+{\displaystyle \sum _{i=1}^4{\gamma }_{\text{3},i}{X}_{3,i}}+{\displaystyle \sum _{i=1}^5{\gamma }_{\text{4},i}{X}_{4,i}}+{\displaystyle \sum _{i=1}^3{\beta }_i{Z}_i+\epsilon }$$ (12)

and the partial linear single-index model

$$Y={\gamma }_{\text{1}}{X}_1+{\gamma }_{\text{2}}{X}_2+{\displaystyle \sum _{i=1}^4{\gamma }_{\text{3},i}{X}_{3,i}}+{\displaystyle \sum _{i=1}^5{\gamma }_{\text{4},i}{X}_{4,i}}+g\left({\displaystyle \sum _{i=1}^3{\beta }_i{Z}_i}\right)+\epsilon .$$ (13)

We require β = (β₁, β₂, β₃)^T in model (13) to have unit length and positive sign for the first non-zero element to ensure identifiability. We applied ordinary least squares to model (12), which corresponds to the estimating equation (a) in Section 4. In addition, we applied estimating equations (b), (c) and (e) to estimate the parameters in model (13). We reiterate here that estimating equation (b) requires condition (2) for consistency of estimation. Both (c) and (e) yield consistent estimators without condition (2), but (e) is more efficient if the data exhibit heteroscedasticity.

The estimated coefficients and their associated standard errors for models (12) and (13) are summarized in Table 6. The ordinary least squares estimate of γ1 in the linear model (12) has a p-value of nearly 0.10, indicating no significant gender effect on salary. The semiparametric inference procedures (b), (c) and (e) suggest a similar conclusion, which is contrary to the two-sample t-test result.

Table 6.

Estimated coefficients and standard errors for the Fifth National Bank data

Parameter	Results for model (12),		Results for model (13) and the following estimators:
	estimator (a)
			Estimator (b)		Estimator (c)		Estimator (e)
	Coefficient	Standard deviation
			Coefficient	Standard deviation	Coefficient	Standard deviation	Coefficient	Standard deviation
γ1	1.4273	0.8504	1.2381	1.3163	−0.1572	1.5864	0.6726	1.5409
γ2	4.5738	1.2258	5.0360	2.2537	4.4178	2.3679	3.4229	2.1513
γ3,1	−3.8173	1.3532	−0.5834	2.2137	1.4330	2.7118	−1.7172	2.4421
γ3,2	−4.1015	1.3018	−1.1123	2.1733	0.1020	2.5062	−2.9037	2.5332
γ3,3	−2.7977	0.9749	−1.7869	1.7624	−0.4008	1.8991	−2.2040	1.7955
γ3,4	−3.1605	1.8026	−0.5708	3.3598	−0.9586	3.5150	−2.1893	3.2231
γ4,1	−26.1685	2.3418	−24.1351	2.0737	−30.2798	3.4069	−24.9195	2.9111
γ4,2	−24.5755	2.2937	−22.6682	1.9986	−28.3341	3.2557	−23.1889	2.8851
γ4,3	−21.3149	2.2023	−18.7183	1.8050	−23.7748	3.1097	−19.2959	2.7476
γ4,4	−17.9505	2.0632	−14.0674	1.9868	−18.5167	3.0344	−14.9075	2.7432
γ4,5	−13.0403	1.9952	−8.2875	2.0998	−11.4228	3.1984	−9.0453	2.6962
β1	3.9500	0.5570	0.7787	19.6816	0.2329	0.1963	0.5546	0.0220
β2	−0.1526	0.4909	−0.6020	15.3779	0.4854	0.3464	0.4647	0.0268
β3	0.5729	0.3664	0.1765	4.4941	−0.8427	0.6024	0.6902	0.0218
R2	0.8342		0.8569		0.8446		0.9194

Because model (12) is nested within model (13), we first examine whether the link function g(·) in model (13) is linear. The estimated link function along with its pointwise confidence band is shown in Fig. 1(a), where the bandwidth is determined by leave-one-out cross-validation. We can see that there are quite a few data points in the upper right-hand part of Fig. 1(a) which exhibit a clear non-linear pattern. A closer inspection of these data points reveals that these mainly correspond to the executives who earned handsome salaries at the Fifth National Bank. The linear model (12) fails to capture this feature, indicating that it is insufficient to describe the data. Therefore, the results of semiparametric inference procedures obtained from estimating equations (b), (c) and (e) is more trustworthy.

Fig. 1.

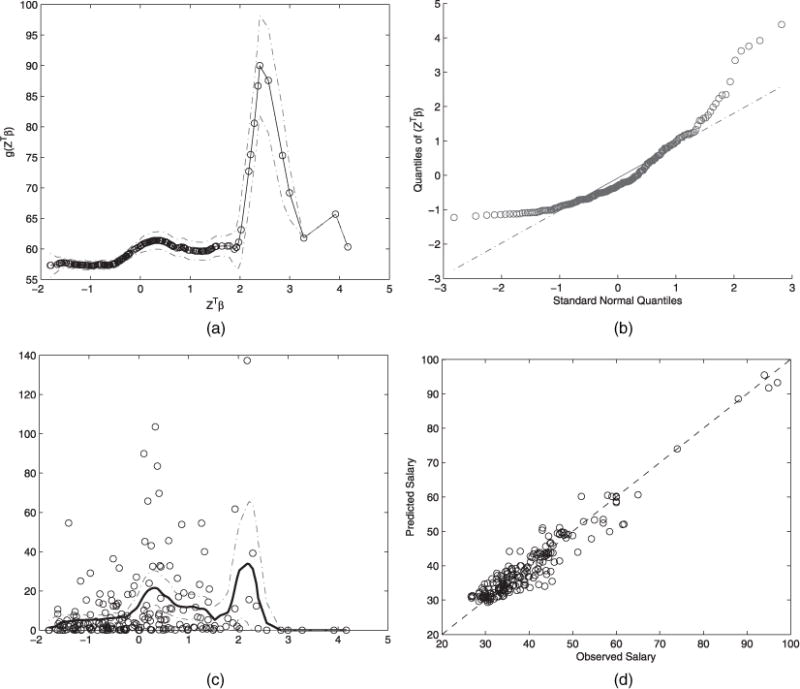
(a) Estimated link function (h = 0.3788), (b) Q–Q-plot of z^Tβ, (c) scatter plot of the residuals (h = 0.3618) and (d) scatter plot of salaries for the fifth National Bank data

From Table 6, we can see that both estimator (b) and estimator (c) indicate that none of the covariates in z has any effect on the employee’s salary, which contradicts our common sense because we would expect the working experience, for example, to be an important factor for salary. We suspect that estimator (b) failed to produce a consistent estimator, which would be so if the linearity condition (2) was not satisfied. To verify this conjecture, we examine whether z satisfies the linearity condition (2). The Q–Q-plot of z^Tβ that is presented in Fig. 1(b) indicates that the linearity condition (2) is probably violated because the distribution of z^Tβ deviates from a normal population significantly.

We next compare (c) with (e). We note that (c) differs from (e) in that (e) accounts for the heteroscedasticity. We calculated the residuals of model (13) to examine the existence of heteroscedasticity. Fig. 1(c) reports the scatter plot of the squared residuals versus the component z^Tβ. The full curve in Fig. 1(c) is the fitted variance function w(·)⁻¹ obtained from standard non-parametric smoothing, where the bandwidth is determined by leave-one-out cross-validation. We can clearly see from Fig. 1(c) that the data points were heteroscedastic, which was ignored by estimator (c). Thus, estimator (e) offers a more efficient estimate than (c). It also complies with the results in Table 6 because the standard errors of the estimates obtained from estimator (e) are smaller than those obtained from (c).

The last row of Table 6 summarizes the R²-values for all procedures. We can see that estimator (e) has the largest R²-value, which suggests the best performance among all estimation procedures. Fig. 1(d) shows a nice fit of the predicted salaries from estimator (e) and the observed salaries of all employees.

Considering all the above discussion, we believe that the results of estimator (e) based on model (13) are convincing. In fact, Fan and Peng (2004) analysed the same data by using another semiparametric model and reached the same conclusion that there is no significant evidence supporting gender discrimination in salary.

6. Conclusion

We have studied the partially linear single-index model with possibly high dimensional covariates, which can be viewed as a generalization of the model in Carroll et al. (1997), with the normality and homoscedasticity assumptions relaxed. We proposed a class of estimators that do not rely on the profile likelihood method. In addition, estimators in this class have a double-robustness property, which enables us to misspecify some of the non-parametric components. We also derived a computationally simple estimation procedure that achieves semiparametric efficiency. This further generalizes the efficiency result of Carroll et al. (1997). The presence of the popular linearity condition further simplifies the computation. However, we have shown that this additional condition does not contribute to the theoretical property of the estimator. In other words, the benefit of the linearity condition is purely computational. This does not come as a surprise since it is a very weak condition that always holds in the asymptotic sense (Hall and Li, 1993).

To preserve the usual optimal bandwidths h_i = O(n^−1/5) for i = 1,2,3, we have intentionally avoided the undersmoothing condition $n{h}_1^4\to 0$. A more careful but tedious analysis than that in the on-line supplementary document shows that, to guarantee the root n consistency of the resulting estimates, the valid bandwidth range is between $n{h}_1^2\to \infty$ and $n{h}_1^8\to 0$. Hence, if one feels comfortable in using an undersmoothing bandwidth in estimating β and γ, then the computation of consistent estimates can be relaxed because of the double robustness. Specifically, if we use a bandwidth between $n{h}_1^2\to \infty$ and $n{h}_1^4\to 0$, then we can opt to estimate either the g-function or the appropriate conditional expectation E(·|z^Tβ). This is computationally beneficial when we are not willing to propose a model for either of the two quantities, in that it is not necessary to estimate both. If g or E(·|z^Tβ) is of interest, one can always perform an additional standard non-parametric regression after obtaining the β- and γ-estimates.

Equivalent arguments and conclusions hold when model (1) is generalized to the scenario in which the partially linear function ${\mathbf{x}}_i^T\gamma +g({\mathbf{z}}_i^T\beta )$ is replaced by an arbitrary semiparametric function $m({\mathbf{x}}_i,{\mathbf{z}}_i^T\beta ,\text{γ,}g)$. The estimator will have the form

$$\begin{array}{c}{\displaystyle \sum _{i=1}^n\{Y_i-{\widehat{m}}_i(\theta )\}{\widehat{w}}_i\left[\frac{\partial {\widehat{m}}_i(\theta )}{\partial \gamma }-\frac{\widehat{E}\{{\widehat{w}}_i\partial {\widehat{m}}_i(\theta )/\partial \gamma |{\mathbf{z}}_i\}}{\widehat{E}({\widehat{w}}_i|{\mathbf{z}}_i)}\right]=0},\\ {\displaystyle \sum _{i=1}^n\{Y_i-{\widehat{m}}_i(\theta )\}{\widehat{w}}_i{\mathbf{z}}_i\left[\frac{\partial {\widehat{m}}_i(\theta )}{\partial ({\mathbf{z}}_i^T\theta )}-\frac{\widehat{E}\{{\widehat{w}}_i\partial {\widehat{m}}_i(\theta )/\partial ({\mathbf{z}}_i^T\beta )|{\mathbf{z}}_i\}}{\widehat{E}({\widehat{w}}_i|{\mathbf{z}}_i)}\right]=0},\end{array}$$

where ${\widehat{m}}_i(\theta )=m({\mathbf{x}}_i,{\mathbf{z}}_i^T\beta ,\text{γ,}\widehat{g})$. The estimator remains consistent and efficient provided that $E(\widehat{w}\partial \widehat{m}/\partial \theta |\mathbf{z})$ and $E(\widehat{w}|\mathbf{z})$ are properly estimated non-parametrically.

We did not expand our model to allow common components in x and z, which actually leads to very different results. This will be investigated in our subsequent work, and readers are referred to Xia et al. (1999) for related discussion and results. Finally, when z^Tβ is not sufficient to describe the regression, the partially linear additive model or partially linear multi-index model represent common strategies to overcome the curse of dimensionality. Recent work in this area includes Xia (2008) and Li et al. (2011).