Abstract
The heart of oxygenic photosynthesis is photosystem II (PSII), a multisubunit protein complex that uses solar energy to drive the splitting of water and production of molecular oxygen. The effectiveness of the photochemical reaction center of PSII depends on the efficient transfer of excitation energy from the surrounding antenna chlorophylls. A kinetic model for PSII, based on the x-ray crystal structure coordinates of 37 antenna and reaction center pigment molecules, allows us to map the major energy transfer routes from the antenna chlorophylls to the reaction center chromophores. The model shows that energy transfer to the reaction center is slow compared with the rate of primary electron transport and depends on a few bridging chlorophyll molecules. This unexpected energetic isolation of the reaction center in PSII is similar to that found in the bacterial photosystem, conflicts with the established view of the photophysics of PSII, and may be a functional requirement for primary photochemistry in photosynthesis. In addition, the model predicts a value for the intrinsic photochemical rate constant that is 4 times that found in bacterial reaction centers.
As the site of water splitting and oxygen production, photosystem II (PSII) is essential for oxygenic photosynthesis. This multisubunit protein complex consists of at least 17 polypeptides and catalyzes the oxidation of water and the reduction of plastoquinone (1). The PSII holocomplex of higher plants and green algae contains 200–300 chlorophyll (Chl) molecules and various carotenoids that are noncovalently bound to a variety of PSII polypeptides (2). The minimal functionally active PSII complex contains the reaction center (RC) polypeptides (D1, D2, cytochrome b559), the Chla core antenna polypeptides (CP43 and CP47), and the polypeptides of the oxygen-evolving complex. The total number of Chls in this PSII core complex is less than 40 per RC (3). Light energy absorbed by any PSII Chl generates an excited state, which is ultimately transferred to the primary electron donor in photosystem II, the RC photoactive pigment P680. Within the excited-state lifetime, primary charge separation [formation of P680+ and pheophytin− (Pheo−)] and charge stabilization (reduction of the primary quinone electron acceptor, QA, by Pheo−) occur with greater than 90% efficiency.
The kinetics of excited-state decay in PSII are highly dependent on the redox state of the RC (4). Accordingly, these kinetics contain valuable information about rates and mechanisms of excited-state energy transfer, primary charge separation, and stabilization reactions in the RC complex. Unfortunately, it is very difficult to measure directly these rates by using time-resolved spectroscopic techniques because of the complications of excited-state transfer processes that precede the electron transfer steps. In addition, transient absorption measurements in the Qy band of Chl are complicated by spectral congestion and also by competing absorption, bleaching, and stimulated emission. Although the Qx band of Pheo is relatively narrow and isolated from chlorophyll absorption, transient absorption measurements in this band cannot distinguish between the loss of Pheo ground-state population caused by the production of an ion pair or by the formation of electronically excited Pheo. Nevertheless, determination of the rate constants describing these intrinsic photophysical and photochemical processes is essential to the construction of a comprehensive kinetic model of PS II and thus to a fundamental understanding of biological energy transduction in photosynthesis.
Previously, kinetic models applied to the analysis of excited-state processes in PSII have been based on a concept of rapid spectral equilibration—that is, the excited state reaches a thermal equilibrium among the various spectral forms of Chl in the antenna and RC on a time scale that is short compared with the photochemically limited lifetime of the excited state (5–7). A model for PSII based on these assumptions, known also as the Reversible Radical Pair (RRP) model, was introduced by Schatz and Holzwarth (5) in 1988. Simulations based on the Förster inductive resonance mechanism (8) with randomly assigned positions and orientations of chromophores restricted by volumes of pigment–protein complexes also supported the concept of fast spectral equilibration (9). However, a detailed kinetic description of excited-state dynamics within and between pigment–protein complexes of PS II is impossible without knowing the actual positions and orientations of all Chls. This same information is required if one is to extract the intrinsic rate constant for photochemical charge separation (kp) by using the constraints of experimentally determined lifetimes.
The availability of high-resolution x-ray crystallographic data for the PSII core complex (10) permits a quantitative analysis of our commonly held assumptions about excited-state dynamics in PSII. The rationale for questioning the concept of rapid equilibration of the excited state is immediately obvious on inspection of the PSII x-ray structure (Fig. 1). Here one observes a large gap between the electron transfer pigments and the antenna Chl that may act as a physical barrier to the fast spectral equilibration so commonly assumed in PSII. In this paper, we apply this recently acquired structural knowledge to critically evaluate our understanding of excited-state transfer and primary electron transport in PSII. We present a detailed kinetic model of excitation dynamics in PSII based on the coordinates of the 35 Chls and 2 Pheos in the PSII x-ray structure. Comparison of our simulations with the available experimental data clearly shows that there is no fast spectral equilibration among the antenna and the RC pigments. A critical consequence of slower energy transfer steps in PSII is that the kp for primary charge separation is much larger than previously assumed.
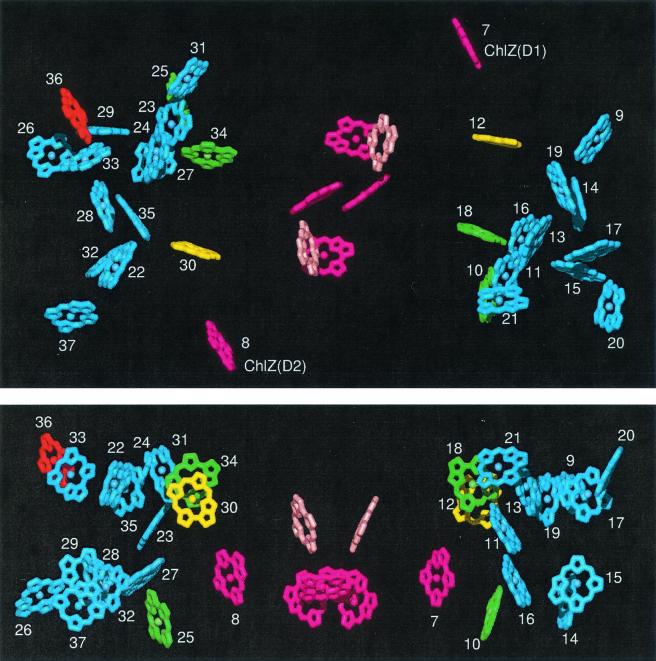
Figure 1.
X-ray structure of PSII showing all chromophores. Yellow and green, Chls efficiently transferring excitation to the RC (yellow, most efficient); blue, peripheral Chls not coupled directly to the RC; dark pink, RC Chls; pale pink, RC Pheos; red, long-wavelength Chl of CP47 coordinated by His-114. Chls numbered from 9 to 21 are associated with the CP43 polypeptide; Chls numbered from 22 to 37 are associated with the CP47 polypeptide. (Upper) View from the stromal side of the membrane. (Lower) Side view (stromal surface above).
Materials and Methods
Plant Material and Thylakoid Membrane Isolation.
A PSI-less strain of the cyanobacterium Synechocystis 6803 (a generous gift of W. Vermaas, Arizona State University, Phoenix, AZ) was grown at 30°C in BG-11 growth media in the presence of 15 mM glucose at a light intensity of 5 μE (E = einstein, mol of photons) m−2 s−1 (11). Thylakoid membranes were prepared from the cells according to the method of Tang and Diner (12). Immediately after isolation, the thylakoid membranes were frozen in liquid nitrogen and stored at −80°C until use.
Picosecond Fluorescence-Decay Kinetics and Global Lifetime Analysis.
Fluorescence-decay kinetics were measured with the time-correlated single-photon counting apparatus as described (13). Details of measurement conditions and the global lifetime analysis used to extract the PSII-associated decay components are as described (14). PSII kinetic parameters that we measured for Synechocystis 6803 were very close to the same parameters reported previously for PSII membrane particles from Synechococcus sp. (5).
Kinetic Modeling.
The rates for pairwise excited-state transfer between chromophores were
calculated by using the analytical expression of Shipman and Housman
(15). A refractive index of 1.3 was assumed for pairs with >15-Å
spacing and 1.0 for <15-Å spacing (16). The Stokes shift was set to
127 cm−1. Distances between chromophores and
orientation factors (kij =
e⃗i⋅
e⃗j−
3[e⃗j⋅
r⃗ij][e⃗j⋅ r⃗ij], where
e⃗i and
e⃗j are unit vectors in the direction
of the Qy transition dipole moment and
r⃗ij is the unit vector in the
direction of the line connecting the centers of the two molecules) were
calculated from the x-ray structural data (10). Excited-state
relaxation kinetics were obtained by using a numerical solution to the
Pauli master equation (17, 18). To account for reversible charge
separation and charge stabilization, we introduced two additional
states corresponding to
[P680+Pheo−] and
[P680+Q ]. We assumed a rate
constant for electron transfer from Pheo− to
QA of (0.48 ns)−1 (5, 19)
and used the rate constants for charge separation and charge
recombination as parameters to fit the excited-state decay kinetics
predicted by the model to experimental fluorescence decay kinetics. The
excitation wavelength for model simulations was set to 664 nm, the
wavelength at which experimental fluorescence-decay kinetics were
acquired.
]. We assumed a rate
constant for electron transfer from Pheo− to
QA of (0.48 ns)−1 (5, 19)
and used the rate constants for charge separation and charge
recombination as parameters to fit the excited-state decay kinetics
predicted by the model to experimental fluorescence decay kinetics. The
excitation wavelength for model simulations was set to 664 nm, the
wavelength at which experimental fluorescence-decay kinetics were
acquired.
Results and Discussions
PSII Chromophore Coordinates.
To build a detailed kinetic model based on Förster theory requires information on the positions and orientations of all pigments in PSII. Previous models making explicit reference to individual chromophores have used random positions and orientations of chromophores restricted to known volumes of the CP43 and CP47 polypeptides (14). The coordinates used for all chromophores in our current model were obtained from the x-ray structure of PSII from Synechococcus elongatus shown in Fig. 1. Each chromophore has a positional error of 1 Å and a rotational error of 10° in plane and 5° in all other directions. This structure is a refinement of the structure originally determined to 3.8-Å resolution (10). The RC complex, consisting of the D1, D2, and cytochrome b559 proteins, contains 6 Chls and 2 Pheos. The CP47 and CP43 core antenna complexes flank the RC complex and bind 16 and 13 Chls, respectively.
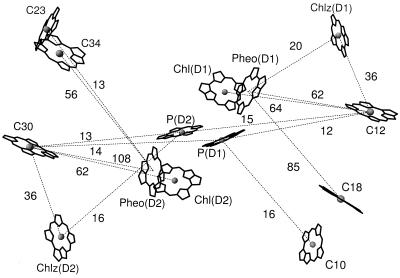
Structure factors [k2/R6, where k is the orientation factor (see Materials and Methods) and R is the distance between pigments] are a convenient way to quantify the contribution of distance and relative orientation to the rate of energy transfer between two pigments. For PSII, only a few Chls are positioned in such a way as to contribute significantly to the coupling between the antenna and RC complexes (Fig. 2). Two of these Chls (C12 and C30) have the largest sum of structure factors for transfer to RC electron transfer pigments and are especially tuned for transfer to Pheo and Chl of the RC.
Figure 2.
X-ray structure of PSII showing the RC pigments and the antenna Chls most important for energy transfer to the RC. Numbers refer to the structure factors (k2/R6, see text for details) for pairwise energy transfer between pigments connected with dotted lines and are given in units of 105 nm−6. Only structure factors greater than 10 × 105 nm−6 are shown.
The limited coupling observed between the antenna pigments and the RC pigments is a first indication that the typical assumption of exciton equilibration within the PSII core may be incorrect, and that the core may behave more like a three-component system.
Spectral Assignments for the 35 Chl and 2 Pheo Molecules in PSII.
The rate of excited-state transfer between pigments also depends on their respective spectral assignments. For the RC complex, we assigned the spectroscopic properties of P680 and Pheos as follows: P680, 680 nm; Pheo(D1), 679.6 nm; and Pheo(D2), 669 nm (20, 21). The spectral characteristics of Chl(D1) and Chl(D2) and the two peripheral RC Chls (ChlZ; Figs. 1 and 2) have not been identified unambiguously; therefore, we studied the effects of their energy levels on excited-state decay. Variation in the absorption maxima of both ChlZ molecules in the range 668–684 nm did not affect excited-state dynamics in simulations; however, placing Chl(D1) or Chl(D2) at 682 nm (21) accelerated the decay kinetics. For all subsequent simulations, we used the spectral arrangement of the RC pigments that yielded the fastest excited-state decay: ChlZ(D1), 684 nm (20); ChlZ(D2), 670 nm (22); Chl(D1), 673 nm; and Chl(D2), 682 nm (21).
As the spectroscopic properties of each Chl in CP43/47 are presently unknown, we investigated how the arrangement of the Chl spectral forms affects excited-state decay. Spectral assignment of Chls in the CP43 and CP47 antenna complexes was constrained by the absorption maxima and relative pigment numbers derived from Gaussian deconvolution of their absorption spectra (23). For CP43, we set the peak absorption of three Chls to 661 nm, three Chls to 671 nm, four Chls to 678 nm, and three Chls to 683 nm. For CP47, we set the peak absorption of three Chls to 661 nm, four Chls to 671 nm, four Chls to 678 nm, four Chls to 683 nm, and one Chl to 688 nm.
Based on a site-directed mutant study (24), we assigned C36 to the long-wavelength absorbing (688 nm) and emitting pigment (F695) of CP47 coordinated by His-114. An alternative assignment for F695 was the neighboring C33, whose transition dipole was perpendicular to the membrane plane. This second assignment is consistent with early spectroscopic studies with oriented samples (25) that showed the F695 transition dipole to be perpendicular to the membrane plane. Although the data presented are from simulations using the first assignment, results were very similar using either assignment.
All other spectral assignments first were made randomly. Of more than
105 random spectral configurations, we analyzed
those configurations that exhibited either the lowest or the highest
photochemical yield in simulations with fixed rate constants of charge
separation and recombination. In contrast with the prediction of models
based on fast spectral equilibration, we found the excited-state
dynamics in PSII to be sensitive to the location of Chl spectral forms.
The fastest excited-state decays were always found when lower energy
spectral forms of Chla were placed closest to the RC
complex. Spectroscopic properties of the four Chls (C12, C18, C34, and
C30) closest to the RC pigments were found to have the highest impact
on the excited-state decay. Placing the long-wavelength pigments of the
core antenna complexes at these sites helped to accelerate trapping of
the excited state by the RC. The efficiency of formation of
Q in our simulations ranged from 91% to 95% for
nonoptimal to optimal spectral arrangements, respectively.
in our simulations ranged from 91% to 95% for
nonoptimal to optimal spectral arrangements, respectively.
Calculation of Rates of Primary Electron Transport in PSII.
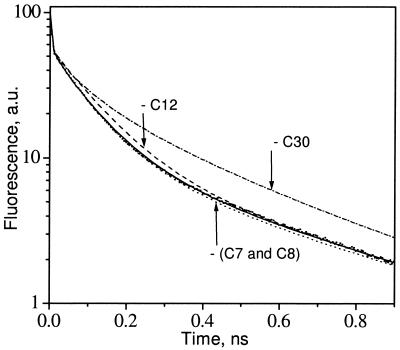
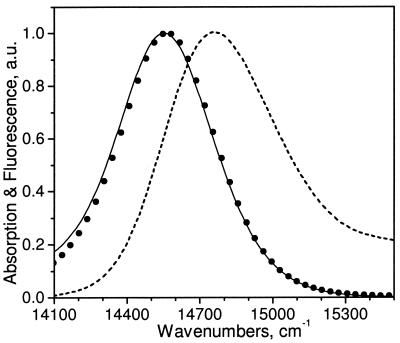
By choosing the spectral arrangement with the highest photochemical yield, we were able to determine a lower limit for the kp in PSII by using the rates of primary charge separation and recombination as variable parameters to obtain the best fit for the excited-state decay of the simulations to the experimental data (Fig. 3). For the optimal spectral configurations described above, the lower limit for the kp was (0.7 ps)−1. All other spectral configurations required even larger rate constants to match the experimental lifetimes. This value for kP is more than a factor of 3 larger than the corresponding value (2.7 ps)−1 in bacterial reaction centers, measured directly by experiment (26), but is in good agreement with recent transient absorption and fluorescence studies of isolated D1–D2–cytochrome b559 complexes in which (0.4 ps)−1 (27) and >(1.25 ps)−1 (28) rates of charge separation were reported. It is the presence of the slow transfer steps (>5 ps) from the CP47 and CP43 antenna pigments into the RC complex that forces the use of a higher kp, as compared with previous simulations, to keep the predicted lifetime and photochemical yield in line with experimental measures. The difference in photochemical rate must be attributed to subtle differences in protein structure and to the differences in the electronic properties of Chl and Pheo compared with their bacterial counterparts (29).
Figure 3.
PSII fluorescence-decay kinetics obtained from a global lifetime analysis of the PSI-less strain of Synechocystis 6803 (small filled dots) compared with the decay calculated with the kinetic model (solid line). Dashed, dash-dotted, and dotted lines represent fluorescence decays predicted with the model if C12, C30, or both ChlZ (C7 and C8), correspondingly, were removed. a.u., arbitrary units.
Equilibration of the Excited State.
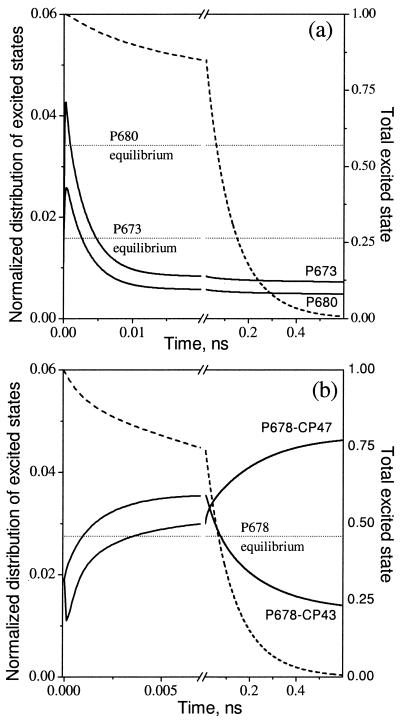
In a thermally equilibrated system of interacting pigments, the probability of excitation at any particular pigment depends on the energy level of the pigment and follows the Boltzmann law. Dissipation of excitation energy by charge separation at a photochemically active pigment (photochemical trapping) leads to deviations from this Boltzmann equilibrium. However, if excitation transfer within an ensemble of interacting pigments is fast compared with the rate of photochemical trapping, the system will reach a quasi-equilibrium (transfer equilibrium) state that may deviate from thermal equilibrium. For PSII, fast equilibration within the core antenna and between the core and RC chromophores has been the commonly accepted paradigm that led to the development and use of the RRP model. The x-ray structure of PSII challenges these assumptions and raises the following questions. How far from thermal equilibrium are the chromophores of PSII? Are transfer equilibrium states reached within the photochemically limited lifetime? Equilibration among the spectral forms in the model can be followed by plotting the fraction of the total excited states on each pigment as a function of time after excitation (Fig. 4). In this way, the redistribution of excited state from the initial excitation condition can be visualized without the dominant contribution of excited-state decay. Fig. 4 compares the spectral equilibration processes for representative pigments (solid lines) in the RC (Fig. 4a) and core antenna complexes (Fig. 4b) with the rate of excited-state decay (dashed line). For each pigment, the corresponding Boltzmann level is also shown. It is immediately apparent that none of the pigments reach any sort of equilibrium distribution during the lifetime of the excited state. For pigments in the RC complex, strong coupling to the photochemical losses on P680 causes a depletion of the excited state to as much as 7 times below their respective Boltzmann levels. In contrast, the excited-state distributions on the core antenna pigments are generally above their respective Boltzmann levels. In both the core antenna and RC complexes, the process of spectral redistribution exhibits two kinetic phases: a rapid (<5-ps) phase of redistribution within a complex, and a slower (100-ps) redistribution between the antenna and RC complexes. The latter phase is a consequence of the relatively weaker coupling between the antenna and RC complexes; the direction of the slow equilibration step (toward CP47) is driven by the presence of the low energy pigment in CP47.
Figure 4.
Time-resolved excited-state distributions (solid lines) calculated from the kinetic model with 664-nm excitation compared with the Boltzmann equilibrium distributions for the same pigments (dotted lines). The excited-state distributions are presented for P680 and a representative pigment P673 (the D1 Chl) in the RC (a), and for a representative antenna pigment (P678) in CP43 and in CP47 (b). The excited-state distributions have been normalized to the total amount of excitation remaining at any given time (dashed lines).
This description of excited-state dynamics in PS II would seem to be in direct conflict with a wealth of experimental data that has supported the concept of rapid spectral equilibration in PS II, including both steady-state (4, 6) and time-resolved (5, 30) measurements. One of the strongest arguments supporting rapid spectral equilibration in PS II is the observation that the steady-state fluorescence emission spectrum of PS II is indistinguishable from the emission spectrum predicted by the Kennard–Stepanov (K-S) relation (4, 6). The K-S relation, as extended to photosynthetic systems (31), predicts the steady-state fluorescence-emission spectrum from the absorption spectrum on the assumption of complete thermal equilibration among all coupled pigments and their respective vibrational states. We have compared emission spectra for our model simulation with the emission predicted from the K-S transform of the absorption and found that, as was previously observed experimentally (6), the two emission spectra strongly overlap (Fig. 5). However, the data in Fig. 4 clearly indicate that in the same model the RC and core antenna pigments are far from the expected Boltzmann levels (i.e., thermally equilibrated). On the basis of the crystallographic data (Fig. 1), the PSII RC/core antenna complex is clearly a three-compartment model in which the kinetics of excited-state transfer within each compartment are rapid compared with either kp or the rates of transfer between the compartments. The reason the K-S analysis and all experimental data to date fail to indicate this lack of spectral equilibration is that the spectral compositions of the three compartments of the model are so similar. Without significant spectral distinctions between compartments, neither steady-state nor time-resolved measurements can be used reliably to assess spectral equilibration.
Figure 5.
Absorption (dashed line) and emission (solid line) calculated from the kinetic model, and the emission predicted from the Kennard–Stepanov transform of the absorption (●).
The Role of ChlZ.
In analyses of energy transfer in PSII, before determination of the x-ray structure, it was assumed that the peripheral ChlZ of the RC complex played a central role in energy transfer from CP47 and CP43 to the RC complex (11, 14). However, the crystallographic structure clearly shows that this assumption cannot be valid (Figs. 1 and 2). The orientations and positions of both ChlZ molecules are not favorable for transfer to the RC. Compared with C12 and C30, both ChlZ molecules are weakly coupled to the RC and also are weakly coupled to the antenna Chls. Accordingly, the equilibration kinetics of both peripheral ChlZ molecules were found to be very slow (data not shown). This result is consistent with the earlier study of Schelvis and van Gorkom (32) that pointed out that energy transfer from ChlZ is likely to be slow (on the order of 30 ps).
Mapping the Major Pathways of Energy Transfer from Antenna to RC.
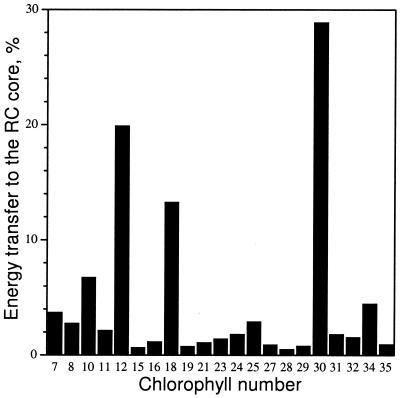
We used the kinetic model to determine the major routes for energy transfer from antenna to RC. For each core antenna Chl, the product of excitation probability with the sum of energy transfer rates from that Chl to each RC electron transfer pigment (excluding the ChlZ) was integrated over time and expressed as a percentage of the total transfer to the RC pigments from all core antenna Chls. Chls C12 and C30 were found to be most important in coupling the antenna and RC complexes, with about 50% of excitation energy transferred via these pigments (Fig. 6). Removal of either of these pigments from the model caused a pronounced slowdown of the excited-state decay (Fig. 3). Four other Chls, C18, C34, C10, and C25, transferred another 25%. We have examined how orientations of the pigments most important for energy transfer (C12 and C30) would affect the predicted excitation dynamics and found that variation of the direction of the dipoles within ±10% in the plane of the porphyrin ring did not change the dynamics of the system significantly. Optimization of orientations within these limits resulted in less than a 6% decrease of the rate constant for charge separation predicted by the model and did not change any of the basic conclusions of our study.
Figure 6.
Histogram showing the amount of excitation energy transferred from the antenna to the RC (see text for details) through some of the most important Chls.
Conclusions
We have built a model for excited-state dynamics and photochemical trapping in PSII that takes into account available spectral and x-ray structural data. Our kinetic model differs from the simpler RRP model in that it makes explicit reference to individual energy transfer steps between all chromophores in PSII rather than neglecting them on the assumption of fast transfer between all pigments (compared with the photochemically limited lifetime). Under conditions of fast equilibration between all pigments, the RRP model provided simple algebraic (empirical) terms that link the overall decay of the excited state, the yield of fluorescence, and most other model parameters to the intrinsic rate constants for photochemistry and radical pair recombination. The lack of rapid spectral equilibration described in this work does not mean that antenna emission is no longer sensitive to or representative of the redox state of the P680 reaction center. In the present model, the slow transfer step or steps from the core antenna to the RC pigments do not uncouple the antenna from the RC. This result is reflected by the high photochemical quantum yield predicted by the model. The decay of the excited state (and thus fluorescence emission) remains a function of these rate constants, but it is clear now that this function is strongly affected by the spatial organization of pigments within PSII. Results of our simulations show that the validity of the RRP model is limited to the RC core, where equilibration between six pigments is achieved rapidly. The relatively weak coupling between the antenna and RC complexes dictated by the structure of PSII has required the use of a significantly larger kp [>(0.7 ps)−1] to simulate fluorescence decay data than ever could have been predicted by the RRP model with its assumption of rapid thermal equilibration (5, 33).
The physical separation between chromophores with antenna and electron transfer functions that has been observed in bacterial (34, 35) and PSI (36) complexes previously is seen now in PSII as well—a structural feature that seems to have been conserved through evolution. One possible explanation for this common theme is that the electron transfer pigments must be physically isolated from the antenna pigments to retain the remarkable efficiency of their photochemical function.
Acknowledgments
D.B. gratefully acknowledges the support of research and equipment grants from the Natural Sciences and Engineering Research Council of Canada.
Abbreviations
- PSII
photosystem II
- Chl
chlorophyll
- RC
(photosynthetic) reaction center
- P680
primary electron donor in photosystem II
- Pheo
pheophytin
- RRP
Reversible Radical Pair
- ChlZ
peripheral reaction center chlorophylls
Footnotes
Data deposition: The atomic coordinates have been deposited in the Protein Data Bank, www.rcsb.org (PDB ID code 1ILX).
References
- 1.Barry B A, Boerner R J, de Paula L C. In: The Molecular Biology of Cyanobacteria. Bryant D A, editor. Dordrecht, The Netherlands: Kluwer; 1994. pp. 217–257. [Google Scholar]
- 2.Bassi R, Pineau B, Dainese P, Marquardt J. Eur J Biochem. 1993;212:297–303. doi: 10.1111/j.1432-1033.1993.tb17662.x. [DOI] [PubMed] [Google Scholar]
- 3.Ohno T, Satoh K, Katoh S. Biochim Biophys Acta. 1986;852:1–8. [Google Scholar]
- 4.Dau H. Photochem Photobiol. 1994;60:1–23. [Google Scholar]
- 5.Schatz G H, Brock H, Holzwarth A R. Biophys J. 1988;54:397–405. doi: 10.1016/S0006-3495(88)82973-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Dau H, Sauer K. Biochim Biophys Acta. 1996;1273:175–190. [Google Scholar]
- 7.Briantais J M, Dacosta J, Goulas Y, Ducruet J M, Moya I. Photosynth Res. 1996;48:189–196. doi: 10.1007/BF00041008. [DOI] [PubMed] [Google Scholar]
- 8.Förster T. In: Modern Quantum Chemistry. Sinano-glu O, editor. Vol. 3. New York: Academic; 1965. pp. 93–137. [Google Scholar]
- 9.Laible P D, Zipfel W, Owens T G. Biophys J. 1994;66:844–860. doi: 10.1016/s0006-3495(94)80861-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Zouni A, Witt H-T, Kern J, Fromme P, Krauss N, Saenger W, Orth P. Nature (London) 2001;409:739–743. doi: 10.1038/35055589. [DOI] [PubMed] [Google Scholar]
- 11.Lince M T, Vermaas W. Eur J Biochem. 1998;256:595–602. doi: 10.1046/j.1432-1327.1998.2560595.x. [DOI] [PubMed] [Google Scholar]
- 12.Tang X-S, Diner B. Biochemistry. 1994;33:4594–4603. doi: 10.1021/bi00181a021. [DOI] [PubMed] [Google Scholar]
- 13.Vasil'ev S, Bruce D. Biochemistry. 1998;37:11046–11054. doi: 10.1021/bi9806854. [DOI] [PubMed] [Google Scholar]
- 14.Vasil'ev S, Bruce D. Biochemistry. 2000;39:14211–14218. doi: 10.1021/bi000476v. [DOI] [PubMed] [Google Scholar]
- 15.Shipman L L, Housman D L. Photochem Photobiol. 1979;29:1163–1167. [Google Scholar]
- 16.Moog R S, Kuki A, Fayer M D, Boxer S G. Biochemistry. 1984;23:1564–1571. doi: 10.1021/bi00302a034. [DOI] [PubMed] [Google Scholar]
- 17.Jean J M, Chan C-K, Fleming G R, Owens T G. Biophys J. 1989;56:1203–1215. doi: 10.1016/S0006-3495(89)82767-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Holcomb C T, Knox R S. Photosynth Res. 1996;50:117–131. doi: 10.1007/BF00014883. [DOI] [PubMed] [Google Scholar]
- 19.Leibl W, Breton J, Deprez J, Trissl H-W. Photosynth Res. 1989;22:257–275. doi: 10.1007/BF00048304. [DOI] [PubMed] [Google Scholar]
- 20.Jankoviac R, Rästep M, Picorel R, Seibert M, Small G J. J Phys Chem. 1999;103:9759–9769. [Google Scholar]
- 21.Konermann L, Holzwarth A R. Biochemistry. 1996;35:829–842. doi: 10.1021/bi9513158. [DOI] [PubMed] [Google Scholar]
- 22.Vacha F, Joseph D M, Durrant J R, Telfer A, Klug D, Porter G, Barber J. Proc Natl Acad Sci USA. 1995;92:2929–2933. doi: 10.1073/pnas.92.7.2929. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Jennings R C, Bassi R, Garlaschi F M, Dainese P, Zucchelli G. Biochemistry. 1993;32:3203–3210. doi: 10.1021/bi00064a002. [DOI] [PubMed] [Google Scholar]
- 24.Shen G, Eaton-Rye J J, Vermaas W. Biochemistry. 1993;32:5109–5115. doi: 10.1021/bi00070a019. [DOI] [PubMed] [Google Scholar]
- 25.Kramer H J M, Amesz J. Biochim Biophys Acta. 1982;682:201–207. [Google Scholar]
- 26.Fleming G R, Martin J L, Breton J. Nature (London) 1988;333:190–192. [Google Scholar]
- 27.Groot M L, van Mourik F, Eijckelhoff C, van Stokkum I H M, Dekker J P, van Grondelle R. Proc Natl Acad Sci USA. 1997;94:4389–4394. doi: 10.1073/pnas.94.9.4389. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Donovan B, Walker L A, Kaplan D, Bouvier M, Yocum C F, Sension R J. J Phys Chem. 1997;101:5232–5238. [Google Scholar]
- 29.Dekker J P, van Grondelle R. Photosynth Res. 2000;63:195–208. doi: 10.1023/A:1006468024245. [DOI] [PubMed] [Google Scholar]
- 30.van Amerongen H, Valkunas L, van Grondelle R. Photosynthetic Excitons. Singapore: World Scientific; 2000. [Google Scholar]
- 31.Laible P D, Knox R S, Owens T G. J Phys ChemB. 1998;102:1641–1648. [Google Scholar]
- 32.Schelvis J P M, van Noort P I, Aartsma T J, Van Gorkom H J. Biochim Biophys Acta. 1994;1184:242–250. [Google Scholar]
- 33.Roelofs T A, Lee C-H, Holzwarth A R. Biophys J. 1992;61:1147–1163. doi: 10.1016/s0006-3495(92)81924-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Visscher K J, Bergstöm H, Sundström V, Hunter C N, van Grondelle R. Photosynth Res. 1989;22:211–217. doi: 10.1007/BF00048300. [DOI] [PubMed] [Google Scholar]
- 35.Hu X, Damjanovic A, Ritz T, Schulten K. Proc Natl Acad Sci USA. 1998;95:5935–5941. doi: 10.1073/pnas.95.11.5935. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Krauss N, Schubert W-D, Klukas O, Fromme P, Witt H-T, Saenger W. Nat Struct Biol. 1996;3:965–973. doi: 10.1038/nsb1196-965. [DOI] [PubMed] [Google Scholar]