Classification of fMRI patterns—A study of the language network segregation in pediatric localization related epilepsy

Abstract

This article describes a pattern classification algorithm for pediatric epilepsy using fMRI language‐related activation maps. 122 fMRI datasets from a control group (64) and localization related epilepsy patients (58) provided by five children's hospitals were used. Each subject performed an auditory description decision task. Using the artificial data as training data, incremental Principal Component Analysis was used in order to generate the feature space while overcoming memory requirements of large datasets. The nearest‐neighbor classifier (NNC) and the distance‐based fuzzy classifier (DFC) were used to perform group separation into left dominant, right dominant, bilateral, and others. The results show no effect of age, age at seizure onset, seizure duration, or seizure etiology on group separation. Two sets of parameters were significant for group separation, the patient vs. control populations and handedness. Of the 122 real datasets, 90 subjects gave the same classification results across all the methods (three raters, LI, bootstrap LI, NNC, and DFC). For the remaining datasets, 18 cases for the IPCA‐NNC and 21 cases for the IPCA‐DFC agreed with the majority of the five classification results (three visual ratings and two LI results). Kappa values vary from 0.59 to 0.73 for NNC and 0.61 to 0.75 for DFC, which indicate good agreement between NNC or DFC with traditional methods. The proposed method as designed can serve as an alternative method to corroborate existing LI and visual rating classification methods and to resolve some of the cases near the boundaries in between categories. Hum Brain Mapp 35:1446–1460, 2014. © 2013 Wiley Periodicals, Inc.

INTRODUCTION

The functional anatomy of language processing networks has been extensively studied through fMRI [Binder et al., 1995; Bookheimer, 2002; Cabeza and Nyberg, 2000; Just et al., 1996]. For normal healthy persons, language activation is typically left dominant, but there are known variants (bilateral or right dominance) in right handed populations and left handed populations: 4% right handed and 24% left handed in Pujol et al., 1999; 4% right handed and 30% left handed in Rasmussen and Milner, 1977; 6% right handed in Springer et Al., 1999; and 22% left handed in Szaflarski et al., 2002. Furthermore, patients with localization‐related epilepsy (LRE) exhibit a higher incidence of atypical language activations (20–30%) based either on quantitative region of interest (ROI) analysis [Frost et al., 1999; Gaillard et al., 2007; Woermann et al., 2003] at hemisphere [Binder et al., 1996], sub region levels [Abbott et al., 2010; Gaillard et al., 2002; Ramsey et al., 2001; Spreer et al., 2002], or visual rating [Fernandez et al., 2001; Gaillard et al., 2002, 2004]. The reorganization of language networks from canonical areas (i.e., Broca's and Wernicke's areas) to distinct locations either in the same or in the contra lateral hemisphere is a consequence of underlying structural lesions (e.g., stroke) or the functional processes of epilepsy [Gaillard, 2004; Liegeois et al., 2004; Szaflarski et al., 2006]. We have implemented data driven methods free of a priori assumptions and limitations of ROI and visual methods, to achieve subgroup classification and characterization [Mbwana et al., 2009; You et al., 2011].

One such method, principal component analysis (PCA), is a valuable mathematical method used for exploring and analyzing multidimensional datasets. It enables computation of a linear transformation that maps data from a high dimensional space to a lower dimensional orthogonal space, maximizing variance as a consequence [Jolliffe, 2002]. These characteristics of the PCA are incorporated in our method to transform the fMRI activation map from its spatial space into the eigenvector feature space, which we use as the feature space for classification. Previous studies have shown that this feature space facilitates classification by means of different algorithms including the K‐means approach [Mbwana et al., 2009], neural networks [Samanwoy and Adeli, 2008], and nonlinear decision functions [Cabrerizo et al., 2011; Tito et al., 2010, 2009] to name a few.

Another advantage of the PCA feature space is its independence of a priori assumptions and biases inherent to ROI and visual rating. In our previous study [You et al., 2011], we performed PCA on 122 fMRI activation maps with regional masking, and identified three primary activation pattern groups or clusters: left dominant with higher intensity, left dominant with lower intensity, and right dominant. Then, through a Euclidean distance method, we associated the remaining undecided subjects to the primary clusters that were previously determined. This study aims to overcome limitations identified during our previous study, namely the need (1) to include bilateral activation and (2) to resolve those challenging activation patterns that are at the boundaries in between categories and are therefore difficult to classify.

DATA AND SUBJECTS

A multisite consortium with pediatric epilepsy programs at five children's hospitals: Miami Children's Hospital (MCH), Children's National Medical Center (CNMC), Hospital for Sick Children (HSC), British Columbia Children's Hospital(BCCH), and Children's Hospital of Philadelphia (CHOP) built a repository for pediatric epilepsy data (http://mri-cate.fiu.edu) to investigate the effects of epilepsy on brain function and structure [Lahlou et al., 2006]. Procedures were followed in accordance with local institutional review board requirements; all parents gave written informed consent and children gave assent. The control subjects were right handed, determined by clinical assessment or handedness inventories such as the Harris tests of lateral dominance or the modified Edinburgh inventory [Harris, 1974; Oldfield, 1971], and free of any current or past neurological or psychiatric disease. Since demographic and clinical information are required for statistical analysis, the requirements for the usable data include: (1) at least two of the three variables (gender, age, and handedness) in demographic information are available; (2) at least two of the three variables (age at seizure onset, seizure focus, and seizure etiology) are also available. With these requirements, 64 controls and 58 patients were included in the study. Among all subjects, the following are the number of missing cases for variables: 0 in gender, 2 in age, 4 in handedness, 9 in seizure onset, 9 in duration of epilepsy, 8 in seizure focus, and 11 in seizure etiology.

Each participant performed an auditory description decision task‐ADDT (a word definition task) which was designed to activate both temporal (Wernicke's area) and inferior frontal (Broca's area) cortex [Gaillard et al., 2007]. The task required comprehension of a phrase, semantic recall, and a semantic decision. The block design paradigm is consisted of 100 (TR = 3 s) or 150 (TR = 2 s) time‐points, with experimental and baseline periods alternating every 30 s for five cycles, totaling 5 min.

To perform the group analysis of datasets collected from several sites, datasets were matched into Neuroimaging Informatics Technology Initiative (NIFTI) format using the transversal view and radiology convention, and were registered into the standard Montreal Neurological Institute (MNI) [Burgund et al., 2002; Faria et al, 2010; Muzik et al., 2000] brain with 3 × 3 × 3 (mm³) in voxel size and 61 × 73 × 61 (axial × coronal × sagittal) in resolution. The fMRIB software Library (FSL) was used to perform the pre‐processing required for obtaining the 3D activation maps [Jenkinson et al., 2002; Jenkinson and Smith, 2001; Woolrich et al., 2001].

Of the 64 control datasets and 58 children with focal epilepsy (patient population) included in this study, 63.79% of the patients and 54.69% of the controls are males. Moreover, 19% of the patients had atypical handedness (left or mixed). The mean age of patients was 13.86 years (standard deviation 3.37 years, age range 4.5–19 years), and the mean age of controls was 8.65 years (standard deviation 2.65, range 4.2–12.9). The patients had mean age seizure onset of 8.23 years (standard deviation 4.28, range 1–18 years). There were 26 left localized patients; 17 (65%) had a temporal focus and the rest an extra‐temporal focus. There were 18 right localized patients; seven (39%) had a temporal focus and the rest had an extra‐temporal focus. Three patients had bilateral seizure focus. Twenty‐two patients had abnormal MRIs: seven tumors, five mesial temporal sclerosis, four focal cortical dysplasia, one vascular malfunction, three focal gliosis, and two atrophy. Of the 45 patients with seizure etiology information, 21 had remote symptomatic seizure cause, three an acute symptomatic cause, and 21 no known cause. Eleven patients (out of the 54 available) had atypical handedness (left or mixed).

METHODS

Artificial Data Generation and Validation

In this study, artificial activation patterns were generated based on different combinations of activations in the typical language related areas of Broca's and Wernicke's. These artificial patterns are created as the training data to classify the 122 real datasets in the testing phase. First, we obtained left and right Broca's [BA: 44, 45, 47] and Wernicke's [BA 21, 22, 39] masks separately from BA templates provided by MRIcro (Rorden and Brett, 2000). In accordance with the clinical notion of typical and atypical language patterns (Fig. 1), the top five combinations of Broca's and Wernicke's masks were regarded as typical (left dominant if both regions are left, or one region is left and the other is bilateral or with no activity), and the rest were considered atypical (bilateral for both bilateral or lateralized in opposite sides; or right dominant when both regions are right lateralized, or when one is right and the other is bilateral or with no activity). Moreover, activation patterns which are considered as “others” (nondiagnostic) include null activation and noise.

Figure 1.

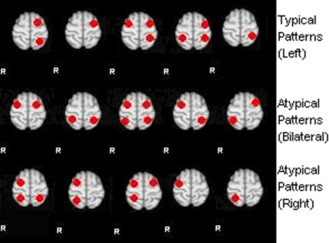
Suggested standard fMRI language activation patterns: Anterior and lateral dots represent expressive language areas (Broca); posterior and lateral dots represent receptive language areas (Wernicke). Note: Null‐activation and noise (pseudo activation) are not displayed in this figure. [Color figure can be viewed in the online issue, which is available at http://wileyonlinelibrary.com.]

Activations are then generated randomly within the four ROIs (left and right Brocas' and Wernicke's) in accordance to the following rules:(i) the center of activation must be within the ROI; (ii) the covariance matrix is randomly generated, and the number of activations is randomly chosen from 1 to 10. (iii) the generated clusters satisfy the Gaussian distribution; These datasets were generated taking into consideration only the extent of volume and masked regions, while disregarding any demographic or clinical information of the real data. The reason is to remove any inference to the available real data, so that the classification method as designed can be generalized in its use to other real fMRI data. The procedure for generating artificial data consists of the following steps:

• Generate related parameters following the set rules.

• Resample the original volume size 61*73*61 into 244*292*244.

• Randomly generate points in the resampled volume (2500 points in this case is generated for each activation pattern).

• Accumulate the number of points on each voxel as the value of that voxel.

• Resample the volume back to its original size 61*73*61.

• Apply the mask to obtain the artificial data.

Four hundred activation samples within each of the four basic masks (left Broca, right Broca, left Wernicke, and right Wernicke) were generated initially for a total of 1,600. Random combinations from those basic activation patterns were thereafter generated yielding 580 artificial datasets. Since the goal is to classify the data into four categories: left dominant, right dominant, bilateral, and others (noise and NA), the artificial datasets which satisfy the characteristics of the three main categories (left dominant, right dominant, and bilateral) were generated with close numbers in volumes in each category for a balanced analysis. In order to focus on activation region differences instead of activation intensity as we did in our previous study [You et al., 2011], the intensity of all artificial activation maps was normalized. The intensity normalization was achieved by changing the range of pixel intensity values to range between 0 and 1. More specifically, we divide each pixel by the maximum value of the whole volume.

Incremental PCA‐Based Method and Feature Space for Classification

Feature space generation has been studied extensively with different applications in medical imaging, as well as for object recognition and pattern classifications problems [Joliffe and Morgan, 1992; Turk and Pentland, 1991]. With the due consideration to the concept and merit of subject loading [Alexander and Moeller, 1994], we intended to perform the PCA on the artificial datasets to obtain the eigenvectors for projecting the data into a dimensionally reduced feature space. However, the number of artificial datasets considered initially in this study was too large to be loaded into the program at once. Consequently, the Incremental PCA was used instead. Implementation details of the IPCA are provided in the Appendix.

The inputs for the classifiers are the basis projections of the data into the IPCA leading eigenvector feature space.

Nearest Neighbor Classifier

The nearest neighbor classifier (NNC) searches for the minimum distance in the Eigen space or feature space between a testing dataset and the training datasets. Suppose the projection of one testing activation data is y _t and the projection of the p _th training activation data is y _p. Then the distance between projections of the two data is determined as d _p=||y _t − y _p||. The index of minimum(d) gives the recognition result in the training data for the given test data.

Distance‐Based Fuzzy Classifier

Clinical decisions or rating of activation patterns that fall at or near the boundary in between categories are difficult to make. In the case of the four categories considered here, it may be important to know such matters as this data has 0.56 similarity to left dominant patterns and 0.44 similarity to bilateral patterns to facilitate the decision making or at least proceed at scrutinizing the activation patterns of that particular subject or patient. To achieve this goal, a distance‐based fuzzy classifier (DFC) for this specific study was introduced, which is based on the K‐nearest neighbor algorithm [Dasarathy, 1991; Shakhnarovish et al., 2008].

This DFC follows the same steps as the NNC until the distance vector is obtained between all the training data and the testing dataset. In this case, we consider the nearest m distances (d _i with i = 1, 2,…,m where d ₁ < d ₂ < …< d _m) instead of the nearest distance. For this particular implementation, we opted for the nearest 3 distances (m = 3). The statistical analysis for other m will be discussed in the result section.

For the nearest m distances, different weights are given according to their nearest order following Eq. (3):

$$w_i=\frac{i}{{\sum }_{j=1}^{m}j}$$ (1)

where i is the index of the nearest m distances. For example, when m = 3, the nearest distance d ₁ is given the weight 1/6, the second nearest distance d ₂ is given the weight 2/6 and the third nearest distance d ₃ is given the weight 3/6, and so on for other nearest distances if considered. The reason for the choice of weights is because in Eq. (4), the smaller is the weight (i.e., distance) the higher is the similarity.

The similarity for the ith distance (i = 1, 2, …, m) is given by the following relation:

$$S_i=\frac{e^{-d_i{w}_i}}{{\sum }_{j=1}^m{e}^{-d_j{w}_j}}$$ (2)

Then to determine the percentage similarity of a given real dataset to any one of the four categories, the following equation was used:

$$\text{Category}\hspace{1em}x\hspace{1em}\text{similarity}=\sum _{j\in x}{S}_j$$ (3)

Assume a real dataset is now to be categorized after we determined the 3 nearest distances d ₁, d ₂ and d ₃. Assume further as an example that it was determined that d ₁ and d ₃ are computed from artificial patterns in category L, and that d ₂ on the other hand is from an artificial pattern in category B. Equation (4) is then used to compute the similarity percentage S ₁, S ₂, S ₃ based on d ₁, d ₂ and d₃, respectively. Then according to equation (5), S ₁ and S₃ are summed together to yield the similarity percentage for category L, and similarity S ₂ alone will the similarity percentage for category B and the similarity percentages for the remaining categories will be 0. In this case, only such similarity percentages will be tabulated as will be detailed in the Results section. The larger similarity percentage for the category means the test data has a higher probability of belonging to that category. A special case that should be considered is when one of the d _i is very small or near zero in contrast to the other d _is, then the category similarity gives 1 to the pattern corresponding to the near zero d _i. For example if d ₁ ≤ 0.01 with d ₂ ≥10d ₁, then a similarity of 100% is given to the category nearest to the pattern corresponding to d ₁.

Visual Rating System

We used a visual rating system to categorize each subject's activation map into the dominance patterns used for LI assignment. An access‐based tool was used to score images to a predetermined set of language network patterns representing the differing combinations of activations in canonical frontal and temporal regions. Each subject's activation map interpreted using set threshold, Z > 2.3 with P = 0.05 cluster corrected [Forman et al., 1995; Friston et al., 1994; Worsley et al., 1992], and then overlaid on top of the brain template. Three clinical raters, blinded to subject identity, categorized the laterality of activation in language related areas, and provided the level of confidence in the rating (confidence scale was from 1 to 5: 5 being most confident, 1 least (i.e., not) confident of rating). Comments on observations when there was concern about noise or null activation were noted [Guillen et al., 2009]. Raters were instructed to rate each subject's map independently and categorize the map into one of the 20 available activation patterns present in the tool (Fig. 2), and mark their selection, if necessary, with personal comments.

Figure 2.

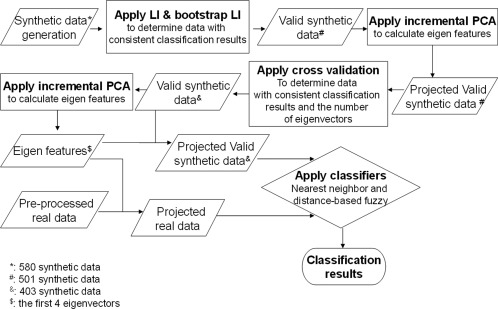
Structure of the classification process combining synthetic and real data.

Laterality Indices

For quantitative assessments, we used two approaches to calculate regional LIs: (1) a fixed threshold (the threshold at which visual rating was performed) [Adcock et al., 2003; Holland et al., 2001; Liegeois et al., 2004; Price, 2000] and (2) a bootstrap method with the weighted mean measure with the option “no optional steps” [Wilke and Schmithorst, 2006] (postulated to be more versatile than a fixed threshold). With these measures we then categorized the regional activation maps into a specific laterality category using these following criteria: LI ≥ 0.2 is deemed left; LI ≤ −0.2 is deemed right; |LI | < 0.2 is deemed bilateral [Gaillard et al., 2002; Wilke and Schmithorst, 2006].We defined typical language related area Broca's (BA: 44, 45, 47) and Wernicke's (BA 21, 22, 39) areas as our two ROIs. These specific regions were extracted from BA templates provided by MRIcro [Rorden and Brett, 2000].

The LI measure was derived using the following equation:

$$\text{LI}=\frac{\sum V_{\text{Left}}-\sum V_{\text{Right}}}{\sum V_{\text{Left}}+\sum V_{\text{Right}}}$$ (4)

where V denotes either the activation magnitude to yield LI_magnitude or voxel count to yield LI_voxel. Average LI that accounts for both voxel and magnitude can be obtained as follows:

$${\text{LI}}_{\text{avg}}=1/2\hspace{1em}({\text{LI}}_{\text{voxel}}+{\text{LI}}_{\text{magnitude}})$$ (5)

Once the two LIs from the Broca's and Wernicke's areas were calculated (for fixed threshold and bootstrap methods) we then used the following criteria for determining hemispheric language dominance: (1) left dominance when activation patterns in both Broca's and Wernicke's areas are left lateralized, or when one region is deemed left and the other bilateral or with no activity (NA); (2) right dominance when both regions of the activation patterns are right, or one region is right and the other is bilateral or with NA; (3) bilateral if both regions of the activation patterns are bilateral, or one is bilateral and the other is with NA, or one is left and the other is right; (4) “other,” when both regions of the activation patterns are with NA or noise/artifact.

Post‐Processing for Artificial Data

Artificial datasets were post‐processed to determine which ones were to be used as training data in the classification process. The following steps are considered:

• Calculate LI and bootstrap LI to re‐group the artificial data.

• Collect the data that match the group in both LI and bootstrap‐LI.

• Perform the cross validation for the data through nearest neighbor classifier based on the PCA dimensionally‐reduced decision space. In this test, the repeated random sub‐sampling validation is used (50% for training and 50% for testing). A total of twenty trials were performed.

• Determine the number of eigenvectors by the most frequent number of eigenvectors that gives the highest recognition rate.

• Examine the number of eigenvectors that will be used in order to exclude the wrongly classified testing data from the final artificial data group which is used for classification of real data.

• A null activation data is added into the artificial data.

The artificial null activation data is used to classify the null activation data in the real datasets. And for the artificial datasets, we know where the activation should be located, therefore wrongly classified artificial datasets means that the classified category of the datasets is not the one initially assigned to it (after verification of two LI methods). Therefore, there should be four categories in the classification results.

Processing Procedure

Randomly generated artificial data were utilized in this study to complement the classification process of the 122 real datasets used in study. To validate these artificial datasets, LI based on a fixed threshold at which visual ratings was determined, and a LI based on a bootstrap threshold was performed. The two LIs served as a first filter to keep, for further consideration, only those artificial datasets that yielded consistent classification results from both methods. Cross validation was then applied to the IPCA using the nearest neighbor classifier to determine the optimal number of eigenvectors (optimal feature space) that would yield the highest classification accuracies in different trials. Once the number of components was determined, wrongly classified artificial datasets in the optimal feature space were excluded from further consideration. In this selection process, we started with 580 artificial datasets, which were reduced to 501 after the LI and bootstrap LI classification consistency test, and then further reduced to 403 after the cross validation test in the IPCA feature space [Wang et al., 2011]. Then the NNC and DFC were both implemented, and the latter addressed those activation patterns that were located in the boundaries between categories. Also, for comparable assessments, we also used fixed LI, bootstrap LI, and visual rating to categorize the activation maps.

Figure 2 illustrates the overall classification process as it is implemented. In this figure, projected data (i.e., validated artificial data and real data) are the data that are projected into the reduced 4‐D feature space determined through the IPCA method.

Methods Used for Statistical Analysis

Because of the limited sample size, Fisher's exact test was applied to analyze the association of categorical factors with the group distribution, while continuous numerical factors are analyzed by Friedman or Mann‐Whitney U test as nonparametric alternatives to the ANOVA and independent t‐test. And the agreement between the LI, visual rating and the IPCA results were quantified using Kappa coefficient κ [Belle et al., 2004; Cohen, 1960]. The interpretation from the Kappa value follows: >0.81 as “excellent agreement”, 0.61–0.80 as “good agreement,” 0.41–0.60 as “moderate agreement,” 0.21–0.40 as “fair agreement,” <0.20 as “poor agreement”.

RESULTS

Artificial Data

For the artificial data considered, there were initially 580 datasets generated with 190 volumes for left dominant, 190 volumes for right dominant and 200 volumes for bilateral, with no duplicate basic activation patterns. After the LI and bootstrap LI validation, 501 out of 580 data were kept for further consideration. Of these 182 were found to be left dominant, 196 were right dominant and 123 were bilateral.

With the cross validation using the IPCA, in 16 out of the 20 trials among 1–10 eigenvectors, the highest accuracy values ranged from 91.1% to 95.1% when four eigenvectors were used. Therefore, four eigenvectors were deemed sufficient as a feature space for deploying the classification process. After this cross validation, and using the four‐dimensional feature space, 403 out of 501 data were classified correctly using the nearest neighbor classifier. Of these, 140 were left dominant, 158 were right dominant and 105 were bilateral. Comparing to left dominant and right dominant patterns, bilateral patterns are more likely to be eliminated as shown in the results. Since the first three patterns from the left in middle row of Figure 1 could be considered as ambiguous cases. While for left and right dominant patterns, there are only two such ambiguous cases (left dominant: third and fourth patterns from the left in top row; right dominant: first and third patterns from the left in the bottom row in Fig. 1).

Figure 3 shows the plots for the recognition accuracy rate in the cross validation based on the 20 trials and across one through ten eigenvectors. In this figure, each plot represents the recognition accuracy rate of a single trial as the accuracy changes from using one eigenvector up to ten eigenvectors. Each “cross” in the graph represents the highest value found for each trial.

Figure 3.

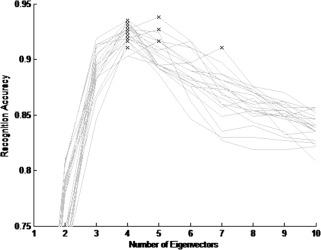
Plots of the recognition accuracy rate for the 20 trials in the cross validation across 1 through 10 eigenvectors.

Assessment of IPCA Results and Key Cases

Of the 122 real datasets, 90 subjects (81 left, 5 right, 3 bilateral, and 1 others) had the same classification results across all the methods (three raters, LI, bootstrap LI, NNC, DFC). For the remaining datasets, there were 18 cases for the IPCA‐NNC and 21 cases for the IPCA‐DFC that agreed with the majority of the five classification results, including three visual ratings and two LI results. For example, if there were three classification results identified as bilateral, bilateral became the majority choice of the classification results.

The categorization results of IPCA‐NNC, comparing with other methods, are shown in Table 1 with L, left dominant, R, right dominant, B, bilateral, and O, others.

Table 1.

Categorization results between each method and the IPCA‐based method

	Rater1				Rater2				Rater3a				LI				LI
													(Fixed threshold)				(Bootstrap)
IPCA	L	R	B	O	L	R	B	O	L	R	B	O	L	R	B	O	L	R	B	O
L	90	0	5	4	92	0	4	3	88	1	5	4	88	2	9	0	90	3	6	0
R	0	9	0	0	0	9	0	0	0	8	0	1	0	7	2	0	0	8	1	0
B	1	2	5	0	2	3	3	0	3	2	3	0	0	3	5	0	0	0	8	0
O	1	0	0	5	1	0	0	5	1	1	0	5	2	1	0	3	2	0	0	4

^aThere is a special case for rater 3 in the others category.

For the IPCA‐DFC which relies on the similarity percentage to a given category, the highest similarity percentage determines the category to which the activation pattern belongs. The following categorization results were obtained:

Considering the ten cases that the IPCA‐DFC did not agree with the majority results, four cases were found to be special cases, where more than one category was designated as a majority choice. For example, two results claimed the activation pattern was left dominant, two other results determined that the same activation pattern was bilateral, and one result identified the activation as others (NA, noise). Two out of these four cases can thus be considered as an agreement with the majority.

Some of these results are exemplified in Table 3 for comparative purposes (in this table, four‐category classification was considered). Moreover, the similarity for the DFC is shown as a percentage number. Among the highlighted cases (Table 3 and Figs. 4–11, representative slices), the first three illustrate examples where all results were in agreement throughout the methods. The next two cases illustrate examples where the discrepancy happened between LI methods or among LI methods and the other methods. Another set of three cases demonstrates examples where the inconsistency existed among the three visual raters.

Table 3.

Example results from LI, visual rating, nearest neighbor classifier and distance‐based fuzzy classifier

Case #	Fixed LI	Bootstrap LI	Rater 1	Rater 2	Rater 3	PCA
						NNC	Fuzzy
1	L	L	L	L	L	L	100%:L
2	R	R	R	R	R	R	100%:R
3	B	B	B	B	B	B	100%:B
4	B	B	L	L	L	L	100%:L
5	B	R	R	R	R	R	100%:R
6	L	L	L	L	B	L	100%:L
7	L	L	L	O	L	O	65.5%:L
							34.5%:O
8	L	L	L	R	B	L	100%:L
9	R	B	R	R	R	B	68.7%:B
							31.3%:R

Figure 4 shows examples where the proposed method and all other methods agreed and classified the given activation patterns into the same category.

Figure 4.

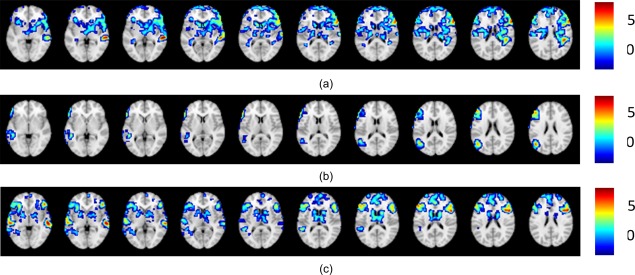
Cases where agreement is reached among all methods. (a) Left dominant case; (b) right dominant case; (c) bilateral case.

For Case 4 (Fig. 5), both LI methods resulted in a left dominant classification, while all the other methods classified this activation as bilateral. By comparing the original data in Figure 5a and the masked data in Figure 5b, the mismatch is believed to be due to the predefined regional mask selected and potentially relevant to (or irrelevant) activation adjacent to the Broca's area.

Figure 5.

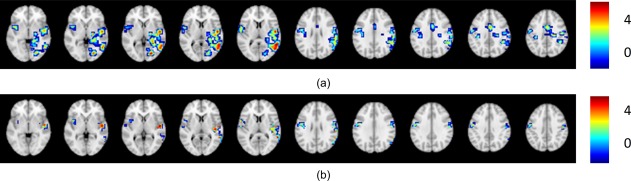
Case 4, illustrating activation pattern yielding the same results for all other methods, except for the two LI methods: (a) original data; (b) masked data.

For case 5 (Fig. 6a), only the LI method yielded bilateral language classification; all the other methods classified as left dominant. It is likely that this misclassification is largely due to the fixed threshold of the LI algorithm, since the bootstrap LI correctly classified this pattern as left dominant. The LI value for the Wernicke's area is 0.18, which is close to the boundary in between the categorical determination of left dominant and bilateral.

Figure 6.

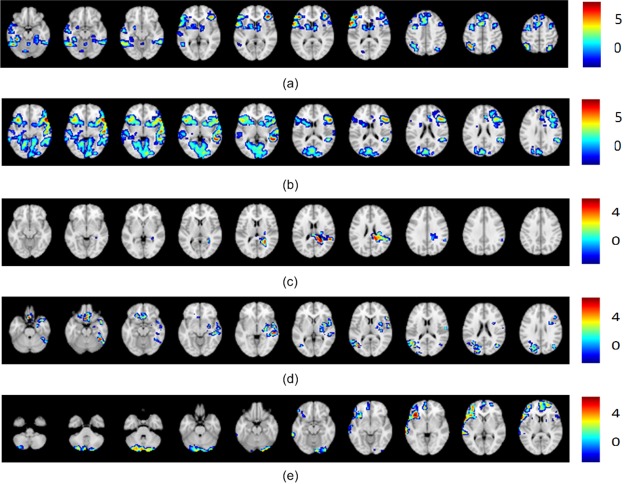
Other interesting cases: (a) Case 5 illustrating activation pattern slices where only the fixed LI method yielded the bilateral classification and all the other methods classified the activation as right dominant. (b) Case 6 illustrating an activation pattern where all the results agree on left dominant except for the classification of one rater as bilateral. (c) Case 7 illustrating slices of an activation pattern that received a majority classification for left dominant with the rest of the classifications being null activation, and with the IPCA‐Fuzzy method reflecting in percentages the similarities of this pattern to both classifications. (d) Case 8 illustrating slices of activation pattern where there is complete disagreement among the raters (three of them give three different classification results), and yet the data driven methods, IPCA‐NNC and IPCA‐Fuzzy, as well as both LI methods come in support of one of the rater that classified this pattern as left dominant. (e) Case 9 illustrating an activation pattern where fixed LI and all the raters identified it as right dominant disagreeing with the data driven methods and bootstrap LI who identified it as bilateral.

For case 6 (Fig. 6b), one rater scored bilateral classification while the two other raters, and the other methods classified this activation as left dominant. This result from one rater highlights subjective judgment and motivates the development of a data driven method to augment the decision making and minimize misclassifications. Raters varied in the confidence in their classification (scored 3,4,2) perhaps made problematic by low intensity activation in the right Broca's ROI.

Case 7 (Fig. 6c) provides slices of an activation pattern that has different classifications, including the “others” category. All slices that exhibit activation are shown. Both LI methods as well as two of the three raters classified the pattern as left dominant, one of the raters as well as the IPCA‐NNC method classified the pattern as null activation. However, the IPCA‐Fuzzy method provided a 65.5% similarity to the left dominant classification and 34.5% similarity to the null activation, which reflects the trend in the way the different methods classified the pattern and indicates that the pattern is more likely to be left dominant. Raters had low confidence in their assignment (scored 2,3,2). In this case, the results of our method sided with 65.5% similarity with the majority classification results for left dominant. It did however provide a 34.5% similarity for other which is compatible with the low confidence ratings.

The activation pattern in Figure 6d (case 8) also shows disagreement in the visual rating results—each rater gave a different classification result. Both LI methods as well as both IPCA‐NNC and IPCA‐Fuzzy methods agree with a left dominant classification. The IPCA‐Fuzzy gave a 100% similarity to both LI methods and thus augment the decision making process. All three raters gave the lowest confidence rating (scored 1,1,1).

The activation patterns of case 9 (Fig. 6e) show the limitation of the proposed IPCA‐NNC and IPCA‐Fuzzy methods, where IPCA–NNC and the IPCA‐DFC disagreed with the majority classification for right dominant language. All three raters and the fixed threshold LI agreed on right dominant classification, while the bootstrap LI agreed with the IPCA‐NNC and the high similarity provided by the IPCA‐DFC method for bilateral classification (68.7%).We believe that this may have been caused by the nature of the generated artificial data, where there may not have been a pattern in category R generated that was closer to the test data. Although more artificial data means more variability, a fixed amount of artificial data that is large enough should be sufficient. It is important to note however that the IPCA‐DFC did provide a similarity 31.3% to the right dominant classification. Such limitation is unavoidable even in data driven method even when a sizable number of artificial datasets was considered.

Statistical Analysis for Group Separation

The statistical analysis related to group separation is performed on the basis of the aforementioned four groups. Since intensity normalization is performed, scanner and site effects on group separation are also examined.

Demographic and Clinical Variables

Previous studies have examined the association between demographic data and clinical variables with the laterality of the language activation patterns; however, the participants in those studies were not restricted to pediatric populations [Gaillard et al. 2007; Springer et al., 1999; Woermann et al., 2003]. In this study, we seek to investigate such associations within a pediatric population.

Patients versus control populations affected significantly results of group separation (Fisher's Exact test, P = 0.0029). Furthermore, handedness also affected significantly the results of group separation (with right handedness considered typical and the rest as atypical, with a Fisher's Exact test, P = 1.25e‐5 for all subjects and P = 0.013 for patients only). The results also show that the patient population and atypical handedness have more cases classified into the right dominant category. Excluding the right dominant category, the same tests were carried out with the patient vs. control populations (Fisher's Exact test, P = 0.67) and handedness (Fisher's Exact test, P = 0.086 for all subjects and P = 0.12 for patient only), and the results show no difference. There was no association for gender with the group separation (Fisher's Exact test, P = 0.59 for all, P = 1 for controls, and P = 0.51 for patients), or for age (Friedman Test, χ²(3)=3.048, P = 0.384 for all subjects, and χ²(3) = 0.624, P = 0.891 for patients only).

We found no effects of age at seizure onset (Friedman Test, χ²(2) = 0.401, P = 0.818), duration of epilepsy (Friedman Test, χ²(2) = 0.638, P = 0.727), seizure focus (Fisher's Exact test, P = 0.90), seizure etiology (Fisher's Exact test, P = 0.87) on group separation.

Comparison to Results of Traditional Methods

According to the results in Table 1, the three raters revealed good inter‐rater agreement with IPCA in the four categories (Kappa 0.61–0.71). Furthermore, the ROI LI showed good inter‐rater agreement with IPCA in the four categories (Kappa 0.59 from LI and 0.73 from bootstrap LI). The special case is one noise activation map, which is correctly recognized as belonging to the bilateral category.

As shown in Table 2, the three raters exhibited good inter‐rater agreement with the IPCA‐DFC (Kappa 0.63–0.73). The LIs also showed good inter‐rater agreement with IPCA‐DFC (Kappa 0.61 from LI and 0.75 from bootstrap LI).

Table 2.

Categorization results between each method and the IPCA‐DFC

	Rater1				Rater2				Rater3a				LI				LI
													(Fixed threshold)				(Bootstrap)
PCA	L	R	B	O	L	R	B	O	L	R	B	O	L	R	B	O	L	R	B	O
L	91	0	5	4	93	0	4	3	89	1	5	4	89	2	9	0	91	3	6	0
R	0	9	0	0	0	9	0	0	0	8	0	1	0	7	2	0	0	8	1	0
B	1	2	5	0	2	3	3	0	3	2	3	0	0	3	5	0	0	0	8	0
O	0	0	0	5	0	0	0	5	0	1	0	5	1	1	0	3	1	0	0	4

^aThere is a special case for rater 3 in other category.

As mentioned previously, 90 cases exhibited agreement, and 32 cases exhibited disagreement among all results (obtained from all methods). Results of rater 1 shows no difference in confidence rating between agree and disagree groups at significant level of 0.017 based on Bonferroni correction (Mann‐Whitney U test, P = 0.43). However for the other two raters, there are significant differences in confidence rating (Mann‐Whitney U test, P = 0.012 for rater 2 and P = 1.47e‐5 for rater 3), and we can further conclude that the mean confidence rating in the agreed upon cases is higher than in the disagreed upon cases. Also for LI and bootstrap LI, we compared the differences between the boundary values (−0.2 and 0.2) and the LI values of the Broca's area and Wernicke's area respectively. Differences are calculated between the LI value and its nearest boundary value, and shows differences between the agreed upon cases and disagreed upon cases at significant level of 0.025 based on Bonferroni correction (Mann‐Whitney U test, P = 0.02 for LI Broca's area, P = 0.02 for LI Wernicke's area). However, the results show no differences for bootstrap LI in both Broca's and Wernicke's areas (Mann‐Whitney U test, P = 0.04 for bootstrap LI Broca's area; and P = 0.61 in Wernicke's area). The results show that it is statistically significant for fixed LI that the values of disagreed upon cases are closer to these boundary values. However, the bootstrap LI shows no such significance possibly due to the weighted mean results based on only 50% of the data points at the central part of the histogram or the stringency of the Bonferroni correction process.

Comparison Among Different $m$ in DFC

The aforementioned results are based on $m=3$ in DFC. In our case, we use different $m$ values in the DFC to do the group separation on the samples, and perform the test on the results when $m=3,4,5,6,7$ respectively to examine if there is difference among different values of $m$. We find that the $m$ value has no significant effects on the group separation (Friedman Test, χ²(4) = 6.4, P = 0.171). The result shows that the model is insensitive to the value of $m$, and a probable reason for this may be related to the generated artificial data and the weight values chosen.

DISCUSSION

This study extended our previous work (1) from a 2D feature space to a 4D feature space (number of eigenvectors by using the incremental PCA method); (2) from a two‐category (left dominant and right dominant) classification to a four‐category classification (left dominant, right dominant, bilateral, and others); (3) from using only the real data to including a large number of artificial data that was integrated in the classification process; (4) from using solely the nearest neighbor classifier to including the distance‐based fuzzy classifier to resolve cases near the boundary in between categories; and (5) examining the relation between the classified groups and demographic and clinic information.

Another important contribution of this work is in the way the artificial data was generated then reassessed for inclusion. The main purpose for using synthetic data is based on increasing certainty in defining the different data patterns as defined in Figure 1. When we generate the data according to these patterns, steps used to remove specific synthetic data are taken in order to reduce the error in the training phase, as the initial label used for the synthetic data might be the wrong one to begin with. It is important to know that through this procedure, we did not affect any information related to the real‐world data but only strengthened the process for classifying it, since the synthetic data used in the classification process reflect the four categories (L, R, B, and O) in a more meaningful way. As more patients and control subjects are included in the collaborative repository, the more thorough the IPCA analysis will become; eventually recourse to artificial data may not be necessary.

There are several methods for determining language dominance, qualitative/subjective by visual rating, or by quantitative LI based whether on hemisphere or regions [Seghier, 2008]. There is no agreed upon method; there is some evidence the regional LI rather than hemispheric LI is better [Seghier, 2008], the former is based on a priori assumptions. Some investigators use a generous regional ROI [Jansen et al., 2006] others more restricted [Fernandez, et al., 2001, 2003]. In practice when one rates visually, one focuses on activation in classical (canonical) areas. Here we are using a data driven method to overcome these obstacles. For these reasons we have compared our results with commonly used methods. For most patients all methods agree; we are able to comment on when, and how they partially disagree. These limitations are important and informative. In retrospect, this is both a strength and a limitation as visual analysis allows looking outside canonical areas [Fernandez et al., 2001] obtained the visual rating results from six senior neurologists, and achieved fully concordant results except for one patient. And [Gaillard et al., 2002] also proved that clinical visual interpretation of language lateralization is comparable to quantitative ROI analysis.

At this juncture of data availability, and for this particular study, the inclusion of the artificial data allowed the proposed IPCA‐based methods to encompass the four‐category classification, including bilateral and others categories. For the large majority of cases (90 out of 122), there is agreement across all methods; the small minority (32 out of 122) occasions where one or other methods do not agree are illustrative of the limitations of current methods as well as the approach proposed here. As reported by others, it is rare to have overt disagreement; most differences are where one method is lateralized and another is bilateral. When the LI is near 0.2, the boundary between typical and atypical language, there is rare disagreement between the LI methods as activation is known to change according to threshold used (fixed vs. bootstrap, case 4). Similarly, when activation maps are poor or LI is close to 0.2, there may be subjective differences among raters (cases 6‐8) or with objective LI assessment differences including the extent of regional mask employed (cases 4‐5). These differences also highlight the clinical use of rigid criteria that in fact rests on a continuum. With the parceling methods proposed here, differences, when they occur, are also found at boundaries (case 9).Knowing the circumstances where uncertainties may occur, allows for more judicious use of fMRI data. We found that the confidence rating in the agreed upon cases is higher than in the disagreed upon cases (mean confidence rating of agreed upon cases is higher than that of the disagreed upon cases). The values of disagreed upon cases are closer to these boundary values.

There are few comparison studies of which we are aware that examine the different rating system (in [Gaillard et al., 2002], we compared visual rating at several thresholds and a LI at several thresholds). The boot strap method is designed to effectively examine data at several thresholds and select the optimal threshold for that person, and this is what we now use in practice. However some centers and reviewers prefer to use a single threshold, therefore we have provided a range of assessments and we believe this helps contribute to the literature in this way. In the absence of invasive tests (Wada procedure), which are also imperfect, we thought it best to provide comparison to commonly used assessments. The LI method provided by [Fernandez et al., 2001, 2003] uses an adjusted threshold to identify the activated pixels based on inter‐subjects variability in general activation levels. On the other hand, [Adcock et al., 2003, Branco et al., 2006, Suarez et al., 2009, and Pillai and Zaca, 2011] all included weighted voxels to calculate the LI value. Yet, different weighting functions were adopted and compared. As discussed in [Arora et al., 2009], it showed that proper consideration of midline exclusion was necessary due to the higher concordance with WADA test.

The merits of the proposed data driven methods include artificial data generation, as a means to overcome the subjective nature of visual rating, and the shortcomings of ROI‐based LI methods. Furthermore, corollary contributions can be derived from the observation that the DFC can give the similarity percentage to the categories for better representation of the pattern, especially for those patterns near the boundaries in between categories, where raters may disagree and LI methods (fixed LI and bootstrap LI) may not converge on classification.

Although some mismatches were observed among the IPCA‐based algorithms, the visual rating and LI‐based methods, the IPCA‐based algorithm in most cases classified the activation pattern in the same category as the one found in the majority results across all methods. Furthermore, when disagreement happened, the IPCA‐DFC method provided similarity percentages that always included the majority category across methods (visual rating and LI methods). It is useful for the cases that have close similarity percentages in more than one category. For those cases, verification process may be utilized such as visual rating by the physician to assure proper category assignment. Unfortunately, there is no golden standard that would allow us to assess which method is better. Conventional ratings have excellent but not complete agreement with invasive methods [Gaillard et al., 2002; Pouratian et al., 2002]. Moreover, there are clear limitations to the use of invasive methods – the Wada test or electrocorticography — as “gold standards”, like fMRI, may be flawed and under various circumstances yield faulty information [Gaillard et al., 2011]. Finally, recent clinical practice [De Ribaupierre et al., 2012; Szaflarski et al., 2012; Wilke et al., 2011] in most pediatric epilepsy centers, especially for younger patients, has de‐emphasized the Wada test. As the standard is not established we present data for commonly used methods and report our observations on their concordance, not their “correctness.” Further, we have made some observations about when and how partial discordance arises. We find they are mostly boundary issues hence our efforts to seek data driven means to segregate and classify datasets. As there are few such comparison studies, IPCA‐based methods could thus serve as an alternative method to corroborate existing LI and visual rating classification methods.

The fuzzy classifier for group separation is empirically proven to improve classification and may overcome human rating errors as well as the limitation of a priori assumptions upon re‐evaluation. Furthermore, instead of a blind clustering of the given real datasets, the idea of using artificial activation patterns helps the method to be language patterns‐oriented. Since both classifiers of the proposed data driven methods (IPCA‐NNC and IPCA‐DFC) were distance based, the generation of the artificial data does affect the results as we have indicated in at least one of the cases. Such is the limitation in the inclusion of artificial data in terms of the way it is generated and in determining how large such a dataset should be to make the classification process more effective. With all these issues in mind, the proposed approach to classify pediatric fMRI datasets could promote objective assessments of large datasets and can serve to interrogate data for a multitude of clinical variables.

We observed no effect of age, age at seizure onset, duration of epilepsy, seizure focus, or seizure etiology to the group separation. However, based on the clinical information, these results are taken with some caution as the sample size, although coming from five different hospitals, is still limited. We intend to pursue this type of analysis as more data is collected within our consortium of hospitals. It is also important to note that just as reported in other reported studies, we found patient/control populations as well as handedness to have significant effect on group separation, with patient population and atypical handedness as having more cases being classified as right dominant. Also, some of our patients had a very diverse range of problems, including brain tumors and vascular malformations, which might affect the functional MRI. However, the data from previous studies suggests this may be so for larger lesions, generally absent in this study [Liegeois, 2004], evidence is mixed for smaller lesions but likely small [Duke et al., 2012; Wellmer et al., 2009]. In addition data from ¹⁵O water and FDG PET suggests these abnormalities do not disrupt the BOLD signal [Duke et al, 2012; Gaillard et al, 2011].

This study also emphasizes that a single site is unlikely to evaluate a sufficient number of patients to identify the array of variant activation patterns; the consortium of imaging epilepsy centers provides the necessary collaborative effort to overcome this limitation to optimizing the role of advanced technologies for improved clinical care. Thus, with a large sample, inter‐subject variability can be more reliably characterized for control populations as well as heterogeneous patient groups. With the growing data source from the consortium, more meaningful classifications and statistical analysis can be expected. New associations between the demographic as well as clinic information and the activation maps are expected to be discovered. Moreover, with the proposed IPCA, which progressively includes more eigenvectors without re‐computing the entire Eigen system, there is an opportunity to break down the three classes into more specific categories to include, perhaps, all the 15 patterns shown in Figure 1, at least in theory, which are needed to describe more fully the lateralization of brain activation related to language tasks.

INCREMENTAL PCA ALGORITHM

Each volume was transformed into a 1D vector with q elements where q is defined as the product M* N* L, where M, N, and L are the resolutions of the activation map in the x, y, and z axes, respectively. The i ^th subject is represented by a specific column x _i in matrix X. The mean matrix $M_{\mathrm{Xn}}=[{\mu }_x,{\mu }_x,{\mu }_x,\dots {\mu }_x]$ is composed of n column‐wise mean ${\mu }_x$, which means the mean vector ${\mu }_x$ is composed of the mean voxels on every row of matrix X. Consequently, the centered matrix $\overline{X}$ is obtained by $\overline{\mathrm{X}}=\mathrm{X}-{\mathrm{M}}_{\mathrm{Xn}}$. Suppose there are two matrices A and B and that M _An1 and M_Bn2 are their mean matrices, respectively. To compute the eigenvector of matrix C which concatenates matrices A and B, denoted as C = [A, B] where C is now too large to be loaded, the largest k eigenvectors and eigenvalues of matrix C, will be computed following the procedural steps given in Table AI.

The core of the algorithm is based on partitioning the Singular Value Decomposition (SVD) of a large matrix. Suppose we already performed the SVD of the centered matrix A denoted by $\overline{A}=U_{\overline{A}}{V}_{\overline{A}}{Q}^T$, where $\overline{A}=A-M_A$. The goal is to now compute the SVD of matrix $\overline{C}=C-M_{{\mathrm{Cn}}_C}=[A-M_{{\mathrm{Cn}}_A},B-M_{{\mathrm{Cn}}_B}]$, where k ₁ and k ₂ are the number of columns in A and B respectively and $n_C=n_A+n_B$.Only $U_{\overline{A}}$ and $V_{\overline{A}}$ are considered for efficient storage and fast computing since $Q$ is no longer saved as it is no longer needed in the decomposition of $\overline{C}$. Note that if we use $A-M_{{\mathrm{Cn}}_A}$ directly, we will lose this computational gain. Therefore, an alternative of $\overline{C}$ defined as $\stackrel{\wedge }{C}=[\overline{A},\overline{B}\sqrt{\left(\frac{n_A{n}_B}{n_A+n_B}\right)({\mu }_B-{\mu }_A)}]$, which has been proven to have the same covariance matrix as $\overline{C}$, is utilized instead for implementing this particular incremental algorithm.

Given that $B{}^{\stackrel{\wedge }{}}=[(\overline{B}),\surd (n_{{}_A}{n}_{{}_B})/(n_{{}_A}+n_B)({\mu }_B-{\mu }_A)$ (step 5 in the Table IV), then $\stackrel{\wedge }{C}=[\overline{A},\stackrel{\wedge }{B}]=[U_{\overline{A}}\tilde{E}]\left[\begin{array}{cc}\multicolumn{1}{c}{V_{\overline{A}}}& \hfill U_{\overline{A}}^T\stackrel{\wedge }{B}\hfill \\ \multicolumn{1}{c}{0}& \hfill {\tilde{E}}^T\stackrel{\wedge }{B}\hfill \end{array}\right]\left[\begin{array}{cc}\multicolumn{1}{c}{Q^T}& \hfill 0\hfill \\ \multicolumn{1}{c}{0}& \hfill I\hfill \end{array}\right]$(it should be noted that 0 in the equation means a nested matrix where all its elements are zero). Also, $\tilde{E}=\text{orth}(\stackrel{\wedge }{B}-U_{\overline{A}}{U}_{\overline{A}}^T\stackrel{\wedge }{B})$ (step 6 through 8 in the Table IV). Let $R=\left[\begin{array}{cc}\multicolumn{1}{c}{V_{\overline{A}}}& \hfill U_{\overline{A}}^T\stackrel{\wedge }{B}\hfill \\ \multicolumn{1}{c}{0}& \hfill {\tilde{E}}^T\stackrel{\wedge }{B}\hfill \end{array}\right]$, on which we perform the SVD to get $R=\tilde{U}\tilde{V}{\tilde{Q}}^T$. Then we obtain $\stackrel{\wedge }{C}=([U_{\overline{A}}\tilde{E}]\tilde{U})\tilde{V}\left({\tilde{Q}}^T\left[\begin{array}{cc}\multicolumn{1}{c}{Q^T}& \hfill 0\hfill \\ \multicolumn{1}{c}{0}& \hfill I\hfill \end{array}\right]\right)$ (step 9 through 12 in the Table IV). It should be noted that if only the first k largest eigenvectors are considered, those parameters such as U, V will only contain the first k largest eigenvectors and eigenvalues instead of all.