A Selective Sweep across Species Boundaries in Drosophila

Abstract

Adaptive mutations that accumulate during species divergence are likely to contribute to reproductive incompatibilities and hinder gene flow; however, there may also be a class of mutations that are generally advantageous and can spread across species boundaries. In this study, we characterize a 15 kb region on chromosome 3R that has introgressed from the cosmopolitan generalist species Drosophila simulans into the island endemic D. sechellia, which is an ecological specialist. The introgressed haplotype is fixed in D. sechellia over almost the entirety of the resequenced region, whereas a core region of the introgressed haplotype occurs at high frequency in D. simulans. The observed patterns of nucleotide variation and linkage disequilibrium are consistent with a recently completed selective sweep in D. sechellia and an incomplete sweep in D. simulans. Independent estimates of both the time to the introgression and sweep events are all close to 10,000 years before the present. Interestingly, the most likely target of selection is a highly occupied transcription factor binding region. This work confirms that it is possible for mutations to be globally advantageous, despite their occurrence in divergent genomic and ecological backgrounds.

Introduction

Allopatric speciation sensu stricto begins when gene flow between geographically isolated populations ceases simultaneously at all loci throughout the genome. Cessation of gene flow can lead to the accumulation of mutations that may ultimately cause reproductive isolation, as envisioned by the Bateson–Dobzhansky–Muller model of genetic incompatibility (Bateson 1909; Dobzhansky 1937; Muller 1940). However, when incipient species are loosely connected by migration, the rate of genetic exchange is determined by the interactions of the strength of disruptive selection, recombination, and the number and distribution of existing genetic incompatibilities in the genome (Barton and Bengtsson 1986; Pinho and Hey 2010). In this sense, speciation in the face of ongoing gene flow can be called “complex speciation.” In Drosophila, multilocus and, more recently, whole-genome resequencing efforts have identified loci that appear inconsistent with strictly allopatric speciation and show evidence for recent gene flow (Machado and Hey 2003; Llopart et al. 2005; Garrigan et al. 2012).

Although gene flow works to homogenize genetic variation between diverging populations, it is countered by disruptive selection against hybrid genotypes. This conflict can only be ameliorated by recombination, which allows for the introgression of genomic regions between populations. Introgressing regions are therefore unlinked to mutations causing incompatibilities, and the majority are expected to be effectively neutral with respect to fitness, whereupon their fate is subject to the vagaries of genetic drift. However, there may also be instances when mutations are either globally or locally adaptive in the recipient species, and natural selection facilitates the introgression of a genomic region.

Although adaptive introgression has been known for decades (Arnold 2004), it is receiving renewed attention in the postgenomic era and has been recently reported in a wide variety of plant and animal species. Examples include the vkorc1 locus that confers warfarin resistance in mice (Song et al. 2011) and the regulatory gene RAY that controls floret distribution in the genus Senecio (Kim et al. 2008). It has even been demonstrated that self-incompatibility alleles can introgress across species boundaries in the genus Arabidopsis, initially driven by balancing selection rather than directional selection (Castric et al. 2008). Finally, adaptive introgression has been implicated in radiations in the genus Heliconius. Wing color patterns are highly similar across species, as Heliconius butterflies use Müllerian mimicry to evade predators (Heliconius Genome Consortium 2012). There is evidence that the genes controlling wing color pattern have introgressed between diverse Heliconius species, resulting in convergent wing color patterns (Heliconius Genome Consortium 2012; Pardo-Diaz et al. 2012).

The three species of the Drosophila simulans clade have long served as a model for speciation genetics: interspecific crosses produce fertile females and sterile males (Lachaise et al. 1986) and their close phylogenetic relationship with D. melanogaster enables the use of many genetic tools. The ancestors of D. melanogaster and the D. simulans clade are estimated to have diverged approximately 2–3 kya (Lachaise et al. 1988; Li et al. 1999). Within the last 200–300 kya, the D. simulans-like ancestor gave rise to two island endemic species, D. sechellia and D. mauritiana, and the cosmopolitan D. simulans (Garrigan et al. 2012). Although both D. melanogaster and D. simulans are human commensals, D. sechellia specializes on the host plant Morinda citrifolia and has evolved both a preference for and a resistance to the toxic long-chained fatty acids (e.g., octanoic acid) found in the Morinda fruit (R'Kha et al. 1991). Despite such behavioral and physiological adaptations, gene flow is thought to occur between D. simulans and D. sechellia. Kliman et al. (2000) found that D. sechellia possessed a sequence at the In(2L)t locus that closely resembled sequences from D. simulans. More recently, a whole-genome resequencing study of the D. simulans clade species conservatively estimated that almost 5% of the genome has experienced recent gene flow. Genomic regions of introgression are particularly abundant between D. simulans and D. sechellia, demonstrating a history of complex speciation (Garrigan et al. 2012).

A whole-genome scan for introgression between the three species of the D. simulans clade identified a candidate region on chromosome 3R that statistically rejected a model of strict allopatry (Garrigan et al. 2012). This region encompasses at least 15 kb of sequence that is closely shared between D. simulans and D. sechellia. Because this genome scan relied upon only a single sequence per species, outstanding questions remain about the timing and mode of introgression in this large genomic region. In this study, we collect more than 15 kb of sequence polymorphism data from both D. simulans and D. sechellia. The frequencies of the introgressed haplotype in the two species provide valuable insights into the direction of the introgression event and the role natural selection plays in complex speciation.

Results

Unusual Haplotype Structure

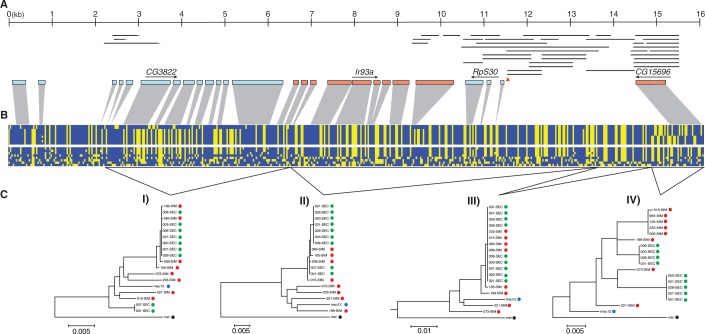
The total resulting sequence alignment is 15,406-bp long and includes nine lines of D. sechellia from the Seychelles archipelago, eight lines of D. simulans from Madagascar, a single D. mauritiana, and the D. melanogaster reference sequence. This region includes four genes, CG3822 and Ir93a (fig. 1A), both of which encode ionotropic glutamate receptors (Benton et al. 2009), as well as RpS30, a ribosomal protein-coding gene (Brogna et al. 2002), and CG15696 a putative transcription factor with a conserved Homeobox domain. Hereafter, we refer to this genomic region by its cytological band 93A2. We identify a shared haplotype that extends from position 1 to position 14378; this shared haplotype has a core region that is fixed in D. sechellia and segregates at high frequency in D. simulans (fig. 1B and C—tree III). We will refer to the shared core haplotype as “Ht1.”

Fig. 1.

A trans-specific haplotype occurs at high frequency in both Drosophila simulans and D. sechellia. (A) The resequenced region of chromosome 3R with gene models and TFB sites projected onto the polymorphism table below. Arrows indicate the direction of transcription and thin lines above the gene models are annotated TFB sites. The triangle denotes the location of a class II insulator. The resequenced region corresponds to 3R: 16692096–16672738 of the D. melanogaster genome. (B) A polymorphism table with variable sites coded as ancestral (blue) and derived (yellow) states. The top matrix contains sequences from D. sechellia and the bottom matrix is from D. simulans. (C) Four maximum likelihood trees representing regions with distinct histories. Green circles represent the D. sechellia samples, red circles are the D. simulans samples, blue is D. mauritiana, and black is the D. melanogaster sequence.

The extended Ht1 haplotype spans the entire resequenced region for three of the D. simulans samples. Three additional D. simulans samples carry recombinant Ht1/non-Ht1 sequences, whereas the remaining two D. simulans samples have non-Ht1 haplotypes (fig. 1B). The two D. simulans recombinant Ht1/non-Ht1 sequences have recombination break points at 7190 and 12457, respectively. Both sequences have non-Ht1 sequence distal to the breakpoint and convert to Ht1 sequence proximal to the breakpoint. The other D. simulans recombinant sequence experienced a double recombination event: there is Ht1 sequence before a recombination breakpoint at 7163, at which point it converts to non-Ht1 sequence, followed by an additional recombination event near breakpoint 13377, where the sequence reverts back to Ht1.

In D. sechellia, the core region of the Ht1 haplotype extends from position 9850 to 14378 and is fixed in the sample. However, there are a total of four haplotypes in D. sechellia, the additional variation is localized to four distinct regions (fig. 1B). The first three regions occur between positions 0–529, 2559–6946 (fig. 1C—tree I) and between 9517 and 9850, in which two D. sechellia samples have non-Ht1 sequence. If, as we argue later, the Ht1 haplotype originated in D. simulans, then it is likely that these tracts arose through gene conversion between Ht1 and endogenous non-Ht1 D. sechellia-specific sequence. The last region containing polymorphism within D. sechellia begins at position 14378 and extends to the end of our resequenced region. In this region, there are two haplotypes encompassing the CG15696 gene that segregate at intermediate frequency (fig. 1C—tree IV). Finally, it is important to note that there is no linkage disequilibrium between sites in this final region and the first three regions of variation in D. sechellia.

Across both D. sechellia and D. simulans, the core Ht1 haplotype reaches its highest frequency between coordinates 12765–14364, which is located between the RpS30 and CG15696 genes. In this region, all nine D. sechellia and six D. simulans samples can be characterized as Ht1, whereas two D. simulans samples carry non-Ht1 sequence (fig. 1B and C—tree III). This intergenic region is known to bind a large number of developmental transcription factors (Negre et al. 2011). Across the entire 15 kb alignment, there are a total of 15 nonsynonymous polymorphisms (supplementary table S2, Supplementary Material online). Three of the nonsynonymous polymorphisms are shared between species, two in Ir93a and one in CG15696, whereas nine are polymorphic exclusively in D. simulans and three in D. sechellia. The two shared nonsynonymous changes in Ir93a occur on the Ht1 background and both are conservative amino acid changes. Finally, the shared nonsynonymous polymorphism in CG15696 is not in linkage disequilibrium with mutations on the Ht1 haplotype.

Origin and Introgression of the Shared Ht1 Haplotype

A previous study found that the 93A2 region was the most extreme outlier in its deviation from expectations of an allopatric model and therefore there is a low probability that the patterns of haplotype sharing in this genomic region are due to incomplete lineage sorting (Garrigan et al. 2012). Given this evidence, it is also useful to establish whether the introgressed 93A2 region originated in D. simulans or in D. sechellia. To infer the origin of the Ht1 haplotype and, hence, the directionality of the putative introgression event, we performed a phylogenetic analysis of the largest region harboring variation within D. sechellia (positions 2559–6946, in the CG3822 gene). The resulting maximum likelihood tree shows that the Ht1 sequences are nested within the non-Ht1 D. simulans sequences, whereas the two D. sechellia samples with non-Ht1 sequence are basal to all of the D. simulans sequences (fig. 1C—tree I). These two basal D. sechellia sequences group together in 99% of bootstrap replicates, to the exclusion of all other D. sechellia and D. simulans sequences. This relationship suggests that the Ht1 haplotype originated in D. simulans and was later introduced into D. sechellia through hybridization and introgression. Thus, the non-Ht1 sequence present in this region of the D. sechellia ortholog likely represents endogenous D. sechellia sequence. Under the alternative hypothesis of Ht1 originating in D. sechellia, the time to a most recent common ancestor of our D. sechellia sample would have to be older than that of D. simulans. This would be unexpected because of the well-documented reduced effective population size of the island endemic specialist compared with its cosmopolitan sister species (Kliman et al. 2000; Legrand et al. 2009; Garrigan et al. 2012).

The time of the putative introgression event is estimated using coalescent simulations of a two-population model with a divergence time of 242 kya (Garrigan et al. 2012). For the introgression model, the mode of the posterior distribution for the population mutation rate is θ = 161.663 for D. simulans and θ = 28.364 for D. sechellia, whereas the mode of the population recombination rate is ρ = 48.664 for D. simulans and ρ = 3.011 for D. sechellia. By fitting the simulated inter-specific haplotype mismatch distributions to the observed distribution, we estimate that the introgression event occurred approximately 11 kya (fig. 2). The marginal posterior probability distribution for time of the putative introgression event has a highest probability density interval of 2.6–18.6 kya.

Fig. 2.

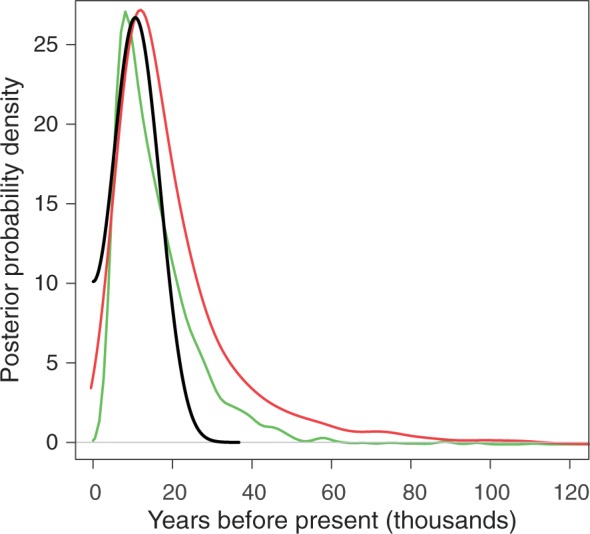
Marginal posterior probability densities for the time to the putative introgression and selective sweep events. Curves represent posteriors of introgression time for the shared haplotype (black line), the time of the selective sweep in Drosophila sechellia (green line), and the time of the partial sweep in D. simulans (red line).

Evidence for Selective Sweeps in both D. simulans and D. sechellia

Selection in D. sechellia

We can reject the hypothesis that polymorphism at the 93A2 region in D. sechellia is the result of neutral mutation-drift equilibrium. In D. sechellia, the region contains a total of 86 segregating sites distributed among four haplotypes. There are high levels of linkage disequilibrium (Z_nS = 0.673; P < 0.05) and haplotype structure (Wall’s Q = 0.9778; P < 0.05). Additionally, the D. sechellia polymorphism data set has an excess of high frequency derived mutations (H_FW = −36.972; P < 0.05). It is also interesting to note that for local regions harboring polymorphism in D. sechellia (fig. 3B), nucleotide diversity is 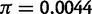, which is approximately five times higher than previously reported autosomal estimates (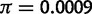) for this species (Kliman et al. 2000; Legrand et al. 2009). This observation is consistent with the trans-specific nature of the Ht1 haplotype.

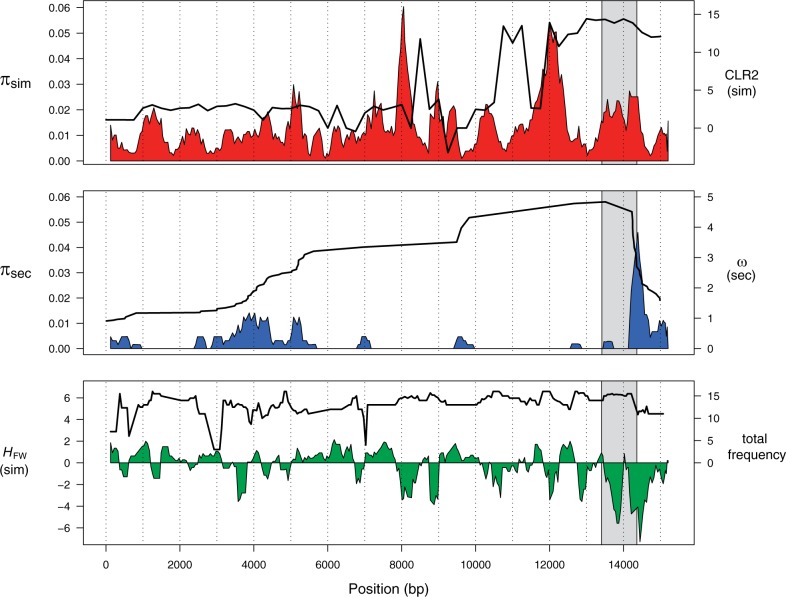
Fig. 3.

Spatial analysis of polymorphism across the 93A2 region and the putative target of natural selection. (A) Nucleotide diversity (π) for Drosophila simulans (red) and the CLR test of selection comparing the partial sweep to the complete sweep model (black line). (B) π for D. sechellia (blue) and the ω linkage disequilibrium statistic (black line). (C) Fay and Wu’s H statistic for D. simulans (green) and the frequency of derived sites shared by D. simulans and D. sechellia (black line). All analyses are performed in 250 bp windows with a step size of 50 bp. The gray box highlights the genomic region with the highest frequency of the core Ht1 haplotype (positions 12765–14364).

A composite likelihood ratio (CLR) test rejects neutral evolution of the 93A2 region in D. sechellia. For the parameters in the CLR test, we assume a population mutation rate (θ) that is equal to Watterson’s moment estimator 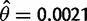per site (Watterson 1975) and we also assume two different population recombination rates (ρ). The reason for assuming both a high and low values of ρ is to obtain a range of estimates of the effects of natural selection, since hitchhiking models are often sensitive to the assumed rate of crossing-over (Kim and Stephan 2002). We took the low value of ρ to be a point estimate 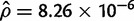per site, obtained by the method of Hudson (1987). Alternatively, for a high estimate, we assume that ρ is of the same order as θ (see rationale for D. simulans below).

Table 1 summarizes the CLR test statistics for both the D. sechellia and D. simulans data sets considering both the complete selective sweep model (CLR1) and the partial sweep model (CLR2). When ρ is assumed to be low, CLR1 = −147.317 (P > 0.05 in a one-tailed test) and CLR2 = 163.582 (P < 0.05). Thus, coalescent simulations indicate that the standard neutral model cannot be rejected in favor of a complete sweep model, whereas the partial sweep model offers significant improvement over the complete sweep model, and by extension, the standard neutral model. The estimated parameters of the best-fitting partial sweep model are 2Ns = 2.70, X = 317, and B = 0.2167. By assuming low levels of recombination, the partial sweep model assumes that the recombined region, that we are assuming to be endogenous D. sechellia variation, does not represent a recombination event but rather the true frequency of natural intraspecific polymorphisms. However, when ρ is assumed to be on the same order as θ, CLR1 = 28.8103 (P < 0.05) and CLR2 = 0.002 (P > 0.05), the coalescent simulations indicate that the complete sweep is favored over the neutral model, whereas the partial sweep does not represent a significant improvement over the complete sweep model. For the higher value of ρ, the estimated parameters are 2Ns = 26.72 and X = 7702. Additionally, under this best-fitting complete sweep model, the Λ_GOF = 276.25 (P > 0.05), indicating that an arbitrary demographic model is not a better fit to the data than the selective sweep model. Finally, the linkage disequilibrium statistic ω_max = 4.835 in the D. sechellia sample, which rejects the neutral expectation, given either high or low levels of recombination (P < 0.05) and this maximum value of ω occurs when partitioning the data on either side of site 13327 (fig. 3B).

Table 1.

CLR Analysis of a Complete Selective Sweep Model and a Partial Selective Sweep Model.

Sample	Recombination Ratea	Complete Sweep			Partial Sweep
		CLR1	2Nsb	Positionc	CLR2	2Nsb	Positionc
D. sechellia	Low	−147.317	NA	NA	163.582*	2.70	317
	High	28.810*	26.72	7702	0.002	NA	NA
D. simulans	Low	4.874*	5.68	15087	8.092*	14.98	14370
	High	11.822*	20.19	14459	4.586*	41.44	14323

Note.—Both high and low values of the population recombination rate are used to obtain a range of estimates for each of the two CLRs.

^aSee Results section for definition of low and high recombination rate.

^bAn estimate of the population-scaled selection coefficient.

^cThe base pair position of putatively selected site (15,406 bp total).

*P < 0.05.

NA = not applicable

Selection in D. simulans

Polymorphism within D. simulans is more complex because the core Ht1 haplotype is not fixed but still segregates at high frequency. Figure 1B shows that three D. simulans samples carry the extended Ht1 haplotype across the entirety of the resequenced 93A2 region. Under a strictly neutral model with recombination, it is unexpected to observe a single haplotype extending over such a large genetic distance. A post hoc test suggests that this subsample of three sequences has significantly elevated homozygosity compared with the neutral expectation. There are 32 segregating sites observed in this subsample of three D. simulans chromosomes. The significance of this observation is assessed by simulating neutral genealogies with 444 segregating sites (the total number of segregating sites in D. simulans) and calculating the minimum number of segregating sites among all possible subsamples of three sequences (note there are 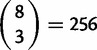partitions of the data possible). From these simulations, the probability of obtaining a subsample with 32 or fewer segregating sites is P < 0.05, even with low levels of recombination. Finally, across the entire 93A2 region, H_FW = −19.500, Wall’s Q = 0.208, and Z_nS = 0.220 (P > 0.05 for all three statistics).

Table 1 shows the results for the CLR test in the D. simulans data set. In this case, we assume the population mutation rate is again Watterson’s estimator 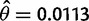per site and, as we did with the D. sechellia analysis mentioned earlier, we also assume two different values of ρ. For the low value of ρ, we again used the estimator of Hudson (1987), 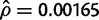per site. For the high value of ρ, we assume that it is of the same order as θ (although the ratio ρ/θ is generally expected to be greater than unity in D. simulans [Andolfatto and Przeworski 2000]). When recombination is assumed to be low, CLR1 = 4.874 and CLR2 = 8.092; in both cases, coalescent simulations indicate that P < 0.05. Therefore, the standard neutral model is rejected in favor of a complete sweep model and the complete sweep model can, in turn, be rejected in favor of the partial sweep model. The estimated parameters of the partial sweep model are 2Ns = 14.98, X = 14370, and B = 0.711. In the case where ρ is assumed to be on the same order as θ, then CLR1 = 11.822 and CLR2 = 4.586. Again, in both cases, coalescent simulations indicate that the complete sweep model is favored over the neutral model and the partial sweep is favored over the complete sweep model. Additionally, when recombination is assumed to occur more frequently, the estimated parameters are 2Ns = 41.44, X = 14323, and B = 0.827. Under the best-fitting partial sweep model, the Λ_GOF = 658.79 (P > 0.05), also confirming that an arbitrary demographic model does not provide a better fit to the data than does the partial selective sweep model. Finally, the ω_max = 3.358 in the D. simulans sample, which does not reject neutral expectations, given either high or low levels of recombination. Given the results of the CLR test, this last result is expected because ω_max is most sensitive to complete selective sweeps (Kim and Nielsen 2004).

Timing and Strength of Selection

Polymorphism data from each species reject an equilibrium neutral model due to the elevated frequency of the core Ht1 haplotype in both D. sechellia and D. simulans, as well as the low levels of within-Ht1 haplotype nucleotide diversity. On this basis, a leading alternative hypothesis is that natural selection has recently caused a sweep of this trans-specific haplotype in both species. Although there is undoubtedly a universe of alternative models to explore, these analyses find that the data are consistent with a complete sweep in D. sechellia and a partial sweep in D. simulans. Under the hypothesis of a selective sweep, we estimate both the timing and intensity of the sweep events using coalescent approximations to a model of positive selection.

To estimate the time since the selective sweep, we are particularly interested in the number of mutations that have accumulated on the putatively swept background (e.g., the core Ht1 region). Thus, for D. sechellia, we exclude the putatively recombined region between positions 2559 and 6946 and the polymorphic sites in the CG15696 gene, beyond position 14364. This modified data set harbors only one segregating site at position 808, for which the derived allele is present in two samples. If the population mutation rate in D. sechellia is assumed to be θ = 0.0021 per site, then the mode for the posterior probability distribution for the time since the selective sweep event is 10.2 kya, with a selection coefficient of s = 0.046. Similarly, if we consider only the three D. simulans samples with the full Ht1 haplotype sequence, there are 32 segregating sites. If we assume that the population mutation rate in D. simulans is θ = 0.0113 per site, then the mode of the posterior probability distribution for the time at which the sweep began is 13.7 kya with s = 0.022 (fig. 2).

Discussion

A previous study using single-genome sequences from the four species of the D. melanogaster subgroup identified the 93A2 region as one that statistically rejects a model of strict allopatry between D. simulans and D. sechellia (Garrigan et al. 2012). In this study, we collect additional polymorphism resequence data from the 93A2 region in nine lines of D. sechellia from the Seychelles archipelago and eight lines of D. simulans from Madagascar (fig. 1). Fitting a model of divergence with secondary contact to these new data confirms that the patterns of haplotype sharing in the 93A2 region can be best explained by an introgression event from D. simulans into D. sechellia approximately 2.6–18.6 kya (fig. 2). However, the most surprising result is that the core region of the introgressed haplotype (Ht1) occurs at high frequency in both species. Furthermore, there is extended linkage disequilibrium and homozygosity within the Ht1 haplotype, suggesting that it has very recently increased in frequency. Our analyses support a complete selective sweep of the Ht1 haplotype in D. sechellia and a partial sweep in D. simulans (table 1). However, two important outstanding questions remain. First, what is the target of natural selection in the 93A2 region? And second, why is the core Ht1 sequence fixed in D. sechellia but only partially swept in D. simulans?

Target of Natural Selection

We initially attempt to localize the target of selection using patterns of sequence polymorphism. Our inferences rely upon 1) the spatial distribution of within-species allele frequencies and 2) the changes in patterns of linkage disequilibrium across the alignment. The spatial distribution of nucleotide diversity (π) shows regions of depressed polymorphism in both species (fig. 3A and B). However, the composite likelihood analysis of the partial sweep model in D. simulans shows a maximum likelihood ratio (CLR2) at position 14323 (fig. 3A). Furthermore, there is a strong excess of high frequency derived sites surrounding approximate position 14000 in D. simulans (fig. 3C). We have noted that the frequency of the Ht1-like sequence is highest in the region between positions 12765 and 14364 (area shown in grey in fig. 3).

Similarly, the region between positions 12765 and 14364 also contains a breakpoint in the patterns of linkage disequilibrium in D. sechellia as reflected in a significant ω_max value occurring at position 13327 (fig. 3B). This is consistent with a selective sweep producing two independent patterns of strong linkage disequilibrium on either side of a selected region (Kim and Nielsen 2004). Analyses that rely on the site frequency spectrum are less reliable in D. sechellia than D. simulans because of an overall lack of polymorphism in this sequenced region. This is reflected in the results from the composite likelihood analysis in D. sechellia. For example, when we consider low rates of recombination in this species, the composite likelihood method identifies the partial sweep model as the best-fitting model and localizes the selected site to one of the two regions of polymorphism in D. sechellia. This is likely an artifact of the model, which does not consider the effects of inter-specific divergence and gene flow or gene conversion.

By relying only upon the patterns of polymorphism and linkage disequilibrium, we conclude that the best candidate for the target of natural selection lies in the intergenic region between the RpS30 and the CG15696 genes. In this region, there are five single-base mutations and one 20-bp insertion that differentiate the Ht1 and non-Ht1 sequences (only two D. simulans lines do not carry the Ht1-like sequence in this region). Chromatin immunoprecipitation experiments show that a large number of developmental transcription factors bind to this region (Negre et al. 2011). It is therefore likely that the target of selection is a regulatory sequence. The nature of these transcription factor binding (TFB) “hot spots” suggests three distinct possibilities for the phenotype being targeted by natural selection: 1) cis-regulation of nearby genes, 2) regulation of genes outside of the region, or 3) intrinsic function of the TFB hot spot.

If the target of selection is cis-regulatory, the presence of an insulator element, which acts to partition TFB between RpS30 and CG15696 (Negre et al. 2010), suggests that the candidate region regulates expression of CG15696 (fig. 1A). However, preliminary results comparing in situ hybridization of CG15696 in D. simulans embryos that carry Ht1 (vs. the two lines that do not) indicate that there is no difference in the expression of CG15696 (supplementary methods, Supplementary Material online). In lieu of direct evidence for differential expression of CG15696 between D. simulans lines, two additional possibilities remain. TFB hot spots are hypothesized to have functions beyond cis-regulation of adjacent genes. For example, it is thought that TFB hot spots are able to modulate genome-wide transcription factor concentrations by acting as a “sink” for transcription factor protein (Moorman et al. 2006). One additional function of TFB hot spots may be that they can coordinate expression between physically distant loci (Moorman et al. 2006). Further experimentation is required to discern whether either of the above are viable hypotheses.

Partial Selective Sweep in D. simulans

One distinctive feature of our data is that the Ht1 has swept to complete fixation in D. sechellia but has experienced only partial sweep in D. simulans. This observation is consistent with the faster sojourn time of a selected allele that is expected for a species with a small effective population size (Stephan et al. 1992). However, our analyses also suggest that the selection pressure is more intense in D. sechellia. One possible explanation for the increased selection intensity is that the introgressed Ht1 may rescue a loss-of-function mutation in D. sechellia (Garrigan et al. 2012). This explanation is plausible because the reduced effective population size of D. sechellia makes it susceptible to the fixation of slightly deleterious mutations (Kliman et al. 2000; Garrigan et al. 2012). In particular, D. sechellia is known to have experienced more loss-of-function mutations of chemosensory receptors than generalist Drosophila species (McBride 2007).

Alternatively, although the sweep may be ongoing in D. simulans, it is also possible that the progress of selection is inhibited in this species. For example, the Ht1 haplotype may be held at intermediate frequency due to Hill–Robertson interference between two selected sites (Kirby and Stephan 1996). In this case, two beneficial mutations may be present in repulsion phase, or a deleterious mutation may be linked to the beneficial mutation that drove the selective sweep. However, in a Drosophilid with a large effective population size, in which linkage disequilibrium extends merely tens of bases on average (Mackay et al. 2012), this seems particularly unlikely, unless the two mutations are very closely physically linked. One final explanation for this complex pattern of selection may be that the intensity of selection is heterogeneous across the range of our sampled D. simulans lines, resulting in a balanced polymorphism (Linnen et al. 2009). More extensive sampling of the D. simulans population will aid in addressing this last hypothesis.

Significance and Conclusions

To our knowledge, this study provides the first unambiguous support for a trans-specific selective sweep in Drosophila. Others have shown haplotype sharing across smaller genomic regions on the dot chromosomes of D. pseudoobscura and D. persimilis (Machado and Hey 2003), and the three species of the D. simulans clade (Hilton et al. 1994). However, because the dot chromosome experiences negligible levels of recombination, it is difficult to discern whether the lack of both within- and between-species variation is due to a trans-species selective sweep or the effects of strong background selection (Machado and Hey 2003). The fact that our data include residual non-Ht1 variation, due to either incomplete fixation or recombination and gene conversion, is fortuitous because it allows us to establish that divergence has, in fact, occurred at this locus (fig. 1C—tree I).

Although we cannot currently detail the phenotype that is being targeted by natural selection, the 93A2 region stands out as a striking example of how speciation can be accompanied by gene flow in nature. Typically, it is expected that mutations causing reproductive incompatibilities will experience disruptive selection in hybrid individuals, resulting in diminished hybrid fitness (Coyne and Orr 2004). In this study, we find evidence that a large, recombining genomic region can not only cross species boundaries but can also be favored by natural selection in both species simultaneously. This scenario suggests that the 93A2 region harbors a mutation that is globally adaptive and is favored by natural selection, despite divergent genomic backgrounds and ecological conditions.

Materials and Methods

Samples and DNA Sequencing

Genomic DNA was extracted from nine D. sechellia lines from the Seychelles archipelago and eight D. simulans lines from Madagascar (Dean and Ballard 2004) that were founded as isofemale lines and sib-mated for at least nine generations (supplementary table S1, Supplementary Material online). DNA was isolated with DNeasy Blood & Tissue Kit (QIAGEN). To design polymerase chain reaction (PCR) primers, the region of interest in both D. simulans and D. sechellia was downloaded from FlyBase (Tweedie et al. 2009), and primers were chosen using the Primer3Plus software (Untergasser et al. 2007). All PCR primers were anchored in exons in three overlapping amplicons of length 4.5, 5.8, and 6.6 kb (primer sequences are available upon request). We performed PCR in 50 µl reaction volumes using Expand Long Range, dNTPack (Roche) according to the manufacturer’s protocol. The resulting PCR products were visualized on a 2% agarose gel and cleaned using ExoSAP-IT (USB Corp). Sanger sequencing was performed with the Big Dye Terminator Cycle Sequencing Kit (Applied Biosystems) and run on an ABI 3730xl DNA genetic analyzer.

Sequence Polymorphism and Divergence

Sequencing reads were edited and aligned using the Geneious software (http://www.geneious.com, last accessed July 18, 2013). Polymorphism tables and population genetics statistics were generated using the DnaSP program (Librado and Rozas 2009). The population genetics statistics included an unbiased moment estimator of the population mutation rate (θ; Watterson 1975), a summary of the unfolded site frequency spectrum (H_FW; Fay and Wu 2000), and two measures of linkage disequilibrium: congruency among adjacent sites (Wall’s Q; Wall 1999) and the average r² value (Z_nS; Kelly 1997). The significance of the earlier mentioned statistics under a standard neutral model were assessed with 10,000 replicate coalescent simulations with a prior probability distribution for recombination rate (gamma distribution with scale = 2 and rate = 0.04 for D. simulans and rate = 0.08 for D. sechellia). Maximum likelihood gene trees (including 1,000 bootstrap replicates) and pairwise sequence distance estimates were calculated using the MEGA software package (Tamura et al. 2011). A parsimony criterion was used to categorize variable sites as either ancestral or derived, using the D. melanogaster reference genome (FlyBase, build r5.45) as the outgroup. A short read sequence assembly of the 93A2 region from D. mauritiana generated by Garrigan et al. (2012) was also included in the final alignment.

Estimating the Time of Introgression

The time of the putative introgression event was estimated using a coalescent-based model of population divergence and a Markov chain Monte Carlo approach. The model includes two populations with effective population sizes N_sim and N_sec = αN_sim. The two populations initially diverge at time T = 2.42 × N_sim generations before the present (Kliman et al. 2000; Garrigan et al. 2012), and this time is held constant throughout the estimation procedure. The population mutation rates are θ_sim and αθ_sim for D. simulans and D. sechellia, respectively, and the population crossing-over rates are ρ_sim and αρ_sim. Finally, going backward in time, at generation τ, all lineages from D. sechellia are moved into an artificially created third population. Also at this time, half of the remaining D. simulans ancestral lineages are also moved to this third population. The effective size of this third population is set to be 0.001 × N_sim. Because lineages are expected to coalesce rapidly in this third population, this artificial construct is intended to elevate the introgressed segment to high frequency in the sample, before all lineages are moved back into the D. simulans population. Posterior probability distributions for the model parameters were obtained by estimating the likelihood of the model parameters at each step in the Markov chain using coalescent simulation. Replicate coalescent histories were simulated with a modified version of the ms computer program (Hudson 2002; program available from the authors upon request).

The likelihood of the model was estimated using the interspecific mismatch distribution, in which p_i is the probability of getting i mutational differences between a pair of sequences under a given model parameterization. The likelihood is calculated as being proportional to a multinomial probability, using the observed counts of pairs with i differences (f_i), 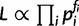. In cases where p_i = 0 and f_i > 0, a pseudocount was added to make the calculation feasible. Ten independently seeded Markov chains, each comprising the four model parameters (θ_sim, ρ_sim, τ, and α), were run for 10⁵ steps, and the likelihoods were estimated at each step from 5,000 replicate coalescent histories. The chains show satisfactory convergence behavior, as measured by the potential scale reduction factor (PSRF) (Gelman and Rubin 1992). The PSRF values are 1.01 for θ_sim, 1.00 for ρ_sim, 1.03 for τ, and 1.01 for α. Similarly, the Markov chains updated via the Metropolis-Hastings criterion and the chains showed good mixing behavior. The autocorrelation at lag 50 is 0.029 for θ_sim, 0.061 for ρ_sim, 0.130 for τ, and 0.007 for α.

Inference of Selective Sweeps

A maximum CLR test was used to estimate the ratio CLR1, which is the CLR of the data under a model of a complete selective sweep compared with that under a standard neutral equilibrium model (Kim and Stephan 2002). We also considered a second CLR statistic, CLR2, which is the CLR under a partial sweep model compared with that under the complete selective sweep model (Meiklejohn et al. 2004). This method requires a priori knowledge of both the population mutation and recombination rates. In this implementation, we estimated the population mutation rate from the data using the method of Watterson (1975) and used two different population recombination rates: one that assumed the recombination rate was of the same order of magnitude as the mutation rate and the other was estimated from the data using the method of Hudson (1987). The significance of the CLR1 test statistic was assessed via coalescent simulation under the standard neutral model and the significance of the CLR2 test statistic was determined via coalescent simulation under a complete selective sweep model with a value of Ns that was determined to be the maximum likelihood estimate resulting from the calculation of CLR1. Each simulation set consisted of 1,000 replicates. Finally, each maximum likelihood estimate of the CLR also produced estimates of 2Ns, X (the position of the selected site), and, in the case of the partial selective sweep, an estimate of the frequency of the selected allele (B). Finally, we adopted the method of Jensen et al. (2005), which uses the ratio Λ_GOF to the assess the goodness-of-fit of the data to the selective sweep model of Kim and Stephan (2002) compared with that expected under an arbitrary demographic model. The significance of the Λ_GOF statistic was assessed via 1,000 simulated replicates under the best-fitting selective sweep model. All CLR tests and goodness-of-fit analyses were performed using a modified version of the CLics program provided by Dr Yuseob Kim.

To localize the strongest signal of putative selective sweeps, we employed two different approaches. First, in the case of complete sweeps, we examined the partitioning of patterns of linkage disequilibrium across the entire 93A2 region. This approach considers each position along the sequence and seeks the position that maximizes the levels of linkage disequilibrium on either side of the position, while minimizing the levels of linkage disequilibrium among pairs of sites across the partition. The statistic is called ω_max and is detailed by Kim and Nielsen (2004), who identified this summary as a reliable statistic with which selective sweeps can be detected from genome-level scans of linkage disequilibrium. Second, local signals of partial selective sweeps were examined using the framework detailed by Meiklejohn et al. (2004). Similar to the method described in the previous paragraph, this method computes the CLR in windows across a desired region.

Finally, the timing of the putative selective sweep was estimated using subsets of the sequence alignment that contained only the core Ht1 haplotype sequence. A rejection algorithm based on the number of haplotypes and segregating sites was used in conjunction with coalescent simulations of natural selection to obtain posterior probability densities for both the time of the selective sweep and the selection coefficient (Przeworski 2003).

Supplementary Material

Supplementary methods, figures S1 and S2, and tables S1 and S2 are available at Molecular Biology and Evolution online (http://www.mbe.oxfordjournals.org/).