Temperature, Not Fine Particulate Matter (PM2.5), is Causally Associated with Short-Term Acute Daily Mortality Rates: Results from One Hundred United States Cities

Abstract

Exposures to fine particulate matter (PM2.5) in air (C) have been suspected of contributing causally to increased acute (e.g., same-day or next-day) human mortality rates (R). We tested this causal hypothesis in 100 United States cities using the publicly available NMMAPS database. Although a significant, approximately linear, statistical C-R association exists in simple statistical models, closer analysis suggests that it is not causal. Surprisingly, conditioning on other variables that have been extensively considered in previous analyses (usually using splines or other smoothers to approximate their effects), such as month of the year and mean daily temperature, suggests that they create strong, nonlinear confounding that explains the statistical association between PM2.5 and mortality rates in this data set. As this finding disagrees with conventional wisdom, we apply several different techniques to examine it. Conditional independence tests for potential causation, non-parametric classification tree analysis, Bayesian Model Averaging (BMA), and Granger-Sims causality testing, show no evidence that PM2.5 concentrations have any causal impact on increasing mortality rates. This apparent absence of a causal C-R relation, despite their statistical association, has potentially important implications for managing and communicating the uncertain health risks associated with, but not necessarily caused by, PM2.5 exposures.

INTRODUCTION: DO CHANGES IN PM2.5 LEVELS CAUSE CHANGES IN MORTALITY RATES?

Many sophisticated statistical models and epidemiological studies of time series data have reported highly statistically significant associations between average ambient concentrations of pollutants such as ozone and particulate matter (PM) and all-cause (non-accidental) acute mortality rates (Daniels et al. 2000; Dominici et al. 2002; Franklin et al. 2007; Katsouyanni et al. 2009; Balakrishnan et al. 2011; EPA 2011). This statistical relation between ambient concentrations and short-term mortality rates, often called the concentration-response (C-R) function, is typically modeled as being approximately linear, and risks are estimated down to the lowest measured or modeled ambient levels, for both fine particulate matter (PM2.5) and coarse particulate matter (PM10). Assuming that the significant associations in these studies reflect an underlying genuine causal C-R relation, a clear policy implication is that further reducing PM2.5 exposures will further improve human health benefits, extending lives and reducing PM2.5-associated deaths per capita-year. For example, Pope et al. (2009) concluded from a regression model of the association between reductions in pollution and changes in life expectancy in 211 county units in the U.S. that “A decrease of 10 μg per cubic meter in the concentration of fine particulate matter was associated with an estimated increase in mean (±SE) life expectancy of 0.61 ± 0.20 year (P = 0.004).” They interpreted the statistical regression coefficient causally, as implying that “A reduction in exposure to ambient fine-particulate air pollution contributed to significant and measurable improvements in life expectancy in the United States,” although without reporting results of formal statistical tests for this causal interpretation.

It is worth revisiting this causal interpretation of the statistical evidence. Do reductions in recent ambient levels of PM2.5 cause reductions in mortality rates (e.g., by reducing cardiovascular disease (CVD) and other inflammatory diseases of the lung and heart that can be exacerbated by high levels of pollutants), or might the historical associations between PM2.5 levels and mortality rates reported in multiple cities and countries reflect coincident trends, modeling artifacts, incomplete control of confounders, or other non-causal explanations? The role of causation in reported associations has often been questioned and discussed, but without an unequivocal resolution (Clyde 2000; NRC 2002; Green and Armstrong 2003; GAO 2006; Koop et al. 2007; Schwartz 2007). For example, Clyde (2000) expressed the following concerns in the context of a reanalysis of reported associations between PM10 and mortality rates in the elderly, similar to ones expressed by the National Research Council (NRC 2002):

“There are many aspects of model choice that are involved in health effect studies of particulate matter and other pollutants. Some of these choices concern which pollutants and confounding variables should be included in the model, what type of lag structure for the covariates should be used, which interactions need to be considered, and how to model nonlinear trends. Because of the large number of potential variables, model selection is often used to find a parsimonious model. Different model selection strategies may lead to very different models and conclusions for the same set of data. As variable selection may involve numerous tests of hypotheses, the resulting significance levels may be called into question, and there is the concern that the positive associations are a result of multiple testing.”

Clyde (2000) recommended applying Bayesian model-averaging (BMA) (i.e., using the data to identify an ensemble of plausible models, all of which are consistent with the data, based on their relative likelihoods; and examining the fraction of them that indicate a significant PM-mortality association) as a more objective way to interpret the data than selecting any single model. She found that BMA results “appear to support lower estimates of relative risk, with intervals that contain 1” (i.e., no effect) for PM10 air pollution and daily mortality in Birmingham, Alabama, where earlier studies (Schwartz 1993) had indicated a significant positive association. Similarly, applying BMA to time series data on daily lung-related hospital admissions in 11 cities in Canada led other investigators to conclude that “Almost all of our estimates of the health effects of air pollution are insignificant. Two pollutant types have significantly negative coefficients, indicating, if interpreted in the standard way, that these pollutants are actually beneficial for health. We do not claim this, but we conclude that the perceived statistical relationship between air pollution and health is not robust” (Koop et al. 2007).

Other investigators have also reported negative C-R relations for various air pollutants when models are left free to reflect the data. For example, Krstić (2011a) observed “a very weak negative association between elderly mortality and air pollution” for fine particulate matter (PM2.5) and concluded that, “Apparent temperature is associated with mortality from circulatory and respiratory causes, while air pollution does not appear to be a reliable predictor of elderly population mortality on the regional level in Metro Vancouver.” Similarly, Krstić (2011b) reported that latitude and total insolation in winter months (which may affect exposure to sunlight and vitamin D deficiency) are strongly associated with prevalence of asthma. By contrast, “The association of asthma prevalence with the annual mean air pollution as PM2.5 is very weak and not statistically significant (r² = 0.002; p=0.66).” In addition, annual air temperature appeared to be a marginally better predictor of asthma prevalence than the annual mean insolation in the studied populations. Powell et al. (2012) noted that, “The health risks associated with short-term exposure to air pollution have been the focus of much recent research, most of which has considered linear concentration–response functions (CRFs) between ambient concentrations of pollution and a health response. A much smaller number of studies have relaxed this assumption of linearity and allowed the shape of the function to be estimated from the data. However, this increased flexibility has resulted in CRFs being estimated that appear unfeasible, often showing decreases in the risk to health with increasing concentrations.” Convictions that it should be regarded as “unfeasible” for health risks of air pollution to decrease with increasing concentrations, and recommendations that statistical models should be constrained by a priori assumptions to prevent such negative dose-response relations from affecting reported results, have previously been expressed specifically for particulate matter. For example, Roberts (2004) recommends “Constraining the concentration-response function to be nondecreasing,” which “rules out the possibility of hormesis.” However, experimental data and mechanistic understanding of the biology of inflammation-induced diseases suggest that hormesis for particulate matter is in fact plausible (Cox 2012), and should not be discarded a priori as being biologically unrealistic. Thus, the question of how strong PM-mortality associations are when BMA (or perhaps other techniques, such as resampling methods (Roberts and Martin 2010)) are used to address model uncertainty and avoid or reduce model selection biases, remains interesting.

More generally, experimental studies and analyses of clinical data have not found clear evidence of a non-zero C-R relation for excess mortalities at current ambient concentration levels for specific pollutants such as PM10 or PM2.5 (Green and Armstrong 2003; Schwartz 2007). Concerns that some previously reported positive, approximately linear, C-R relations could be driven by the expectations and modeling assumptions of analysts, rather than by data alone (NRC 2002; Roberts and Martin 2010), are bolstered by the fact that some re-analyses of data and analyses of new data that attempt to account for model uncertainty (typically, via BMA) have not confirmed clear, positive C-R relations between PM and mortality rates (Clyde 2000; NRC 2002; GAO 2006). Other sources of misgivings include the sensitivity of the statistical significance and estimated size of PM2.5 health effects to model specification and variable-selection choices in key cohort studies (e.g., Moolgavkar 2005); and the high rates of false-positive associations in observational studies, due to multiple sources of bias (Ottenbacher 1998; Imberger et al. 2011, Sarewitz 2012, Yong 2012), such as from unmodeled errors in explanatory variables, confirmation and publication biases, model uncertainties and model selection biases, omitted confounders or residual confounding, and unmodeled correlations between explanatory variables and error terms in regression models. The high prevalence of false-positive biases has led some commentators to worry that “science is failing us,” due largely to misunderstandings about causation (Lehrer 2012); and that, especially in the past two decades (Sarewitz 2012), “Most published research findings are wrong” (Ioannidis 2005), with the most sensational and publicized claims being most likely to be wrong. Thus, the most important scientific question about the C-R relation remains: Do changes in current ambient concentrations of pollutants cause changes in mortality rates?

Our contribution is to attempt a fresh look at the question by analyzing PM2.5-mortality associations and evidence of causation in daily time series data for over 100 U.S. cities. To avoid or reduce potential model selection biases, our main analysis emphasizes simple nonparametric comparisons of death rates on high- vs. matched low-pollution days. We deliberately avoid what has become the standard approach to PM2.5-mortality data analysis (applying generalized linear models and/or generalized additive models to daily mortality counts, with statistical adjustments for meteorological covariates and smoothed seasonal and longer-term trends), since this approach requires making many modeling choices, and thus raises the issues of model selection and multiple testing biases noted above. Instead, we apply classification tree analysis and a modified version of a simple sign test for our main results. However, we do first briefly check whether multiple linear regression and BMA modeling reproduce the appearance of a significant linear association, and its absence, respectively, in this data set. Finally, we report the results of Granger tests for a potential causal relation between daily and lagged values of PM2.5 and daily mortality rates.

THE “HUNDRED CITIES” DATA SET FOR C-R RELATIONS IN U.S. CITIES

Most C-R data are less than ideal. They are available at the level of cities and metropolitan areas, but not at the level of accurately measured individual exposures and responses. Analysis of such aggregate data runs a risk of potential ecological biases, leading to false-positive associations (e.g., due to unmeasured confounders or unmodeled measurement errors); or to distortions (false negatives as well as false positives) in estimated statistical associations due to unmodeled differences between aggregate exposure concentrations (based on measurements at a fixed set of monitoring locations) and the spatially resolved true exposures of individuals (Sheppard et al. 2012). In multiple regression models, measurement error in explanatory variables can cause biases in either direction (Wooldridge 2008, Section 9.4). Yet, city-level C-R data seem too informative about potentially important causal relations to simply ignore; thus, the question arises of how best to use them to address the fundamental scientific question of how changing C (e.g., by reducing average ambient concentrations of PM2.5) would change R (e.g., by reducing the average age-specific mortality rates) in different locations, while bearing in mind the limitations of such data. The following sections present new analyses of a large data base on C-R relations in over 100 U.S. cities, with the goals of (a) Independently testing/verifying conclusions about C-R relations for PM2.5 drawn from other data sets; and (b) Performing additional analyses and tests emphasizing potential causation between changes in PM2.5 and changes in mortality rates.

A large, publically accessible, data base (the National Morbidity, Mortality, and Air Pollution Study, NMMAPS) for studying city-level C-R relations is the iHAPSS (internet-based Health and Air Pollution Surveillance System) data base of pollutant levels and mortality rates for U.S. cities made available on-line by Johns Hopkins at www.ihapss.jhsph.edu/. This data base provides historical daily data (from January 1,1987 through December 31 2000) on meteorological (temperature and humidity) variables, pollutant concentration measurements, and mortality counts for 108 U.S. cities, of which 101 are currently populated with at least some PM2.5 data. (PM2.5 data was not collected in all years and days in all cities and often had several-day gaps between data points.) The mortality data include all-cause mortality (excluding accidents) and cause-specific mortality counts, as follows:

• accident – accidental death

• copd – Chronic Obstructive Pulmonary Disease

• cvd – cardiovascular deaths

• death – all non-accidental death

• inf - influenza

• pneinf – pneumonia and influenza

• pneu – pneumonia

• resp – respiratory deaths

We divided the original daily mortality count values for the above variables (from NMMAPS) by the population base for each city, year, and age category (from US Census data) to obtain corresponding daily mortality rates by cause, city, year, and age category; see Appendix A for details. (Issues such as heteroscedasticity are dealt with in the subsequent data analysis.) Since most deaths occur among people over 75, we focus on the exposure-mortality association in this age group. For completeness, however, Bayesian Model Averaging and Granger-Sims causality analyses also consider the two younger age categories in the NMMAPS data set: people under 65 (agecat = 1 in NMMAPS) and between 65 and 75 (agecat = 2 in NMMAPS).

Because the data span over a decade for multiple cities (although most of the data are for 1999 and 2000), they are well suited for examining associations between historical changes in PM2.5 concentrations, C, (from day to day, month to month, and year to year) and changes in daily mortality rates, R, for different cities and time scales. Because they are collected from many cities, the NMMAPS data also provide an excellent opportunity to study heterogeneity in city-level C-R relations. We will refer to the resulting combined data set as the “Hundred Cities” data set (although, to be precise, it contains data from 101 cities.)

The NMMAPS data uses a derived variable, pm25Reconstruct, to estimate PM2.5 concentration levels. As explained at the iHAPSS web site (http://www.ihapss.jhsph.edu/data/FAQ.html):

“The median of the trends is stored in a variable with suffix “mtrend”. Adding a variable ending in “tmean” with its corresponding “mtrend” variable should get you something resembling the original averaged values. Adding the “tmean” and “mtrend” variables adds the average detrended series with the median of the long term trends from each monitor. It is not an exact reconstruction of any particular series.”

Accordingly, we computed pm25Reconstruct = pm25tmean + pm25mtrend from the original data, to facilitate cross-city comparisons.

RESEARCH QUESTIONS AND METHODS

The remainder of this paper examines the following research questions by applying exploratory, descriptive, hypothesis-testing, and estimation statistical methods to the Hundred Cities data set. All data files used can be retrieved from the cited web sites (or, if desired, from the authors as .xls/.csv files. R scripts used in data preparation and analysis are also available upon request).

1. Is there evidence of a statistically significant, positive, model-free association between PM2.5 levels and mortality rates? For example, are mortality rates higher on days with high PM2.5 levels (e.g., top quartile of PM2.5 concentrations) than on matched days (e.g., for the same city, month, temperature, and humidity quartiles) with low PM2.5 levels? This is perhaps the most fundamental, and least assumption-laden, question that can be asked about the PM2.5-mortality relation. It provides an alternative to more model-dependent questions, such as whether regression coefficients in particular models are significantly different from zero.

2. Does BMA change the conclusions about PM2.5-mortality from model-selection methods? Do Bayesian Model Averaging (BMA) models (which attempt to control for model uncertainty) produce similar evidence of a positive PM2.5-mortality association in the Hundred Cities study to the results of selecting a single model, e.g., a best-fitting regression model? (Clyde 2000; Koop and Tole 2004) To address this, we first tested for a significant positive linear association between PM2.5 and mortality (e.g., Ostro et al. 2006) in the simplest way possible: by fitting multivariate linear regression models for mortality rates vs. PM2.5 and other covariates and testing whether the regression coefficients for current or lagged PM2.5 values are significantly positive. Next, we test whether any such associations disappear in BMA analyses of the same data. This preliminary exercise is intended only to test the methodological claim that BMA diminishes the significance of effects seen in best-fitting models (within some family, such as linear regression models); our main analyses do not assume a linear regression specification, as we wish to avoid the potential for model specification errors and model selection biases pointed out by others (Clyde 2000, Roberts and Martin 2010).

3. Is there evidence of a causal relation between changes in PM2.5 concentrations, C, and changes in all-cause or cause-specific mortality rates, R? To address this question, we borrow from time series econometrics the Granger test for potential causation between two time series. This test is based on the intuitive criterion that there is evidence that exposure concentrations C might contribute to causing adverse responses R only if the future time series of R values can be predicted better from past and present values of R and C than from past and present values of R alone. We also apply nonparametric conditional independence tests (using classification tree analysis), which test whether observed associations between R and C are fully explained away by other variables (e.g., confounders) that are associated with both of them.

RESULTS ON C-R STATISTICAL ASSOCIATIONS AND BMA

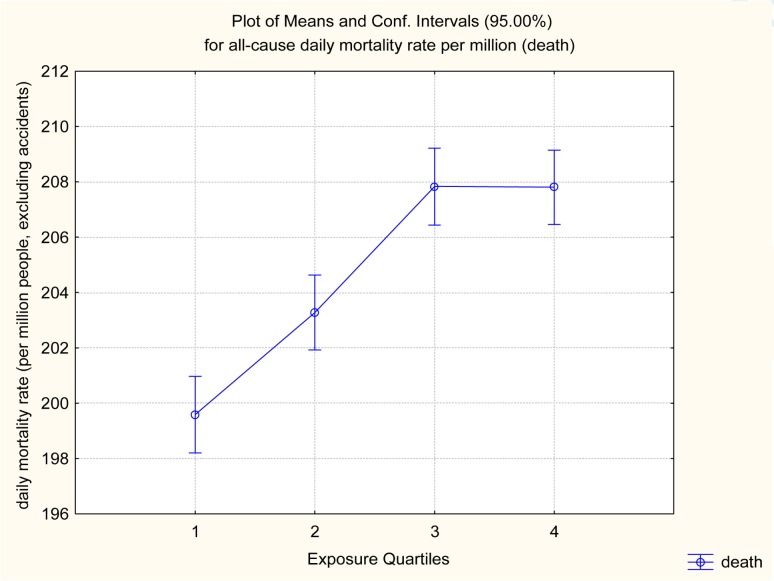
Figure 1 plots the aggregate C-R relation for all-cause mortality rates (per million people per day, excluding accidents), pooled across all 101 cities. The horizontal axis shows quartiles of the estimated PM2.5 frequency distribution, and the y axis shows daily mortality rates. Vertical bars around mean values indicate 95% confidence intervals. Figure 1 shows that the crude C-R relation is strong, positive, and apparently linear down to the lowest exposures (first quartile) examined. (The same holds when resolution is increased to show deciles, and also holds for lagged PM2.5 levels.) Although there is apparent saturation at higher exposure levels (quartiles 3 and 4), a linear regression model would show a strong, significant, C-R relation. The difference is about 4%, based on about 200 deaths per million person-days for the lowest exposure quartile compared to about 208 deaths per million person-days at the highest exposure quartile, and is statistically significant.

FIGURE 1.

Average PM2.5 level is significantly positively associated with average all-cause daily mortality rate (both same-day, as shown here, and on subsequent days)

As an example of a simple parametric statistical model controlling for potential confounders, Table 1 summarizes a multivariate linear regression model fit to the data. pm25Reconstruct remains a highly significant predictor of all-cause mortality rate, even after adjusting (via linear regression) for a variety of other variables. The regression in Table 1 was performed using the commercial statistical software environment Statistica 9.0 with backward stepwise variable selection. The b coefficients are ordinary least squares (OLS) regression coefficients, and the b* coefficient are their standardized values. To save space, Figure 1 and Table 1 show results only for pooled data from all cities, but city-by-city analysis confirms a significant positive statistical association (linear regression coefficient) between estimated PM2.5 levels and mortality rates in most cities. (All data and R code are freely available from the authors upon request.)

TABLE 1.

Multiple linear regression of non-accident mortality rates (death) against estimated pm2.5 levels (pm25Reconstruct), controlling for other variables, shows a statistically significant linear C-R association between them

N=54089	Regression Summary for Dependent Variable: death R= .26579752 R2= .07064832 Adjusted R2= .07039052 (All cities, Age > 75)
	b*	Std.Err. of b*	b	Std.Err. of b	t(54073)	p-value
Dec–Feb	0.14	0.01	27.24	1.00	27.3	0.000
Phighschool2000	0.13	0.01	169.99	10.48	16.2	0.000
tmin	0.12	0.02	0.56	0.09	6.5	0.000
dptp	0.09	0.02	0.43	0.08	5.3	0.000
pm25Reconstruct	0.04	0.00	0.32	0.03	9.2	0.000
pHisp	0.04	0.01	29.19	4.88	6.0	0.000
medianlncome	0.03	0.01	0.00	0.00	3.9	0.000
pBlack	0.02	0.01	14.13	3.80	3.7	0.000
Year	−0.03	0.01	−0.81	0.14	−5.7	0.000
Month	−0.05	0.00	−1.13	0.10	−11.1	0.000
pOther	−0.05	0.00	−44.65	4.10	−10.9	0.000
Purban2000	−0.05	0.00	−70.62	6.34	−11.1	0.000
mnrh	−0.06	0.01	−0.27	0.04	−7.1	0.000
Pdegree2000	−0.13	0.01	−149.41	8.92	−16.7	0.000
tmpd	−0.30	0.02	−1.42	0.11	−12.4	0.000
Intercept			1838.17	284.36	6.5	0.000

Key: Dec–Feb = 1 for days in December–February, else 0; tmin = minimum daily temperature; dptp = dew point temperature; mnrh = mean relative humidity; pOther = proportion of ethnic groups other than black, white, or Hispanic; see NMMAPS documentation for further definitions.

Of course, daily time series mortality data should be, and are, analyzed by more sophisticated and appropriate time series modeling methods (e.g., to deal with serially correlated errors, errors in independent variables, heteroscedasticity and other model specification errors and uncertainties). We have not attempted to replicate such models, although Table 1 identifies many of the same significant predictors (including temperature, humidity, PM2.5, and socioeconomic variables) noted by others (e.g., Krewski et al. 2000) in other data sets. The regression in Table 1 is proposed only to confirm that even simple statistical models indicate a highly statistically significant C-R association in the Hundred Cities data set. It also allows us to examine the effects of BMA on this association. To this end, we applied a BMA algorithm, bicreg (Bayesian Model Averaging for Linear Regression Models) available in the R library – BMA (http://cran.r-project.org/web/packages/BMA/BMA.pdf) – to 200 randomly selected days of data from each city and age category (600 total for each city). Each record contained the concentrations of PM2.5 and other contaminants, along with mortalities by type, for the selected day; to these we appended the values for the mortalities on the next five as additional variables. This sampling allowed us to obtain the same number of valid records for each city and age category (where we only selected days with non-missing values for PM2.5) and provided a tractable data set. (The raw data contains 5115 records per city, including NA values, and would be cumbersome to try to analyze in its entirety, e.g., using multiple imputation for missing data. The sampled data set is relatively easy to analyze.)

All analyses were performed within the R 2.13 programming environment. The BMA algorithm determines the fraction of all models that fit the data – here, linear regression models – in which each candidate independent variable is a significant predictor of the dependent variable (here, daily mortality rates).

Table 2 shows the fraction of models in which the coefficient of same-day pm25Recostruct for each mortality rate exceeds zero, averaged over all cities. (These only count cases where the posterior mean coefficient was nonnegative; it was significantly negative for several cities. The number of negatives depends on the specific cell of the table (age category and mortality type). There were 17 negatives for all-cause mortality in age category 3 (elderly), 25 negatives for age category 2 (middle age) and 13 for age category 1 (young).)

TABLE 2.

BMA-derived probabilities of significant PM2.5 association averaged over 101 individual NMMAPS cities (nonnegative associations only)

	Age Category
Indicator Variable	1	2	3	Average
accident	0.07	0.06	0.04	0.06
copd	0.05	0.04	0.07	0.05
cvd	0.06	0.05	0.08	0.06
death	0.10	0.08	0.12	0.10
inf	0.02	0.02	0.02	0.02
pneinf	0.07	0.04	0.07	0.06
pneu	0.07	0.04	0.06	0.06
resp	0.03	0.04	0.07	0.05
Average	0.06	0.04	0.07	0.06

The fractions in Table 2 can be interpreted roughly as estimated probabilities that same-day pm25Reconstruct would be a significant predictor of each mortality rate in the correct model, if it were known. Table 2 shows that it is unlikely (probabilities range from 2% to 12%) that PM2.5 is a predictor of all-cause or cause-specific mortality rates when BMA is used to try to account for model uncertainty. (An analogous table (not shown) for Month of year shows that it has a 100% probability of being a predictor of CVD and all-cause mortality rates.) Most individual cities exhibit a zero (or negative) association in BMA between estimated PM2.5 (pm25Reconstruct) levels and all-cause mortality rate (death), even in the relatively elderly group (agecat = 3). For over 90% of cities, it is more likely than not that PM2.5 is not a predictor of mortality rate. The ten cities with a probability of significant association greater than 50% in this analysis were New York, Rochester, Corpus Christi, Stockton, Oakland, Buffalo, Tampa, Salt Lake City, Topeka, and San Francisco.

In this data set, “best-fit” (here, OLS) statistical models indicate significant associations between estimated PM2.5 levels and same-day mortality rates that vanish in BMA analyses. This analysis shows that a C-R coefficient that is significantly positive in a single best-fitting multiple linear regression model (Table 1) is no longer significantly different from zero when model uncertainty is taken into account using BMA. This emphasizes the importance of accounting for model uncertainty before drawing conclusions about whether a C-R coefficient differs significantly from zero. The same methodological point holds for more sophisticated models: published findings about significant C-R coefficients, whether positive or negative, have uncertain validity when model uncertainty has not been explicitly accounted for. This applies to most of the published literature on PM2.5 health effects. We turn to model-free (non-parametric) analyses to better understand associations and potential causation in this data set.

MAIN FINDINGS: RESULTS OF NONPARAMETRIC ANALYSIS OF CITY-SPECIFIC C-R ASSOCIATIONS AND CONDITIONAL INDEPENDENCE RELATIONS

Average PM2.5 and mortality rate values for the cities in the Hundred Cities data base (pooled over all months and years) exhibit substantial heterogeneity, as shown in Figure 2. Average PM2.5 levels differ by more than a factor of 4 across cities, and average mortality rates among inhabitants over 75 years old differ by more than 2-fold across cities. There is no overall aggregate (ecological) positive association between average PM2.5 and average mortality rates across the cities, suggesting that the clear positive association shown in Figure 1 results from within-year correlations (e.g., daily PM2.5 levels and mortality rates tending to move together within a year in each city), rather than across-city correlations (cities with higher PM2.5 levels having higher average mortality rates).

FIGURE 2.

Different cities have very different PM2.5 exposure levels and death rates

To assess the C-R relations in different cities, we applied the non-parametric nonlinear modeling technique of classification and regression tree (CART) analysis (Lemon et al. 2003) to data for each city separately. Classification tree analysis successively conditions on the levels of statistically significant predictors to quantify how the dependent variable (mortality rate) varies with different combinations of predictor values. In classification trees for all-cause mortality rate (generated by the commercial data mining program KnowledgeSeeker™ Angoss Software 2005), PM2.5 (pm25Reconstruct) is a significant, though weak (compared to other variables) predictor of all-cause-mortality when considered alone, consistent with Figure 1 and Table 1. However, in most cities, it provides no additional predictive power (does not appear in the tree) after conditioning on other variables. In other words, mortality rate appears to be conditionally independent of PM2.5 exposure levels (at least within the power of the CART program to discover), given the levels of other variables, as explained next. Such conditional independence indicates that PM2.5 exposure level does not make a detectable causal contribution to mortality rate (Ellis and Wong 2008; Frey et al. 2003; Shipley 2000; Wood et al. 2006), despite their statistical association.

More specifically, 21 of 101 cities – Bakersville, Birmingham, Chicago, Denver, El Paso, Fresno, Los Angeles, Las Vegas, Louisville, Minneapolis, New Orleans, New York, Phoenix, Sacramento, San Diego, San Jose, Salt Lake City, Santa Anna, Stockton CA, Topeka, and Tucson – showed significant associations (p < 0.05, after using a simple conservative (Bonferroni inequality) adjustment for multiple testing) between PM2.5 and mortality rate when the only candidate predictor considered was pm25Reconstruct. In Birmingham and Louisville, the associations are significantly negative (lower mortality risks at higher exposure levels); in Los Angeles and Topeka they are J-shaped (significantly lower at intermediate concentrations than at the low and high ends); at other locations, they are generally positive. After conditioning on Month (the first, strongest split) in classification tree analysis, however, only 6 of the 21 cities still showed a significant C-R association with PM2.5: Chicago, El Paso, Los Angeles, New York, Stockton CA, and Topeka (with a J-shaped C-R curve for Topeka).

Six out of the 101 cities might show a positive C-R association either because one really exists (although one would then wonder why it is not apparent at the other 95 cities); or by chance (at a p < 0.05 level for the classification tree analysis); or because of confounders other than Month. Indeed, further conditioning on mean daily temperatures (tmpd), as well as on Month, eliminates all significant C-R associations in classification tree analysis, suggesting that there is no detectable causal relation between them, as causal associations typically remain even after conditioning on other factors (Ellis and Wong 2008; Frey et al. 2003; Shipley 2000; Wood et al. 2006).

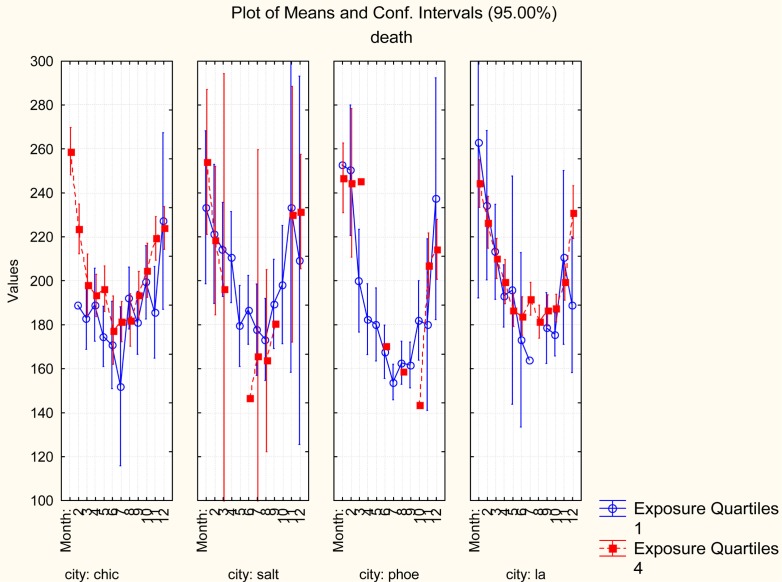
To help visualize and understand this finding, Figure 3 shows average mortality rates by month for four individual cities, for both the highest PM2.5 exposure quartile (solid dots) and the lowest exposure quartile (open circles). In Chicago, which was one of six cities that still showed a positive association between PM2.5 exposure and mortality rate after conditioning on month, the majority of month-specific mortality rates are higher for days with high estimated exposure levels (quartile 4) than for days with low estimated exposure levels (quartile 1). (Classification tree analysis confirms this pattern without restricting the comparison to quartiles.) By contrast, in Phoenix and Salt Lake City, month-specific mortality rates are not systematically higher on high-exposure days than on low-exposure days; hence, these cities no longer show a clear positive C-R association after conditioning on Month.

FIGURE 3.

Conditioning on Month eliminates the C-R relation in most cities

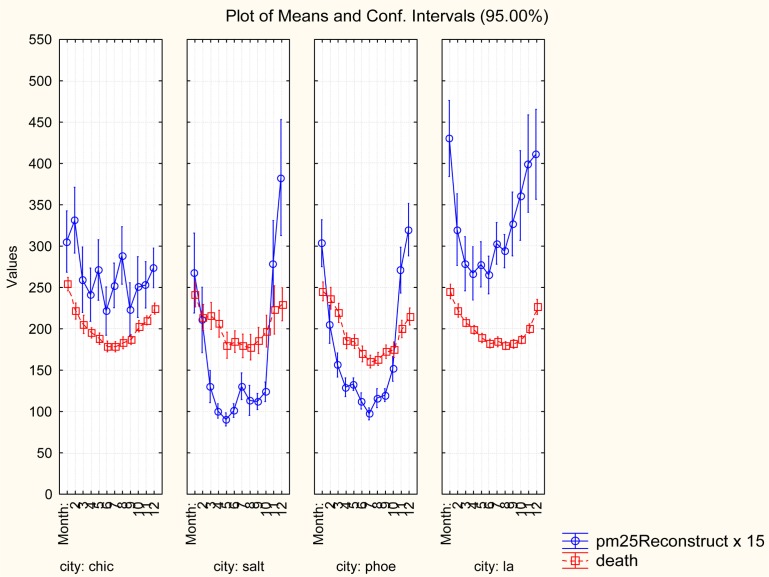
Figure 4 illustrates why only six cities showed a significant positive C-R relation after conditioning on Month: month-of-year (especially, the coldest winter months December–February) is a strong, non-linear confounder of the C-R relation. (PM2.5 levels are multiplied by 15 in Figure 4 to display them on the same vertical scale as mortality rates.) Month is significantly associated with PM2.5 levels and also, independently, with mortality rates. The associations are U-shaped, with nadirs occurring in different months for different cities. Comparing daily mortality rates for high- and low- PM2.5 exposure concentration days within the same month shows that neither daily PM2.5, nor its lagged values (not shown), are significant predictors of mortality rates within a month.

FIGURE 4.

Month is a strong, nonlinear confounder of C-R relations

This apparent conditional independence relation – that the city-specific daily mortality rate does not appear to depend on current or lagged daily PM2.5 levels, after conditioning on month and daily temperature –is surprising. It appears to contradict other analyses that have modeled the effects of covariates and concluded that PM2.5-mortality associations are probably not explained by confounders such as temperature and month, when their effects are estimated (e.g., using penalized or natural splines) and statistically adjusted for (e.g., Ostro et al. 2006). It is therefore worth critically examining this finding, using different analyses that do not depend on the exploratory techniques of classification tree analysis or on the use of statistical models.

Scrutiny of the conditional independence finding can be conducted via model-free methods, even without a classification tree program, by cross-tabulating the daily mortality rates by city (all 101), month (all 12), tmpd (4^th quartile vs. 1^st quartile) and PM2.5 (pm25Reconstruct) (4^th quartile vs. 1^st quartile). A variation on the nonparametric sign test then provides a model-free test of the hypothesis that mortality rates are higher on high-PM2.5 days than on matched low-PM2.5 days (for the same city, month, and temperature quartile) against the null hypothesis that they are not higher (which would hold if mortality rates are conditionally independent of PM2.5, given city, month, and temperature). The test is based on the observed fraction of all combinations (101 cities × 12 months × 2 temperature quartiles) for which days in the upper (4^th) quartile of exposure have a higher average daily mortality rate than days in the lowest (1^st) quartile of exposure. (This procedure controls for city, month, and temperature (tmpd) quartile variables by directly conditioning on them, rather than by statistically modeling, and subtracting out, their estimated effects. This eliminates the need for modeling choices, such as the degree of smoothness for spline curves, or the interaction terms to be included in parametric statistical models.) The null hypothesis that PM2.5 has no effect on mortality rate corresponds to a fraction of 0.5 in this nonparametric test. The alternative hypothesis being tested is model-free, in that it specifies only that high-pollution days should have higher death rates than matched low-pollution days.

The result of applying this non-parametric test to the Hundred Cities data was that 0.51 (95% CI [0.47, 0.55]) of the city-month-temperature combinations had a greater mortality rate for the high PM2.5 exposure days than for the matched low-exposure days. This evidence does not allow the null hypothesis of no difference to be rejected. The mean difference between mortality rates on high-exposure vs. low-exposure days matched for city, month, and mean daily temperature also has a 95% confidence interval that includes zero, and hence leads to the same conclusion.

If these nonparametric results are accepted at face value, it appears that, in this data set, the highly statistically significant association between PM2.5 and all-cause mortality is largely or completely explained by the confounding effects of temperature and month in model-free analysis. (The converse is not true: differences in PM2.5 levels do not explain away the effect of Month, as shown in classification tree analysis.) The same conclusion also holds for cardiovascular and other cause-specific mortality risks and for lagged as well as unlagged PM2.5 levels: In this large data set, in the nonparametric analyses performed, it does not appear that current or lagged PM2.5 values have statistically significant positive associations with all-cause or cause-specific mortality rates, after conditioning on month and temperature-related variables. Thus, the significant statistical C-R associations between PM2.5 and mortality rates do not appear to reflect a causal relation, based on these conditional independence tests.

Of course, it is impossible to prove a negative (no causal relation between PM2.5 and mortality rates). However, the large sample sizes and many cities in the NMMAPS data set suggest that, if there is a causal relation between PM2.5 and daily mortality rate, it is too weak to easily detect; and that significant positive statistical C-R associations between PM2.5 and mortality rates do not necessarily provide evidence that PM2.5 causes excess mortalities.

When an expected effect is not found, it is worth asking whether this is because it is not present, or because the methods used are not powerful enough to detect it, even though it is present. To better understand how to interpret our negative findings (no apparent statistically significant association between PM2.5 and daily mortality rates after conditioning on other variables) we used simulation to estimate the smallest effect size that would be expected to be detected if it were present. The usual way of describing the effects of PM2.5 on mortality rate is to state that every increase of 10 μg/m³ in average daily PM2.5 exposure concentrations increases daily mortality rate by a certain percent, typically on the order of 1% (Ostro et al. 2006). We therefore tested the power of our nonparametric test to detect such effects, by generating random samples of data points in the top quartile of the exposure distribution, for each city/month/tmpd combination, and setting their simulated mortality rates equal to randomly generated values from distributions with mean values based on different hypothesized effect sizes (average increases in mortality per 10 μg/m³ above the mean), and with variance equal to the empirical variance of mortality rates for each combination. (The empirical distributions of mortality rates are approximately normal for each combination.)

Because of the large sample sizes in this study, the non-parametric test we used was able to reliably detect effects below 0.1% increase in mortality rate per 10 μg/m³ increase in average daily PM2.5 exposure concentrations, far smaller than previously estimated effect sizes. Thus, the absence of any detected significant effect suggests that the expected effect (of about 1% increase in mortality rate among elderly people per 10 μg/m³ increase in average daily PM2.5) is not apparent in this data set. If an effect is present, it must be smaller than this size to have escaped detection.

TESTING FOR TIME SERIES CAUSATION

The unexpected finding that nonparametric conditional independence tests do not indicate a causal relation between PM2.5 levels and mortality rates can be reexamined using more detailed time series analysis. The intuition that causes should (a) precede their effects; and (b) help to predict their effects, provides the conceptual basis for the Granger test, developed in econometrics, for investigating potential causal relations in time series. To test for a possible causal C-R relation between PM2.5 and mortality rates, we extracted from NMMAPS city data all sequences of days for which pm25mean values were provided daily for at least 50 consecutive days. This produced 190 data sequences, distributed over 56 cities and various time periods within 1998–2000 (when regular data collection became more common). For each sequence, we performed a Granger statistical test for potential causality between pm25Reconstruct and the all-cause (except accidents) and seven cause-specific mortality rates calculated from the NMMAPS data set and Census data, using the granger.test (bivariate Granger causality testing for multiple time series) algorithm available in the R library (http://rss.acs.unt.edu/Rdoc/library/MSBVAR/html/granger.test.html). (We modified the algorithm to also report the direction – positive or negative – of the gradient relationship between changes in PM2.5 and changes in mortality rates.)

As explained in the R documentation for granger.test,

“Bivariate Granger causality tests for two variables X and Y evaluate whether the past values of X are useful for predicting Y once Y’s history has been modeled. The null hypothesis is that the past p values of X do not help in predicting the value of Y. The test is implemented by regressing Y on p past values of Y and p past values of X. An F-test is then used to determine whether the coefficients of the past values of X are jointly zero. …Tests are estimated using single equation OLS models.”

Because the Granger tests for the NMMAPS data set use daily data, rather than monthly or yearly time steps, they test for potential short-run causal relations, with lags ranging from a day to a week. Running this test for each age category in NMMAPS for 7 different maximum lags (the test includes each independent variable at each lag up to a maximum) yielded a total of 3990 tests (1330 for each age category). Table 3 summarizes the fraction of them in which the p-value was less than 0.05 and the gradient relation between PM2.5 and each mortality rate was positive. This fraction (average value of 0.037) was less than p = 0.05 for each cause of death, consistent with no evidence of a significant positive causal relation between PM2.5 exposures and mortality rates. (Among 24 tests of PM2.5 as a possible cause for each of 8 types of death (including accidental) in each of 3 age groups, borderline significance was achieved for accidental deaths among 65–75 year olds and for COPD and all-cause mortality in the over-75 age group, but multiple testing without adjustment of the significance levels weakens the significance of these borderline cases.)

TABLE 3.

Granger tests show no significant causal association between PM2.5 and mortality rates in daily time series

	Age Category
Relation	< 65	65–75	> 75	Avg.
PM.25 -> accident	0.044	0.058	0.048	0.050
PM.25 -> copd	0.029	0.038	0.050	0.039
PM.25 -> cvd	0.009	0.044	0.041	0.031
PM.25 -> death	0.023	0.036	0.051	0.037
PM.25 -> inf	0.002	0.022	0.014	0.013
PM.25 -> pneinf	0.052	0.041	0.036	0.043
PM.25 -> pneu	0.055	0.039	0.038	0.044
PM.25 -> resp	0.037	0.039	0.045	0.040

(Fractions of sequences with p-value < 0.05 and positive correlation)

Table 4 shows the analogous results for temperature (specifically, tmin). In this case, there is strong evidence of a Granger-causal relation between temperature and mortality rates: the null hypothesis of no effect is rejected in all 24 of 24 cases for tmin, as the fraction of data sequences in which Granger-causation appears to be present is greater than p = 5% in every case.

TABLE 4.

Granger tests strongly reject the null hypotheses of no significant causal association between temperature (tmin) and mortality rates in daily time series

	Age Category
Relation	< 65	65–75	> 75	Avg.
tmin -> accident	0.17	0.09	0.15	0.14
tmin -> copd	0.25	0.34	0.49	0.36
tmin -> cvd	0.33	0.41	0.69	0.48
tmin -> death	0.40	0.45	0.77	0.54
tmin -> inf	0.14	0.14	0.37	0.22
tmin -> pneinf	0.37	0.29	0.63	0.43
tmin -> pneu	0.34	0.27	0.62	0.41
tmin -> resp	0.40	0.42	0.66	0.49

(Fractions of sequences with p-value < 0.05; most correlations are negative)

Unlike our main results based on nonparametric methods, the granger.test procedure in this section uses parametric regression models, and hence is vulnerable to model selection and specification errors. No tests or transformations were attempted to correct for possible nonlinearities, heteroscedasticity, measurement error, nonstationarities, interactions of temperatures over time, or other issues: we simply applied the off-the-shelf granger.test procedure (modified to report the direction, as well as the significance, of associations). Notwithstanding these potential limitations, the results are consistent with the main findings from nonparametric analyses, that temperature (unlike PM2.5) has a clear causal impact on health outcomes.

DISCUSSION: SUMMARY AND IMPLICATIONS FOR PUBLIC HEALTH POLICY AND RISK COMMUNICATION

A fundamental scientific question about air pollution health effects is whether changes in ambient levels of pollutants cause changes in short-term daily mortality rates. A substantial body of literature concludes that there is a significant positive, approximately linear, statistical association between ambient levels of PM2.5 and mortality rates in multiple cities. Other studies have noted that much of this apparent association disappears when Bayesian Model Averaging is used to try to account for model uncertainty, although the most appropriate use of BMA and other (e.g., resampling) methods in air pollution health effects analysis is still being worked out (Roberts and Martin 2010). We have found, using NMMAPS data and multiple linear regression both the presence of an apparent small but highly statistically significant positive linear C-R association between PM2.5 (same-day or lagged) and daily mortality rates in multiple cities, and also the absence of such an association when BMA is applied.

More surprisingly, it appears that the statistical association between PM2.5 and mortality rates is explained in this data set by confounding by variables such as the month the daily record falls within and average daily temperature (with the cold winter months having both higher pollution levels and, independently of pollution level, higher mortality in most cities). The nonparametric technique of classification tree analysis showed that statistically significant C-R associations disappear after conditioning on city, time of year, and other variables; this unexpected apparent conditional independence is also seen in simple, model-free, cross-tabulation analyses.

To further test for evidence of a causal C-R relation between PM2.5 and mortality rates, we applied Granger-Sims tests to examine whether changes in daily PM2.5 levels preceded, and helped to explain, subsequent changes in daily mortality rates. They did not, according to these tests. The results did not suggest a significant (non-random) causal association between changes in PM2.5 concentrations and changes in mortality rates, despite the clear statistical associations between them (since both vary similarly with time).

The contrast between our negative findings and conclusions from previous analyses of the NMMAPS data set, and other data sets, requires some explanation. We propose that the following factors may contribute to the differences in conclusions.

• Residual confounding. The standard approach to analysis of PM and mortality time series data, e.g., using splines to model effects of seasonality, does not necessarily control as completely as conditioning does for the effects of Month. How flexible a spline is affects how well it can fit highly non-linear relations, and different degrees of smoothing may create different degrees of residual confounding. Indeed, as noted in relatively recent analyses of PM2.5-mortality associations in California (Ostro et al. 2006), “greater degrees of freedom for time trend tended to lower the effect estimates,” which are not significantly different from zero, for natural splines, unless the degrees of freedom are chosen to be small enough (e.g., 4) so that the spline is relatively inflexible. The multiple linear regression analysis in Table 1 and the conditioning-on-month approach illustrated in Figures 3 and 4 stand at opposite extremes of flexibility in modeling temporal effects, with the usual spline approaches somewhere in between. Imposing a linear model on the data produces an apparently significant PM2.5-mortality association, but without removing the effects of residual confounding by month and temperature (created because these nonlinear confounding effects cannot be fully estimated and removed using a linear model). Conditioning on month controls more fully for its effects, but does no smoothing across months. Splines provide some smoothing, and eliminate more confounding than a linear model, but may leave some residual confounding, especially if the spline is relatively stiff. The non-parametric CART analysis estimates a constant risk level for each group (each “leaf” node in a classification tree), reducing the potential for residual confounding (since there are no high or low risk estimates within each group that could be associated with high or low values of predictors). It does not rule out the possibility that some confounders have been omitted from the analysis, but offers a constructive response: since conditioning on the observed confounders (e.g., daily temperature) already suffices to render mortality risk conditionally independent of PM2.5 exposures, conditioning on any further, omitted confounders (if there are any) would only reinforce this conclusion.

• Causality tests. To the best of our knowledge, this is the first published analysis to apply Granger-Sims tests for potential causation to the NMMAPS data on PM2.5 levels and mortality rates. We anticipate that testing for causation in other data sets may confirm that significant statistical associations between PM2.5 and mortality rates are present, even if causation is not.

• No consistent effect. Although BMA results have sometimes been challenged, e.g., by investigators who prefer using expert judgment or substantive knowledge to guide model selection, such more objective techniques can potentially play a useful role in understanding PM and health effects data (Roberts and Martin 2010). That BMA eliminates the apparently significant PM2.5-mortality association seen when a single “best-fitting” (e.g., OLS) model in some family of models is selected suggests that including PM2.5 as a predictor improves the fit of the single best-fitting model (perhaps by helping to compensate for residual confounding), yet has no systematic effect of its own when examined in the ensemble of best-fitting models.

• Heterogeneity and model-free analysis. Wide heterogeneity of PM-mortality associations across cities (see Figure 2) has been previously noted, with stronger associations in the East than in the West of the U.S., and with zero (or negative) associations seen in a substantial minority of cities (Franklin et al. 2007; Davis et al 2011; Dominici et al. 2007). This suggests that any description of PM effects in terms of a national average increase in mortality rate per unit increase in PM2.5 concentrations is likely to be too simple, as no such consistent effect exists in reality. The causes of such heterogeneity are not yet well understood, although one can speculate that differences in PM2.5 composition and errors in estimated exposures may contribute to differences across cities (Davis et al. 2011). Another possibility could be a J-shaped concentration-response curve, giving inconsistent signs of effects across cities with different daily exposure levels (Cox 2012). Hence, it is not yet known how to specify families of models that correctly describe PM2.5-mortality associations in different locations. In this context, it is perhaps not surprising that model-free analyses such as CART and cross-tab based conditional independence tests might produce different results from model-based approaches that require model specifications and assumptions of uncertain validity.

Whatever the explanations for differences across studies, the implications for risk-based policy and communication seem clear. Suggesting that each unit of increase in PM2.5 corresponds to (or produces) a certain proportional increase in daily mortality rate, as is now commonly done in reporting study results (e.g., Ostro et al. 2006; Katsouyanni et al. 2009; Balakrishnan et al. 2011; EPA 2011; Fann et al. 2012), is overly simple and misleading. Rather, such correspondences appear to exist in some cities but not in others, and for some models and analyses but not for others (Clyde 2000; Koop and Tole. 2004; Franklin et al. 2007; Schwartz 2007). Policy makers should not be led to expect that further reducing exposure PM2.5 concentrations will necessarily further reduce daily mortality rates, as the actual effects caused by such a change are neither as known nor as consistent as such a statement suggests. Even where positive associations do exist, they may not be causal. The results of our BMA, classification tree (CART), conditional independence, and Granger-Sims analyses suggest that, at least in this study of many U.S. cities, the causal impact of PM2.5 on daily mortality rates is far less clear than might previously have been expected.

Some other studies, with different designs (e.g., prospective cohort studies) and models, report positive PM2.5 mortality rate associations (as do our Figure 1 and Table 1), although such associations might well be explained by residual confounding and modeling and other biases (Moolgavkar 2005; Sarewitz 2012); and although negative associations are also reported when models are left unconstrained in describing the data (e.g., Krstić 2011a; Powell et al. 2012). But the methodological point is that, if a clear, robust causal relation exists – one that does not depend on details of modeling choices – then it is puzzling that it is not more apparent when model-free methods and other analyses are used to look for it in this large data set. This may add new weight to previously expressed concerns (Clyde 2000; NRC 2002; Roberts and Martin 2006; Koop et al. 2007) that the usual current approaches to analyzing time series data on exposures and mortality rates may be identifying associations that do not necessarily reflect reliable causal relations.

APPENDIX A. DATA SOURCES

NMMAPS Data and Functions

• NMMAPS = National Mortality, Morbidity, and Air Pollution Study

• NMMAPSData R package version 0.4-2 downloaded from http://www.ihapss.jhsph.edu/publications/publication.htm

• Run on R version 2.9.2 (note NMMAPSData R package will not run on later versions of R)

Specification of Relevant Counties and Aggregation into Cities

• Counties.txt file from NMMAPS: http://www.ihapss.jhsph.edu/data/NMMAPS/Data/data_download_gz.htm

Poverty and Income Data

• By state and by county of the US

• Years available: 1989 1993 1995 1997 1998 1999 2000

• US Census State and Small Area Poverty Estimates downloaded from http://www.census.gov/did/www/saipe/data/statecounty/data/index.html

• Fields used:

  • - 35– 38 Estimated percent of people of all ages in poverty

  • - 134–139 Estimate of median household income

• Years 1990–1992 1994, and 1996 are computed via linear interpolation between the nearest endpoint years.

• Years 87–88 used the values from 1989

Hispanic Origin

• 1987–89

  • - By Age (category), Year, and State of US

  • - Race/Hispanic Origin Codes: 5 + 6 (White Hispanic + Black Hispanic)

  • - US Census Estimates of the Population of States by Age, Sex, Race, and Hispanic Origin: 1981 to 1989 downloaded from http://www.census.gov/popest/archives/1980s/80s_st_detail.html.

  • - To obtain county level data, we used the distribution by counties within each state in 1990 and applied the same distribution to state totals for 87–89. This was performed separately within each of the 3 age categories.

• 1990–99

  • - By Age (category), Year, and US County

  • - Hispanic Status as a separate code

  • - Intercensal State and County Characteristics Population Estimates with 1990-Base Race Groups downloaded from http://www.census.gov/popest/datasets.html (each year in a separate file)

• 2000

  • - By Age (category) and US County

  • - Hispanic Status in combination with each race category

  • - Modified Race Data Summary File 2000 Census of Population and Housing downloaded from http://www.census.gov/popest/archives/files/MRSF-01-US1.html.

Race (Black and Other)

• 87–89

  • - By Age (category), Year, and US County

  • - Intercensal County Estimates by Age, Sex, Race: 1980–1989 downloaded from http://www.census.gov/popest/archives/1980s/PE-02.html.

• 90–99 (same as Hispanic Origin above)

• 2000 (same as Hispanic Origin above)

Educational Attainment and Urban vs. Rural

• Year 2000 only for each city

• Extracted from NMMAPS database