Abstract
INTRODUCTION
ACL reconstructions are frequently performed following ACL injury. The most common treatment is single bundle reconstruction. While ACL reconstructions have been studied clinically and experimentally, quantitative information regarding the local biomechanics the knee following ACL reconstruction is generally lacking. Specifically, the role of graft size on joint stability and soft tissue injury propensity is currently unknown.
METHODS
Therefore, a non-linear contact finite element model was developed to systematically evaluate the relationship between ACL graft size and knee joint biomechanics following ACL reconstruction. A simulated Lachman maneuver was utilized to assess knee joint laxity, meniscal stress, in situ graft loading, and peak articular cartilage contact pressure for ACL graft sizes between 5 and 9 mm, as well as an ACL-deficient knee. The model was validated by corroboration with previously published experimental (cadaveric) data on ACL reconstruction.
RESULTS
The 5 mm graft resulted in 30% greater relative AP translation compared to the 9 mm graft; the ACL deficient knee resulted in 2.56-times greater AP translation than the average graft reconstruction. Contact pressure and peak meniscal stresses decreased monotonically for increased values of ACL graft diameter. For all graft diameters, soft tissue stress and articular contact pressure was reduced versus the ACL-deficient knee.
Conclusions
ACL reconstruction dramatically affects the local biomechanics of the knee. Stresses occurring in the soft tissues, as well as contact pressure at the articular surfaces, were found to be highly sensitive to ACL graft size. Larger grafts were associated with lower meniscal stress, decreased joint laxity, and less articular cartilage contact stress. Therefore, the current data suggests that increased graft size confers a biomechanical advantage in the ACL reconstructed knee.
Introduction
Anterior cruciate ligament (ACL) injury is common in the athletic patient population, occurring 200,000 times annually in the United States1. ACL reconstruction is a common treatment modality, with an estimated 60,000 to 175,000 surgical cases performed per year in the United States1-3. The ACL is the primary restraint to anterior tibial translation with respect to the femur, absorbing approximately 90% of the anterior displacement force during knee flexion4. The Lachman test is an important clinical exam to evaluate the soft tissue integrity of the ACL, by assessing anterior tibial translation relative to the femur at typically 20-30° of knee flexion5. It is the most reliable clinical test to assess both anterior cruciate ligament injuries and the state of reconstructions5-7. The test can be quantified in the clinical setting using KT-1000 arthrometer (MEDmetric, San Diego, California) measurements of anterior tibial translation8.
However, a reliable method to assess the mechanics associated with ACL reconstruction integrity is generally lacking. Perhaps the most frequent guide for surgical practice is the clinical study, which can give insight into apparent causality of events and outcomes. However, inherent weaknesses of clinical studies, including limited patient populations and uncontrolled confounders, often prevent systematic analysis. Therefore such studies are frequently limited in terms of their immediate clinical utility. By contrast, experimental biomechanical analyses allow for precise and controlled investigation. However, conventional biomechanical investigation, whether by simulator or cadaveric studies, is greatly resource-intensive, both in terms of labor and cost. Additionally, experimental studies must be sufficiently robust to parametrically address individual factors associated with biomechanical outcomes, further increasing their cost and complexity. Computational models – specifically finite element (FE) analyses – enable unique advantages in the realm of biomechanical investigation. Provided sufficient model robustness, FE analysis grants the ability for unlimited parametric simulations, at a minimum of time and economic expenses. While cadaveric studies of ACL reconstruction have generally focused on whole-joint kinematics8-10, quantitative data regarding the local biomechanics associated with variances in reconstruction technique are generally unavailable9, 11-13. Therefore, a non-linear three-dimensional contact FE model of single-bundle ACL reconstruction was developed, and used to assess the effect of ACL graft size on local joint kinetics and kinematics.
Methods
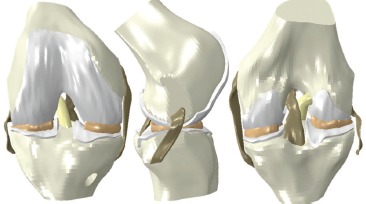
The ACL reconstruction FE model consisted of bony anatomy, native soft tissues, and the ACL graft (Fig. 1). Surface geometries of the knee joint were obtained from the open-source OpenKnee project14. These surfaces, which consisted of bony anatomy (distal femur, proximal tibia), cartilage, menisci and additional soft tissues (lateral collateral ligament, medial collateral ligament, posterior cruciate ligament), were obtained from MRI imaging of a donor knee specimen. These surfaces were imported into the preprocessing software TrueGrid (XYZ Scientific Applications, Livermore, CA), appropriately modified, and discretized into 8-noded hexahedral continuum elements, with a mesh density based on convergence sensitivity studies.
Fig. 1. The ACL reconstruction FE model consisted of bony anatomy, articular cartilage, menisci, native collateral ligaments, PCL and the ACL graft. The graft was attached to 9-mm tunnels placed in the femur and tibia, to facilitate parametric evaluation of single-bundle ACL grafts up to 9-mm in diameter. Ligament attachments were defined by computationally pinning the nodes at the insertion-and originsite to their respective bony attachment site. The attachment site for the LCL was at the approximate location of the fibular head.
Initial locations of the ACL graft tunnel was determined from experimental analyses of the femoral ACL footprint15 and established CT based data of arthroscopically identified loci for the tibial footprint16. To permit parametric evaluation of the effect of graft sizes up to 9.0 mm diameter, the femoral and tibial tunnels were modeled at 9.05 mm in diameter. The ACL graft was constructed as a single cylindrical solid (i.e., single bundle graft). The graft was manipulated within TrueGrid to penetrate approximately 1 cm into the femoral and tibial tunnel sites. The axial centroid of the graft was then aligned with a cubic spline spanning from the femoral to tibial tunnels, producing a natural strain-free anatomic geometry, permitting simulation of intraoperative tautening of the graft during reconstruction. The meshed structures were then aligned in a knee-joint coordinate orientation system17with an approximate Q angle of 14.1°. In this orientation, the origin of the model is defined as the midpoint of the medial and femoral condyles. the x-axis is the flexion axis, the y-axis the anterior-posterior axis, and the z-axis the mechanical axial axis14.
Anisotropic (fiber direction-dependent) representation of the knee joint soft tissues were implemeated using the micromechanically based hyperelastic constitutive model introduced by Holzapfel, Gasser and Ogden (HGO)18. In the HGO-formulation, the strain-energy potential U takes the form
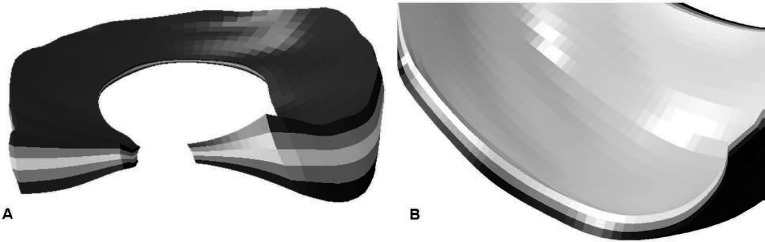
where Ī1 is the first strain invariant, and Ī4αα are pseudo-invariants of the deviatoric part of the right Cauchy-Green deformation tensor, Jel is the elastic volume ratio, N is the number of fiber families; C10, D, k1, k2 are material coeffi cients, and k is a parameter quantifying the degree of heterogeneity in the distribution of fiber directions locally within the material. A similar material model has been successfully implemented for modeling of the hip capsule following total hip arthroplasty19. The prevailing collagen fiber orientation of the ACL was assumed to run parallel to the long axis of the graft. An element-by-element continuous fiber orientation was defined for the graft (Fig. 2), allowing for appropriate material response from tensile loads acting through the soft tissue. Material coefficients for the ACL model were optimized such that the resulting load-displacement data from a simulated tensile test matched physical load-displacement20 and stiffness21 data for corresponding cadaveric native ACL specimens. The remaining cruciate and collateral ligamentous structures were similarly assigned prevailing fiber orientations and assigned these HGO material coefficients. The menisci were discretized such that appropriate fiber orientations in the superficial, lamellar and central layers22 could be defined (Fig. 3A). An optimization routine was used to determine the appropriate material coefficients for the HGO model of the menisci based on literature values13. Meniscal horn attachments to the tibia were approximated as a series of spring elements attaching each node on the surface of the meniscal horn to a node on the tibia acting approximately orthogonal to the horn face centroid14. The spring constants were determined from the Young’s modulus for horn attachments23. Additional spring elements, representing the meniscal coronary ligaments were similarly prescribed. Appropriate collagen fiber orientations of the articular cartilage were assigned to the deep, middle, and superficial layers (Fig. 3B), and HGO material parameters were also determined by an optimization routine to match literature cartilage mechanical behavior12. Given the several-order higher stiffness of bone versus soft-tissue stiffness, the bony structures were assumed rigid.
Fig. 2. Implementation of the anisotropic hyperelastic constitutive material model requires determination of prevailing fiber orientations. Fiber directions for the ligaments were assumed to align with the long-axis of the tissue. These directions were defined as a continuous element-by-element function, resulting in smooth transitions between sections with varying initial geometry as well as during large-scale deformations during the simulation. Shown here are representative sections of a 7 mm ACL graft, demonstrating the continuation of fiber direction (small black arrows) along the long axis of the ligament.
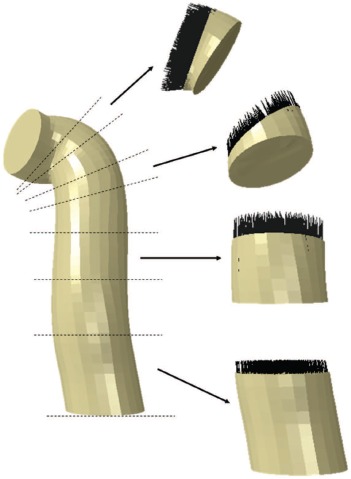
Fig. 3. (A) the lateral and medial menisci were discretized into superficial, lamellar and central layers, allowing for accurate replication of the variance in prevailing fiber orientation for each layer. Similar layering of the articular cartilage (B) allows for accurate fiber representation in the deep, middle and superficial cartilage zones. By varying the dispersion parameter k, fiber orientations within the lamellar layers (more dispersed) and central/superficial layers (less dispersion) could be reproduced.
The FE model was kinematically controlled using rigid body definitions. Reference nodes were ascribed to the tibia, the femur and the ACL graft. Attachments of the soft tissues to bones (e.g., cartilage to bone and ligaments to bone) were applied using these rigid body interfaces. Additionally, all prescribed boundary conditions (six total degrees of freedom) were applied to these reference nodes. The Lachman simulation consisted of two steps: the first step begins with the knee in full extension, and flexes the knee to 30° while an axial load of 50N is applied. To accurately represent the native ACL’s U-shaped tension curve, as well as intraoperative ACL reconstruction technique24-26, the ACL graft is tautened (pretensioned) with 20 N tensile load at approximately 20° of knee flexion. The second step is the application of 89 N of posteriorly directed load on the flexed femur, simulating the Lachman maneuver. During both steps, all degrees of freedom at the tibia were constrained; therefore displacement of the femur relative to the tibia determined in the FE simulation is analogous to anterior displacement of the tibia during the clinical exam. To ensure the highest level of model realism, kinematic contact definitions were specified for all possible perturbations of bone, cartilage and soft-tissue engagement.
The FE model was used to parametrically assess the effect of graft size on knee joint mechanics. A total of ten FE models were generated, consisting of an ACL-deficient knee, and nine variants of ACL graft diameter (5.0 mm to 9.0 mm in 0.5 mm increments). Output metrics for each simulation included: (1) anterior-posterior displacement of the femur relative to the tibia; (2) ACL reaction forces (analogous to in situ ACL load bearing during the Lachman maneuver); (3) von Mises (vM) stresses in the ACL graft and menisci; and (4) contact pressure at the articular cartilage. The FE simulations were run using Abaqus/Explicit 6.11 (SIMULIA, Providence, RI), executed on a 64-bit Suse Linux operating system with twin dual quad-core Intel Xeon platforms configured with 24 GB of RAM. Each simulation required approximately 21 processor-hrs of computation time.
Results
During knee flexion and the Lachman simulation, in situ stresses developed within the ACL graft (Fig. 4). These stresses were shown to be highly dependent upon the ACL graft diameter (Fig. 5), in which increased ACL graft bundle size generated substantially less peak stress within the tissue. During the Lachman simulation, the posteriorly-directed load on the femur is taken up by the ACL graft, with summation loads (i.e., the ACL reaction force) also highly dependent upon graft diameter (Fig. 6). These in situ loads, within the range of 75-90N, agree well with experimental cadaveric data [9] with similar testing parameters.
Fig 4. von Mises (vM) stresses developed in the ACL graft during the Lachman simulation varied throughout the entire input sequence. In the initial unloaded state (A), the ligament is tension-free. At the conclusion of the 20 N pretensioning step at 20° (B), contact between the graft and the femoral tunnel generates a stress concentration at this site. Posterior translation of the femur relative to the tibia occurs following application of the posteriorly-directed force during the Lachman simulation. This relative translation generated increased contact pressures and graft tension shown here at 45 N (C) and 89 N (D) of load.

Fig. 5. Peak von Mises (vM) stresses occurring in the ACL graft decreased for increased values of ACL graft diameter.
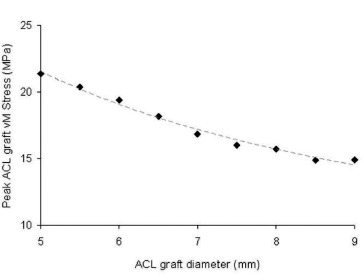
Fig. 6. ACL reaction force, representative of the in situ load-burden received by the ACL graft during the Lachman simulation, increased monotonically as a function of ACL graft diameter. Computational results agreed favorably from those measured experimentally. [9].
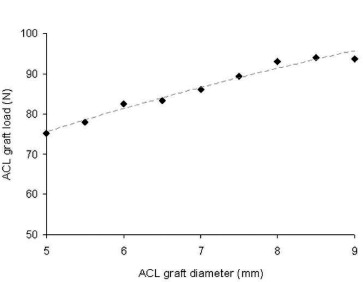
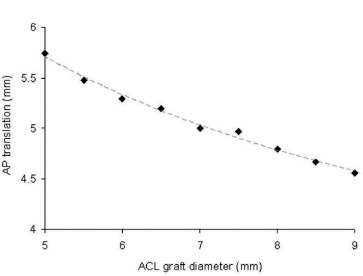
The increased reaction forces and stresses seen with increased graft diameters also influenced the posterior translation of the femur relative to the tibia during the Lachman simulation (Fig. 7). The 5.0 mm graft resulted in nearly 30% greater relative translation compared to the 9.0 mm graft. The ACL-deficient knee resulted in substantially greater translation (12.8 mm) than that seen with the smallest graft simulated (5.75 mm with the 5.0 mm graft). The magnitude of relative translation reported here also agrees favorably with that seen experimentally.9
Fig. 7. Femoral translation in the anterior-posterior (AP) direction relative to the constrained tibia resulted from the application of the posteriorly-directed load on the femur. There was a strong inverse correlation between graft size and AP translation during the simulated Lachman maneuver. In the ACL-deficient knee, 12.8 mm of translation was observed, greatly exceeding those obtained in ACL-reconstructed simulations.
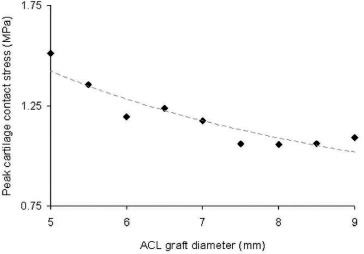
Owing to the considerably altered local mechanics resulting from ACL graft size variance, discrepancies in peak meniscal stress (Fig. 8) and articular cartilage contact pressure (Fig. 9) were also observed. In general, both peak meniscal stress and peak articular cartilage contact pressure decreased with increased graft diameter.
Fig. 8. Peak von Mises (vM) stresses occurring in both the medial and lateral mensici decreased for increased values of graft diameter. The maximum meniscal stress occurring during the ACL-deficient simulation was 5.0 MPa, exceeding all simulations performed with a reconstructed ACL.
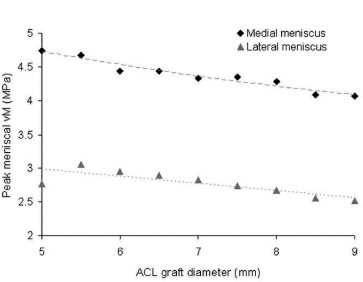
Fig. 9. In general, the peak contact stress occurring at the articular cartilage decreased for increased values of ACL graft diameter. The peak cartilage stress in the ACL-deficient simulation was 1.6 MPa, exceeding all simulations performed with a reconstructed ACL.
Discussion
ACL reconstructions are common procedures in orthopaedics and are generally associated with good results. Although several techniques exist, single bundle ACL reconstructions remain the mainstay of treatment27. However, objective evidence regarding the influence of patient-and surgical-specific variables on outcomes following ACL reconstruction is very limited. Therefore, the ability to perform efficient systematic and parametric biomechanical analysis of ACL reconstructed knees is a desirable goal. Toward objectively analyzing knee joint mechanics following ACL reconstruction, a three-dimensional contact FE model of single-bundle reconstruction was developed, and utilized to investigate the role of graft size on joint stability and soft tissue stresses. Model validation was conducted by corroboration of the FE model with published studies of ACL reconstructions. In a cadeveric study, Kato et al9. found anterior tibial translation at 30° with 89 N of force to be 5.9-6.1 ± 2mm for intact ACLs and anatomic single bundle reconstructions. Prophy and Pearle28 reported anterior tibial translations of 4 ± 1 mm with conventional ACL graft placement. Under similar conditions in the present investigation, translations of 4.6-5.7 mm were observed with similarly-sized graphs. In situ forces from the present study also agree well with the established literature. Yagi et al10. demonstrated 2.67-times greater AP tranlation of an ACL deficient knee compared to a single bundle reconstruction. This compares favorably with the 2.56-times greater AP translation observed in the present FE study. After single bundle ACL recon-sturctions under similar loading conditions, in situ forces have been reported between 65 N and 110 N9, 10. In situ ACL graft forces of 75-90N were observed in the present investigation. The excellent agreement acheived between the computational and experimental results reinforces the validity of the current FE model.
The present data indicate that even small changes to ACL graft size used for reconstruction can result in large variation in the local biomechanics of the knee. Increased ACL integrity, as simulated with increased ACL graft diameter, resulted in substantially less joint laxity during Lachman simulation by increasing the load burden of the ACL. Owing to decreased translation across the articular surface and concomitant compressive loads on the menisci, increased ACL graft integrity was found to decrease the stresses generated in the lateral and medial meniscal structures. Contact pressures generated at the articular surface demonstrated a similar dependence upon ACL graft size. Additionally, in all cases, the soft-tissue stresses generated during the simulation of ACL-deficient knees were substantially greater than that observed for any simulation involving reconstructed ACLs. Given the well-established clinical association of the development of osteoarthritis in ACL-deficient29 and in some reconstructed ACLs30, 31 the ability to systemically evaluate the effects of surgical variables on the local-and whole-joint mechanics of the ACL-injured knee deserve further attention. The present study, which to the authors’ knowledge represents the first computational model of Lachman testing in ACL-reconstructed knees, provides the first quantitative data in this regard. Of course, numerous other surgical variables – such as tunnel location, tunnel angle, graft pretensioning, graft choice, etc. – can similarly affect the biomechanics of the ACL-reconstructed knee. Parametric investigation of these variables is an attractive avenue for further investigation with the present FE model.
Despite every effort to attain the highest level of realism with the computational formulation, several modeling limitations merit attention. First, the present study evaluated joint mechanics only for a Lachman-type maneuver. Several clinical examinations are available for evaluation of joint laxity prior to, and following, ACL-reconstruction. However, the Lachman test was chosen owing to the availability of experimental data for model corroboration. Additionally, while alterations in cartilage, meniscal and ligament stresses were reported for Lachman testing, it is perhaps more clinically relevant to determine the effect of ACL-reconstruction variables on potentially deleterious soft tissue engagements for more clinically relevant joint motions, such as gait, stair descent, etc. While the relative complexities of these additional maneuvers would plausibly increase the complexity associated with computational simulation, a distinct advantage of the present FE model is its relative robustness, permitting the systematic computational evaluation of complex kinematic and kinetic challenges. This represents another attractive area for further investigation. Finally, while the anisotropic fiber-dominated material models used in the present model were attentively defined – and consequently represents one of the more sophisticated knee FE models in the orthopaedic literature – several simplifications were necessarily involved with model development. Defining the material response of the articular cartilage as a three-layer fibril-reinforced hyperelastic material may be an over-simplification, as the mechanobiology of articular cartilage is often represented as a biphasic poroelastic viscous (time-dependent) material32. Additionally, all ligaments in the present study were assumed to have the same material model coefficients. While the effect of these simplifications at the whole-joint level is unknown, given the excellent agreement of the current model with experimental data, their influences are assumed negligible.
In summary, the present investigation has quantified the effects of ACL graft size on knee joint stability and soft-tissue stresses. Increased graft size was associated with substantially greater joint stability, and considerably lower meniscal stress and articular cartilage contact pressures. Given the high costs and technical complexities involved with cadaveric biomechanical investigations, the present study offers an attractive alternative modality for systematic evaluation of ACL-reconstructed knees.
Acknowledgments
The authors would like to express their sincerest gratitude to Dr. Ahmet Erdemir for his generosity in developing the freely-available OpenKnee project (available from https://simtk.org/home/openknee). Finite element model development is a laborious process, often prohibitively so. OpenKnee was a potent springboard for this investigation, greatly facilitating initial model development. The authors would also like to thank Dr. Austin Ramme for his assistance during model development. We would also like to thank The National Center for Research Resources (UL1 RR024979) for research support.
References
- 1.Lyman S, Koulouvaris P, Sherman S, Do H, Man-dl LA, Marx RG. Epidemiology of anterior cruciate ligament reconstruction: trends, readmissions, and subsequent knee surgery. The Journal of bone and joint surgery. American volume. 2009;91(10):2321–8. doi: 10.2106/JBJS.H.00539. doi: 10.2106/JBJS.H.00539[published Online First: Epub Date]|. [DOI] [PubMed] [Google Scholar]
- 2.Frank CB, Jackson DW. The science of reconstruction of the anterior cruciate ligament. The Journal of bone and joint surgery. American volume. 1997;79(10):1556–76. doi: 10.2106/00004623-199710000-00014. [DOI] [PubMed] [Google Scholar]
- 3.Spindler KP, Wright RW. Clinical practice. Anterior cruciate ligament tear. The New England journal of medicine. 2008;359(20):2135–42. doi: 10.1056/NEJMcp0804745. doi: 10.1056/ NEJMcp0804745[published Online First: Epub Date]|. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Butler DL, Noyes FR, Grood ES. Ligamentous restraints to anterior-posterior drawer in the human knee. A biomechanical study. The Journal of bone and joint surgery. American volume. 1980;62(2):259–70. [PubMed] [Google Scholar]
- 5.Torg JS, Conrad W, Kalen V. Clinical diagnosis of anterior cruciate ligament instability in the athlete. The American journal of sports medicine. 1976;4(2):84–93. doi: 10.1177/036354657600400206. [DOI] [PubMed] [Google Scholar]
- 6.Benjaminse A, Gokeler A, van der Schans CP. Clinical diagnosis of an anterior cruciate ligament rupture: a meta-analysis. The Journal of orthopaedic and sports physical therapy. 2006;36(5):267–88. doi: 10.2519/jospt.2006.2011. [DOI] [PubMed] [Google Scholar]
- 7.Gurtler RA, Stine R, Torg JS. Lachman test evaluated. Quantification of a clinical observation. Clinical orthopaedics and related research. 1987;(216):141–50. [PubMed] [Google Scholar]
- 8.Rangger C, Daniel DM, Stone ML, Kaufman K. Diagnosis of an ACL disruption with KT-1000 arthrometer measurements. Knee surgery, sports traumatology, arthroscopy : official journal of the ESSKA. 1993;1(1):60–6. doi: 10.1007/BF01552161. [DOI] [PubMed] [Google Scholar]
- 9.Kato Y, Maeyama A, Lertwanich P, et al. Biomechanical comparison of different graft positions for single-bundle anterior cruciate ligament reconstruction. Knee surgery, sports traumatology, arthroscopy: official journal of the ESSKA. 2012 doi: 10.1007/s00167-012-1951-4. doi: 10.1007/ s00167-012-1951-4[published Online First: Epub Date]|. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Yagi M, Wong EK, Kanamori A, Debski RE, Fu FH, Woo SL. Biomechanical analysis of an anatomic anterior cruciate ligament reconstruction. The American journal of sports medicine. 2002;30(5):660–6. doi: 10.1177/03635465020300050501. [DOI] [PubMed] [Google Scholar]
- 11.Kopf S, Forsythe B, Wong AK., et al. Non-anatomic tunnel position in traditional transtibial single-bundle anterior cruciate ligament reconstruction evaluated by three-dimensional computed tomography. The Journal of bone and joint surgery. American volume. 2010;92(6):1427–31. doi: 10.2106/JBJS.I.00655. doi: 10.2106/ JBJS.I.00655[published Online First: Epub Date]|. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Donahue TL, Hull ML, Rashid MM, Jacobs CR. A finite element model of the human knee joint for the study of tibio-femoral contact. Journal of biomechanical engineering. 2002;124(3):273–80. doi: 10.1115/1.1470171. [DOI] [PubMed] [Google Scholar]
- 13.yao J, Snibbe J, Maloney M, Lerner AL. Stresses and strains in the medial meniscus of an ACL deficient knee under anterior loading: a finite element analysis with image-based experimental validation. Journal of biomechanical engineering. 2006;128(1):135–41. doi: 10.1115/1.2132373. [DOI] [PubMed] [Google Scholar]
- 14.Sibole S, Bennetts C., Borotikar B., Maas S., van den Bogert A.J., Weiss J.A., Erdemir A. Open knee: a 3D finite element representation of the knee joint. 34th Annual Meeting of the American Society of Biomechanics. 2010 [Google Scholar]
- 15.Westermann R, Sybrowsky C., Ramme A., Wolf B. Three-Dimensional Characterization of the Native Femoral Footprint of the Anterior Cruciate Ligament. Manuscript Submitted fot Publication. 2013 [Google Scholar]
- 16.Forsythe B, Kopf S, Wong AK., et al. The location of femoral and tibial tunnels in anatomic double-bundle anterior cruciate ligament reconstruction analyzed by three-dimensional computed tomography models. The Journal of bone and joint surgery. American volume. 2010;92(6):1418–26. doi: 10.2106/JBJS.I.00654. doi: 10.2106/ JBJS.I.00654[published Online First: Epub Date]|. [DOI] [PubMed] [Google Scholar]
- 17.Grood ES, Suntay WJ. Ajoint coordinate system for the clinical description of three-dimensional motions: application to the knee. Journal of biomechanical engineering. 1983;105(2):136–44. doi: 10.1115/1.3138397. [DOI] [PubMed] [Google Scholar]
- 18.Gasser TC, Ogden RW, Holzapfel GA. Hyperelastic modelling of arterial layers with distributed collagen fibre orientations. Journal of the Royal Society, Interface / the Royal Society. 2006;3(6):15–35. doi: 10.1098/rsif.2005.0073. doi: 10.1098/rsif.2005.0073[published Online First: Epub Date]|. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Elkins JM, Stroud NJ, Rudert MJ, et al. The capsule’s contribution to total hip construct stability-a finite element analysis. Journal of orthopaedic research : official publication of the Orthopaedic Research Society. 2011;29(11):1642–8. doi: 10.1002/jor.21435. doi: 10.1002/ jor.21435[published Online First: Epub Date]|. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Woo SL, Hollis JM, Adams DJ, Lyon RM, Takai S. Tensile properties of the human femur-anterior cruciate ligament-tibia complex. The effects of specimen age and orientation. The American journal of sports medicine. 1991;19(3):217–25. doi: 10.1177/036354659101900303. [DOI] [PubMed] [Google Scholar]
- 21.Noyes FR, Grood ES. The strength of the anterior cruciate ligament in humans and Rhesus monkeys. The Journal of bone and joint surgery. American volume. 1976;58(8):1074–82. [PubMed] [Google Scholar]
- 22.Fox AJ, Bedi A, Rodeo SA. The basic science of human knee menisci: structure, composition, and function. Sports health. 2012;4(4):340–51. doi: 10.1177/1941738111429419. doi: 10.1177/1941738111429419[published Online First: Epub Date]|. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Hauch KN, Oyen ML, Odegard GM, Donahue TLH. Nanoindentation of the insertional zones of human meniscal attachments into underlying bone. J Mech Behav Biomed. 2009;2(4):339–47. doi: 10.1016/j.jmbbm.2008.10.005. doi: DOI 10.1016/j.jmbbm.2008.10.005[published Online First: Epub Date]|. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Arnold MP, Lie DT, Verdonschot N, de Graaf R, Amis AA, van Kampen A. The remains of anterior cruciate ligament graft tension after cyclic knee motion. The American journal of sports medicine. 2005;33(4):536–42. doi: 10.1177/0363546504269938. doi: 10.1177/0363546504269938[published Online First:Epub Date]|. [DOI] [PubMed] [Google Scholar]
- 25.Arnold MP, Verdonschot N, van Kampen A. ACL graft can replicate the normal ligament’s tension curve. Knee surgery, sports traumatology, arthroscopy : official journal of the ESSKA. 2005;13(8):625–31. doi: 10.1007/s00167-004-0601-x. doi: 10.1007/s00167-004-0601-x[published Online First: Epub Date]|. [DOI] [PubMed] [Google Scholar]
- 26.Arnold MP, Verdonschot N, van Kampen A. The normal anterior cruciate ligament as a model for tensioning strategies in anterior cruciate ligament grafts. The American journal of sports medicine. 2005;33(2):277–83. doi: 10.1177/0363546504265909. [DOI] [PubMed] [Google Scholar]
- 27.Lewis PB, Parameswaran AD, Rue JP, Bach BR Jr. Systematic review of single-bundle anterior cruciate ligament reconstruction outcomes: a baseline assessment for consideration of double-bundle techniques. The American journal of sports medicine. 2008;36(10):2028–36. doi: 10.1177/0363546508322892. doi: 10.1177/0363546508322892[published Online First:Epub Date]|. [DOI] [PubMed] [Google Scholar]
- 28.Brophy RH, Pearle AD. Single-bundle anterior cruciate ligament reconstruction: a comparison of conventional, central, and horizontal single-bundle virtual graft positions. The American journal of sports medicine. 2009;37(7):1317–23. doi: 10.1177/0363546509333007. doi: 10.1177/0363546509333007[published Online First: Epub Date]|. [DOI] [PubMed] [Google Scholar]
- 29.Chaudhari AM, Briant PL, Bevill SL, Koo S, Andriacchi TP. Knee kinematics, cartilage morphology, and osteoarthritis after ACL injury. Medicine and science in sports and exercise. 2008;40(2):215–22. doi: 10.1249/mss.0b013e31815cbb0e. doi: 10.1249/mss.0b013e31815cbb0e[published Online First: Epub Date]|. [DOI] [PubMed] [Google Scholar]
- 30.Ferretti A, Conteduca F, De Carli A, Fontana M, Mariani PP. Osteoarthritis of the knee after ACL reconstruction. International orthopaedics. 1991;15(4):367–71. doi: 10.1007/BF00186881. [DOI] [PubMed] [Google Scholar]
- 31.Stergiou N, Ristanis S, Moraiti C, Georgoulis AD. Tibial rotation in anterior cruciate ligament (ACL)-deficient and ACL-reconstructed knees: a theoretical proposition for the development of osteoarthritis. Sports medicine. 2007;37(7):601–13. doi: 10.2165/00007256-200737070-00004. [DOI] [PubMed] [Google Scholar]
- 32.Carter DR, Wong M. Modelling cartilage mechanobiology. Philosophical transactions of the Royal Society of London. Series B, Biological sciences. 2003;358(1437):1461–71. doi: 10.1098/rstb.2003.1346. doi: 10.1098/ rstb.2003.1346[published Online First: Epub Date]|. [DOI] [PMC free article] [PubMed] [Google Scholar]


