Skip to main content
PMC home page
British Journal of Cancer logoLink to British Journal of Cancer
. 2013 Aug 6;109(4):1056–1062. doi: 10.1038/bjc.2013.336

Evolutionary game theory of growth factor production: implications for tumour heterogeneity and resistance to therapies

M Archetti 1,*
PMCID: PMC3749558  PMID: 23922110

Abstract

Background:

Tumour heterogeneity is documented for many characters, including the production of growth factors, one of the hallmarks of cancer. What maintains heterogeneity remains an open question that has implications for diagnosis and treatment, as drugs that target growth factors are susceptible to the evolution of resistance.

Methods:

I use evolutionary game theory to model collective interactions between cancer cells, to analyse the dynamics of the production of growth factors and the effect of therapies that reduce their amount.

Results:

Five types of dynamics are possible, including the coexistence of producer and non-producer cells, depending on the production cost of the growth factor, on its diffusion range and on the degree of synergy of the benefit it confers to the cells. Perturbations of the equilibrium mimicking therapies that target growth factors are effective in reducing the amount of growth factor in the long term only if the reduction is extremely efficient and immediate.

Conclusion:

Collective interactions within the tumour can maintain heterogeneity for the production of growth factors and explain why therapies like anti-angiogenic drugs and RNA interference that reduce the amount of available growth factors are effective in the short term but often lead to relapse. Alternative strategies for evolutionarily stable treatments are discussed.

Keywords: anticancer therapy, evolutionary game theory, growth factors, public goods, cooperation, heterogeneity

Self-sufficiency of growth factor production is one of the hallmarks of cancer (Hanahan and Weinberg, 2000) and, like for other characters, there is evidence of intra-tumour heterogeneity in the ability of cells to produce growth factors (Achilles et al, 2001; Marusyk and Polyak, 2010). Jouanneau et al (1994) have shown that tumour cells cooperate for the production of FGF, that is, cells that do not produce the growth factor can benefit from the products of their neighbours. As they are diffusible molecules, it stands to reason that this is the case for other growth factors as well (Axelrod et al, 2006). What maintains heterogeneity? Given that cancer progression is a process of clonal selection (Cairns, 1975; Nowell, 1976; Crespi and Summers, 2005; Merlo et al, 2006; Greaves and Maley, 2012) in which cells compete for resources, space and nutrients, how can more than one clone stably coexist in a neoplasm? Current explanations include the possibility that different clones are evolutionarily neutral (Iwasa and Michor, 2011), specialise on different niches (Nagy, 2004; Gatenby and Gillies, 2008) or are not in equilibrium (Gonzalez-Garcia et al, 2002); which, if any, of these mechanisms are at work in neoplasms remains an open question (Merlo et al, 2006).

Heterogeneity has also implications for disease progression (Maley et al, 2006), diagnosis and therapy (Dexter and Leith, 1986). As diagnostic biopsies sample only a small region of the tumour, treatments based upon such samples might not be effective against all tumour cells. Understanding the origin, extent and dynamics of tumour heterogeneity, therefore, is essential for the development of successful anticancer therapies. It has been suggested that treatments that attack growth factors may be less susceptible than traditional drugs to the evolution of resistance (Pepper, 2012; Aktipis and Nesse, 2013). Current drugs that target growth factors, however, like the anti-angiogenic drug Avastin, extend overall survival by only a few months (Amit et al, 2013), as resistance often arises.

We develop a model of growth factor production in the framework of evolutionary game theory and show how the evolutionary dynamics of the system can explain the maintenance of stable heterogeneity, how this affects the development of resistance to anticancer therapies that target growth factors, and show the implications for the development of stable therapies.

A fundamental analytical method in evolutionary biology, game theory has often been mentioned (for example, Gatenby and Maini, 2003; Axelrod et al, 2006; Merlo et al, 2006; Basanta and Deutsch, 2008; Lambert et al, 2011) as a promising avenue for cancer research, but only a few papers actually develop game theoretical models of cancer. Tomlinson (1997) and Tomlinson and Bodmer (1997) developed a mathematical model of a population consisting of two types of cells, with one type producing a factor that confers a proliferative advantage to both cells. Subsequent papers have extended this model up to four types of cells (Dingli et al, 2009; Basanta et al, 2008a, 2008b, 2011; 2012; Gerstung et al, 2011) and allowed stochastic and spatial effects (Bach et al, 2003). These models, however, describe interactions between pairs of cells, whereas interactions among cancer cells are not normally pairwise and should be described by public goods games (PGGs) with collective interactions. It is known that results from the theory of two-player games cannot be extended to multiplayer PGGs and that this can actually lead to fundamental misunderstandings (Archetti and Scheuring, 2012).

Models of PGGs in evolutionary game theory, on the other hand (reviewed by Archetti and Scheuring (2012)) assume that the benefit of the public good is a linear function of the number of contributors (the N-person Prisoner's Dilemma: NPD) or a step function with a fixed threshold (Archetti, 2009a, 2009b). As the effect of enzyme production is generally a saturating function of its concentration (Hemker and Hemker, 1969; Ricard and Noat, 1986; Mendes, 1997; Eungdamrong and Iyengar, 2004), however, the public good produced by growth factors is likely to be a sigmoid function of the number of producer cells. We must therefore resort to a model with sigmoid benefits, which has been so far beyond the reach of evolutionary game theory (Archetti and Scheuring, 2011, 2012). As the dynamics of the NPD and that of threshold PGGs is radically different, it is not clear a priori, what the dynamics of PGGs with sigmoid benefits could be.

The model we use here, therefore, goes beyond current game theory models of cancer in that it is a multiplayer, collective action (public goods) game, rather than a game with two players; and it goes beyond standard models in evolutionary biology in that it assumes nonlinear, sigmoid benefits, and investigates the effect of therapies that affect the dynamics. To make the analysis possible, we must assume that cells maintain a large and constant population size, which may describe cancer cell populations that have reached a carrying capacity, due, for example, to resource limitation or immune response. The model is relevant for insulin-like growth factor (IGF) and other growth factors that confer direct benefits by inducing a growth advantage or by protecting against apoptosis. Other growth factors like vascular endothelial growth factor (VEGF) whose benefits are less direct will have more complicated dynamics.

Materials and methods

We consider the case in which cells can be either producers of the growth factor (cooperators; C) or non-producers (defectors; D); producers pay a cost of production c>0 and the benefit b(j) for a cell is an increasing function of the number of contributors j among the other cells in the group (of size n) defined by the diffusion range of the growth factor, that is, Δbj=b(j+1)−b(j)>0 for j=0, …, n−1. More specifically, we assume that the benefit function has a sigmoid shape (for a given j*, j⩽j*⇒Δbj+1⩾Δbj, j⩾j*⇒Δbj+1⩽Δbj). We use the simplest and most natural sigmoid function, the logistic function b(j)=1/[1+es(k−j)], where k is the inflection point at which the function has steepness s (with 0<k⩽n and s>0). A normalised version of the logistic function, given by bN(j)=[b(j)−b(0)]/[b(n)−b(0)], delivers the case of a fixed threshold (a benefit is produced if and only if at least k producers are present; s→∞) and of a linear function (s→0) as limit cases. In a large population with no assortment, we can approximate the analysis by assuming an infinite, well-mixed population, and the fitness of producers and non-producers is given as follows:

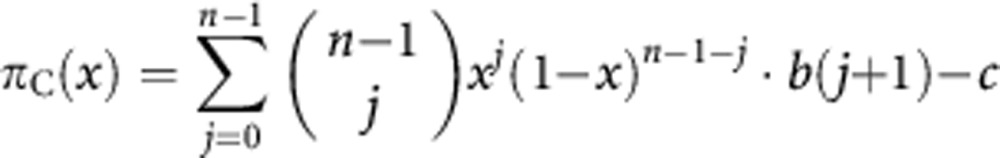graphic file with name bjc2013336e1.jpg
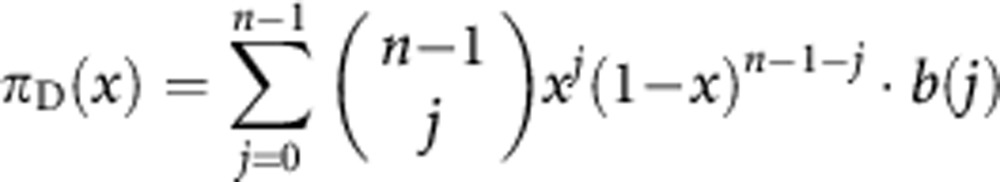graphic file with name bjc2013336e2.jpg

where 0⩽x⩽1 is the fraction of producers in the population, as a producer pays a cost c that a non-producer does not pay, but its group has one more contributor (itself).

In a clonal population, the replicator dynamics (Hofbauer and Sigmund, 1998) of this game is given by

graphic file with name bjc2013336e3.jpg

where the fitness difference πC(x)−πD(x) is written in the form β(x)−c, and

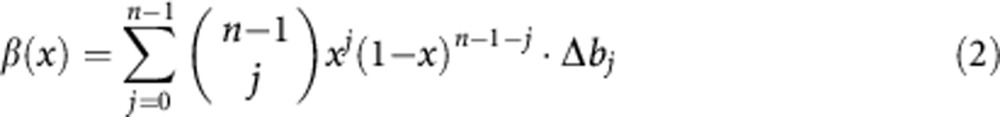graphic file with name bjc2013336e4.jpg

The dynamics (1) has two trivial rest points x=0 and x=1; further possible, interior rest points are given by the roots of the equations

graphic file with name bjc2013336e5.jpg

For the logistic function (or any other sigmoid function), an exact analytical solution is not possible. As β(x) is a polynomial in Bernstein form, we can resort to the properties of Bernstein polynomials (Lorentz, 1953; Philips, 2003) to characterise the dynamics and find an approximate solution.

The benefit for having a fraction x of producer cells is b(x)=1/[1+ens(h−x)], the extension of b(j/n) to all x∈[0,1], with h=k/n. As β(x) is a Bernstein polynomial (Bernstein, 1912; Lorentz, 1953; Philips, 2003) of the coefficient Δbj=b((j+1)/n)−b(j/n), by Bernstein theorem (Bernstein, 1912) we know that β(x) converges uniformly to Δbj in [0,1]. Furthermore, because Δbj is the forward difference of the benefit function with spacing 1/n, for large enough n we can approximate Δbj≈(1/n)b′(j/n). For any x, j/n converges in probability to x as n→∞ therefore, by Bernstein theorem β(x) converges to (1/n)b′(x), and equation (3) can be approximated by

graphic file with name bjc2013336e6.jpg

We can obtain an analogous solution using equation (4) for the normalised benefit function bN(x), and actually for any sigmoid function.

Because of the variation-diminishing property of Bernstein polynomials, we also know that the number of internal equilibria of β is less than the number of sign changes of Δb by an even amount; because of our assumption of sigmoid benefits, we know that β(x) has a unique maximiser x* in (0,1); finally, because of the end point values property of Bernstein polynomials, we know that β(0)=Δb0 and β(1)=Δbn−1.

Results

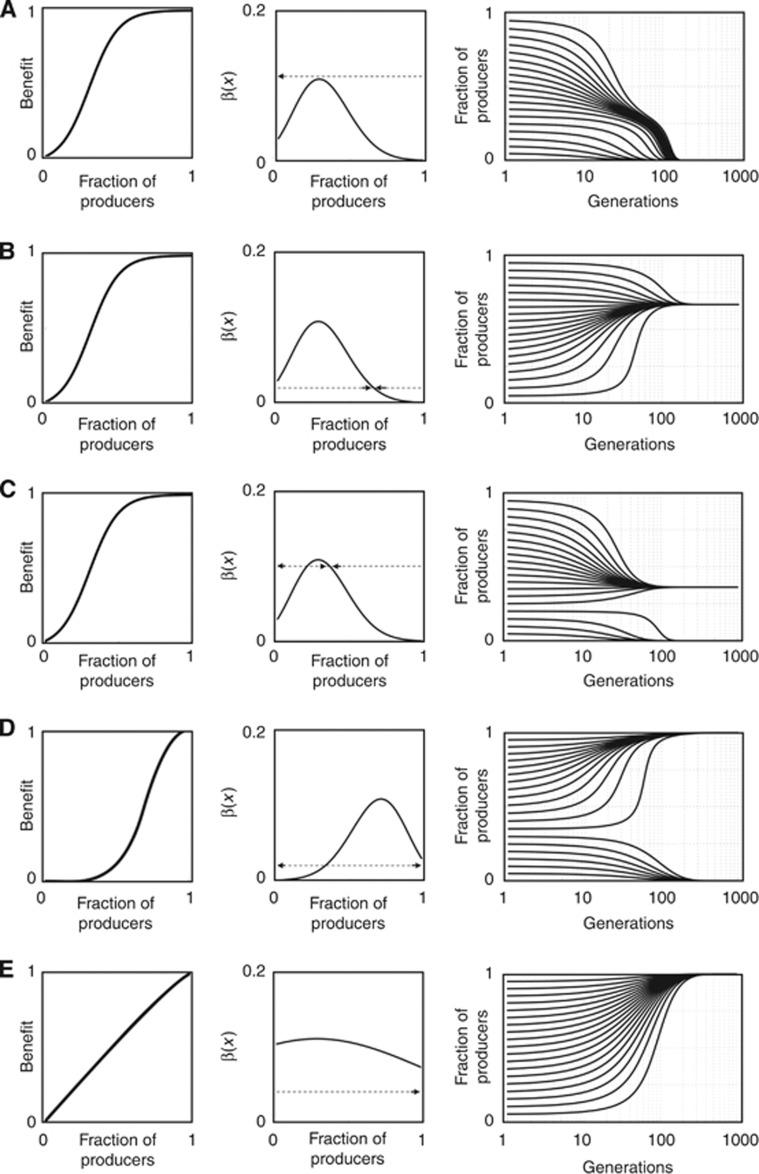
It follows that x=0 is a stable rest point of (1) if and only if Δb0<c, and that x=1 is a stable rest point of (1) if and only if Δbn−1⩾c. In addition, any interior stable rest point xs must satisfy equation (3) and β′(xs)<0. It follows that there is at most one interior stable rest point xs and that, if such a rest point exists, it satisfies x*<xs<1. These conclusions define, for any sigmoid benefit function, the following five types of dynamics (Figure 1), where we simplify notation by defining β*=β(x*):

  • If c>β*, then β(x)<c 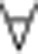Inline graphic x, and x=0 is the only stable equilibrium.

  • If c<min[Δb 0, Δb n−1], then β(x)>c 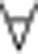Inline graphic x, and x=1 is the only stable equilibrium.

  • If min[Δb 0,Δb n−1]<c<max[Δb 0,Δb n−1], and Δb 0<Δb n−1, then β(x)>c for x>x u and β(x)<c for x<x u; therefore, the unique interior unstable equilibrium x u divides the basin of attraction of the two stable equilibria x=1 and x=0.

  • If min[Δb 0,Δb n−1]<c<max[Δb 0, Δb n−1], and Δb 0>Δb n−1, then β(x)>c for x<x s and β(x)<c for x>x s; therefore, the unique interior stable equilibrium x s divides the basin of attraction of the two unstable equilibria x=1 and x=0.

  • If max[Δb 0, Δb n−1]<c<β*, then β(x)>c for x u<x<x s, whereas β(x)<c for x<x u and for x>x s; therefore, the interior unstable equilibrium x u divides the basins of attraction of the two stable equilibria x=0 and x=x s.

Figure 1.

Figure 1

Open in a new tab

The five types of dynamics of growth factor production. The evolutionary dynamics of growth factor production depends on how the benefit of the growth factor changes as a function of the fraction of producer cells. The equilibria are found where β(x)−c=0, that is, where β(x) intersects the constant line c (the cost of producing the growth factor; dashed line); the fraction of producers increases if β(x)>c and decreases if β(x)<c; the arrows show the direction of the change. There are five possible types of dynamics: (A) only x=0 is stable; s=0.5, h=0.3, c=0.12. (B) Only x=xs is stable; s=0.5, h=0.7, c=0.02. (C) Both x=0 and x=xs are stable; s=0.5, h=0.3, c=0.1. (D) Both x=0 and x=1 are stable; s=0.5, h=0.3, c=0.02. (E) Only x=1 is stable; s=0.1, h=0.3, c=0.02. n=20.

The internal equilibria for the normalised logistic function are given by (from equation (4))

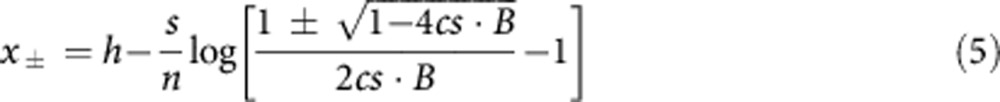graphic file with name bjc2013336e9.jpg

with xs=x− for the stable equilibrium and xu=x+ for the unstable equilibrium, where B=b(1)−b(0).

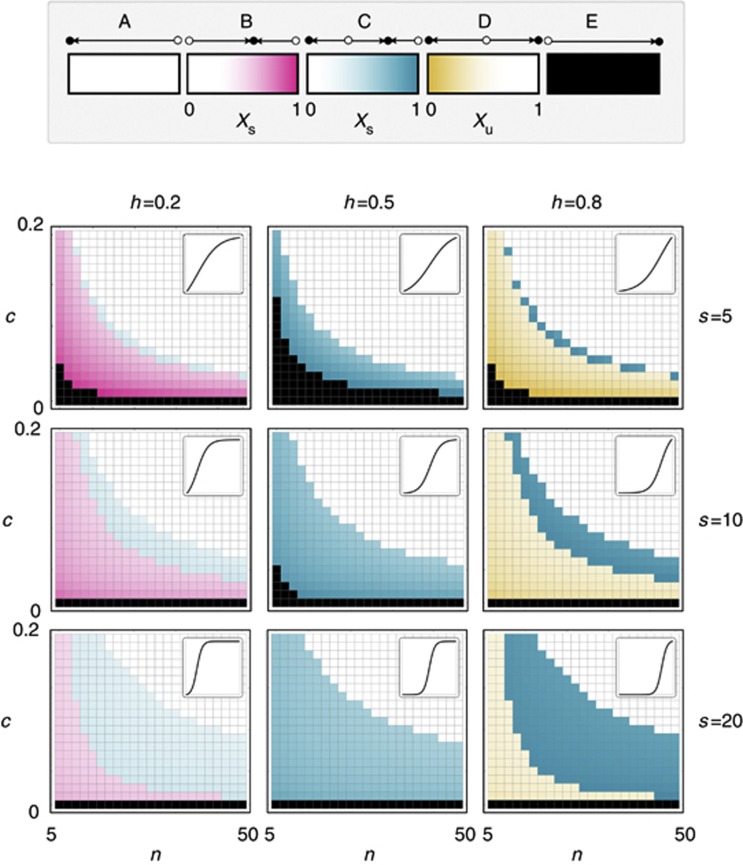
The results described so far reveal that stable heterogeneity can arise simply as a consequence of the fact that growth factors are diffusible public goods. Stable heterogeneity is more likely to occur for low levels of h (that is, when few producer cells are enough to confer a benefit to the whole group; Figure 2).

Figure 2.

Figure 2

Open in a new tab

Types of evolutionary dynamics as a function of the parameters. Each plot is drawn for different values of s (the steepness of the benefit function) and h (the threshold of the benefit function), that is, for different types of benefit of the growth factor (a function of the fraction of producers, represented by the small panels on the top right; see Figure 1), and shows the type of dynamics as a function of c (the cost of producing the growth factor) and n (group size). There are five types of dynamics (see Figure 1). (A) Only x=0 is stable. (B) Only x=xs is stable. (C) Both x=0 and x=xs are stable. (D) Both x=0 and x=1 are stable. (E) Only x=1 is stable. Colours show the values of the stable (xs) or unstable (xu) equilibria.

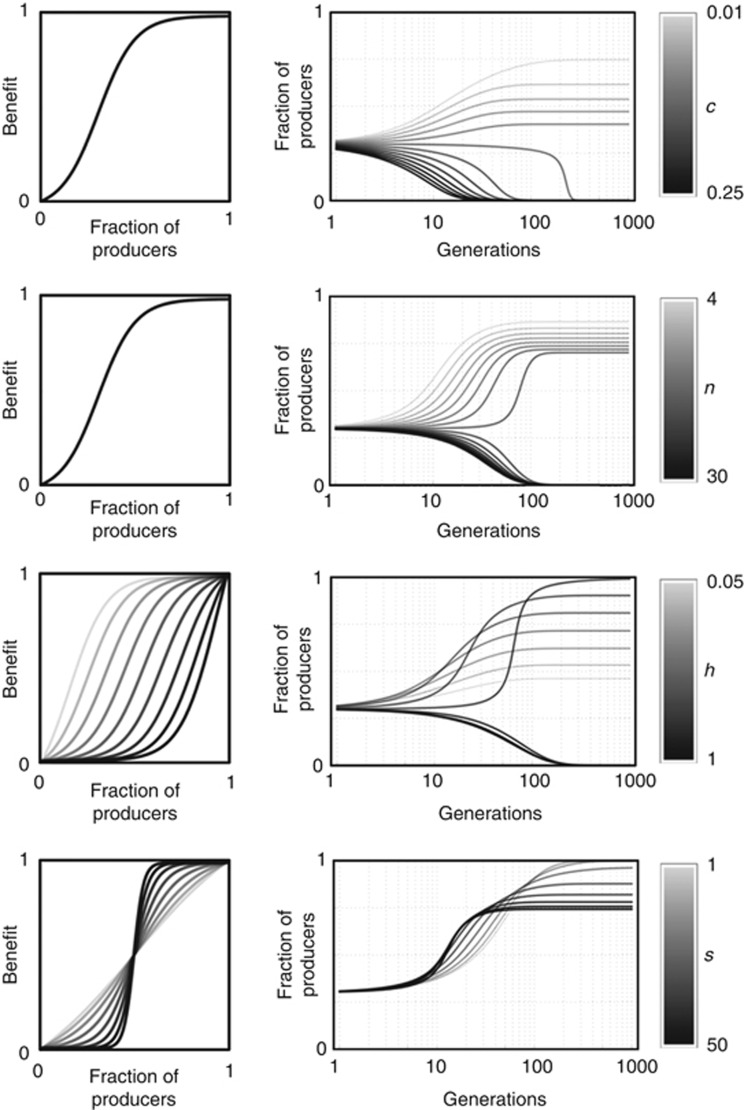
To conclude the comparative statics of the system, we note that (Figure 3) the equilibrium frequency of producers is always a decreasing function of c and n (the number of cells within the diffusion range of the growth factor); the effect of s (the steepness of the benefit function) is more complex because the equilibrium can be a monotonic or a single-peaked function of s depending on the other parameters (it is clear, however, that stable heterogeneity is possible only if s is not too low); finally, the equilibrium frequency of producers is an increasing function of h (the inflection of the benefit function). This has a implications for the dynamics of anticancer therapies that target growth factors and for the evolution of resistance against such therapies.

Figure 3.

Figure 3

Open in a new tab

Effect of the parameters on the equilibrium fraction of producers. The fraction of producers is plotted over time for different values of c (the cost of production), n (the number of cells within the diffusion range of the growth factor), h (the inflection of the benefit function) and s (the steepness of the benefit function), starting from the same initial frequencies.

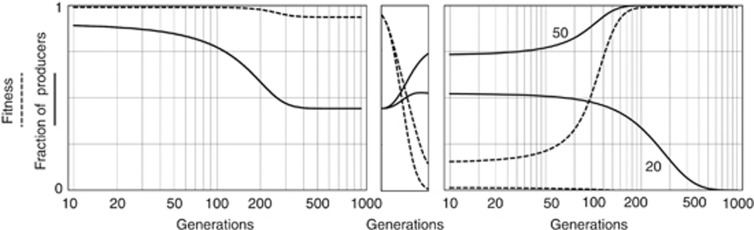
An anticancer drug that acts by impairing growth factors will increase the amount of growth factors that the cells must produce to achieve a certain benefit, that is, it will increase h. If the threshold is high, producers can go to fixation, whereas they remain at a mixed equilibrium if the threshold is lower (compare, for example, Figures 1B and D). Specifically, an anticancer drug that acts by reducing the amount of circulating growth factor may lead to the opposite of the desired effect: although the immediate effect is, of course, a sudden reduction in tumour growth (because there are not enough circulating growth factors), the amount of growth factors that must be produced to achieve the same benefit (h) is now increased, which leads to an increase in frequency of the C cells, which eventually leads to a new equilibrium (Figure 4). In case of bistability, the final outcome will depend on the initial frequency of producers.

Figure 4.

Figure 4

Open in a new tab

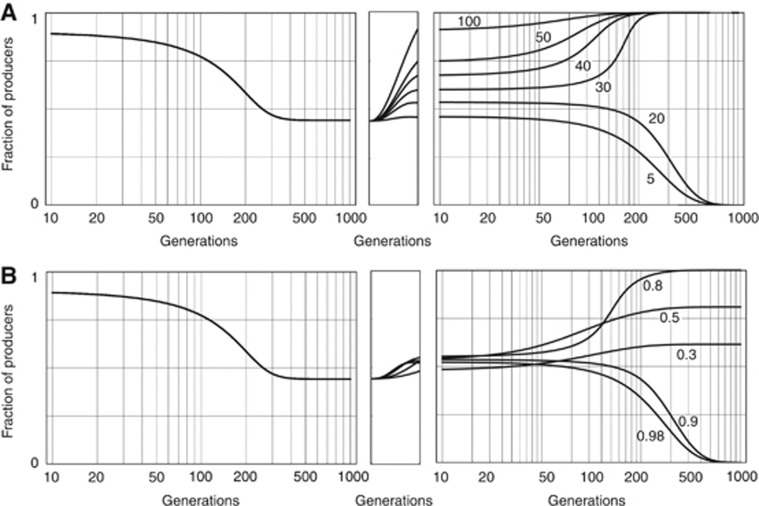
Evolution of resistance to anticancer treatments that target growth factors. A population reaches an equilibrium (after about 200 generations) in which producers and non-producers of growth factors coexist. When, at generation 1000, a drug is introduced that increases the threshold h from 0.1 to 0.98 (i.e., it impairs almost completely the growth factor produced by the tumour), fitness immediately declines and remains low for a few generations; if the transition to the new dynamics is fast enough (20 generations), producers go extinct. If the transition is slower, however, (50 generations) the frequency of producers increases, and after a few generations fitness reaches levels comparable to the pre-drug treatment, as the fraction of producers approaches a new equilibrium. n=50; c=0.01; s=0.2.

Even if a drug induces an almost complete annihilation of available growth factors, the speed of the transition from the original to the new threshold is essential for the success of the therapy. Although a fast transition to the new threshold can lead to a successful, stable therapy, a slower delivery of the anti-growth factor drug, or inefficient RNA interference (RNAi) delivery systems that require multiple treatments over an extended period of time, can make the system evolve back to relapse, even if the treatment itself is extremely efficient at impairing the growth factor (Figure 5A). Even therapies that are almost immediately effective will fail if the reduction in circulating growth factor is not large enough (Figure 5B).

Figure 5.

Figure 5

Open in a new tab

Designing evolutionarily stable anti-growth factor treatments. At generation 1000, a drug is introduced that increases the threshold h from 0.1 to h*, in t generations. n=50; c=0.01; s=0.2. (A) h*=0.9; variable t, from 5 to 100 generations. If the transition is not fast enough, producers reach a new equilibrium (here, the transition must occur in 20 generations or less). (B) t=20; variable h*, from 0.3 to 0.98. If the treatment does not reduce enough the available amount of growth factor, producers reach a new equilibrium (here, the reduction must be strong enough to change the threshold from 0.1 to at least 0.9).

Conclusion

Analysing the production of growth factors as a nonlinear PGG reveals that tumour heterogeneity can be maintained by the frequency-dependent selection that arises as a natural consequence of the fact that growth factors are diffusible, and therefore public goods, with no need to invoke neutral mutations (Iwasa and Michor, 2011), niche specialisation (Nagy, 2004; Gatenby and Gillies, 2008) or non-equilibrium (Gonzalez-Garcia et al, 2002). Five types of dynamics are possible, including the coexistence of producers and non-producers at a stable equilibrium. This diversity of dynamics was not captured by previous game theory models based on pairwise interactions or by previous models of public goods in evolutionary game theory.

Tumour heterogeneity has important implications for diagnosis and treatment. The results help us understand anticancer therapies that attack growth factors, either directly (using drugs like avastin that target the growth factors) or indirectly (using RNAi). Although it was suggested that attacking growth factors may be less susceptible to the evolution of resistance (Pepper, 2012; Aktipis and Nesse, 2013), the results shown here suggest that the issue is not so simple. In fact, it is clear that, in spite of the initial enthusiasm, anti-angiogenic drugs, one of the most prominent examples of therapies based on the disruption of growth factors, have been disappointing. A drug like Avastin, which was the best selling drug for Roche (Basel, Switzerland) in the past few years, only extend overall survival of patients with certain types of cancer by a few months, which are followed by relapse (Amit et al, 2013).

The rationale of the analysis is that when one reduces the amount of a growth factor, the immediate result is a sudden reduction in tumour growth, because the threshold necessary to achieve the original benefit is not reached; as a consequence, the growth rate of the tumour immediately declines. At the same time, however, the amount of growth factors necessary for the population to grow increases (because part of them are disrupted by the therapy), which changes the dynamics of the system; unfortunately, it changes in the wrong direction: by increasing the threshold, one increases the frequency of producers at equilibrium, which explains relapse simply as the new equilibrium reached by the system under the new conditions. Analysing anti-growth factor drugs as methods that increase the threshold of a PGG reveals that the initial expectations of stability for these therapies were based on faulty evolutionary predictions. Although it is too early to evaluate the efficacy of RNAi treatments, it seems reasonable that even silencing the gene for a growth factor should incur a similar problem and be susceptible to the evolution of resistance. As pointed out by Pepper (2012), therapies that target growth factors are certainly a more evolutionary robust approach than conventional drugs that target cells directly. As we have shown, however, an anti-growth factor drug must be evolutionarily stable in order to be effective. Besides efficacy, latency was also shown here to be fundamental for the success of such therapies.

In order to have quantitative results that may help design proper therapies, the methods used here should be extended to take into account more realistic features of cancer development, including, for example, spatial structure, as cells will form clusters of producers and non-producers with their own dynamics. It is known, however, that assortment in spatially structured populations does not change the dynamics qualitatively if benefits are sigmoid (which is our case; Archetti and Scheuring, 2012; Perc et al, 2013).

Drugs that target growth factors may be used in combination with other therapies, such as chemotherapy. As chemotherapy is more effective against rapidly dividing cells, it will affect preferentially non-producing cells (which grow faster), and therefore confer a benefit to producer cells, which would not help the treatment. An evolutionarily stable therapy should modify the dynamics to lead to the extinction of the producer cells. As we have seen, extinction of the producer cells is possible, depending on the shape of the benefit function, if the cost/benefit ratio of producing the growth factor is high enough, group size is large enough and if the initial amount of non-producer cells is above a critical threshold. The cost/benefit ratio could be changed by varying the amount of exogenous growth factor; group size could be changed by varying the diffusion range of the factor; the critical amount of non-producer cells can be achieved by autologous cell therapy, using cancer cells collected from the patient, in which genes coding for growth factors have been knocked out. Such therapy would be stable against the evolution of resistance because mutants that produce growth factors, having a higher cost, would not invade. The very reason why most current therapies fail in the long term, the evolutionary response of the tumour, in this case would lead to the desired effect: the extinction of the producer cells and the long-term stability of the treatment.

Acknowledgments

This work was funded in part by NERC grant NE/H015701/1.

Footnotes

This work is published under the standard license to publish agreement. After 12 months the work will become freely available and the license terms will switch to a Creative Commons Attribution-NonCommercial-Share Alike 3.0 Unported License.

References

  1. Achilles EG, Fernandez A, Allred EN, Kisker O, Udagawa T, Beecken WD, Flynn E, Folkman J. Heterogeneity of angiogenic activity in a human liposarcoma: a proposed mechanism for "no take" of human tumors in mice. J Natl Cancer Inst. 2001;93:1075–1081. doi: 10.1093/jnci/93.14.1075. [DOI] [PubMed] [Google Scholar]
  2. Aktipis CA, Nesse RM. Evolutionary foundations for cancer biology. Evol Appl. 2013;6 (1:144–159. doi: 10.1111/eva.12034. [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Amit L, Ben-Aharon I, Vidal L, Leibovici L, Stemmer S. The impact of bevacizumab (avastin) on survival in metastatic solid tumors - a meta-analysis and systematic review. PLoS ONE. 2013;8 (1:e51780. doi: 10.1371/journal.pone.0051780. [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Archetti M. Survival of the steepest: hypersensitivity to mutations as an adaptation to soft selection. J Evol Biol. 2009a;22:740–750. doi: 10.1111/j.1420-9101.2009.01697.x. [DOI] [PubMed] [Google Scholar]
  5. Archetti M. The volunteer's dilemma and the optimal size of a social group. J Theor Biol. 2009b;261:475–480. doi: 10.1016/j.jtbi.2009.08.018. [DOI] [PubMed] [Google Scholar]
  6. Archetti M, Scheuring I. Coexistence of cooperation and defection in public goods games. Evolution. 2011;65:1140–1148. doi: 10.1111/j.1558-5646.2010.01185.x. [DOI] [PubMed] [Google Scholar]
  7. Archetti M, Scheuring I. Review: game theory of public goods in one-shot social dilemmas without assortment. J Theor Biol. 2012;299:9–20. doi: 10.1016/j.jtbi.2011.06.018. [DOI] [PubMed] [Google Scholar]
  8. Axelrod R, Axelrod De, Pienta KJ. Evolution of cooperation among tumor cells. Proc Natl Acad Sci USA. 2006;103:13474–13479. doi: 10.1073/pnas.0606053103. [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Bach LA, Sumpter DJT, Alsner J, Loeschke V. Spatial evolutionary games of interaction among generic cancer cells. J Theor Med. 2003;5:47–58. [Google Scholar]
  10. Basanta D, Deutsch A.2008A Game Theoretical Perspective On The Somatic Evolution Of CancerIn: Bellomo N, Chaplain M, De Angelis E, (eds),Selected Topics On Cancer Modelling: Genesis Evolution Inmune Competition Therapy Birkhauser: Boston, MA, USA [Google Scholar]
  11. Basanta D, Hatzikirou H, Deutsch A. Studying the emergence of invasiveness in tumours using game theory. Eur Phys J. 2008a;63:393–397. [Google Scholar]
  12. Basanta D, Scott JG, Fishman MN, Ayala G, Hayward SW, Anderson AR. Investigating prostate cancer tumour-stroma interactions: clinical and biological insights from an evolutionary game. Br J Cancer. 2012;106:174–181. doi: 10.1038/bjc.2011.517. [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Basanta D, Scott JG, Rockne R, Swanson KR, Anderson AR. The role of IDH1 mutated tumour cells in secondary glioblastomas: an evolutionary game theoretical view. Phys Biol. 2011;8:015016. doi: 10.1088/1478-3975/8/1/015016. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Basanta D, Simon M, Hatzikirou H, Deutsch A. Evolutionary game theory elucidates the role of glycolysis in glioma progression and invasion. Cell Prolif. 2008b;41:980–987. doi: 10.1111/j.1365-2184.2008.00563.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Bernstein S. Démonstration du théorème de Weierstrass fondée sur le calcul des probabilities. Comm Soc Math Kharkov. 1912;13:1–2. [Google Scholar]
  16. Cairns J. Mutation selection and the natural history of cancer. Nature. 1975;255:197–200. doi: 10.1038/255197a0. [DOI] [PubMed] [Google Scholar]
  17. Crespi B, Summers K. Evolutionary biology of cancer. Trends Ecol Evol. 2005;20:545–552. doi: 10.1016/j.tree.2005.07.007. [DOI] [PubMed] [Google Scholar]
  18. Dexter DL, Leith JT. Tumor heterogeneity and drug resistance. J Clin Oncol. 1986;4:244–257. doi: 10.1200/JCO.1986.4.2.244. [DOI] [PubMed] [Google Scholar]
  19. Dingli D, Chalub FA, Santos FC, Van Segbroeck S, Pacheco JM. Cancer phenotype as the outcome of an evolutionary game between normal and malignant cells. Br J Cancer. 2009;101:1130–1136. doi: 10.1038/sj.bjc.6605288. [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Eungdamrong NJ, Iyengar R. Modeling cell signalling networks. Biol Cell. 2004;96:355–362. doi: 10.1016/j.biolcel.2004.03.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Gatenby R, Gillies RJ. A microenvironmental model of carcinogenesis. Nat Rev Cancer. 2008;8:56–61. doi: 10.1038/nrc2255. [DOI] [PubMed] [Google Scholar]
  22. Gatenby RA, Maini P. Cancer summed up. Nature. 2003;421:321. doi: 10.1038/421321a. [DOI] [PubMed] [Google Scholar]
  23. Gerstung M, Nakhoul H, Beerenwinkel N. Evolutionary games with affine fitness functions: applications to cancer. Dynam Games Appl. 2011;1:370–385. [Google Scholar]
  24. Gonzalez-Garcia I, Sole RV, Costa J. Metapopulation dynamics and spatial heterogeneity in cancer. Proc Natl Acad Sci USA. 2002;99:13085–13089. doi: 10.1073/pnas.202139299. [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. Greaves M, Maley CC. Clonal evolution in cancer. Nature. 2012;481:306–313. doi: 10.1038/nature10762. [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. Hanahan D, Weinberg RA. The hallmarks of cancer. Cell. 2000;100:57–70. doi: 10.1016/s0092-8674(00)81683-9. [DOI] [PubMed] [Google Scholar]
  27. Hemker HC, Hemker PW. General kinetics of enzyme cascades. Proc R Soc Lon Ser B. 1969;173:411–420. doi: 10.1098/rspb.1969.0068. [DOI] [PubMed] [Google Scholar]
  28. Hofbauer J, Sigmund K.1998Evolutionary Games and Population Dynamics Cambridge University Press: Cambridge, UK. [Google Scholar]
  29. Iwasa Y, Michor F. Evolutionary dynamics of intratumor heterogeneity. PLoS One. 2011;6:e17866. doi: 10.1371/journal.pone.0017866. [DOI] [PMC free article] [PubMed] [Google Scholar]
  30. Jouanneau J, Moens G, Bourgeois Y, Poupon MF, Thiery JP. A minority of carcinoma cells producing acidic fibroblast growth factor induces a community effect for tumor progression. Proc Natl Acad Sci USA. 1994;91:286–290. doi: 10.1073/pnas.91.1.286. [DOI] [PMC free article] [PubMed] [Google Scholar]
  31. Lambert G, Estévez-Salmeron L, Oh S, Liao D, Emerson BM, Tlsty TD, Austin RH. An analogy between the evolution of drug resistance in bacterial communities and malignant tissues. Nat Rev Cancer. 2011;11:375–382. doi: 10.1038/nrc3039. [DOI] [PMC free article] [PubMed] [Google Scholar]
  32. Lorentz GG. Bernstein Polynomials. University of Toronto Press: Toronto, Canada; 1953. [Google Scholar]
  33. Maley CC, Galipeau PC, Finley JC, Wongsurawat VJ, Li X, Sanchez CA, Paulson TG, Blount PL, Risques RA, Rabinovitch PS, Reid BJ. Genetic clonal diversity predicts progression to esophageal adenocarcinoma. Nat Genet. 2006;38:468–473. doi: 10.1038/ng1768. [DOI] [PubMed] [Google Scholar]
  34. Marusyk A, Polyak K. Tumor heterogeneity: causes and consequences. Biochem Biophys Acta. 2010;1805:105–117. doi: 10.1016/j.bbcan.2009.11.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
  35. Mendes P. Biochemistry by numbers: simulation of biochemical pathways with Gepasi 3. Trends Biochem Sci. 1997;22:361–363. doi: 10.1016/s0968-0004(97)01103-1. [DOI] [PubMed] [Google Scholar]
  36. Merlo LMF, Pepper JW, Reid BJ, Maley CC. Cancer as an evolutionary and ecological process. Nat Rev Cancer. 2006;6:924–935. doi: 10.1038/nrc2013. [DOI] [PubMed] [Google Scholar]
  37. Nagy JD. Competition and natural selection in a mathematical model of cancer. Bull Math Biol. 2004;66:663–687. doi: 10.1016/j.bulm.2003.10.001. [DOI] [PubMed] [Google Scholar]
  38. Nowell PC. The clonal evolution of tumor cell populations. Science. 1976;194:23–28. doi: 10.1126/science.959840. [DOI] [PubMed] [Google Scholar]
  39. Pepper JW. Drugs that target pathogen public goods are robust against evolved drug resistance. Evolut Appl. 2012;5 (7:757–761. doi: 10.1111/j.1752-4571.2012.00254.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
  40. Perc M, Gómez-Gardeñes J, Szolnoki A, Floría LM, Moreno Y. Evolutionary dynamics of group interactions on structured populations: a review. J R Soc Interface. 2013;10:20120997. doi: 10.1098/rsif.2012.0997. [DOI] [PMC free article] [PubMed] [Google Scholar]
  41. Phillips GM.2003Interpolation and Approximation by PolynomialsChapter 7.Springer: Berlin, Germany [Google Scholar]
  42. Ricard J, Noat G. Catalytic efficiency, kinetic co-operativity of oligometric enzymes and evolution. J Theor Biol. 1986;123:431–451. doi: 10.1016/s0022-5193(86)80212-0. [DOI] [PubMed] [Google Scholar]
  43. Tomlinson IP. Game-theory models of interactions between tumour cells. Eur J Cancer. 1997;33:1495–1500. doi: 10.1016/s0959-8049(97)00170-6. [DOI] [PubMed] [Google Scholar]
  44. Tomlinson IP, Bodmer WF. Modelling consequences of interactions between tumour cells. Br J Cancer. 1997;75:157–160. doi: 10.1038/bjc.1997.26. [DOI] [PMC free article] [PubMed] [Google Scholar]

Articles from British Journal of Cancer are provided here courtesy of Cancer Research UK

RESOURCES